Electric field tuning of the anomalous Hall effect at oxide interfaces

Abstract

Anomalous Hall effect is the phenomenon where the transport properties of the spin-polarized electrons are governed by the spin-orbit coupling that couples the orbital and spin degrees of freedom of the electron. Here we show that the anomalous Hall effect at a magnetic interface with strong spin-orbit coupling can be tuned with an external electric field. By altering the strength of the inversion symmetry breaking, the electric field changes the Rashba interaction, which in turn modifies the magnitude of the Berry curvature, the central quantity in determining the anomalous Hall conductivity. The effect is illustrated with a square lattice model, which yields a quadratic dependence of the anomalous Hall conductivity for small electric fields. Explicit density-functional calculations were performed for the recently grown iridate interface, viz., the (SrIrO₃)₁/(SrMnO₃)₁ (001) structure, both with and without an electric field, which show a strong electric field dependence. The effect may be potentially useful in spintronics applications.

Introduction

The anomalous Hall effect (AHE) occurs in solids with broken time-reversal symmetry, such as the ferromagnets, as a result of the spin-orbit coupling (SOC). Although the effect was noticed in the original work of Hall himself,^1,2 the explanation of the phenomenon came from the seminal paper of Karplus and Luttinger,³ where they identified the anomalous contribution to arise from the SOC, which results in the left-right asymmetry in the scattering of the spin-polarized electrons. Currently, there is a considerable interest on the AHE from a technological point of view because of potential applications in spintronics such as for magnetic sensors and memory devices.⁴

The interface between 3d anti-ferromagnetic insulator SrMnO₃ (SMO)⁵ and 5d paramagnetic metal SrIrO₃ (SIO)^6,7,8 is one of the notable examples among several attempts^{9,10,11,12,13} to engineer the electronic and magnetic properties at the 3d-5d interfaces, where the strong coupling is achieved by the charge transfer from SIO to the SMO side,^9,14 as sketched in Fig. 1. This results in electron doped SMO and hole doped SIO, which leads to an emergent ferromagnetism at the interface. The ferromagnetism at the interface in turn gives rise to the AHE, which has been measured for the short-period superlattices of SIO/SMO.⁹

Fig. 1

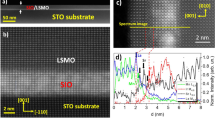
Electronic and magnetic structure of the (SIO)₁/(SMO)₁ interface, both sides consisting of a single layer each, considered here as a specific example for the tuning of the AHC. The charge transfer across the interface leads to electron or hole doping, which in turn results in an emergent ferromagnetism at the interface, leading to an anomalous Hall effect

In this paper, we show that the AHE can be tuned by an external electric field by modifying the strength of the Rashba interaction. The idea that the Rashba interaction can modify the AHE is a reasonable expectation, since any kind of magnetic field would affect the Hall conductivity and the Rashba interaction is equivalent to a magnetic field, albeit k dependent. Here, we study the effect using general arguments as well as from density-functional calculations of the anomalous Hall conductivity (AHC) for a specific interface structure (SIO)₁/(SMO)₁. Similar interface structures have already been grown experimentally.⁹ Such a perovskite hetero-structure is a good candidate for the electric field control of the Rashba effect,^15,16 providing an excellent platform for the manipulation of the AHE.

Results and discussions

To illustrate the effect of the electric field on AHE, consider the motion of electrons in a simplified tight-binding (TB) model of a ferromagnetic square lattice [Fig. 2a], relevant for the transition metal atoms at the interface. The Hamiltonian is

$$\begin{array}{*{20}{l}} {\cal{H}} \hfill & = \hfill & {{\cal{H}}_{kin} + {\cal{H}}_{ex} + {\cal{H}}_{SOC} + {\cal{H}}_E} \hfill \\ {} \hfill & = \hfill & {\mathop {\sum}\limits_{i\mu \sigma ,j\nu \sigma } {t_{ij}^{\mu \nu }} c_{i\mu \sigma }^\dagger c_{j\nu \sigma } - J_{ex}\mathop {\sum}\limits_{i\mu } {\mathop {\sum}\limits_{\sigma ,\sigma \prime } {c_{i\mu \sigma }^\dagger } } \sigma _{\sigma \sigma \prime }^zc_{i\mu \sigma \prime }} \hfill \\ {} \hfill & {} \hfill & { + \frac{\lambda }{2}\mathop {\sum}\limits_\eta {\mathop {\sum}\limits_{i\mu \sigma ,\nu \sigma \prime } {c_{i\mu \sigma }^\dagger } } L_{\mu \nu }^\eta \sigma _{\sigma \sigma \prime }^\eta c_{i\nu \sigma \prime } + {\cal{H}}_E,} \hfill \end{array}$$

where we consider d electrons, $c_{i\mu \sigma }^\dagger$ creates an electron at the i-th site with spin σ and orbital index μ, $t_{ij}^{\mu \nu }$ is the spin independent hopping between near neighbors, J_ex describes the spin splitting of up and down electrons in the ferromagnet, and $\lambda \vec L \cdot \vec S$ is the SOC term. In the TB model, the electric field induces asymmetry of the orbital lobes, which opens up new inter-orbital hopping channels,^15,16,17 that were zero before. This is incorporated in the final term ${\cal{H}}_E$, having the same form as ${\cal{H}}_{kin}$, but with new matrix elements $t_{ij}^{\mu \nu }$, viz., $\alpha = \left\langle {xy|{\cal{H}}_E|yz} \right\rangle _{\hat x} = \left\langle {xy|{\cal{H}}_E|xz} \right\rangle _{\hat y}$, $\beta = \left\langle {xz|{\cal{H}}_E|z^2} \right\rangle _{\hat x} = \left\langle {yz|{\cal{H}}_E|z^2} \right\rangle _{\hat y}$, $\gamma = \left\langle {xz|{\cal{H}}_E|x^2 - y^2} \right\rangle _{\hat x} = \left\langle {x^2 - y^2|{\cal{H}}_E|yz} \right\rangle _{\hat y}$, which are roughly proportional to the electric field with the subscript $\hat x$ or $\hat y$ indicating the location of the nearest neighbor.

Fig. 2

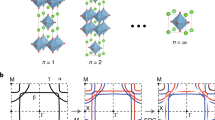
Illustration of the electric field dependence of the Berry curvature and AHC, computed from Eqs. (2) and (3), for the square-lattice TB model. a The square lattice and the electric-field induced TB hopping integral α. b The TB band structure with both large crystal field Δ_cf and SOC parameter λ, which is relevant for SIO, where the J_eff = 1/2 state is partially occupied. c Dispersion of the J_eff = 1/2 bands with and without an electric field (black and red lines, respectively). d Computed AHC for small electric fields, characterized by the parameter α, indicating the $\sigma _{xy}^{AHC} \propto |E|^2$ dependence. The Fermi energy E_F corresponded to the electron concentration n_e = 0.9 in the J_eff = 1/2 bands. e, f Berry curvature ${\mathrm{\Omega }}_n^z(\vec k)$ (in units of Ų) for the lower J_eff = 1/2 band without and with the electric field, respectively. ${\mathrm{\Omega }}_n^z(\vec k)$ is large near a crossing point K_c (here close to X) and has a dominant contribution to AHC. The TB parameters are: V_σ = −0.2 eV (1NN), −0.1 eV (2NN), V_σ/V_π = −1.85, J_ex = 0.5 eV, λ = 0.4 eV, α = β = γ = 0.01 eV (0 if E = 0), and Δ_cf = 3 eV

Te electric field breaks the inversion symmetry and leads to a Rashba interaction in the presence of SOC. The TB form ${\cal{H}}_E$ leads^15,16 to the equivalent Rashba Hamiltonian in the momentum space^18,19

$${\cal{H}}_R = \alpha _R(\vec \sigma \times \vec k) \cdot \hat z,$$

(1)

which results in the linear-k splitting of the band structure $\varepsilon _k = \frac{{\hbar ^2k^2}}{{2m}} \pm \alpha _Rk$, when J_ex = 0. The Rashba coefficients, which are different for different bands, depend on the strength of the SOC and can be expressed in terms of the matrix elements α, β, and γ, all roughly proportional to E; For instance, in the present case with strong SOC, α_R ≈ 4α/3 for the J_eff = 1/2 states. In 3D continuum, the SOC term ${\cal{H}}_{SO} = \frac{{\hbar ^2}}{{2m^2c^2}}(\vec \nabla V \times \vec k) \cdot \vec \sigma ,$ with the potential gradient $\vec \nabla V = - E\hat z$, immediately leads to the linear field dependence $\alpha _R = \frac{{\hbar ^2E}}{{2m^2c^2}}$. In fact, the linear dependence is seen from the results of the full DFT calculations as shown in Fig. 4e. Note that Eq. (1) can be rewritten as ${\cal{H}}_R = \vec B_k \cdot \vec \sigma$, where $\vec B_k = \alpha _R(\vec k \times \hat z)$ can be thought of as a momentum dependent magnetic field, as stated in the Introduction, so that the Rashba interaction is anticipated to modify the AHC because an extra magnetic field has been introduced.

Another point to note here is that the origins of the SOC term $\lambda \vec L \cdot \vec S$ and the Rashba interaction are fundamentally the same, viz., the relativistic effect, where the electron sees an electric field (nuclear field or an applied field) as a magnetic field $\vec B = (\vec v \times \vec E)/c^2$ in its rest frame, which interacts with the spin of the electron. In fact, for a weak SOC, it can be shown that the Rashba coefficient α_R is directly proportional to the strength of the SOC λ.^15,16 For the case of a strong SOC, the eigen states become spin-orbital entangled, and as a result |α_R| ≈ 4α/3 for the J_eff = 1/2 state, as stated above, is huge but independent of λ.^15,16

The AHC is computed^20,21 from the momentum sum of the Berry curvature

$$\sigma _{xy}^{{\mathrm{AHC}}} = - \frac{{e^2}}{\hbar }\frac{1}{{N_kV_c}}\mathop {\sum}\limits_{n\vec k} {{\mathrm{\Omega }}_n^z} \left( {\vec k} \right),$$

(2)

where the sum is over the occupied states, and the Berry curvature ${\mathrm{\Omega }}_n^z(\vec k)$ for the nth band can be evaluated using the Kubo formula²²

$$\Omega _n^z(\vec k) = - 2\hbar ^2\mathop {\sum}\limits_{n^{\prime} \ne n} {\frac{{{\mathrm{Im}}\langle \psi _{n\vec k}|v_x|\psi _{n^{\prime} \vec k}\rangle \langle \psi _{n^{\prime} \vec k}|v_y|\psi _{n\vec k}\rangle }}{{(\varepsilon _{n^{\prime} \vec k} - \varepsilon _{n\vec k})^2}}} .$$

(3)

Here v_η = ħ⁻¹∂H/∂k_η, V_c is the unit cell volume, and N_k is the number of k points used in the BZ sum. Near a band crossing point close to E_F, which we denote by K_c [see Fig. 2b, c], the denominator in (3) becomes small, leading to a large contribution to the AHC. For a crossing point deep below E_F, the contributions to the AHC from the two crossing bands cancel due to the opposite signs of the matrix elements.

The computed values of the Berry curvature using these expressions for the TB model in absence and presence of electric field are shown in Fig. 2e, f respectively, from which it is clear that the band crossing points have the dominant contributions to the Berry curvature. The calculated AHC for small electric fields, characterized by the field-induced TB parameter α in ${\cal{H}}_E$, is shown in Fig. 2d, which indicates the square-law dependence $\sigma _{xy}^{{\mathrm{AHC}}} = \sigma _0 + cE^2$. The AHC can also be tuned by doping, which adds carriers to the system. The results obtained for the TB model are summarized in Fig. 3, indicating the strong dependence of the AHC on the applied electric field, characterized by the parameter α, as well as the electron concentration n_e, which can be modified by doping. Note that our TB model addresses the electric field dependence of the AHC using a general ferromagnetic square lattice. It is not a model for the bilayer structure considered in our DFT calculations, and therefore does not reproduce the specific band structure.

Fig. 3

Variation of the AHC with electric field, parametrized by α, and the carrier concentration n_e [electrons in the J_eff = 1/2 band; see Fig. 2c], computed for the TB model. The star corresponds to parameters for SIO/SMO and units of AHC are Ω⁻¹cm⁻¹

The fact that $\sigma _{xy}^{{\mathrm{AHC}}} \propto |E|^2$ for small electric fields can be understood by considering a two-band model near the crossing point $\vec K_c$

$${\cal{H}}(\vec q) = \left[ {\begin{array}{*{20}{c}} {\eta q} & {h_{12}} \\ {h_{12}^ \ast } & { - \eta q} \end{array}} \right],$$

(4)

where for E = 0, we have the conical bands ε_± = ±ηq, and h₁₂ is the electric field dependent term. Explicitly, we take the crossing point in the J_eff= 1/2 band, so that the TB form of ${\cal{H}}_E$ yields the expression h₁₂ = α_R(sink_y + isink_x), where α_R = 4α/3, obtained straightforwardly from the Bloch functions corresponding to the J_eff = 1/2 wave functions: $\psi _ \pm = (|yz,\bar \sigma \rangle \pm i|xz,\bar \sigma \rangle \pm |xy,\sigma \rangle )/\sqrt 3$. From the eigenvalues of Eq. (4), viz., $\varepsilon _ \pm = \pm \sqrt {\eta ^2q^2 + |h_{12}|^2}$, and the corresponding wave functions, we find the Berry curvature from Eq. (3) to be

$${\mathrm{\Omega }}_ \pm ^z = \pm \frac{\eta }{2} \times \frac{{ - \alpha _1\alpha _2q + c_1{\mathrm{sin}}\theta - c_2{\mathrm{cos}}\theta - \alpha _1\alpha _2q{\mathrm{cos}}(2\theta )}}{{(\eta ^2q^2 + |h_{12}|^2)^{3/2}}}$$

(5)

where we have kept the terms to the lowest order in $\vec q \equiv \vec k - \vec K_c$, so that $h_{12} = {\mathrm{\Delta }} + \alpha _1q_y + i\alpha _2q_x$, where $\alpha _1 = \alpha _R{\mathrm{cos}}K_y$, $\alpha _2 = \alpha _R{\mathrm{cos}}K_x$, and ${\mathrm{\Delta }} = \alpha _R({\mathrm{sin}}K_y + i{\mathrm{sin}}K_x)$. In Eq. (5), $c_1 = \alpha _2{\mathrm{Re}}({\mathrm{\Delta }})$, $c_2 = \alpha _1{\mathrm{Im}}({\mathrm{\Delta }})$, and the ± sign refers to the upper and the lower bands. For $\alpha \ll \eta$, valid for small electric fields, we immediately find the angle-integrated Berry curvature to be

$$I_ \pm (q) \equiv {\int}_0^{2\pi } {{\mathrm{\Omega }}_ \pm ^z} (q,\theta )\,d\theta = \mp \frac{{f\alpha _R^2q\eta }}{{2(\eta ^2q^2 + |{\mathrm{\Delta }}|^2)^{3/2}}},$$

(6)

where f = cosK_x × cosK_y. This equation together with Eq. (2) clearly shows that $\sigma _{{\mathrm{x}}y}^{{\mathrm{A}}HC} \propto |E|^2$, since the Rashba coefficient α_R scales as the electric field strength. Furthermore, it is clear that I_±(q) is sharply peaked close to the band crossing point. In the square-lattice model, we find the AHC to scale as: $\sigma _{xy}^{{\mathrm{AHC}}} = \sigma _0 + cE^2$ [see Fig. 2d] for very small electric field, where σ₀≠0 due to the broken time-reversal symmetry, which is present even with E = 0. Note that this result is valid only for small E. For sufficiently large E, the bands can realign which can shift the Fermi level, and the pre-factor c can get modified as well, sometimes even becoming negative, as seen from the DFT results (Fig. 5) for a large positive electric field. This is further elaborated in the Supplementary Information.

We now turn to the DFT calculations for the (001) (SIO)₁/(SMO)₁ slab to illustrate the field tuning effect for a real material. We used the plane wave methods to solve the DFT equations within the GGA + SOC + U approximation.^23,24,25 The AHC was calculated by computing the Berry curvature using the Wannier interpolation approach as implemented in the Wannier90 code.²⁶ Further details are given in the Supplementary Information.

A key feature of the electronic structure of the (001) (SIO)₁/(SMO)₁ interface is the charge transfer^14,27 from the spin-orbital entangled J_eff = 1/2 state on the SIO side to the empty Mn-e_g states on the SMO side [Fig. 1b]. The charge transfer is important because it helps drive ferromagnetism at the interface, thereby breaking the time-reversal symmetry, which is an essential ingredient for AHC. The electron-doped SMO becomes ferromagnetic due to the Anderson-Hasegawa-DeGennes double exchange,^28,29 as is well known from the manganite physics, while SIO becomes ferromagnetic due to a combination of the magnetic proximity effect and hole doping. The magnetic proximity effect arising from the presence of the neighboring ferromagnetic SMO layer is due to the exchange interaction across the interface, while the hole doping, in addition, has a tendency to drive the SIO part ferromagnetic due to the Nagaoka physics, where in the infinite-U limit, a single doped carrier in the half-filled Hubbard model destroys the anti-ferromagnetic insulating ground state, driving the system into a ferromagnetic metal.³⁰ In fact, a short range ferromagnetic interaction has been observed experimentally in the hole-doped SIO.³¹ Both our DFT calculation as well as X-ray magnetic circular dichroism measurement⁹ show that the Ir and Mn spins are antiparallel to each other as indicated in Fig. 1a.

For the (001) (SIO)₁/(SMO)₁ slab, we find that there is a transfer of about 0.08 |e| across the interface, enough to make the SMO side ferromagnetic via double exchange. The charge transfer is consistent with the fraction of the area in the Brillouin zone occupied by the Mn (e_g) states as indicated by the purple region in Fig. 4a. Such a charge transfer has indeed been observed in the experiments. However, the magnitude of the observed charge transfer 0.5 |e| is significantly higher, which may be attributed to the fact that charge partitioning in the solid is an ill-defined quantity because creation of disjoint volumes associated with ions is not unique. Note that, the experiments were performed for the superlattice structure as opposed to the (SIO)₁/(SMO)₁ slab considered here.

Fig. 4

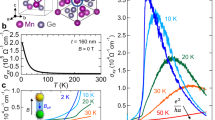
DFT results for the AHC of the (SIO)₁/(SMO)₁ slab with an applied electric field E. a Band structure for E = −0.3 V/Å, with the colored regions indicating the Ir t_2g holes and Mn e_g electrons, and the band crossing point K_c. b The Berry curvature ${\mathrm{\Omega }}_n^z(\vec k)$ summed over the occupied bands n at each $\vec k$ point along the specified line in the BZ. c Contours of the same quantity in (b) in the k_x−k_y plane, indicating the large contributions from regions around M and K_c points in the BZ, with the latter providing the dominant contribution to the field dependence of the AHC as discussed in the text. d Rashba splitting of the DFT band structure for the non-magnetic state, used for extracting α_R. e Variation of the computed α_R with the applied electric field

The magnetic structure is in good agreement with the measured value for the superlattice. We find the spin (orbital) moment to be 3.12 μ_B (0.03 μ_B) for Mn, while for Ir, it is 0.14 μ_B (0.08 μ_B), which are similar to the values for the superlattice structure. Total energy calculations with constrained spin directions indicate the moments to be aligned along $\hat z$ (normal to the plane) in agreement with the experimental results as well.⁹ In order to test the results from the DFT calculations, we first computed the AHC for the (001) (SIO)₁/(SMO)₁ superlattice structure with E = 0, for which the AHC has been measured. The computed value $\sigma _{{\mathrm{xy}}}^{{\mathrm{AHC}}} \approx 26\,{\mathrm{\Omega }}^{ - 1}\,{\mathrm{cm}}^{ - 1}$ is in reasonable agreement with the experimental value of ~18 Ω⁻¹ cm⁻¹.⁹

The typical band structure for the (SIO)₁/(SMO)₁ is shown in Fig. 4a, where the Ir holes and the Mn electrons are shown, which is consistent with the charge transfer across the interface, as sketched in Fig. 1. It is essential to optimize the crystal structure for each case in order to take into account the electrostatic screening effect, which reduces the applied field. The only changes in the band structure occur around $\vec K_c$, for different electric fields, but the overall band structure remains the same, and there is no substantial change of the charge transfer up to the electric fields we used in the calculations.

As already mentioned, large contributions to the AHC comes from regions in the BZ, where both occupied and unoccupied bands occur near the Fermi energy for same $\vec k$, which can be seen from the small energy denominator in the Kubo formula (3). As seen from Figs. 4b and 5, there are two regions with significant contributions to the AHC, σ_c from the region around the four crossing points K_c, which strongly varies with the electric field, and the remaining part σ_rest, which remains more or less unaffected because unlike near K_c, the bands change very little at M, which is the major contributor to σ_rest (see the Fig. 3 of the Supplementary Information for the evolution of the band structure with E). The electric field is expected to modify the Rashba coefficient as $\alpha _R = \frac{{\hbar ^2E}}{{2m^2c^2}}$ in the free particle model as mentioned already. To evaluate this for the solid, we computed the Rashba coefficient α_R as a function of the electric field from the linear band splitting Δ_k = 2α_Rk near the Γ point from additional DFT calculations for the non-magnetic structure. The results, Fig. 4d, e, show the anticipated linear E dependence of α_R. Note that for E = 0, α_R is large, which can be attributed to an intrinsic electric field E₀ that exists at the interface due to the broken inversion symmetry.

Fig. 5

The variation of total AHC $\left( {\sigma _{{\mathrm{xy}}}^{{\mathrm{AHC}}} = \sigma _{\mathrm{c}} + \sigma _{{\mathrm{rest}}}} \right)$, and the partial contributions, σ_c from the crossing point K_c in the BZ, and the remaining part σ_rest, as a function of the applied electric field E. The dashed parabola indicates the remnant of the square electric field dependence for the small electric field. It is clear that σ_rest shows little change with E, while σ_c changes significantly, controlling the electric field behavior of the AHC

The computed $\sigma _{{\mathrm{xy}}}^{{\mathrm{AHC}}}$, presented in Fig. 5, shows a strong electric field dependence. Even though the band structure of the slab is much more complex than the single band crossing in the model, still the remnant of a square electric-field-dependence is seen for small electric fields. This is indicated by the dashed parabola in Fig. 5, with the relation $\sigma _{{\mathrm{xy}}}^{{\mathrm{AHC}}} \approx \sigma _0 + c(E + E_0)^2$, where E₀ ≈ 0.05 V/Å is the intrinsic electric field at the interface and E is the applied electric field. For large positive electric fields, the band structure changes a lot, resulting in a large change in the AHC, as discussed in the Supplementary Information. Thus the tuning of AHC is achievable in the real material over a range of electric field as evident from Fig. 5. We note that calculations with a larger value of the Coulomb U (U = 4 eV for Mn and U = 3 eV for Ir) yields a larger AHC (55.3, 57, 57.9 Ω⁻¹ cm⁻¹ for E = −0.05, 0, and 0.05 V/Å, respectively); however, the trend obtained for the electric field dependence remains intact.

Note that we used the Γ point to evaluate the strength of the Rashba interaction because of the characteristic linear band splitting, which allows for a convenient evaluation of α_R there. At other points in the Brillouin zone, such as X or M, the Rashba coefficient will be proportional. This point can be argued by considering the expression for the relativistic magnetic field $(\vec v \times \vec E)/c^2$ seen by the electron in its rest frame, which leads to the Rashba interaction (1) for a parabolic band ε_k = ħ²k²/2m. For a general k point in the Brillouin zone, $\vec v = \frac{1}{\hbar }\vec \nabla _k\varepsilon _k$ which leads to the form $H_R = \alpha _R^\prime (\vec \sigma \times \vec v) \cdot \hat z$, where $\alpha _R^\prime$ is proportional to α_R.

So far, we described the electric field tuning via the modification of the Rashba SOC by the applied electric field. A second way to alter the AHC is by manipulating the carrier density by doping. This is verified by shifting the Fermi energy in the DFT calculations to a lower value, thereby increasing the Ir-hole concentration. In presence of an electric field E, shifting of Fermi energy downwards by Δε_F = −0.1 eV enhances the AHC by 15% to about 38 Ω⁻¹ cm⁻¹. For Δε_F = −0.15 eV, it is further increased to the value 85 Ω⁻¹ cm⁻¹. This offers an additional tool for the manipulation of the AHC.

In conclusion, we have shown that the anomalous Hall effect at the 3d-5d interfaces can be tuned by modifying the Rashba spin-orbit interaction with the application of an external electric field. The major contribution to the electric-field dependence comes from the band-crossing points close to the Fermi energy. In addition, the AHC can be tuned by manipulating the electron density with doping. We illustrated the results with a ferromagnetic square-lattice model as well as with density-functional calculations for the recently grown manganite-iridate interface, viz., (001) (SIO)₁/(SMO)₁. In fact, several recent experiments^32,33 have found evidence for the electric field dependence of the AHC in the oxide heterostructures. It would be valuable to develop this effect further, both theoretically and experimentally, with an eye towards potential spintronics applications.

Methods

The magnetic properties of SIO/SMO are studied using DFT calculations based on the plane-wave based projector augmented wave (PAW)^34,35 method as implemented in the Vienna ab initio simulation package (VASP)²³ within the generalized gradient approximation (GGA)²⁵ including Hubbard U³⁶ and SOC. The kinetic energy cut-off of the plane wave basis was chosen to be 550 eV. Following the previous report,¹⁴ all the calculations have been performed using U = 2 eV for Ir and U = 3 eV for Mn-d states respectively unless stated otherwise. In order to take into account the electrostatic screening effects, we have relaxed the structure in presence of each of the electric fields using VASP until the Hellman-Feynman forces on each atom becomes less than 0.01 eV/Å. For the calculations in presence of electric field, a sawtooth-like potential is applied.

The AHC of the slabs in presence and absence of electric field are calculated using QUANTUM ESPRESSO and the Wannier interpolation approach.^24,26 In order to compute the AHC, BZ integration of the Berry curvature is performed with a k-mesh of 400 × 400 × 80, and in the region where the Berry curvature is sharply peaked (as indicated by a Berry curvature sum over the occupied states being larger than 100 Ų), an “adaptively refined” mesh²⁶ of 7 × 7 × 7 is used. The convergence is confirmed by using finer mesh points.