Introduction

Dzyaloshinskii–Moriya interaction (DMI) is an asymmetric magnetic exchange between magnetic moments with a Hamiltonian \({\cal{H}}_{{\mathrm{DMI}}} = \mathop {\sum}\nolimits_{i \ne j} {{\mathbf{D}}_{ij}} \cdot ({\mathbf{S}}_i \times {\mathbf{S}}_j)\),1,2 in which Dij is the DMI vector with respect to the moments Si and Sj. The summation covers all different pairs of moments but is usually restricted to the nearest magnetic neighbors due to their dominant role.3,4 The DMI favors a chiral perpendicular orientation between two neighboring moments, competing against the Heisenberg exchange that tends to align the moments in parallel, which results in the formation of spin spirals. Skyrmions can be obtained by applying external magnetic field to the spin spirals and sometimes can occur spontaneously.5 They are stable circular spin textures in which moments rotate chirally from one to another across the center. The configuration is topologically protected characterized by a winding number, which cannot be changed by continuous deformation of the configuration.6 Skyrmions are promising candidates for memory and logic elements because they are highly mobile when manipulated by spin-polarized electric currents, of which the threshold magnitude (102 A cm−2) is several orders smaller than that needed to drive a conventional magnetic domain wall.7,8 Undoubtedly, DMI is critical to the special topology of skyrmions.

DMI exists in many skyrmionic materials such as MnSi,9 FeCoSi,10 FeGe,11 Cu2OSeO3,12 and GaV4S8,13 as well as Fe (Co) ultrathin films deposited on heavy metals.5 All these materials have nonmagnetic components. The presence of nonmagnetic components contributes to a broken inversion symmetry with respect to the midpoint between two magnetic sites, which is necessary for the occurence of DMI. However, the introduction of nonmagnetic components generally weakens the total ferromagnetic (FM) exchange and thus lowers the Curie temperature (TC) due to the lack of magnetic coordinations around magnetic atoms. To hold strong DMIs with meanwhile enough magnetic coordinations around a magnetic atom is usually difficult for bulk materials. Deposition of magnetic films on heavy metals is an alternative way since the heavy metals have a strong spin–orbit coupling (SOC) and the scattering of which will result in strong DMIs between adjacent magnetic atomic pairs.3,14,15,16,17 However, the interfacial DMI is basically confined in one or two atomic layers at the interface.3

Recently, Tokunaga et al.18 found that β-Mn-type (space group P4132) Co-Zn-Mn alloys can be tuned to have a TC above room temperature while DMI is present.19 Increasing Zn and Mn reduced the FM exchange in the alloy because Zn is nonmagnetic and Mn usually has strong tendency to be antiferromagnetically coupled. A noteworthy fact is that Co also possesses a metastable β-Mn-type structure named as ε-Co, which can be prepared by chemical synthesis and can be stabilized well beyond room temperature.20 Its band structure allows conduction of highly spin-polarized electrons, which may be useful for domain manipulation.21 Hence, it will be interesting to investigate the magnetic interactions in ε-Co even if there is no nonmagnetic component. In this paper, we performed calculations on the Heisenberg exchange and DMI interactions of ε-Co by employing first-principles methods. In addition to a high TC, strong DMIs between Co atoms have been found. The net effect of the DMIs can result in stable spin spirals. Atomistic spin dynamics simulations showed that skyrmions are fully achieved under a critical magnetic field of 2.9 T (0 K) but will be (partially) polarized by the field above 8 T.

Results

Exchange interactions and spin spirals

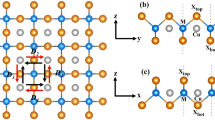
There are two crystallographic sites, i.e., 8c and 12d, in the cubic ε-Co structure as shown in Fig. 1 with a relaxed lattice constant of a = 6.055 Å. ε-Co can be seen as a derivative structure of face-centered cubic (fcc) or hexagonal close packed (hcp) Co as each atom has also 12 nearest neighbors (NNs) within 0.43a (2.60 Å) despite their positions are somehow displaced. Owing to the threefold and twofold rotation axes across Co(8c) and Co(12d), respectively, there are six inequivalent exchange paths within 0.43a around the Co atoms, as marked in Fig. 1a, while all the other ones can be replicated by symmetry operations.

Fig. 1
figure 1

Magnetic interactions and electronic hopping. a The six inequivalent NN exchange paths in ε-Co around the two sites with blue and blown atoms being Co(8c) and Co(12d), respectively. b The Heisenberg exchange interactions between Co pairs centered on Co(8c) and Co(12d). An overlapped circle with a square indicates equivalent exchange paths. The calculated ones for fcc-Co are also shown in the inset for comparison. c The DMI strengths of the six exchange paths. d The magnitude of hopping between atoms considering all spin-down spd orbitals

Full size image

By using the magnetic force theorem implemented in EMTO (see Methods), the pairwise exchange interactions are calculated centered on each site with a distance up to 0.63a, as shown in Fig. 1b. For both Co(8c)- and Co(12d)-centered cases, the exchange interaction is very strong (higher than 7.5 meV) for the 12 atomic pairs within the distance of 0.43a; out of that reach, it decreases fast to <1.5 meV. These results are similar to those calculated in fcc-Co [see the inset in Fig. 1b], where the exchange interaction between an atom and its 12 first NNs is much higher than the other ones. The obtained mean-field TC of ε-Co is 1209 K, comparable to the 1303 K of fcc-Co (1388 K in experiment) calculated in the same way. Considering only the 12 NNs, we still get a mean-field TC of 1193 K for ε-Co and 1162 K for fcc-Co, which verifies the dominant role of the magnetic interactions within these NNs. Significant differences are found in the Heisenberg exchange within 0.43a for ε-Co due to the splitting of the 12-fold degeneracy by atomic displacements with respect to fcc-Co. The variation of the exchange is basically governed by the change of atomic distance, i.e., the FM exchange is enhanced when Co atoms get closer and is weakened otherwise. Strong direct exchange is thus expected to be dominant due to their short distances.

The DMIs can be evaluated by using first-principles methods in different ways.3,22,23 Here, we calculate the DMIs of the six inequivalent exchange paths using the energy-mapping analysis developed by Xiang et al.23,24,25 combined with the constrained moment approach implemented in VASP code (see Methods). DMIs are found to differ significantly for different exchange paths. The DMIs for path II and V are remarkably strong with a vector of −(4.36, 4.35, 4.87) meV and (3.91, 3.37, 2.93) meV, respectively, while the other DMIs are much weaker (see Supplementary Table 1 and Note 1). Accordingly, |D/J| is found to be 0.85 for path II and 0.42 for path V, which are far larger than those considered by Moriya.2 Since path II connects Co(8c) and Co(12d), and path V connects Co(12d) and Co(12d), it can be concluded that Co(12d) is critical for the material to have strong DMIs. These results are interesting because there is no heavy metal present to provide strong scattering of SOC.

Assuming that Moriya’s theory applies to the present case, the DMI is given by the difference of electronic hopping forward and backward between two spin sites in the presence of SOC as follows2

$$D_{R,R^{\prime}} = \frac{{4i}}{U}[b_{nn^{\prime}}C_{n^{\prime}n} - C_{nn^{\prime}}b_{n^{\prime}n}],$$
(1)

with bnn′ being the hopping integral without SOC between ground states represented by n and n′ of sites R and R′, respectively. C is a sum of indirect hoppings between n and n′ states via excited states m and m′ of sites R and R′, respectively. For instance,

$$C_{n^{\prime}n} = - \frac{\lambda }{2}\left( {\frac{{L_{m^{\prime}n^{\prime}}^ \ast }}{{\epsilon _{m^{\prime}} - \epsilon _{n^{\prime}}}}b_{m^{\prime}n} + \frac{{L_{mn}}}{{\epsilon _m - \epsilon _n}}b_{n^{\prime}m}} \right) + c_{n^{\prime}n}.$$
(2)

Lmn is the matrix element of orbital angular momentum of atom on R and λ is the SOC constant. cn′n is the SOC-induced hopping between n and n′ states, which is usually much weaker. If there are multiple ground states and excited states for an atom, all possible hopping processes should be summed up in the above equations. Apparently, DR,R′ is not zero if the midpoint between the two spin sites is not an inversion center. This is the case in all six exchange paths here. DR,R′ results from both the hopping between the two sites and on-site mixing of ground states with excited states. Different SOC strength contributes to a different DR,R′. Nevertheless, the SOC strength of Co is a constant (15.5 meV) because it is mainly contributed by the electrons close to the nucleus, which is weak compared to those of heavy metals.26 Another fact is that the spin moment is 1.66 μB for Co(8c), which is close to the 1.76 μB for Co(12d), and the orbital moment is basically 0.065 μB for both sites. Hence, the difference in the DMI strength for the six exchange paths can be attributed to the difference in hopping due to the low symmetry that influences the spatial distribution of electrons.2 Larger hopping generally results in stronger DMI strength.24 This can be evaluated by using the maximally localized Wannier functions.27,28 For each pair of orbitals, the hopping magnitude is calculated by summing up the absolute hopping integrals between different decomposed orbitals. Both the DMI strengths and the top three significant hopping magnitudes of each exchange path are shown in Fig. 1c, d. The hopping magnitudes of path II and V are far greater than other ones, which correspond very well to the strong DMIs of these paths. It can be seen that the p states play a very important role in the hopping. The hopping magnitudes of p–p, p–d, d–p, and d–d for exchange path II and V are exceptionally significant. The hopping processes involving these orbitals are analyzed in detail with the electronic structure (Supplementary Fig. 1 and Supplementary Note 1).

A DMI vector must be distinguishable by the geometry of the structure.2,29 With the absence of inversion symmetry, if there is an n-fold (n ≥ 2) rotation axis along the two magnetic sites, the DMI vector is not allowed by the symmetry to have a perpendicular component to the polar vector rij connecting the magnetic sites i and j.29 The DMI vector thus lies in parallel to rij, such as the case of α-Fe2O3 discussed by both Dzyaloshinskii and Moriya.1,2 If there is no such rotation axis along rij, the ligands around the two sites contribute to a certain perpendicular component of the DMI vector to rij and the DMI vector is driven away from rij. The tilt angle will be 90° if there is a mirror plane bisecting rij, such as the cases of β-MnS and Co/Pt interfaces.3,29 Taking the exchange path II and V for instance, no n-fold (n ≥ 2) rotation axis along rij or mirror plane bisecting rij is present. It is thus understandable that the DMI vector has an angle of 148° and 83° with respect to rij for the exchange path II and V, respectively.

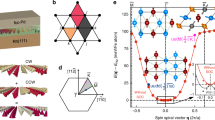
Turning now to the magnetic structures, we model the spirals by a continuous rotation of the spins characterized by a magnetic propagation vector q similar to that used in ref. 30. Both Bloch-type and Néel-type spirals (see Fig. 2a) are considered in the calculation. The spin direction of the kth site in the unit cell with a lattice vector R is \(S_{k,{\mathbf{R}}} = \cos [2\pi {\mathbf{q}}\cdot ({\mathbf{R}} + {\mathbf{r}}_k)]{\mathbf{e}}_y^q + \sin [2\pi {\mathbf{q}}\cdot ({\mathbf{R}} + {\mathbf{r}}_k)]{\mathbf{e}}_x^q\) and \(S_{k,{\mathbf{R}}} = \cos [2\pi {\mathbf{q}}\cdot ({\mathbf{R}} + {\mathbf{r}}_k)]{\mathbf{e}}_z^q + \sin [2\pi {\mathbf{q}}\cdot ({\mathbf{R}} + {\mathbf{r}}_k)]{\mathbf{e}}_x^q\) for Bloch-type and Néel-type spirals, respectively. The x, y, and z are orthogonal axes with z aligning along q. \({\mathbf{e}}_x^q\), \({\mathbf{e}}_y^q\), and \({\mathbf{e}}_z^q\) are the unit vectors accordingly. The propagation direction is chosen to be [100]* and [110]* in the reciprocal space. While the Néel-type spirals have higher energies than the FM state (q = 0), left-handed Bloch-type spirals can be stabilized for both propagation directions, as shown in Fig. 2b, c. The energy reduction relative to the FM state is 1.66 meV/cell and 1.64 meV/cell for q||[100]* and q||[110]*, respectively, which are greater than that in Cu2OSeO3 but are weaker than those in single Fe layers on heavy metals.15,30 At q = 2π/(30a), both spirals have the lowest energy. These spirals thus are almost degenerate in energy and q. This feature may benefit the generation of skyrmions since the skyrmions result from superpositions between spirals with different propagation directions. Correspondingly, a spiral period of L = 18.2 nm is obtained, which is larger than L = 3 nm found in Fe/Ir(111)15 but is much smaller than L = 125 nm in Co8Zn8Mn4 and L = 185 nm in Co10Zn10.18,19 Propagation direction [111]* has also been considered in the calculation, but no stable spiral was found. Moreover, it is found that the DMIs of exchange path II and V dominate the stabilization of the spirals because removing the DMIs of other paths from the calculation makes no difference in the period of stable spirals, although the energy reduction changes to be 2.37 meV/cell and 2.25 meV/cell for q||[100]* and q||[110]*, respectively.

Fig. 2
figure 2

Energy of spirals. a A schematic picture of Bloch-type and Néel-type spirals. b, c show the energies of spirals (in meV/atom) propagating along [100]* and [110]* directions, respectively

Full size image

The DMI contributions from different Co sites to the stable spin spirals are given in Fig. 3. For the spin spiral propagating along [100]*, all Co(8c) sites have the same negative DMI energy. The reason is that a threefold rotation axis lying in one of the four [111] axes through a Co(8c) site results in an equal projection of total DMI energy in each [100] direction. In contrast, there is a twofold rotation axis along one of the six [110] axes through each Co(12d) site. Apparently, regarding the projection in [100] direction, four of these axes with an angle of 45° are equivalent and the other two with an angle of 90° are degenerate, leading to a ratio of 2:1. The DMI energies of Co(12d) sites are thus separated into two groups with one of them having eight negative DMI energies and another having four positive ones, as shown in Fig. 3a. A similar way can be used to understand how the DMI energies are grouped for the spin spiral propagating along [110]* direction (Fig. 3b). A noteworthy fact is that these DMI energies are more inhomogeneous with two of the Co(12d) sites having strong negative values. Although the DMI energies partially cancel with each other for both cases, a net effect is clearly shown. The overall DMI energies of the two spirals are negative and are close to each other.

Fig. 3
figure 3

DMI energies of stable spirals. a, b are the DMI energies (in meV/atom) of different atomic sites for the stable Bloch-type spin spirals propagating along [100]* and [110]* directions, respectively

Full size image

Spin dynamics simulations

To demonstrate the formation of skyrmions explicitly, the Heisenberg exchange and DMIs are transferred to the spin dynamics simulation implemented in the SPIRIT code, which solves the Landau–Lifshitz–Gilbert equation at 0 K (See Methods). The operation plane (to simulate skyrmions within) is chosen to be (001) by constructing a 100 × 100 × 1 supercell (60.5 nm by width) since skyrmions are most likely to be generated in this plane. Periodic boundary condition is adopted in the simulation. The external field is varied from 0 to 10 T and is applied along +z direction. The initial spin configuration for each simulation is randomized. The energies and patterns of the stabilized spin configurations with an external field ranging from 0 and 6 T are given in Fig. 4. Under zero field, there are stripe-like domains separated by chiral domain walls, which may be characterized as a helix state since the width of domain walls are close to half the spiral period (Red scale bar in Fig. 4). Some domains spontaneously form circular skyrmions due to the natural superposition between spirals with different propagation directions as they are almost degenerate in energy and q. When the external field increases from 0 to 1 T, the patterns do not vary much, but the energy increases. Further increasing the external field results in an expansion of the favored domains by the Zeeman effect, which also reduces the energy of the spin configuration. The unfavored domains shrink and finally, at 2.9 T, only skyrmions are found in the patterns. This critical field is about half that predicted in Fe single layers on heavy metals.15 The number of skyrmions increases when the external field increases from 2.9 T and reaches its maximum at 8 T, which is also verified by the calculation of topological charge (see Supplementary Figs 2 and 3). A field larger than 8 T results in (partial) polarization of the skyrmions (patterns not shown here) as can be expected since the diameter of skyrmions shrinks from 16 nm at 2.9 T to be only 8 nm at 6 T. The evolution of the magnetic configurations may be interpreted by the energy analysis given below.

Fig. 4
figure 4

Total energy of magnetic patterns under external field. The energies (in meV/atom) and patterns of magnetic configurations under different external fields applied along +z direction. The white spins point to +z and the black ones denote the opposite. The red scale bar (18.2 nm) is the spiral period obtained by energy calculation

Full size image

Discussion

The simulation of magnetic configuration is based on the Hamiltonian

$${\cal{H}} = - \mu _0H\mathop {\sum}\limits_i {{\mathbf{S}}_i} - \mathop {\sum}\limits_{i \ne j} {J_{ij}} {\mathbf{S}}_i\cdot {\mathbf{S}}_j - \mathop {\sum}\limits_{i \ne j} {{\mathbf{D}}_{ij}} \cdot ({\mathbf{S}}_i \times {\mathbf{S}}_j),$$
(3)

which includes Zeeman effect, Heisenberg exchange, and DMI. The demagnetization effect and magnetic anisotropy are expected to be minor effects on the formation of skyrmions and are neglected here. As shown in Fig. 5, at the beginning, the external field results in an increase in the Heisenberg energy. This is because the external field tends to enlarge the favored domains and narrow the unfavored ones in the helix state, which will inevitably increase the angles of neighboring spins that rotate chirally across the domain wall. In contrast, the DMI energy is lower when the increasing angles get closer to 90°. At this stage, no significant change happens in the pattern and the Zeeman energy varies slowly. As the external field increases further, Zeeman energy decreases rapidly since the coverage of favored domain expands quickly. The amount of domain wall thus becomes less, which results in a dropping Heisenberg energy but a rising DMI energy. Around the critical external field of 2.9 T, kinks occur in the energy profiles because skyrmions are fully achieved as shown in Fig. 5. Beyond this critical field, the Zeeman energy continuously decreases partially due to the shrinking skyrmions (Even if there is no change in pattern, the Zeeman energy still decreases as external field increases if the coverage of favored domains is larger than that of the unfavored). Meanwhile, the resulting increase in angles between spins in the skyrmions contributes to an increasing Heisenberg energy and a decreasing DMI energy. However, the DMI energy does not vary much from 4 to 8 T due to the energy compensation by more skyrmions as shown in Fig. 5. The Zeeman effect is a driving force in the formation of skyrmions, which resembles the undercooling in solidification: a larger Zeeman effect tends to nucleate more skyrmions with smaller sizes in a shorter time (Supplementary Note 2). However, too high external field will simply polarize the skyrmions and result in the decreasing Heisenberg energy and increasing DMI energy, as shown in Fig. 5. This result indicates a potential method to manipulate the number of skyrmions in the future.

Fig. 5
figure 5

Evolution of different energies under external field. The Zeeman, Heisenberg and DMI energies (in meV/atom) of magnetic configurations are represented by squares, circles and triangles, respectively. The dashed line gives the critical field needed to fully induce skyrmions. The reference is the energy of the magnetic configuration with zero field

Full size image

In summary, strong DMIs are predicted in a high-TC and noncentrosymmetric Co phase, which can be attributed to the strong hopping between certain neighboring atomic pairs, where Co-p orbitals play an important role. Stable left-handed spirals propagating along [100]* and [110]* are found to be almost degenerate in energy and propagation vector. A spiral period of 18.2 nm is obtained from energy calculation. A critical external field of 2.9 T is found to trigger the formation of skyrmions from a randomized magnetic configuration by spin dynamics simulation. The stable skyrmions result from the competition between Heisenberg exchange and DMI mediated by the Zeeman effect.

Methods

First-principles calculations

Two first-principles tools are involved in the calculations: the Vienna ab initio simulation package (VASP)31,32 and the exact muffin-tin orbitals (EMTO).33,34 The former was used to fully relax the ε-Co structure and calculate the Dzyaloshinskii–Moriya interactions (DMIs), while the latter was used to calculate the Heisenberg exchange based on the relaxed structure. Although combining different computation tools will suffer from certain inconsistency of accuracy, it is expected that the resulting error is stable and not significant. The carefully tested computational parameters are introduced below in detail.

The projector augmented wave (PAW) pseudopotentials are used here for the calculations related to VASP. The exchange-correlation energy is calculated with generalized gradient approximation (GGA) in the Perdew-Burke-Ernzerhof (PBE) form.35 A Γ-centered 9 × 9 × 9 Monkhorst-Pack k-point mesh is adopted for the calculation. The energy cut for the plane waves is chosen to be 320 eV.3 The relaxation obtains a lattice constant of 6.055 Å for ε-Co when the maximum force of atoms is lower than 0.001 eV/Å, which is close to the measured 6.097 Å.20 In order to obtain the DMIs, the constrained moment approach with spin–orbit coupling (SOC) implemented in VASP is used to calculate the energies of different spin orientations starting from the charge distribution obtained by collinear calculation. This technique has been proved to be powerful in DMI calculations in magnetic oxides and Co films on heavy metals.3,23,24,30 Test calculations with respect to the supercell size indicate that adopting the unit cell (20 atoms) is a good compromise between efficiency and accuracy.

The emto calculations are performed by using Green’s function technique based on an improved screened Koringa–Kohn–Rostoker (KKR) method.33,36 The one-electron Kohn–Sham equation is solved with soft-core approximation. The exchange-correlation energy is also calculated with the GGA parameterized by Perdew et al.35 The spdf orbitals are included in the EMTO basis sets to construct the wave functions. The Co-3d74s2 are treated as valence states. A Gaussian mesh of 16 energy points on a semicircle (1.0 Ry in diameter) comprising the valence states is used for energy integration. The Brillouin Zone is sampled by a special k-point technique with a dense mesh of 17 × 17 × 17. The technique to calculate pairwise Heisenberg exchange is based on magnetic force theorem,34 which does not require a supercell and can calculate the Heisenberg exchange between atoms with an arbitrary distance.

Spin dynamics simulation

The spin dynamics simulation was performed by solving the below Landau–Lifshitz–Gilbert (LLG) equation using a 100 × 100 × 1 supercell (60.5 nm by width) at 0 K (The SPIRIT code is availabe from site: https://spirit-code.github.io/).

$$\frac{dM}{dt} = - \gamma M\, \times H_{\mathrm{eff}}\, +\, \frac{\alpha }{Ms}M\, \times \frac{\partial M}{\partial t},$$
(4)

in which M is the magnetic moment, γ the electronic gyromagnetic ratio and α the damping factor. The effective field Heff includes Heisenberg exchange, DMI, and Zeeman effect. The initial orientations of the magnetic moments were randomized. The damping factor was chosen to be 0.3. The time step was set as 1 femtosecond.