Introduction

Glass-ceramics consist of crystals embedded in a glassy matrix, which can create a wide range of products with tunable thermal, optical, and mechanical properties. Controlling the crystallization process allows glass-ceramic properties to range from highly transparent to opaque with unique properties such as ultra-low thermal expansion, tunable fluorescence, chemical durability, or improved mechanical properties compared to their base glass compositions.1 These properties have led glass-ceramics to be used in an ever expanding list of applications 2,3,4,5 including dental and medical implants, aerospace equipment, nuclear waste mediation, cooktop panels, and personal armor protection. Furthermore, understanding how to suppress nucleation during glass manufacturing would led to fewer devitrified wasted products.6 A better understanding of the nucleation and crystallization mechanisms will therefore lead to improved materials and manufacturing processes for both glass and glass-ceramic products.

Nucleation is a rare event occurring on nanometer length scales 7,8,9,10 and particularly challenging to understand. One of the key challenges is decoupling the nucleation and crystal growth mechanisms 3,11 To investigate nucleation experimentally, a combination of techniques need to be used to construct a more complete picture of the nucleation event. These include transmission electron microscopy (TEM) 12,13 differential scanning calorimetry (DSC) 14,15 X-ray diffraction 9,16 and magic angle spinning nuclear magnetic resonance spectroscopy (MAS NMR).17 Observing the kinetics of the nucleation event directly is especially difficult, since the volume fraction of nuclei in the material is typically well below the experimental detection limit. In the two-stage heat treatment process,18 where the sample is first nucleated at a lower temperature, and then the crystals are grown at a higher temperature, completely missing the initial nucleation event. In situ ultrafast X-ray is an emerging and powerful experimental technique that has promise to probe the evolving microstructure during nucleation. However, this technique requires specialized equipment that is not easily accessible and has its own technical challenges, e.g., time synchronization to resolve the dynamics at the angstrom and picosecond scale.19

Atomic scale modeling of the nucleation and growth processes can provide new insights into the formation of these materials and their physical properties. As with the experimental approaches discussed above, current modeling techniques have severe limitations related to capturing the nucleation barrier 7,20 for a new phase to appear. The accuracy of the model depends on the force field’s description of the true physical system, and the precision of the simulation depends on sampling a representative volume of the relevant phase space.20 Time and length scales challenges result from the fact that crystal nucleation is a rare event occurring on a longer length scale compared to that associated with liquid motion.

To determine the nucleation barrier, one must find the critical cluster size that differentiates the crystal and liquid phases. The main difficulty of modeling nucleation is that the fast time scale of molecular dynamics (MD) simulations leads to an over-prediction of nucleation rates.21 Techniques such as a brute-force method 8 and enhanced sampling simulations 22 have been considered to address the time and length scale issues; however, these techniques are challenging due to finite size effects and the choice of collective variables. For an excellent review of liquid nucleation modeling techniques and challenges, see Ref. 7

The modeling of liquid environments, which pertains to time and length scales of nucleation can become computationally expensive due to the solute size (e.g., the crystal seed) and the solvent’s many degrees of freedom (e.g., the glass or liquid matrix). As one increases the size of the solute, more solvent particles are required to prevent the solute from interacting with its periodic image, which would increase the apparent nucleation rate. To overcome this problem, a larger simulation box is required, along with additional computational time associated with the movement of solvent particles, which does not contribute significantly to the nucleation event. To reduce the number of solvent particles and lower the computational expense, implicit solvent models 23,24,25,26,27 have been developed. Implicit solvent models have traditionally focused on water-protein interactions, but the concept can also be extended to other liquid systems, such as supercooled liquids. In this case, instead of the protein solute, the solute may be impurities, nucleating agents, or crystal-like clusters. Our aim is to expand upon the previously discussed implicit glass model 28 allowing simulation models to focus on the important phase space regions.

The implicit solvation method, also known as continuum solvation, is a technique that approximates the behavior of explicit solvent particles to an effective continuum medium. To create an implicit solvent model, two approaches have been used based on solute accessible surface area 29 (ASA) and continuum electrostatics. The ASA method calculates the free energy of solvation from the atom’s surface area using a linear relationship. This approach highlights the importance of solute structure and has been deployed for protein folding, where each amino acid experiences a different solvent environment. On the other hand, continuum electrostatics, such as the Poisson-Boltzmann (PB) method, views the solvent as a dielectric continuum that screens the solute’s electrostatic interactions. The PB equation (Eq. 1) combines the Poisson equation, that connects the solvent medium’s electrostatic potential variation in a constant dielectric to the charge density, with the Boltzmann distribution governing the system’s ion distribution:30

$$\nabla \cdot \left[ {\varepsilon \left( {\vec r} \right)\nabla \varphi \left( {\vec r} \right)} \right] = - 4\pi \rho \left( {\vec r} \right) - 4\pi \mathop {\sum }\nolimits_i c_i^Bq_i{\mathrm{\lambda }}\left( {\vec r} \right)\exp \left[ {\frac{{ - q_i\varphi \left( {\vec r} \right)}}{{k_BT}}} \right]$$
(1)

The PB equation (Eq. 1) incorporates divergence operator ∇, solving for the position dependent electrostatic field, \(\varphi \left( {\vec r} \right)\), the ion’s charge, qi, bulk charge density, \(c_i^B\), the solute charge density, \(\rho \left( {\vec r} \right)\), the accessibility of the ions at point \(\vec r\) is described by \({\mathrm{\lambda }}\left( {\vec r} \right)\), and the position dependent dielectric coefficient, \(\varepsilon \left( {\vec r} \right)\). The PB equation can exactly solve for the electrostatic field of a charge distribution in a dielectric medium; however, it is computationally expensive to solve due to mesh quality and convergence for a given configuration. Approximations have been made to simplify the PB equation; the most notable approximation is the Generalized Born (GB) solvation model 24 This model describes the electrostatic solvation energy as a function of the solute’s pairwise interaction via their effective Born radii, which signifies a characteristic distance from the atom to the solute’s surface.

Both ASA and continuum electrostatics techniques have their relative merits. ASA incorporates the free energy of solvation while the continuum methods use only the enthalpic component of the free energy (via charge distribution). A disadvantage of the ASA technique is incomplete sampling of the solvent and surface configurations leading to errors in solvent averaging. The PB equation is straightforward to calculate; however, for complex geometries it is expensive to solve thus making the use of the GB approximation attractive. These techniques have been combined in the Generalized Born/Solvent Accessible method 31,32 and have been shown to correctly model the tertiary structure of peptides.33 Nevertheless, this technique has a deficiency where the electrostatic screening is too weak depending on the surface area, resulting in stronger electrostatic configurations between the solute and solvent.34 For our problem of interest (crystal growth in a liquid or glassy medium) the solute crystal is spherical-like (compared to the complex protein configuration of alpha helixes and beta sheets), and applying the GB methodology is deemed to be a good first order approximation to the solvation energy.

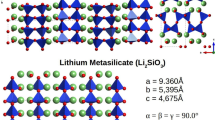
For this study, we expand the GB method to glasses by selecting three systems of study: barium silicate, lithium disilicate, and soda lime silicate (Table 1). The remainder of this article covers the results, discussion, and methods. The discussion includes an overview of the assumptions used, validation of IGM’s predicted structural features, computational savings, influence of the crystal cluster solvation energy on nucleation, and a comparison of a lithium metasilicate crystal with the IGM approach to SEM experiments for comparing morphology and volume. The methods section is divided into two parts: (1) the development of the Implicit Glass Model (IGM) based on the GB approximation and (2) the experimental section includes glass melting, dielectric measurement, and Scanning Electron Microscopy (SEM) setups.

Table 1 List of systems for IGM development
Full size table

Results

To study the stability of a nucleating crystal, we perform molecular dynamics simulations under the conditions listed in Table 2. The isothermal-isobaric (NPT) ensemble is used with the Berendsen thermostat with a time constant of 0.1 fs and a relaxation constant of 100 fs. The temperature is set to the nucleation temperature of the glass to study the stability of the crystal using a time step of 2 fs which ensures stability of simulation.28 Two simulations are carried out for each system: an explicit solvent simulation and an implicit solvent simulation. In the explicit solvent simulation, we place a crystal of the compound surrounded by a melt of the same stoichiometric ratio as the crystal (Table 2), and NPT simulations are carried out. In the second simulation, we simulate a crystal under NPT conditions, adding the IGM parameters to the existing forcefield to simulate an implicit glass environment.

Table 2 Simulation setup parameters used in test of the crystal structure
Full size table

It was found that the average potential energies per atom of all systems are within 0.003% of each other indicating the underlying energetics remains similar. Examining the resulting structure, we observe that the implicit solvent model captures short range and medium order accurately (Figs. 1 and 2). There is a mismatch in the medium range order for the explicit smaller crystal within a melt (gray curves in Figs. 1 and 2). This can be attributed to the finite size of the crystal placed in the melt, as shown by comparing the larger melt systems (gray and black curves in Figs. 1 and 2). System size effects play a role in computational expense estimations. By defining a service unit (SU) as one central processing unit (CPU)-core per hour, it was found that the Systems 3-c, 3-m1, 3-m2 requires 8, 960, and 7250 SU, respectively, to model 1 ns of simulation time.

Fig. 1
figure 1

Barium silicate radial distribution function comparison between systems 1-m1 (gray), 1-m2 (black), and 1-c (red). In panels a, b, and d the gray curve overlaps with the black curve

Full size image
Fig. 2
figure 2

Lithium silicate radial distribution function comparison between systems 3-m1 (gray), 3-m2 (black), and 3-c (red). In panels a-d and f the gray and black curves overlap

Full size image

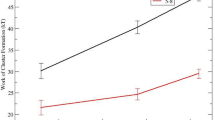
As an alternative to measuring the nucleation rates and processes directly via the brute force approach 8,7 we measure the solvation energy of the cluster to determine if it would be stable in the melt. To determine the contributions of the solvation energy to the total energy, we consider 2–3 unit cell crystals (to have close to 30 atoms total for comparison) using the nucleation code (described in 28 using the nucleation code 35) with the Pedone et al. 36 force field and IGM parameters and allowed the system to relax via Monte Carlo translational moves. There is a lack of experimental solvation energies for silicate systems. Only small molecules aqueous solvation energies are known experimentally, and larger solutes are typically parameterized based on the smaller molecular fragment representations.37 Knowledge of crystal dissolution and high temperature solid solutions from phase diagrams offer an insight into a solvation metric. The calculated crystal solvation energies are presented in Table 3. Note, these values are on the same low MJ/mol solvation energies as ions in aqueous solutions.38

Table 3 Calculated solvation energy from the implicit glass model of small (approximately 30-atom) clusters
Full size table

Experimentally, Fokin and Zanotto studied 39 this system and found compositional changes of the sodium calcium silicate crystals during the crystallization process. They showed that the crystallization pathway of the composition of a CaO SiO2–Na2O SiO2 pseudo-binary (Table 3, System B) does not start with the nucleation of CaO SiO2 (Table 3, System C) or Na2O 2CaO 3SiO2 (Table 3, System D) but instead begins with an enriched sodium solid solution (Table 3, System A). In Table 3, we show the solvation energies of these small clusters and found the sodium rich structure (System A) requires the most solvation energy (the higher positive solvation energy, the compound is more insoluble). This agrees with Fokin and Zanotto’s observations. In a similar argument, lithium disilicate (Table 3, System F) may co-precipitate or an intermediate 40 lithium metasilicate (System E). The metasilicate requires more solvation energy to stay in solution (i.e., in the melt); hence it precipitates out. In the barium silicate system, it has been postulated 41 that the nucleating phase for both barium disilicate (B1S2, Table 1, System 1) and the pentabarium octasilicate (B5S8, Table 1 System 2) initiates from B5S8 spherulites. This is reasonable according to the barium silicate phase diagram, in that the first phase that comes out of solution, for all barium oxide compositions, is the B5S8 phase.42 We found the B5S8 has a more positive solvation energy than the B1S2, indicating B5S8 is more insoluble. This provides credence that this system first forms B5S8 clusters.

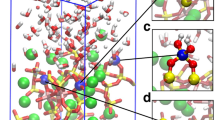
Another test of the IGM is to compare cluster shape with experiment. The lithium metasilicate nucleation experiment (873 K for 2 h) created a hazy sample due to large population of small crystals. Following a previous study,28 we continued to grow a lithium metasilicate cluster to larger tens of nanometer sizes. The modeled 80-formula unit sized cluster of lithium metasilicate is created, using the IGM parameters from a 10-formula unit cluster. The cluster is grown by adding 10-formula units at a time (randomly around the cluster) and allowing the atoms to translate to obtain a minimum energy configuration (40 million Monte Carlo translational moves). The SEM experiment shows squat needle-like structures (Fig. 3a). Further increasing the SEM resolution, these needle-like structures are more rounded and appear to be made of smaller spheroid-crystallites (Fig. 3b). The model created an oblong spheroid having the greatest axial lengths of 27 Å × 24 Å × 28 Å (Fig. 3c). Comparing all the panels in Fig. 3, the lithium metasilicate shapes begin to converge, this implies the IGM parameters are effective at solvating the cluster and able to predict the growing cluster shape.

Fig. 3
figure 3

SEM images and model of lithium metasilicate clusters. The SEM scale bar is 200 nm and 100 nm for panels a and b, respectively. Panel c shows different viewing angles of a 80 formula units of lithium metasilicate cluster. Coloring scheme is Si (yellow), O (red), and Li (pink). Longest axial measurements are 27 Å × 24 Å × 28 Å

Full size image

Discussion

Before discussing the validation of IGM, it is important to review the assumptions so that readers can make a better assessment of the model for their own needs. The assumptions used in the development of IGM are listed in Table 4. These include the implicit solvent model, GB model, choice of force field, and use of an experimental dielectric instead of explicit computation. For each of these points, we list their advantages, disadvantages, and possible remedies should the assumptions prove ungrounded for a given system.

Table 4 Assumptions and their advantages/disadvantages with possible remedies used in the IGM creation
Full size table

Implicit models, including GB, are computationally cost effective, assuming the solvent is of uniform density, relative motion, and charge. Increased shear flow, or hydrodynamic forces, around a solute could distort the solvent shape and break uniformity. For fast solvent degrees of freedom, a better implicit-like treatment would be the use of Stokesian dynamics,43 though this approach has its own assumptions. Another disadvantage of these implicit solvent methods comes from the solute shape. If the solute becomes aspherical, the simple distance dependent implicit model would under-predict important solvent contribution. Incorporating the GB/ASA technique mentioned in the background section would be able to alleviate this matter.

Note this IGM formulation would have to be modified depending on the atomic force field used. Silicate glasses have bonding with mixed covalent and ionic character. The Pedone force field36 represents this balance through the magnitude of partial atomic charges. Silicon atoms have a charge of 2.4 balanced by oxygen’s–1.2 charge, indicating the silicate ions have more of a covalent bond character. While modifiers typically have a charge of 0.6 (more imbalanced with silicon, more ionic bond character). In fact, this simplified view makes the development of the IGM easier as one does not have to explore many different systems having many different charge magnitudes. Moreover, Pedone is a non-bonded force field and a bonded force field would require additional sampling of the bonded degrees of freedom with respect to the work of solvation. Depending on the physics needed to model the science, one can use a different force field that would be more appropriate.

Using the experimental dielectric constant versus a computed value has a variety of consequences. There are a few methods to compute this quantity: density functional theory (DFT), polarizable force field model, and estimation based on the Kirkwood factor. For DFT, it would require large systems and long trajectories, which is computationally prohibitive. Also, using this route to obtain the system’s dielectric constant may not agree with a reformulation using a fixed charge classical potential. The dielectric constant is sensitive to the electrostatic environment, and a polarizable fluctuating charge model could be used as an alternate approach. Unfortunately, the few fluctuating charge silicate force fields44,45,46 only contain at most three elements and cannot model the multicomponent systems of interest. One could estimate the dielectric constant with the fixed charge model via an ensemble average of the fixed charge positions used to estimate the Kirkwood factor. However, this method severely underestimates the dielectric constant by 50% 47,48 to 70% 49 of the experimental value. The failure is due to the mean field approximation for the fixed charge to account for polarization. Previous aqueous GB models 23,24,31,50 have used the experimental dielectric constant of water with good success. From these considerations and prior work, it is reasonable to use the macroscopic dielectric constant.

We have developed the implicit glass model (IGM) that relies on accurate differences of atomic solvation energies and dielectric constant. The major findings are:

  • This approach enables one to focus on the key physics governing each step in the nucleation process, providing critical insights for the design of new glass-ceramic materials.

  • Significant computational savings is achieved by treating the liquid/glass matrix as an implicit solvent using an extended Generalized Born Model.

  • IGM allows MC methods to work efficiently in condensed phased systems.

  • Predicted the correct solid phases according to the phase diagram.

  • Experimental validation was performed with SEM measurements and the phase diagram.

  • While the focus in this work has been on glass-ceramic (oxide) systems, the approach is generally applicable to crystal nucleation in any liquid, supercooled liquid, or glassy system.

This work opens a new door for the use of Monte Carlo simulations in dense phase systems where traditionally it would struggle due to low acceptance rates on translational moves. Now the full use of the Monte Carlo techniques can focus on the important features such as liquid to cluster exchange processes (e.g., cluster growth/shrinkage), changes in the cluster composition, cluster solvation, cluster to crystal organization, stabilities of impurities in a glass melt, and the exploration of the developing crystal microstructure from many small cluster aggregates. From opening this door, new and unexpected challenges may arise in the form of glass complexity, solute shape, and understanding the change of residual glass chemistry with growing crystals. The complexity of the glass solution, for instance having many components with single molar oxide concentrations, may require a much longer and larger simulation to obtain accurate free energy estimates.

There are many opportunities for IGM, and this work serves as a step towards a new way to study atomistic microstructural evolution and mechanical properties, crystal precipitation, bubble nucleation, and broadening the inorganic-organic modeling techniques. For instance, if we consider when the GB method may not be accurate, via solute becoming non-spherical. Creating a GB/ASA model to extend the solvent predictability, one can apply this to the developing crystal microstructures. Another aspect the IGM approach can provide solutions to materials science research is to understand why certain crystal phases, like jadeite, are difficult to precipitate as a glass-ceramic. A more immediate geologic issue concerns volcanic eruption, as seen in Hawaii where toxic gases are emitted that causes much destruction. A pertinent question is the pressure and mechanics of bubble formation needed to de-gas these toxic species. A step in such an endeavor would be to extend IGM to other inorganic force fields, e.g., the Interface force field 51,52 so that an atomic representation of the gas can be utilized. By doing so, this would expand the IGM scope to organic-inorganic systems that are important to understand geologic processes.

Methods

IGM development

An approximation to the PB equation (Eq. 1), the GB model is based on representing the solute as a set of spheres in that the internal dielectric constant differs from the external solvent. We begin with the GB equation below.32

$$\Delta G_{\mathrm{{solv}}} = \frac{1}{{8{\mathrm{\pi \varepsilon }}_0}}\left( {{\mathrm{1 - }}\frac{1}{\varepsilon }} \right)\mathop {\sum }\limits_{i,j}^N \frac{{q_iq_j}}{{\sqrt {r_{ij}^2 + a_ia_j{\mathrm{exp}}\left( { - \frac{{r_{ij}^2}}{{4a_ia_j}}} \right)} }}$$
(2)

The variables i and j are atom indices for a total of N atoms. Each atom has a charge, q, and a separation from other solute atoms, rij. ɛ0 and ɛ are the permittivity of free space and the dielectric constant of the solvent being modeled, respectively. The effective Born radii for atoms i and j are represented by ai and aj, respectively. It should be noted that a larger Born radius indicates a lower screening environment.

The IGM parameters for three different chemical systems are shown in Tables 1 and 5. The dielectric constant is sensitive to the glass composition; therefore, we select two barium silicate compositions to explore its impact on the Born radii. We need to find the solution dielectric constant and calculate the Born radii from the work of solvation performed per atom (Eq. 3). Using the computed work of solvation from Eq. 3, the effective Born radius ai is found. This parameter tunes the local screening for the pairwise computation between atoms (Eq. 2).

$$W_{\mathrm{{solvation}}} = - \frac{1}{2}\left( {1 - \frac{1}{\varepsilon }} \right)\frac{{q_i^2}}{{a_i}}$$
(3)

The work of per atom solvation (Eq. 3) involves simulating a well equilibrated liquid box containing a few thousand atoms (Table 1) with LAMMPS53 using the Pedone set of interatomic potentials.36 The glass is melted at 4000 K using the canonical (NVT) ensemble for 20 ns. Another 20 ns is used to quench the melt to the system’s nucleating temperature, viz., 980 K, 732 K, and 750 K, for the barium silicate, lithium silicate, and soda lime silicate systems, respectively. An isobaric-isothermal ensemble is then used to continue relaxation of the melt system at the nucleating temperature for another 20 ns. The calculated energy differences from the melt to vacuum and calculated Born radii are shown in Table 5. This solvation potential term (Equation 1) is added to the total potential energy by converting Table 5 into a tabulated potential for LAMMPS.

Table 5 Simulation output from the estimation of solvation work done and the resulting Born radii
Full size table

Experiment setup

The barium and lithium silicate samples were prepared by crucible melting. The batch materials (barium carbonate for barium, lithium carbonate for lithium, and high purity silica sand for silicon) were turbula mixed for 30 min and then melted in platinum crucible at 1873 K for 6 h. The molten glass was roller quenched, crushed, and re-melted at 1873 K for increased homogeneity. After second melting, the glasses were poured in 254 mm × 127 mm patties. The patties were annealed at 923 K to reduce stress. Induced Coupled Plasma (ICP) was conducted on each glass to analyze the composition.

The two barium silicate samples for dielectric measurement are made into 25.4 mm diameter disks and polished to 1 mm thickness. The sample surfaces are sputtered with gold to make electrical contact. The samples are placed inside a custom build furnace where platinum leads are in contact with the gold electrodes on the sample. The measurements are taken under slow heating (~1 K/min) so that sufficient thermal equilibration is achieved at each measurement temperature. The dielectric constants are measured with an impedance analyzer, and frequency sweeps from 1 kHz to 1 MHz were performed. The data presented in Table 1 are measured at 773 K.

Scanning Electron Microscope (SEM) experiments were conducted to study the shape of small lithium metasilicate crystals. A lithium silicate composition was analyzed by high temperature X-ray diffraction and the first detectable lithium metasilicate phase was observed at 600 °C. Quenched samples of this composition also showed that the glass was hazy after heating at 600 °C for 2 h. A specimen of the sample that was heated at 600 °C for two hours was prepared as a polished cross-section using only fixed abrasives with a final polish using 0.05 μm fixed silica abrasives. A conductive carbon coating was evaporated on to the polished specimen to reduce charging. The polished and coated specimen was imaged using a Zeiss 1550VP field emission scanning electron microscope operated at 2 kV accelerating potential. Secondary electron images were acquired showing the crystal morphology at a field width as small as 1.14 μm and pixel resolution of 1.12 nm.