Abstract
We present a combination of machine learning and high throughput calculations to predict the points defects behavior in binary intermetallic (A–B) compounds, using as an example systems with the cubic B2 crystal structure (with equiatomic AB stoichiometry). To the best of our knowledge, this work is the first application of machine learning-models for point defect properties. High throughput first principles density functional calculations have been employed to compute intrinsic point defect energies in 100 B2 intermetallic compounds. The systems are classified into two groups: (i) those for which the intrinsic defects are antisites for both A and B rich compositions, and (ii) those for which vacancies are the dominant defect for either or both composition ranges. The data was analyzed by machine learning-techniques using decision tree, and full and reduced multiple additive regression tree (MART) models. Among these three schemes, a reduced MART (r-MART) model using six descriptors (formation energy, minimum and difference of electron densities at the Wigner–Seitz cell boundary, atomic radius difference, maximal atomic number and maximal electronegativity) presents the highest fit (98 %) and predictive (75 %) accuracy. This model is used to predict the defect behavior of other B2 compounds, and it is found that 45 % of the compounds considered feature vacancies as dominant defects for either A or B rich compositions (or both). The ability to predict dominant defect types is important for the modeling of thermodynamic and kinetic properties of intermetallic compounds, and the present results illustrate how this information can be derived using modern tools combining high throughput calculations and data analytics.
Similar content being viewed by others
Introduction
In crystalline compounds, point defects often play a central role in governing a wide variety of physical properties. Whether one is considering intrinsic carrier types in semiconductor compounds, optical properties of insulators, or the resistance of an intermetallic phase to high-temperature deformation processes, knowledge of the type and concentrations of dominant point defects is essential for understanding and controlling materials behavior. The difficulties inherent in performing experimental measurements of equilibrium point defect properties can thus present a significant barrier to the accelerated development of materials for targeted applications. In recent years, this situation has benefited significantly from the development of computational tools based on electronic DFT that provide a framework for accurate prediction of the equilibrium concentrations, electronic structure, and kinetic properties of point defects.1,2,3,4 While such tools have advanced significantly, they remain relatively computationally costly, due to the need to employ supercell models,5 particularly when expensive functionals6 are employed. Thus the use of such computational techniques in high throughput (HT) calculations in the context of materials discovery and design7,8,9 has remained limited.
In the present work, we demonstrate a strategy for predicting point-defect properties over a large composition space, employing machine-learning (ML) methods on a relatively small training set. ML approaches have found rapidly increasing use in computationally-assisted materials discovery and design in recent years,10,11,12,13,14,15,17, but to the best of our knowledge the application of such models for point defect properties has not yet been undertaken. In this work, we present a general framework for applying ML algorithms to the important problem of predicting the dominant point-defect type in an inorganic crystalline compound. This approach is demonstrated specifically for equilibrium intrinsic point defects in binary intermetallic compounds with the B2 crystal structure, but can be readily generalized to multicomponent intermetallic systems, as well as to semiconductors and insulators employing standard schemes for charged point defect calculations.4 Further, the approach described here provides a basis also for extending ML algorithms to non-equilibrium defect properties such as those related to diffusion in alloys.18
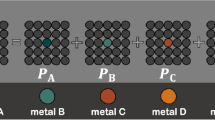
As mentioned above, we demonstrate the ML strategy for defect types in this work by focusing on the modeling of dominant intrinsic point defect types in intermetallic compounds displaying the simple cubic B2 crystal structure illustrated in Fig. 1. B2-structured intermetallics have been extensively researched for a range of applications, including as strengthening precipitates19,20,21 in advanced alloys, and as lightweight materials for high-temperature applications relevant to the aerospace industry22,23. Considering the B2 crystal structure for an AB compound (Fig. 1a) there are four types of point defects commonly observed: a vacancy on the A-type sublattice (VA) or on the B-type sublattice (VB), or antisite defects of A on the B sublattice (AB) or B on the A sublattice (BA). Self-interstitials will also form as an intrinsic point defect in B2 compounds, but in the present work, we assume their formation energies in the relatively close-packed B2 compound are significantly higher than those for vacancies or substitutional antisites, such that their concentrations will be sufficiently low so as not to influence the predicted dominant defect type. We thus focus on the antisites and vacancies in the present work. The equilibrium concentration of point defects, and which type is dominant (i.e., has the highest equilibrium concentration), is influenced by the temperature as well as the overall composition of the compound: for example a B2-AB compound that is slightly rich in A will tend to have either AB antisites or VB vacancies as a dominant defect type, and similarly for B-rich compositions, either BA antisites or VA vacancies are the possible dominant defects. When the vacancies form as the dominant defect to accommodate changes in composition, they are typically referred to as constitutional vacancies.
The interest in understanding whether a compound will form constitutional vacancies stems from the important role that these defects play in mechanisms governing atomic transport, which underlie high-temperature deformation and degradation processes. To our best knowledge, even for simple B2 intermetallics, the available experimental and computational data for their defect properties is still limited, while for ternary and quaternary system, the knowledge is even more limited. Due to the importance of identifying whether an intermetallic will intrinsically form high concentrations of vacancies, previous efforts have aimed to develop empirical rules to predict such tendencies in B2 compounds. Specifically, in the work by Neumann,24 based on data for 19 such compounds, it was shown that a threshold value of the compound formation enthalpy (ΔE f, the difference in energy between the ordered intermetallic compound and the concentrated weighted average of the energy of the constituent elemental solids) could be identified such that for ΔE f, more negative than −0.31 eV/atom, the material would form antisites as the dominant point defect type for both A and B rich compositions. This empirical relationship ends up with about 80 % classification accuracy for the 19 intermetallics considered, while the predictive accuracy beyond this data set has not been explored.
In what follows, we will classify B2 intermetallic compounds according to whether the vacancies are a dominant defect type at either A or B rich compositions, or whether the dominant defects are always of antisite type. We employed HT DFT and subsequent thermodynamic calculations to identify the dominant point defects for 100 B2-type compounds over a wide range of intermetallic chemistries. This established a minimal dataset with proper sampling size for subsequent data mining work.25 To classify the B2 compounds with respect to the dominant defects, we utilized three different ML models: a simple decision tree (DT) model and two models that utilize the gradient boosting technique. In the gradient boosting technique, the classification result is derived by combining a forest of DTs obtained in an iterative manner. While the performance of the DT model is found to be lacking, one of the gradient boosting classifiers with minimal model parameters resulted in a good fit and predictive accuracies. This gradient-boosted classifier is further used to predict the dominant defect types in other B2 compositions in order to explore trends across a broad range of chemistries.
Results and discussion
From the Materials Project database,26 100 B2-type intermetallic compounds (as listed in Supplementary Information (SI) Table 3) were first selected for high throughput defect property calculations. At a representative temperature T = 1000 K, the equilibrium defect concentrations in these B2-type intermetallic compounds were computed using the grand-canonical, dilute-solution thermodynamic formalism27 as implemented in PyDII28 for compositions deviating from stoichiometry by up to 1 %. The dilute solution formalism allows us to predict dominant defect types at off-stoichiometric compositions using DFT supercell calculations based on the ideal stoichiometry of the B2 compound (with only a single defect in each supercell calculation). The formalism is applicable to multicomponent and multisublattice intermetallics as well. The required DFT calculations were automated with a high throughput FireWorks29 workflow. Based on the dominant defects in the A and B rich compositions, the compounds are classified into two groups: those that contain vacancies as the dominant defect type at either A or B rich compositions (or both), and those for which the antisites are the dominant defects at both compositions. The classification of B2 compounds is illustrated in Fig. 1b. For example, Be–Ni having antisites as dominant defects in both composition regions are classified into the latter class, and both Al–Co (having Co vacancies as dominant defects in Al-rich compositions and Co antisites as dominant defects in Co-rich regions) and Al-Rh (having vacancies as the dominant defects in both composition regions) are grouped into the former class.
Our calculations indicate that among the one hundred compounds, half of them belong to the antisite dominant category (labeled with 0 in the defect-type classification (DTC) column of SI Table 3), in which antisite defects are the dominant ones in both off-stoichiometric composition (A-rich and A-poor) regions. The other half belong to non-antisite dominant type (labeled with 1 in the DTC column of SI Table 3), as vacancy defects are dominant in one side of off-stoichiometric composition region (41 compounds) or in both regions (9 compounds). Henceforth, based on these computational results, we established a basic B2-type intermetallic defect property database containing these 100 compounds, which was used to evaluate the empirical defect classification model developed by Neumann,24 as well as to construct new machine-learning models to explore the underlying DTC for B2 compounds.25
We first assessed the accuracy of Neumann's model in classifying the defect types. In this model, Neumann assumed a constant vacancy formation energy (ΔH v) of about 0.5 eV/atom for all intermetallics, which leads to the classification rule that the intermetallics with formation energy, ΔE f, less than −0.31 eV/atom exhibit antisite dominant defects, whereas those with ΔE f greater than −0.31 eV/atom will have non-antisite dominant defects. When tested against the 100 B2 compounds considered in the present calculations, Neumann's classification model yields an accuracy of 61 %. This accuracy is statistically a good improvement over the 50 % probable accuracy obtained with random guesses. The confusion matrix pertaining to Neumann's classification model displaying the number of correct and incorrect predictions in comparison with the DFT-based classifications in the database is shown in Fig. 2a. It can be noticed that this model is relatively more accurate in identifying the non-antisite dominant type B2 compounds (38 out of 50), whereas its performance is poor (23 out of 50) for the other type. Also, we find that Neumann’s model is biased towards non-antisite defects as it predicts 65 compounds belong to non-antisite dominant type.
To improve upon this model, we applied ML techniques on the computed data. The classification problem in ML is to construct an estimate of the function, which maps different properties associated with each compound to discrete values representing the possible classes of interest; in this case, the defect types. The input properties, called “descriptors” here were chosen from compound properties (CPs) and linear combinations of the constituent elemental properties (EPs). Most prior studies used either differences (denoted by Δ) between or averages (denoted by subscript ‘avg’) of the EPs as descriptors,30,31,32 while in this work we also considered the minimum and the maximum of the EPs as potential descriptors. The initial set of CPs and EPs used to generate the fit model, along with the corresponding univariate predictive powers (explained later) can be found in SI Table 1.
The minimum, maximum, average, and differences can be thought of as derived descriptors. The average and differences are the linear combinations of the initial set of descriptors. These in principle can be obtained from principle component analysis (PCA), however minimum and maximum type of derived descriptors are not obtainable from PCA. Derived descriptors are found to often generate significantly improved ML models for a broad set of applications.
According to Villars,33 the EPs used in machine-learning of intermetallics can be classified into five main groups related to atomic number, atomic size, electrochemical properties, valence electron properties, and cohesive energy properties. The EPs chosen for this work included one or more EPs from each of these five groups. Among these, we note that Mooser and Pearson used n av (the average of principle quantum numbers) and ΔX (difference in Pauling electronegativities) to evaluate the structural stability,30 and Miedema et al.31 developed \(\Delta {n}_{WS}^{\mathrm{1/3}}\) (difference in the cube roots of the electron densities at the Wigner–Seitz cell boundary) to predict the heat of formation. In addition to the EPs, we also considered a few CPs, such as alloy density, volume, and formation energy, which are simple to evaluate based on DFT calculations.
Many previous ML studies have been guided by heuristic approaches in scrutinizing the potential descriptor space, in order to include only the descriptors thought to be relevant to the prediction of the target property.32,34,35 For example, Kong et al. used 7 preselected descriptors to predict the crystal structure of AB2 compounds32 and Seko et al. used 23 preselected descriptors to predict the melting temperatures of binary solids.35 In this work, we made no attempt to make any a priori selection for these descriptors. However with only 100 data points, including all of them in the analysis would result in a very large model space and potentially reduced predictive accuracy. It becomes important to identify the appropriate descriptors to develop a reliable model with minimal data-sets.34
Dimensionality reduction—removing some descriptors before applying a given ML algorithm—is an important pre-processing step in many problems. For example, ML algorithms cannot distinguish between two nearly perfectly correlated descriptors. So, highly correlated descriptors should be removed (or averaged). PCA could be applied to identify projections of the descriptor data, which have the greatest variance and, therefore, possibly, the most information. The problem with this approach is that, because the outcome of interest is not taken into consideration, the projections found by PCA might be (nearly) orthogonal to the projections which are actually useful in predicting the outcome.
Two different techniques were therefore applied to reduce the number of descriptors passed to the classification schemes. One is Spearman’s’s correlation36 between pairs of descriptors and the other is based on the predictive value of individual descriptors as measured by the the Mann–Whitney–Wilcoxon (MWW) rank-sum statistic.37 In the first case, we attempted to identify sets of descriptors highly correlated with one another, allowing us to select one element from each set for possible inclusion in the fitted model with little or no reduction in predictive power. The distance between two potential descriptors was computed as \({d}_{ij}\mathrm{=1}-{\rho }_{ij}^{2}\), where ρ ij is the Spearman’s correlation between the two descriptors. This distance takes values in the range [0,1], with smaller values corresponding to higher correlation. Considering that classification trees and other tree-based regression methods used later in this work are invariant under monotone transformation of descriptors, this Spearman’s distance approach is well-suited to dimensionality reduction. The Spearman’s’s distance between any two potential descriptors, plotted in Fig. 3, reveals several correlated descriptors. Among descriptors that are strongly correlated with others based on computed Spearman’s correlation values, only one of them was selected for use in classification. For example, average Zunger pseudopotential radius (R Z,avg)38 and average atomic radius (R avg) are highly correlated. In this case only R avg was retained for future data mining. Likewise, differences in principle quantum numbers (Δn), atomic numbers (ΔZ), and Clementi effective nuclear charges (ΔZ eff)39 are also highly correlated, and thence only ΔZ was considered for further use.
The second technique is based on the Mann–Whitney–MWW rank-sum statistic (or corresponding p-value),37 which is computed by ranking the observations of a descriptor and then summing the ranks corresponding to the observations belonging to only one defect type (or the other). Very small or very large sums correspond to very little or no overlap between the descriptor distributions of the two defect types. A lack of overlap between the two distributions implies that the corresponding descriptor can be used to distinguish the defect types. Therefore, these descriptors can easily be ranked according to the value of their MWW statistic or, better yet, the corresponding p-value, with small values indicating that a certain descriptor is useful in discriminating between the two defect types. By ranking the descriptors in this way, we can eliminate those with the largest p-values; i.e. those descriptors that are less diagnostically useful than the others. The MWW rank sum values, shown in SI Table 1 for all the descriptors, suggest that the “minimal” or “maximal” types of various descriptors, together with “difference” types are the most predictive. Only in specific cases, “average” type of descriptors, carried along with “minimal” or “maximal” types of descriptors, are predictive. Therefore, descriptors that are the average of various EPs were dropped in favor of the maximum and minimum of the descriptors. The dimensionality reduction based on Spearman’s correlation and p-value analysis left us with 35 descriptors (listed in SI Table 2) for further data mining studies.
Based on the retained descriptors, we fitted a classification tree (described in detail in the Methods section) to the binary outcome of the dominant point defects type using the recursive partitioning routine rpart in R programming language.40 We also applied a 10-fold cross-validation to obtain unbiased estimates of the predictive accuracy of the fitted model. According to cross-validation, the optimal DT has three splits as shown in Fig. 4, with the corresponding three descriptors: the minimum of Miedema's electron density parameter \(({\rm{\min }}({n}_{{\rm{WS}}}^{\mathrm{1/3}}))\), formation energy per atom (ΔE f) and normalized difference in Allred electronegativity (ΔX A). The root classification rule in the DT is based on Miedema's electron density parameter, which is the cube root of elementary electron density at the Wigner–Seitz boundary, and is given as \({\rm{\min }}({n}_{{\rm{WS}}}^{\mathrm{1/3}})\,\ge \,1.45\). We classified all the metallic elements with the corresponding \({n}_{{\rm{WS}}}^{1/3}\) values (can be seen in SI Fig. S1) and found that almost all elements with \({n}_{{\rm{WS}}}^{1/3}\,\ge \,1.45\) are transition metal elements (except Be). This makes intuitive sense as the EPs of these transition metal elements are relatively similar and the formation of antisite defects (BA or AB) will be favored as it does not significantly change local intermetallic bonds in comparison with bond breaking status in vacancy defects. The next-level decision rule obtained from the classification, ΔE f ≥ −0.502 eV/atom, is based on the compound formation energy. This descriptor is the same as what was chosen by Neumann for his model. As shown in ref. 24, the nearest-neighbor interaction approximation gives rise to the estimation of antisite defect formation energy being proportional to ΔE f, where a larger magnitude of ΔE f corresponds to larger antisite defect formation energy, which tends to make the formation of vacancy defects energetically more favorable. The last classification rule based on elementary electronegativity difference between A and B is given as ΔX A ≥ −0.68. This also agrees with intuitive assumptions that a smaller elementary electronegativity difference corresponds to relatively similar properties between the two compositional elements and thus antisite defects may be more preferred. Overall, we can see that the classification rules proposed in this DT model are in general consistent with intuitive assumptions and analytical approaches.
The accuracy of the aforementioned DT model was again evaluated with computed defect types of these 100 compounds. The confusion matrix of the DT model is presented in Fig. 2b. In contrast to Neumann’s model, the DT model exhibits a bias towards antisite dominant type prediction, as it predicts 59 compounds to be antisite dominated, and the remaining 41 compounds to be non-antisite dominant types. This DT model correctly predicts antisites as the dominant defects in 45 out of the 59 compounds, indicating a 76 % accuracy on predicting this type, while for the non-antisite dominant type, the model correctly predicted 36 compounds, indicating a 87 % accuracy. For the other 14 antisite dominant and 5 non-antisite dominant compounds, this DT model yielded the opposite (wrong) predictions. Overall, this DT classifier correctly classified the defect types with 81 % accuracy.
Unfortunately, while a single DT may be easy to interpret and use, it tends to be unstable, with small changes in the input data set producing large changes in the fitted tree. To ameliorate this and other problems, we considered models based on large collections of trees. There are several techniques for producing these collections but the one we used is based on “gradient boosting”.41 Another technique, which also produces a collection of trees, called bagging41 was recently used by Meredig et al. to predict formation energies.42 The gradient boosting technique, fits trees of fixed depth, one after the next; first, to the observed data, and then to the residuals from the previous step. In this way, the observed prediction error decreases as each new tree is added to the fitted model, where k-fold cross-validation is used to compute unbiased estimates of the prediction error as a function of the total number of trees in the fitted model. The model with the lowest estimated prediction error is finally selected as the optimal classifier.
In order to obtain a better model with improved predictive accuracy, we applied the gradient boosting technique to generate a MART model. Again, 10-fold cross-validation was used for model selection and prediction accuracy estimation. The generated MART model using all the 35 descriptors is called full MART (f-MART), being composed of 997 DTs. It has a fit accuracy of 94 % as shown by the confusion matrix given in Fig. 2c and a predictive accuracy of 71 %. This f-MART model, though being relatively accurate, may suffer from some critical problems. In particular, gradient boosting assigns a value to each descriptor included in the model, which measures that descriptor's influence on the model. This assesses the magnitude of the effect that small changes in each descriptor may bring to the final predictions of the model: the higher the number is, the more important the corresponding descriptor is to yield accurate predictions. When the influence of the 35 descriptors on the f-MART model was examined, we found many descriptors, e.g. min(X) and Δn, have relatively small influence (≤1 %) on the predictive accuracy of the f-MART model. Besides, larger number of descriptors passed to the fitting procedure may give rise to higher variance in the MART model, i.e. less stability. In addition, using a large number of descriptors relative to the training set can lead to overfitting, where the developed model becomes too tailored to the input sample. An overfitted model can perform poorly against compounds not used in the generation of the model, despite high accuracies obtained during model generation. By limiting the input descriptors to the MART model, more stable and accurate models can often be produced.
In this context, we limited the descriptors in the f-MART model using the “influence trimming” approach, where low-influence descriptors were removed iteratively such that at each step, the descriptor with the lowest relative influence factor was removed, the model was refitted and the relative influence factor of remaining descriptors was recalculated. We carried out this procedure until further iteration would result in a model with less accuracy in comparison with the previous ones. The resulting MART model, called r-MART, is comprised of 2496 trees and retains only six descriptors. The confusion matrix for the r-MART model is given in Fig. 2d, and it shows that the r-MART model has a fit accuracy of 98 % and predictive accuracy of 75 %. In comparison with the f-MART model, both fit and predictive accuracies are improved. In particular, the r-MART model correctly classifies 49 B2 compounds as antisite dominant and the other 49 ones as non-antisite dominant intermetallics, except the two alloy systems, i.e. RuAl and PdBe. It is also encouraging that the r-MART model does not exhibit any bias in classification, in contrast to what has been observed in both Neumann's and the simple DT models.
The systems for which the predictions of ML models do not agree with the outcomes from the DFT calculations are given in SI Table 4. It can be noticed that all three models wrongly predict the dominant defects in BePd. Both the f-MART and DT models wrongly predict the dominant defects in LiAg, TiFe, and NiZn.
To validate that the r-MART model is not biased by the input set of B2 intermetallic compounds, the accuracy of the r-MART is tested against fourteen additional B2 intermetallics (given in SI Table 5) that are not used in the generation of the model. For the selected fourteen compounds, DFT calculations were performed to determine the dominant defect types and the DFT computed dominant defect types are compared with the r-MART predictions. For 11 of the 14 compounds, r-MART predictions match with the results from DFT calculations giving a success rate of 78.6 %, which is in agreement with the 75 % predictive accuracy estimated from the 10-fold CV.
The six descriptors retained in the r-MART model and corresponding relative influence factors are given in Table 1. Within these six descriptors, all the five main groups of EPs as defined by Villars33 are represented. Among these six descriptors, the two descriptors present in the top nodes of the DT classifier in Fig. 4, ΔE f and \({n}_{\text{WS},\,\min }^{\mathrm{1/3}}\), are also having the two largest influence factors of 22.89 and 12.37 %, respectively. However, the third descriptor ΔX A in the DT classifier is replaced by ΔR Z, max(Z), \(\Delta {n}_{{\rm{WS}}}^{1/3}\), and X A,max in the r-MART model. This shows that the r-MART model, instead of being completely different from the simpler DT model, can be considered as a refinement over the DT model. The presence of \(\Delta {n}_{{\rm{WS}}}^{1/3}\) and ΔR Z in the r-MART model implies that the differences in the electronic properties and the sizes of the constituent elements affect the nature of the dominant defects. It can also be understood that max(Z) and X A,max are partitioning the chemical space similar to \({n}_{\text{WS},\,\min }^{\mathrm{1/3}}\) and ΔE f. As a whole, the r-MART model can be thought of as a function that maps a complex combination of chemical space partitioning and electronic and size differences between the constituent elements to the dominant defects in the B2 intermetallics.
The occurrence of ΔE f and \({n}_{\text{WS},\,\min }^{\mathrm{1/3}}\) in both the DT and the r-MART as the two most influential descriptors suggests that the DT model can be used as a physically intuitive first order approximation for defect classification with reasonable confidence.
It is worth noticing that the three descriptor DT model and the f-MART model with its 35 descriptors are both sensitive to any errors or biases in the input data for the different reasons listed earlier. On the other hand, the r-MART model containing only six descriptors is a more robust model, and any small deviations in the training set should not significantly affect the prediction power of the r-MART model generated.
Taking advantage of its stability and predictive power, we considered next the application of the r-MART model for predicting the defect behaviors of other possible B2 compounds. Here, a total of 44 common metallic elements were chosen to form possible B2 composition space. It can be seen that the present prediction covers (44 × 43)/2 = 946 B2 compounds. Instead of performing relatively time-consuming defect property computations, the unit cells of the rest of B2 compounds, 946−100 = 846 in number, were simply optimized with DFT to obtain the formation energies, ΔE f , and the resulting formation energy values were fed to the current r-MART model to predict their defect behavior. It should be noted that a comparison of the ΔE f values with those for other compounds in the same systems in the Materials Project database42 shows that only 44 of the systems form stable B2 intermetallics, as indicated in Fig. S2 in the SI. The predictions for the remainder of the systems are still relevant in the sense that compounds that are not on the ground-state hull can become stabilized at finite temperatures, or they can form as metastable phases in materials processing.
The final prediction of the r-MART model, and its comparison with the DTC based on DFT calculations for the 100 calculated compounds are illustrated in Fig. 5. It can be seen that, among all compounds considered here, 525 compounds are predicted to be the antisite dominant type and the other 421 compounds are classified as the non-antisite dominant type. For the compounds consisting of only transition metal elements, 305 out of 378 compounds (81 %) are predicted to be antisite dominant defect types, which is consistent with the trend drawn from the classification rule derived from the DT model.
Figure 5 affords us to understand why the ML models failed for the systems listed in SI Table 4. The failure systems are located at either the top central region or in the lower middle region. The dominant defect types rapidly change in the top central region, and the lower middle region contains the complex shaped boundary separating the regions that contain antisite forming compounds with those that form vacancies. Making predictions near a boundary/transition is inherently difficult. While the MART models are able to capture these high frequency variations to a maximum extent, DT model is not up to the task. The failure systems of the f-MART and r-MART models also lie in the same regions. Higher number of failures in f-MART model can be ascribed to overfitting.
We would like to note that the methods and the approach presented here are quite general and can be adapted for various scenarios. The MART models presented here can be used for both regression as well as classification, which makes them a suitable choice to predict other properties of materials that are computationally intensive.
The dilute solution model is applicable to multi-component systems with arbitrary crystal structure. By combining the flexibility of the dilute solution model with the ML models based on DTs, which are additive, one could extend the model to include all binary systems by computing similar models for other binary compounds with different crystal structures (phases) and combine the generated models into a single model with a crystal structure-based root-node partition at the top. Due to the above mentioned advantages, we believe the approach presented here would be particularly powerful when applied over much larger ternary and quaternary configurational space. For compositions that go beyond the dilute deviations from the stoichiometric compositions of various phases, where phase stability and structural variations need to be accounted for, for situations involving concentrated disorder, other models that account for defect-defect interaction such as special quasirandom structures approach should be applied.43
An interesting extension of the proposed approach would be to predict the dominant defects over a broader range of temperatures. Calculating the point defect concentrations at different temperatures is straightforward with the thermodynamic formalisms employed here. The results for different temperatures could be incorporated into a unified model using temperature as an additional descriptor during the ML model building stage. Another interesting extension of the work would be the prediction of the site preferences of the ternary solutes, such as those added to improve low-temperature ductility in intermetallic compounds.44 In binary B2 intermetallics, the solute atom can occupy either of the two B2 sublattices. By ordering the sublattices based on the property of the native element of the sublattice, such as atomic number, atomic weight, or Mendeleev number, the site preference of solutes in different intermetallics could be converted to a binary form (0/1) in a consistent manner. These binary outcomes enable development of simple yet robust ML models for solute site preference in intermetallics in a manner similar to that employed in the present work. For compounds exhibiting a different structure (i.e., beyond the B2 structure), additional properties such as elemental composition, site multiplicity and site coordination number are appropriate as descriptors to the ML models.
Conclusions
In this work, we demonstrated an approach combining the high throughput DFT calculations with ML algorithms to predict dominant defect types in inorganic compounds. The approach was illustrated for the specific case of binary intermetallic compounds with the cubic B2 crystal structure. We computed intrinsic point defect properties for 100 B2 intermetallics using a recently developed python tool for high throughput density functional theory computations of dominant defect types. We subsequently classified the compounds into two categories: antisite or non-antisite defect dominating intermetallics, depending on the dominant defects in off-stoichiometric regions. Neumann's classification model, the only empirical model available for identifying the dominant defects, when assessed with this data set, shows a 61 % accuracy. To develop classification schemes with better accuracy and understand the underlying principles, we applied ML techniques on the computed data. In particular, with a simple binary DT- based classification scheme we obtained a better fit accuracy of 81 %. Besides the formation energy, ΔE f, used in Neumann's model, two additional descriptors, \({\rm min}({n}_{WS}^{\mathrm{1/3}})\) and ΔX A, are found to be relevant for predicting the defect types more accurately in the developed tree-based classification scheme. We further introduced the MART classification models, and through iterative removal of low-influence descriptors, we established a robust r-MART model with only six descriptors, which yields a much higher fit accuracy (98 %) and prediction accuracy (75 %). The ML methods presented here are quite general and can be used for either classification or regression of other properties of interest in materials. Finally, the power of this predictive model is applied to classify the defect type of the other 846 possible B2 compounds as shown in Fig. 5. The approach presented here can be extended to multicomponent and multisublattice intermetallics, where the configuration space is much larger than that considered here, as well as to charged point defects in semiconducting and insulating compounds.
Methods
Defect concentrations in a grand-canonical dilute-solution formalism
The intrinsic point defect properties in B2 intermetallic compounds were evaluated using the computational framework recently implemented in the python code PyDI.I 28 This framework uses the grand-canonical, dilute-solution thermodynamic formalism described in Ref. 27 to predict intrinsic point defect concentrations in ordered intermetallic compounds as a function of temperature and composition deviating slightly from stoichiometry. In this formalism, defect concentrations and therefore dominant defect types can be computed at off-stoichiometric compositions using DFT calculations for supercells based on the ideal stoichiometric compound, with only a single defect present. In the present work, we computed the point-defect concentrations at the temperature of 1000 K, and limited the composition ranges to +\−1 % around the stoichiometric 50/50 composition. The resulting defect concentrations are much lower than those required for the B2 intermetallic compounds to form a solid-solution phase. For both concentration regions, i.e. A-poor (B-rich) and A-rich (B-poor), the dominant defect type, which can be either vacancy or antisite, are identified. In the remainder of this section, we briefly review the computational formalism.
For binary B2-type intermetallic compounds, with the crystal structure shown in Fig. 1a, each site p in the structure can be occupied by one of two atom types (A or B) or a vacancy. The occupation at each site is denoted by a local concentration variable c i (p) which takes a value of 1 if atom type i is at site p and zero otherwise. In the current application, i = 1 or 2 denotes atom of type A or B, respectively. For a stoichiometric, perfectly ordered B2 structure, \({c_1(p)\equiv c_i^0(p)=1}\) for all sites p on the A-type sublattice, and zero otherwise, and \({c_2(p)\equiv c_2^0(p)=1}\) for all sites p on the B-type sublattice, and zero otherwise. More generally, for a compound at finite temperature of off stoichiometry, the values of c i (p) will differ from the values \({c}_{i}^{0}(p)\) due to the presence of nonzero equilibrium point defect concentrations, and the total number of atoms of type i, N i, is given by the following sum: \({N_{\rm i}={\sum }_{p=1,2}{c}_i(p)}\). The overall mole fraction of atoms of type B is then defined as x 2 = N 2/(N 1 + N 2), and similarly for the mole fraction of species 1 (x 1 = 1−x 2).
In the dilute-solution model, a first-order low-temperature expansion of the grand potential, Ω, yields
Here, E 0 denotes the ground-state energy for a perfectly ordered stoichiometric B2 compound, μ i is the chemical potential of element i, k B is Boltzmann's constant and T is temperature. The variable ε in the second sum for the third term on the right hand side of Eq. (1) denotes a possible point defect (i.e., an antisite or vacancy) leading to an energy change δE ϵ(p) and change in the site occupation variables \(\delta {c}_{i}^{\varepsilon }\). Following the terminology used in ref. 27, hereafter, δE ϵ(p) and \(\delta {E}^{\epsilon }(p)-{\sum }_{i}{\mu }_{i}\delta {c}_{i}^{\epsilon }(p)\) will be referred to as defect “excitation energy” and defect formation energy, respectively. From Eq. (1), the following relation can also be derived:
where 〈c i (p)〉 denotes the ensemble averaged concentration of element i at site p; note that by symmetry 〈c i (p)〉 will be equal for all sites p belonging to a given sublattice. For any composition, by specifying the mole fractions between the two constituent elements and by setting the grand-potential Ω in Eq. (1) equal to zero (corresponding to thermodynamic equilibrium relative to the number of lattice sites under zero stress conditions), we obtain the two equations needed for determining the chemical potentials of the two elements in a B2 compound. Substituting the resulting chemical potentials into Eq. (2) yields the equilibrium defect concentrations for a given temperature and input values of chemical potentials (which determine the overall composition of the alloy).
Density functional theory (DFT) calculations
Periodic supercells were used to compute the defect energies arising in Eqs. (1) and (2). In this approach, the defect excitation energy, δE ϵ(p), for either an antisite or a vacancy defect is given by
where \({E}_{{\rm{def}}}^{\epsilon }(p)\) is the energy of the supercell with defect ϵ at site p, and E 0 is the energy of the non-defected bulk supercell. Bulk and defect supercells were generated with PyDII28 from the optimized structures in the Materials Project database.26
The energies of supercells were computed within the framework of DFT using the Vienna ab initio simulation package.45,46,47 We used the projector augmented wave method48,49 and the Perdew, Burke and Ernzerhof50 generalized-gradient approximation (GGA) for the exchange-correlation functional. For all the calculations, a cut-off value of 520 eV was used for plane-wave basis set. Spin polarization with ferromagnetic spin ordering was considered as the starting point for all calculations. Based on our tests (the details are presented in SI Table 6), accounting for anti-ferromagnetic ordering for those systems where it was energetically favorable, did not lead to changes in the predictions for the dominant DTC.
The defect supercells were optimized by relaxing the atomic positions at constant volume until the individual forces on each atom were minimized to be less than 0.01 eV/Å. Based on convergence tests of defect energies with respect to supercell size and k-point sampling mesh, we used 4 × 4 × 4 B2 supercells (128 atoms) with 4 × 4 × 4 Monkhorst-Pack k-point grid for all calculations. We tested the influence of the supercell size on dominant DTC by computing the defect energetics of five B2 systems for different supercell sizes given in SI Table 7. The selected five systems are on ground state hull, and have large size differences between the host atoms which helps us to check the effect of strain-induced interactions. In the compounds considered, the difference in the excitation energies of a defect in 4 × 4 × 4 supercell and the corresponding defect in larger 6 × 6 × 6 supercell was found to be much less than the differences in the excitation energies of the defects. As an example, composition-dependent defect concentrations in ScPt for the different supercell sizes listed in SI Table 7 are plotted in SI Fig. S3. In all the systems considered, the dominant defect types have been found to remain unaffected by increasing the supercell size beyond the 4 × 4 × 4 setting used in this study. The first-order Methfessel Paxton method51 with a smearing width of 0.2 eV was used for electronic smearing.
Machine learning: Decision trees
To predict the defect types of B2 intermetallics, we developed three classifiers, each of which uses binary DTs41 as base learners. A binary DT is a function which maps descriptors X ≡ {x i } to classes {c}, which, in our case, take only two values (c = 0 or 1): antisite or non-antisite types. The key advantage of tree-based classification schemes is their interpretability, because each non-leaf node in the tree corresponds to answering a simple question of the form “is x i ≤ s?”, where s is some value in the domain of x i. If the answer to this question is yes, then one looks at the question posed by the left-hand child node, assuming it is not a leaf, and if the answer to the question is no, then one looks at the question posed by the right-hand child node. Final predictions are simply read from the leaf nodes, where each one specifies either c = 0 or c = 1.
Mathematically, each node m of the classification tree represents a subset of the descriptor space X m which contains N m data points and the corresponding outcomes, \(\{{y}_{m1},\ldots ,{y}_{m{N}_{m}}\}\). Taking I(y i = c) = 1 if i th observation, y i , is of class c and 0 otherwise, we can define
to be the proportion of class c observations in node m. The data points in node m are then assigned to the majority class \({c}^{\ast }={{\rm{argmax}}}_{c}\,{\hat{p}}_{m,c}\). Recursive partitioning is used to construct DTs. Starting with the root node, which contains the entire data set, the data at each node is split by splitting descriptor x j at a split point s j such that the resulting partition defines two child nodes, m1 and m 2, whose descriptor data is given by
The objective at each node is to engineer the split such that the child nodes are as homogeneous as possible. This homogeneity can be measured in various ways, including entropy, the so-called Gini index (which is another measure of entropy), and (raw) classification error. The splitting is stopped when any one of the following criteria is met: (a) no descriptor can be found which produces a useful split of the data, in which case splitting really cannot continue; (b) there are fewer than some number of observations in the current node—here, we use the number of 6; (c) the tree has reached a pre-specified depth so as to minimize overfitting. To avoid overfitting, k-fold cross-validation is used to identify the tree with the lowest estimated prediction error.
References
Carling, K. et al. Vacancies in metals: from first-principles calculations to experimental data. Phys. Rev. Lett. 85, 3862–3865 (2000).
Nguyen-Manh, D., Horsfield, A. P. & Dudarev, S. L. Self-interstitial atom defects in bcc transition metals: Group-specific trends. Phys. Rev. B 73, 020101 (2006).
Ding, H., Razumovskiy, V. I. & Asta, M. Self diffusion anomaly in ferromagnetic metals: a density-functional-theory investigation of magnetically ordered and disordered Fe and Co. Acta Mater. 70, 130–136 (2014).
Freysoldt, C. et al. First-principles calculations for point defects in solids. Rev. Mod. Phys. 86, 253–305 (2014).
Angsten, T., Mayeshiba, T., Wu, H. & Morgan, D. Elemental vacancy diffusion database from high throughput first-principles calculations for fcc and hcp structures. New J. Phys. 16, 015018 (2014).
Medasani, B., Haranczyk, M., Canning, A. & Asta, M. Vacancy formation energies in metals: a comparison of MetaGGA with LDA and GGA exchangecorrelation functionals. Comput. Mater. Sci. 101, 96–107 (2015).
Morgan, D., Ceder, G. & Curtarolo, S. High throughput and data mining with ab initio methods. Meas. Sci. Technol. 16, 296–391 (2004).
Jain, A. et al. A high throughput infrastructure for density functional theory calculations. Comput. Mater. Sci. 50, 2295–2310 (2011).
Jain, A., Shin, Y. & Persson, K. A. Computational predictions of energy materials using density functional theory. Nat. Rev. Mater 1, 15004 (2016).
Mueller, T., Kusne, A. & Ramprasad, R. In Reviews in Computational Chemistry, Vol 29 (eds Parrill, A. L. & Lipkowitz, K. B.) Ch. 4 (John Wiley & Sons, Inc, 2015).
Hautier, G., Fischer, C. C., Jain, A., Mueller, T. & Ceder, G. Finding natures missing ternary oxide compounds using machine learning and density functional theory. Chem. Mater. 22, 3762–3767 (2010).
Rupp, M., Tkatchenko, A., Müller, K. R. & Von Lilienfeld, O. A. Fast and accurate modeling of molecular atomization energies with machine learning. Phys. Rev. Lett. 108, 058301 (2012).
Meredig, B. & Wolverton, C. A hybrid computational-experimental approach for automated crystal structure solution. Nat. Mater. 12, 123–127 (2013).
Isayev, O. et al. Materials cartography: representing and mining materials space using structural and electronic fingerprints. Chem. Mater. 27, 735–743 (2015).
Simon, C. M., Mercado, R., Schnell, S. K., Smit, B. & Haranczyk, M. What are the best materials to separate a xenon/krypton mixture?. Chem. Mater. 27, 4459–4475 (2015).
Pilania, G., Gubernatis, J. E. & Lookman, T. Classification of octet AB-type binary compounds using dynamical charges: a materials informatics perspective. Sci. Rep. 5, 17504 (2015).
Ward, L. et al. A general-purpose machine learning framework for predicting properties of inorganic materials. npj Comput. Mater. 2, 16028 (2016).
Choudhury, S. et al. Ab-initio based modeling of diffusion in dilute bcc FeNi and FeCr alloys and implications for radiation induced segregation. J. Nucl. Mater. 411, 1–14 (2011).
Choe, H. & Dunand, D. C. Synthesis, structure, and mechanical properties of Ni--Al and Ni-Cr-Al superalloy foams. Acta Mater. 52, 1283–1295 (2004).
Teng, Z. et al. Characterization of nanoscale nial-type precipitates in a ferritic steel by electron microscopy and atom probe tomography. Scr. Mater 63, 61–64 (2010).
Song, G. et al. Ferritic alloys with extreme creep resistance via coherent hierarchical precipitates. Sci. Rep. 5, 16327 (2015).
Subramanian, P., Mendiratta, M. & Dimiduk, D. The development of Nb-based advanced intermetallic alloys for structural applications. JOM 48, 33–38 (1996).
Clemens, H. & Smarsly, W. Light-weight intermetallic titanium aluminides-status of research and development. Adv. Mat. Res. 278, 551–556 (2011).
Neumann, J. On the occurrence of substitutional and triple defects in intermetallic phases with the B2 structure. Acta Metall. 28, 1165–1170 (1980).
Steinberg, D. Rules of thumb when working with small data samples. https://www.salford-systems.com/blog/dan-steinberg/rules-of-thumb-when-working-with-small-data-samples. Accessed: 29 June 2016.
Jain, A. et al. Commentary: the materials project: a materials genome approach to accelerating materials innovation. APL Mater 1, 011002 (2013).
Woodward, C., Asta, M., Kresse, G. & Hafner, J. Density of constitutional and thermal point defects in L12 Al3Sc. Phys. Rev. B 63, 094103 (2001).
Ding, H. et al. PyDII: a python framework for computing equilibrium intrinsic point defect concentrations and extrinsic solute site preferences in intermetallic compounds. Comput. Phys. Commun. 193, 118–123 (2015).
Jain, A. et al. Fireworks: a dynamic workflow system designed for high throughput applications. Concurr. Comput. 27, 5037–5059 (2015).
Mooser, E. & Pearson, W. B. On the crystal chemistry of normal valence compounds. Acta Crystallogr. 12, 1015–1022 (1959).
Miedema, A. R., Boom, R. & Boer, F. R. D. On the heat of formation of solid alloys. J. Less-Common Met 41, 283–298 (1975).
Kong, C. S. et al. Information-theoretic approach for the discovery of design rules for crystal chemistry. J. Chem. Inf. Model. 52, 1812–1820 (2012).
Villars, P. In Intermetallic Compounds, Vol. 1, Crystal Structures of (eds Westbrook, J. C. & Fleischer, R. L.) Ch. 1 (Wiley, 2000).
Pilania, G., Gubernatis, J. E. & Lookman, T. Structure classification and melting temperature prediction in octet ab solids via machine learning. Phys. Rev. B 91, 214302 (2015).
Seko, A., Maekawa, T., Tsuda, K. & Tanaka, I. Machine learning with systematic density-functional theory calculations: application to melting temperatures of single- and binary-component solids. Phys. Rev. B 89, 054303 (2014).
Spearman, C. The proof and measurement of association between two things. Am. J. Psychol. 15, 72–101 (1904).
Mann, H. B. & Whitney, D. R. On a test of whether one of two random variables is stochastically larger than the other. Ann. Math. Statist 18, 50–60 (1947).
Zunger, A. Systematization of the stable crystal structure of all AB-type binary compounds: a pseudopotential orbital-radii approach. Phys. Rev. B 22, 5839–5872 (1980).
Clementi, E. & Raimondi, D. L. Atomic screening constants from scf functions. J. Chem. Phys. 38, 2686–2689 (1963).
R Development Core Team. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing: Vienna, Austria, 2008. ISBN 3-900051-07-0, http://www.R-project.org/.
Hastie, T., Tibshirani, R. & Friedman, J. The Elements of Statistical Learning, 2nd edn (Springer, 2013).
Meredig, B. et al. Combinatorial screening for new materials in unconstrained composition space with machine learning. Phys. Rev. B 89, 094104 (2014).
Jiang, C., Chen, L.-Q. & Liu, Z.-K. First-principles study of constitutional point defects in B2 NiAl using special quasirandom structures. Acta Mater. 53, 2643–2652 (2005).
Jiang, C. Site preference of transition-metal elements in B2 NiAl: A comprehensive study. Acta Mater. 55, 4799–4806 (2007).
Kresse, G. & Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 47, 558–561 (1993).
Kresse, G. & Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metal21amorphous-semiconductor transition in germanium. Phys. Rev. B 49, 14251–14269 (1994).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Methfessel, M. & Paxton, A. T. High-precision sampling for brillouin-zone integration in metals. Phys. Rev. B 40, 3616–3621 (1989).
Acknowledgements
This work was intellectually led by the Department of Energy (DOE) Basic Energy Sciences (BES) program—the Materials Project—under Grant No. EDCBEE. This research used resources of the National Energy Research Scientific Computing Center, which is supported by the Office of Science of the U.S. Department of Energy under Contract No. DEAC02-05CH11231.
Author contributions
M.A., M.H., A.C., and K.A.P. conceived the research and provided guidance. B.M., H.D., and W.C. performed simulations of material properties. A.G. and B.M. performed ML analysis. B.M., H.D., A.G., and M.A. wrote the paper. All authors analyzed the results and revised the paper.
Competing interests
The authors declare that they have no conflict of interest.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Medasani, B., Gamst, A., Ding, H. et al. Predicting defect behavior in B2 intermetallics by merging ab initio modeling and machine learning. npj Comput Mater 2, 1 (2016). https://doi.org/10.1038/s41524-016-0001-z
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-016-0001-z