Abstract
A nonvolatile optical phase shifter is a critical component for enabling the fabrication of programmable photonic integrated circuits on a Si photonics platform, facilitating communication, computing, and sensing. Although ferroelectric materials such as BaTiO3 offer nonvolatile optical phase shift capabilities, their compatibility with complementary metal-oxide-semiconductor fabs is limited. Hf0.5Zr0.5O2 is an emerging ferroelectric material, which exhibits complementary metal-oxide-semiconductor compatibility. Although extensively studied for ferroelectric transistors and memories, its application to photonics remains relatively unexplored. Here, we show the optical phase shift induced by ferroelectric Hf0.5Zr0.5O2. We observed a negative change in refractive index at a 1.55 μm wavelength in a pristine device regardless of the direction of the applied electric field. The nonvolatile phase shift was only observed once in a pristine device. This non-reversible phase shift can be attributed to the spontaneous polarization within the Hf0.5Zr0.5O2 film along the external electric field.
Similar content being viewed by others
Introduction
Silicon (Si) photonics have experienced remarkable advancements over the past two decades, playing a pivotal role in facilitating the exponential growth of optical fiber communication traffic1,2. This progress has led to an exponential increase in the integration capacity of optical elements on a Si photonic integrated circuit (PIC), fueling expectations for the development of programmable PICs, catering to not only optical communication but also computing and sensing applications3,4,5,6,7,8. An essential component in reconfiguring the functionality of a programmable PIC is the optical phase shifter. This component plays a crucial role in adjusting the phase of a light signal as it propagates through an optical waveguide. In the context of a Si programmable PIC, the thermo-optic (TO) phase shifter is the most commonly used type of optical phase shifter. While the TO phase shifter has a simple structure and can be easily integrated, its drawback lies in its large power consumption, which poses challenges for large-scale integration9. However, alternative approaches have been explored to address this issue. Low-power and low-loss optical phase shifters have been fabricated using III-V/Si hybrid integration10, micro-electro-mechanical systems (MEMS)11, ferroelectrics12,13,14,15, phase change materials16,17, 2D materials18,19, and piezoelectric actuation20. Among these alternatives, the optical phase shifter based on ferroelectric BaTiO3 shows promise, particularly owing to its low-loss, nonvolatile operation driven by an external electric field12,13. The nonvolatile nature of the BaTiO3-based phase shifter allows for zero static power consumption and simplification of electric wiring through a crossbar configuration21. Moreover, the non-volatility of a phase shifter is essential for an energy-efficient deep learning accelerator based on a programmable PIC utilizing an in-memory computing architecture, which helps overcome the von Neumann bottleneck22. However, a challenge arises with BaTiO3, as it is incompatible with the complementary metal-oxide-semiconductor (CMOS) process, making it difficult to fabricate BaTiO3-based optical phase shifters in CMOS fabs. Hence, there is a strong desire for a CMOS-compatible ferroelectric material.
In this work, we investigate the nonvolatile optical phase shift in orthorhombic Hf0.5Zr0.5O2 (HZO), which was first reported to exhibit ferroelectricity in 201123,24,25. Since HfO2-based ferroelectrics are CMOS-compatible, a wide variety of electron devices such as ferroelectric transistors and ferroelectric memories have been investigated intensively26,27. However, the optical properties of HfO2-based ferroelectrics have not been fully explored yet28,29,30. Therefore, it is of utmost importance to evaluate the refractive index change induced by the electric field in ferroelectric HZO, as it has the potential to be applied as a CMOS-compatible Si optical phase shifter.
Results
Device structure and fabrication
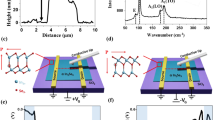
To evaluate the electric-field-induced refractive index change in HZO, we prepared a SiN optical waveguide surrounded by HZO (10 nm)/Al2O3 (1 nm) stacks (See Methods and Supplementary Fig. S1a and S1b) with a Mach–Zehnder interferometer (MZI), as shown in Fig. 1a, b. The SiN waveguide operating at a 1.55 μm wavelength was fabricated on a thermally oxidized Si wafer. The ferroelectricity in HZO reaches its maximum when crystalizing at a film thickness of 10 nm31. To enhance the overlap between the confined light in the waveguide and the HZO layers, we stacked 10 nm-thick HZO films in three cycles with 1 nm-thick Al2O3 interlayers by atomic layer deposition (ALD) so that the total ferroelectric thickness achieves 30 nm while each 10 nm-thick layer is separately crystallized32. The Al2O3 interlayer induces the generation of oxygen vacancies in the HZO layers, thereby promoting the HZO layers to exhibit ferroelectric behavior33, in conjunction with the stress-induced crystallization of the HZO layers by TiN capping34. Note that annealing temperature of 400 °C for achieving ferroelectricity of HZO is much lower than the maximum temperature of the front-end-of-line (FEOL) process for CMOS transistors. Therefore, there are no major difficulties in integrating HZO into the FEOL process, as reported in ref. 35. While we anticipate that increasing the number of cycles will augment the refractive index change and potentially reduce device length, achieving robust ferroelectric behavior might require meticulous process optimization. A bias voltage was applied to generate a horizontal electric field across the waveguide, as shown in Fig. 1b. Figure 1c shows a plan view of the fabricated SiN waveguide devices. We prepared an asymmetric Mach-Zehnder interferometer (AMZI) with 4.5 mm-long phase modulators, enabling us to evaluate the phase shift through the resonance wavelength peak shift in the transmission spectrum of the AMZI. To evaluate the change in optical loss with respect to the application of a bias voltage, we also prepared straight optical phase modulators. We also fabricated samples with a nonferroelectric HfO2 or SiO2 cladding layer as references (See Supplementary Fig. S1c and S1d). The width of the SiN waveguide was designed to be 1.2 μm for a single-mode operation (See Supplementary Fig. S2). The multimode interference couplers employed in AMZIs and the grating couplers for fiber coupling were designed for the transverse-electrical (TE) mode of the SiN waveguide (See Supplementary Fig. S2e and S2f).
a 3D view of a Mach-Zehnder interferometer based on a SiN waveguide with Hf0.5Zr0.5O2-based optical phase shifters. Al electrodes are formed for applying an electric field to Hf0.5Zr0.5O2. b Cross-sectional structure of the optical phase shifter with Hf0.5Zr0.5O2/Al2O3 stacks deposited on a SiN waveguide. An external electric field is applied along the transverse direction through the Al electrodes. c Plan-view microscopy image of the fabricated device. An AMZI and straight waveguides with grating couplers are prepared for optical phase and loss evaluation. d Cross-sectional TEM image of the SiN waveguide with Hf0.5Zr0.5O2/Al2O3 stacks. e Phase map of the Hf0.5Zr0.5O2 layers.
Figure 1d presents a cross-sectional transmission electron microscopy (TEM) image of the SiN waveguide with the conformally deposited HZO/Al2O3 layers. Magnified TEM images clearly revealed three polycrystalline HZO layers separated by Al2O3 interlayers (See Supplementary Fig. S3). Automated crystal orientation mapping in transmission electron microscopy (ACOM-TEM)36 with a precession electron diffraction angle of 0.5° was conducted to analyze the phase and orientation of the polycrystalline HZO layers, as depicted in Fig. 1e. We found that the majority of the HZO layers on the top and sidewalls of the SiN waveguide were in the orthorhombic crystal phase, which exhibits ferroelectric properties. Since the thickness of each Al2O3 layer is only 1 nm, which is significantly smaller than the operating wavelength, the influence of the presence of the Al2O3 layers on the waveguide property is negligible.
Ferroelectric properties
First, we evaluated the properties of the HZO/Al2O3 stacks prepared on a Si substrate, as shown in Fig. 2. To evaluate the crystallinity of the poly HZO/Al2O3 stacks, we performed grazing-incidence X-ray diffraction, as shown in Fig. 2a. An orthorhombic phase or rhombohedral phase is expected for ferroelectric HZO37. We found that the diffraction peaks correspond to the orthorhombic phases25. Polarization−voltage (PV) characteristics of the metal–insulator–semiconductor capacitor composed of the HZO/Al2O3 stacks in various voltage ranges are shown in Fig. 2b. As expected for the measured orthorhombic phase in Figs. 1d and 2a, a clear hysteresis of PV characteristics was observed, confirming the ferroelectricity of HZO/Al2O3 stacks. When a bias voltage was swept between −15 V and +15 V, the remnant polarization of the HZO/Al2O3 stacks was approximately 20 μC/cm2, comparable to that of a 10 nm-thick HZO single layer38,39. By inserting a 1 nm Al2O3 layer for every 10 nm HZO layer40,41, we obtained good ferroelectricity even in the HZO layer with a total thickness of 30 nm (See Supplementary Fig. S4).
a Grazing-incidence X-ray diffraction of the Hf0.5Zr0.5O2/Al2O3 stacks deposited on a Si substrate. The orthorhombic phase of the Hf0.5Zr0.5O2 layer is confirmed by the diffraction peaks. b PV characteristics of the metal–insulator–semiconductor capacitor composed of the Hf0.5Zr0.5O2/Al2O3 stacks. The hysteresis PV curves clearly indicate the ferroelectricity of the Hf0.5Zr0.5O2 layer.
Optical properties
Next, we measure the transmission of the fabricated waveguide devices to evaluate the refractive index change of the HZO layer in response to an applied voltage. The measurement was conducted by injecting a continuous-wave laser light with wavelengths ranging from 1480 nm to 1580 nm through grating couplers (see Methods). As shown in Supplementary Fig. S5a, S5b, the propagation loss of the SiN waveguide with SiO2 cladding was evaluated to be 6.1 dB/cm. The propagation loss with HZO is nearly identical to that with SiO2, as shown in Supplementary Fig. S5c. The ellipsometry measurements shown in Supplementary Fig. S6 present the refractive index and extinction coefficient of a 10 nm-thick HZO film. Given HZO’s wide-bandgap nature, ellipsometry at a wavelength of 1.55 µm didn’t reveal any distinct extinction coefficient, further supporting the notion of negligible optical loss associated with HZO. Since the TO effect could potentially contribute to the change in the effective refractive index of the propagating light, we measured the leakage current when applying a bias voltage between the two electrodes of the phase shifter. Our findings revealed a leakage current of less than approximately 300 pA with a 200 V bias voltage (See Supplementary Fig. S7). Considering that the TO effect typically requires more than 10 mW to induce a π phase shift in a SiN waveguide42, we can confidently conclude that the TO effect is negligible in our experiments. We also investigated the impact of free-carrier plasma dispersion and absorption induced by an applied electric field, which is particularly significant in the case of Si. This investigation involved measuring the transmission of a 10 mm-long straight waveguide in response to the bias voltage applied, as shown in Fig. 3a. Notably, we observed no optical intensity modulation even with the application of a 210 V bias voltage, suggesting that the free-carrier effect in the SiN waveguide is negligible.
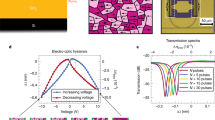
a Optical transmission measurement of the 10 mm-long straight device with respect to the voltage applied. No significant intensity modulation was observed, indicating that the free-carrier effects are negligible. b Transmission spectra of AMZI with the 4.5 mm-long phase shifter. A blue shift in the resonance wavelength peak is observed when 210 V is applied once, showing the nonvolatile optical phase shift. c Change in the effective refractive index when a voltage is swept between +210 and −210 V. When a voltage increases from 0 V to 210, a significant negative refractive index change is observed. Following the initial significant refractive index change, only a small positive change is observed, which can be attributed to the Kerr effect in SiN. A similar Kerr effect is also observed in the HfO2 and SiO2 devices. d Retention characteristics of the nonvolatile refractive index change after a voltage application of 120 V or 160 V.
Then, we proceeded to directly assess the optical phase shift using the AMZI configuration by applying a bias voltage to one of the MZI arms, as illustrated in Fig. 3b. The transmission spectrum of the AMZI before bias voltage application is shown as the black line in Fig. 3b. Notably, the spectrum exhibits periodic wavelength resonance peaks attributed to the length difference between the two MZI arms. Subsequently, we applied a bias voltage of 210 V to a 4.5 mm-long optical phase shifter within the longer AMZI arm, as indicated by the red line in Fig. 3b. The direction of the applied electric field is illustrated as a green arrow in the inset of Fig. 3b. The Simulation result of the electric field distribution at 200 V is illustrated in Supplementary Fig. S8a. The electric field in the HZO layer atop the SiN waveguide is proportional to an applied voltage, as shown in Supplementary Fig. S8b. The external electric field reaches approximately 0.35 MV/cm at 200 V. The transmission spectrum, in this case, reveals a distinctive blue shift in the resonance wavelength peak, clearly indicating a negative change in the effective refractive index of the propagating light. Importantly, the blue-shifted wavelength peak remained unchanged even upon returning the bias voltage to 0 V, indicating the attainment of a nonvolatile optical phase shift. The change in the effective refractive index of the pristine HZO device in response to an applied voltage is depicted by the green circular symbols in Fig. 3c. In this measurement, a bias voltage was applied to the shorter AMZI arm, as depicted in the inset of Fig. 3c. Although no notable change in the effective refractive index occurred within the range of applied voltages from 0 V to 120 V, a substantial negative change in the effective refractive index became evident when the applied voltage exceeded 120 V. Upon reverting the applied voltage from 210 V back to 0 V, the change in the effective refractive index remained relatively constant, as depicted in Fig. 3b, with a magnitude of approximately −1.5 × 10−4 even at 0 V. In this measurement, the direction of the electric field is opposite to that in Fig. 3b, yet the refractive index change remains negative, as similarly observed in Fig. 3b. Therefore, the initial substantial change in the refractive index is consistently negative, irrespective of the electric field direction. Continuing to sweep the voltage down to −210 V did not result in the same large change in the effective refractive index as initially observed. Note that the HfO2 and SiO2 reference devices exhibited a positive change in the effective refractive index, which is approximately 10 times smaller than that in the HZO device, as shown by the black line in Fig. 3c and in Supplementary Fig. S9. The refractive index change increased with the square of the voltage, which can be attributed to the Kerr effect in SiN43. From this comparison, we can deduce that the substantial negative change in the effective refractive index originates from the ferroelectric HZO layer. Since the nonvolatile phase shift was observed only when a voltage was applied to the pristine sample as shown in Fig. 3c, the presented phase shifter works as a one-time memory. Consequently, a wake-up process might not yield any significant benefits. Supplementary Fig. S10 illustrates the refractive index change in a couple of the samples. As depicted in this figure, we observed a basically similar one-time unidirectional phase shift, indicating the reproducibility of our findings. The variations in the amount of refractive index change and the voltage at which the refractive index change begins could be attributed to variations in device fabrication. The retention characteristics of the nonvolatile refractive index changes observed in the HZO sample were then evaluated. Figure 3d shows the results of measuring the change in refractive index over time after a voltage of 120 V or 160 V was applied and then the voltage was returned to 0 V again. It can be seen that there is no significant change in the refractive index throughout measurements up to 104 s. This retention time is comparable to that of the BaTiO3-based optical phase shifter12. We expect a longer retention time as reported in ref. 44. As shown in Fig. 3c, the refractive index remains nearly unchanged when the applied voltage is reverted to 0 V. This suggests the potential to achieve a minimum of 10 intermediate states, as evidenced by the measured points between 110 V and 210 V in Fig. 3c. Therefore, we can realize a multilevel nonvolatile optical phase shifter using ferroelectric HZO. Measuring the small change in optical loss during the retention measurement is challenging due to the significant impact of optical fiber alignment changes on the loss measurement for optical input and output. The retention is dominated by polarization change in HZO. Since we observed no change in optical loss during the polarization change induced by applying voltage, as shown in Fig. 3a, it is reasonable to expect a negligible change in optical loss during the retention measurement.
Discussion
To delve into the physical mechanism underlying the nonvolatile optical phase shift in ferroelectric HZO, we conducted ACOM-TEM of the HZO layer. This analysis enabled us to explore the alteration in the orientation of the orthorhombic phase induced by the application of an electrical field. Figure 4a illustrates a grain map of the orthorhombic HZO layer on the SiN waveguide before the application of any electrical field. In Fig. 4b, an inverse pole figure of the HZO layer along the direction of the electrical field shown in Fig. 1a, defined as the transverse direction, is presented; here, the (001) orientation is defined as the polarization axis of an orthorhombic HZO crystal. Figure 4c, d show a grain map and an inverse pole figure of the HZO layer, respectively, after the application of 210 V. From the comparison of Fig. 4b, d, it becomes evident that the polarization axis shifts more toward the transverse direction owing to the applied voltage45,46. Figure 4e shows the product of the normalized distribution density of the orientation angle θ of the orthorhombic phase and cosθ, which is regarded as the component contributing to the refractive index change. Here, θ is defined as the angle between the polarization axis and the transverse direction. It is clearly seen that the product-sum of the normalized distribution density and cosθ increased by approximately 30% after the voltage application. We observed a similar trend in the HZO layer at the sidewall of the SiN waveguide, as shown in Supplementary Fig. S11.
a Grain map and (b) inverse pole figure of the orthorhombic Hf0.5Zr0.5O2 layer before voltage application. c Grain map and (d) inverse pole figure of the orthorhombic Hf0.5Zr0.5O2 layer after voltage application. e Product of the normalized distribution density of the orientation angle θ of the orthorhombic phase and cosθ. The polarization axis rotates toward the direction of an external electric field owing to the voltage application, which contributes to the change in refractive index.
Taking into account the rotation of the polarization axis of HZO along the direction of the applied electric field, as observed in Fig. 4, the negative change in the refractive index, as depicted in Fig. 3c, regardless of the electric field direction, can be elucidated using two physical models. One such model is the quadratic electro-optic effect induced by the spontaneous polarization of HZO47,48,49. As observed in LiNbO3, the refractive index reduction is proportional to the square of the spontaneous polarization through the quadratic electro-optic effect in ferroelectric materials. When a voltage is applied to a pristine device, the spontaneous polarization is expected to evolve along the transverse direction, as depicted in Fig. 4. As a result, we expect to observe a negative refractive index change that is independent of the direction of voltage application. With the TE-mode light predominantly confined in the SiN core, the optical confinement factor within the HZO layer stands at approximately 4.5%. Taking the quadratic electro-optic coefficient of HZO as the same value as that of LiNbO3 (0.09 m4C−2)49, and considering a spontaneous polarization of 10 μC/cm2 and an optical confinement factor within the HZO layer, the estimated effective refractive index change stands at approximately −1.8 × 10−4, which is close to the experimental value shown in Fig. 3c. Hence, the quadratic electro-optic effect induced by the spontaneous polarization in HZO after the first voltage sweep presents a plausible explanation for the nonvolatile optical phase shift. During the second voltage sweep, the spontaneous polarization in HZO remains undisturbed, while an external electric field modulates only the paraelectric component of the polarization in HZO. As shown in Supplementary Fig. S8, the external electric field at 200 V is approximately 0.35 MV/cm. With this electric field and a dielectric constant of 30, the polarization from the paraelectric component is calculated to be approximately 0.9 μC/cm2, which is approximately 10 times smaller than a spontaneous polarization of 10 μC/cm2. The refractive index change caused by the quadratic electro-optic effect is proportional to the square of the polarization49. Therefore, the refractive index change by the paraelectric polarization through the quadratic electro-optic effect in HZO, resulting from an external electric field in the second voltage sweep, is expected to be roughly 100 times smaller than the nonvolatile refractive index change observed in the first voltage sweep due to the spontaneous polarization in HZO. Thus, the refractive index change induced by an external electric field through the quadratic electro-optic effect of the paraelectric polarization in HZO remains unobservable due to the presence of the quadratic electro-optic effect in SiN.
The other model pertains to the birefringence of HZO. According to numerical predictions, the refractive index of orthorhombic HfO2 along the polarization axis is 2.081 at a wavelength of 633 nm, whereas the refractive indices along the other two axes are expected to be 2.059 and 2.12230. Even at a wavelength of 1550 nm, the refractive indices are expected to be close to that at 633 nm50. In directions perpendicular to the polarization axis, HZO crystals are assumed to be randomly oriented. Consider the scenario in which the polarization axis is oriented perpendicular to the transverse direction. Since the measurement in Fig. 3 employs TE-mode light, in which the optical electric field is predominantly polarized along the transverse direction, the refractive index for the propagating light becomes the average of the refractive index perpendicular to the polarization axis, i.e., 2.0905. Upon rotating the polarization axis along the transverse direction through voltage application, the refractive index for the propagating light changes to that along the polarization axis, i.e., 2.081. Considering the optical confinement factor within the HZO layer, the maximum estimated change in effective refractive index reaches approximately −4.3 × 10−4, which is approximately three times higher than the experimental value depicted in Fig. 3c. This discrepancy indicates that the polarization axis does not completely rotate toward the direction of the external electric field due to insufficient field strength. The same logic applies to ZrO2. Consequently, the refractive index reduction observed regardless of the direction of voltage application can also be explained by the birefringence of orthorhombic HZO.
In conclusion, we successfully demonstrated the nonvolatile optical phase shift induced by applying a voltage to ferroelectric HZO deposited on a SiN waveguide. This observed phenomenon can be attributed to the rotation of the polarization axis of orthorhombic HZO along the direction of the external electric field. Notably, the nonvolatile phase shift was only observed once in a pristine HZO sample. Additionally, the consistent negative refractive index change, regardless of the electric field direction, signifies unidirectional phase shifting. Although such a one-time unidirectional phase shift may indeed have limited applications, our discovery of the nonvolatile optical phase shift observed in HZO remains valuable for one-time optical memory applications in programmable PICs. For instance, it can be utilized to store the weights of a matrix for multiply-accumulation operations. This is particularly relevant because the weights for inference purposes remain unchanged once the learning process is completed. Another potential application of our discovery is the correction of initial phase errors in programmable PICs. Given that initial phase errors are inevitable due to fabrication variations, the one-time unidirectional phase shifter proves to be useful in this regard. Presently, owing to limitations in the measurement equipment, applying a voltage higher than 210 V is not feasible. Nevertheless, it is anticipated that employing a larger electric field for HZO could yield an even more substantial optical phase shift. Since the leakage current was less than 300 pA even at 200 V, the switching energy could be very small even with a slow switching time. For instance, assuming the switching speed of 10 s at 200 V, the estimated switching energy amounts to approximately 0.6 μJ. This level of energy consumption might not be significant for the reconfiguration purpose of PICs. In this study, no linear electro-optic effect, i.e., the Pockels effect, was observed in HZO. However, there is a possibility of observing the Pockels effect in HZO by applying a larger electric field using a slot waveguide51 or plasmonic waveguide52. For instance, the device structure of the Si slot waveguide with HZO in the slot gap is illustrated in Supplementary Fig. S12a. The simulated electric field distribution at 20 V in Supplementary Fig. S12b shows that the external electric field is concentrated in the slot gap. As shown in Supplementary Fig. S12c, the slot device, with bias voltages exceeding 10 V, allows an external electric field of 1 MV/cm, which is close to the coercive electric field of HZO53. Since ALD facilitates the conformal deposition of HZO, it allows HZO to be deposited on both sidewalls of the slot. Consequently, the HZO film grows laterally from the sidewall. In this scenario, a 50 nm-thick HZO layer is necessary on one side to fill the 100 nm-wide gap of the slot. Such a thickness is realistic for maintaining the ferroelectric behavior of HZO. The utilization of a Si slot waveguide also facilitates a reduction in the switching time of the nonvolatile optical phase shift observed in this study. Based on transient measurements shown in Supplementary Fig. S13a and S13b, the observed switching speed appears slow, ranging from 10 to 100 s due to an insufficient electric field in the SiN waveguide device. Referring to the nucleation-dominated switching model in HZO54, the switching time follows an exponential reduction relative to the square of the external electrical field. Extrapolating from the measured switching speeds, a switch time of less than 1 μs could be achieved with an external electric field of approximately 0.7 MV/cm, as shown in Supplementary Fig. S13c. As mentioned earlier, such a field strength can be attained using the slot device. Hence, the utilization of a slot waveguide or plasmonic waveguide demonstrates potential in achieving switching times below 1 μs. We anticipate that our findings will trigger and promote the study of optical nonlinear effects in HZO, leading to the progress of Si PICs employing ferroelectric HZO and making significant contributions to the evolution of communication, computing, and sensing.
Methods
The SiN waveguide with the HZO/Al2O3 stack was fabricated as follows (See Supplementary Fig. S1 for the detailed fabrication procedure). First, a 330 nm-thick SiN layer was deposited on a thermally oxidized Si wafer by plasma–enhanced chemical vapor deposition (PECVD). The thickness of the thermally oxidized SiO2 layer was 4 μm. SiN waveguides were fabricated by electron-beam (EB) lithography and inductively coupled plasma (ICP) dry etching. Three HZO/Al2O3 multilayer stacks were then deposited on the Si waveguide by ALD. After depositing TiN on the HZO/Al2O3 stacks, annealing at 400 °C for 1 min was performed to achieve the ferroelectricity of HZO. TiN was removed by wet etching, and SiO2 passivation was carried out by PECVD. The thickness of the SiO2 cladding was 600 nm. Finally, Al electrodes were formed by metal sputtering and lift-off. For optical intensity and phase modulation measurements, a continuous-wave light from a tunable laser source (Santec, TSL-510) was injected into the SiN waveguide from a single-mode optical fiber through a SiN grating coupler. The polarization of the input light was tuned to the TE mode of the SiN waveguide using an in-line polarization controller. The output from the SiN waveguide was coupled back to the optical fiber through a grating coupler and measured by an InGaAs power meter (Agilent, 81624 A). A precision source/measure unit (Agilent, B2902A) was used for voltage application and current measurement.
Data availability
The data that support the findings of this study have been included in the main text and Supplementary Information. All other relevant data supporting the findings of this study are available from the corresponding authors upon request.
References
Siew, S. Y. et al. Review of silicon photonics technology and platform development. J. Lightwave Technol. 39, 4374–4389 (2021).
Stojanović, V. et al. Monolithic silicon-photonic platforms in state-of-the-art CMOS SOI processes [Invited]. Opt. Express 26, 13106 (2018).
Bogaerts, W. et al. Programmable photonic circuits. Nature 586, 207–216 (2020).
Huang, C. et al. A silicon photonic–electronic neural network for fibre nonlinearity compensation. Nat. Electron. 4, 837–844 (2021).
Shastri, B. J. et al. Photonics for artificial intelligence and neuromorphic computing. Nat. Photonics 15, 102–114 (2021).
Shen, Y. et al. Deep learning with coherent nanophotonic circuits. Nat. Photonics 11, 441–446 (2017).
Qiang, X. et al. Large-scale silicon quantum photonics implementing arbitrary two-qubit processing. Nat. Photonics 12, 534–539 (2018).
Zhang, X., Kwon, K., Henriksson, J., Luo, J. & Wu, M. C. A large-scale microelectromechanical-systems-based silicon photonics LiDAR. Nature 603, 253–258 (2022).
Takenaka, M. et al. III–V/Si Hybrid MOS optical phase shifter for Si photonic integrated circuits. J. Lightwave Technol. 37, 1474–1483 (2019).
Han, J.-H. et al. Efficient low-loss InGaAsP/Si hybrid MOS optical modulator. Nat. Photonics 11, 486–490 (2017).
Edinger, P. et al. Silicon photonic microelectromechanical phase shifters for scalable programmable photonics. Opt. Lett. 46, 5671–5674 (2021).
Geler-Kremer, J. et al. A ferroelectric multilevel nonvolatile photonic phase shifter. Nat. Photonics 16, 491–497 (2022).
Abel, S. et al. Large Pockels effect in micro- and nanostructured barium titanate integrated on silicon. Nat. Mater. 18, 42–47 (2019).
Wang, C. et al. Integrated lithium niobate electro-optic modulators operating at CMOS-compatible voltages. Nature 562, 101–104 (2018).
He, M. et al. High-performance hybrid silicon and lithium niobate Mach–Zehnder modulators for 100 Gbit s−1 and beyond. Nat. Photonics 13, 359–364 (2019).
Delaney, M., Zeimpekis, I., Lawson, D., Hewak, D. W. & Muskens, O. L. A new family of ultralow loss reversible phase-change materials for photonic integrated circuits: Sb2S3 and Sb2Se3. Adv. Funct. Mater. 30, 1–10 (2020).
Miyatake, Y. et al. Proposal of low-loss nonvolatile mid-infrared optical phase shifter based on Ge2Sb2Te3S2. IEEE Trans. Electron Devices 70, 2106–2112 (2023).
Sorianello, V. et al. Graphene–silicon phase modulators with gigahertz bandwidth. Nat. Photonics 12, 40–44 (2018).
Datta, I. et al. Low-loss composite photonic platform based on 2D semiconductor monolayers. Nat. Photonics 14, 256–262 (2020).
Dong, M. et al. High-speed programmable photonic circuits in a cryogenically compatible, visible–near-infrared 200 mm CMOS architecture. Nat. Photonics 16, 59–65 (2021).
Ribeiro, A. et al. Column-row addressing of thermo-optic phase shifters for controlling large silicon photonic circuits. IEEE J. Sel. Top. Quantum Electron. 26, 6100708 (2020).
Ríos, C. et al. In-memory computing on a photonic platform. Sci. Adv. 5, eaau5759 (2019).
Böscke, T. S., Müller, J., Bräuhaus, D., Schröder, U. & Böttger, U. Ferroelectricity in hafnium oxide thin films. Appl. Phys. Lett. 99, 102903 (2011).
Müller, J. et al. Ferroelectric Zr0.5Hf0.5O2 thin films fornonvolatile memory applications. Appl. Phys. Lett. 99, 112901 (2011).
Müller, J. et al. Ferroelectricity in simple binary ZrO2 and HfO2. Nano Lett. 12, 4318–4323 (2012).
Khan, A. I., Keshavarzi, A. & Datta, S. The future of ferroelectric field-effect transistor technology. Nat. Electron. 3, 588–597 (2020).
Park, M. H., Lee, Y. H., Mikolajick, T., Schroeder, U. & Hwang, C. S. Review and perspective on ferroelectric HfO2-based thin films for memory applications. MRS Commun. 8, 795–808 (2018).
Kondo, S. et al. Linear electro-optic effect in ferroelectric HfO2-based epitaxial thin films. Jpn. J. Appl. Phys. 60, 070905 (2021).
Kondo, S. et al. Influence of orientation on the electro-optic effect in epitaxial Y-doped HfO2 ferroelectric thin films. Jpn. J. Appl. Phys. 60, SFFB13 (2021).
El Boutaybi, A. et al. Electro-optic properties of ZrO2, HfO2, and LiNbO3 ferroelectric phases: A comparative density functional study. Phys. Rev. B Condens. Matter 107, 045140 (2023).
Migita, S. et al. Polarization switching behavior of Hf–Zr–O ferroelectric ultrathin films studied through coercive field characteristics. Jpn. J. Appl. Phys. 57, 04FB01 (2018).
Chen, H.-H. et al. Ferroelectric polarization enhancement in hafnium-based oxides through capping layer engineering. IEEE J. Electron Devices Soc. 10, 947–952 (2022).
Pal, A. et al. Enhancing ferroelectricity in dopant-free hafnium oxide. Appl. Phys. Lett. 110, 022903 (2017).
Kim, S. J. et al. Large ferroelectric polarization of TiN/Hf0.5Zr0.5O2/TiN capacitors due to stress-induced crystallization at low thermal budget. Appl. Phys. Lett. 111, 242901 (2017).
Trentzsch, M. et al. A 28nm HKMG super low power embedded NVM technology based on ferroelectric FETs. in 2016 IEEE International Electron Devices Meeting (IEDM) 11.5.1–11.5.4 (IEEE, 2016).
Viladot, D. et al. Orientation and phase mapping in the transmission electron microscope using precession-assisted diffraction spot recognition: state-of-the-art results. J. Microsc. 252, 23–34 (2013).
Wei, Y. et al. A rhombohedral ferroelectric phase in epitaxially strained Hf0.5Zr0.5O2 thin films. Nat. Mater. 17, 1095–1100 (2018).
Toprasertpong, K. et al. Improved ferroelectric/semiconductor interface properties in Hf0.5Zr0.5O2 ferroelectric FETs by low-temperature annealing. IEEE Electron Device Lett. 41, 1588–1591 (2020).
Toprasertpong, K. et al. Low operating voltage, improved breakdown tolerance, and high endurance in Hf0.5Zr0.5O2 ferroelectric capacitors achieved by thickness scaling down to 4 nm for embedded ferroelectric memory. ACS Appl. Mater. Interfaces 14, 51137–51148 (2022).
Kim, H. J. et al. Grain size engineering for ferroelectric Hf0.5Zr0.5O2 films by an insertion of Al2O3 interlayer. Appl. Phys. Lett. 105, 192903 (2014).
Ali, T. et al. Tuning hybrid ferroelectric and antiferroelectric stacks for low power FeFET and FeRAM applications by using laminated HSO and HZO films. Adv. Electron. Mater. 8, 2100837 (2022).
Mohanty, A. et al. Reconfigurable nanophotonic silicon probes for sub-millisecond deep-brain optical stimulation. Nat. Biomed. Eng. 4, 223–231 (2020).
Krückel, C. J. et al. Linear and nonlinear characterization of low-stress high-confinement silicon-rich nitride waveguides. Opt. Express 23, 25827–25837 (2015).
Mikheev, V., Kondratyuk, E. & Chouprik, A. Retention Model and Express Retention Test of Ferroelectric HfO2-Based Memory. Phys. Rev. Appl. 18, 064084 (2022).
Grimley, E. D., Schenk, T., Mikolajick, T., Schroeder, U. & LeBeau, J. M. Atomic structure of domain and interphase boundaries in ferroelectric HfO2. Adv. Mater. Interfaces 5, 1701258 (2018).
Li, Z. et al. A 3D vertical-channel ferroelectric/anti-ferroelectric FET with indium oxide. IEEE Electron Device Lett. 43, 1227–1230 (2022).
DiDomenico, M. Jr & Wemple, S. H. Oxygen-octahedra ferroelectrics. I. Theory of electro-optical and nonlinear optical effects. J. Appl. Phys. 40, 720–734 (1969).
Åhlfeldt, H., Webjörn, J., Thomas, P. A. & Teat, S. J. Structural and optical properties of annealed proton‐exchanged waveguides in z‐cut LiTaO3. J. Appl. Phys. 77, 4467–4476 (1995).
Hu, H. et al. Extraordinary refractive-index increase in lithium niobate caused by low-dose ion implantation. Appl. Opt. 40, 3759–3761 (2001).
Tang, W. T. et al. Synthesis and characterization of HfO2 and ZrO2 thin films deposited by plasma assisted reactive pulsed laser deposition at low temperature. Thin Solid Films 518, 5442–5446 (2010).
Alloatti, L. et al. 100 GHz silicon–organic hybrid modulator. Light Sci. Appl. 3, e173 (2014).
Melikyan, A. et al. High-speed plasmonic phase modulators. Nat. Photonics 8, 229–233 (2014).
Materano, M. et al. Polarization switching in thin doped HfO2 ferroelectric layers. Appl. Phys. Lett. 117, 262904 (2020).
Mulaosmanovic, H. et al. Switching Kinetics in Nanoscale Hafnium Oxide Based Ferroelectric Field-Effect Transistors. ACS Appl. Mater. Interfaces 9, 3792–3798 (2017).
Acknowledgements
This work was partly based on results obtained from projects (JPNP16007 received by M.T.) commissioned by the New Energy and Industrial Technology Development Organization (NEDO) and partly supported by JST, CREST (JPMJCR2004 received by M.T.), JST, MIRAI (JPMJMI20A1 received by M.T.), and “Advanced Research Infrastructure for Materials and Nanotechnology in Japan (ARIM)” of the Ministry of Education, Culture, Sports, Science and Technology (MEXT) (JPMXP1222UT1028).
Author information
Authors and Affiliations
Contributions
K.Ta. contributed to fabrication, measurement, and manuscript preparation, N.S. contributed to ideas, K.W. contributed to fabrication and measurement, Y.M. contributed to design and measurement, T.A. contributed to the simulation and manuscript preparation, and H.S. contributed to the simulation. K.To and S.T. contributed to the overall discussion. M.T. contributed to ideas and to discussion, and manuscript revision and also provided high-level project supervision.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks the anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Taki, K., Sekine, N., Watanabe, K. et al. Nonvolatile optical phase shift in ferroelectric hafnium zirconium oxide. Nat Commun 15, 3549 (2024). https://doi.org/10.1038/s41467-024-47893-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-024-47893-2
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.