Abstract
Strongly correlated spin systems can be driven to quantum critical points via various routes. In particular, gapped quantum antiferromagnets can undergo phase transitions into a magnetically ordered state with applied pressure or magnetic field, acting as tuning parameters. These transitions are characterized by z = 1 or z = 2 dynamical critical exponents, determined by the linear and quadratic low-energy dispersion of spin excitations, respectively. Employing high-frequency susceptibility and ultrasound techniques, we demonstrate that the tetragonal easy-plane quantum antiferromagnet NiCl2 ⋅ 4SC(NH2)2 (aka DTN) undergoes a spin-gap closure transition at about 4.2 kbar, resulting in a pressure-induced magnetic ordering. The studies are complemented by high-pressure-electron spin-resonance measurements confirming the proposed scenario. Powder neutron diffraction measurements revealed that no lattice distortion occurs at this pressure and the high spin symmetry is preserved, establishing DTN as a perfect platform to investigate z = 1 quantum critical phenomena. The experimental observations are supported by DMRG calculations, allowing us to quantitatively describe the pressure-driven evolution of critical fields and spin-Hamiltonian parameters in DTN.
Similar content being viewed by others
Introduction
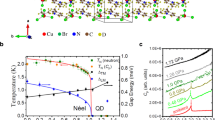
Magnetic insulators with their short-range interactions and well-controlled effective Hamiltonians offer an ideal playground for studying quantum critical phenomena induced by various stimuli1,2,3. Nowadays, great attention is attracted by antiferromagnetic (AF) ordering, which can be induced, e.g., by magnetic field in gapped quantum magnets4,5. On the other hand, especially tantalizing is the possibility of magnetic ordering, accompanied by spontaneous spin-symmetry break-down without the aid of magnetic field, while keeping the spectrum degenerate in the absence of Zeeman splitting6. Such transitions are known to appear in certain quantum antiferromagnets under applied pressure. As Fig. 1a illustrates, both the magnetic field and pressure can be regarded as a tuning parameter. Contrary to the field-induced transitions, the pressure-induced case belongs to another class of universality7,8,9. The key distinction is the dynamic critical exponent z that links the characteristic energy of spin excitations to the momentum relative to the critical one:
a The generic phase diagram (η is the tuning parameter; QCP is the quantum critical point). The critical value of the tuning parameter is labeled ηc. b Schematic view of magnetic excitation spectra for the field- and pressure-induced quantum phase transitions (q is the momentum; ℏω is the excitation energy; z is the dynamic critical exponent, see Eq. (1)).
Field-induced phase transitions are characterized by z = 2 and a quadratic low-energy excitation spectrum, while the pressure-induced case has z = 1 and a linear spectrum6,8. The realizations of these two scenarios are illustrated in Fig. 1b. The z = 1 regime is very remarkable. It should have mean-field critical exponents8 and the universal scaling of dynamic fluctuations at the same time10. This quantum critical point (QCP) is also a natural habitat for a well-defined order-parameter amplitude mode11,12.
There is a number of gapped quantum antiferromagnets, demonstrating field-induced AF ordering with z = 25. If the spin Hamiltonian of a system has axial symmetry with respect to the applied field, the field-induced AF ordering can be formally described as the Bose–Einstein condensation of magnons by mapping the spin-1 system into a gas of semi-hard-core bosons4,13. In order to perform an accurate comparison with the theory, high-symmetry spin systems are highly demanded. The compound NiCl2 ⋅ 4SC(NH2)2 (dichloro–tetrakis thiourea–nickel(II), known as DTN) is one of them, having a tetragonal crystal structure (space group I4) and easily accessible critical fields.
A good realization of the true z = 1 QCP is actually hard to find. Most of the materials known to show such a transition (TlCuCl311,12, KCuCl314,15, (C4H12N2)Cu2Cl616, and (C9H18N2)CuBr417) suffer from unwanted anisotropies. For TlCuCl3 and (C9H18N2)CuBr4 biaxial anisotropy was experimentally detected18,19. In KCuCl3 the presence of biaxial anisotropy follows from symmetry considerations, and is indirectly evidenced by a peculiar orientation of sublattice magnetization in the ordered phase14. Such anisotropies eventually lead to the criticality of the Ising universality class20, different from the target QCP. This does not seem to be the case for CsFeCl321,22, but there, one has to deal with geometric exchange frustration.
In the present study, utilizing high-pressure tunneling-diode oscillator (TDO) susceptibility, ultrasound-propagation measurements, and high-field electron spin resonance (ESR) techniques, we demonstrate a pressure-induced phase transition in DTN, which we ascribe to the long-sought z = 1 criticality. This transition resides at an easily accessible pressure of about 4.2 kbar. Neutron-diffraction measurements confirm the absence of a structural transition and reveal an undistorted tetragonal symmetry near this QCP. At higher pressure, we actually find an irreversible distortion of the lattice occurring. We describe the experimentally measured phase boundaries employing a quasi-1D numerical approximation, circumventing a renormalization of the spin-Hamiltonian parameters by quantum fluctuations.
Results
Magnetism in DTN: brief introduction
Magnetism in DTN originates from the spin-1 Ni2+ ions forming a tetragonal lattice (we refer the reader to Supplemental Material S1 for detailed crystallographic information). The magnetic properties are defined by the competition between the strong single-ion planar anisotropy D, and the antiferromagnetic exchanges interactions Jc and Ja ≡ Jb along the corresponding c and a, b directions. The effective Hamiltonian is
Here, r runs along the nickel positions in the tetragonal sublattice; a, b, and c are the primitive lattice translation vectors towards the neighboring spins. Importantly, the symmetry prohibits any in-plane second-order anisotropic terms. The planar anisotropy protects the spin-singlet state \(\left\vert {S}^{z}=0\right\rangle\) on every magnetic ion, thus preventing Neél order in zero field, otherwise favored by the exchange interactions. The set of constants describing DTN at ambient pressure was initially obtained from zero-field neutron spectroscopy and thermodynamic studies23,24, and later refined as D/kB = 8.9 K, Jc/kB = 1.82 K, and Ja/kB = 0.34 K25 based on the spectroscopic properties at high magnetic fields (where the effect of quantum renormalization is not present). The zero-field gap Δ/kB ≃ 3.5 K26 is relatively small compared to the excitation-doublet bandwidth of ~ 8 K. If the magnetic field is applied along the c (z) direction, the degeneracy of the doublet is removed due to Zeeman splitting (as shown in Fig. 1b), triggering eventually the onset of low-temperature magnetic order at μ0Hc1 ≃ 2.1 T23,27. At stronger magnetic field, μ0Hc2 ≃ 12.2 T, DTN undergoes the transition into the fully spin-polarized state. We would like to stress that the zero-field gap in DTN is dominantly determined by the single-ion anisotropy (in contrast to Haldane spin-chain materials), making DTN a rare example of a large-D spin-1 system.
High-pressure neutron diffraction
As the pressure increases, the parameters of Hamiltonian Eq. (2) are expected to change. However, it is necessary to check first whether the lattice remains undistorted. To this end, we have performed a series of structural neutron diffraction studies28. As shown in Fig. 2, the DTN lattice is smoothly compressible up to about 6 kbar. Interestingly, the compression goes in a rather uniaxial manner, with shrinking of the sample mostly along the c axis (∂c/∂P = −0.038 ± 0.003 Å/kbar at 1.8 K). This implies the compression of the main Ni–Cl–Cl–Ni superexchange pathway and the deformation of the Ni2+ local environment. Such changes must affect D and Jc in the first place. The lattice parameter a remains nearly constant with ∂a/∂P = ( −4.1 ± 1.5) ⋅ 10−3 Å/kbar. At Pirr ≃ 6 kbar, an irreversible structural transition occurs, evidenced by discontinuities in the lattice parameters. A more detailed discussion is given in the Supplemental Material (S2 and S3).
a Pressure dependence of the lattice parameter a. b Pressure dependence of the lattice parameter c. Open and closed symbols correspond to 300 and 1.8 K data, respectively. Dotted lines denote the irreversible structural phase transition at Pirr ~ 6 kbar. Red lines are fit results (see text for details).
High-pressure TDO measurements
The TDO susceptibility technique is well established as a versatile tool for detecting field-induced phase transitions in solids under applied pressure29,30,31,32.
The results of our measurements are shown in Fig. 3. At low pressures, two anomalies, corresponding to the boundaries of the long-range AF ordered phase at Hc1 and Hc2, respectively, are well discernible. To extract the critical fields in a reliable way we use a set of empirical functions (red lines, a detailed description is given in the Supplemental Material). With applied pressure, we observe a decrease and increase of the first and second critical field, respectively. Above 4.2 kbar, the low-field transition is not visible anymore. This is a strong evidence of the spin-gap closure. The critical field Hc2 increases linearly up to Pirr, where a discontinuity appears. The high-field part of the curve at 6 kbar (about Pirr) features a double-dip structure. This reflects the coexistence of two structurally different phases at the first-order crystallographic transition. In the structurally distorted phase above Pirr, we observe only one anomaly.
High-pressure ultrasound measurements
In order to reveal the nature of the pressure-induced gapless phase, we performed high-pressure ultrasound measurements. The magnetic ordering in DTN at zero pressure was thoroughly investigated with ultrasound by Chiatti et al.33,34, firmly establishing the connection between the long-range-order onset and the sound velocity anomalies in DTN. These anomalies reflect the spin-susceptibility divergence in the vicinity of the critical temperature35, as a result of the pronounced magnetoelastic coupling in DTN.
We studied the longitudinal sound mode along the c direction (mode c33) at high pressures. The field-induced changes of its velocity are shown in Fig. 4a. Similar to our TDO data (Fig. 3), there are two anomalies at low pressures. As revealed previously33,34, they evidence the transitions from disordered gapped to AF ordered gapless state at Hc1, and the subsequent transition to the fully spin-polarized state at Hc2.
a Relative change of the sound velocity Δv/v of the longitudinal acoustic mode as function of the magnetic field (zero-pressure data are taken from ref. 33 and were measured at 0.3 K). The data are offset for clarity. b Relative change of the sound velocity Δv/v of the longitudinal acoustic mode as function of temperature. The data are offset for clarity. The onset of magnetic order is marked by red arrows.
At higher pressures (above 3.8 kbar), we only observe the high-field phase transition, while the gapless AF ordered phase becomes extended to zero magnetic field. An additional evidence for the pressure-induced magnetic ordering in zero fields is our observation of the sound–velocity anomaly below 1 K (red arrows in Fig. 4b). As expected, the ordering temperature grows with increasing pressure.
Electron spin resonance
The applied pressure in DTN should affect not only the ground state but the spin dynamics as well. Electron spin resonance (ESR) has recently proven to be a powerful tool to probe the excitation spectra in strongly correlated spin systems under applied pressure 29,36. Selected examples of ESR spectra in DTN are shown in Fig. 5a (adopting the naming convention from ref. 25, we label the observed modes B and C). Excitation modes corresponding to ΔSz = 1 transitions remain well visible up to 6 kbar. With the pressure increase both modes demonstrate a gradual shift towards higher fields (as illustrated in Fig. 5b) until they vanish in the structurally distorted phase above about 6 kbar. The complete frequency-field diagrams can be found in the Supplemental Material S6.
Discussion
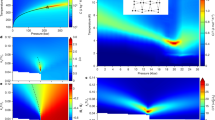
The results of our TDO and ultrasound experiments on DTN are summarized in the phase diagram in Fig. 6. The data ensure that near 4 kbar the spin gap does close and antiferromagnetic order emerges. One can theoretically describe the pressure-dependent spin Hamiltonian, consistent with these observations. The saturation field Hc2 is known to follow the linear spin wave theory (LSWT) description without any quantum renormalization25:
Given the overall smallness of Ja and lack of a significant pressure-induced length change in this direction, we can neglect possible variations in this interaction. Thus, the phase-diagram evolution is due to the changes in D and Jc:
With the g-factor being 2.26, the measured slope μ0∂Hc2/∂P = 0.78 ± 0.03 T/kbar (upper red line in Fig. 6 below the instability pressure Pirr) quantifies the linear pressure dependence of D and Jc.
The analysis of the first critical field poses a greater challenge: since gμ0μBHc1 = Δ, it requires evaluating the zero-field spin gap for the given set of Hamiltonian (2) parameters. No exact theory is available for that to the best of our knowledge. We overcome this challenge employing a random-phase approximation (RPA)37 based ansatz combined with density matrix renormalization group (DMRG) calculations38,39. The starting point is the determination of the zero-field gap value Δ0(D/Jc) in the Ja = 0 limit of a single anisotropic chain, utilizing the latter technique. As far as we know, only a particular range close to the quantum critical point at D/Jc ~ 1 was thoroughly accessed with DMRG earlier40. The next step of the model is to apply the RPA treatment to interacting chains in order to estimate the critical value of the coupling \({J}_{a}^{{{{{{{{\rm{crit}}}}}}}}}\) that closes the gap. The details of the calculations (based on large-D approximation for the dynamic structure factor41,42,43 and the Kramers–Kronig relations) are given in the Supplemental Material (S4).
The main result is the approximation for the order-disorder zero-field phase boundary:
We find that the numerical value \(1/4{{{{{A}}}}}\simeq 0.14\) provides an excellent description of this phase boundary, previously obtained by extensive quantum Monte–Carlo (QMC) simulations44,45. This comparison can be seen in Fig. 7d, where the calculation result using Eq. (5) is shown as the red line. Then, it follows from our approach that the value of the gap, renormalized by Ja, is
Hence, the first critical field can be expressed through the pressure-dependent Hamiltonian parameters as
The ambient pressure Hc1 evaluated by this procedure agrees with the experimental value, ensuring the validity of the approach for the smaller gap values as well.
a Pressure dependence of the anisotropy parameter D/kB. b Pressure dependence of the exchange coupling parameter Jc/kB. c Pressure dependence of the transverse exchange coupling parameter Ja/kB. The calculation results are shown for the pressures, matching the experiments. d The Sakai–Takahashi phase diagram for a quasi-1D spin-1 antiferromagnet44. The red open points correspond to QMC calculations for the phase boundary45; the red line is a prediction based on the ansatz as described in the text. The purple circles correspond to estimates of the spin Hamiltonian parameters at given pressures. The dotted cross marks the critical parameter values at 4.2 kbar.
The ability to predict both critical fields using Eqs. (3) and (7) finally opens a route to a self-consistent treatment of the measured phase diagram without any “effective” parameters. We numerically optimize the agreement between (7) and the experimental Hc1 data by varying the choice of the critical pressure Pc at which the gap closes completely. This fixes a unique combination of ∂(D, Jc)/∂P. The optimization results in the critical pressure Pc = 4.2 ± 0.3 kbar (see Supplemental Material S5 for more details). The magnetic phase diagram (Fig. 6) is fully captured with \({k}_{{{{{{{{\rm{B}}}}}}}}}^{-1}\partial D/\partial P=0.16\pm 0.03\) K/kbar and \({k}_{{{{{{{{\rm{B}}}}}}}}}^{-1}\partial {J}_{c}/\partial P=0.25\pm 0.01\) K/kbar. Figure 7a–c illustrate how the spin-Hamiltonian parameters of DTN are pressure-tuned up to Pirr. In the phase diagram of Fig. 7d, we show how the corresponding ground state (illustrated by purple points) is changing from gapped to long-range ordered at Pc in accordance with the previous discussion.
The rich high-pressure physics of DTN under pressure invites further investigations, related to the interplay of quantum and thermal fluctuations near z = 1 quantum criticality9,12,46,47,48. In particular, it would be important to access the order parameter (e.g., with neutron diffraction or nuclear magnetic resonance) and the extended field-temperature-pressure phase diagram32. This would open the possibility to establish a direct connection between the minimalistic and highly symmetric spin Hamiltonian of DTN and the effective field theory used to describe the static and dynamic properties of critical quantum magnets49,50. The undistorted symmetry also makes DTN a perfect candidate for investigating of the effect of thermal and quantum fluctuations on the amplitude mode12 in the absence of Ising-type anisotropy. One can also expect chemically substituted DTNX51,52 to be a fruitful playground for the interplay of quantum z = 1 criticality and quenched disorder, similarly to (C4H12N2)Cu2(Cl1−xBrx)653, (NH4)xK1−xCuCl354, and Cs1−xRbxFeCl355. The higher symmetry and a simpler, well-understood Hamiltonian make the case of DTNX much more appealing for such studies.
To summarize, we have identified the material DTN as a unique platform for studies of the exotic z = 1 universality class in a three-dimensional magnetic material. By means of TDO, ultrasound, and ESR measurements we have confirmed the existence of pressure-induced criticality, separating gapped disordered and gapless long-range ordered magnetic phases in the material. The nearly ideal axial symmetry of the structure is retained at that point, which makes DTN to stand out among the non-frustrated quantum magnets. In addition to that, we have extracted the pressure dependence of the spin Hamiltonian parameters from the data, and have achieved a quantitative theoretical understanding of the transition mechanism.
Methods
Sample growth
Samples for the thermodynamic measurements and the electron spin resonance spectroscopy were synthesized in the University of Saõ Paulo from aqueous solution using a thermal-gradient method56,57. Samples used in the neutron diffraction studies were synthesized at ETH Zürich. Fully deuterated chemicals (water and thiourea) were used. The crystals were crushed into powder for these experiments.
High-pressure neutron diffraction
Neutron-diffraction experiments with the powder samples were performed at instrument HB2a at the High Flux Isotope Reactor, Oak Ridge National Laboratory (Oak Ridge, Tennessee, USA). Up to a few grams of deuterated DTN powder material were used. A Ge[113] or Ge[115] vertically focussing wafer-stack monochromator was used to produce a neutron beam with 2.41 Å or 1.54 Å wavelength, respectively. A 4He Orange cryostat with an aluminum He-gas pressure cell (capable of producing pressures up to 6 kbar) and a CuBe clamp cell (capable of producing pressures up to 20 kbar) were used. The pressure in the gas cell was measured in situ using a manometer. For the clamp cell a rock salt (halite) calibration curve was used for the pressure estimate, resulting in an error bar of about 1 kbar. After initial data reduction, the FULLPROF package58 was used for the intensity profile analysis and structure determination. More details of these experiments can be found in ref. 28.
High-pressure TDO
High-pressure TDO measurements were conducted at the National High Magnetic Field Laboratory, Florida State University (Tallahassee, Florida, USA) in magnetic fields up to 18 T using a TDO susceptometer59. The magnetic field was applied along the c axis of the crystal placed in a tiny copper-wire coil with 0.8 mm diameter and 1 mm height. This assembly was immersed into Daphne 7575 oil and encapsulated in a Teflon cup inside the bore of a piston-cylinder pressure cell made of a chromium alloy (MP35N). The pressure created in the cell was calibrated at room temperature and again at low temperature using the fluorescence of the R1 peak of a small ruby chip as a pressure marker60 with an accuracy better than 0.15 kbar. The pressure cell was immersed directly into 3He, allowing TDO measurements down to 350 mK.
High-pressure ultrasound measurements
We performed ultrasound measurements using the pulse-echo method with phase-sensitive detection technique35,61. Overtone polished LiNbO3 transducers with 36° Y-cut (longitudinal sound polarization) were used to generate and detect ultrasonic signals with a frequency of about 35 MHz. The transducers were bonded to natural (001) crystal surfaces of a DTN sample with Thiokol 32, providing k∥u∥H∥c experiment geometry. The crystal dimensions were 0.3 × 0.3 × 2.95 mm3. We determined the low-T sound velocity at zero field and pressure to v ≃ 2600 m/s, in agreement with33,34. A commercially available piston-cylinder cell with CuBe outer sleeve, NiCrAl inner sleeve, and tungsten carbide inner pistons (C&T Factory Co.,Ltd) was adapted for ultrasound experiments following 62, with Daphne oil 7373 as a pressure medium. The pressure cell (with a calibrated RuO2 temperature sensor on the outer side) was thermally anchored to the 3He pot of the cryostat via a copper rod. The pressure was estimated from the pressure-dependent superconducting transition of tin63,64.
High-pressure ESR
High-pressure ESR studies of DTN were performed employing a 25 T cryogen-free superconducting magnet ESR setup (25T-CSM) at the High Field Laboratory for Superconducting Materials, Institute for Materials Research, Tohoku University (Sendai, Japan)65,66. Gunn diodes were utilized as microwave sources for frequencies up to 405 GHz; the transmitted radiation power was detected using a hot-electron InSb bolometer operated at 4.2 K. A DTN crystal was loaded into a Teflon cup filled with Daphne 7474 oil as a pressure medium. A two-section piston-cylinder pressure cell made from NiCrAl (inner cylinder) and CuBe (outer sleeve) has been used. The key feature of the pressure cell is the inner pistons, made of ZrO2 ceramics. The applied pressure was calibrated against the superconducting transition temperature of tin63,64, detected by AC susceptometer. The actual pressure during the experiment was calculated using the relation between the load at room temperature and the pressure obtained at around 3 K; the pressure calibration accuracy was better than 0.5 kbar67.
DMRG calculations
The DMRG calculations utilized the Julia version of the ITensors package68,69. A 249-site anisotropic S = 1 chain was simulated. The calculations were performed on the hemera cluster (HZDR).
Data availability
The data that support the findings of this study are available from the corresponding author upon request.
References
Sachdev, S. Quantum Phase Transitions (Cambridge Univ. Press, 2011).
Vojta, M. Quantum phase transitions. Rep. Prog. Phys. 66, 2069 (2003).
Sachdev, S. Quantum criticality: competing ground states in low dimensions. Science 288, 475 (2000).
Giamarchi, T., Rüegg, C. & Tchernyshyov, O. Bose–Einstein condensation in magnetic insulators. Nat. Phys. 4, 198 (2008).
Zapf, V., Jaime, M. & Batista, C. D. Bose–Einstein condensation in quantum magnets. Rev. Mod. Phys. 86, 563 (2014).
Matsumoto, M. & Koga, M. Longitudinal spin-wave mode near quantum critical point due to uniaxial anisotropy. J. Phys. Soc. Jpn. 76, 073709 (2007).
Matsumoto, M., Normand, B., Rice, T. M. & Sigrist, M. Field- and pressure-induced magnetic quantum phase transitions in TlCuCl3. Phys. Rev. B 69, 054423 (2004).
Zhang, Z. et al. Phase diagram and magnetic excitations of anisotropic spin-one magnets. Phys. Rev. B. 87, 174405 (2013).
Scammell, H. D. & Sushkov, O. P. Multiple universalities in order-disorder magnetic phase transitions. Phys. Rev. B. 95, 094410 (2017a).
Zheludev, A. Quantum critical dynamics and scaling in one-dimensional antiferromagnets. J. Exp. Theor. Phys. 131, 34 (2020).
Rüegg, C. et al. Quantum magnets under pressure: controlling elementary excitations in TlCuCl3. Phys. Rev. Lett. 100, 205701 (2008).
Merchant, P. et al. Quantum and classical criticality in a dimerized quantum antiferromagnet. Nat. Phys. 10, 373 (2008).
Mills, D. L. Comment on “Bose–Einstein condensation of magnons in Cs2CuCl4”. Phys. Rev. Lett. 98, 039701 (2007).
Goto, K. et al. Pressure-induced magnetic quantum phase transition in gapped Spin system KCuCl3. J. Phys. Soc. Jpn. 75, 064703 (2006).
Matsumoto, M. et al. First ESR detection of Higgs amplitude mode and analysis with extended Spin-Wave theory in Dimer system KCuCl3. Appl. Magn. Reson. 52, 523 (2021).
Thede, M. et al. Pressure-induced quantum critical and multicritical points in a frustrated spin liquid. Phys. Rev. Lett. 112, 087204 (2014).
Hong, T. et al. Evidence for pressure induced unconventional quantum criticality in the coupled spin ladder antiferromagnet C9H18N2CuBr4. Nat. Comm. 13, 3073 (2022).
Glazkov, V. N., Smirnov, A. I., Tanaka, H. & Oosawa, A. Spin-resonance modes of the spin-gap magnet TlCuCl3. Phys. Rev. B. 69, 184410 (2004).
Glazkov, V. N., Yankova, T. S., Sichelschmidt, J., Hüvonen, D. & Zheludev, A. Electron spin resonance study of anisotropic interactions in a two-dimensional spin-gap magnet (C4H12N2)(Cu2Cl6). Phys. Rev. B. 85, 054415 (2012).
Dell’Amore, R., Schilling, A. & Krämer, K. U(1) symmetry breaking and violated axial symmetry in TlCuCl3 and other insulating spin systems. Phys. Rev. B. 79, 014438 (2009).
Kurita, N. & Tanaka, H. Magnetic-field- and pressure-induced quantum phase transition in CsFeCl3 proved via magnetization measurements. Phys. Rev. B. 94, 104409 (2016).
Hayashida, S. et al. Novel excitations near quantum criticality in geometrically frustrated antiferromagnet CsFeCl3. Sci. Adv. 5, eaaw5639 (2019a).
Zapf, V. S. et al. Bose-Einstein condensation of S = 1 nickel spin degrees of freedom in \({{{{{{{{\rm{NiCl}}}}}}}}}_{2}-4{{{{{{{\rm{SC}}}}}}}}{({{{{{{{{\rm{NH}}}}}}}}}_{2})}_{2}\). Phys. Rev. Lett. 96, 077204 (2006).
Zapf, V. S. et al. Direct measurement of spin correlations using magnetostriction. Phys. Rev. B. 77, 020404 (2008).
Psaroudaki, C. et al. Magnetic excitations in the spin-1 anisotropic antiferromagnet NiCl2–4SC(NH2)2. Phys. Rev. B. 85, 014412 (2012).
Paduan-Filho, A., Gratens, X. & Oliveira, N. F. High-field magnetization in the quantum spin magnet \({{{{{{{{\rm{NiCl}}}}}}}}}_{2}\cdot 4{{{{{{{\rm{SC}}}}}}}}{({{{{{{{{\rm{NH}}}}}}}}}_{2})}_{2}\). J. Appl. Phys. 95, 7537 (2004a).
Paduan-Filho, A., Gratens, X. & Oliveira, N. F. Field-induced magnetic ordering in \({{{{{{{{\rm{NiCl}}}}}}}}}_{2}\cdot 4{{{{{{{\rm{SC}}}}}}}}{({{{{{{{{\rm{NH}}}}}}}}}_{2})}_{2}\). Phys. Rev. B. 69, 020405 (2004b).
Mannig, A. Experimental Studies of Zero-field Phase Transitions in Quantum Magnets. PhD thesis, ETH Zürich (2017).
Zvyagin, S. A. et al. Pressure-tuning the quantum spin Hamiltonian of the triangular lattice antiferromagnet Cs2CuCl4. Nat. Commun. 10, 1064 (2019).
Shi, Z. et al. Emergent bound states and impurity pairs in chemically doped Shastry–Sutherland system. Nat. Commun. 10, 2439 (2019).
Shi, Z. et al. Discovery of quantum phases in the Shastry-Sutherland compound SrCu2(BO3)2 under extreme conditions of field and pressure. Nat. Commun. 13, 2301 (2022).
Coak, M. J. et al. Asymmetric phase diagram and dimensional crossover in a system of spin-\(\frac{1}{2}\) dimers under applied hydrostatic pressure. Phys. Rev. B. 108, 224431 (2023).
Chiatti, O. et al. Character of magnetic excitations in a quasi-one-dimensional antiferromagnet near the quantum critical points: Impact on magnetoacoustic properties. Phys. Rev. B. 78, 094406 (2008).
Chiatti, O. et al. Ultrasonic investigation of \({{{{{{{{\rm{NiCl}}}}}}}}}_{2}-4{{{{{{{\rm{SC}}}}}}}}{({{{{{{{{\rm{NH}}}}}}}}}_{2})}_{2}\). J. Phys. Conf. Ser. 150, 042016 (2009).
Lüthi, B. Physical Acoustics in the Solid State, Solid State Sciences (Springer, 2005).
Sakurai, T. et al. Direct observation of the quantum phase transition of SrCu2(BO3)2 by high-pressure and terahertz electron spin resonance. J. Phys. Soc. Jpn. 87, 033701 (2018a).
Jensen, J. & Mackintosh, A. R. Rare Earth Magnetism: Structures and Excitations (Clarendon Press, 1991).
White, S. R. Density matrix formulation for quantum renormalization groups. Phys. Rev. Lett. 69, 2863 (1992).
Schollwöck, U. The density-matrix renormalization group. Rev. Mod. Phys. 77, 259 (2005).
Albuquerque, A. F., Hamer, C. J. & Oitmaa, J. Quantum phase diagram and excitations for the one-dimensional S = 1 Heisenberg antiferromagnet with single-ion anisotropy. Phys. Rev. B 79, 054412 (2009).
Papanicolaou, N. & Spathis, P. Quantum spin-1 chains with strong planar anisotropy. J. Phys. Cond. Mat. 2, 6575 (1990).
Lindgård, P.-A. Correlation theory of crystal field and anisotropic exchange effects. J. Magn. Magn. Mater. 52, 47 (1985).
Zaliznyak, I. & Lee, S. In Modern Techniques for Characterizing Magnetic Materials (ed. Zhu, Y.) Ch.1 (Springer, 2005).
Sakai, T. & Takahashi, M. Effect of the Haldane gap on quasi-one-dimensional systems. Phys. Rev. B. 42, 4537 (1990).
Wierschem, K. & Sengupta, P. Characterizing the Haldane phase in quasi-one-dimensional spin-1 Heisenberg antiferromagnets. Mod. Phys. Lett. B. 28, 1430017 (2014).
Scammell, H. D. & Sushkov, O. P. Asymptotic freedom in quantum magnets. Phys. Rev. B. 92, 220401 (2015).
Scammell, H. D. & Sushkov, O. P. Nonequilibrium quantum mechanics: a “hot quantum soup” of paramagnons. Phys. Rev. B. 95, 024420 (2017b).
Hong, T. et al. Field induced spontaneous quasiparticle decay and renormalization of quasiparticle dispersion in a quantum antiferromagnet. Nat. Commun. 8, 15148 (2017).
Scammell, H. D. et al. Unifying static and dynamic properties in three-dimensional quantum antiferromagnets. Phys. Rev. B. 96, 174414 (2017).
Qin, Y. Q., Normand, B., Sandvik, A. W. & Meng, Z. Y. Amplitude mode in three-dimensional dimerized antiferromagnets. Phys. Rev. Lett. 118, 147207 (2017).
Povarov, K. Y. et al. Quantum criticality in a three-dimensional spin system at zero field and pressure. Phys. Rev. B. 96, 140414 (2017).
Mannig, A., Povarov, K. Y., Ollivier, J. & Zheludev, A. Spin waves near the edge of halogen substitution induced magnetic order in \({{{{{{{\rm{Ni}}}}}}}}{({{{{{{{{\rm{Cl}}}}}}}}}_{1-x}{{{{{{{{\rm{Br}}}}}}}}}_{x})}_{2}\cdot 4{{{{{{{\rm{SC}}}}}}}}{({{{{{{{{\rm{NH}}}}}}}}}_{2})}_{2}\). Phys. Rev. B 98, 214419 (2018).
Mannig, A. et al. Effect of disorder on a pressure-induced z = 1 magnetic quantum phase transition. Phys. Rev. B. 94, 144418 (2016).
Kinyon, J. S., Dalal, N. S., Clark, R. J., Zhou, H. & Choi, K. Y. Closing the spin gap of \({({{{{{{{{\rm{NH}}}}}}}}}_{4})}_{x}{{{{{{{{\rm{K}}}}}}}}}_{1-x}{{{{{{{{\rm{CuCl}}}}}}}}}_{3}\) through chemical substitution. Phys. Rev. Mater. 5, 054413 (2021).
Hayashida, S. et al. Chemical composition induced quantum phase transition in Cs1−xRbxFeCl3. Phys. Rev. B. 99, 224420 (2019b).
Paduan-Filho, A., Chirico, R. D., Joung, K. O. & Carlin, R. L. Field-induced magnetic ordering in uniaxial nickel systems: a second example. J. Chem. Phys. 74, 4103 (1981).
Yankova, T. et al. Crystals for neutron scattering studies of quantum magnetism. Philos. Mag. 92, 2629 (2012).
Rodríguez-Carvajal, J. Recent advances in magnetic structure determination by neutron powder diffraction. Phys. B. 192, 55 (1993).
Clover, R. B. & Wolf, W. P. Magnetic susceptibility measurements with a tunnel diode oscillator. Rev. Sci. Instr. 41, 617 (1970).
Piermarini, G. J., Block, S., Barnett, J. D. & Forman, R. A. Calibration of the pressure dependence of the R1 ruby fluorescence line to 195 kbar. J. Appl. Phys. 46, 2774 (1975).
Wolf, B. et al. New experimental techniques for pulsed magnetic fields - ESR and ultrasonics. Phys. B. 294-295, 612 (2001).
Mombetsu, S. et al. Study of localized character of 4f electrons and ultrasonic dispersions in SmOs4Sb12 by high-pressure high-frequency ultrasonic measurements. Phys. Rev. B. 94, 085142 (2016).
Smith, T. F. & Chu, C. W. Will pressure destroy superconductivity? Phys. Rev. 159, 353 (1967).
Eiling, A. & Schilling, J. S. Pressure and temperature dependence of electrical resistivity of Pb and Sn from 1–300 K & 0–10 GPa-use as continuous resistive pressure monitor accurate over wide temperature range; superconductivity under pressure in Pb, Sn and In. J. Phys. F: Met. Phys. 11, 623 (1981).
Sakurai, T., Ohta, H., Hara, S. & Saito, Y. High-pressure THz ESR. Appl. Magn. Reson. 52, 267 (2021).
Sakurai, T. et al. Development and application of 2.5 GPa-25 T high-pressure high-field electron spin resonance system using a cryogen-free superconducting magnet. J. Magn. Reson. 296, 1 (2018b).
Sakurai, T. et al. Development of multi-frequency ESR system for high-pressure measurements up to 2.5 GPa. J. Magn. Reson. 259, 108 (2015).
Bezanson, J., Edelman, A., Karpinski, S. & Shah, V. Julia: a fresh approach to numerical computing. SIAM Rev. 59, 65 (2017).
Fishman, M., White, S. R. & Stoudenmire, E. M. The ITensor software library for tensor network calculations. SciPost. Phys. Codebases https://doi.org/10.21468/SciPostPhysCodeb.4 (2022).
Acknowledgements
We thank A. Mannig, J. Möller, and G. Perren for their involvement at the early stage of the ETH Zürich part of the project. This work was supported by the Deutsche Forschungsgemeinschaft through ZV 6/2-2, the Würzburg-Dresden Cluster of Excellence on Complexity and Topology in Quantum Matter - ct.qmat (EXC 2147, Project No. 390858490) and the SFB 1143 (Project No. 247310070), as well as by HLD at HZDR, member of the European Magnetic Field Laboratory (EMFL) [K.Yu.P., S.A.Zv., S.Zh., A.H., J.W.]. The neutron-diffraction experiments at HB2a used resources at the High Flux Isotope Reactor, a Department of Energy Office of Science User Facility operated by the Oak Ridge National Laboratory. This work was partially supported by the Swiss National Science Foundation, Division II [A.Z.]. A portion of this work has been performed at the National High Magnetic Field Laboratory, which is supported by the National Science Foundation Cooperative Agreement DMR-1644779 and the State of Florida [D.E.G.]. ESR experiments were performed at the High Field Laboratory for Superconducting Materials, Institute for Materials Research, Tohoku University (proposal 19H0501 and 20H0501). Support of the ICC-IMR Visitor Program at Tohoku University is acknowledged [S.A.Zv.]. This work was partially supported by the Brazilian agencies CNPq (grant 304455-2021-0) and FAPESP (grant 2021-12470-8) [A.P.F.]. We also thank M. E. Zhitomirsky for fruitful discussions.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
S.A.Zv. conceived the project and performed the TDO (together with D.E.G.) and ESR (together with T.S., S.K. and H.N.) measurements; K.Yu.P. performed the analysis of this data and the numeric simulations. V.O.G. has performed the neutron diffraction measurements and analyzed the data. A.H. and S.Zh. have performed the ultrasound propagation measurements. M.N. has contributed to the preliminary high-pressure thermodynamic measurements. A.P.F. has synthesized the non-deuterated single crystals used in the study. H.O., H.N., A.Z. and J.W. administered at work at Kobe University and Tohoku University, ETH Zürich, and HZDR, respectively. All the authors have contributed to the discussions and manuscript writing.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Tao Hong and Lei Zhang for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Povarov, K.Y., Graf, D.E., Hauspurg, A. et al. Pressure-tuned quantum criticality in the large-D antiferromagnet DTN. Nat Commun 15, 2295 (2024). https://doi.org/10.1038/s41467-024-46527-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-024-46527-x
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.