Abstract
Electrons at the border of localization generate exotic states of matter across all classes of strongly correlated electron materials and many other quantum materials with emergent functionality. Heavy electron metals are a model example, in which magnetic interactions arise from the opposing limits of localized and itinerant electrons. This remarkable duality is intimately related to the emergence of a plethora of novel quantum matter states such as unconventional superconductivity, electronic-nematic states, hidden order and most recently topological states of matter such as topological Kondo insulators and Kondo semimetals and putative chiral superconductors. The outstanding challenge is that the archetypal Kondo lattice model that captures the underlying electronic dichotomy is notoriously difficult to solve for real materials. Here we show, using the prototypical strongly-correlated antiferromagnet CeIn3, that a multi-orbital periodic Anderson model embedded with input from ab initio bandstructure calculations can be reduced to a simple Kondo-Heisenberg model, which captures the magnetic interactions quantitatively. We validate this tractable Hamiltonian via high-resolution neutron spectroscopy that reproduces accurately the magnetic soft modes in CeIn3, which are believed to mediate unconventional superconductivity. Our study paves the way for a quantitative understanding of metallic quantum states such as unconventional superconductivity.
Similar content being viewed by others
Introduction
The Kondo lattice model has been key in qualitatively demonstrating how a myriad of correlated quantum matter states emerge1,2,3,4,5,6,7,8 from the interplay of local and itinerant electrons8,9,10. Beyond the strongly correlated electron materials for which this archetypal model was conceived, it applies to a growing list of novel quantum systems with potential for applications including the electronic transport through quantum dots11, voltage-tunable magnetic moments in graphene12, magnetism in twisted-bilayer graphene13 and in two-dimensional organometallic materials14, the electronic structure in layered narrow-electronic-band materials15, electronic resonances of Kagome metals16, metallic spin liquid states17,18,19 that may even be of chiral character20, skyrmions in centrosymmetric magnets21,22 and fully tunable electronic quasiparticles in semiconductor moiré materials23. Further, Kondo lattice models have been used to study flat-band materials24 and predict novel topological states such as topological superconductivity25 and quantum spin liquid states26, including the highly sought-after fractional quasiparticles27. Despite this continued relevance, quantitative predictions for real materials based on Kondo lattice models remain a formidable computational hurdle.
Metals containing cerium are firmly established model systems for the interplay between itinerant and localized electronic degrees of freedom and are ideal candidates to make progress on this issue. A prototypical case is CeIn3, whose phase diagram as a function of temperature T and hydrostatic pressure p is shown in Fig. 1a28. The formation of well-localized magnetic moments occurs due to Ce 4f orbitals that are buried close to the nuclei. A weak hybridization with conduction electron bands leads to a long-range magnetic exchange interaction between the moments known as the Ruderman–Kittel–Kasuya–Yosida (RKKY) interaction29,30,31 (see Fig. 1b). By increasing the strength of the hybridization, one can screen the magnetic moment through the Kondo effect, leading to a strongly renormalized electronic density of states near the Fermi energy. This heavy Fermi-liquid state borders the magnetically ordered state, from which it is separated by a magnetic quantum phase transition (QPT) that can be accessed via an external control parameter (here: pressure). Interestingly, novel quantum states (here: superconductivity32) emerge generically in the vicinity of the QPT suggesting that they are mediated by the associated magnetic quantum critical fluctuations8. To understand this emergence near QPTs in a quantitative manner requires a materials-specific microscopic model that incorporates relevant interactions to account for the magnetically ordered state and the resulting fluctuations.
a The magnetic phase diagram of the heavy electron material CeIn3 as a function of pressure p exemplary of many Kondo lattice materials. The Ruderman–Kittel–Kasuya–Yosida (RKKY) interaction arises when local cerium 4f moments polarize the surrounding conduction electron spins, which, in turn, interact with local moments on neighboring Ce sites (see b). At ambient pressure this results in antiferromagnetic (AFM) order. However, increasing pressure increases the overlap of neighboring 4f electron wave functions, and the hybridization with the conduction electrons. The Kondo effect then leads to the quenching of the local Ce moments, and the formation of strongly-renormalized non-magnetic heavy Fermi liquid (FL). The AFM and FL state are separated by a magnetic quantum phase transition (QPT). The underlying magnetic interactions are therefore not only responsible for the AFM order at ambient pressure, but the associated magnetic quantum fluctuations at the QPT drive the emergence of novel quantum states, in this case, of unconventional superconductivity (SC) and lead to non-Fermi liquid (NFL) behavior. b Because the RKKY interaction is mediated via conduction electrons (top panel) it is extremely long-range (bottom panel), compared to the lattice parameter a. It is also oscillatory in nature as we illustrate for a spherical Fermi-surface with radius kF (right panel), which results in a period λ ≈ π/kF in real space (bottom panel). However, as we demonstrate in Fig. 2, magnetic order on a Kondo lattice is not only mediated by RKKY interactions but additionally requires short-range superexchange and fourth-order particle-particle interactions.
Both for experiment and theory, the challenge in understanding real materials is the extreme energy resolution (~meV) required to capture the inherently small energy scales that emerge in the renormalized electronic state (see Fig. 2a). On the non-magnetic side of the QPT, a pioneering time-of-flight (TOF) neutron spectroscopy study33, complemented by a subsequent resonant inelastic X-ray (RIXS) scattering measurement34, on a selected material with a relatively large Kondo interaction (≈60 meV) has only recently achieved quantitative agreement with dynamical mean field theory (DMFT). In contrast, for the magnetic (or superconducting) state of interest here, the relevant energy scale is typically of the order of meV, making this a formidable issue. Materials-specific theoretical investigations of emergent phenomena in f-electron materials35,36 are often limited by the difficulty of validating low-energy effective models derived from complex high-energy input. Consequently, studies of such emergent states of matter are generally restricted to oversimplified models of real materials. Experimentally, in addition to the demand for energy resolution, the pivotal requirement is state-of-the-art momentum-transfer resolution. Notably, the long-range nature of RKKY exchange in real space (Fig. 1b) universally results in extremely sharp magnetic excitations in momentum space, as we elucidate below.
a Materials-specific microscopic parameters are contained in the multi-orbital periodic Anderson lattice model (MO-PAM), where f-electrons are well localized due to a strong Coulomb repulsion. These states, however, still fluctuate through hybridization with the conduction electron bands. By integrating out the high-energy conduction band states, one arrives at a minimal Kondo + Heisenberg lattice model (KHM). The Kondo interaction contains the spin exchange interaction with the conduction electrons (blue dashed line), while the Heisenberg interaction is a combination of short-range interactions arising from completely filled or completely unoccupied conduction bands (purple p-like orbital between the local moments) and a long-range interaction due to particle-particle processes not captured through the Kondo exchange (right process in the MO-PAM sketch, and pink wavy line in the KHM sketch). This Hamiltonian encapsulates the physics of heavy-fermion materials such as CeIn3. Finally, the low-energy conduction electrons can be integrated out to yield an effective spin Hamiltonian between local f-moments, which contains both the long-range RKKY interaction from the Kondo exchange (blue wavy line), and the other contributions explained above. b Results derived for CeIn3 using this approach are shown. The upper panel shows the electronic bandstructure that serves as input for the MO-PAM along the path RΓXMΓ. The inset on the right illustrates the position of these high symmetry points in the Brillouin zone. The cut-off Λ = 0.5 eV around the Fermi-energy EF allows short-range superexchange and long-ranged interactions to be seperated (see text for details). The lower panel shows the various contributions to the net magnetic interaction \({\tilde{I}}_{{{{{{{{\bf{q}}}}}}}}}\) in CeIn3 shifted by the indicated energies for visibility. The color of each contribution denotes the corresponding process of the same color in a.
Here we illustrate an approach to reduce a multi-orbital periodic Anderson model (MO-PAM) imbued with materials-specific hopping parameters to a minimal Kondo-Heisenberg lattice model that can form the basis for understanding emergent states of matter in various Kondo lattice materials (Fig. 2a). Using controlled fourth-order perturbation theory and the high combined momentum-transfer and energy resolution of the latest-generation TOF spectrometers, we resolve the full magnetic interaction over the entire range of relevant length scales. We thereby demonstrate that we can determine accurately the emergent energy scales four orders of magnitude smaller than the bare parameters of the initial MO-PAM. In doing so, we critically evaluate the assumptions made to date about heavy-fermion materials.
Results
Due to a simple cubic structure that facilitates numerical calculations and its characteristic Doniach phase diagram as a function of pressure p (Fig. 1a), CeIn3 is ideally suited to revisit the role of magnetic interactions on a Kondo lattice. As the MO-PAM was originally conceived to explain the localization of shielded electron shells37 and, in turn, offers a realistic theoretical treatment of coupled charge and spin degrees of freedoms in correlated metals, we begin with a 25-orbital PAM for CeIn3,
where \({c}_{{{{{{{{\bf{k}}}}}}}},s}^{{{{\dagger}}} }\) (ck,s) is the creation (annihilation) operator of band electrons with wavevector k and band index s, which includes the spin index. \({f}_{i,m\sigma }^{{{{\dagger}}} }\) (fi,mσ) denotes the creation (annihilation) operator of an f-electron state with lz = m (−3 ≤ m ≤ 3) and spin σ on lattice site i. The matrix elements \({h}_{{m}^{{\prime} }{\sigma }^{{\prime} };m\sigma }^{{{{{{{{\rm{SI}}}}}}}}}\) of the single-ion f-electron Hamiltonian include the crystal-field coefficients and intra-atomic spin-orbit coupling (see Methods for details). For CeIn3 and related materials, it is well established that the f2 state is energetically considerably less favorable than the f0 excited state38,39. Thus, we assume that the on-site repulsive interaction between f-electrons is infinitely large, implying that f2 configurations are excluded from the Hilbert space: \({f}_{i,m\sigma }^{{{{\dagger}}} }\,{f}_{i,{m}^{{\prime} }{\sigma }^{{\prime} }}^{{{{\dagger}}} }=0\). The dispersion of the conduction electrons (ϵk,s) and the hybridization between f and conduction electron states (Vk,mσs) are obtained from a tight-binding fit to the ab initio bandstructure calculation (see Methods and Supplementary Information for details). We find it important to include 18 conduction electron orbitals per spin (9 In-p, 3 In-s, 5 Ce-d and 1 Ce-s) to account fully for the electronic structure of the conduction bands near the Fermi level EF, and to obtain well localized f-orbitals. The spin-orbit coupling and crystal fields of CeIn3 allow that, out of the 14 f states, only the Γ7 ground state doublet needs to be included, which is separated by 12 meV from the Γ8 quartet excited state40. Hence, the energy of the Γ7 state (\({\epsilon }_{{{{\Gamma }}}_{7}}^{f}\)) is the one remaining free parameter in our model. We further demonstrate in the Supplementary Information that our ab initio band structure calculation is in agreement with the electronic structure determined via angle-resolved photo emission spectroscopy (ARPES) experiments41.
As the hybridization between the conduction electrons and the f-electrons is small, we can use degenerate perturbation theory (see Supplementary Information for details) to derive an effective Kondo-Heisenberg Hamiltonian,
where \({\tilde{f}}_{i,\sigma }^{{{{\dagger}}} }\) creates an f-electron in the lowest energy Γ7 doublet state (σ = {↑, ↓}) of site \(i,{S}_{{{{{{{{\bf{q}}}}}}}}}^{\nu }\) is the Fourier transform of the effective spin-1/2 operator \({S}_{i}^{\nu }\) (see Methods). The Kondo coupling is \({J}_{i,\sigma {\sigma }^{{\prime} }}^{{{{{{{{\bf{k}}}}}}}}s,{{{{{{{{\bf{k}}}}}}}}}^{{\prime} }{s}^{{\prime} }}=\frac{1}{N}{e}^{i({{{{{{{\bf{k}}}}}}}}-{{{{{{{{\bf{k}}}}}}}}}^{{\prime} })\cdot {{{{{{{{\bf{r}}}}}}}}}_{i}}{\tilde{V}}_{{{{{{{{\bf{k}}}}}}}},\sigma s}{\tilde{V}}_{{{{{{{{{\bf{k}}}}}}}}}^{{\prime} },{\sigma }^{{\prime} }{s}^{{\prime} }}^{*}/({E}_{F}-{\varepsilon }_{{{{\Gamma }}}_{7}}^{f})\) where \({\tilde{V}}_{{{{{{{{\bf{k}}}}}}}},\sigma s}\) is the hybridization projected to the Γ7 doublet. \({{{{{{{{\mathcal{H}}}}}}}}}_{{{{{{{{\rm{KH}}}}}}}}}\) contains effectively only the two conduction-electron bands that are close to the Fermi energy (the sum \({\sum }^{{\prime} }\) is restricted to band states within a cut-off Λ = 0.5 eV: ∣ϵk,s − EF∣ ≤ Λ and \(| {\epsilon }_{{{{{{{{{\bf{k}}}}}}}}}^{{\prime} },{s}^{{\prime} }}-{E}_{F}| \le {{\Lambda }}\); cf. top of Fig. 2b), as opposed to the 18 conduction bands in the MO-PAM. The remaining bands have been integrated out by including all fourth-order particle-hole and particle-particle processes that give rise to two types of magnetic interactions between the f-moments in \({I}_{{{{{{{{\bf{q}}}}}}}}}^{\mu \nu }\) (last term of Eq. (2)). Notably, in addition to short-ranged superexchange involving particle-hole and particle-particle processes with excited states outside the cut-off Λ (\({I}_{{{{{{{{\bf{q}}}}}}}}}^{{{{{{{{\rm{SE}}}}}}}}}\)), long-ranged interactions arise from fourth-order particle-particle processes with excited states inside the cut-off (\({\hat{I}}_{{{{{{{{\bf{q}}}}}}}}}^{({{{{{{{\rm{pp}}}}}}}})}\)) (cf. Fig. 2). This derivation provides the microscopic justification for including a Heisenberg term in model studies of the Kondo lattice (e.g.42,43). As we shall see below, it also plays an important role in understanding the magnetically ordered state of CeIn3. Importantly, this minimal Kondo-Heisenberg model still contains the materials-specific information through the dispersion relation of the conduction electrons and the Heisenberg exchange coupling.
To validate this new minimal Kondo-Heisenberg model for CeIn3 against experiments, and to illustrate the importance of the different contributions to magnetic interactions identified above, we further derive the RKKY Hamiltonian from the Kondo lattice term (first two terms of Eq. (2)) via an additional Schrieffer–Wolf transformation (see Supplementary Information)44,45. The resulting effective spin Hamiltonian is
The effective exchange interaction \({\tilde{I}}_{{{{{{{{\bf{q}}}}}}}}}\) is then a sum of the RKKY interaction \({I}_{{{{{{{{\bf{q}}}}}}}}}^{{{{{{{{\rm{RKKY}}}}}}}}}\), the superexchange \({I}_{{{{{{{{\bf{q}}}}}}}}}^{{{{{{{{\rm{SE}}}}}}}}}\) and the particle-particle contribution \({\hat{I}}_{{{{{{{{\bf{q}}}}}}}}}^{\,({{{{{{{\rm{pp}}}}}}}})}\). It turns out to be practically isotropic, \({\tilde{I}}_{{{{{{{{\bf{q}}}}}}}}}^{\mu \nu }\approx \,{\delta }_{\mu \nu }{\tilde{I}}_{{{{{{{{\bf{q}}}}}}}}}\), as a consequence of the weak influence of the spin-orbit interaction on the f−c hybridization amplitudes and the suppression of the f2 magnetic virtual states. In Fig. 2b, we show all resulting contributions along the path RΓXMΓ. The inset on the upper right corner of Fig. 2b shows the position of these high symmetry points in the Brillouin zone that define this path. For comparison with experiment, we note that the antiferromagnetic order of CeIn3 below a Néel temperature TN = 10 K is characterized by a magnetic propagation vector \({{{{{{{{\bf{q}}}}}}}}}_{{{{{{{{\rm{AFM}}}}}}}}}=\left(\frac{1}{2},\frac{1}{2},\frac{1}{2}\right)\)46 corresponding to the R point (cf. Figs. 1 and 2). Crucially, as shown in Fig. 2b, the RKKY interaction (blue line) typically thought to mediate magnetic order in Kondo lattice materials, has a global minimum near Γ = (0, 0, 0) and only a local minimum at R, demonstrating that it is not responsible for the onset of the observed order. Instead, the superexchange \({I}_{{{{{{{{\bf{q}}}}}}}}}^{{{{{{{{\rm{SE}}}}}}}}}\) (purple line) exhibits a global minimum at the R point. Finally, the particle-particle contribution near EF (\({\hat{I}}_{{{{{{{{\bf{q}}}}}}}}}^{({{{{{{{\rm{pp}}}}}}}})}\), pink line) is mostly flat, but is characterized by a pronounced, cusplike maximum at Γ. It is then essential to note that the global minimum of the net interaction \({\tilde{I}}_{{{{{{{{\bf{q}}}}}}}}}\) (bold cyan line) at the ordering wavevector R arises from the combination of two effects: a compensation between low-energy particle-particle and particle-hole contributions around the Γ point and the short-range antiferromagnetic superexchange interaction generated by the high-energy processes in both channels.
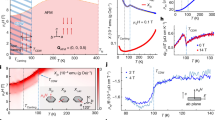
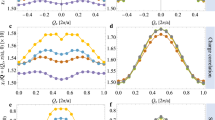
To go beyond the magnetic ground state and to test the theoretically calculated exchange interaction \({\tilde{I}}_{{{{{{{{\bf{q}}}}}}}}}\) quantitatively against experiment, we have carried out high-resolution neutron spectroscopy to measure the dispersion of the magnons in CeIn3, which is determined by the magnetic interactions derived above. Notably, the dispersion is given by \({E}_{{{{{{{{\bf{q}}}}}}}}}=S\sqrt{\left({\tilde{I}}_{{{{{{{{{\bf{q}}}}}}}}}_{{{{{{{{\rm{AFM}}}}}}}}}}-{\tilde{I}}_{{{{{{{{\bf{q}}}}}}}}}\right)\left({\tilde{I}}_{{{{{{{{{\bf{q}}}}}}}}}_{{{{{{{{\rm{AFM}}}}}}}}}}-{\tilde{I}}_{{{{{{{{{\bf{q}}}}}}}}}_{{{{{{{{\rm{AFM}}}}}}}}}+{{{{{{{\bf{q}}}}}}}}}\right)}\) with S = 1/2 and is shown as the solid blue line in Fig. 3a, which presents an overview of our results at T = 1.8 K. The key signature predicted by our model is a extremely dispersive magnon around the R point arising due to the steep local minimum of the long-ranged RKKY contribution; this was not identified in a previous study with modest resolution by Knafo et al., who instead reported a large magnon gap of more than 1 meV40. In contrast, the magnon dispersion determined from our neutron spectroscopy data as well as the observed magnetic intensity are in quantitative agreement with the calculated dispersion and intensity, respectively (see Fig. 3). Here the neutron intensities in Fig. 3 are expressed as the dynamic magnetic susceptibility \({\tilde{\chi }}^{{\prime\prime} }({{{{{{{\bf{Q}}}}}}}},\, E)\) and were converted to absolute units of \({\mu }_{{{{{{{{\rm{B}}}}}}}}}^{2}{{{{{{{{\rm{meV}}}}}}}}}^{-1}\) for comparison to theory. In particular, the energy and momentum transfer cuts through the magnon spectrum shown in Figs. 3c and d, respectively, demonstrate the excellent agreement between experiment and theory. Figure 4 showcases the steep magnon dispersion in a small region around the R point, which could only be uncovered by the most modern spectrometers (see Methods). Here panels a1, b1, and c1 show slices through the R point along the three cubic high-symmetry directions and confirm that the magnon gap is either absent or substantially smaller than the experimental resolution (ΔE = 106 μeV) as we show in detail in the Supplementary Information. A single fit parameter, \({\epsilon }_{{{{\Gamma }}}_{7}}^{f}=12.009\,{{{{{{{\rm{eV}}}}}}}}\), reproduces the experimental dispersion both with regard to the bandwidth and the magnon velocity. This showcases that our microscopic model, which starts with an ab initio bandstructure calculation with energy scales of 10 eV, is able to predict magnetic interactions on the order of meV. In addition to being quantitatively accurate, our calculations are robust against small changes of the chemical potential of the order of 10 meV (resolution of our band structure calculation), which modify the slope and bandwidth of the magnon dispersion by less than 1
Panels a and b show the imaginary part of the dynamic magnetic susceptibility \({\tilde{\chi }}^{{\prime\prime} }({{{{{{{\bf{Q}}}}}}}},\, E)\) obtained by our experiments and calculated via the MO-PAM model, respectively. Solid lines denote the magnon dispersion on the path γ = RΓXMΓ as calculated based on the effective spin interaction \({\tilde{I}}_{{{{{{{{\bf{q}}}}}}}}}\) [Eq. (3)] derived from the MO-PAM (blue solid line, see text for details), a Heisenberg model with a single nearest-neighbor exchange constant J1 (light green line), and the dispersion inferred from our neutron spectroscopy measurements (symbols). We refer to the inset on the upper right corner of Fig. 2b for the position of the high symmetry positions R, Γ, X, M, and Γ in the Brillouin zone. Experimental data points and error bars represent the location and standard deviation of the Gaussian peaks inferred from neutron spectroscopy data sets with incident neutron energies 3.315 meV (high-resolution, triangles) and 12 meV (high-energy, circles), by means of constant-energy and constant-momentum transfer cuts, respectively. All cuts investigated and the corresponding fits are shown in the Supplementary Information. The color-scale provides \({\tilde{\chi }}^{{\prime\prime} }({{{{{{{\bf{Q}}}}}}}},\, E)\) in absolute units of \({\mu }_{{{{{{{{\rm{B}}}}}}}}}^{2}{{{{{{{{\rm{meV}}}}}}}}}^{-1}\) along the path γ, as inferred from neutron spectroscopy data taken in the high-energy setting. For details see Methods. c Typical constant-momentum-transfer cuts through \({\tilde{\chi }}^{{\prime\prime} }({{{{{{{\bf{Q}}}}}}}},\, E)\) as illustrated for the two positions Q1 and Q2 on the paths XΓ and XM, respectively. Square symbols denote high-intensity neutron spectroscopy data and the blue solid lines MO-PAM calculations. Error bars represent the statistical error. The orange line corresponds to a Gaussian fit to the INS data. The orange and blue bars denote the systematic error in the conversion of the neutron intensity to absolute units and uncertainties in the calculation of the MO-PAM intensities, respectively (see Supplementary Information for details). d The integral of \({\tilde{\chi }}^{{\prime\prime} }({{{{{{{\bf{Q}}}}}}}},\, E)\) over energy, denoted \({\tilde{\chi }}_{{{{{{{{\bf{Q}}}}}}}}}^{{\prime\prime} }\). Circle symbols and the blue solid line correspond to \({\tilde{\chi }}_{{{{{{{{\bf{Q}}}}}}}}}^{{\prime\prime} }\) from high-intensity neutron data and MO-PAM calculations, respectively. Error bars represent the statistical error.
a1–c1 Magnon dispersion near the magnetic zone center R along the respective lines RΓ, RX, and RM. The color-coding reflects the imaginary part of the dynamic susceptibility, \({\tilde{\chi }}^{{\prime\prime} }({{{{{{{\bf{Q}}}}}}}},E)\), recorded with incident neutron energy Ei = 3.315 meV (see Methods for details). Squares and circles correspond to the locations of Gaussian profiles inferred from constant-energy cuts with one and two Gaussian profiles, respectively. All cuts investigated and the corresponding fits are shown in the Supplementary Information. The solid blue and light green lines denote the magnon dispersions calculated from our microscopic model and a fit of a short-range Heisenberg model with a single nearest-neighbor exchange constant J1 to our data, respectively. The dashed black line is a linear fit of the magnon dispersion close to the zone center used to extract the magnon velocity. a2–c2 At higher energies, where the splitting is larger than the FWHM of the experimental resolution, the profiles of constant-energy cuts were fitted by two Gaussian profiles. a3–c3 At energies below 0.6 meV for the RΓ and RX direction and below 0.4 meV for the RM direction, the splitting is restricted by the experimental resolution as indicated by the shaded profile. Error bars in panels a2–c2 and a3–c3 represent the statistical error.
Finally, we consider the role of short-range Heisenberg superexchange. Although the long-range RKKY interaction is widely credited with mediating magnetic order in Kondo lattice materials8, short-range superexchange interactions are commonly employed to fit the observed magnon dispersion47,48,49,50,51,52 and have been also used for CeIn340. As expected short-range superexchange allows us to model the magnon dispersion at high energy and the zone boundary well (cf. Fig. 3). Besides providing a microscopic justification for including short-range superexchange interactions, our model also demonstrates that they are not sufficient to explain the magnons near the magnetic zone center. We quantify this statement via the dimensionless parameter η that describes ratio of the magnon velocity v to the magnon bandwidth W. The experimental magnon bandwidth is \({W}_{\exp }=2.75(3)\,{{{{{{{\rm{meV}}}}}}}}\), as determined from the energy cuts in Fig. 3b. The experimental magnon velocity, \({v}_{\exp }=38.6(8)\,{{{{{{{\rm{meV/r.l.u.}}}}}}}}\), was inferred from linear fits to the measured dispersion near to the R point along the different high-symmetry directions and averaged over all directions (black dashed lines in Fig. 4 and Supplementary Information). The parameter \({\eta }_{\exp }=2.23(6)\) derived from our experiments compares favorably with ηMO−PAM = 2.27(5) computed from our model. In contrast, fits of the magnon dispersion with a single exchange constant J1 result in \({\eta }_{{J}_{1}}=0.58\), which stems from a substantial underestimation of the magnon velocity near the R point (cf. light green line in Fig. 4). We note that even adding a large number of additional higher-order exchange terms does not allow the large observed magnon velocity to be modeled accurately (see Supplementary Information), as was noted in previous studies47,51.
Discussion
Our study demonstrates that it is now possible to derive a minimal microscopic Kondo lattice model for a real material starting from ab initio electronic bandstructure calculations starting at energy scales of eV. This enables us to reproduce quantitatively the magnetic order and all relevant magnetic interactions in the prototypical Kondo lattice CeIn3 at energy scales 10,000 times smaller. Thus, it provides a tractable path for the accurate calculation of the low-energy spin excitations that arise due to strong electronic correlations, and are believed to mediate the emergence of novel quantum phases (cf. Fig. 1). Due to the long-range nature of the RKKY interaction, these magnetic soft modes are remarkably steep. This is also borne out by neutron scattering studies on further f-electron materials, which highlight the broad relevance of our results. Either steep magnon dispersions were observed directly47,51,53 or this key feature is concealed due to inadequate resolution, resulting in reports of potentially spurious magnon gaps48,52,54 similar to CeIn340. We note that the ability to resolve these steep low-energy spin excitations also ushers in high-resolution TOF spectroscopy as a complementary technique to access the electronic band structure of magnetically ordered heavy-fermion materials.
A further remarkable insight revealed by our calculations is that, in addition to the RKKY interaction, contributions from the particle-particle channel are equally crucial to quantitative description of the magnetic order and the magnon spectrum. In turn, our approach resolves several puzzles concerning magnetic order in heavy-fermion materials. First, it is consistent with neutron scattering studies of the magnon spectrum of various heavy fermion-materials, where the dispersion towards the zone boundary is well explained using short-range interactions47,48,49,49,50,51,52. Second, the presence of short-range interactions highlights why a large collection of heavy fermion materials exhibit commensurate AFM order46,48,55,56,57, even though RKKY interactions arising from generic Fermi surfaces typically favor incommensurate order. Finally, the apparent lack of 4f-based metallic ferromagnets is now understood quite simply by the presence of particle-particle interactions in metals, which generically disfavor the ferromagnetic ground state.
In summary, the combination of our MO-PAM approach with TOF spectroscopy establishes a straightforward recipe to obtain a quantitative, yet relatively simple, effective Kondo-Heisenberg Hamiltonian, which for CeIn3 includes only 2+1 orbitals (two conduction electron bands and one f level). In turn, studying this effective model as a function of pressure has the promising prospect of establishing the emergence of unconventional superconductivity in CeIn3 quantitatively. Notably, the short-range interaction promotes a local-moment magnetic state relative to the bare Kondo temperature, which may fundamentally alter the nature of the magnetic QPT observed under pressure58. Adding the Γ8 f-state to our calculation should equally allow us to reproduce the magnetic anisotropy emerging as a function of magnetic field59. Considering the ever-increasing computational power available, our approach is equally in reach for more complex materials with lower symmetry and more orbitals, which will allow us to unlock the microscopic understanding of a large number of quantum matter states with functional properties8. Further, our discovery that both short- and long-range interactions are key to understanding magnetic order in heavy fermion materials offers a straightforward explanation of their rich magnetic phase diagrams, where changing the balance of interactions by applying external tuning parameters allows us to select distinct magnetic ground states. Similarly, we anticipate that the combination of short- and long-ranged interactions will turn out to be a generic feature of metallic systems whose starting point is the periodic Anderson model. Finally, our study paves the way for ab initio modeling of quantum systems described by Kondo lattices and therefore suggests an avenue beyond a phenomenological description of the ground states of their strongly correlated electron systems.
Methods
Multi-orbital periodic Anderson model
The input parameters for the multi-orbital periodic Anderson model (MO-PAM) presented in Eq. (1) specific to CeIn3 were obtained by deriving a tight-binding model based on density functional theory (DFT) that accurately captures the electronic structure of the conduction bands near the Fermi level EF, and yields the hybridization between these bands and the 4f-orbitals. The underlying DFT band structure calculations were performed using the QUANTUM ESPRESSO package60 and fully relativistic projector augmented-wave (PAW) pseudopotentials with the Perdew-Burke-Ernzerhof (PBE) exchange-correlation functional, which are available in PSlibrary61. A realistic tight-binding Hamiltonian with 50 Wannier functions (25 orbitals times 2 for spin) was constructed using the Wannier90 package62. Details for all steps are provided in the Supplementary Material.
The low-temperature magnetic properties of CeIn3 at zero field are dominated by the low-energy Ce 4f Γ7 doublet that results from diagonalizing the single-site f-electron Hamiltonian [second term of Eq. (1)],
which includes the crystal field coefficients \({B}_{m,{m}^{{\prime} }}\) and the intra-atomic spin-orbit coupling λ (\({\zeta }_{{m}^{{\prime} }{\sigma }^{{\prime} };m\sigma }={\delta }_{{m}^{{\prime} },m}{\delta }_{{\sigma }^{{\prime} },\sigma }m\sigma /2+{\delta }_{{m}^{{\prime} },m+\sigma }{\delta }_{{\sigma }^{{\prime} },-\sigma }\sqrt{12-m(m+\sigma )}/2\)). The resulting Γ7 doublet reads
By taking the limit of infinite intra-atomic f-f Coulomb repulsion which eliminates the f2 configurations, we project \({{{{{{{{\mathcal{H}}}}}}}}}_{{{{{{{{\rm{MO}}}}}}}}-{{{{{{{\rm{PAM}}}}}}}}}\) into the low-energy subspace generated by the Γ7 doublet and obtain the periodic Anderson model
where the constrained operators \({\tilde{f}}_{i,\sigma }^{{{{\dagger}}} }\) (\({\tilde{f}}_{i,\sigma }\)) create (annihilate) an f-electron in the Γ7 doublet with σ = {↑, ↓} and \({\tilde{f}}_{i,\sigma }^{{{{\dagger}}} }{\tilde{f}}_{i,{\sigma }^{{\prime} }}^{{{{\dagger}}} }=0,\, {\epsilon }_{{{{\Gamma }}}_{7}}^{f}\) is the energy of the Γ7 states, and \({\tilde{V}}_{{{{{{{{\bf{k}}}}}}}},\sigma s}\) is the hybridization between the Γ7 doublet and the conduction electron states (1 ≤ s ≤ 36).
By treating the small hybridization \({\tilde{V}}_{{{{{{{{\bf{k}}}}}}}},\sigma s}\) as a perturbation, the periodic Anderson model can be reduced to the effective Kondo–Heisenberg Hamiltonian shown in Eq. (2). Furthermore, for strongly localized f-electrons, the Kondo lattice model can be further reduced to the RKKY Hamiltonian via second order degenerate perturbation theory in the Kondo interaction (see Supplementary Information for details). The final effective spin Hamiltonian \({{{{{{{{\mathcal{H}}}}}}}}}_{{{{{{{{\rm{spin}}}}}}}}}\) is presented in Eq. (3), where the pseudo spin-\(\frac{1}{2}\) operator is defined as \({{{{{{{{\bf{S}}}}}}}}}_{i}\equiv \frac{1}{2}{\tilde{f}}_{i,\alpha }^{{{{\dagger}}} }{{{{{{{{\boldsymbol{\sigma }}}}}}}}}_{\alpha \beta }{\tilde{\,f}}_{i,\beta }\) (σν are the Pauli matrices with ν = x, y, z), and its Fourier transform is defined as \({S}_{{{{{{{{\bf{q}}}}}}}}}^{\nu }=\frac{1}{N}{\sum }_{i}{e}^{i{{{{{{{\bf{q}}}}}}}}\cdot {{{{{{{{\bf{r}}}}}}}}}_{i}}{S}_{i}^{\nu }\). N is the total number of Ce atoms on the lattice (we take N → ∞ in the following calculation).
Sample preparation
To overcome the high absorption of cold neutrons by indium, plate-like single crystalline samples of CeIn3 were grown by the indium self-flux method and polished to a thickness of around 0.7 mm. To maximize the total scattering intensity 24 pieces were carefully coaligned on an aluminum sample-holder using a hydrogen-free adhesive (CYTOP) (see Sec. II.A of the Supplementary Information).
Neutron spectroscopy
Inelastic neutron scattering was carried out at the cold neutron chopper spectrometer CNCS at ORNL63. For the measurements, the crystal array was oriented in such a way that the crystallographic \(\left[1\overline{1}0\right]\) axis was vertical. Momentum transfers of neutrons are given in the reference frame of the sample by means of Q = Hb1 + Kb2 + Lb3, where H, K, and L denote the Miller indices and \({{{{{{{{\bf{b}}}}}}}}}_{\nu }=\frac{2\pi }{a}{\hat{{{{{{{{\bf{a}}}}}}}}}}_{\nu }\) (ν = 1, 2, 3) represent primitive translation vectors of the reciprocal cubic lattice (a = 4.689 Å). Throughout the manuscript and the SI, when stating components of momentum transfers the reciprocal lattice unit (\(1\cdot {{{{{{{\rm{r.l.u.}}}}}}}}:=\frac{2\pi }{a}\)) is omitted. To a given momentum transfer Q (upper-case letter), the reduced momentum transfer that equals the equivalent reciprocal space position in the cell 0 ≤ qν < 1, is given by q = q1b1 + q2b2 + q3b3 (labeled by a lower-case letter). Δq denotes the modulus of Δq. Reciprocal-space distances are also given in units \(1\cdot {{{{{{{\rm{r.l.u.}}}}}}}}:=\frac{2\pi }{a}\).
Time-of-flight neutron spectroscopy was performed with two different incident neutron energies. High-resolution experiments with incident neutron energy Ei,1 = 3.315 meV (ΔE = 106 μeV) permitted the study of the steep magnon dispersion in the vicinity of the reciprocal space position \({{{{{{{{\bf{Q}}}}}}}}}_{0}=\left(-\frac{1}{2},-\frac{1}{2},\frac{1}{2}\right)\), which represents the R point. A “high-energy” setting with incident neutron energy Ei,2 = 12 meV was performed to determine the magnon dispersion across the entire Brillouin zone. Data were collected in terms of a so-called Horace scan64, where the crystal is rotated around the vertical axis. In combination with the CNCS detector, which has large horizontal (from -50 to 140 degrees) and vertical ( ± 16 degrees) coverage, this allows one to obtain four dimensional data sets covering all three momentum transfer directions and energy transfer. Detailed information is provided in Sec. II of the Supplementary Information.
For Figs. 3, 4 the neutron intensity recorded in our experiments has been expressed as the imaginary part of the dynamic magnetic susceptibility \({\tilde{\chi }}^{{\prime\prime} }({{{{{{{\bf{Q}}}}}}}},\, E)\) in absolute units of \({\mu }_{{{{{{{{\rm{B}}}}}}}}}^{2}{{{{{{{{\rm{meV}}}}}}}}}^{-1}\) to enable direct comparison with the calculations of the dynamic magnetic susceptibility via the Multi-Orbital Periodic Anderson Model (see above). For this purpose, the recorded neutron intensities have been corrected for neutron absorption, put on an absolute scale via comparison to the well-known incoherent scattering of the sample, and finally background subtracted via data sets obtained below TN(for details of this procedure, we refer to the Supplementary Information). Further, the resulting corrected and normalized magnetic intensity was then corrected by the Bose factor accounting for the thermal population of magnon states, and subsequently divided by the square of the magnetic form-factor for Ce3+ as well as the ratio \(\left|{{{{{{{{\bf{K}}}}}}}}}_{f}\right|/\left|{{{{{{{{\bf{K}}}}}}}}}_{i}\right|\), whereby Ki and Kf denote the wavevectors of incident and scattered neutrons, respectively. For further information, we refer to the Supplementary Information. In the following, we additionally detail the integration ranges for the data shown in Figs. 3, 4. The data in Fig. 3a on the paths ΓR, RΓ, ΓX, XM, and MΓ were taken from the reciprocal space lines between the Q-positions \(\left(-1,-1,\,1\right)\) and \(\left(-\frac{1}{2},-\frac{1}{2},\,\frac{1}{2}\right)\), between \(\left(-\frac{1}{2},-\frac{1}{2},\, \frac{1}{2}\right)\) and \(\left(0,\, 0,\, 0\right)\), between \(\left(1,1,0\right)\) and \(\left(1,\, 1,\, \frac{1}{2}\right)\), between \(\left(-1,\,-\frac{1}{2},\, 1\right)\) and \(\left(-\frac{1}{2},-\frac{1}{2},\, 1\right)\), and between \(\left(\frac{1}{2},\, \frac{1}{2},\, 0\right)\) and \(\left(1 \,,\, 1,\,0\right)\), respectively. The intensity was integrated within a distance of ± 0.17 r.l.u. along the two Q-directions that are perpendicular to the path ΓXM and a distance of ± 0.09 r.l.u. along the two Q-directions that are perpendicular to the paths RΓ and MΓ. For the energy cuts shown Fig. 3b the intensity was integrated within a distance of ± 0.17 r.l.u. along three different reciprocal space directions. For the reduced momentum transfer cuts and slices shown in Fig. 4, the intensity was integrated within a distance of 0.08 r.l.u. along the two reciprocal space directions that are perpendicular to the reduced momentum transfer q. For the cuts in the lower panels, intensity was integrated over energies ± 0.1 meV.
We note that to resolve the sharp magnon dispersion high momentum resolution is required in addition to extreme energy resolution. Although triple-axis neutron spectroscopy is often credited with the best combined momentum-energy-transfer resolution, it fails to properly identify the dispersion even when used with the best resolution due to so-called Currat-Axe spurions65. To demonstrate this we have carried out additional measurements on the multiplexing triple axis spectrometer CAMEA at Paul Scherrer Institute66 using the identical sample and incident energies Ei = 4.15 meV, 4.8 meV, and 5.5 meV. Details of these measurements and the spurious features close to the zone center are shown in the Supplementary Information. This highlights the importance of modern TOF spectroscopy for the investigation of strongly correlated metals.
Data availability
The datasets generated during and/or analyzed during the current study have been deposited on the ONCat platform of Oak Ridge National Laboratory (ORNL) under the following digital object identifier: 10.14461/oncat.data.64d61647fd6850c0afce4da3/1994514 (https://doi.org/10.14461/oncat.data.64d61647fd6850c0afce4da3/1994514). Currently, the DOI-minting functionality in ONCat is still in beta and behind a firewall and you need to be on ORNL’s network to access it. This can be achieved going to https://analysis.sns.gov/ and registering an account, signing and starting a session. As soon as the DOI-minting functionality is publically available the data will directly available via the link above. The processed neutron spectroscopy data shown in the manuscript are available at the Zenodo database under accession code digital object identifier: 10.5281/zenodo.10146787 (https://zenodo.org/records/10146787)67.
Code availability
All code for the absorption correction of the neutron spectroscopy data is available in the Zenodo database under accession code digital object identifier: 10.5281/zenodo.10147126 (https://zenodo.org/records/10147126)68.
References
Pfleiderer, C. Superconducting phases of f-electron compounds. Rev. Mod. Phys. 81, 1551 (2009).
Ronning, F. et al. Electronic in-plane symmetry breaking at field-tuned quantum criticality in CeRhIn5. Nature 548, 313 (2017).
Seo, S. et al. Nematic state in CeAuSb2. Phys. Rev. X 10, 011035 (2020).
Mydosh, J. A. & Oppeneer, P. M. Colloquium: Hidden order, superconductivity, and magnetism: the unsolved case of URu2Si2. Rev. Mod. Phys. 83, 1301–1322 (2011).
Pirie, H. et al. Imaging emergent heavy Dirac fermions of a topological Kondo insulator. Nat. Phys. 16, 52 (2020).
Lai, H.-H., Grefe, S. E., Paschen, S. & Si, Q. Weyl–kondo semimetal in heavy-fermion systems. Proc. Natl Acad. Sci. 115, 93–97 (2018).
Jiao, L. et al. Chiral superconductivity in heavy-fermion metal UTe2. Nature 579, 523 (2020).
Paschen, S. & Si, Q. Quantum phases driven by strong correlations. Nat. Rev. Phys. 3, 9–26 (2021).
Kotliar, G. & Vollhardt, D. Strongly correlated materials: Insights from dynamical mean-field theory. Phys. Today 57, 53–59 (2004).
Dagotto, E. Complexity in strongly correlated electronic systems. Science 309, 257–262 (2005).
Cronenwett, S. M., Oosterkamp, T. H. & Kouwenhoven, L. P. A tunable kondo effect in quantum dots. Science 281, 540–544 (1998).
Jiang, Y. et al. Inducing kondo screening of vacancy magnetic moments in graphene with gating and local curvature. Nat. Commun. 9, 2349 (2018).
Vahedi, J., Peters, R., Missaoui, A., Honecker, A. & de Laissardière, G. T. Magnetism of magic-angle twisted bilayer graphene. SciPost Phys. 11, 83 (2021).
Tuerhong, R. et al. Two-dimensional organometallic kondo lattice with long-range antiferromagnetic order. J. Phys. Chem. C 122, 20046–20054 (2018).
Shen, S. et al. Inducing and tuning kondo screening in a narrow-electronic-band system. Nat. Commun. 13, 2156 (2022).
Zhang, S. S. et al. Many-body resonance in a correlated topological kagome antiferromagnet. Phys. Rev. Lett. 125, 046401 (2020).
Nakatsuji, S. et al. Metallic spin-liquid behavior of the geometrically frustrated kondo lattice Pr2Ir2O7. Phys. Rev. Lett. 96, 087204 (2006).
Tokiwa, Y., Ishikawa, J. J., Nakatsuji, S. & Gegenwart, P. Quantum criticality in a metallic spin liquid. Nat. Mater. 13, 356–359 (2014).
Tokiwa, Y., Stingl, C., Kim, M.-S., Takabatake, T. & Gegenwart, P. Characteristic signatures of quantum criticality driven by geometrical frustration. Sci. Adv. 1, e1500001 (2015).
Machida, Y., Nakatsuji, S., Onoda, S., Tayama, T. & Sakakibara, T. Time-reversal symmetry breaking and spontaneous hall effect without magnetic dipole order. Nature 463, 210–213 (2010).
Kurumaji, T. et al. Skyrmion lattice with a giant topological Hall effect in a frustrated triangular-lattice magnet. Science 365, 914 (2019).
Khanh, N. D. et al. Nanometric square skyrmion lattice in a centrosymmetric tetragonal magnet. Nat. Nanotechnol. 15, 444 (2020).
Zhao, W. et al. Tgate-tunable heavy fermions in a moiré kondo lattice. Nature 616, 61–65 (2023).
Kumar, P., Chen, G. & Lado, J. L. Kondo lattice mediated interactions in flat-band systems. Phys. Rev. Res. 3, 043113 (2021).
Seifert, U. F. P., Meng, T. & Vojta, M. Fractionalized fermi liquids and exotic superconductivity in the Kitaev–Kondo lattice. Phys. Rev. B 97, 085118 (2018).
Hsieh, T. H., Lu, Y.-M. & Ludwig, A. W. W. Topological bootstrap: fractionalization from kondo coupling. Sci. Adv. 3, e1700729 (2017).
Han, C. et al. Fractional entropy of multichannel kondo systems from conductance-charge relations. Phys. Rev. Lett. 128, 146803 (2022).
Knebel, G., Braithwaite, D., Canfield, P. C., Lapertot, G. & Flouquet, J. Electronic properties of CeIn3 under high pressure near the quantum critical point. Phys. Rev. B 65, 024425 (2001).
Ruderman, M. A. & Kittel, C. Indirect exchange coupling of nuclear magnetic moments by conduction electrons. Phys. Rev. 96, 99–102 (1954).
Kasuya, T. A Theory of Metallic Ferro- and Antiferromagnetism on Zener’s Model. Prog. Theor. Phys. 16, 45–57 (1956).
Yosida, K. Magnetic properties of Cu-Mn alloys. Phys. Rev. 106, 893–898 (1957).
Mathur, N. D. et al. Magnetically mediated superconductivity in heavy fermion compounds. Nature 394, 39 (1998).
Goremychkin, E. A. et al. Coherent band excitations in CePd3: a comparison of neutron scattering and ab initio theory. Science 359, 186 (2018).
Rahn, M. C. et al. ondo quasiparticle dynamics observed by resonant inelastic x-ray scattering. Nat. Commun. 13, 6129 (2022).
Zwicknagl, G. Quasi-particles in heavy fermion systems. Adv. Phys. 41, 203–302 (1992).
Nomoto, T. & Ikeda, H. Fermi surface evolution and d-wave superconductivity in CeCoIn5: analysis based on LDA+DMFT method. Phys. Rev. B 90, 125147 (2014).
Anderson, P. W. Localized magnetic states in metals. Phys. Rev. 124, 41 (1961).
Sundermann, M. et al. Quantitative study of the f occupation in CeMIn5 and other cerium compounds with hard X-rays. J. Electron Spectrosc. Relat. Phenom. 209, 1–8 (2016).
Braicovich, L. et al. Spectroscopy of strongly correlated systems: resonant x-ray scattering without energy resolution in the scattered beam. Phys. Rev. B 75, 073104 (2007).
Knafo, W. et al. Study of low-energy magnetic excitations in single-crystalline CeIn3 inelastic neutron scattering. J. Phys.: Condens. Matter 15, 3741 (2003).
Zhang, Y. et al. Three-dimensional bulk electronic structure of the Kondo lattice CeIn3 revealed by photoemission. Sci. Rep. 6, 33613 (2016).
Si, Q., Rabello, S., Ingersent, K. & Smith, J. L. Locally critical quantum phase transitions in strongly correlated metals. Nature 413, 804 (2001).
Senthil, T., Sachdev, S. & Vojta, M. Fractionalized Fermi liquids. Phys. Rev. Lett. 90, 216403 (2003).
Fazekas, P. Lecture Notes on Electron Correlation and Magnetism (World Scientific Publishing Co. Pte. Ltd., 1999).
Yamada, T. & Hanzawa, K. Derivation of RKKY interaction between multipole moments in CeB6 by the effective Wannier model based on the bandstructure calculation. J. Phys. Soc. Japan 88, 084703 (2019).
Lawrence, J. M. & Shapiro, S. M. Magnetic ordering in the presence of fast spin fluctuations: a neutron scattering study of CeIn3. Phys. Rev. B 22, 4379 (1980).
Broholm, C. et al. Spin fluctuations in the antiferromagnetic heavy-fermion system U2Zn17. Phys. Rev. Lett. 58, 917 (1987).
van Dijk, N. H., Fåk, B., Charvolin, T., Lejay, P. & Mignot, J. M. Magnetic excitations in heavy-fermion CePd2Si2. Phys. Rev. B 61, 8922–8931 (2000).
Fåk, B., Raymond, S., Braithwaite, D., Lapertot, G. & Mignot, J.-M. Low-energy magnetic response of the noncentrosymmetric heavy-fermion superconductor CePt3Si studied via inelastic neutron scattering. Phys. Rev. B 78, 184518 (2008).
Stockert, O. et al. Magnetically driven superconductivity in CeCu2Si2. Nat. Phys. 7, 119 (2011).
Houmann, J. G., Rainford, B. D., Jensen, J. & Mackintosh, A. R. Magnetic excitations in praseodymium. Phys. Rev. B 20, 1105 (1979).
Das, P. et al. Magnitude of the magnetic exchange interaction in the heavy-fermion antiferromagnet CeRhIn5. Phys. Rev. Lett. 113, 246403 (2014).
Wiebe, C. R. et al. Gapped itinerant spin excitations account for missing entropy in the hidden-order state of URu2Si2. Nat. Phys. 3, 96 (2007).
Osborn, R., Loewenhaupt, M., Rainford, B. & Stirling, W. Magnons in CeAl2. J. Magn. Magn. Mater. 63-64, 70–72 (1987).
Kawarazaki, S. et al. Ground-state magnetic structure of CeRh2Si2 and the response to hydrostatic pressure as studied by neutron diffraction. Phys. Rev. B 61, 4167–4173 (2000).
Bao, W. et al. Magnetic structure of heavy-fermion Ce2RhIn8. Phys. Rev. B 64, 020401 (2001).
Gauthier, N. et al. Investigation of the commensurate magnetic structure in the heavy-fermion compound CePt2In7 using magnetic resonant x-ray diffraction. Phys. Rev. B 96, 064414 (2017).
Settai, R. et al. Change of the Fermi surface across the critical pressure in CeIn3: the de Haas-van Alphen study under pressure. J. Phys. Soc. Japan 74, 3016–3026 (2005).
Moll, P. J. W. et al. Emergent magnetic anisotropy in the cubic heavy-fermion metal CeIn3. Npj Quantum Mater. 2, 1 (2017).
Giannozzi, P. et al. Advanced capabilities for materials modelling with quantum ESPRESSO. J. Phys.: Condens. Matter 29, 465901 (2017).
Dal Corso, A. Pseudopotentials periodic table: From H to Pu. Comput. Mater. Sci. 95, 337–350 (2014).
Pizzi, G. et al. Wannier90 as a community code: new features and applications. J. Phys.: Condens. Matter 32, 165902 (2020).
Ehlers, G., Podlesnyak, A. A., Niedziela, J. L., Iverson, E. B. & Sokol, P. E. The new cold neutron chopper spectrometer at the Spallation Neutron Source: design and performance. Rev. Sci. Instrum. 82, 085108 (2011).
Ewings, R. A. et al. Horace: Software for the analysis of data from single crystal spectroscopy experiments at time-of-flight neutron instruments. Nucl. Instrum. Methods Phys. Res. A: Accelerators Spectrom. Detectors Assoc. Equipment 834, 132 (2016).
Shirane, G., Shapiro, S. M. & Tranquada, J. M. Neutron Scattering with a Triple-Axis Spectrometer: Basic Techniques (Cambridge University Press, 2002).
Lass, J. et al. Design and performance of the multiplexing spectrometer camea (2020). 2007.14796.
Simeth, W. et al. Dataset package for the manuscript “A microscopic Kondo lattice model for the heavy fermion antiferromagnet CeIn3". https://doi.org/10.5281/zenodo.10146787 (2023).
Simeth, W. wolfgangsimeth/NeutronAbsorptionPlatelikeSamples: Neutron Absorption in Platelike Samples. https://doi.org/10.5281/zenodo.10147126 (2023).
Acknowledgements
M.J. would like to thank Georg Ehlers for useful discussions concerning the setup of the CNCS experiment and acknowledges fruitful discussions with Bruce Normand. Work at Los Alamos National Laboratory was performed under the U.S. DOE, Office of Science, BES project “Quantum Fluctuations in Narrow Band Systems”. This research used resources at the Spallation Neutron Source, a DOE Office of Science User Facility operated by the Oak Ridge National Laboratory. WS is supported through funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No 884104 (PSI-FELLOW-III-3i). Z.W. was supported by funding from the Lincoln Chair of Excellence in Physics. During the writing of this paper, Z.W. was supported by the U.S. Department of Energy through the University of Minnesota Center for Quantum Materials, under Award No. DE-SC-0016371. FR thanks the hospitality of the University of Tokyo. Y.N. and R.A. acknowledge funding through Grant-in-Aids for Scientific Research (JSPS KAKENHI, Japan) [Grant No. 20K14423 and 21H01041, and 19H05825, respectively] and “Program for Promoting Researches on the Supercomputer Fugaku” (Project ID:hp210163) from MEXT, Japan.
Author information
Authors and Affiliations
Contributions
C.D.B., F.R., and M.J. conceived the study. Y.N., R.A., and F.R. carried out the electronic band structure calculations. Z.W., E.A.G., and C.D.B. derived the multi-orbital periodic Anderson model and Kondo–Heisenberg model. D.M.F. and M.J. designed the TOF experiments. W.S., D.G.M., and M.J. designed the CAMEA experiments. D.M.F., W.S., A.P., J.L., S.F., J.V., D.G.M., C.N., and M.J. carried out the experiments. J.V. comissioned and set up the low-temperature sample environment for CAMEA. N.H.S. and E.D.B. synthesized and characterized the samples. D.M.F. assembled the single-crystal mosaic. W.S. and M.J. analyzed the data. W.S., Z.W., C.D.B., F.R., and M.J. interpreted the results. W.S., Z.W., C.D.B., F.R., and M.J. wrote the paper with input from all the authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer?review
Peer review information
Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Simeth, W., Wang, Z., Ghioldi, E.A. et al. A microscopic Kondo lattice model for the heavy fermion antiferromagnet CeIn3. Nat Commun 14, 8239 (2023). https://doi.org/10.1038/s41467-023-43947-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-023-43947-z
This article is cited by
-
Machine learning assisted derivation of minimal low-energy models for metallic magnets
npj Computational Materials (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.