Abstract
Understanding metal-metal bonding involving f-block elements has been a challenging goal in chemistry. Here we report a series of mixed-valence di-metallofullerenes, ThDy@C2n (2n = 72, 76, 78, and 80) and ThY@C2n (2n = 72 and 78), which feature single electron actinide-lanthanide metal-metal bonds, characterized by structural, spectroscopic and computational methods. Crystallographic characterization unambiguously confirmed that Th and Y or Dy are encapsulated inside variably sized fullerene carbon cages. The ESR study of ThY@D3h(5)-C78 shows a doublet as expected for an unpaired electron interacting with Y, and a SQUID magnetometric study of ThDy@D3h(5)-C78 reveals a high-spin ground state for the whole molecule. Theoretical studies further confirm the presence of a single-electron bonding interaction between Y or Dy and Th, due to a significant overlap between hybrid spd orbitals of the two metals.
Similar content being viewed by others
Introduction
Metal-metal bonding is a classic research topic in chemical bonding studies and has been applied as a tool for developing molecular magnets as well as for addressing challenges in biology, energy, and catalysis1,2. Thus far, most of the metal-metal bonding studies have focused on the interactions involving d orbitals. By contrast, direct bonds between f-block metals are extremely difficult to prepare by conventional synthetic methods due to the limited extension of 4f or 5f orbitals, and remained elusive until the very recent isolation of a dilanthanide complex featuring lanthanide metal-metal bonds3. In this study, Long, Harvey, and Chilton et al. significantly demonstrated that single electron lanthanide metal-metal bonds, which give rise to an enormous coercive magnetic field at liquid nitrogen temperature, can be obtained in mixed-valence dilanthanide complexes (CpiPr5)2Ln2I3 (Ln = Gd, Tb, or Dy) via salt metathesis reaction4. On the other hand, Liddle et al. also reported the synthesis of a tri-thorium cluster with a delocalized 3-center-2-electron Th-Th bond very recently by using K2[C4(SiMe3)4] as the reduced reagent to generate thorium(III)-containing complexes which contains low-valence thorium ions in close proximity5.
Endohedral doping of fullerenes with a variety of metal atoms or metallic clusters to form endohedral metallofullerenes (EMFs) provides many possibilities for the investigation of metal-metal interactions6,7,8. In particular, di-metallofullerenes (di-EMFs), with only two metal atoms trapped inside the carbon cages, i.e. M2@C2n, provide a unique platform to study these bonding interactions. In these di-EMFs, the two metal atoms generally adopt relatively long metal-metal distances, dictated by the metal-cage interactions as well as by the repulsion between the partially ionized atoms due to electron density transfer to the carbon cages9,10,11,12,13. However, despite the long distances and the repulsion forces, the metal dimers cannot be dissociated inside the nano-scale fullerene cage, thus direct lanthanide metal-metal bonds, which are hardly accessible by conventional synthetic methods so far, can form inside the fullerene cages14. Recently, much progress has been made in the study of lanthanide metal-metal bonds inside fullerene cages15,16,17,18,19. In addition to the σ2 lanthanide metal-metal bond found for Lu2, Er2, and Sc2 inside the C3v(8)-C82 fullerene cage15,20, single electron lanthanide metal-metal bonds have attracted much attention because of their potential in the preparation of novel molecular magnets. A particular array of lanthanide metal dimers, i.e., Y2, Dy2, Gd2, Tb2, etc. were found to form single-electron bonds inside fullerene cages19,21. These di-EMFs were synthesized by arc-discharge method similar to those of other EMFs, but their carbon cages are either doped with N or attached with functional groups to obtain the stable compound in solution22,23. These results offered an evidence of single electron lanthanide metal-metal bonds and also showed that the outstanding single molecular magnetism of the corresponding di-EMFs arises from this unique bonding interaction18,19,24,25.
Metal-metal bonding between f-block elements, actinides, have also been proposed and studied by theoreticians26,27,28,29,30. Similar to the lanthanides, the synthesis and characterization of a molecular compound containing an actinide-actinide bond is still a great challenge5,31. Our recent studies show that two U atoms, as predicted by computational studies32, can be encapsulated inside an Ih(7)-C80 cage to form a stable di-metallic actinide EMF U2@Ih(7)-C8033. Moreover, the two low oxidation states of Th(III) were found to form a strong σ2 single actinide-actinide metal-metal bond in Th2@Ih(7)-C8034. These studies provide the experimental proof of actinide-actinide metal-metal bonds in a molecular compound and again demonstrates the advantage of using fullerenes as template structures to study these elusive metal-metal bonds involving f elements.
We wondered if this paradigm could be further extended to heteronuclear di-metallofullerene compounds with direct metal-metal bonding between a lanthanide and an actinide. The possibility of obtaining and characterizing lanthanide-actinide metal-metal bonds is not only interesting for endohedral fullerene studies, but more importantly, they may offer a potentially powerful platform for the fundamental understanding of f-block elemental chemistry.
Herein, we report the formation of unprecedented actinide-lanthanide single electron metal-metal bonds inside fullerene cages, giving rise to a series of mixed di-metallofullerenes, ThDy@C2n (2n = 72, 76, 78, and 80) and ThY@C2n (2n = 72 and 78). These mixed actinide-lanthanide di-EMFs were synthesized and characterized by single-crystal X-ray diffraction and multiple spectroscopic methods. In particular, SQUID magnetometry, ESR spectra, and computational analyses were performed to probe the actinide-lanthanide single-electron metal-metal bonding.
Results
Synthesis and isolation of ThX@C2n (X = Dy and Y; 2n = 72, 76, 78, and 80)
ThDy@C2n (2n = 72, 76, 78, and 80) and ThY@C2n (2n = 72 and 78) were synthesized by a modified arc-discharge method. Graphite, mixed with ThO2 and Dy2O3/Y2O3 (molar ratio of Th:Dy/Y:C = 1:1:24) were evaporated in a 200 Torr He atmosphere using a current of 90 A. The resulting soot was extracted with CS2 for 12 h. A multistage HPLC procedure was employed to isolate and purify the ThDy@C2n and ThY@C2n samples (Supplementary Figs. 2–8). The positive-ion mode MALDI-TOF mass spectra of purified ThDy@C2n (2n = 72, 76, 78, and 80) and ThY@C2n (2n = 72 and 78) (Supplementary Fig. 1) show single peaks at m/z = 1260.091, 1308.092, 1332.103, 1356.097, 1184.960, and 1256.961, respectively, and the experimental isotopic distributions agree well with the calculated ones. The purities of ThDy@C2n and ThY@C2n were confirmed by the observation of HPLC single peaks (Supplementary Fig. 1).
Molecular structures of ThX@C2n·[NiII(OEP)] (X = Dy and Y; 2n = 72, 76, 78, and 80)
The molecular structures of the obtained EMFs were determined by single-crystal X-ray diffraction studies. Black crystals with suitable sizes were obtained by slow diffusion from a benzene solution of NiII(OEP) (OEP = 2, 3, 7, 8, 12, 13, 17, 18-octaethylporphyrin anion) into a CS2 solution of the EMFs. As shown in Figs. 1 and 2, the six EMFs were all co-crystallized with one NiII(OEP) molecule, with substantial π − π interactions between them, and unambiguously refined as ThDy@D2(10611)-C72, ThDy@Cs(17490)-C76, ThDy@D3h(5)-C78, ThDy@Ih(7)-C80, ThY@D2(10611)-C72, and ThY@D3h(5)-C78. Among them, ThDy@D2(10611)-C72 and ThY@D2(10611)-C72 share the same non-isolated pentagon rule (non-IPR) fullerene cage, D2(10611)-C729. The cages of Cs(17490)-C76 and Ih(7)-C80 are fully ordered, and the other four cages are disordered over two orientations (cage A and cage B), as listed in Supplementary Table 1. The metal ions inside all the fullerene cages also show some disorder. Interestingly, due to the strong metal-pentalene interactions, the metal ions in the three non-IPR cages i.e. D2(10611)-C72 and Cs(17490)-C76, show less disorder than in the three IPR cages. Details of the metallic occupancies are summarized in Supplementary Table 2. Only the major cage orientations and metal sites are discussed below.
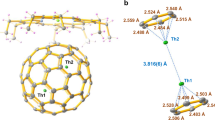
ORTEP drawings of a ThDy@D2(10611)-C72, b ThDy@Cs(17490)-C76, c ThDy@D3h(5)-C78, and d ThDy@Ih(7)-C80 with the co-crystallized NiII(OEP) molecule (upper) and the relative positions of the major Th1/Dy1 dimer to a partial region of the fullerene cage (below). Only the major cage orientations and metal sites, Th1 (green) and Dy1 (purple) are shown. Solvent molecules and hydrogen atoms are omitted for clarity. Metal-cage, metal-centroid, and metal-metal distances (in Å) are indicated.
a and c ORTEP drawings of ThY@D2(10611)-C72 and ThY@D3h(5)-C78 with the co-crystallized NiII(OEP) molecule. Only the major cage orientations and metal sites, Th1 (green) and Y1 (blue) are shown. Solvent molecules and hydrogen atoms are omitted for clarity. b and d Relative positions of the major Th1/Y1 unit localized in a region of the fullerene cage. Metal-cage, metal-centroid, and metal-metal distances (in Å) are indicated. e Isosurface (±0.002 au) of the spin density distribution for ThY@D3h(5)-C78. f ESR X-band spectra measured for a CS2 solution of ThY@D3h(5)-C78 under different temperatures (in K) with simulated results represented with smooth solid lines. Calculated (Calc.) EPR spectrum at the DFT level is also plotted, which is downfield 45 G shifted.
Figures 1 and 2 illustrate the enlarged regions showing the interactions between the encapsulated Th/Ln (Ln = Dy and Y) units and their corresponding cage moieties and for the dimers themselves. The Th/Ln ions are located over the [5, 5] bonds in non-IPR C72 and C76 cages and two parallel symmetrical hexagons in the IPR C78 and C80 cages. The lanthanide ions have slightly shorter metal-cage distances than the Th ions (Supplementary Tables 3 and 4). Th-cage distances are very close for all six fullerene cages, indicating that there is little influence of the cage size and shape on the metal-cage interactions. Further structural analyses show that the Th/Dy and Th/Y units have similar metal-metal distances when encapsulated in the same cage, 4.166(3)/4.183(1) Å in D2(10611)-C72 and 4.135(9)/4.144(8) Å in D3h(5)-C78. The results suggest that the lanthanide ions have a minor effect on the Th-Ln interactions, which may result from the similar lanthanide ionic radii, Y3+(0.90 Å) vs. Dy3+(0.91 Å)35. However, the Th/Dy unit has a metal-metal separation of 3.932(7) Å in Ih(7)-C80, which is notably shorter than those in D2(10611)-C72 (4.166(3) Å), Cs(17490)-C76 (4.193(2) Å), and D3h(5)-C78 (4.135(9) Å). This correlates with the fact that the longest axis of 7.84 Å inside the Ih(7)-C80 is much shorter than those of the D2(10611)-C72 (8.87 Å), Cs(17490)-C76 (8.58 Å), and D3h(5)-C78 (8.03 Å). This indicates that, while metal-cage distances are identical for the different cages, the Th-Ln interactions are largely cage-dependent.
It is noteworthy that the Th/Dy distance in Ih(7)-C80 of 3.932(7) Å is comparable to those of the Dy2 dimer in Dy2@C80(CH2Ph) (3.898(3) Å)18 and Dy2@C79N (3.89 Å)36 with a two-center single-electron (2c-1e) bond, but longer than that of the Th2 dimer that contains a covalent Th-Th bond in the same cage (3.816 Å)34. It might indicate that the Th/Dy interaction is likely comparable to those for Dy2@C80(CH2Ph) (3.898(3) Å)18 and Dy2@C79N (3.89 Å)36 with a 2c-1e single-electron bond.
Electronic structures of ThX@C2n (X = Dy and Y; 2n = 72, 76, 78, and 80) and electrochemical properties
DFT calculations show a spin-septet configuration for ThDy@D2(10611)-C72, ThDy@Cs(17490)-C76, ThDy@D3h(5)-C78 and ThDy@Ih(7)-C80 (Supplementary Fig. 10). The optimized Th-Dy distances, 4.187 Å for ThDy@D2(10611)-C72, 4.209 Å for ThDy@Cs(17490)-C76, 4.151 Å for ThDy@D3h(5)-C78, and 3.939 Å for ThDy@Ih(7)-C80, as well as the metal-cage distances are very close to the experimental values (Table 1). Different from ThDy@C2n, a spin-doublet electronic state is found for ThY@D2(10611)-C72 and ThY@D3h(5)-C78. Th and Y ions are located within the D2(10611)-C72 and D3h(5)-C78 cages in the same positions as the ThDy analogs. Th-Y and metal-cage distances are also shown in Table 1. Th-cage distances are nearly identical for the different sized cages, however, the Th-Y distances within the D2(10611)-C72 and D3h(5)-C78 are about 0.02 Å shorter than for ThDy, therefore there are longer Y-Ccage contacts than for Dy-Ccage.
The spin density distribution for ThDy@C2n and their individual Mulliken spin populations at metal atoms (~5.5 for Dy and ~0.5 for Th), computed for the septet state, show that the unpaired electrons are mainly localized on Dy with a contribution around half an electron at Th (Supplementary Figs. 10 and 13). These data indicate that the Dy and Th atoms have formal oxidation states of 2.5+ and 3.5+ , respectively. The ThDy cluster formally transfers six electrons to the fullerene, with a resulting electronic structure of (ThDy)6+@(C2n)6−. Figure 3a shows a rather simplified molecular orbital (MO) diagram for the ground spin-septet state of ThDy@D2(10611)-C72, ThDy@D3h(5)-C78 and ThDy@Ih(7)-C80 with one electron in the delocalized \(\sigma\) orbital. For simplicity, the corresponding MO diagram for ThDy@Cs(17490)-C76 is shown in the Supplementary Fig. 14a. Supplementary Figs. 15–18 provide the MOs associated with the Dy f9 for the ThDy@C2n series, which are localized on Dy and are found to be lower in energy compared to the σ-bonding orbital. For ThY@C2n, there is also a transfer of six electrons from ThY to the C2n cage. The corresponding MO diagrams for the ground spin-doublet state are also plotted in Fig. 3a, with one electron in the delocalized \(\sigma\) orbital. An interesting correlation between the ThX distances and the energies of the \(\sigma\) orbital for the different C2n cages was found, with the shortest metal-metal distance showing the \(\sigma\) bonding orbital with the lowest energy (C80 for ThDy and C78 for ThY, Fig. 3). This trend is confirmed by measuring the redox potentials, which are very different from those of EMFs containing pairs of lanthanides as La2 or Ce2 because of different electron occupations of the metal-metal (spd) sigma molecular orbitals, providing more evidence of the Ln-An single electron bond inside fullerene cages (see Supplementary Information).
a Molecular orbital (MO) diagrams for ThDy@D2(10611)-C72 and ThY@D2(10611)-C72. The energy levels of the delocalized sigma orbital a1 (for alpha- and beta-spins) are drawn in red and the associated MO isosurfaces (±0.03 a.u.) with the corresponding MO energy (in eV) are shown on the side. The energy levels for the highest six electrons (in black) from the cage are also represented. For more detailed MO diagrams, see Supplementary Fig. 12. b Spin density distribution with an isosurface of ±0.002 au for ThDy@D2(10611)-C72 and ThY@D2(10611)-C72. c MO isosurfaces (±0.03 a.u.) and MO energies (in eV) for the delocalized sigma orbital a1 for alpha- and beta-spins of ThDy@D2(10611)-C72, ThDy@D3h(5)-C78, ThDy@Ih(7)-C80, ThY@D2(10611)-C72 and ThY@D3h(5)-C78. d Molecular orbital contributions of the \(\sigma\)-type bonding orbital formed essentially by ns, np and (n-1)d metal orbitals.
The computed first oxidation and reduction potentials for ThY@C2n (2n = 72 and 78) show good agreement with the experimental data (see Supplementary Table 10). As expected from Fig. 3, the first oxidation process for both ThY@C72 and ThY@C78 involve MOs of the fullerene, with the triplet spin-state configuration being, by far, the lowest in energy. The first reduction process is predicted to take place at the Th-Y sigma orbital, which is the HOMO in the singlet spin configuration of the reduced system of ThY@C78 (see Supplementary Figs. 22 and 23 and Supplementary Table 11). We predict that the first reduction for all ThX@C2n (2n = 72, 78, and 80; X = Y and Dy) reported in this article occurs at the sigma Th-Ln orbital in line with the correlation between the energies of these orbitals and the first reduction potentials (Table 1).
Similar bonding has been previously reported for some Ln2@C2n species14. As shown in Fig. 3 and Supplementary Fig. 11, the a1 orbital exhibits similar electron distributions of s, p and d populations for the two metal atoms, so the single electron is shared by the two metals. Furthermore, Bader’s Quantum Theory of Atoms in Molecules37 was used to characterize the An(Th)-Ln(Dy) interaction. The bond critical point (BCP) postulated by Bader between two atoms is a necessary and sufficient condition for the atoms to be bonded. At the BCP, the corresponding values of electron density ρbcp and Laplacian of the electron density ∇2ρbcp for ThX@C2n series (X = Dy and Y) are also displayed in Table 1, confirming the presence of an accumulation of charge density in the center of the metal-metal bonds caused by a significant overlap between hybrid spd orbitals of the two metals. Note that we get smaller values than for Th2@Ih(7)-C8034, which also shows a smaller Th-Th distance and two electrons in the sigma bond.
ESR analysis of ThY@D 3h(5)-C78
The ESR spectra of ThY@D3h(5)-C78 as a function of temperature show a doublet, as expected for an unpaired electron mainly interacting with Y (nuclear spin I = 1/2 of 89Y, 100% natural abundance), while the nuclear spin of 232Th is 0 in 100% natural abundance. The smooth solid lines are simulated results using a hyperfine constant Aiso = 200 MHz and giso = 1.825 (for 220, 190 and 150 K) with EasySpin software package based on Hamiltonian (1).
DFT calculations are in full agreement with experiments, resulting in a calculated A of 206 MHz and a g value of 1.803 (Fig. 2f and Supplementary Fig. 20). The large hyperfine coupling constant indicates that there is a significant amount of spin density located on yttrium38,39. The isotropic signal with giso = 1.825 is somewhat smaller than the g value of a 6d single electron in traditional Th-based monometallic complexes40. Below 150 K, no signal was observed due to the frozen motion of ThY@D3h(5)-C78, which may broaden the spectral peaks. These results indicate that the unpaired electron is not on the fullerene cage but it is mainly confined to yttrium and partially delocalized on thorium, an indication that a single electron bond is formed between Y and Th, consistent with the electronic structure observed in the computations (Supplementary Fig. 13). The hyperfine coupling constant of ThY@D3h(5)-C78 is very similar to that found for Y2@C79N, in which a two-center single-electron sigma bond is also present39.
SQUID magnetometry of ThDy@D 3h(5)-C78
To further explore the electronic structure of the obtained dimetallo-EMFs, direct current (dc) magnetic measurements were performed for polycrystalline sample of ThDy@D3h(5)-C78. The temperature-dependent susceptibility data were collected under 1 kOe dc field in the temperature range of 2–300 K. The magnetic susceptibility χ at first remains almost constant as the temperature decreases (Supplementary Fig. 27), while the χT products slowly decrease as temperature changes from 300 K to around 10 K (Fig. 4c). The effect of crystal-field splitting is dominant with further cooling, and χT drops rapidly from 10 K to 2 K due to the depopulation of Stark sublevels. This variation tendency has been reported in many literatures4,41,42,43. Magnetization data were collected at 2, 3, 5, 8, and 10 K in the field range of 0∼50 kOe (Fig. 4b). The non-superposition of magnetization curves at different temperatures suggest magnetic anisotropy caused by the crystal field. Magnetic measurements showed that no hysteresis could be observed even at 2 K with the sweep rate of 500 Oe s−1. This is different from what previously observed for Ln2@C79N and Ln2@C80(CH2Ph) (Ln = Dy, Tb)19,36, which exhibit exceptionally high blocking temperatures at ca. 20 K. Compared with Dy(III) and Tb(III) ions, the f orbital of Th is more diffuse, and Th is more susceptible to the external crystal field (fullerene cage). The orbital angular momentum of Th is easily quenched, and thus the anisotropy is usually weak, leading to different electronic structure and magnetic behavior from Ln(III) ions. Therefore, the introduction of Th may cause ThDy@D3h(5)-C78 to exhibit completely different hysteresis behaviors from dilanthanide metallofullerenes. Besides, the Dy-to-ring-centroid distances in ThDy@D3h(5)-C78 (1.867 Å) is shorter than that in Dy2@C79N36 (average: 1.916 Å) and Dy2@C80(CH2Ph)18 (average: 1.988 Å) (Supplementary Table 13), indicating that the fullerene cage may have a stronger effect on the inner Dy ions, which likely reduce the uniaxial anisotropy and cause a much lower blocking temperature.
a Spin distributions and relative energies (in kcal·mol−1) for the lowest two spin states determined from CASSCF calculations. Atomic Mulliken spin densities are given for the lowest-energy spin state of each spin configuration. The arrow in the middle of the two metal atoms represents that the unpaired electron in the sigma bond is delocalized between the two centers. b Calculated magnetization curves measured at various temperatures (0.5, 1, 2, 3, 5, 8, and 10 K). Corresponding experimental curves at T = 2, 3, 5, 8, and 10 K are plotted in dashed lines. c Experimental vs. calculated normalized χT. d Low-energy spectrum with transition probabilities visualized as lines of different thicknesses (thicker lines correspond to higher probabilities), the x axis is the projection of magnetic moment upon the main anisotropy axis. Calculations in Fig. 4b–d include spin-orbit coupling.
CASSCF calculations for the ThDy@D3h(5)-C78 molecule were performed to corroborate the DFT results, as well as to determine the magnetic properties arising from the magnetic anisotropy of the Dy center. We used an active space with eight orbitals and ten electrons and explored the lowest quintet and septet states (Supplementary Table 7). For ThDy@D3h(5)-C78, in the spin-orbit free description, the spin-septet state is the lowest-energy state, confirming the results obtained from the DFT calculations, and it is followed by the spin-quintet state at 3850 cm−1 (11.0 kcal·mol−1) higher in energy (Fig. 5 and Supplementary Table 8). The spin distributions of the active orbitals for the lowest-energy spin states of ThDy@D3h(5)-C78 are displayed in Fig. 4a and Supplementary Table 8, being the spins parallel for all of the septet states. For the quintet states, the spin of the delocalized electron in the a1 orbital is antiparallel to the five f electrons localized on Dy. At PBE0 level, the energy difference between the high and low spin states is reduced to 1400 cm−1 (4.0 kcal mol−1), which is rather similar to the value reported for a related digadolinium endofullerene (1220 cm−1, 3.5 kcal·mol−1)19. When the spin-orbit coupling is considered at CASSCF level, the energy difference increases by 2100 cm−1 (6 kcal·mol−1, Fig. 5). In Fig. 5, we have correlated the spin-orbit states (SOC ≠ 0) with the spin-orbit free states (SOC = 0) computed at CASSCF level. We have named the states as if they were spherical atoms, 2S+1L, with SOC within a LS coupling scheme, which helps us in the interpretation of the results. Once the SOC is included, the level with J = 8 from septet state is the ground state multiplet (17 MJ states split in 450 cm−1 range), followed by J = 7 level from septet state (15 MJ states) at 2850 cm−1 (8 kcal·mol−1), and the J = 7 level (15 MJ states) from quintet state is found at 6000 cm−1 (17 kcal·mol−1). The lowest SO-levels show contributions dominated mainly from the SO-free septet states with a slight degree of mixing with quintet states.
The spin-orbit-free (left, SOC = 0) and the spin-orbit (right, SOC ≠ 0) states are represented in blue for the septet spin state and green for the quintet spin state. The number of spin-orbit-free states of each type, described as 2S+1L as if they were spherical atoms, are indicated. Relative energies in parentheses are in kcal·mol−1. The total angular momentum J (spherical atom approximation) is indicated in the SOC \(\ne\)0 section. We make the assignment of these atomic-like J values according to the manifold of MJ states for each level. The energy difference between the septet and quintet states (SOC = 0) is in bold, as well as the energy difference between the lowest-energy spin-orbit states derived from the septet and the quintet. For the lowest-energy level (J = 8), the representation of its 17 MJ states with their corresponding energies is plotted on the side showing the energy barrier (312 cm−1) and the energy splitting among these 17 states (450 cm−1). A scheme of the magnetic moment of Dy3+ (JDy = 15/2) and the spin in the sigma orbital (s = j = 1/2) alignment in the ground state is also shown. For sake of interpretation, we consider that the delocalized electron in the sigma a1 orbital has no first-order angular momentum (l = 0).
Figure 4b compares the calculated normalized magnetization vs. the experimental normalized magnetization at 2, 3, 5, 8, and 10 K, resulting in a good agreement between calculations and experiments with a saturation of the magnetization at a magnetic field between 1 and 2 T. In addition, calculated normalized χT curve was obtained and compared with the experimental normalized χT curve (Fig. 4c). Some discrepancies between calculation and experiment were observed in the χT vs T curves at low temperatures. These deviations are challenging to avoid due to the limited sample yield and the difficulty in accurately calculating the magnetic energy levels of 4f or 5f ions18,43,44. Nevertheless, from that, we corroborate (i) the spin-septet ground state of this system; and (ii) the high energy of the spin-quintet state that makes it to be non populated at room temperature. Such an energy difference likely comes from the nearly atomic-like Hund coupling between the sigma electron and the unpaired 4f electrons on Dy. As a consequence, the behavior of \(\chi\)T vs T plot is like a high-spin state with magnetic anisotropy in contrast to the \(\chi\)T curves reported for Dy2@C80(CH2Ph)18. For the latter, two centers (Dy) with magnetic anisotropy are coupled through a ferromagnetic interaction with the spin of the electron in the sigma Dy-Dy bond. Different from our systems, the reported studies of endohedral dilanthanofullerenes18,23,45,46 all contain two centers with magnetic anisotropy that could explain the larger values computed for the barrier of magnetization (426 cm−1 and 582 cm−1 for Dy2@C80(CH2Ph) and Dy2@C79N, respectively, vs. 312 cm−1 for ThDy@D3h(5)-C78), see Fig. 4d and Fig. 5. Magnetic studies are underway for other members of the An-Ln@C2n series to evaluate the relevance of the number of magnetic centers and metal-metal distances. Preliminary calculations show that the barrier of 400 cm−1 can be easily overcome.
Discussion
In summary, we report the synthesis and characterization of a series of mixed-valence dimetallo-EMFs, ThDy@C2n (2n = 72, 76, 78, and 80) and ThY@C2n (2n = 72 and 78), featuring single-electron actinide-lanthanide metal-metal bonds. These mixed-dimetallic EMFs were successfully isolated and structurally characterized by single-crystal X-ray diffraction and various spectroscopic methods. Crystallographic characterization unambiguously confirmed that Th and Ln metals (Y, Dy) can be encapsulated inside variable fullerene carbon cages with different size and symmetry and revealed the cage-dependent metal-metal distances. The ESR study of ThY@D3h(5)-C78 shows a doublet as expected for an unpaired electron interacting with the Y, and a SQUID magnetometric study of ThDy@D3h(5)-C78 revealed the high-spin ground state of the whole molecule. DFT and CASSCF calculations identify the presence of a single-electron bonding interaction between Y or Dy and Th, due to a significant overlap between hybrid spd orbitals of the two metals. Moreover, computational studies further suggest that the characteristic flexibility of Th in terms of oxidation states permits its sharing of an electron with the other metal, resulting in a formal oxidation state of +3.5.
The dimetallo-EMFs we report provide the experimental proof of direct lanthanide-actinide metal-metal bonding, which will add to our understanding of metal-metal bonding involving f-block elements. In fact, the six dimetallo-EMFs reported in this article represent only a small fraction of the many possible members of this new An-Ln@C2n family. Our preliminary studies show that single-electron metal-metal bonding can be formed between an array of lanthanides and U or Th. Computational studies predict that the coupling of a single electron in the sigma-bonding orbital with 4fn and 5fn on different lanthanides and actinides may give rise to exceptional magnetic properties to the bulk materials, which may help in the design and synthesis of next generation molecular magnets.
Methods
Synthesis and isolation of ThDy@C2n (2n = 72, 76, 78, and 80) and ThY@C2n (2n = 72 and 78)
The carbon soot containing thorium-dysprosium/yttrium-based EMFs was synthesized by the direct-current arc-discharge method. Graphite, mixed with ThO2 and Dy2O3/Y2O3 (molar ratio of Th:Dy/Y:C = 1:1:24) were evaporated in a 200 Torr He atmosphere with the current of 90 A. The resulting soot was extracted with CS2 for 12 h. The separation and purification of ThDy@C2n (2n = 72, 76, 78, and 80) and ThY@C2n (2n = 72 and 78) were achieved by a multistage HPLC procedure (Supplementary Figs. 2–8). Multiple HPLC columns, including Buckyprep-M (25 × 250 mm, Cosmosil, Nacalai Tesque Inc.), Buckyprep (10 × 250 mm, Cosmosil, Nacalai Tesque, Japan), 5PBB (10 × 250 mm, Cosmosil, Nacalai Tesque, Japan), and Buckyprep-M (10 × 250 mm, Cosmosil, Nacalai Tesque, Japan), were utilized in this procedure. Toluene was used as the mobile phase and the UV detector was adjusted to 310 nm for fullerene detection. The HPLC traces and single peaks of MALDI-TOF spectra for purified samples are shown in Supplementary Figs. 2–8.
Spectroscopic and electrochemical studies
The positive-ion mode matrix-assisted laser desorption/ionization time-of-flight (Bruker, Germany) was employed for mass characterization. UV-vis-NIR absorption spectra were measured in carbon disulfide at room temperature with a Cary 5000 UV-vis-NIR spectrophotometer (Agilent, U.S.). Cyclic voltammetry was performed in 1,2-dicholorbenzene (o-DCB) with 0.05 M (n-Bu)4NPF6 using a CHI-660E instrument.
X-ray crystallographic study
Black co-crystals of ThDy@C2n (2n = 72, 76, 78, and 80)·[NiII(OEP)] and ThY@C2n (2n = 72 and 78)·[NiII(OEP)] were obtained by allowing the benzene solution of [NiII(OEP)] and the CS2 solution of each sample to slowly diffuse at 4 °C for 2-3 weeks. X-ray diffraction data were collected at 120/130 K using a diffractometer (Bruker, D8 Venture) equipped with a CCD detector. The structures were solved by a direct method and refined with SHELXL-201547. The cif files of the six crystals in this work are shown in Supplementary Data 1 and ORTEP-style illustration with probability ellipsoids are shown in Supplementary Fig. 26.
ESR and SQUID magnetometry
Continuous-wave (CW) EPR experiments were performed on a Bruker ElexSys E580 spectrometer at the X-band (ω = 9.36 GHz) with the samples dissolved in CS2. The low-temperature environment was achieved by using an Oxford Instruments ESR900 and CF935 liquid helium cryostat. The EPR spectra were all simulated using the “EasySpin” toolbox based on MATLAB48. DC magnetic properties were determined using a Quantum Design MPMS3 VSM magnetometer. The sample was prepared by drop-casting from CS2 solution onto a slice of Al foil (3.224 mg), which is paramagnetic to minimize the background of the sample holder. Fast evaporation of the carbon disulfide afforded a black powder. After that, the Al foil was folded into a small cube and stuck on the inner wall of a plastic straw with very small amount of N grease (less than 1 mg).
Computational details
Kohn-Sham density functional theory (DFT) calculations were performed with the Amsterdam Density Functional (ADF, v. 2019) package49 using the PBE0 exchange correlation functional50,51,52, in conjunction with all-electron triple-ζ polarized (TZP) Slater-type orbital (STO) basis sets quality53,54. Scalar relativistic (SR) zero-order regular approximation (ZORA) was included for relativistic effects55. ‘D3’ dispersion corrections by Grimme were also performed56,57. ESR calculations were performed using an all-electron basis set with ADF and simulated with EasySpin package. Single points CASSCF calculations were carried out for the ThDy@C78 system using a PBE0 geometry with OpenMolcas14. The active space contains eight orbitals and ten electrons. Extended relativistic ANO-RCC-type basis sets were employed, in particular we used the ANO-RCC-VDZ for Dy and Th, and the ANO-RCC-MB for C. Scalar relativistic effects were considered with the Douglas-Kroll-Hess Hamiltonian37. Calculations of the magnetic properties for ThDy@C78 were performed at the CASSCF/SO-RASSI level of theory with the use of the SINGLE_ANISO module58.
Data availability
The X-ray crystallographic coordinates for structures reported in this study have been deposited at the Cambridge Crystallographic Data Centre (CCDC), under deposition numbers CCDC-2108663 (ThDy@D2(10611)-C72), CCDC-2108664 (ThDy@Cs(17490)-C76), CCDC-2108688 (ThDy@D3h(5)-C78), CCDC-2108689 (ThDy@Ih(7)-C80), CCDC-2108690 (ThY@D2(10611)-C72) and CCDC-2108694 (ThY@D3h(5)-C78). Copies of the data can be obtained free of charge via https://www.ccdc.cam.ac.uk/structures/. The Source Data files contain spectroscopy, chromatography, DC magnetic data, and xyz data of simulated structures. All other data supporting the findings of this study are available from the corresponding authors on request. Source data are provided with this paper.
References
Pfleiderer, C. et al. Coexistence of superconductivity and ferromagnetism in the d-band metal ZrZn2. Nature 412, 58–61 (2001).
Powers, I. G. & Uyeda, C. Metal–metal bonds in catalysis. ACS Catal 7, 936–958 (2017).
Liddle, S. T. Molecular metal-metal bonds: compounds, synthesis, properties (John Wiley & Sons, 2015).
Gould Colin, A. et al. Ultrahard magnetism from mixed-valence dilanthanide complexes with metal-metal bonding. Science 375, 198–202 (2022).
Boronski, J. T. et al. A crystalline tri-thorium cluster with σ-aromatic metal-metal bonding. Nature 598, 72–75 (2021).
Bao, L., Peng, P. & Lu, X. Bonding inside and outside fullerene cages. Acc. Chem. Res. 51, 810–815 (2018).
Popov, A., Yang, S. & Dunsch, L. Endohedral Fullerenes. Chem. Rev. 113, 5989–6113 (2013).
Lu, X., Feng, L., Akasaka, T. & Nagase, S. Current status and future developments of endohedral metallofullerenes. Chem. Soc. Rev. 41, 7723–7760 (2012).
Lu, X. et al. Chemical understanding of a non-IPR metallofullerene: Stabilization of encaged metals on fused-pentagon bonds in La2@C72. J. Am. Chem. Soc. 130, 9129–9136 (2008).
Cao, B. et al. Addition of adamantylidene to La2@C78: Isolation and single-crystal X-ray structural determination of the monoadducts. J. Am. Chem. Soc. 130, 983–989 (2008).
Yamada, M. et al. Metal atoms collinear with the spiro carbon of 6,6-open adducts, M2@C80(Ad) (M = La and Ce, Ad = adamantylidene). J. Am. Chem. Soc. 130, 1171–1176 (2008).
Beavers, C. M. et al. Very large, soluble endohedral fullerenes in the series La2C90 to La2C138: isolation and crystallographic characterization of La2@D5(450)-C100. J. Am. Chem. Soc. 133, 15338–15341 (2011).
Yamada, M. et al. Sc2@C66 revisited: an endohedral fullerene with scandium ions nestled within two unsaturated linear triquinanes. J. Am. Chem. Soc. 136, 7611–7614 (2014).
Popov, A. A., Avdoshenko, S. M., Pendás, A. M. & Dunsch, L. Bonding between strongly repulsive metal atoms: an oxymoron made real in a confined space of endohedral metallofullerenes. Chem. Commun. 48, 8031–8050 (2012).
Shen, W. et al. Lu2@C2n (2n = 82, 84, 86): Crystallographic evidence of direct Lu–Lu bonding between two divalent lutetium ions inside fullerene cages. J. Am. Chem. Soc. 139, 9979–9984 (2017).
Pan, C. et al. Crystallographic characterization of Y2C2n (2n = 82, 88–94): direct Y–Y bonding and cage-dependent cluster evolution. Chem. Sci. 10, 4707–4713 (2019).
Yang, T., Zhao, X. & Osawa, E. Can a metal–metal bond hop in the fullerene cage? Chem. Eur. J. 17, 10230–10234 (2011).
Liu, F. et al. Single molecule magnet with an unpaired electron trapped between two lanthanide ions inside a fullerene. Nat. Commun. 8, 16098 (2017).
Liu, F. et al. Air-stable redox-active nanomagnets with lanthanide spins radical-bridged by a metal–metal bond. Nat. Commun. 10, 571 (2019).
Yao, Y.-R. et al. Atomically precise insights into metal–metal bonds using comparable endo-units of Sc2 and Sc2C2. CCS Chem. 3, 294–302 (2020).
Hu, Z. et al. Endohedral metallofullerene as molecular high spin qubit: diverse rabi cycles in Gd2@C79N. J. Am. Chem. Soc. 140, 1123–1130 (2018).
Liu, F. et al. Single-electron lanthanide-lanthanide bonds inside fullerenes toward robust redox-active molecular magnets. Acc. Chem. Res. 52, 2981–2993 (2019).
Fu, W. et al. Gd2@C79N: Isolation, characterization, and monoadduct formation of a very stable heterofullerene with a magneticspin state of S = 15/2. J. Am. Chem. Soc. 133, 9741–9750 (2011).
Velkos, G. et al. Giant exchange coupling and field-induced slow relaxation of magnetization in Gd2@C79N with a single-electron Gd-Gd bond. Chem. Commun. 54, 2902–2905 (2018).
Wang, Y. et al. Electrophilic trifluoromethylation of dimetallofullerene anions en route to air-stable single-molecule magnets with high blocking temperature of Magnetization. J. Am. Chem. Soc. 143, 18139–18149 (2021).
Knecht, S., Jensen, H. J. A. & Saue, T. Relativistic quantum chemical calculations show that the uranium molecule U2 has a quadruple bond. Nat. Chem. 11, 40–44 (2019).
Roos, B. O., Malmqvist, P.-Å. & Gagliardi, L. Exploring the actinide−actinide bond: theoretical studies of the chemical bond in Ac2, Th2, Pa2, and U2. J. Am. Chem. Soc. 128, 17000–17006 (2006).
Wang, C.-Z. et al. Actinide (An = Th–Pu) dimetallocenes: promising candidates for metal–metal multiple bonds. Dalton Trans. 44, 17045–17053 (2015).
Gagliardi, L. & Roos, B. O. Quantum chemical calculations show that the uranium molecule U2 has a quintuple bond. Nature 433, 848–851 (2005).
Hu, H.-S. & Kaltsoyannis, N. The shortest Th–Th distance from a new type of quadruple bond. Phys. Chem. Chem. Phy. 19, 5070–5076 (2017).
Szczepanik, D. W. Bonding in a crystalline tri-thorium cluster: not σ-aromatic but still unique. Angew. Chem. Int. Ed. 61, e202204337 (2022).
Foroutan-Nejad, C. et al. Unwilling U–U bonding in U2@C80: cage-driven metal–metal bonds in di-uranium fullerenes. Phys. Chem. Chem. Phys. 17, 24182–24192 (2015).
Zhang, X. et al. U2@Ih(7)-C80: crystallographic characterization of a long-sought dimetallic actinide endohedral fullerene. J. Am. Chem. Soc. 140, 3907–3915 (2018).
Zhuang, J. et al. Characterization of a strong covalent Th3+–Th3+ bond inside an Ih(7)-C80 fullerene cage. Nat. Commun. 12, 2372 (2021).
Shannon, R. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Crystallogr. A 32, 751–767 (1976).
Wang, Y. et al. Dy2@C79N: a new member of dimetalloazafullerenes with strong single molecular magnetism. Nanoscale 12, 11130–11135 (2020).
Bader, R. F. W. Atoms in Molecules: a Quantum Theory (Clarendon Press, 1990).
Zhao, C. et al. Synthesis and structural studies of two paramagnetic metallofullerenes with isomeric C72 cage. Inorg. Chem. 58, 8162–8168 (2019).
Zuo, T. M. et al. M2@C79N (M = Y, Tb): Isolation and characterization of stable endohedral metallofullerenes exhibiting M-M bonding interactions inside aza[80]fullerene cages. J. Am. Chem. Soc. 130, 12992–12997 (2008).
Langeslay, R. R. et al. Synthesis, structure, and reactivity of the sterically crowded Th(3+) complex (C5Me5)3Th including formation of the thorium carbonyl, [(C5Me5)3Th(CO)][BPh4]. J. Am. Chem. Soc. 139, 3387–3398 (2017).
Vincent, A. H., Whyatt, Y. L., Chilton, N. F. & Long, J. R. Strong axiality in a dysprosium(III) bis(borolide) complex leads to magnetic blocking at 65 K. J. Am. Chem. Soc. 145, 1572–1579 (2023).
Liu, B.-C. et al. An imido ligand significantly enhances the effective energy barrier of dysprosium(iii) single-molecule magnets. Chem. Commun. 55, 9355–9358 (2019).
Goodwin, C. A. P. et al. Molecular magnetic hysteresis at 60 kelvin in dysprosocenium. Nature 548, 439–442 (2017).
Norel, L. et al. A terminal fluoride ligand generates axial magnetic anisotropy in dysprosium complexes. Angew. Chem. Int. Ed. 57, 1933–1938 (2018).
Singh, M. K., Yadav, N. & Rajaraman, G. Record high magnetic exchange and magnetization blockade in Ln2@C79N (Ln = Gd(III) and Dy(III)) molecules: a theoretical perspective. Chem. Commun. 51, 17732–17735 (2015).
Cimpoesu, F. et al. On exchange coupling and bonding in the Gd2@C80 and Gd2@C79N endohedral dimetallo-fullerenes. Mol. Phys. 113, 1712–1727 (2015).
Zhao, H. & Schuck, P. Combining biophysical methods for the analysis of protein complex stoichiometry and affinity in SEDPHAT. Acta Crystallogr. D 71, 3–14 (2015).
Stoll, S. & Schweiger, A. EasySpin, a comprehensive software package for spectral simulation and analysis in EPR. J. Magn. Reson. 178, 42–55 (2006).
Te Velde, G. et al. Chemistry with ADF. J. Comput. Chem. 22, 931–967 (2001).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple [Phys. Rev. Lett. 77, 3865 (1996)]. Phys. Rev. Lett. 78, 1396–1396 (1997).
Adamo, C. & Barone, V. Toward reliable density functional methods without adjustable parameters: the PBE0 model. J. Chem. Phys. 110, 6158–6170 (1999).
Perdew, J. P. Density-functional approximation for the correlation energy of the inhomogeneous electron gas. Phys. Rev. B 33, 8822–8824 (1986).
Becke, A. D. Density functional calculations of molecular bond energies. J. Chem. Phys. 84, 4524–4529 (1986).
Lenthe, E. V., Baerends, E. J. & Snijders, J. G. Relativistic regular two-component Hamiltonians. J. Chem. Phys. 99, 4597–4610 (1993).
Grimme, S., Antony, J., Ehrlich, S. & Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 132, 154104 (2010).
Grimme, S., Ehrlich, S. & Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 32, 1456–1465 (2011).
Aquilante, F. et al. Molcas 8: new capabilities for multiconfigurational quantum chemical calculations across the periodic table. J. Comput. Chem. 37, 506–541 (2016).
Acknowledgements
N. C. thanks the National Science Foundation China (NSFC NO. 52172051, 91961109) and the NSF of Jiangsu Province (BK20200041), the Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD). A.R.-F., J.M.P., and C.d.G. thank the Spanish Ministry of Science (grants PID2020-112762GB-I00 and PID2020-113187GB-I00), the Generalitat de Catalunya (grant 2021SGR00110) and the URV for support. Y.R.Y thanks the National Natural Science Foundation of China (22301288), the Anhui Provincial Natural Science Foundation (2308085MB31), and the Fundamental Research Funds for the Central Universities (WK2060000051). L.A. thanks the AGAUR for a Beatriu de Pinós fellowship. L.E. thanks the NSF for the generous support of this work under Grant CHE-1801317. The Robert A. Welch Foundation is also gratefully acknowledged for an Endowed Chair to L.E. (Grant AH-0033).
Author information
Authors and Affiliations
Contributions
N.C. conceived and designed the experimental work. Y.J.Y. synthesized and isolated all the compounds. Y.R.Y., Y.J.Y., and Q.Y.M. performed the crystallographic analysis. L.A., Y.R., A.R.-F., C.d.G., and J.M.P. performed the computations and theoretical analyses. S.G., B.W.W., R.S., and Y.H.F. performed the SQUID and ESR magnetometry. Y.J.Y. performed the electrochemical test. N.C., A.R.-F., J.M.P., L.E., Y. J.Y., L.A., S.R., Y.R.Y., Y.S., and M.H.J. co-wrote the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Eugenio Coronado and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Source data
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Yan, Y., Abella, L., Sun, R. et al. Actinide-lanthanide single electron metal-metal bond formed in mixed-valence di-metallofullerenes. Nat Commun 14, 6637 (2023). https://doi.org/10.1038/s41467-023-42165-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-023-42165-x
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.