Abstract
In non-interacting systems, bands from non-trivial topology emerge strictly at half-filling and exhibit either the quantum anomalous Hall or spin Hall effects. Here we show using determinantal quantum Monte Carlo and an exactly solvable strongly interacting model that these topological states now shift to quarter filling. A topological Mott insulator is the underlying cause. The peak in the spin susceptibility is consistent with a possible ferromagnetic state at T = 0. The onset of such magnetism would convert the quantum spin Hall to a quantum anomalous Hall effect. While such a symmetry-broken phase typically is accompanied by a gap, we find that the interaction strength must exceed a critical value for this to occur. Hence, we predict that topology can obtain in a gapless phase but only in the presence of interactions in dispersive bands. These results explain the recent quarter-filled quantum anomalous Hall effects seen in moiré systems.
Similar content being viewed by others
Introduction
Although topological insulators1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16 represent a new class of bulk insulating materials with gapless conducting edges, their physics is completely entailed by the band theory of non-interacting electrons. The new twist is that should two atoms reside in each unit cell, the standard insulating gap that obtains at half-filling, full lower band, does not tell the whole story when spin-orbit coupling1,2,3 is present. As long as time-reversal invariance is maintained, two spinful counter-propagating edge modes exist and exhibit a quantized conductance proportional to e2/h, thereby giving rise to a quantum spin Hall (QSH) effect in two dimensions. Within the Kane–Mele (KM)1,2 and Bernevig–Hughes–Zhang (BHZ)3 models, the QSH effect obtains only at half-filling. In a general non-interacting system, this physics obtains at a filling equal to the inverse number of atoms per unit cell, 1/q. This physics is robust to perturbations that yield only smooth deformations16 of the Hamiltonian. Additionally, the quantum anomalous Hall (QAH) effect, that is, the existence of a quantized Hall conductance with zero net magnetic field, also requires half-filling of the Haldane model17. As the QAH effect breaks time-reversal symmetry while the QSH effect does not, it is difficult for them to be realized in the same material.
However, recently, both effects18,19 have been observed in the same material in direct contrast to predictions of standard non-interacting models1,2,3. In the AB-moiré-stacked transition metal dichalcogenide (TMD) bilayer MoTe2/WSe218,19, the QSH insulator is observed at ν = 2 with the QAH effect residing at ν = 1. To date, this constitutes the first observation of the intertwining of these effects in the same material and hence the question of the minimal model required to explain the conflation of both is open. In terms of the 4-band KM/BHZ model, ν = 2 and ν = 1 correspond to half-filling and quarter-filling, respectively. Numerous theories20,21,22,23,24,25,26,27,28,29,30,31 have been put forth in this context, and the most recent experiment32 shows that both valleys contribute to the QAH effect and hence valley coherence rather than valley polarization is the operative mechanism. The striking deviation from the standard theory raises the question: can interactions drive either of these transitions away from half- to quarter-filling in the KM/BHZ models?
It is this question that we address here. We show quite generally that at a temperature above any ordering tendency, strong interactions shift the QSH effect to quarter filling with a decrease of the spin Chern number by a factor of two. However, the spin susceptibility exhibits a peak indicating a tendency to ferromagnetism as the temperature is lowered. Such an ordered ground state would be consistent with the Lieb–Schultz–Mattis33,34 (LSM) theorem and recent exact diagonalization35 on one of the models treated here. Whether or not such a ground state is gapped depends on the flatness of the band and interaction strength. In the flat-band limit, the ferromagnetic ground state is always gapped whereas for a dispersive band, the interactions must exceed a critical value for a gap to obtain. These results raise the possibility of a gapless topological semi-metallic state with non-trivial temperature corrections to the Hall conductance36. Generally, We argue that when the interactions dominate, the QSH must give way to a ferromagnetic QAH state at T = 0 at 1/4-filling. Since this is a generic conclusion on the most general models proven to undergird the QSH effect, we analyze the experiments19,32 in this context. Our model yields a quarter-filled QAH effect which coexists with a QSH effect at half-filling as is seen experimentally, in the presence of a flat lower band and intermediate interaction.
A brief survey of interacting topological systems is in order as our key result hinges on the interplay between the two. Most studies on the KM-Hubbard37,38,39,40 and the BHZ-Hubbard41,42,43,44 models focused on the half-filled system and found a transition from a QSH insulator to a topologically trivial anti-ferromagnetic Mott insulator as the interaction strength U increases. In addition, for models more relevant to flat-band twisted bilayer graphene, refs. 45,46 have provided a strong-coupling analysis and a density-matrix-renormalization group study47 has found that the gapless state at half-filling in the spinless (and hence Mottless) Bisritzer–MacDonald (BM) model48 yields a quantum anomalous Hall state in the presence of Coulomb interactions. In an extensive49 exact diagonalization study on an 8-band BM model, U(4) ferromagnets were observed always with the onset of a gap. Quantum Monte Carlo50,51 on the spinful model reveals a series of insulating states at half-filling. In the mean-field context, models focused on layered graphene systems have addressed the origin of quantum Hall ferromagnetism in the interacting BM model45,52,53 while others have argued that a topological Mott insulators (TMI) emerges at half-filling in the presence of on-site and nearest neighbor interactions in the tight-binding model (with only nearest-neighbor hopping) on a honeycomb lattice54. However, the latter proposal has not been substantiated by subsequent numerical studies55,56,57,58 that have found half-filling to be a trivial Mott insulator when interactions are sufficiently large. Interactions also lie at the heart of fractional topological insulators4,10,59,60,61 built from fractional Chern insulators62,63,64,65,66 which resemble the fractional quantum Hall effect but with no net magnetic field. Such phases appear at a fractional filling in a flat-band Δ0 ≫ W0 (where Δ0 is the non-interacting topological gap and W0 is the bandwidth) and require nearest-neighbor interactions. A recent study on the strongly interacting spinful Haldane model67 demonstrates that a Chern Mott insulator originates at quarter-filling with Chern number C = ± 1. This physics arises as a general consequence of an interplay between Mottness and topology.
Motivated by refs. 19,32,67, we explore the general phenomena that emerge from the interplay between Mottness and the QSH effect in the context of the KM and BHZ models. To demonstrate that the quarter-filled state is a TMI with a strongly correlated QSH effect, we numerically solve both the KM-Hubbard and BHZ-Hubbard Hamiltonians using determinantal quantum Monte Carlo (DQMC) as well as dynamical cluster approximation (DCA) and construct an analytically solvable Hamiltonian for a general interacting QSH system and obtain consistent results for sufficiently large interactions.
Results
Hubbard interaction
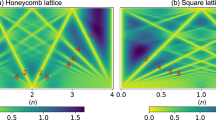
The DQMC simulation results for the generalized KM–Hofstadter–Hubbard (KM-HH) model (see “Methods”) on a honeycomb lattice at ψ = 0.81 and \({t}^{{\prime} }/t=0.3\) are shown in Fig. 1. For this choice of parameters, the non-interacting lower band is rather flat with bandwidth W0− ≈ 0.28 and the topological gap is Δ0 ≈ 1.62, the upper bandwidth is W0+ ≈ 4.37, where the subscript 0 indicates non-interacting. This mimics the flat-bands in moiré TMD experiments. The tunability of bandwidths in the KM model (unlike the bands in the BHZ model which are always dispersive W0+ = W0− ≥ Δ0) makes the KM model ideal for studying both flat-band and dispersive physics.
DQMC results for the flat-band generalized KM-HH model (\({t}^{{\prime} }=0.3,\psi=0.81\)) at U = 0, β = 7/t (a–c), U = 3t, β = 7/t (d–f) and U = 12t, β = 3/t (g–i). In each row, the compressibility, spin susceptibility and magnetization are presented in order from left to right as a function of magnetic flux and electron density. The dashed green lines in panels f and i serve as a guide to the eye for the crossing pairs of Landau levels in the QSH effect.
A key quantity that helps discern the topology in the presence of a probe magnetic field is the charge compressibility,
where the sublattice and spin summations are implied in ni. Regardless of density, the inverse slope of the leading straight-line incompressible valley that extends to the zero-field limit67 provides the Chern number. As a probe, this field does not alter our claim of a QSH phase at zero field. In the non-interacting case (Fig. 1a) at β = 7, there is a short middle vertical straight line at low fields which indicates a Chern number C0 = 0 at 〈n〉 = 2. This state bifurcates into two lines or equivalently two Landau levels (LLs) at higher magnetic flux. This crossing pair of zero-mode LLs is a reliable fingerprint for the QSH effects observed in experiments11. Note the asymmetry around 〈n〉 = 2 arises entirely because the lower band is flat while the upper band is dispersive. In this regime, the lines with finite slopes all represent the standard integer quantum Hall states.
The second quantity we calculate is the spin susceptibility defined as
where \({m}_{z}={\sum }_{{{{{{{{\bf{i}}}}}}}}}\langle {S}_{{{{{{{{\bf{i}}}}}}}}}^{z}\rangle /N\) is the magnetization per spin. The non-interacting spin susceptibility is related to the compressibility by χs = χ/(4β) as shown in Fig. 1b with reverse color scale. Fig. 1c shows the magnetization. Even though the Zeeman field is absent, a non-zero Peierls flux can magnetize the system since the spin-up and -down electron bands have different Chern numbers. The non-interacting results at lower temperatures can be found in the Supplement. What we alert the reader to is the absence of any topologically non-trivial states at 〈n〉 = 1.
In the presence of interactions U = 3t (already strongly correlated for the lower band), the new feature and hence prediction is the emergence of a topologically non-trivial state at 〈n〉 = 1. In Fig. 1d, the inverse slope of the trace extending to 〈n〉 = 1 is ± 1 and thus gives the Chern number. The absence of the right-moving counterpart signifies a QAH effect rather than a QSH effect. At 〈n〉 = 2, the standard QSH effect remains. Consequently, we have a system in which both the QAH and QSH effects obtain simply by changing the filling. For 〈n〉 > 2, the physics is weakly interacting as U < W0+. The bright peak in the spin susceptibility in Fig. 1e indicates a possible tendency for ferromagnetism at 〈n〉 = 1. This is supported by the asymmetry in the dotted lines that cross at zero field and 〈n〉 = 1 in the magnetization in Fig. 1f. Such asymmetry signifies that an infinitesimal field would lead to a polarization of the spins and hence ferromagnetism.
We then further increase the interaction strength but have to raise the temperature to β = 3 due to the Fermion sign problem in DQMC (see Supplement). In the final row of Fig. 1 for the compressibility when U = 12t, which far exceeds W0− + W0+ + Δ0 ≈ 6, the non-interacting QSH Landau fan vanishes for 〈n〉 = 2 turning into a trivial Mott insulator and most strikingly, a new LL emerges corresponding to the mirror image of the QAH state that terminates at 〈n〉 = 1. The presence of both Landau components completes the high-temperature QSH features at quarter filling. The magnetization (Fig. 1i) shows a more dramatic change than does the compressibility; namely it vanishes at 〈n〉 = 2 as a result of the anti-ferromagnetic Mott insulator. Further, the magnetization splits into peaks on either side of 〈n〉 = 1 that continues to be asymmetrical and hence is consistent with a tendency for spontaneous Ising ferromagnetism despite the presence of both LLs. This physics in Fig. 1d–f is only present in the flat-band limit when U is much larger than the bandwidth but comparable to the topological gap. Consequently, our theoretical work here is consistent with the sudden onset of the QAH state. Since the temperature for Fig. 1g–i is higher than the previous row, their features are softer.
To confirm the tendency for ferromagnetism, it is important to compute the temperature dependence of the spin susceptibility. Shown in Fig. 2a is the inverse spin susceptibility as the temperature is lowered with zero external magnetic flux. Displayed clearly is a possible divergence of the susceptibility (1/χs → 0) consistent with ordering. With extrapolation, we find that it supports a finite-temperature transition to ferromagnetism. Note that this does not violate the Mermin–Wagner theorem which forbids the spontaneous breaking of continuous symmetries at finite temperature in low-dimensional (d ≤ 2) systems with short-range interactions. In the KM-Hubbard model with spin-orbit coupling, the system no longer has the full SU(2) symmetry but only conserves \({\hat{S}}^{z}\). Then it is the Ising symmetry that is spontaneously broken in this transition and thus allowed at a finite temperature. As this is an interaction-driven effect, we expect an enhancement of the susceptibility as U increases. This is also borne out in Fig. 2b. Together these figures justify our claim of interaction-driven ferromagnetism as the temperature is lowered. A ferromagnetic QAH state will stabilize at zero temperature even though QSH features could be present at high temperatures when U is sufficiently large (Fig. 1g–i). We also observe a similar high-temperature phenomenon in the dispersive case ψ = 0.5 (see Supplement).
To show the generality of the 1/4-filled topological state, we consider the BHZ-Hofstadter-Hubbard (BHZ-HH) model (see “Methods”) on a square lattice. Note in this model, both bands are dispersive and have the same bandwidth. Without loss of generality, we set M/t = 1, then W0− = W0+ = Δ0 = 2t (t = 1 as the energy scale). The non-interacting 1/2-filled system is a QSH insulator with Cs = 2. It is the spin Chern number that describes a QSH insulator. To measure this quantity, we use a spin-dependent time-reversal-invariant (TRI) magnetic field inspired by cold-atom experiments68,69, namely ϕi,j → σϕi,j. The compressibility measured in this way we refer to as TRI compressibility. The minus sign coupled to spin-down electrons changes the corresponding Chern number \({C}_{\downarrow }^{{{{{{{{\rm{TRI}}}}}}}}}=-{C}_{\downarrow }\). Thus, the “TRI" Chern number measured in the TRI compressibility \({C}^{{{{{{{{\rm{TRI}}}}}}}}}={C}_{\uparrow }^{{{{{{{{\rm{TRI}}}}}}}}}+{C}_{\downarrow }^{{{{{{{{\rm{TRI}}}}}}}}}={C}_{\uparrow }-{C}_{\downarrow }={C}_{s}\) corresponds to the spin Chern number in the BHZ-HH model. This method overcomes the breakdown of the simple additivity formula for Cs when the spin channels are mixed and k is no longer a good quantum number in the presence of interactions. Through this quantity, we can read the spin Chern number from the inverse slope of the TRI compressibility (see the Supplement for the non-interacting examples).
The simulation results for the BHZ-HH models at U = 8t, β = 4/t are presented in Fig. 3. In Fig. 3a, two (red) straight lines appear from the zero-field 1/4 − and 3/4 − filled system, whose inverse slope indicates that the corresponding zero-field 1/4 − and 3/4 − filled BHZ-HH systems present QSH feature with Cs = 1 while the 1/2 − filled system becomes a topologically trivial Mott insulator with Cs = 0. This physics becomes much clearer by studying the standard charge compressibility in Fig. 3b which reveals identical features at 〈n〉 = 1 and 〈n〉 = 3 of left and right moving LLs indicative of the QSH effect. Also, the spin susceptibility exhibits a peak both at 〈n〉 = 1 and 〈n〉 = 3. The simultaneous appearance of compressibility minima and spin-susceptibility maxima are key features of this Mottness-driven QSH effect, in contrast to its non-interacting counterpart. The magnetization in Fig. 3d is also asymmetrical indicating a possible tendency towards ferromagnetism at 〈n〉 = 1 and 〈n〉 = 3. We return to this in a later section.
To corroborate our findings, we conducted a finite-size analysis (see Supplement) and confirm that the same spin Chern number survives in system sizes as large as Nsite = 12 × 12 with insignificant finite-size effects and hence our results are valid in the thermodynamic limit. We conclude then that the DQMC exhibits the QSH effect at high temperatures at 1/4-filling when U is sufficiently large.
Exactly solvable model for interacting quantum spin Hall insulators
The natural question arises: why is 1/4-filling the new topologically relevant filling and can it be understood in a simple way? The answer is yes. For a system with 2 atoms per unit cell, there should be interaction-induced insulating states at any integer filling up to 4 charges in each unit cell. The first such state should be at 1/4-filling. This physics arises naturally from a momentum-space formulation of the interactions which will result in 4-poles of the Green function, each corresponding to the four insulating states possible.
We now introduce the Hatsugai–Kohmoto (HK) interaction70,71,72 into a general QSH Hamiltonian,
Without loss of generality, we use the dispersions from the BHZ model (see Methods) setting M = 1 as an example. This interaction introduces Mottness by tethering double occupancy to k-space rather than the usual real space as in the well-known Hubbard model. As we will show, this model yields physics for strong interactions consistent with the Hubbard model. The reason for this consilience72 is that both models break the underlying \({{\mathbb{Z}}}_{2}\) (distinct from the classification scheme for topological insulators) symmetry of the non-interacting Fermi surface73. As the interaction commutes with the kinetic term, the original non-interacting wave function is untouched and momentum k remains a good quantum number. Therefore, it makes sense to extract the Chern number from an integration over the Brillouin zone. The interacting Green function can be written down analytically67,71 as
The Green function immediately reveals the effect of the correlations. The non-interacting lower and upper bands which were degenerate for spin-up and spin-down electrons split into singly and doubly occupied sub-bands as a result of Mottness. In the following, we use the abbreviation LSB and LDB for lower singly and doubly occupied sub-bands respectively, and likewise USB and UDB for the upper bands. The energy of the LSB and USB remains at the non-interacting value, while the LDB and UDB move up by a value equal to U. For a large enough U, the quarter-filled system emerges as an insulator with a filled LSB. This physics falls out naturally from the HK model because of the 4-pole structure of the Green function.
Since the interaction mixes the spin channels, leading to a huge degeneracy (\(d={2}^{{N}_{c}}\)) in the ground state (Nc is the number of unit cells), we need to average over all degenerate ground states74 to rigorously calculate the spin Chern number: \({\bar{C}}_{s}={\bar{C}}_{\uparrow }-{\bar{C}}_{\downarrow }\). For each spin, the contribution is
where fxy,σ is the normal Berry curvature defined with Bloch wave function75 because k remains a good quantum number in the HK model, and (1/2π)∫d2kfxy,σ = C0σ. When U = 0, 〈Ω∣nk,σ∣Ω〉 = 1 below the chemical potential. When U is finite, 〈Ω∣nk,σ∣Ω〉 can be 0 or 1. We can conduct the average first for Eq. (5). When U is large enough to fully separate the singly and doubly occupied bands, \((1/d)\mathop{\sum }\nolimits_{{{\Omega }}=1}^{d}\langle {{\Omega }}| {n}_{{{{{{{{\bf{k}}}}}}}},\sigma }| {{\Omega }}\rangle=\langle {n}_{{{{{{{{\bf{k}}}}}}}},\sigma }\rangle=\langle {n}_{\sigma }\rangle=1/2\). Then Eq. (5) becomes
Thus, the spin Chern number Cs = C0s/2 (we will drop the average bar symbol in the following text.). This result demonstrates that each momentum state is equivalently occupied by half spin-up and half spin-down electrons on average. Similarly, the LDB has the same Cs, while the USB and UDB have the opposite Cs. In short, the strongly correlated quarter-filled system becomes a Mott insulator with a spin Chern number Cs = C0s/2 should the interaction exceed the bandwidth.
To visualize how this phase emerges, we plot the band structure in Fig. 4 for varying U. With M = 1, the bandwidth for the lower and upper BHZ bands is W0+(−) = 2 and Δ0 = 2 is the topological gap. The non-interacting lower band has C0s = 2, while the upper band carries the opposite spin Chern number. We separate the non-interacting lower and upper bands into LSB (red-unmeshed), LDB (red-meshed), USB (green-unmeshed) and UDB (green-meshed). As derived above, the red and green sub-bands have the spin Chern number Cs = 1 and − 1 respectively. Turning on the interaction causes the doubly occupied sub-bands to increase in energy while the singly occupied sub-bands remain unchanged. For small interactions W0− > U > 0 (Fig. 4a), the band structure only slightly departs from the non-interacting case. As U increases to W0+ + W0− + Δ0 ≥ U ≥ W− (Fig. 4b), the same-color sub-bands fully separate, leading to a gap opening at quarter-filling. Then both the 1/4- and 3/4-filled systems become a TMI with a spin Chern number Cs = 1, while the 1/2-filled case becomes a conductor. Upon further increasing U to U > W0+ + W0− + Δ0 (Fig. 4c), the 1/2-filled state becomes a topologically trivial Mott insulator. All the while, the QSH Mott insulator at 1/4- and 3/4-fillings persists with a gap equal to Δ. For a different M, the intermediate panel b may change, while panel c is always valid for a large enough U. This indicates that generally in the presence of strong interactions, the system becomes a QSH Mott insulator at 1/4- and 3/4-filling with spin Chern number Cs = C0s/2 and a trivial Mott insulator at 1/2-filling.
Different phases emerge as U increases: a 1/2-filled QSH insulator for W0− > U > 0 (U = 0.5), b 1/4-filled TMI and 1/2-filled metal for W0− + W0+ + Δ0 ≥ U ≥ W0− (U = 3), and c 1/4-filled QSH Mott insulator and 1/2-filled topologically trivial Mott insulator for U > W0− + W0+ + Δ0 (U = 7). The red (or green) color represents Cs = 1 (or −1). The unmeshed (meshed) band consists of only singly (doubly) occupied states. It is the splitting of these bands by the interaction that gives rise to the Mott-derived topological physics.
As we compute in the Supplement, the spin susceptibility for the HK model diverges at T = 0 indicating that the HK model is unstable to ferromagnetic order in this limit. Note that this conclusion applies to a general QSH Hamiltonian (not only to the BHZ model) with HK interactions. This result is consistent with the divergence of the spin-susceptibility of the flat-band KM-Hubbard models. Ultimately this means that the 1/2-filled QSH effect would give rise to a 1/4-filled QAH effect at T = 0.
To summarize, this simple model offers a way of understanding why 1/4-filling is special in the Hubbard model. Note the agreement with the Hubbard simulations is non-trivial because momentum mixing is not present in HK model but is in the Hubbard model. Hence, the agreement demonstrates that it is the ultimate 4-pole structure of the underlying single-particle Green function that dictates the physics. As we have shown previously72,76, the HK model represents a fixed point in which no short-range repulsions are relevant not even Hubbard interactions. Hence, the HK model is the fixed point for Mott physics. Possible ferromagnetism at T = 0 would eventually turn the QSH effect into the QAH effect. Hence, as a result of interactions, the QAH effect appears as the symmetry-broken phase of the QSH effect much the way antiferromagnetism is the low-temperature symmetry-broken phase of a Mott insulator. Equal drivers of this spontaneous symmetry breaking are consistency with the LSM theorem and the restriction that the Chern number must be an integer. As is evident at 1/4-filling, the QAH always dominates as the symmetry-broken ground state. This is the primary conclusion of this work.
In a previous exact diagonalization study77 on a strict flat band model with Hubbard interactions and spin-orbit interaction, it was noticed that ferromagnetism emerged at 1/4-filling. This result can be viewed as a special case of HK physics because in the strict flat-band limit of the model studied, any value of U will necessarily prohibit double occupancy thereby producing a gapped state. The HK result is more general than this result as the gap persists even when the bands disperse.
Gap opening
In the previous sections, we have shown that both simulations on the Hubbard model and analytical calculations on the HK model indicate the emergence of non-trivial topology at 1/4-filling driven by strong correlations. In the non-interacting case, the topology appears with a bulk gap. In the strongly correlated case, however, this is not necessarily true. While a gap opens in the HK model as long as U exceeds the total bandwidth, the precise condition for opening a gap in the Hubbard model is much more subtle because of the dynamical mixing between the bands. In the Hubbard case, the interaction strength needs to exceed a critical value (\({U}_{c}^{{{{{{{{\rm{topo}}}}}}}}}\gg {W}_{0-}\)) to induce the topology at 1/4-filling and a separate critical value (\({U}_{c}^{{{{{{{{\rm{gap}}}}}}}}}\)) to open a gap. In general, we find \({U}_{c}^{{{{{{{{\rm{topo}}}}}}}}} \, < \,{U}_{c}^{{{{{{{{\rm{gap}}}}}}}}}\).
From the dip of the high-temperature compressibility computed by DQMC, we can tell roughly when the non-trivial topology appears and hence we are able to extract \({U}_{c}^{{{{{{{{\rm{topo}}}}}}}}}\). However, to access the gap information, one has to explore much lower temperatures. This can not be done by DQMC as we are restricted by the Fermion sign problem and finite-size effects (see Supplement for details). To address this problem, we resort to DCA78,79,80,81. We computed the value of the gap defined as
in the vicinity of the quarter-filled state in the generalized KM-Hubbard model using DCA on a 2 × 2 × 2 cluster at low temperature β = 20/t. To make contact with previous work on flat-band systems, we define the ratio r = Δ0/W0− and study the evolution of the gap as a function of the complex hopping phase, ψ in the generalized KM model (fixing \({t}^{{\prime} }=0.3\)). The results are summarized in Fig. 5a. We only plot the data when Δ(〈n〉 = 1) ≳ 0.2 because Δ(〈n〉 = 1) by definition remains a small value even when the state is metallic and obtain the \({U}_{c}^{{{{{{{{\rm{gap}}}}}}}}}\) by extrapolation to zero gap. In all cases, Δ(〈n〉 = 1) is significantly smaller than Δ0 even when U > W0− + W0+ + Δ0 ( ≈ 6). As the band becomes more dispersive (ψ decreases, or r decreases), Δ(〈n〉 = 1) reduces and \({U}_{c}^{{{{{{{{\rm{gap}}}}}}}}}\) grows as shown in Fig. 5a (Δ0 = 2 for all cases). Now we consider the relation between \({U}_{c}^{{{{{{{{\rm{gap}}}}}}}}}\) and \({U}_{c}^{{{{{{{{\rm{topo}}}}}}}}}\). Take ψ = 0.63 as an example (Δ0 = 2, W0− = 1). Already at U = 2t, the corresponding KM-HH model shows QAH topology at β = 8 in Fig. 5b, while \({U}_{c}^{{{{{{{{\rm{gap}}}}}}}}} \, \approx \,3.25\). The DQMC compressibility at zero field is shown in Fig. 5c at various \(U \, < \,{U}_{c}^{{{{{{{{\rm{gap}}}}}}}}}\). It exhibits that a dip at 〈n〉 = 1 starts to develop (and therefore the topological magnetic response) at a smaller U before the gap actually opens (see Supplement for a benchmark between DCA and DQMC). This supports a topological Mott semimetal (TMSM). In Fig. 5d, we find that for the semi-metallic state, the inverse spin susceptibility 1/χs decreases slowly with temperature and is unlikely to reach 0 at finite temperatures, while for the insulating state, the 1/χs drops much sharper with temperature so that its extrapolation supports a finite-temperature transition. We conclude that while the Chern numbers remain the same in the TMSM and insulating QAH phases, the TMSM phase lacks a gap and ferromagnetism as well.
a Estimated gap of the generalized KM-Hubbard model at quarter-filling as a function of the interaction strength U and the hopping phase ψ. These results are obtained from DCA simulations at a temperature of β = 20/t. b The DQMC compressibility for the KM-HH model at U = 2t, β = 8 around quarter-filling. c The zero-field DQMC compressibility for the KM-Hubbard model at various U and β = 8 as a function of the density. d The inverse temperature-dependent spin susceptibility from DQMC for KM-Hubbard model at U = 2t and 5t. b–d fix ψ = 0.63. All DQMC simulations are done on a 6 × 6 × 2 cluster while the DCA simulations are on a 2 × 2 × 2 cluster.
In Fig. 5a, at any finite value of r > 1, U must exceed a critical value \({U}_{c}^{{{{{{{{\rm{gap}}}}}}}}}\) for the gap to form. In general, \({U}_{c}^{{{{{{{{\rm{gap}}}}}}}}}\) increases as r decreases. When r = 1 (ψ = 0.5), we find the gap barely opens for U < 12 (Δ(〈n〉 = 1, U = 12) = 0.2). This situation is directly applicable to the BHZ-Hubbard model because in the topologically relevant region ( − 2 < M < 2), r ≤ 1. At M = 1 (which means r = 1), Δ(〈n〉 = 1, U = 12) = 0.22. However, we already observe the emergence of non-trivial topology at 1/4- and 3/4-filling in Fig. 3 at U = 8 and even U = 6 (see Supplement). Thus, such phases with non-trivial topology in actuality are semi-metals. Similar to the KM-Hubbard model, the spin susceptibility for these semi-metallic states only shows a soft peak and their temperature evolution does not support a finite-temperature transition (see Supplement). In such a system, the Hall conductance will have finite temperature corrections36 and hence deviate from the value dictated by the Chern number. This observation is in contrast with the recent exact diagonalization study on the BHZ-Hubbard model (with system size up to 3 × 4) which observes gap opening and ferromagnetic order for U > 4. As we show in the Supplement, the finite size effects are sizeable for the cluster size used in this study.
Experimental realization
While the interactions in ultracold atoms in optical traps82 can be adjusted to mimic the physics here, the most obvious synergy is with the moiré TMD experiments18,19,32 discussed previously. Our DQMC simulation result in Fig. 1 for the flat-band KM-HH model is consistent with this experiment in the existence of QAH and QSH at 1/4- and 1/2-filling, respectively.
However, we cannot make direct contact with the observation of valley coherence32 within a single-layer KM model in which spin-valley locking obtains. Note relaxing the spin-valley locking constraint of the KM model by reversing the spins in one of the bands relative to the other, as indicated in the experiment32 (see Supplement), would lead to a contradiction with a non-zero Chern number per spin in the band insulator limit. That is, the moiré band structure of AB stacked MoTe2/WSe2 bilayer can not be captured by a strict four-band model such as the KM model. The remedy is to construct an eight-band model (details in Supplement) consisting of two copies of the KM model, one for each layer with an effective voltage difference between the layers. For completeness, we recomputed the compressibility for the bilayer flat-band KM-HH model at an intermediate U = 1.5t. Clearly shown in Fig. 6a is the QAH at 〈n〉 = 1, the QSH at 〈n〉 = 2 and 〈n〉 = 4. Besides, there is also an emergent QAH state at 〈n〉 = 3. This prediction has been confirmed in a recent experiment on a moiré TMD material83.
The accompanying magnetization in Fig. 6b is also consistent with these assignments. Within the eight-band model, spin polarization requires layer coherence because the interaction does not commute with the interlayer hopping and since the same spin is assigned to different valleys in each layer, layer coherence necessarily entails valley coherence. Hence, a simple two-layer extension of our results is sufficient to account for the QAH effect in TMD moiré systems. This reasoning motivates first-principle calculations to determine how the 8-band model should be tailored to apply to specific moiré materials.
Discussion
Interactions play a non-trivial role in topology in two distinct ways. First, they lead to a TMSM/TMI with a high-temperature QSH effect characterized by a spin Chern number of Cs = 1 at quarter filling in the interacting BHZ and KM models. We use the term “Mott" because it is the interactions that lead to a lifting-up of the doubly occupied sector thereby exposing the topology of the 1/4-filled band. The resultant Cs = 1 poses a problem as this number must be even for a non-degenerate ground state84 with time-reversal symmetry. The resolution of this dilemma lies in the divergence of the spin susceptibility in the HK model at zero temperature and in the Hubbard model at finite temperature. Both of these indicate a possible spontaneous ferromagnetic phase at T = 0. The onset of ferromagnetism results with a unit Chern number indicative of the QAH effect and would offer a route around the LSM restriction33,34 that a unique featureless gapped ground state is impossible with an odd number of fermions per unit cell. Consequently, our results point to a fundamental reason why the QSH effect at high temperatures must resort to the QAH effect as temperature decreases if a gap opens. Namely, while at high temperatures, a paramagnetic symmetry-unbroken state obtains, for the ground state to be unique, the symmetry must be spontaneously broken. We refer to this onset of the symmetry-broken state as a consequence of topological Mottness85, in direct analogy with the traditional Mott state which has an antiferromagnetic ground state. Therefore, we argue that the 1/4-filled state is a TMI or TMSM. In analogy with the traditional Mott insulator with an antiferromagnetic ground state, a TMI exhibits the QSH phase which turns into the symmetry-broken QAH at low temperature as illustrated in Table 1. A TMI is qualitatively distinct from the fractional topological insulators4,10,59,60,61 driven by at least nearest-neighbor interactions. The fractional topological insulator usually consists of two decoupled fractional Chern insulators with opposite spins. However, in the TMI, spin-up and -down electrons are correlated to form the inseparable singly occupied states giving rise to the high-temperature QSH feature and a QAH ground state. Second, we showed that in the flat-band limit, a high-temperature QAH state exists also at 1/4-filling with an intermediate U. In the double-layer extension of this model, the QAH state exhibits valley coherence as is seen experimentally in moiré TMD materials32.
Methods
The model
All QSH models are based on Hamiltonians of the form,
where \({{{\Phi }}}^{{{{\dagger}}} }=\{{c}_{{O}_{1},\uparrow }^{{{{\dagger}}} }{c}_{{O}_{2},\uparrow }^{{{{\dagger}}} },{c}_{{O}_{1},\downarrow }^{{{{\dagger}}} }{c}_{{O}_{2},\downarrow }^{{{{\dagger}}} }\}\) is a four-component spinor, where O1/2 stands for different orbitals or sub-lattices, respectively. Eq. (8) means that the spin-up and spin-down electrons are described by a QAH Hamiltonian hQAH(k) = ha(k)τa (τa is the Pauli matrix for orbital/sublattice space) and its TR conjugate counterpart \({h}_{{{{{{{{\rm{QAH}}}}}}}}}^{*}(-{{{{{{{\bf{k}}}}}}}})\) with opposite chirality. As a result, the system is TR invariant and the half-filled case can be a topologically trivial and non-trivial insulator, categorized by a \({{\mathbb{Z}}}_{2}\) invariant or the spin Chern number Cs if \({\hat{S}}_{z}\) is conserved. As a consequence, any ferromagnetism here will be of the Ising type rather than U(4) as in the BM model49,53. To introduce Hubbard on-site interactions, we need to resort to a real-space representation of the QSH model. For concreteness, consider the generalized KM model18 in the honeycomb lattice under an external magnetic field, namely the KM-Hubbard-Hofstadter (KM-HH) model:
where ti,j contains the nearest-neighbor hopping t = 1 (as the energy scale) and next-nearest-neighbor hopping \({t}^{{\prime} }{{{{{{{{\rm{e}}}}}}}}}^{\pm i\psi \sigma }\) as the spin-orbit coupling with ± iψ following the convention in the Haldane model17. If we set ψ = 0.5 (in the unit of π), the hopping term reduces to the original KM model1,2. λν is the sub-lattice potential difference. For simplicity, we fix λν = 0 for this study. Non-trivial topology arises as long as \({t}^{{\prime} }\,\ne \,0\), ψ ≠ 0, 1. The phase factor \(\exp (i{\phi }_{{{{{{{{\bf{i}}}}}}}},{{{{{{{\bf{j}}}}}}}}})\) which arises from the standard Peierls substitution contains the effect of the external magnetic field, which is introduced to measure the magnetic response of the incompressible states at high temperature to determine the topology. Here \({\phi }_{{{{{{{{\bf{i}}}}}}}},{{{{{{{\bf{j}}}}}}}}}=(2\pi /{{{\Phi }}}_{0})\int\nolimits_{{r}_{{{{{{{{\bf{i}}}}}}}}}}^{{r}_{{{{{{{{\bf{j}}}}}}}}}}{{{{{{{\bf{A}}}}}}}}\cdot d{{{{{{{\bf{l}}}}}}}}\), where Φ0 = e/h is the magnetic flux quantum, the vector potential \({{{{{{{\bf{A}}}}}}}}=(x\hat{y}-y\hat{x})B/2\) (symmetric gauge), and the integration is along a straight-line path.
The other model we study is the BHZ-Hofstadter-Hubbard (BHZ-HH) model:
where t = 1 (energy scale), τa is the Pauli matrix in the orbital basis and α is the orbital index. Non-trivial topology arises as long as ∣M∣ < 2.
At zero field, a general QSH Hamiltonian can be diagonalized into
where μ is the chemical potential and
represents the upper ( + ) and lower ( − ) bands for each spin. In the BHZ3 model,
The spin-up and -down electrons have the same dispersion but different wave functions with opposite chirality. For 2 > M > 0 (or − 2 < M < 0), the half-filled system is a QSH insulator3 with C0s = 2 (or − 2) related to the spin Hall conductance3,9.
Numerical simulations
We use the DQMC method86,87,88 to simulate the KM-HH and BHZ-HH models on an Nsite = 6 × 6 × 2 cluster (two sublattices or orbitals per unit cell) with modified periodic boundary conditions89. A single-valued wave function requires the flux quantization condition Φ/Φ0 = nf/Nc (with nf an integer). We also use DCA to calculate the charge gap at low temperatures on a Nsite = 2 × 2 × 2 cluster of the KM-MM model. The DCA represents the infinite lattice in the thermodynamic limit by a finite cluster embedded in a self-consistent dynamical mean field. It has a much milder finite-size effect and Fermion sign problem. The technical details of these two methods are provided in the Supplement.
Data availability
The DQMC and DCA data generated in this study have been deposited in the Zenodo under the accession code https://doi.org/10.5281/zenodo.8275156.
Code availability
The DQMC code used for this project can be obtained at https://doi.org/10.5281/zenodo.8275145. The DCA code for this study can be obtained at https://doi.org/10.5281/zenodo.8275154.
References
Kane, C. L. & Mele, E. J. Z2 topological order and the quantum spin Hall effect. Phys. Rev. Lett. 95, 146802 (2005).
Kane, C. L. & Mele, E. J. Quantum spin Hall effect in graphene. Phys. Rev. Lett. 95, 226801 (2005).
Bernevig, B. A., Hughes, T. L. & Zhang, S.-C. Quantum spin Hall effect and topological phase transition in HgTe quantum wells. Science 314, 1757–1761 (2006).
Bernevig, B. A. & Zhang, S.-C. Quantum spin Hall effect. Phys. Rev. Lett. 96, 106802 (2006).
Roy, R. Topological phases and the quantum spin Hall effect in three dimensions. Phys. Rev. B 79, 195322 (2009).
Moore, J. E. & Balents, L. Topological invariants of time-reversal-invariant band structures. Phys. Rev. B 75, 121306 (2007).
Fu, L., Kane, C. L. & Mele, E. J. Topological insulators in three dimensions. Phys. Rev. Lett. 98, 106803 (2007).
Fu, L. & Kane, C. L. Topological insulators with inversion symmetry. Phys. Rev. B 76, 045302 (2007).
Qi, X.-L., Hughes, T. L. & Zhang, S.-C. Topological field theory of time-reversal invariant insulators. Phys. Rev. B 78, 195424 (2008).
Qi, X.-L. & Zhang, S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2011).
König, M. et al. Quantum spin Hall insulator state in HgTe quantum wells. Science 318, 766–770 (2007).
Hsieh, D. et al. A topological Dirac insulator in a quantum spin Hall phase. Nature 452, 970–974 (2008).
Hsieh, D. et al. Observation of unconventional quantum spin textures in topological insulators. Science 323, 919–922 (2009).
Xia, Y. et al. Observation of a large-gap topological-insulator class with a single Dirac cone on the surface. Nat. Phys. 5, 398–402 (2009).
Chen, Y. L. et al. Experimental realization of a three-dimensional topological insulator, Bi2Te3. Science 325, 178–181 (2009).
Hasan, M. Z. & Kane, C. L. Colloquium: Topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
Haldane, F. D. M. Model for a quantum hall effect without Landau levels: condensed-matter realization of the “parity anomaly". Phys. Rev. Lett. 61, 2015–2018 (1988).
Zhao, W. et al. Realization of the Haldane Chern insulator in a moiré lattice. Preprint at https://doi.org/10.48550/arXiv.2207.02312 (2022).
Li, T. et al. Quantum anomalous Hall effect from intertwined moiré bands. Nature 600, 641–646 (2021).
Su, Y., Li, H., Zhang, C., Sun, K. & Lin, S.-Z. Massive Dirac fermions in moiré superlattices: a route towards topological flat minibands and correlated topological insulators. Phys. Rev. Res. 4, L032024 (2022).
Dong, Z. & Zhang, Y.-H. Excitonic Chern insulator and kinetic ferromagnetism in a MoTe2/WSe2 moiré bilayer. Phys. Rev. B 107, L081101 (2023).
Xie, Y.-M., Zhang, C.-P. & Law, K. T. Topological px + ipy inter-valley coherent state in moiré MoTe2/WSe2 heterobilayers. Preprint at https://doi.org/10.48550/ARXIV.2206.11666 (2022).
Chang, Y.-W. & Chang, Y.-C. Theory of quantum anomalous Hall effect and electric-field-induced phase transition in AB-stacked MoTe2/WSe2 moire heterobilayers. Phys. Rev. B 106, 245412 (2022).
Xie, M., Pan, H., Wu, F. & Sarma, S. D. Nematic excitonic insulator in transition metal dichalcogenide moiré heterobilayers. Phys. Rev. Lett. 131, 046402 (2023).
Pan, H., Xie, M., Wu, F. & Das Sarma, S. Topological phases in ab-stacked mote2/wse2: \({{\mathbb{z}}}_{2}\) topological insulators, Chern insulators, and topological charge density waves. Phys. Rev. Lett. 129, 056804 (2022).
Devakul, T. & Fu, L. Quantum anomalous Hall effect from inverted charge transfer gap. Phys. Rev. X 12, 021031 (2022).
Zhang, Y., Devakul, T. & Fu, L. Spin-textured Chern bands in ab-stacked transition metal dichalcogenide bilayers. Proc. Natl Acad. Sci. USA 118, e2112673118 (2021).
Devakul, T., Crépel, V., Zhang, Y. & Fu, L. Magic in twisted transition metal dichalcogenide bilayers. Nat. Commun. 12, 6730 (2021).
Xie, Y.-M., Zhang, C.-P., Hu, J.-X., Mak, K. F. & Law, K. T. Valley-polarized quantum anomalous Hall state in moiré MoTe2/WSe2 heterobilayers. Phys. Rev. Lett. 128, 026402 (2022).
Wu, F., Lovorn, T., Tutuc, E., Martin, I. & MacDonald, A. H. Topological insulators in twisted transition metal dichalcogenide homobilayers. Phys. Rev. Lett. 122, 086402 (2019).
Rademaker, L. Spin-orbit coupling in transition metal dichalcogenide heterobilayer flat bands. Phys. Rev. B 105, 195428 (2022).
Tao, Z. et al. Valley-coherent quantum anomalous Hall state in AB-stacked MoTe2/WSe2 bilayers. Preprint at https://doi.org/10.48550/ARXIV.2208.07452 (2022).
Lieb, E., Schultz, T. & Mattis, D. Two soluble models of an antiferromagnetic chain. Ann. Phys. 16, 407–466 (1961).
Watanabe, H., Po, H. C., Vishwanath, A. & Zaletel, M. Filling constraints for spin-orbit coupled insulators in symmorphic and nonsymmorphic crystals. Proc. Natl Acad. Sci. USA 112, 14551–14556 (2015).
Tzeng, Y.-C., Chang, P.-Y. & Yang, M.-F. Interaction-induced metal to topological insulator transition. Phys. Rev. B 107, 155106 (2023).
Cooper, N. R., Halperin, B. I. & Ruzin, I. M. Thermoelectric response of an interacting two-dimensional electron gas in a quantizing magnetic field. Phys. Rev. B 55, 2344–2359 (1997).
Zheng, D., Zhang, G.-M. & Wu, C. Particle-hole symmetry and interaction effects in the Kane-Mele-Hubbard model. Phys. Rev. B 84, 205121 (2011).
Yu, S.-L., Xie, X. C. & Li, J.-X. Mott physics and topological phase transition in correlated Dirac fermions. Phys. Rev. Lett. 107, 010401 (2011).
Hohenadler, M. et al. Quantum phase transitions in the Kane-Mele-Hubbard model. Phys. Rev. B 85, 115132 (2012).
Lee, D.-H. Effects of interaction on quantum spin Hall insulators. Phys. Rev. Lett. 107, 166806 (2011).
Amaricci, A., Budich, J. C., Capone, M., Trauzettel, B. & Sangiovanni, G. First-order character and observable signatures of topological quantum phase transitions. Phys. Rev. Lett. 114, 185701 (2015).
Yoshida, T., Peters, R., Fujimoto, S. & Kawakami, N. Topological antiferromagnetic phase in a correlated Bernevig-Hughes-Zhang model. Phys. Rev. B 87, 085134 (2013).
Tada, Y. et al. Correlation effects in two-dimensional topological insulators. Phys. Rev. B 85, 165138 (2012).
Budich, J. C., Trauzettel, B. & Sangiovanni, G. Fluctuation-driven topological Hund insulators. Phys. Rev. B 87, 235104 (2013).
Bultinck, N. et al. Ground state and hidden symmetry of magic-angle graphene at even integer filling. Phys. Rev. X 10, 031034 (2020).
Lian, B. et al. Twisted bilayer graphene. IV. Exact insulator ground states and phase diagram. Phys. Rev. B 103, 205414 (2021).
Soejima, T., Parker, D. E., Bultinck, N., Hauschild, J. & Zaletel, M. P. Efficient simulation of moiré materials using the density matrix renormalization group. Phys. Rev. B 102, 205111 (2020).
Bistritzer, R. & MacDonald, A. H. Moiré bands in twisted double-layer graphene. Proc. Natl Acad. Sci. USA 108, 12233–12237 (2011).
Xie, F. et al. Twisted bilayer graphene. VI. An exact diagonalization study at nonzero integer filling. Phys. Rev. B 103, 205416 (2021).
Da Liao, Y. et al. Correlation-induced insulating topological phases at charge neutrality in twisted bilayer graphene. Phys. Rev. X 11, 011014 (2021).
Hofmann, J. S., Khalaf, E., Vishwanath, A., Berg, E. & Lee, J. Y. Fermionic Monte Carlo study of a realistic model of twisted bilayer graphene. Phys. Rev. X 12, 011061 (2022).
Zhang, Y.-H., Mao, D., Cao, Y., Jarillo-Herrero, P. & Senthil, T. Nearly flat Chern bands in moiré superlattices. Phys. Rev. B 99, 075127 (2019).
Bultinck, N., Chatterjee, S. & Zaletel, M. P. Mechanism for anomalous Hall ferromagnetism in twisted bilayer graphene. Phys. Rev. Lett. 124, 166601 (2020).
Raghu, S., Qi, X.-L., Honerkamp, C. & Zhang, S.-C. Topological Mott insulators. Phys. Rev. Lett. 100, 156401 (2008).
Motruk, J., Grushin, A. G., de Juan, F. & Pollmann, F. Interaction-driven phases in the half-filled honeycomb lattice: an infinite density matrix renormalization group study. Phys. Rev. B 92, 085147 (2015).
Varney, C. N., Sun, K., Rigol, M. & Galitski, V. Interaction effects and quantum phase transitions in topological insulators. Phys. Rev. B 82, 115125 (2010).
Varney, C. N., Sun, K., Rigol, M. & Galitski, V. Topological phase transitions for interacting finite systems. Phys. Rev. B 84, 241105 (2011).
Assaad, F. F. & Herbut, I. F. Pinning the order: the nature of quantum criticality in the Hubbard model on honeycomb lattice. Phys. Rev. X 3, 031010 (2013).
Neupert, T., Santos, L., Ryu, S., Chamon, C. & Mudry, C. Fractional topological liquids with time-reversal symmetry and their lattice realization. Phys. Rev. B 84, 165107 (2011).
Levin, M. & Stern, A. Fractional topological insulators. Phys. Rev. Lett. 103, 196803 (2009).
Repellin, C., Bernevig, B. A. & Regnault, N. \({{\mathbb{z}}}_{2}\) fractional topological insulators in two dimensions. Phys. Rev. B 90, 245401 (2014).
Regnault, N. & Bernevig, B. A. Fractional Chern insulator. Phys. Rev. X 1, 021014 (2011).
Tang, E., Mei, J.-W. & Wen, X.-G. High-temperature fractional quantum Hall states. Phys. Rev. Lett. 106, 236802 (2011).
Neupert, T., Santos, L., Chamon, C. & Mudry, C. Fractional quantum Hall states at zero magnetic field. Phys. Rev. Lett. 106, 236804 (2011).
Sun, K., Gu, Z., Katsura, H. & Das Sarma, S. Nearly flatbands with nontrivial topology. Phys. Rev. Lett. 106, 236803 (2011).
Sheng, D. N., Gu, Z.-C., Sun, K. & Sheng, L. Fractional quantum Hall effect in the absence of Landau levels. Nat. Commun. 2, 389 (2011).
Mai, P., Huang, E. W., Yu, J., Feldman, B. E. & Phillips, P. W. Interaction-driven spontaneous ferromagnetic insulating states with odd Chern numbers. npj Quant. Mater. 8, 14 (2023).
Goldman, N. et al. Realistic time-reversal invariant topological insulators with neutral atoms. Phys. Rev. Lett. 105, 255302 (2010).
Aidelsburger, M. et al. Realization of the Hofstadter Hamiltonian with ultracold atoms in optical lattices. Phys. Rev. Lett. 111, 185301 (2013).
Hatsugai, Y. & Kohmoto, M. Exactly solvable model of correlated lattice electrons in any dimensions. J. Phys. Soc. Jpn. 61, 2056–2069 (1992).
Phillips, P. W., Yeo, L. & Huang, E. W. Exact theory for superconductivity in a doped Mott insulator. Nat. Phys. 16, 1175–1180 (2020).
Huang, E. W., Nave, G. L. & Phillips, P. W. Discrete symmetry breaking defines the Mott quartic fixed point. Nat. Phys. 18, 511–516 (2022).
Anderson, P. W. & Haldane, F. D. M. The symmetries of fermion fluids at low dimensions. J. Stat. Phys. 103, 425–428 (2001).
Niu, Q., Thouless, D. J. & Wu, Y.-S. Quantized Hall conductance as a topological invariant. Phys. Rev. B 31, 3372–3377 (1985).
Thouless, D. J., Kohmoto, M., Nightingale, M. P. & den Nijs, M. Quantized Hall conductance in a two-dimensional periodic potential. Phys. Rev. Lett. 49, 405–408 (1982).
Zhao, J., La Nave, G. & Phillips, P. Proof of a stable fixed point for strongly correlated electron matter. Phys. Rev. B (2023). In press.
Neupert, T., Santos, L., Ryu, S., Chamon, C. & Mudry, C. Topological Hubbard model and its high-temperature quantum Hall effect. Phys. Rev. Lett. 108, 046806 (2012).
Maier, T., Jarrell, M., Pruschke, T. & Hettler, M. H. Quantum cluster theories. Rev. Mod. Phys. 77, 1027–1080 (2005).
Hähner, U. R. et al. DCA++: a software framework to solve correlated electron problems with modern quantum cluster methods. Comput. Phys. Commun. 246, 106709 (2020).
Mai, P., Balduzzi, G., Johnston, S. & Maier, T. A. Orbital structure of the effective pairing interaction in the high-temperature superconducting cuprates. npj Quant. Mater. 6, 26 (2021).
Mai, P., Karakuzu, S., Balduzzi, G., Johnston, S. & Maier, T. A. Intertwined spin, charge, and pair correlations in the two-dimensional Hubbard model in the thermodynamic limit. Proc. Natl Acad. Sci. USA 119, e2112806119 (2022).
Tarruell, L. & Sanchez-Palencia, L. Quantum simulation of the Hubbard model with ultracold fermions in optical lattices. C. R. Phys. 19, 365–393 (2018).
Foutty, B. A. et al. Mapping twist-tuned multi-band topology in bilayer WSe2. Preprint at https://doi.org/10.48550/arXiv.2304.09808 (2023).
Lin, K.-S. et al. Spin-resolved topology and partial axion angles in three-dimensional insulators. Preprint at https://doi.org/10.48550/arXiv.2207.10099 (2022).
Bradlyn, B. private communication (2023).
Blankenbecler, R., Scalapino, D. J. & Sugar, R. L. Monte Carlo calculations of coupled Boson-fermion systems. I. Phys. Rev. D 24, 2278–2286 (1981).
Hirsch, J. E. Two-dimensional Hubbard model: numerical simulation study. Phys. Rev. B 31, 4403–4419 (1985).
White, S. R. et al. Numerical study of the two-dimensional Hubbard model. Phys. Rev. B 40, 506–516 (1989).
Assaad, F. F. Depleted Kondo lattices: quantum Monte Carlo and mean-field calculations. Phys. Rev. B 65, 115104 (2002).
Towns, J. et al. Xsede: accelerating scientific discovery. Comput. Sci. Eng. 16, 62–74 (2014).
Acknowledgements
We thank Taylor L. Hughes, Edwin W. Huang, Kin Fai Mak and Kam Tuen Law, Cristian Batista, Thomas Maier, Charlie Kane and Barry Bradlyn for useful discussions. We also thank P. Armitage for help with the pithy title. This work was supported by the Center for Quantum Sensing and Quantum Materials, a DOE Energy Frontier Research Center, grant DE-SC0021238 (P.M., B.E.F., and P.W.P.). P.W.P. also acknowledges NSF DMR-2111379 for partial funding of the HK work, which led to these results. The DQMC calculation of this work used the Advanced Cyberinfrastructure Coordination Ecosystem: Services & Support (ACCESS) Expanse supercomputer through the research allocation TG-PHY220042, which is supported by National Science Foundation grant number ACI-154856290.
Author information
Authors and Affiliations
Contributions
P.M. performed the DQMC and DCA calculations on the Hubbard model, analyzed the data, and carried out the analytic calculations on the HK model; J.Z. provided the method to calculate the spin Chern number in HK model and analyzed the data; B.E.F. provided information on experimental realizations; P.W.P. supervised the project; P.M. and P.W.P. wrote the paper with input from all authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Mai, P., Zhao, J., Feldman, B.E. et al. 1/4 is the new 1/2 when topology is intertwined with Mottness. Nat Commun 14, 5999 (2023). https://doi.org/10.1038/s41467-023-41465-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-023-41465-6
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.