Abstract
Band topology of materials describes the extent Bloch wavefunctions are twisted in momentum space. Such descriptions rely on a set of topological invariants, generally referred to as topological charges, which form a characteristic class in the mathematical structure of fiber bundles associated with the Bloch wavefunctions. For example, the celebrated Chern number and its variants belong to the Chern class, characterizing topological charges for complex Bloch wavefunctions. Nevertheless, under the space-time inversion symmetry, Bloch wavefunctions can be purely real in the entire momentum space; consequently, their topological classification does not fall into the Chern class, but requires another characteristic class known as the Stiefel-Whitney class. Here, in a three-dimensional acoustic crystal, we demonstrate a topological nodal-line semimetal that is characterized by a doublet of topological charges, the first and second Stiefel-Whitney numbers, simultaneously. Such a doubly charged nodal line gives rise to a doubled bulk-boundary correspondence—while the first Stiefel-Whitney number induces ordinary drumhead states of the nodal line, the second Stiefel-Whitney number supports hinge Fermi arc states at odd inversion-related pairs of hinges. These results experimentally validate the two Stiefel-Whitney topological charges and demonstrate their unique bulk-boundary correspondence in a physical system.
Similar content being viewed by others
Introduction
Quantum mechanical wavefunctions are written in complex numbers, and so are the Bloch wavefunctions in crystals. These complex Bloch wavefunctions are twisted in momentum space to form band topology, following their mathematical structure of fiber bundles that is characterized by a set of topological invariants corresponding to a characteristic class. A famous example of the topological invariant is the Chern number in the Chern class, which can be treated as a topological charge that induces topological boundary states, following the principle of bulk-boundary correspondence1. Such a correspondence from bulk to boundary is generally one to one, since different topological phases are incompatible and do not exist simultaneously to host different topological charges. Materials classified in the Chern class have been extensively explored for decades, leading to many discoveries such as the Chern insulators, time-reversal-invariant topological insulators, and Weyl semimetals2,3,4,5,6,7.
In the presence of symmetries, the properties of the Hamiltonian eigenspace can be significantly modified8. A prominent example is the spacetime inversion (PT) symmetry. In the field of non-Hermitian physics, PT symmetry has played a central role as it can lead to real eigenenergies that are unexpected for a non-Hermitian Hamiltonian9. In periodic Hermitian systems without spin-orbit coupling, while the eigenenergies are already real, the application of PT symmetry is able to refine the Bloch wavefunctions from complex numbers to real numbers10,11. Accordingly, the Chern number must vanish in such a scenario, and the Chern class classification is no longer applicable. Instead, the Stiefel-Whitney (SW) class is responsible for the topological classification of the PT-symmetric systems with purely real eigenspaces12.
The SW class consists of two topological charges, the first and second SW numbers, classifying 1D and 2D PT-symmetric systems, respectively. A nontrivial first (second) SW number represents the obstruction of finding a global real basis of fiber bundles for Bloch wavefunctions in the 1D (2D) Brillouin zone12. This context is similar to the Chern number in the obstruction of finding a global complex basis for Bloch wavefunctions in the 2D Brillouin zone. While the first SW number is equivalent to the quantized Berry phase13,14, the second SW number is unique to the SW class, being able to protect 2D higher-order topological insulators and 3D topological semimetals15,16,17,18,19,20,21,22,23, as counterparts of Chern insulators and Weyl semimetals protected by the Chern number. More intriguingly, recent theories suggest that nontrivial first and second SW numbers can co-exist in a single system17,18,20,21,23, leading to a doubled bulk-boundary correspondence—the same bulk can be doubly charged with two topological charges simultaneously, which give rise to two kinds of boundary states at different locations.
Here, in a three-dimensional (3D) acoustic crystal, we experimentally realize a nodal-line topological semimetal with a doublet of SW topological charges as illustrated in Fig. 1a, with w1 and w2 the first and second SW numbers, respectively (Supplementary Section 1 and Supplementary Fig. S1). Such a nodal line can be named a real nodal line due to its purely real eigenspace. Because of the nontrivial w2, these nodal lines appear in pairs (see Fig. 1b, c)17,21, resembling the Nielsen-Ninomiya theorem of Weyl points in Weyl semimetals24. The 1D topological charge w1 leads to the first-order drumhead surface states (SSs)25, which also appear in the case of a conventional nodal line (see Fig. 1b). However, the additional 2D topological charge w2, which is unique to the SW class, can give rise to odd PT-related pairs of hinge Fermi arcs. In our experiment, this is demonstrated by a sample of a long rectangular prism that hosts a single pair of PT-related gapless hinges (see Fig. 1c). The novel distribution of hinge states (HSs) distinguishes this unconventional nodal-line semimetal from other existing second-order topological semimetals that host HSs on all four hinges26,27,28. This novelty is further experimentally confirmed on a sample with a more irregular but still PT-invariant geometry.
a Illustration of a nodal line with a doublet of topological charges (w1, w2). w1 and w2 are defined on the chosen S1 and S2 surrounding the nodal line, respectively. b Due to w1 = 1, the surface states (SSs) form drumheads bounded by the projections of bulk nodal lines on the surface Brillouin zone. c w2 = 1 leads to a PT-related pair of hinge state (HS) Fermi arcs bounded by the projections of the bulk nodal lines on the hinge Brillouin zone.
Results
General idea
Let us start with introducing the minimal Dirac model for a nodal line with a doublet of topological charges (w1, w2) (Supplementary section 2 and Supplementary Figs. S2-S4):
Here, γa with a = 1, 2, ⋯ , 5 are the 4 × 4 Hermitian Dirac matrices satisfying the Clifford algebra: {γa, γb} = 2δab14 and k = (kx, ky, kz) is the wavevector. Without loss of generality, we represent the PT operator as \({{{{{{{\mathcal{P}}}}}}}}{{{{{{{\mathcal{T}}}}}}}}={{{{{{{\mathcal{K}}}}}}}}\) with \({{{{{{{\mathcal{K}}}}}}}}\) the complex conjugation. In model (1), we have ordered the Dirac matrices so that γi with i = 1, 2, 3 are real and γ4,5 are purely imaginary. A set of matrices representing γa can be found in Methods. Hence, it is easy to check (1) is indeed a real Hamiltonian preserving PT symmetry. Moreover, since iγ3γ4 anticommutes with γ3 while commutes with γ1,2, we may refer to mziγ3γ4 as the partial mass term along the kz direction. The nodal line lies on the kx-ky plane, and its radius increases monotonically as mz (see Fig. 2a). When mz = 0, the ring shrinks into a Dirac point named a real Dirac point due to its real eigenspace11.
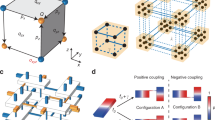
a The fourfold degenerate real Dirac point (DP) is monotonically spread into a real nodal line (NL) by the partial mass term of mziγ3γ4. b Successively implementing operators sends a particle to circle the rectangular plaquette with flux π. Here, positive (negative) hopping amplitudes are colored in purple (blue). c The undimerized lattice with flux π through every rectangular plaquette. The red star denotes the inversion center. A topologically neutral eightfold degenerate crossing point resides at K = (π, π, π) in the Brillouin zone. d, The dimerization \({{\mathfrak{D}}}_{1}\) is added along the x-direction, which is alternative along the y direction and uniform along the z-direction. Hence, the eightfold degenerate crossing point is split into a pair of fourfold degenerate real DPs, each with topological charge w2 = 1. e The dimerization \({{\mathfrak{D}}}_{2}\) along the z direction is further added, which alternates along both x and y directions. Then, each real DP is spread into a real NL.
Inspired by this continuum model, we develop a lattice construction method briefly introduced as follows. First, we shall form an eightfold degenerate band crossing point in the momentum space. Although the crossing point is topologically neutral, we then add appropriate symmetry-breaking dimerization patterns in order to split it into two fourfold degenerate real Dirac points, each with topological charge w2 = 1. The last step is to further spread each point into a nodal line with certain appropriate dimerization patterns.
To achieve a nodal point with high degeneracy, we utilize projective symmetries, which stem from the gauge fluxes on the lattice and can lead to high dimensional irreducible representations29,30. Moreover, the \({{\mathbb{Z}}}_{2}\) lattice gauge fields are highly engineerable in artificial lattices (i.e., the sign of each real hopping amplitude can be flexibly tuned to be + or − ; see Fig. 2b), as demonstrated in recently realized projectively symmetry-protected topological phases in acoustic crystals31,32.
Model construction
As aforementioned, to construct a realizable lattice model, we have recourse to the projective symmetry algebra. We consider a 3D rectangular lattice with the nearest-neighbor hoppings, which has flux π for each rectangular plaquette along any direction. The flux pattern can be described by numerous configurations of signs of hopping amplitudes, and the one we choose is given in Fig. 2c–e. Because of the gauge fluxes, the unit translation operators Li with i = x, y, z, which previously mutually commute, become pairwisely anti-commuting, i.e., {Li, Lj} = 0 for i ≠ j, which constitute the projective symmetry algebra of translations. The anti-commutation relation manifests the Aharonov-Bohm effect, since the equivalent form \({{\mathsf{L}}}_{j}^{-1}{{\mathsf{L}}}_{i}^{-1}{{\mathsf{L}}}_{j}{{\mathsf{L}}}_{i}=-1\) corresponds to that a particle accumulates a phase factor eiπ = − 1 after circling the plaquette spanned by Li and Lj, as illustrated in Fig. 2b. Similar analysis shows the projective algebraic relations {Mi, Mj} = 2δij for mirror reflections Mi, and those between Mi and Lj: \({{\mathsf{M}}}_{i}{{\mathsf{L}}}_{i}{{\mathsf{M}}}_{i}={{\mathsf{L}}}_{i}^{-1}\) and {Mi, Lj} = 0 for i ≠ j (see Fig. 2b). Here, Mi reverses the ith coordinate with the center of the unit cell as the coordinate origin. We now turn to the Brillouin zone, and denote the representations of Li and Mi as \({{{{{{{{\mathcal{L}}}}}}}}}_{i}^{{{{{{{{\bf{k}}}}}}}}}\) and \({{{{{{{{\mathcal{M}}}}}}}}}_{i}\), respectively. Note that \({{{{{{{{\mathcal{L}}}}}}}}}_{i}^{{{{{{{{\bf{k}}}}}}}}}\) depend on k, while \({{{{{{{{\mathcal{M}}}}}}}}}_{i}\) are independent of k. Specializing at the point K = (π, π, π), their projective algebraic relations are given by
Since time reversal T is preserved at K, we further consider its representation \({{{{{{{\mathcal{T}}}}}}}}\), which commutes with all \({{{{{{{{\mathcal{L}}}}}}}}}_{i}^{K}\) and \({{{{{{{{\mathcal{M}}}}}}}}}_{i}\). The projective symmetry algebra generated by \({{{{{{{{\mathcal{L}}}}}}}}}_{i}^{K}\), \({{{{{{{{\mathcal{M}}}}}}}}}_{i}\) and \({{{{{{{\mathcal{T}}}}}}}}\) is equivalent to the real Clifford algebra \({C}^{3,3}\otimes {C}^{1,1}\cong {C}^{4,4}\cong {\mathbb{R}}({2}^{d+1})\), which has a unique complex irreducible representation with dimension 23. That is, there is the desired eightfold degenerate crossing point at K protected by the projective symmetry algebra (2). Since our unit cell consists of 8 sites, all bands are enforced to cross at K to represent (2).
To have a nontrivial SW class, we consider the inversion symmetry P centered at the x-bond of the unit cell in Fig. 2c (indicated by the red star), i.e., P = LyLzMxMyMz. Following the aforementioned method, we should proceed to add PT-invariant dimerization patterns that break some Li and Mj to realize the real nodal lines. Let us consider two dimerization patterns in order. The first pattern \({{\mathfrak{D}}}_{1}\) is the dimerization along the x direction, which alternates along the y direction but is invariant along the z direction as illustrated in Fig. 2d. Adding \({{\mathfrak{D}}}_{1}\) splits the eightfold degenerate topologically “neutral” crossing point into two fourfold degenerate real Dirac points charged by w2, each of which is modeled by (1) with mz = 0. We then introduce the second dimerization pattern \({{\mathfrak{D}}}_{2}\), which gives rise to the partial mass term mziγ3γ4 of (1) and therefore can spread each real Dirac point into a nodal line. \({{\mathfrak{D}}}_{2}\) is designed as the dimerization along the z-direction, which alternates along both the x and y directions, as illustrated in Fig. 2e. Each of the nodal lines, as shown in Supplementary section 3 and Supplementary Fig. S5, carries a nontrivial doublet of topological charges (w1, w2) as expected.
This tight-binding model with π fluxes on a simple rectangular lattice can be implemented using the coupled acoustic cavity structure31,32,33,34,35,36,37,38,39,40. Our designed acoustic crystal is shown in Fig. 3a, with each site in the tight-binding model implemented by a cuboid cavity supporting a dipolar resonance at around 3100 Hz. The coupling between two cavities is enabled by a tube with a square cross-section, with the coupling sign determined by the position of the tube and the coupling amplitude controlled by the width of the tube. Thus, by carefully engineering the coupling tubes, the required gauge fluxes and coupling dimerizations can be realized (see Fig. 3b). The whole structure is filled with air and surrounded by photosensitive resins, which can be treated as rigid walls for sound due to their large impedance mismatch with air (see Methods). Figure 3c shows the equi-frequency surface of the acoustic crystal obtained from full-wave simulation at 3020 Hz (slightly below the minimum frequency of the nodal line), which reveals the existence of two nodal lines forming two rings in the bulk dispersion and suggests the validity of this acoustic design (see Supplementary section 4 and Supplementary Figs. S6-S7 for more details on the dispersion).
a Experimental sample for measuring the surface states (SSs). The lattice constants in the xy plane and along the z direction are a = 140 mm and az = 70 mm, respectively. b Unit cell of the acoustic crystal, with tubes enabling positive and negative couplings colored in purple and blue, respectively. The dimensions of the cuboid cavities are l = 56 mm, w = 28 mm and h = 7 mm. The width parameters of the tubes are dx1 = 3.2 mm, dx2 = 7.8 mm, dy = 6 mm, dz1 = 3.2 mm and dz2 = 4.8 mm. The acoustic crystal is filled with air and surrounded by hard walls. c Equi-frequency surface of the acoustic crystal in b at 3020 Hz (slightly below the frequency range of the nodal ring) calculated from full-wave simulations. d Experimentally measured SS dispersion at 3045 Hz (inside the frequency range of the nodal ring). The solid blue curves denote the projections of the nodal rings. e, f Experimentally measured SS dispersion along the horizontal (vertical) white dashed line in d. The gray and red dots represent simulated eigenfrequencies of the bulk and SSs, respectively. The blue dots denote the projections of the bulk nodal points.
Drumhead surface states
We first demonstrate the existence of conventional drumhead SSs due to the nontrivial first-order topology induced by ω1. To this end, we scan the acoustic fields on the top surface excited by a speaker placed at the surface center (see Methods and Supplementary Fig. S9). Figure 3d shows the corresponding Fourier intensity at 3045 Hz, where the hot spots occur at positions inside the projections of the nodal rings (denoted by the blue lines), consistent with the feature of the drumhead SSs. To further confirm the existence of the drumhead SSs, we also plot in Fig. 3e, f the frequency-resolved Fourier spectra along the kx and ky momenta, respectively (indicated by the two white dashed lines in Fig. 3d). As can be seen, the measured SSs connect the projections of the two bulk nodal points (indicated by the blue dots) from the same nodal ring, matching well with the simulated SS dispersion (indicated by the red dots).
PT-related hinge states
Next, we study the unconventional higher-order topology in this acoustic crystal induced by the nontrivial second SW number w2. Let us first consider a sample with a simple rectangular geometry as shown in Fig. 4a. This sample consists of six (seven) cavities in the x (z) direction, thus preserving the required PT symmetry. By imposing periodic boundary condition along the y direction, we can numerically compute the dispersion for y-directional hinges. The results for ky = π/a are shown in Fig. 4b and the results for all ky are given as colored dots in Fig. 4d–g. As can be seen, there are two bands connecting the projections of the nodal rings. The eigen profiles of these two states are given in Fig. 4c, showing they are indeed the hinge Fermi arcs states. Notably, the HSs only exist on two of the four hinges related by the PT symmetry. Interestingly, the locations of the HSs can be transferred from the two off-diagonal hinges to the two diagonal ones by simply reversing the dimerization along z (i.e., swap the values of dz1 and dz2; see Supplementary Fig. S10).
a Experimental sample for measuring the hinge states (HSs). The numbers—label the four y-directional hinges. b Eigen frequencies for the sample shown in a at ky = π/a, obtained from full-wave simulation. The blue dots represent the bulk and surface states, and the red dots indicate the HSs. c, Eigen profiles for the two states highlighted in red in b (∣p∣ denotes the absolute value of acoustic pressure). The color indicates the amplitude of the acoustic pressure. d–g Experimentally measured dispersions for hinge 1 d, hinge 2 e, hinge 3 f, and hinge 4 g. The gray dots represent simulated eigenfrequencies of the bulk and SSs, and the red dots indicate simulated hinge bands. The solid blue lines denote the projections of the nodal rings. h–k Experimentally measured acoustic intensity distributions on two surfaces adjacent to hinge 1 h, hinge 2 i, hinge 3 j, and hinge 4 k. The red star indicates the position of the speaker and the red dashed line highlights the position of the hinge. The operating frequencies of the speaker are chosen as: 3078 Hz (hinge 1 and hinge 3), 3076 Hz (hinge 2) and 3080 Hz (hinge 4), which are around the eigenfrequencies of the HSs.
To probe the hinge Fermi arcs, we place a speaker at the hinge and scan the acoustic field along the hinge. This experiment is repeated for all four hinges (see the labelings of the hinges in Fig. 4a) and the measured dispersions are plotted in Fig. 4d–g. For hinge 2 (Fig. 4e) and hinge 4 (Fig. 4g), the measured dispersions match with the simulated hinge Fermi arcs (red dots), suggesting the existence of HSs on these two hinges. In contrast, the excited states are bulk states when the speaker is placed at hinge 1 (Fig. 4d) or hinge 3 (Fig. 4f). These results demonstrate the off-diagonal distribution (i.e., only at hinge 2 and hinge 4) of the HSs. In addition to the momentum space results, we also conduct real space measurements to reveal the HSs. For each hinge, a speaker operating at the HS’s frequency is placed at one end and the acoustic field on the two adjacent surfaces is measured. As shown in Fig. 4h–k, the measured acoustic intensity distributions exhibit a hinge localization profile only for hinge 2 (Fig. 4i) and hinge 4 (Fig. 4k), which is consistent with the information from the simulated and measured dispersions. Note that here the HSs do not show a clear propagation along the hinge due to their small group velocity and the system’s loss. Nevertheless, the strong field enhancement along the hinge is a clear signature of the HSs. We also note that the system’s loss, which can be modeled as a uniform imaginary number in the diagonal terms of the Hamiltonian, will not change the band topology.
A fascinating aspect of this acoustic crystal is that the protecting symmetry, i.e., the PT symmetry, can be easily preserved in various geometries, not limited to regular ones like the square and rectangular geometries. Furthermore, under different geometries with the same bulk invariant w2, the forms of the HSs (e.g., the locations and number of HSs) can also be different (see Supplementary section 5 and Supplementary Fig. S8). This allows us to steer the HSs even without changing the system parameters. To demonstrate this property, we construct a sample with an irregular shape in the xz plane, as shown in Fig. 5a. One can imagine a cutting procedure illustrated in Fig. 5b, where the two off-diagonal hinges of a rectangle-shaped sample are cut to get this irregularly-shaped sample. During such a process, the PT symmetry remains intact while the pair of hinges that support the HSs are removed. Interestingly, the generated new sample host three, instead of one, pair of PT-related HSs (see Fig. 5c). To demonstrate this phenomenon, we measure the transmission spectra at the eight hinges of this sample. As shown in Fig. 5d, in the frequency range of the HSs, the signals measured at hinge 1 and hinge 5 are much lower than the signals measured at other six hinges. This indicates there are no HSs at hinge 1 and hinge 5, consistent with the simulation (see Supplementary Fig. S11). The existence/absence of the HS at each hinge is also confirmed by real-sapce field measurements, as given in Supplementary Fig. S13.
a Experimental sample for demonstrating the odd number of pairs of PT-related hinge states (HSs). The numbers—label the eight y-directional hinges. b Illustration of the process of obtaining an irregularly shaped sample supporting three pairs of HSs by cutting two corners of a rectangle sample with one pair of HSs. Here the red circles represent the HSs and the blue circles denote the inversion centers of the samples. c Eigen frequencies for the sample shown in a at ky = π/a, obtained from full-wave simulation. The blue dots represent the bulk and SSs, and the red dots indicate the HSs. d Experimentally measured transmission spectra at the eight hinges. The gray region indicates the frequency range of the HSs.
Discussion
In summary, we have demonstrated an acoustic real nodal-line crystal in the nontrivial SW class, hosting ordinary drumhead SSs and unconventional PT-related HSs featuring exotic properties. Our study opens a new route to experimental studies on band topology constructed from real fiber bundles that were hardly explored previously. While our demonstration is in acoustics, the proposed idea can also be generalized to other classical wave systems with PT symmetry, including photonic, mechanical and circuit systems41,42,43,44. Other intriguing properties such as the fractional charges and filling anomalies can also be demonstrated with more specialized measurements45. Besides, our results reveal the power of projective symmetries in realizing novel topological phases of matter, which could inspire more topological designs using artificial structures with gauge flux. On the practical level, the PT-related HSs, with superior tunability in their number and configuration compared to previous higher-order topological states, can provide robust and reconfigurable control over sound and other classical waves.
Methods
Concrete form of the model and its symmetry operators
Since each unit cell consists of 2 × 2 × 2 sites, we assign three sets of the standard Pauli matrices σ, τ and ρ for the three dimensions x, y, and z, respectively. Moreover, we introduce the seven Hermitian 8 × 8 Dirac matrices as
The Dirac matrices Γα with α = 1, 2 ⋯ , 7 satisfy {Γα, Γβ} = 2δαβ. With the Dirac matrices, the tight-binding Hamiltonian in momentum space is given by
Let t denote the hopping magnitude along the undimerized y direction, and \({J}_{1}^{x,z}\) and \({J}_{2}^{x,z}\) be the two hopping magnitudes along the two dimerized directions x and z, respectively. Then, the dimerization strengths are measured by \({J}_{-}^{x,z}/{J}_{+}^{x,z}\) with \({J}_{\pm }^{x,z}=({J}_{1}^{x,z}\pm {J}_{2}^{x,z})/2\). The coefficient functions are given by \({f}_{x,1}({k}_{x})=-{J}_{+}^{x}(1+\cos {k}_{x})\), \({f}_{x,2}={J}_{+}^{x}\sin {k}_{x}\), \({f}_{y,1}({k}_{y})=-t(1+\cos {k}_{y})\), \({f}_{y,2}({k}_{y})=t\sin {k}_{y}\), \({f}_{z,1}({k}_{z})={J}_{+}^{z}(1+\cos {k}_{z})\), \({f}_{z,2}({k}_{z})=-{J}_{+}^{z}\sin {k}_{z}\), and \({g}_{x,1}({k}_{x})=-{J}_{-}^{x}(1-\cos {k}_{x})\), \({g}_{x,2}({k}_{x})=-{J}_{-}^{x}\sin {k}_{x}\), \({g}_{z,1}({k}_{z})=-{J}_{-}^{z}(1-\cos {k}_{z})\), \({g}_{z,2}({k}_{z})={J}_{-}^{z}\sin {k}_{z}\).
The momentum-space symmetry operators for Mi are given by
where each \({\hat{m}}_{i}\) is the operator sending ki to − ki with i = x, y, z. It is easy to check the desired projective algebraic relations: \(\{{{{{{{{{\mathcal{M}}}}}}}}}_{i},{{{{{{{{\mathcal{M}}}}}}}}}_{j}\}=2{\delta }_{ij}\). The momentum-space operators for the translations Li are given by
We see that \({{{{{{{{\mathcal{L}}}}}}}}}_{i}^{2}={e}^{{{{{{{{\rm{i}}}}}}}}{k}_{i}}\) for i = x, y, z, and \(\{{{{{{{{{\mathcal{L}}}}}}}}}_{i},{{{{{{{{\mathcal{L}}}}}}}}}_{j}\}=0\) if i ≠ j. One can furthermore to check the projective algebraic relations between \({{{{{{{{\mathcal{L}}}}}}}}}_{i}\) and \({{{{{{{{\mathcal{M}}}}}}}}}_{j}\): \(\{{{{{{{{{\mathcal{M}}}}}}}}}_{i},{{{{{{{{\mathcal{L}}}}}}}}}_{j}\}=0\) if i ≠ j, and \({{{{{{{{\mathcal{M}}}}}}}}}_{i}{{{{{{{{\mathcal{L}}}}}}}}}_{i}{{{{{{{{\mathcal{M}}}}}}}}}_{i}=-{{{{{{{{\mathcal{L}}}}}}}}}_{i}^{{{{\dagger}}} }\) for i, j = x, y, z.
It is easy to check that all symmetry operators \({{{{{{{{\mathcal{L}}}}}}}}}_{i}\) and \({{{{{{{{\mathcal{M}}}}}}}}}_{j}\) commute with time-reversal operator \({{{{{{{\mathcal{T}}}}}}}}={{{{{{{\mathcal{K}}}}}}}}\hat{I}\) with \(\hat{I}\) the inversion of k and \({{{{{{{\mathcal{K}}}}}}}}\) the complex conjugation. Specifically at K = (π, π, π), we see
Together with operators \({{{{{{{{\mathcal{M}}}}}}}}}_{i}\) above, we can verify that the projective algebraic relations (2) at K are indeed satisfied.
In the absence of dimerization, i.e., \({J}_{-}^{x}={J}_{-}^{z}=0\), it is straightforward to check that all \({{{{{{{{\mathcal{M}}}}}}}}}_{i}\) and \({{{{{{{{\mathcal{L}}}}}}}}}_{j}\) commute with the Hamiltonian (3). After the dimerization patterns \({{\mathfrak{D}}}_{1}\) and \({{\mathfrak{D}}}_{2}\) are introduced, all Li and Mj are broken, and therefore \({{{{{{{{\mathcal{M}}}}}}}}}_{i}\) and \({{{{{{{{\mathcal{L}}}}}}}}}_{j}\) do not commute with (3) any more. Nevertheless, the off-centered inversion symmetry P = LyLzMxMyMz is preserved, and the momentum-space operator \({{{{{{{\mathcal{P}}}}}}}}\) for P can be derived as a product of the corresponding operators presented above. Then, the PT symmetry operator \({{{{{{{\mathcal{P}}}}}}}}{{{{{{{\mathcal{T}}}}}}}}\) is given by
It is straightforward to check \({{{{{{{\mathcal{P}}}}}}}}{{{{{{{\mathcal{T}}}}}}}}\) commutes with the Hamiltonian (3) even with nonzero \({J}_{-}^{x}\) and \({J}_{-}^{z}\).
With small dimerizations \({{\mathfrak{D}}}_{1}\) and \({{\mathfrak{D}}}_{2}\), the low-energy effective model can be derived in the vicinity of each nodal line. Each low-energy effective model can be cast into the form of (1), namely the real Dirac model with a “partial mass term” along the z direction, by appropriately choosing the basis of four low-energy modes. The 4 × 4 Hermitian Dirac matrices in (1) can be chosen as
Here, σ and τ are two sets of the standard Pauli matrices, which have no direct relation with those used to define Γα.
Full-wave simulation
All numerical simulations of the acoustic model are performed in the commercial software Comsol Multiphysics, pressure acoustics module. The software solves the Helmholtz equation with the finite element method. In the simulations, periodic boundary conditions with Bloch phase shifts are assigned to the periodic boundaries, while other boundaries are set as sound rigid boundaries due to the large impedance mismatch between the printing materials and air. The sound speed and density of air are set to be 347.2 m/s and 1.16 kg/m3, respectively. The geometrical parameters of the acoustic model are given in the caption of Fig. 3.
To get the equi-frequency contour of the bulk bands (Fig. 3c), we compute all the eight bulk bands in area 0.5π/a < kx < 1.5π/a, 0 < ky < π/a and 0.5π/az < kz < 1.5π/az, with 30 computing points in each momentum direction. The contour at the other side of the Brillouin zone is obtained through the time-reversal operation. In the simulation of surface dispersion (Fig. 3d–f), we adopt an acoustic supercell with periodic boundary condition along the x and y directions and 21 cavities along the z direction. In the simulations of the hinge dispersions (Figs. 4b–g and 5c), the simulated geometries in the xz plane are the same as the experimental samples (see Figs. 4a and 5a), with periodic boundary conditions imposed for the y direction.
Sample design and fabrication
To implement the sound rigid walls that surround the air cavities and tubes, we design hard walls with a thickness of 5 mm to cover the whole sample. These walls are thick enough to provide the rigid wall condition. In order to excite and measure the sound signals, we drill two small holes (with radii of 5 mm) on the boundary cavities. These holes are covered with size-matched plugs when they are not in use.
The samples are fabricated through the stereolithography apparatus technique, with a fabrication resolution of around 0.1 mm. The dimensions of the three samples (i.e., the samples shown in Figs. 3a, 4a and 5a) are around 1.5 m × 1.5 m × 0.2 m, 0.4 m × 1.5 m × 0.2 m and 0.7 m × 0.5 m × 0.5 m, respectively. Due to their large sizes, these samples are fabricated as separate parts and then assembled together.
Experimental measurement
All experiments are conducted using the same scheme, as illustrated in Fig. S9 in Supplementary Information. The sound signal is launched by a speaker (Tymphany PMT-40N25AL01-04) placed on the surface (for measuring the SSs) or the hinge (for measuring the HSs). The speaker generates a broadband sound signal from 2000 Hz to 4000 Hz, which covers the frequency range of our interested bands. Two microphones (Brüel & Kjær Type 4182) are used to detect the amplitude and phase of sound in the sample. One of the microphones is placed at the position of the source, serving as a reference probe. To ensure the accuracy of the frequency-resolved spectra, we have also checked that there are no resonances in the spectrum of the source (see Supplementary Fig. S12). The other microphone scan field distributions in the targeted areas in the sample. The measured signal is processed by an analyzer (Brüel & Kjær 3160-A-022 module) to obtain the experimental data with the amplitude and phase of sound at each measured point for the frequencies ranging from 0 Hz to 6400 Hz (the frequency resolution is 1 Hz).
Data availability
The experimental data are available in the data repository for Nanyang Technological University at https://doi.org/10.21979/N9/NEB0G4. Other data that support the findings of this study are available from the corresponding authors upon reasonable request.
References
Thouless, D. J., Kohmoto, M., Nightingale, M. P. & den Nijs, M. Quantized Hall conductance in a two-dimensional periodic potential. Phys. Rev. Lett. 49, 405 (1982).
Hasan, M. Z. & Kane, C. L. Colloquium: Topological insulators. Rev. Mod. Phys. 82, 3045 (2010).
Qi, X.-L. & Zhang, S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057 (2011).
Haldane, F. D. M. Model for a quantum Hall effect without Landau levels: Condensed-matter realization of the" parity anomaly". Phys. Rev. Lett. 61, 2015 (1988).
Qi, X.-L., Hughes, T. L. & Zhang, S.-C. Topological field theory of time-reversal invariant insulators. Phys. Rev. B 78, 195424 (2008).
Wan, X., Turner, A. M., Vishwanath, A. & Savrasov, S. Y. Topological semimetal and Fermi-arc surface states in the electronic structure of pyrochlore iridates. Phys. Rev. B 83, 205101 (2011).
Armitage, N., Mele, E. & Vishwanath, A. Weyl and Dirac semimetals in three-dimensional solids. Rev. Mod. Phys. 90, 015001 (2018).
Chiu, C.-K., Teo, J. C., Schnyder, A. P. & Ryu, S. Classification of topological quantum matter with symmetries. Rev. Mod. Phys. 88, 035005 (2016).
Bender, C. M. & Boettcher, S. Real spectra in non-Hermitian Hamiltonians having PT symmetry. Phys. Rev. Lett. 80, 5243 (1998).
Zhao, Y. X., Schnyder, A. P. & Wang, Z. D. Unified theory of PT and CP invariant topological metals and nodal superconductors. Phys. Rev. Lett. 116, 156402 (2016).
Zhao, Y. X. & Lu, Y. PT-symmetric real Dirac fermions and semimetals. Phys. Rev. Lett. 118, 056401 (2017).
Nakahara, M. Geometry, topology and physics (CRC press, 2018).
Zak, J. Berry’s phase for energy bands in solids. Phys. Rev. Lett. 62, 2747 (1989).
King-Smith, R. & Vanderbilt, D. Theory of polarization of crystalline solids. Phys. Rev. B 47, 1651 (1993).
Benalcazar, W. A., Bernevig, B. A. & Hughes, T. L. Quantized electric multipole insulators. Science 357, 61 (2017).
Schindler, F. et al. Higher-order topological insulators. Sci. Adv. 4, eaat0346 (2018).
Ahn, J., Kim, D., Kim, Y. & Yang, B.-J. Band topology and linking structure of nodal line semimetals with Z2 monopole charges. Phys. Rev. Lett. 121, 106403 (2018).
Ahn, J., Park, S. & Yang, B.-J. Failure of Nielsen-Ninomiya theorem and fragile topology in two-dimensional systems with space-time inversion symmetry: application to twisted bilayer graphene at magic angle. Phys. Rev. X 9, 021013 (2019).
Bzdušek, Tcv & Sigrist, M. Robust doubly charged nodal lines and nodal surfaces in centrosymmetric systems. Phys. Rev. B 96, 155105 (2017).
Wang, Z., Wieder, B. J., Li, J., Yan, B. & Bernevig, B. A. Higher-order topology, monopole nodal lines, and the origin of large Fermi arcs in transition metal dichalcogenides XTe2 (X = Mo, W). Phys. Rev. Lett. 123, 186401 (2019).
Wang, K., Dai, J.-X., Shao, L., Yang, S. A. & Zhao, Y. Boundary criticality of PT-invariant topology and second-order nodal-line semimetals. Phys. Rev. Lett. 125, 126403 (2020).
Wieder, B. J. et al. Strong and fragile topological Dirac semimetals with higher-order Fermi arcs. Nat. Commun. 11, 627 (2020).
Chen, C. et al. Second-order real nodal-line semimetal in three-dimensional graphdiyne. Phys. Rev. Lett. 128, 026405 (2022).
Nielsen, H. B. & Ninomiya, M. Absence of neutrinos on a lattice:(i). proof by homotopy theory. Nucl. Phys. B 185, 20 (1981).
Weng, H. et al. Topological node-line semimetal in three-dimensional graphene networks. Phys. Rev. B 92, 045108 (2015).
Luo, L. et al. Observation of a phononic higher-order Weyl semimetal. Nat. Mater. 20, 794 (2021).
Wei, Q. et al. Higher-order topological semimetal in acoustic crystals. Nat. Mater. 20, 812 (2021).
Qiu, H., Xiao, M., Zhang, F. & Qiu, C. Higher-order Dirac sonic crystals. Phys. Rev. Lett. 127, 146601 (2021).
Wen, X.-G. Quantum orders and symmetric spin liquids. Phys. Rev. B 65, 165113 (2002).
Shao, L. B., Liu, Q., Xiao, R., Yang, S. A. & Zhao, Y. X. Gauge-field extended k ⋅ p method and novel topological phases. Phys. Rev. Lett. 127, 076401 (2021).
Xue, H. et al. Projectively enriched symmetry and topology in acoustic crystals. Phys. Rev. Lett. 128, 116802 (2022).
Li, T. et al. Acoustic Möbius insulators from projective symmetry. Phys. Rev. Lett. 128, 116803 (2022).
Ma, G., Xiao, M. & Chan, C. T. Topological phases in acoustic and mechanical systems. Nat. Rev. Phys. 1, 281 (2019).
Xue, H., Yang, Y. & Zhang, B. Topological acoustics. Nat. Rev. Mater. 7, 974 (2022).
Xue, H., Yang, Y., Gao, F., Chong, Y. & Zhang, B. Acoustic higher-order topological insulator on a kagome lattice. Nat. Mater. 18, 108 (2019).
Ni, X., Weiner, M., Alu, A. & Khanikaev, A. B. Observation of higher-order topological acoustic states protected by generalized chiral symmetry. Nat. Mater. 18, 113 (2019).
Li, F., Huang, X., Lu, J., Ma, J. & Liu, Z. Weyl points and Fermi arcs in a chiral phononic crystal. Nat. Phys. 14, 30 (2018).
Xue, H. et al. Observation of an acoustic octupole topological insulator. Nat. Commun. 11, 2442 (2020).
Ni, X., Li, M., Weiner, M., Alù, A. & Khanikaev, A. B. Demonstration of a quantized acoustic octupole topological insulator. Nat. Commun. 11, 2108 (2020).
Qi, Y. et al. Acoustic realization of quadrupole topological insulators. Phys. Rev. Lett. 124, 206601 (2020).
Serra-Garcia, M. et al. Observation of a phononic quadrupole topological insulator. Nature 555, 342 (2018).
Peterson, C. W., Benalcazar, W. A., Hughes, T. L. & Bahl, G. A quantized microwave quadrupole insulator with topologically protected corner states. Nature 555, 346 (2018).
Noh, J. et al. Topological protection of photonic mid-gap defect modes. Nat. Photon. 12, 408 (2018).
Imhof, S. et al. Topolectrical-circuit realization of topological corner modes. Nat. Phys. 14, 925 (2018).
Peterson, C. W., Li, T., Benalcazar, W. A., Hughes, T. L. & Bahl, G. A fractional corner anomaly reveals higher-order topology. Science 368, 1114 (2020).
Acknowledgements
H.X., Z.C., Y.L., and B.Z. are supported by the Singapore Ministry of Education Academic Research Fund Tier 2 (Grant Nos. MOE2019-T2-2-085) and Singapore National Research Foundation Competitive Research Program (Grant No. NRF-CRP23-2019-0007). Z.Y.C., J.X.D., and Y.X.Z. acknowledge support from the National Natural Science Foundation of China (Grants Nos. 12161160315 and 12174181).
Author information
Authors and Affiliations
Contributions
H.X., Y.X.Z., and B.Z. conceived the idea. Z.Y.C., J.X.D., and Y.X.Z. developed the theory and the lattice model. H.X. constructed the acoustic model and performed numerical calculations. H.X., Z.C., and Y.L. conducted the experiments. H.X., Y.X.Z., and B.Z. wrote the manuscript with input from all authors. Y.X.Z. and B.Z. supervised the project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Xue, H., Chen, Z.Y., Cheng, Z. et al. Stiefel-Whitney topological charges in a three-dimensional acoustic nodal-line crystal. Nat Commun 14, 4563 (2023). https://doi.org/10.1038/s41467-023-40252-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-023-40252-7
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.