Abstract
Charge noise in the host semiconductor degrades the performance of spin-qubits and poses an obstacle to control large quantum processors. However, it is challenging to engineer the heterogeneous material stack of gate-defined quantum dots to improve charge noise systematically. Here, we address the semiconductor-dielectric interface and the buried quantum well of a 28Si/SiGe heterostructure and show the connection between charge noise, measured locally in quantum dots, and global disorder in the host semiconductor, measured with macroscopic Hall bars. In 5 nm thick 28Si quantum wells, we find that improvements in the scattering properties and uniformity of the two-dimensional electron gas over a 100 mm wafer correspond to a significant reduction in charge noise, with a minimum value of 0.29 ± 0.02 μeV/Hz½ at 1 Hz averaged over several quantum dots. We extrapolate the measured charge noise to simulated dephasing times to CZ-gate fidelities that improve nearly one order of magnitude. These results point to a clean and quiet crystalline environment for integrating long-lived and high-fidelity spin qubits into a larger system.
Similar content being viewed by others
Introduction
Spin-qubits in silicon quantum dots are a promising platform for building a scalable quantum processor because they have a small footprint1, long coherence times2,3, and are compatible with advanced semiconductor manufacturing4. Furthermore, rudimentary quantum algorithms have been executed5 and quantum logic at high-fidelity performed6,7,8,9. As the qubit count is increasing, with a six-qubit processor demonstrated10, significant steps have been taken to couple silicon spin qubits at a distance, via microwave photons or spin shuttling11,12,13,14,15,16, towards networked spin-qubit tiles17. However, electrical fluctuations associated with charge noise in the host semiconductor can decrease qubit readout and control fidelity18. Reducing charge noise independently of the device location on a wafer is pivotal to achieving the ubiquitous high-fidelity of quantum operations, within and across qubit tiles, necessary to execute more complex quantum algorithms.
Charge noise is commonly associated with two-level fluctuators (TLF)19 in the semiconductor host. In gated heterostructures with buried quantum wells, TLF may arise from impurities in several locations: within the quantum well, the semiconductor barrier, the semiconductor/dielectric interface, and the dielectrics layers above20,21,22,23,24,25,26. Furthermore, previous work on strained-Si MOSFETs27,28,29, with strained-Si channels deposited on SiGe strain relaxed buffers, has associated charge noise with dislocations arising from strain relaxation, either deep in the SiGe buffer or at the quantum well/buffer interface. Since these impurities and dislocations are randomly distributed over the wafer and are also a main scattering source for electron transport in buried quantum wells30, a holistic approach to materials engineering should be taken to address disorder in two-dimensional electron gases and charge noise in quantum dots.
In this work, we demonstrate thin quantum wells in 28Si/SiGe heterostructures with low and uniform charge noise, measured over several gate-defined quantum dot devices. By linking charge noise measurements to the scattering properties of the two-dimensional electron gas, we show that a quiet environment for quantum dots is obtained by improving the semiconductor/dielectric interface and the crystalline quality of the quantum well. We feed the measured charge noise into a theoretical model, benchmark the model against recent experimental results6,10, and predict that these optimized heterostructures may support long-lived and high-fidelity spin qubits.
Results
Description of 28Si/SiGe heterostructures
Figure 1a illustrates the undoped 28Si/SiGe heterostructures, grown by reduced-pressure chemical vapor deposition, and the gate-stack above. From bottom to top, the material stack comprises a 100 mm Si substrate, a strain-relaxed SiGe buffer layer, a strained 28Si quantum well, a 30 nm thick SiGe barrier, a Si cap oxidized in air to form a SiOx layer, an AlOx layer formed by atomic layer deposition, and metallic gates. The SiGe layers above and below the quantum well have a Ge concentration of ≃0.3 (Methods).
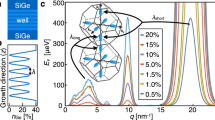
a Schematics of the 28Si/SiGe heterostructure and dielectric stack above. z indicates the heterostructure growth direction. Circles represent remote impurities at the semiconductor/dielectric interface and perpendicular symbols represent misfit dislocations that might arise at the quantum well/buffer interface due to strain relaxation. b, c BF-STEM images from heterostructure C highlighting the semiconductor/dielectric interface and the 5 nm thick 28Si quantum well, respectively. d Mobility μ and e conductivity σxx measured as a function of density n at a temperature of 1.6 K in a Hall bar H-FET from heterostructure C. The red curve in e is a fit to percolation theory.
We consider three 28Si/SiGe heterostructures (A, B, C) to improve, in sequence, the semiconductor/dielectric interface (from A to B) and the crystalline quality of the quantum well (from B to C). Heterostructure A has an ≃9 nm thick quantum well and is terminated with an epitaxial Si cap grown by dichlorosilane at 675 °C. This kind of heterostructure has already produced high performance spin-qubits6,10,31. Heterostructure B misses a final epitaxial Si cap but features an amorphous Si-rich layer obtained by exposing the SiGe barrier to dichlorosilane at 500 °C. Compared to A, heterostructure B supports a two-dimensional electron gas with enhanced and more uniform transport properties across a 100 mm wafer, owing to a more uniform SiOx layer with less scattering centers32. Finally, we introduce here heterostructure C, having the same amorphous Si-rich termination as in heterostructure B, but a thinner quantum well of ≃5 nm (Supplementary Fig. 1). This is much thinner than the Matthews-Blakeslee critical thickness33,34, which is ≃10 nm35 for the relaxation of tensile Si on Si0.7Ge0.3 via the formation of misfit dislocation at the bottom interface of the quantum well. In light of recent morphological characterization by electron channeling constrast imaging of Si/SiGe heterostructures with similar quantum well thickness and SiGe chemical composition36, we expect misfit dislocation segments in heterostructure B because the quantum well approaches the Matthews-Blakeslee critical thickness. Due to the much thinner quantum well, instead, the epitaxial planes may adapt to the SiGe buffer much better in heterostructure C than in heterostructure B, meaning that misfit dislocations are, in principle, suppressed.
Figure 1b, c shows bright-field scanning transmission electron microscopy (BF-STEM) images from heterostructure C after fabrication of a Hall bar shaped heterostructure field effect transistors (H-FET). We observe a sharp SiGe/SiOx semiconductor/dielectric interface (Fig. 1b), characterized by a minor Ge pile up (dark line) in line with ref. 32. The ≃5 nm thick quantum well (Fig. 1c, Supplementary Fig. 1) is uniform, has sharp interfaces to the nearby SiGe, and appears of high crystalline quality.
Electrical characterization of heterostructure field effect transistors
We evaluate the scattering properties of the two-dimensional electron gases by wafer-scale electrical transport measured on Hall-bar shaped H-FETs operated in accumulation mode (Methods). For each heterostructure, multiple H-FETs over a wafer are measured in the same cool-down at a temperature of 1.7 K in refrigerators equipped with cryo-multiplexers37. Figure 1d, e shows typical mobility-density and conductivity-density curves for heterostructure C, from which we extract the mobility measured at high density (n = 6 × 1011 cm−2) and the percolation density (np)38. The mobility rises steeply at low density due to progressive screening of scattering from remote impurities and flattens at higher density (n > 5 × 1011 cm−2), limited by scattering from impurities within or nearby the quantum well, for example uniform background charges, surface roughness, or crystalline defects such as threading or misfit dislocations30,39.
Charge noise measurements in quantum dots
For charge noise measurements, we use devices comprising a double quantum dot and a charge sensor quantum dot nearby, illustrated in Fig. 2a. Using the same device design, two-qubit gates with fidelity above 99% were demonstrated6, silicon quantum circuits were controlled by CMOS-based cryogenic electronics31, and energy splittings in 28Si/SiGe heterostructures were studied with statistical significance40.
a False colored SEM-image of a double quantum dot system with a nearby charge sensor. Charge noise is measured in the multi-electron quantum dot defined by accumulation gates SDLAcc and SDRAcc (blue), plunger P (blue), with the current going along the black arrow. In these experiments, the gates defining the double quantum dot (red) are used as screening gates. There is an additional global top gate (not shown) to facilitate charge accumulation when needed. b Source-drain current ISD through a charge sensor device fabricated on heterostructure C against the plunger gate voltage VP. Colored dots mark the position of the flank of the Coulomb peak where charge noise measurements are performed. The inset shows Coulomb diamonds from the same device, plotted as the differential of the current dI/dV as a function of VP and the source drain bias VSD. c Charge noise spectrum Sϵ measured at the Coulomb peak at VP ≃ 360.3 mV in b and extracted using the lever arm from the corresponding Coulomb diamond. The black trendline is proportional to 1/f. d Sϵ for the same device in b, plotted in 3D as a function of f and VP. The dark gray plane is a fit through the datasets, i.e. the collection of noise spectra as in c measured at different VP and each obtained using a unique lever arm from the corresponding Coulomb diamond. e Line cut through the data in d at f = 1 Hz, showing the experimental noise Sϵ (colored dots) and fit (dark gray line). The black circled data point (also in d) marks the minimum charge noise measured for this specific device (Sϵ,min) at f = 1 Hz.
Here, we electrostatically define a multi-electron quantum dot in the charge sensor by applying gate voltages to the accumulation gates SDRAcc and SDLAcc, the barriers SDLB and SDRB, and the plunger gate P. All other gates (red in Fig. 2a) are set to 0 V for measurements of heterostructure B and C, whereas they are positively biased in heterostructure A to facilitate charge accumulation in the sensor (Methods). Figure 2b shows typical Coulomb blockade oscillations of the source-drain current ISD for a charge sensor from heterostructure C measured at a dilution refrigerator base temperature of 50 mK. We follow the same tune-up procedure (Methods) consistently for all devices and we measure charge noise at the flank of each Coulomb peak within the VP range defined by the first peak observable in transport and the last one before onset of a background channel (Supplementary Figs. 2–4). For example, in Fig. 2b we consider Coulomb peaks within the VP range from 260 mV to 370 mV. The data collected in this systematic way is taken as a basis for comparison between the three different heterostructures in this study.
For each charge noise measurement at a given VP we acquire 60 s (heterostructure A) or 600 s (heterostructures B, C) long traces of ISD and split them into 10 (heterostructure A) or 15 windows (heterostructures B, C). We obtain the current noise spectrum SI by averaging over the 10 (15) windows the discrete Fourier transform of the segments (Methods). We convert SI to a charge noise spectrum Sϵ using, for each measurement at a given VP, the unique lever arm from the corresponding Coulomb diamonds and slope of the Coulomb peak to take into account a possible deformation of the charge sensor with the increasing electron number (inset Fig. 2b, Methods, and Supplementary Fig. 5). A representative charge noise spectrum Sϵ measured at VP = 360.3 mV is shown in Fig. 2c. We observe an approximate 1/f trend at low frequency, pointing towards an ensemble of TLF with a broad range of activation energies affecting charge noise around the charge sensor41,42. Figure 2e shows the charge noise Sϵ at 1 Hz as a function of VP. The charge noise decreases, with a linear trend, with increasing VP, suggesting that, similar to scattering in 2D, screening by an increased electron density shields the electronically active region from noise arising from the heterostructure and the gate stack43. From this measurement we extract, for a given device, the minimum measured charge noise at 1 Hz (Sϵ,min circled data point in Fig. 2e) upon variation of VP in our experimental range. We use Sϵ,min as an informative metric to compare charge noise levels from device to device in a given heterostructure. For a given device, all charge noise spectra Sϵ are plotted in 3D as a function of f and VP (Fig. 2d). To quantify our observations, we fit the data to the plane \(\log {S}_{\epsilon }=-\alpha \log f+\beta {V}_{P}+\gamma\) (Supplementary Note 4). Coefficient α = 0.84 ± 0.01 indicates the spectrum power law exponent and coefficient β = − 15.6 ± 0.1 mV−1 quantifies the change in noise spectrum with increasing plunger gate and, consequently, the susceptibility of charge noise to the increasing electron number in the sensor.
Distribution of transport properties and charge noise
We have introduced key metrics for 2D electrical transport (μ, np) and charge noise (α, β and Sϵ,min) from Hall bar and quantum dot measurements, respectively. In Fig. 3a–e we compare the distributions of all these metrics for the three heterostructures A, B, C. Each box-plot is obtained from the analysis of measurements in Figs. 1d, e, and 2d repeated on multiple H-FETs or quantum dots, on dies randomly selected from different locations across the 100 mm wafers (Methods). To facilitate a comparison with previous studies, the minimum charge noise at 1 Hz is plotted in Fig. 3e as \({S}_{\epsilon,min}^{1/2}\) and therefore in units of μeV/Hz½.
a, b Distributions of mobility μ measured at n = 6 × 1011 cm−2 and percolation density np for heterostructure A (red, 20 H-FETs measured, of which 16 reported in ref. 32), B (blue, 16 H-FETs measured of which 14 reported in ref. 32), and C (green, 22 H-FETs measured). c–e Distributions of noise spectrum power law exponent α, coefficient β indicating the change in noise spectrum with increasing VP, and minimum charge noise \({S}_{\epsilon,min}^{1/2}\) within the range of VP investigated for heterostructure A (red, 4 devices measured), B (blue, 7 devices measured), and C (green, 5 devices measured). Quartile box plots, mode (horizontal line), means (diamonds), 99% confidence intervals of the mean (dashed whiskers), and outliers (circles) are shown.
As reported earlier in ref. 32, the improvement in both mean values and spread for μ and np was associated with a reduction of remote impurities when replacing the epitaxial Si cap in heterostructure A with a Si-rich passivation layer in heterostructure B. Moving to heterostructure C, we measure a high mean mobility of (2.10 ± 0.08) × 105 cm2/Vs and a low mean percolation density of (7.68 ± 0.37) × 1010 cm−2, representing an improvement by a factor ≃1.4 and ≃1.3, respectively (compared to heterostructure A). Most strikingly, the 99% confidence intervals of the mean for μ and np are drastically reduced by a factor ≃9.8 and ≃4.8, respectively. We speculate that these improvements in heterostructure C are associated with the suppression of misfit dislocations at the quantum well/buffer interface, thereby reducing short range scattering and increasing uniformity on a wafer-scale. This interpretation is supported by previous studies of mobility limiting mechanisms as a function of the quantum well thickness in strained Si/SiGe heterostructures39. We speculate that further reducing the quantum well thickness could increase surface roughness scattering from the bottom interface, and therefore disorder. Instead, fine-tuning the quantum well thickness between 5 nm and 9 nm might minimize surface roughness scattering whilst still avoiding the formation of misfit dislocations.
We now shift our attention to the results of charge noise measurements. First, the power law exponent α (Fig. 3c) shows a mean value ≃1, however the 99% confidence interval and interquartile range increase when moving from heterostructure A to B and C. Next, we observe a decreasing trend for the absolute mean value of coefficient β (Fig. 3d), meaning that the noise spectrum is less susceptible to changes in VP. Finally, Fig. 3e shows the distributions for \({S}_{\epsilon,min}^{1/2}\), the minimum charge noise at 1 Hz upon varying VP. We find in heterostructure C an almost order of magnitude reduction in mean \({S}_{\epsilon,min}^{1/2}\) to 0.29 ± 0.02 μeV/Hz½. This trend is confirmed by plotting the distributions of maximum charge noise at 1 Hz upon varying VP (Supplementary Fig. 4). Furthermore, within the distribution of \({S}_{\epsilon,min}^{1/2}\) for heterostructure C, the minimum value of the measured charge noise as a function of VP and across quantum dots is 0.15 μeV/Hz½. These charge noise values are on par or compare favorably to the best values reported previously at 1 Hz in gate defined quantum dots. In multi-electron quantum dots, charge noise of 0.47 μeV/Hz½ was reported for Si/SiGe44, 0.6 μeV/Hz½ (average value, with a minimum of ≤0.2 μeV/Hz½) for Ge/SiGe45, 0.49 ± 0.1 μeV/Hz½ for Si/SiO246, and 1 μeV/Hz½ for InSb47. In single-electron quantum dots, charge noise of 0.33 μeV/Hz½ was reported for Si/SiGe48 and 7.5 μeV/Hz½ for GaAs49.
We understand the charge noise trends in Fig. 3c–e by relating them to the evolution of the disorder landscape moving from heterostructures A to B and C, as inferred by the electrical transport measurements in Fig. 3a, b. The narrow distribution of α in heterostructure A points to charge noise being dominated from many TLFs possibly located at the low quality semiconductor/dielectric interface and above, albeit other sources of charge noise in the surrounding environment of the quantum dot may be present, such as highly localized misfit dislocations arising from partial strain relaxation in the quantum well or other nearby fluctuators. With a better semiconductor/dielectric interface, the effect of these other nearby fluctuators emerges in heterostructure B and C as a larger spread of the frequency exponent α, indicating a nonuniform distribution of activation energies according to the Dutta-Horn model50. Yet, the noise spectra still follow a 1/f-like behavior (Supplementary Fig. 3), suggesting that TLFs also experience slow temperature fluctuations42. The electrical transport measurements support this interpretation: scattering from many remote impurities is dominant in heterostructure A, whereas with a better semiconductor/dielectric interface remote scattering has less impact in the transport metrics of heterostructures B and C.
The decreasing trend in ∣β∣ is in line with the observation from electrical transport. As the impurity density decreases from heterostructure A to B and C, charge noise is less affected by an increasing VP, since screening of electrical noise through adding electrons to the charge sensor becomes less effective. While we are not able to measure directly the electron number in the charge sensor, we deem unlikely the hypothesis that charge sensors in heterostructure A are operated with considerably fewer electrons than in heterostructure C. This is because all operation gate voltages in heterostructure A are consistently larger than in heterostructure C (Supplementary Fig. 4), due to the higher disorder.
Finally, the drastic reduction in mean value and spread of \({S}_{\epsilon,min}^{1/2}\) mirrors the evolution of mean value and spread of np and μ. From heterostructure A to B, a reduction in scattering from remote impurities is likely to result in less charge noise from long-range TLFs. From heterostructure B to C, the reduction in the possible number of dislocations at the quantum well/buffer interface, further reduces the charge noise picked up by quantum dots. This explanation is based on earlier studies of charge noise in strained Si-MOSFETs27,28,29, which showed a correlation between low-frequency noise spectral density and static device parameters. Dislocations at the bottom of the strained channel may act as scattering centers that degrade mobility and as traps for the capture and release of carriers, which causes noise similarly to traps at the dielectric interface.
Calculated dephasing time and infidelity
To emphasize the improvement of the electrical environment in the semiconductor host, we calculate the dephasing time \({T}_{2}^{\star }\) of charge and spin qubits assuming these qubits experience the same fluctuations as our 28Si/SiGe quantum dots. The dephasing time of a qubit (in the quasistatic limit and far-off from a sweet spot) is given by51,52
with the Planck constant h and the standard deviation
Importantly, both the charge noise amplitude \({S}_{\epsilon }^{2}(f)\) and the noise exponent α have a strong impact on the dephasing time while the low and high frequency cut-off, flow and fhigh, given by the duration of the experiment have a weaker impact. The prefactor \(\left|\frac{\partial {{{{{{{\mathcal{E}}}}}}}}}{\partial \mu }\right|\) translates shifts in chemical potential of the charge sensor into energy shifts of the qubit and depends on many parameters such as the type of qubit and the device itself. We find \(\left|\frac{\partial {{{{{{{\mathcal{E}}}}}}}}}{\partial \mu }\right |=1\) for a charge qubit53 and \(\left|\frac{\partial {{{{{{{\mathcal{E}}}}}}}}}{\partial \mu }\right|\approx 1{0}^{-5}\) for an uncoupled spin- qubit44 (see Supplementary Note 7 for a derivation of these numbers and the used frequency bandwidths).
Figure 4a shows the computed dephasing times of charge qubits (circle) and spin qubits (star) for all three heterostructures. These calculations represent a best case scenario, since we use the distribution of measured Sϵ,min from Fig. 3 as input parameter for each heterostructure. The improvements in our material can be best seen by investigating \({T}_{2}^{\star }\) of the charge qubit since it is directly affected by charge noise. Our theoretical extrapolation shows two orders of magnitude improvement in \({T}_{2}^{\star }\) by switching from heterostructures A to heterostructures B and C. One order is gained from the reduced charge noise amplitude and another order is gained through a more beneficial noise exponent α > 1. Note, that the integration regimes differ for spin and charge qubits due to the different experimental setups and operation speeds44,53. For potential spin qubits in heterostructure A the calculated \({T}_{2}^{\star }\) shows an average \({\overline{T}}_{2}^{\star }=8.4\pm 5.6\) μs. This distribution compares well with the distribution \({\overline{T}}_{2}^{\star }=6.7\pm 5.6\) μs of experimental \({T}_{2}^{\star }\) data from state-of-the-art semiconductor spin qubits in materials with similar stacks as in heterostructure A6,10. Note that while such comparisons oversimplify actual semiconductor spin-qubit devices by reducing them to a single number, they fulfill two aims. They allow us to benchmark the computed performance of heterostructure A to past experiments and provide a prognosis on the qubit quality in novel material stacks. Heterostructures B and C, in this case, may support average dephasing times of \({\overline{T}}_{2}^{\star }=24.3\pm 12.5\) μs and \({\overline{T}}_{2}^{\star }=36.7\pm 18\) μs, respectively. The highest values \({T}_{2}^{\star }=70.1\) μs hints towards a possible long dephasing time for spin qubits, previously only reported in ref. 2.
a Computed dephasing times \({T}_{2}^{\star }\) of a charge qubit (circle) and of a spin-qubit (star) using Sϵ,min from heterostructure A (red), B (blue), C (green). Eq. (1) was used to compute \({T}_{2}^{\star }\) as a function of Sϵ and α from Fig. 3 with frequency cutoffs (fmin, fmax) = (1.6 mHz, 33 GHz) and (fmin, fmax) = (1.6 mHz, 10 kHz). Literature values (squares) are taken from refs. 6,10. b Simulated infidelity of a CZ-gate between two spin qubits following the ref. 6 using Sϵ and α from heterostructure A (red), B (blue), C (green) in Fig. 3 as input for barrier fluctuations.
Figure 4b shows the simulated infidelity, a metric to measure the closeness to the ideal operation, of a universal CZ-gate between two spin qubits following ref. 6 and Supplementary Note 7. Note that the device used in ref. 6 has the same architecture as our test devices. In the CZ-gate simulation, noise couples in dominantly via barrier voltage fluctuations which affects the interaction between the electron spins. Again, we use the charge noise amplitude Sϵ,min and exponent α from the quantum dot experiments in Fig. 3 as input for the simulations. The simulations show an averaged average gate infidelity \(1-{\overline{F}}_{{\scriptstyle{{{{{\rm{CZ}}}}}}}}=0.02\pm 0.01\%\) which means on average a single error every 5000 runs. We also observe a saturation value close to 1 − F = 10−4 which arises from single-qubit dephasing \({T}_{2}^{\star }=20\) μs used in the simulations estimated from nuclear spin noise due to a 800 ppm concentration of the 29Si silicon isotope which has a non-zero nuclear spin44.
Discussion
In summary, we have measured electron transport and charge noise in 28Si/SiGe heterostructures where we improve the semiconductor/dielectric interface, by adopting an amorphous Si-rich passivation, and the structural quality of the quantum well, by reducing the quantum well thickness significantly below the Matthew-Blakeslee critical thickness for strain relaxation. We relate disorder in 2D to charge noise in quantum dots by following a statistical approach to measurements. A reduction of remote impurities and dislocations nearby the quantum well is connected with the key improvements in the scattering properties of the 2D electron gas, such as mobility and percolation density, and their uniformity across a 100 mm wafer. The trend observed from electron transport in 2D is compatible with the observations from measurements of charge noise in quantum dots. As remote impurities are reduced, charge noise becomes more sensitive to local fluctuators nearby the quantum well and less subject to screening by an increased number of electrons in the dot. Furthermore, with this materials optimization, we achieve a statistical improvement of nearly one order of magnitude in the charge noise supported by quantum dots. Using the charge noise distribution as input parameter and benchmarking against published spin-qubit data, we predict that our optimized semiconductor host could support long-lived and high-fidelity spin qubits. We envisage that further materials improvements in the structural quality of the quantum well, in addition to the commonly considered semiconductor/dielectric interface, may lead systematically to quantum dots with less noise and to better qubit performance.
Methods
Si/SiGe heterostructure growth
The 28Si/SiGe heterostructures are grown on a 100-mm n-type Si(001) substrate using an Epsilon 2000 (ASMI) reduced pressure chemical vapor deposition reactor. The reactor is equipped with a 28SiH4 gas cylinder (1% dilution in H2) for the growth of isotopically enriched 28Si. The 28SiH4 gas was obtained by reducing 28SiF4 with a residual 29Si concentration of 0.08%54. Starting from the Si substrate, the layer sequence of all heterostructures comprises a 3 μm step-graded Si(1−x)Gex layer with a final Ge concentration of x = 0.3 achieved in four grading steps (x = 0.07, 0.14, 0.21, and 0.3), followed by a 2.4 μm Si0.7Ge0.3 strain-relaxed buffer. The heterostructures differ for the active layers on top of the strain-relaxed buffer. Heterostructure A has a 9 nm tensile strained 28Si quantum well, a 30 nm Si0.7Ge0.3 barrier, and a sacrificial 1 nm epitaxial Si cap. Heterostructure B has an 9 nm tensile strained 28Si quantum well, a 30 nm Si0.7Ge0.3 barrier, and a sacrificial passivated Si cap grown at 500 °C. Heterostructure C has a 5 nm tensile strained 28Si quantum well, a 30 nm Si0.7Ge0.3 barrier, and a sacrificial passivated Si cap grown at 500 °C. A typical secondary ions mass spectrometry of our heterostructures is reported in Supplementary Fig. S13 of ref. 40 and the Ge concentration in the SiGe layers is confirmed by quantitative electron energy loss spectroscopy (EELS).
Device fabrication
The fabrication process for Hall-bar shaped heterostructure field effect transistors (H-FETs) involves: reactive ion etching of mesa-trench to isolate the two-dimensional electron gas; P-ion implantation and activation by rapid thermal annealing at 700 °C; atomic layer deposition of a 10-nm-thick Al2O3 gate oxide; deposition of thick dielectric pads to protect gate oxide during subsequent wire bonding step; sputtering of Al gate; electron beam evaporation of Ti:Pt to create ohmic contacts to the two-dimensional electron gas via doped areas. All patterning is done by optical lithography. Double quantum dot devices are fabricated on wafer coupons from the same H-FET fabrication run and share the process steps listed above. Double-quantum dot devices feature a single layer gate metallization and further require electron beam lithography, evaporation of Al (27 nm) or Ti:Pd (3:17 nm) thin film metal gate, lift-off, ALD of a 5 nm thick Al2O3 insulating layer, and a global top-gate.
Electrical characterization of H-FETs
Hall-bar H-FETs measurements are performed in an attoDRY2100 variable temperature insert refrigerator at a base temperature of 1.7 K32. We apply a source-drain bias of 100 μV and measure the source-drain current ISD, the longitudinal voltage Vxx, and the transverse Hall voltage Vxy as function of the top gate voltage Vg and the external perpendicular magnetic field B. From here we calculate the longitudinal resistivity ρxx and transverse Hall resistivity ρxy. The Hall electron density n is obtained from the linear relationship ρxy = B/en at low magnetic fields. The carrier mobility μ is extracted from the relationship σxx = neμ, where e is the electron charge. The percolation density np is extracted by fitting the longitudinal conductivity σxx to the relation \({\sigma }_{xx}\propto {(n-{n}_{p})}^{1.31}\). Here σxx is obtained via tensor inversion of ρxx at B = 0. The box plots in Fig. 3a, b for heterostructure A (red) and B (blue) expand previously published data in Fig. 2f, e of ref. 32 by considering measurements of 4 additional H-FETs for heterostructure A (20 H-FETs in total) and of 2 additional H-FETs for heterostructure B (16 H-FETs in total).
Electrical characterization of quantum dots
Measurements of the multi-electron quantum dots defined in the charge sensor are performed in a Leiden cryogenic dilution refrigerator with a mixing chamber base temperature TMC = 50 mK40. The devices are tuned systematically with the following procedure. We sweep all gate voltages (VSDRAcc, VSDRB, VP, VSDLB, and VSDLAcc) from 0 V towards more positive bias, until a source-drain current ISD of ≈1 nA is measured, indicating that a conductive channel has formed in the device. We then reduce the barrier voltages to find the pinch-off voltages for each barrier. Subsequently, we measure ISD as a function of VSDLB and VSDRB and from this 2D map we find a set of gate voltage parameters so that Coulomb blockade peaks are visible. We then fix the barrier voltages and sweep VP to count how many clearly defined Coulomb peaks are observed before onset of a background current. The quantum dot is tuned to show at least 9 Coulomb peaks, so that noise spectra may be fitted as in Fig. 2d with meaningful error bars. If we see less than 9 Coulomb peaks we readjust the accumulation gate voltages VSDRAcc, and VSDLAcc, and repeat the 2D scan of VSDLB against VSDRB. In one case (device 2 of heterostructure A), we tuned device to show past 5 Coulomb peaks and still performed the fit of the charge noise spectra similar to the one shown in Fig. 2d. Further details on the extraction of the lever arms and operation gate voltages of the devices are provided in Supplementary Figs 4 and 5. We estimate an electron temperature of 190 mK by fitting Coulomb blockade peaks (see Supplementary Fig. 2 in ref. 32) measured on quantum dot devices.
For heterostructure A we apply a source drain bias of 100 μV (1 device) or 150 μV (3 devices) across the quantum dot, finite gate voltages across the operation gates of the dot, and finite gate voltages across the screening gates. We measure the current ISD and the current noise spectrum SI on the left side of the Coulomb peak where ∣dI/dVP∣ is largest. We use a sampling rate of 1 kHz for 1 min using a Keithley DMM6500 multimeter. The spectra are then divided into 10 segments of equal length and we use a Fourier transform to convert from time-domain to frequency-domain for a frequency range of 167 mHz–500 Hz. We set the upper limit of the frequency spectra at 10 Hz, to avoid influences from a broad peak at around 150 Hz coming from the setup (Supplementary Fig. 3). A peak in the power spectral density at 9 Hz is removed from the analysis since it is an artifact of the pre-amplifier. To convert the current noise spectrum to a charge noise spectrum, we use the formula20
where a is the lever arm and ∣dI/dVP∣ is the slope of the Coulomb peak at the plunger voltage used to acquire the time trace.
The charge noise measurements conditions have been slightly modified from sample A to sample B, C to extend the probed frequency range from 100 μHz to 10 μHz. For heterostructures B and C we apply a source drain bias of 150 μV across the quantum dot, finite gate voltages across the operation gates of the quantum dot, and we apply 0 V to all other gates. We measure the current ISD and the current noise spectrum SI on the left side of the Coulomb peak where ∣dI/dVP∣ is largest. We use a sampling rate of 1 kHz for 10 min using a Keithley DMM6500 multimeter. The spectra are then divided into 15 segments of equal length and we use a Fourier transform to convert from time-domain to frequency-domain for a frequency range of 25 mHz–500 Hz. We set the upper limit of the frequency spectra at 10 Hz, to avoid influences from a broad peak at around 150 Hz coming from the setup. We use Eq. (3) to convert the current noise spectrum to a charge noise spectrum.
(Scanning) Transmission Electron Microscopy
For structural characterization with (S)TEM, we prepared cross-sections of the quantum well heterostructures by using a Focused Ion Beam (Helios 600 dual beam microscope). Atomically resolved HAADF STEM data was acquired in a probe corrected TITAN microscope operated at 300 kV. Quantitative EELS was carried out in a TECNAI F20 microscope operated at 200 kV with approximately 2 eV energy resolution and 1 eV energy dispersion. Principal Component Analysis (PCA) was applied to the spectrum images to enhance S/N ratio.
Data availability
All data included in this work are available from the 4TU.ResearchData international data repository at https://doi.org/10.4121/20418579.
Change history
06 April 2023
A Correction to this paper has been published: https://doi.org/10.1038/s41467-023-37548-z
References
Vandersypen, L. M. K. & Eriksson, M. A. Quantum computing with semiconductor spins. Phys. Today 72, 38–45 (2019).
Veldhorst, M. et al. A two-qubit logic gate in silicon. Nature 526, 410–414 (2015).
Stano, P. & Loss, D. Review of performance metrics of spin qubits in gated semiconducting nanostructures. Nat. Rev. Phys. 4, 672–688 (2022).
Zwerver, A. M. J. et al. Qubits made by advanced semiconductor manufacturing. Nat. Electronics 5, 184–190 (2022).
Watson, T. F. et al. A programmable two-qubit quantum processor in silicon. Nature 555, 633–637 (2018).
Xue, X. et al. Quantum logic with spin qubits crossing the surface code threshold. Nature 601, 343–347 (2022).
Noiri, A. et al. Fast universal quantum gate above the fault-tolerance threshold in silicon. Nature 601, 338–342 (2022).
Ma̧dzik, M. T. et al. Precision tomography of a three-qubit donor quantum processor in silicon. Nature 601, 348–353 (2022).
Mills, A. R. et al. Two-qubit silicon quantum processor with operation fidelity exceeding 99%. Sci. Adv. 8, 5130 (2022).
Philips, S. G. J. et al. Universal control of a six-qubit quantum processor in silicon. Nature 609, 919–924 (2022).
Samkharadze, N. et al. Strong spin-photon coupling in silicon. Science 359, 1123–1127 (2018).
Zajac, D. M. et al. Resonantly driven CNOT gate for electron spins. Science 359, 439–442 (2018).
Borjans, F., Croot, X. G., Mi, X., Gullans, M. J. & Petta, J. R. Resonant microwave-mediated interactions between distant electron spins. Nature 577, 195–198 (2020).
Harvey-Collard, P. et al. Coherent spin-spin coupling mediated by virtual microwave photons. Phys. Rev. X 12, 021026 (2022).
Yoneda, J. et al. Coherent spin qubit transport in silicon. Nat. Commun. 12, 4114 (2021).
Noiri, A. et al. A shuttling-based two-qubit logic gate for linking distant silicon quantum processors. Nat. Commun. 13, 5740 (2022).
Vandersypen, L. M. K. et al. Interfacing spin qubits in quantum dots and donors-hot, dense, and coherent. npj Quantum Inf. 3, 1–13 (2017).
Yoneda, J. et al. A quantum-dot spin qubit with coherence limited by charge noise and fidelity higher than 99.9%. Nat. Nanotechnol. 13, 102–106 (2018).
Paladino, E., Galperin, Y. M., Falci, G. & Altshuler, B. L. 1/f noise: Implications for solid-state quantum information. Rev. Modern Phys. 86, 361 (2014).
Connors, E. J., Nelson, J. J., Qiao, H., Edge, L. F. & Nichol, J. M. Low-frequency charge noise in Si/SiGe quantum dots. Phys. Rev. B 100, 165305 (2019).
Connors, E. J., Nelson, J., Edge, L. F. & Nichol, J. M. Charge-noise spectroscopy of Si/SiGe quantum dots via dynamically-decoupled exchange oscillations. Nat. Commun. 13, 940 (2022).
Culcer, D., Hu, X. & Das Sarma, S. Dephasing of Si spin qubits due to charge noise. Appl. Phys. Lett. 95, 073102 (2009).
Dekker, C. et al. Spontaneous resistance switching and low-frequency noise in quantum point contacts. Phys. Rev. Lett. 66, 2148–2151 (1991).
Sakamoto, T., Nakamura, Y. & Nakamura, K. Distributions of single-carrier traps in GaAs/AlxGa1−xAs heterostructures. Appl. Phys. Lett. 67, 2220 (1998).
Liefrink, F., Dijkhuis, J. I. & Houten, H. V. Low-frequency noise in quantum point contacts. Semiconductor Sci. Technol. 9, 2178–2189 (1994).
Ramon, G. & Hu, X. Decoherence of spin qubits due to a nearby charge fluctuator in gate-defined double dots. Phys. Rev. B 81, 045304 (2010).
Hua, W.-C., Lee, M. H., Chen, P. S., Tsai, M.-J. & Liu, C. W. Threading dislocation induced low frequency noise in strained-Si nMOSFETs. IEEE Electron Device Letters 26, 667–669 (2005).
Lee, M. H. et al. Comprehensive low-frequency and RF noise characteristics in strained-Si NMOSFETs. In: IEEE International Electron Devices Meeting 2003, pp. 3–61364 (2003).
Simoen, E. et al. Processing aspects in the low-frequency noise of nMOSFETs on strained-silicon substrates. IEEE Trans. Electron Dev. 53, 1039–1047 (2006).
Monroe, D. Comparison of mobility-limiting mechanisms in high-mobility Si1−xGex heterostructures. J. Vac. Sci. Technol. B 11, 1731 (1993).
Xue, X. et al. Cmos-based cryogenic control of silicon quantum circuits. Nature 593, 205–210 (2021).
Degli Esposti, D. et al. Wafer-scale low-disorder 2DEG in 28Si/SiGe without an epitaxial Si cap. Appl. Phys. Lett. 120, 184003 (2022).
Matthews, J. W. & Blakeslee, A. E. Defects in epitaxial multilayers: I. Misfit dislocations. J. Crystal Growth 27, 118–125 (1974).
People, R. & Bean, J. C. Calculation of critical layer thickness versus lattice mismatch for GexSi1−x/Si strained-layer heterostructures. Appl. Phys. Lett. 47, 322–324 (1985).
Ismail, K. Effect of dislocations in strained Si/SiGe on electron mobility. J. Vac. Sci. Technol. B 14, 2776 (1996).
Liu, Y. et al. Role of critical thickness in SiGe/Si/SiGe heterostructure design for qubits. J. Appl. Phys. 132, 085302 (2022).
Paquelet Wuetz, B. et al. Multiplexed quantum transport using commercial off-the-shelf CMOS at sub-kelvin temperatures. npj Quantum Inf. 6, 43 (2020).
Tracy, L. A. et al. Observation of percolation-induced two-dimensional metal-insulator transition in a Si MOSFET. Phys. Rev. B 79, 235307 (2009).
Ismail, K. et al. Identification of a mobility-limiting scattering mechanism in modulation-doped Si/SiGe heterostructures. Phys. Rev. Lett. 73, 3447–3450 (1994).
Paquelet Wuetz, B. et al. Atomic fluctuations lifting the energy degeneracy in Si/SiGe quantum dots. Nat. Commun. 13, 7730 (2022).
Kogan, S. Electronic noise and fluctuations in solids (Cambridge University Press, 1996).
Ahn, S., Sarma, S. D. & Kestner, J. P. Microscopic bath effects on noise spectra in semiconductor quantum dot qubits. Phys. Rev. B 103, 041304 (2021).
Thorgrimsson, B. et al. Extending the coherence of a quantum dot hybrid qubit. npj Quantum Inf. 3, 32 (2017).
Struck, T. et al. Low-frequency spin qubit energy splitting noise in highly purified 28Si/SiGe. npj Quantum Inf. 6, 40 (2020).
Lodari, M. et al. Low percolation density and charge noise with holes in germanium. Mater. Quantum Technol. 1, 11002 (2021).
Freeman, B. M., Schoenfield, J. S. & Jiang, H. Comparison of low frequency charge noise in identically patterned Si/SiO2 and Si/SiGe quantum dots. Appl. Phys. Lett. 108, 253108 (2016).
Jekat, F. et al. Exfoliated hexagonal BN as gate dielectric for InSb nanowire quantum dots with improved gate hysteresis and charge noise. Appl. Phys. Lett. 116, 253101 (2020).
Mi, X., Kohler, S. & Petta, J. R. Landau-Zener interferometry of valley-orbit states in Si/SiGe double quantum dots. Phys. Rev. B 98, 161404 (2018).
Basset, J. et al. Evaluating charge noise acting on semiconductor quantum dots in the circuit quantum electrodynamics architecture. Appl. Phys. Lett. 105, 063105 (2014).
Dutta, P., Dimon, P. & Horn, P. M. Energy scales for noise processes in metals. Phys. Rev. Lett. 43, 646–649 (1979).
Shnirman, A., Makhlin, Y. & Schön, G. Noise and decoherence in quantum two-level systems. Phys. Scripta 2002, 147 (2002).
Bermeister, A., Keith, D. & Culcer, D. Charge noise, spin-orbit coupling, and dephasing of single-spin qubits. Appl. Phys. Lett. 105, 192102 (2014).
MacQuarrie, E. R. et al. Progress toward a capacitively mediated CNOT between two charge qubits in Si/SiGe. npj Quantum Inf. 6, 81 (2020).
Sabbagh, D. et al. Quantum Transport Properties of Industrial 28Si/28SiO2. Phys. Rev. Appl. 12, 014013 (2019).
Acknowledgements
We acknowledge helpful discussions with G. Isella, D. Paul, M. Mehmandoost, the Scappucci group and the Vandersypen group. This research was supported by the European Union’s Horizon 2020 research and innovation programme under the Grant Agreement No. 951852 (QLSI project) and in part by the Army Research Office (Grant No. W911NF-17-1-0274). The views and conclusions contained in this document are those of the authors and should not be interpreted as representing the official policies, either expressed or implied, of the Army Research Office (ARO), or the U.S. Government. The U.S. Government is authorized to reproduce and distribute reprints for Government purposes notwithstanding any copyright notation herein. M.R. acknowledges support from the Netherlands Organization of Scientific Research (NWO) under Veni grant VI.Veni.212.223. ICN2 acknowledges funding from Generalitat de Catalunya 2021SGR00457. ICN2 is supported by the Severo Ochoa program from Spanish MCIN / AEI (Grant No.: CEX2021-001214-S) and is funded by the CERCA Programme / Generalitat de Catalunya and ERDF funds from EU. Part of the present work has been performed in the framework of Universitat Autònoma de Barcelona Materials Science PhD program. Authors acknowledge the use of instrumentation as well as the technical advice provided by the National Facility ELECMI ICTS, node “Laboratorio de Microscopias Avanzadas" at University of Zaragoza. M.B. acknowledges support from SUR Generalitat de Catalunya and the EU Social Fund; project ref. 2020 FI 00103. We acknowledge support from CSIC Interdisciplinary Thematic Platform (PTI+) on Quantum Technologies (PTI-QTEP+).
Author information
Authors and Affiliations
Contributions
A.S. grew and designed the 28Si/SiGe heterostructures with B.P.W. and G.S.. M.R. developed the theory. A.S. and D.D.E. fabricated heterostructure field effect transistors measured by B.P.W. and D.D.E.. M.B and J.A. performed TEM characterization. S.A and D.D.E. fabricated quantum dot devices. B.P.W. and D.D.E. measured the quantum dot devices with contributions from A.M.J.Z.. G.S. conceived and supervised the project. B.P.W, D.D.E, M.R, and G.S. wrote the manuscript with input from all authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Yujia Liu and the other anonymous reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Paquelet Wuetz, B., Degli Esposti, D., Zwerver, AM.J. et al. Reducing charge noise in quantum dots by using thin silicon quantum wells. Nat Commun 14, 1385 (2023). https://doi.org/10.1038/s41467-023-36951-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-023-36951-w
This article is cited by
-
Rapid single-shot parity spin readout in a silicon double quantum dot with fidelity exceeding 99%
npj Quantum Information (2024)
-
Low disorder and high valley splitting in silicon
npj Quantum Information (2024)
-
Low charge noise quantum dots with industrial CMOS manufacturing
npj Quantum Information (2024)
-
Impact of interface traps on charge noise and low-density transport properties in Ge/SiGe heterostructures
Communications Materials (2024)
-
Limitations on the maximal level of entanglement of two singlet–triplet qubits in GaAs quantum dots
Quantum Information Processing (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.