Abstract
The recently discovered kagome superconductors AV3Sb5 (A = K, Rb, Cs) exhibit unusual charge-density-wave (CDW) orders with time-reversal and rotational symmetry breaking. One of the most crucial unresolved issues is identifying the symmetry of the superconductivity that develops inside the CDW phase. Theory predicts a variety of unconventional superconducting symmetries with sign-changing and chiral order parameters. Experimentally, however, superconducting phase information in AV3Sb5 is still lacking. Here we report the impurity effects in CsV3Sb5 using electron irradiation as a phase-sensitive probe of superconductivity. Our magnetic penetration depth measurements reveal that with increasing impurities, an anisotropic fully-gapped state changes to an isotropic full-gap state without passing through a nodal state. Furthermore, transport measurements under pressure show that the double superconducting dome in the pressure-temperature phase diagram survives against sufficient impurities. These results support that CsV3Sb5 is a non-chiral, anisotropic s-wave superconductor with no sign change both at ambient and under pressure.
Similar content being viewed by others
Introduction
The kagome lattice, a motif consisting of corner-sharing triangles and hexagonal holes, provides a platform for a rich variety of novel quantum phases of matter. Due to its strong geometrical frustration, it has long been studied in quantum spin systems as a playground for realizing quantum spin liquids1. Recently, however, significant efforts have been devoted to exploring topological metals and semimetals in kagome-lattice systems, in which unique band structures such as flat bands, Dirac cones, and van Hove singularities (vHSs) can lead to Dirac/Weyl fermions2,3, spin/charge ordering, and unconventional superconductivity4,5,6. Although various topological kagome materials have been reported so far2,3, superconductors with kagome lattices are rarely found 7.
The recently discovered AV3Sb5 (A = K, Rb, Cs) is a new family of kagome superconductors with the superconducting transition temperature Tc of 0.9–2.5 K8,9,10. The alkali A atoms are intercalated between sheets consisting of the two-dimensional (2D) kagome networks of V atoms and triangular and hexagonal networks of Sb atoms (Fig. 1a, b). The electronic band dispersions near the Fermi energy EF share characteristic features predicted for an ideal kagome-lattice system such as a vHS at the M point and a Dirac point at the K point8,10,11,12,13. In these materials, EF is located near the vHS point, and multiple Fermi surfaces are formed by the V d-orbitals and Sb p-orbitals (Fig. 1c). Such unique band structures in AV3Sb5 give rise to unconventional charge-density-wave (CDW) orders with the transition temperature T * ~ 78–103 K8,9,10 driven by electron correlation5,14,15,16,17. The CDW transition is accompanied by a 2a0 × 2a0 × 2c0 or 2a0 × 2a0 × 4c0 superlattice composed of modulated star-of-David and inverse star-of-David patterns (where a0 and c0 indicate the lattice constants above T *), which breaks translational symmetry13,18,19,20. More intriguingly, it has been reported that additional symmetries, such as time-reversal symmetry (TRS) and rotational symmetry (RS), can be broken below T*18,21,22,23,24,25. Since the superconducting transition takes place inside the unusual CDW phase, a fundamental question arises as to whether the superconducting pairing mechanism in AV3Sb5 is conventional or not26.
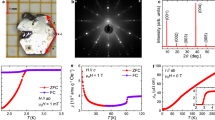
a Crystal structure of CsV3Sb5. b V-Sb1 plane viewed from the c-axis direction. Whereas the V atoms form a two-dimensional kagome network, the Sb1 atoms are located at the hexagonal centers. c Schematic of the 2D Fermi surface of CsV3Sb5. The circular (red) and hexagonal (green) Fermi surfaces around the Γ point are composed of the Sb p-orbitals and V d-orbitals, respectively, while the two triangular Fermi surfaces (blue and green) around the K point are formed by the V d-orbitals. d Temperature dependence of resistivity ρ(T) in CsV3Sb5 single crystals with irradiated doses of 0 (pristine, red), 1.3 (orange), 3.3 (green), and 8.6 (blue) C/cm2. The RRR values for each sample are listed. Arrows indicate the CDW transition temperatures determined from the temperature derivative of ρ(T) (see Fig. 4b, f, j). Note that the ρ(T) curves for the irradiated samples do not shift parallel to that of the pristine sample, which can be naturally understood by considering that CsV3Sb5 is a multiband system (see Supplementary Information Sec. III). e Low-temperature resistivity below 6 K on a logarithmic scale. Arrows indicate the residual resistivity ρ0 for each irradiated sample. f Temperature dependence of normalized frequency shifts of the TDO for each sample. g Superconducting and CDW transition temperatures Tc (left axis) and T* (right axis) as a function of irradiation dose. Tc is defined as the temperature at which the resistivity becomes zero (filled red circles), and the superfluid density becomes finite (open red circles). T* is defined as the temperature at which the derivative dρ/dT shows an abrupt change or dip (filled blue squares). h ρ0 (left axis) and λ(0) (right axis) as a function of irradiation dose. For the estimation of λ(0), see Supplementary Information Sec. IV.
Theories on the kagome lattice near van Hove filling have proposed that unconventional superconductivity beyond the electron–phonon mechanism can be realized by electron correlation effects4,5,6,15,27. Spin and charge fluctuations can lead to spin-triplet p- and f-wave6,15,27 and chiral d-wave superconductivity15, whereas bond-order fluctuations can promote anisotropic s-wave27 and chiral d-wave superconductivity5. In support of the above, first-principle calculations have pointed out that the Bardeen-Cooper-Schrieffer (BCS) theory (electron–phonon mechanism) cannot explain the experimental Tc values, suggesting an unconventional pairing mechanism in AV3Sb528.
Experimentally, however, the superconducting gap symmetry of AV3Sb5 is highly controversial, and whether TRS is broken or not is still elusive. Thermal conductivity measurements in CsV3Sb529 and μSR measurements in Rb/KV3Sb530 have suggested a nodal gap structure. In contrast, magnetic penetration depth31 and scanning tunneling spectroscopy (STS)32 studies in CsV3Sb5 have suggested a nodeless gap structure. Nuclear magnetic/quadrupole resonance (NMR/NQR) measurements in CsV3Sb533 have shown a finite Hebel-Slichter coherence peak in 1/T1T and a decrease in Knight shift below Tc, which exclude spin-triplet superconductivity. Regarding the TRS in the superconducting state, Josephson STS measurements in CsV3Sb534 have suggested a possible roton pair-density wave, corresponding to an unconventional superconducting state with TRS breaking. Contrastingly, μSR studies in CsV3Sb530 have reported that TRS is not broken in the superconductivity state. In addition to the above results at ambient pressure, high-pressure studies35,36 have revealed that the CDW phase is suppressed by the application of pressure, accompanied by the emergence of a superconducting dome, indicating the close relationship between the CDW and superconductivity. Moreover, recent μSR experiments under pressure37,38 have suggested that TRS is broken in the superconducting state when the CDW phase is suppressed by applying pressure. Therefore, to clarify the pairing mechanism of the kagome superconductors, it is crucial to pin down the superconducting gap symmetry of AV3Sb5 both at ambient and high pressure, including whether TRS is broken or not.
In general, the conventional phonon-mediated pairing mechanism leads to a superconducting gap opening all over the Fermi surface, while unconventional pairing mechanisms, such as spin fluctuations, can lead to an anisotropic gap with nodes where the superconducting gap becomes zero. Thus, experimental observations of the low-energy quasiparticle excitations determine whether the gap structure has nodes or not. In addition to clarifying the presence or absence of nodes in the gap, determining the sign of the gap function also provides a strong constraint on the superconducting pairing symmetry. Especially in kagome superconductors, theories have predicted that two degenerated superconducting order parameters, \({d}_{{x}^{2}-{y}^{2}}\) and dxy, give rise to chiral \({d}_{{x}^{2}-{y}^{2}}\pm i{d}_{xy}\)-wave symmetry, where a finite gap opens all over the Fermi surface, but the phase of the order parameter changes by 4π in momentum k space39. Therefore, phase-sensitive probes are highly required to determine the pairing symmetry of AV3Sb5.
There are several experimental probes that are sensitive to the sign of gap functions, such as Josephson junction40, quasiparticle interference41, and neutron scattering techniques42. In general, however, the analysis of such interference effects is complicated in multiband systems due to the complexity of the scattering processes. In addition, most of them require good surface/interface conditions. In contrast, the non-magnetic impurity effect, on which we focus here, is one of the phase-sensitive probes that are applicable to multiband systems and reflect the bulk superconducting properties43,44. In s-wave superconductors with no sign-changing order parameter, the Cooper pairs are not destroyed by non-magnetic impurity scattering, and both Tc and quasiparticle density of states (DOS) are little affected by disorder (the so-called Anderson’s theorem45) (Fig. 2e). In contrast, in the case of nodeless superconductors with sign-changing order parameters, such as chiral d-wave and s±-wave superconductors (note that considering the electronic structure of the present kagome system, one cannot expect sufficient interband interactions to induce the s±-wave superconductivity), the Cooper pairs are destroyed by impurity scattering, which suppresses Tc rapidly and induces impurity states associated with the Andreev bound state (Fig. 2f). In this case, additional low-energy quasiparticle excitations appear near the zero energy, e.g., leading to a change in the temperature dependence of the magnetic penetration depth λ from exponential to T2 43,46.
a–d Temperature dependence of the change in the penetration depth δλ(T) for the pristine (a), 1.3 (b), 3.3 (c), and 8.6 (d) C/cm2 irradiated samples. Solid circles are the experimental data. Black solid and dashed lines are fitting curves of the fully gapped s-wave and power-law analysis. e, f Schematics of the change in the quasiparticle density of states against disorder in the case of fully gapped states without (e) and with (f) sign change. g Gap value Δ0/ kBTc obtained from the s-wave fit to δλ(T) at low tempeartures as a function of irradiation dose. h Exponent value n obtained from the power-law fitting to δλ(T) up to 0.3 Tc as a function of irradiation dose. The exponent n ≤ 2 (gray shaded region) indicates a nodal gap structure, while n ≳ 3 implies a fully gapped state (blue shaded region).
Here, we show that superconductivity in CsV3Sb5 is robust against impurities both at ambient and under high pressure. Our magnetic penetration depth measurements reveal that with increasing impurities, a highly anisotropic fully gapped superconducting state changes gradually to an isotropic full-gap state without showing impurity-induced Andreev bound states, which excludes any of sign-changing symmetries. Moreover, transport measurements under high pressure show that the superconducting dome in the pressure-temperature (P-T) phase diagram survives against sufficient impurities. These results suggest that the superconducting gap function in CsV3Sb5 is non-chiral and non-sign-changing s-wave.
Results
Electron irradiation effects on the CDW and superconducting transition temperatures
In this study, we used electron irradiation to systematically introduce non-magnetic impurities into CsV3Sb5 single crystals (see Methods and Supplementary Information Sec. I). In this method, high-energy electron beam irradiation creates vacancies in the crystal43, acting as point defects without changing the electronic structure and lattice constants (see Supplementary Information Sec. II). Figure 1d, e shows the temperature dependence of resistivity ρ(T) at ambient pressure in samples with irradiated doses of 0 (pristine), 1.3, 3.3, and 8.6 C/cm2. The residual resistivity ratio (RRR) of the pristine sample is ~84, indicating the high quality of our crystals. As the dose increases, the residual resistivity ρ0 increases (also see Fig. 1h), and the RRR value decreases. The change in ρ(T) with impurities is successive for the irradiation dose in the whole temperature range. Furthermore, our X-ray structural analysis and Hall coefficient measurements show the absence of any change in the lattice parameters and carrier density induced by electron irradiation. These results indicate that the non-parallel shift with impurities in ρ(T) is most likely due to the multiband nature of the present kagome system (for more details, see Supplementary Information Sec. III). Along with this, both the CDW and superconducting transition temperatures T* and Tc shift to a lower temperature (Fig. 1g). In general, non-magnetic impurity scattering can suppress long-range orders because the introduced defects shorten the coherence length. Indeed, the suppression of CDW order by impurities has been theoretically studied47. The suppression of Tc has also been confirmed by the Meissner effect measured by the normalized frequency shift of a tunnel diode oscillator (TDO) (Fig. 1f). Note that the superconducting transition becomes sharper with increasing dose, which may be related to the suppression of superconducting phase fluctuations7,48 or the change in skin depth due to impurity scattering. The sharp superconducting transition width in the 8.6 C/cm2 irradiated sample with sufficient disorder indicates that the defects are introduced quite uniformly inside the crystals.
Non-magnetic impurity effects on low-energy quasiparticle excitations in the superconducting state
Next, we turn to the impurity effect on low-energy quasiparticle excitations in the superconducting state. Magnetic penetration depth λ is one of the most fundamental properties of superconductors sensitive to low-energy quasiparticle excitations7,31,43. In this study, we measured the magnetic penetration depth of the pristine and irradiated CsV3Sb5 single crystals down to 50 mK by using the TDO in a dilution refrigerator (see Methods). Figure 2a–d shows the change in the magnetic penetration depth δλ(T) ≡ λ(T) − λ(0) (where λ(0) is the absolute value of the penetration depth at 0 K) at low temperatures for the pristine and 1.3, 3.3, and 8.6 C/cm2 irradiated samples. In the pristine sample, δλ(T) shows a flat temperature dependence at low temperatures below 0.1Tc (Fig. 2a), indicating a fully gapped superconducting state in CsV3Sb5. To examine the low-energy quasiparticle excitations in the pristine sample, we applied a power-law fit δλ(T) ∝ Tn to the experimental data. In general, in the case of nodal superconductors with line and point nodes, the exponent value n gives 1 and 2 in the clean limit, respectively. We obtained n ~ 2.8 from the fitting (Fig. 2a), indicating the absence of nodes in the gap (or conversely, the presence of a finite gap). Then, to quantitatively evaluate the gap value, we tried to fit the data with the fully gapped s-wave model \(\delta \lambda (T)\propto {T}^{-1/2}\exp (-{\Delta }_{0}/{k}_{{{{{{{{\rm{B}}}}}}}}}T)\), where kB is the Boltzmann constant and Δ0 is the superconducting gap. We obtained an extremely small gap value Δ0 = 0.47kBTc (which is consistent with the previous study31), suggesting the existence of gap minima \({\Delta }_{\min }\) coming from the anisotropic gap nature of CsV3Sb5, as discussed later. One of our key findings is that the fully gapped behavior in δλ(T) is robust against disorder (Fig. 2b–d). The flat temperature region at low temperatures expands to a higher temperature region with increasing dose. In the case of fully gapped superconductors with sign-changing order parameters, δλ(T) is expected to change from an exponential to a T2 dependence with increasing impurities because of the impurity-induced DOS (Fig. 2f)43. In sharp contrast, our experimental observations show that Δ0 and n obtained from the fitting rather increase with increasing dose (Fig. 2g, h), indicating no impurity-induced DOS in the superconducting gap. These results provide strong bulk evidence that the superconducting gap structure of CsV3Sb5 is nodeless without a sign-changing gap.
For a more detailed analysis of the superconducting gap structure, we derived the normalized superfluid density ρs(T) ≡ λ2(0)/λ2(T). We used λ(0) = 387 nm for the pristine sample estimated in the previous study31 and calculated λ(0) for the irradiated samples by using the relation λ(0) = λL(0)(1+ξ/l)1/2 (Fig. 1h), where the London penetration depth λL(0) is assumed to be equal to λ(0) = 387 nm for the pristine sample, and l and ξ are the mean free path and coherence length, respectively (for more details, see Supplementary Information Sec. IV). Figure 3a shows the obtained ρs(T) curve as a function of T/Tc for each sample. In all the samples, ρs shows a flat temperature dependence at low temperatures, which extends to a higher temperature region with increasing dose. This is again inconsistent with a nodal gap structure.
a The Temperature dependence of normalized superfluid density ρs(T) ≡ λ2(0)/λ2(T) for the pristine (red), 1.3 (orange), 3.3 (green), and 8.6 (blue) C/cm2 irradiated samples. Black solid lines are the fitting curves of the multigap model (clean limit). The black dashed line is the curve for the dirty s-wave (single gap) case. Note that ρs(T) for the 8.6 C/cm2 irradiated sample with the relatively large value of ξ/l = 2.3 approaches the dirty limit (see Supplementary Information Sec. V). b Schematic picture of the change in the superconducting gap structure against disorder. The introduction of electron irradiation changes the anisotropic superconducting gap structure to an isotropic one. c Gap sizes obtained from the fitting analysis of the superfluid density as a function of dose. Red circles and blue diamonds represent the maximum and minimum values of the anisotropic gap, \({\Delta }_{{{{{{{{\rm{1,max}}}}}}}}}\) and \({\Delta }_{{{{{{{{\rm{1,min}}}}}}}}}\), respectively. Green squares represent the gap values of the isotropic gap Δ2. Dotted lines are guides for the eyes. d Suppression of Tc in CsV3Sb5 (red circles) as a function of pair breaking parameter g = ℏ/(τimpkBTc0). For comparison, the results for Sn-substituted CeCoIn5 (yellow triangles)51 and electron-irradiated YBa2Cu3O7-δ (brown triangles)52 are plotted as examples of d-wave superconductors. Black solid line represents the suppression of Tc expected in the Abrikosov-Gor'kov (AG) theory. Also, the results of neutron-irradiated MgB2 (green diamonds)49 and electron-irradiated CeCu2Si2 (purple diamonds)50 are plotted as examples of multigap s-wave superconductors. Dotted lines are guides for the eyes.
Here, we consider a multigap model to analyze the overall temperature dependence of ρs. In CsV3Sb5, the Fermi surfaces are formed by two different orbitals: one is derived from the d-orbitals of V, forming a hexagonal Fermi surface around the Γ point and two triangular Fermi surfaces around the K point, while the other is from the p-orbitals of Sb, forming a circular Fermi surface around the Γ point (Fig. 1c)13. The Fermi surfaces derived from the V d-orbitals determine the physical properties of this material, and three equivalent q vectors18,21,23,24 are considered to give rise to anisotropic pairing interactions5,27. Indeed, recent STM measurements32 have reported the emergence of an anisotropic superconducting gap as well as an isotropic gap below Tc. We therefore consider a multigap model with an anisotropic but nodeless superconducting gap with six-fold symmetry (\({\Delta }_{1}\propto 1+\alpha \,\cos (6\phi )\)) and an isotropic superconducting gap (\({\Delta }_{2}={{{{{{{\rm{const.}}}}}}}}\)) on two cylindrical Fermi surfaces (Fig. 3b). Note that an isotropic two-gap model cannot produce reasonable results for irradiated samples (for more details, see Supplementary Information Sec. V). We fitted the experimental data with the anisotropic multigap model (Fig. 3a) and obtained the gap values Δ1 and Δ2 as a function of dose (Fig. 3c). As the dose increases, the difference between the maximum and minimum values of Δ1 decreases, and eventually, all the gaps become almost identical. This is due to the averaging effect between the two gaps introduced by impurity-induced intra/interband scattering, and a very similar behavior has been observed in the prototypical multigap superconductor MgB249. This evidences nodeless multigap superconductivity with a sign-preserving order parameter in CsV3Sb5, which excludes the possibility of spin-triplet p- and f-wave and chiral d-wave superconductivity.
Pair-breaking effect
To discuss the impurity effect on Tc more quantitatively, we next introduce a pair-breaking parameter g = ℏ/(τimpkBTc0), where \({\tau }_{{{{{{{{\rm{imp}}}}}}}}}={\mu }_{0}{\lambda }_{{{{{{{{\rm{L}}}}}}}}}^{2}(0)/{\rho }_{0}\) is the impurity scattering time and Tc0 is the superconducting transition temperature of the pristine sample44,50. The suppression of Tc is plotted as a function of g and compared to other superconductors with and without sign-changing order parameters (Fig. 3d). Tc of CsV3Sb5 is rapidly suppressed at a low irradiation dose but starts to saturate at moderate irradiation doses. The initial rapid suppression of Tc is considered to be related to the reduction of the anisotropy of Δ1 (Fig. 3c), as discussed later. The Tc suppression above 1.3 C/cm2 irradiation dose is much slower than those in superconductors with sign-changing order parameters such as d-wave, rather similar to those in s-wave superconductors without sign-changing gaps. These results also support that multigap s-wave superconductivity with no sign change is realized in CsV3Sb5 at ambient pressure.
Impurity effects on the high-pressure superconducting phase
To further investigate the non-magnetic impurity effect on the superconducting phase of CsV3Sb5 under pressure, we constructed the P-T phase diagram in the pristine sample and 4.8 and 8.6 C/cm2 irradiated samples. Figure 4a shows the ρ(T) curve of the pristine sample at several pressures. The CDW transition temperature T*, which is determined from a jump or dip in dρ(T)/dT (Fig. 4b), decreases monotonically with increasing pressure (Fig. 4d). In contrast, the superconducting transition temperature Tc shows a non-monotonic pressure dependence (Fig. 4c), and a double superconducting dome is observed, as reported in previous high-pressure studies35,36 (Fig. 4d). The first peak of the superconducting double dome locates at P1 ~ 0.7 GPa inside the CDW phase, while the second peak locates at P2 ~ 2 GPa near the CDW endpoint. We conducted the same experiments for the 4.8 and 8.6 C/cm2 irradiated samples (Fig. 4e–l) and obtained the P-T phase diagrams as shown in Fig. 4h, l. T* is suppressed in the 4.8 and 8.6 C/cm2 irradiated samples, and the CDW endpoint shifts to lower pressure with increasing irradiation dose. Tc is also suppressed by disorder, but the superconducting dome survives even after 8.6 C/cm2 irradiation.
a, e, i ρ(T) curves below 200 K at several pressures for the pristine (a), 4.8 (e), and 8.6 (i) C/cm2 irradiated samples. Arrows indicate the CDW transitions determined from the dρ/dT curves in b, f, j. b, f, j Temperature dependence of dρ/dT below 100 K for the pristine (b), 4.8 (f), and 8.6 (j) C/cm2 irradiated samples. Arrows indicate the CDW transitions. c, g, k Low-temperature ρ(T) curves below 10 K at several pressures for the pristine (c), 4.8 (g), and 8.6 (k) C/cm2 irradiated samples. Note that the resistivity at 2.38 GPa does not reach zero at low temperatures in g. This may come from distortion such as microcracks to the sample and damage to the terminals caused by solidification of daphne 7373 above 2 GPa. d, h, l P-T phase diagrams of the pristine (d), 4.8 (h), and 8.6 (l) C/cm2 irradiated samples. For clarity, Tc is doubled. The phase diagram of the pristine sample includes data from Chen et al.35. The CDW (superconducting (SC)) phase is shaded in blue (red). Note that the double superconducting dome becomes broader for the irradiated samples. In the intermediate pressure region between P1 and P2, a significant broadening of the superconducting transition has been observed, and Tc shows a strong sample dependence35, 36. These behaviors indicate that the superconducting state in the intermediate pressure region is inhomogeneous and sensitive to the microscopic disorder within the crystal. Therefore, the broadening of the double superconducting dome may come from the introduction of disorders.
As already discussed in Fig. 3d, the irradiation dose of 8.6 C/cm2 introduces enough defects to suppress superconductivity with a sign-changing order parameter. To investigate the impurity effect on the high-pressure superconducting phase, we evaluated the pair-breaking parameter g at P2 for each dose (Fig. S5). Our results display that the suppression of Tc at the second dome is slower than that of the d-wave case with a sign-changing order parameter; it rather traces the trend in MgB2. Therefore, these results suggest that the superconducting gap symmetry of CsV3Sb5 at high pressure is also non-sign-changing s-wave.
Discussion
Recent μSR measurements under pressure37 have reported that the superconducting pairing symmetry near P2 has a finite superconducting gap across the Fermi surface and breaks TRS. As a possible symmetry, chiral \({d}_{{x}^{2}-{y}^{2}}\pm i{d}_{xy}\) or px ± ipy-wave superconductivity has been discussed37,38. However, such unconventional superconductivity is expected to be sensitive to disorder, because the chiral states have sign-changing order parameters which would produce Andreev bound states by impurities. Our present results show that the superconducting state under high pressure is robust against disorder. These findings seem to be inconsistent with the chiral \({d}_{{x}^{2}-{y}^{2}}\pm i{d}_{xy}\) and px ± ipy-wave states. To fully understand the relationship between our impurity effects and the μSR results, further theoretical and experimental studies on the high-pressure phase in the kagome systems are highly desired. We note that the TRS breaking has been observed in the CDW phase, and thus the possible fluctuations of chiral CDW order in the high-pressure phase on the time scale of μSR measurements may be an important issue.
Another important aspect of our findings is that the CDW endpoint shifts to lower pressure with irradiation, followed by the second peak of the superconducting double dome (Fig. 4d, h, l), suggesting that the CDW is closely related to the superconductivity in the present system. Recent theoretical calculations in AV3Sb5 27 have proposed that bond-order fluctuations originating from the triple-q vectors corresponding to the (inverse) star of David pattern induce anisotropic pairing interactions, leading to anisotropic s-wave superconductivity. This theory can explain the relatively high Tc in AV3Sb5 that cannot be reproduced by the BCS theory 28 and the anisotropic superconducting gap structure in CsV3Sb5 obtained in the present study. Moreover, in such anisotropic s-wave superconductivity, the introduction of impurity scattering averages out the anisotropic gap, changing to the isotropic gap. In this case, Tc drops rapidly at an initial introduction of impurities, but as the gap becomes isotropic, the reduction of Tc saturates and becomes much slower than that expected in the Abrikosov-Gor’kov (AG) theory. These expectations are in good agreement with our observations of the Tc suppression in CsV3Sb5. We note that a possible transition from a p-wave to an s-wave state caused by impurities27 may explain the initial rapid suppression of Tc. However, our present results exclude the possibility of a nodal superconducting state in the pristine sample, which is at odds with the p-wave state. The gradual change in the superconducting gap inferred from the temperature dependence of the superfluid density suggests that an impurity-induced transition from a full-gap chiral state to a non-chiral s-wave state is also unlikely. This is reinforced by the μSR measurements at ambient pressure30, which report that chiral superconductivity in the pristine sample at ambient pressure can be ruled out. Thus, our present results support a new type of unconventional superconductivity due to bond-order fluctuations on the kagome lattice in CsV3Sb5, where the gap function is non-sign-changing s-wave. In the present kagome superconductors, the possibility of a loop-current phase with broken TRS and a nematic phase with broken RS has been pointed out above the superconducting phase18,21,22,23,24,25. Therefore, elucidating the intertwining of these unusual normal and superconducting phases, which is commonly seen in high-Tc cuprates and iron-based superconductors, will pave the way to understanding novel quantum phases of matter in condensed matter physics.
Methods
Single crystal growth
High-quality single crystals of CsV3Sb5 were synthesized using the self-flux method. All sample preparations are performed in an argon glovebox with oxygen and moisture < 0.5ppm. The flux precursor was formed through mechanochemical methods by mixing Cs metal (Alfa 99.98%), V powder (Sigma 99.9%), and Sb beads (Alfa 99.999%) to form a mixture which is ~50 at.% Cs0.4Sb0.6 (near eutectic composition) and 50 at.% VSb2. Note that prior to mixing, as-received vanadium powders were purified in-house to remove residual oxides. After milling for 60 min a pre-seasoned tungsten carbide vial, flux precursors are extracted and sealed into 10 mL alumina crucibles. The crucibles are nested within stainless steel jackets and sealed under argon. Samples are heated to 1000 °C at 250 °C/h and soaked for 24 h before dropping to 900 °C at 100 °C/h. Crystals are formed during the final slow cool to 500 °C at 1 °C/h before terminating the growth. Once cooled, the crystals are recovered mechanically. Samples are hexagonal flakes with a brilliant metallic luster. The elemental composition of crystals was assessed using energy-dispersive X-ray spectroscopy (EDS) using an APREO-C scanning electron microscope.
Electron irradiation
Electron irradiation with the incident electron energy of 2.5 MeV was performed on SIRIUS Pelletron accelerator operated by the Laboratoire des Solides irradiés (LSI) at École Polytechnique. To prevent defect migration and agglomeration, the sample temperature was kept at ~20 K during irradiation which produces stable vacancy-interstitial Frenkel pairs. Subsequent warming to room temperature causes annealing of interstitials, which have a lower migration energy, leaving a uniform population of vacancy type defects. The electron irradiation of 1.3, 3.3, and 8.6 C/cm2 was performed at the same beam time (run#1), while the irradiation of 4.8 C/cm2 was conducted at another beam time (run#2).
Electrical resistivity measurements
The electrical resistivity was measured at ambient and high pressure by the 4-terminal method using a Physical Property Measurement System (PPMS) from Quantum Design with the lowest temperature of about 1.8 K. The resistivity under pressure was measured using a piston cylinder cell to generate pressure up to ~2.5 GPa and daphne 7373 as a pressure medium in PPMS. The pressure value in the sample was determined from the superconducting transition temperature Tc of Pb under pressure, using the relation P = (7.20 − Tc)/0.365. Note that when the 4.8 C/cm2 irradiated sample was set in the piston cell, even before pressure was applied, the resistivity value changed, probably due to cracks, so we have corrected it to the value before pressure was applied.
Magnetic penetration depth measurements
The temperature variation of the in-plane magnetic penetration depth δλ(T) = λ(T) − λ(0) was measured by using a tunnel diode oscillator technique (TDO) with the resonant frequency of ~13.8 MHz in a dilution refrigerator down to ~50 mK. The sample was mounted on a sapphire rod with Apiezon N grease, then inserted into a copper coil in the LC circuit. The frequency shift δf in the TDO is related to the change of magnetic susceptibility δχ by the following equation, δf = − (f0Vs/(2Vc(1 − N)))δχ, where f0 is the resonant frequency without the sample, Vs and Vc are the sample and coil volume, respectively, and N is the demagnetization factor. δχ is related to δλ by the following equation, δχ = δλ/R, where R is a constant determined by the geometry of the sample from the calculation. Thus, δf is related to δλ by the following equation, δf = − (f0Vs/(2RVc(1 − N)))δλ.
Data availability
All data supporting the findings of this study are available within the paper and its Supplementary Information. Source data are provided with this paper.
References
Norman, M. R. Colloquium: Herbertsmithite and the search for the quantum spin liquid. Rev. Mod. Phys. 88, 041002 (2016).
Ye, L. et al. Massive Dirac fermions in a ferromagnetic kagome metal. Nature 555, 638–642 (2018).
Nakatsuji, S., Kiyohara, N. & Higo, T. Large anomalous Hall effect in a non-collinear antiferromagnet at room temperature. Nature 527, 212–215 (2015).
Kiesel, M. L. & Thomale, R. Sublattice interference in the kagome Hubbard model. Phys. Rev. B 86, 121105 (2012).
Wang, W.-S., Li, Z.-Z., Xiang, Y.-Y. & Wang, Q.-H. Competing electronic orders on kagome lattices at van Hove filling. Phys. Rev. B 87, 115135 (2013).
Kiesel, M. L., Platt, C. & Thomale, R. Unconventional Fermi surface instabilities in the kagome Hubbard model. Phys. Rev. Lett. 110, 126405 (2013).
Takenaka, T. et al. Strongly correlated superconductivity in a copper-based metal-organic framework with a perfect kagome lattice. Sci. Adv. 7, eabf3996 (2021).
Ortiz, B. R. et al. CsV3Sb5: A \({{\mathbb{Z}}}_{2}\) topological kagome metal with a superconducting ground state. Phys. Rev. Lett. 125, 247002 (2020).
Yin, Q. et al. Superconductivity and normal-state properties of kagome metal RbV3Sb5 single crystals. Chin. Phys. Lett. 38, 037403 (2021).
Ortiz, B. R. et al. Superconductivity in the \({{\mathbb{Z}}}_{2}\) kagome metal KV3Sb5. Phys. Rev. Mater. 5, 034801 (2021).
Ortiz, B. R. et al. New kagome prototype materials: discovery of KV3Sb5, RbV3Sb5, and CsV3Sb5. Phys. Rev. Mater. 3, 094407 (2019).
Kang, M. et al. Twofold van Hove singularity and origin of charge order in topological kagome superconductor CsV3Sb5. Nat. Phys. 18, 1–8 (2022).
Ortiz, B. R. et al. Fermi surface mapping and the nature of charge-density-wave order in the kagome superconductor CsV3Sb5. Phys. Rev. X 11, 041030 (2021).
Li, H. et al. Observation of unconventional charge density wave without acoustic phonon anomaly in kagome superconductors AV3Sb5 (A = Rb, Cs). Phys. Rev. X 11, 031050 (2021).
Wu, X. et al. Nature of unconventional pairing in the kagome superconductors AV3Sb5 (A = K, Rb, Cs). Phys. Rev. Lett. 127, 177001 (2021).
Park, T., Ye, M. & Balents, L. Electronic instabilities of kagome metals: Saddle points and Landau theory. Phys. Rev. B 104, 035142 (2021).
Christensen, M. H., Birol, T., Andersen, B. M. & Fernandes, R. M. Theory of the charge density wave in AV3Sb5 kagome metals. Phys. Rev. B 104, 214513 (2021).
Jiang, Y.-X. et al. Unconventional chiral charge order in kagome superconductor KV3Sb5. Nat. Mater. 20, 1353–1357 (2021).
Hu, Y. et al. Coexistence of tri-hexagonal and star-of-David pattern in the charge density wave of the kagome superconductor AV3Sb5. Phys. Rev. B 106, L241106 (2022).
Kang, M. et al. Charge order landscape and competition with superconductivity in kagome metals. Nat. Mat. 22, 186–193 (2023).
Zhao, H. et al. Cascade of correlated electron states in the kagome superconductor CsV3Sb5. Nature 599, 216–221 (2021).
Mielke, C. et al. Time-reversal symmetry-breaking charge order in a kagome superconductor. Nature 602, 245–250 (2022).
Nie, L. et al. Charge-density-wave-driven electronic nematicity in a kagome superconductor. Nature 604, 59–64 (2022).
Li, H. et al. Rotation symmetry breaking in the normal state of a kagome superconductor KV3Sb5. Nat. Phys. 18, 265–270 (2022).
Xiang, Y. et al. Twofold symmetry of c-axis resistivity in topological kagome superconductor CsV3Sb5 with in-plane rotating magnetic field. Nat. Commun. 12, 6727 (2021).
Neupert, T., Denner, M. M., Yin, J.-X., Thomale, R. & Hasan, M. Z. Charge order and superconductivity in kagome materials. Nat. Phys. 18, 137–143 (2022).
Tazai, R., Yamakawa, Y., Onari, S. & Kontani, H. Mechanism of exotic density-wave and beyond-Migdal unconventional superconductivity in kagome metal AV3Sb5 (A = K, Rb, Cs). Sci. Adv. 8, eabl4108 (2022).
Tan, H., Liu, Y., Wang, Z. & Yan, B. Charge density waves and electronic properties of superconducting kagome metals. Phys. Rev. Lett. 127, 046401 (2021).
Li, S. et al. Nodal superconductivity and superconducting domes in the topological kagome metal CsV3Sb5. Preprint at arXiv https://doi.org/10.48550/arXiv.2102.08356 (2021).
Gupta, R. et al. Microscopic evidence for anisotropic multigap superconductivity in the CsV3Sb5 kagome superconductor. npj Quantum Mater. 7, 49 (2022).
Duan, W. et al. Nodeless superconductivity in the kagome metal CsV3Sb5. Sci. China Phys., Mech. Astron. 64, 1–6 (2021).
Xu, H.-S. et al. Multiband superconductivity with sign-preserving order parameter in kagome superconductor CsV3Sb5. Phys. Rev. Lett. 127, 187004 (2021).
Mu, C. et al. S-wave superconductivity in kagome metal CsV3Sb5 revealed by 121/123Sb NQR and 51V NMR measurements. Chin. Phys. Lett. 38, 077402 (2021).
Chen, H. et al. Roton pair density wave in a strong-coupling kagome superconductor. Nature 599, 222–228 (2021).
Chen, K. Y. et al. Double superconducting dome and triple enhancement of Tc in the kagome superconductor CsV3Sb5 under high pressure. Phys. Rev. Lett. 126, 247001 (2021).
Yu, F. et al. Unusual competition of superconductivity and charge-density-wave state in a compressed topological kagome metal. Nat. Commun. 12, 1–6 (2021).
Gupta, R. et al. Two types of charge order with distinct interplay with superconductivity in the kagome material CsV3Sb5. Commun. Phys. 5, 232 (2022).
Guguchia, Z. et al. Tunable unconventional kagome superconductivity in charge ordered RbV3Sb5 and KV3Sb5. Nat. Commun. 14, 1–10 (2023).
Yonezawa, S. Bulk topological superconductors. AAPPS Bull. 26, 3 (2016).
Tsuei, C. C. & Kirtley, J. R. Pairing symmetry in cuprate superconductors. Rev. Mod. Phys. 72, 969–1016 (2000).
Hanaguri, T., Niitaka, S., Kuroki, K. & Takagi, H. Unconventional s-wave superconductivity in Fe(Se,Te). Science 328, 474–476 (2010).
Christianson, A. et al. Unconventional superconductivity in Ba0.6K0.4Fe2As2 from inelastic neutron scattering. Nature 456, 930–932 (2008).
Mizukami, Y. et al. Disorder-induced topological change of the superconducting gap structure in iron pnictides. Nat. Commun. 5, 1–6 (2014).
Prozorov, R. et al. Effect of electron irradiation on superconductivity in single crystals of \({{{{{{{\rm{Ba}}}}}}}}{({{{{{{{{\rm{Fe}}}}}}}}}_{1-x}{{{{{{{{\rm{Ru}}}}}}}}}_{x})}_{2}{{{{{{{{\rm{As}}}}}}}}}_{2}\) (x = 0.24). Phys. Rev. X 4, 041032 (2014).
Anderson, P. W. Theory of dirty superconductors. J. Phys. Chem. Solids 11, 26–30 (1959).
Bonn, D. A. et al. Surface impedance studies of YBCO. Czechoslov. J. Phys. 46, 3195–3202 (1996).
Gómez-Santos, G. & Ynduráin, F. élix Effects of impurities on charge-density waves: a mean-field calculation. Phys. Rev. B 29, 4459–4467 (1984).
Emery, V. J. & Kivelson, S. A. Importance of phase fluctuations in superconductors with small superfluid density. Nature 374, 434–437 (1995).
Putti, M. et al. Observation of the crossover from two-gap to single-gap superconductivity through specific heat measurements in neutron-irradiated MgB2. Phys. Rev. Lett. 96, 077003 (2006).
Yamashita, T. et al. Fully gapped superconductivity with no sign change in the prototypical heavy-fermion CeCu2Si2. Sci. Adv. 3, e1601667 (2017).
Bauer, E. D. et al. Thermodynamic and transport investigation of \({{{{{{{\rm{Ce}}}}}}}}{{{{{{{\rm{Co}}}}}}}}{{{{{{{{\rm{In}}}}}}}}}_{5-x}{{{{{{{{\rm{Sn}}}}}}}}}_{x}\). Phys. Rev. B 73, 245109 (2006).
Rullier-Albenque, F., Alloul, H. & Tourbot, R. Influence of pair breaking and phase fluctuations on disordered High Tc cuprate superconductors. Phys. Rev. Lett. 91, 047001 (2003).
Acknowledgements
We thank R. Tazai, Y. Yamakawa, S. Onari, and H. Kontani for fruitful discussions. This work was supported by Grants-in-Aid for Scientific Research (KAKENHI) (Nos. JP22K20349, JP22K18681, JP22K18683, JP22J21896, JP22H00105, JP21H01793, JP21KK0242, JP20H02600, JP19H00649, JP19H00648, JP18H05227, JP18KK0375), Grant-in-Aid for Scientific Research on innovative areas “Quantum Liquid Crystals” (No. JP19H05824) and Grant-in-Aid for Scientific Research for Transformative Research Areas (A) “Condensed Conjugation” (No. JP20H05869) from Japan Society for the Promotion of Science (JSPS), and CREST (No. JPMJCR19T5) from Japan Science and Technology (JST). S.D.W. and B.R.O. acknowledge support via the UC Santa Barbara NSF Quantum Foundry funded via the Q-AMASE-i program under award DMR-1906325. Electron irradiation was conducted at the SIRIUS accelerator facility at École Polytechnique (Palaiseau, France) and was supported by EMIR&A French network (FR CNRS 3618) (proposal No. 22-8950).
Author information
Authors and Affiliations
Contributions
K.H. and T.S. conceived the project. M.R., K.I., K. Ogawa, K. Okada, Y.M., K.H., and T.S. performed magnetic penetration depth measurements and analyzed the data. Y.T., K. Okada, K.M., and Y.U. carried out high-pressure measurements. M.R. and S.L. performed electrical transport and X-ray diffraction measurements. R.G. and M.K. conducted electron irradiation experiments. B.R.O. and S.D.W. carried out sample preparation. M.R., K.H., and T.S. prepared the manuscript with inputs from R.G., M.K., B.R.O., and S.D.W. All authors discussed the experimental results.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Ronny Thomale and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Source data
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Roppongi, M., Ishihara, K., Tanaka, Y. et al. Bulk evidence of anisotropic s-wave pairing with no sign change in the kagome superconductor CsV3Sb5. Nat Commun 14, 667 (2023). https://doi.org/10.1038/s41467-023-36273-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-023-36273-x
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.