Abstract
The lanthanum-hydrogen system has attracted significant attention following the report of superconductivity in LaH10 at near-ambient temperatures and high pressures. Phases other than LaH10 are suspected to be synthesized based on both powder X-ray diffraction and resistivity data, although they have not yet been identified. Here, we present the results of our single-crystal X-ray diffraction studies on this system, supported by density functional theory calculations, which reveal an unexpected chemical and structural diversity of lanthanum hydrides synthesized in the range of 50 to 180 GPa. Seven lanthanum hydrides were produced, LaH3, LaH~4, LaH4+δ, La4H23, LaH6+δ, LaH9+δ, and LaH10+δ, and the atomic coordinates of lanthanum in their structures determined. The regularities in rare-earth element hydrides unveiled here provide clues to guide the search for other synthesizable hydrides and candidate high-temperature superconductors. The hydrogen content variability in lanthanum hydrides and the samples’ phase heterogeneity underline the challenges related to assessing potentially superconducting phases and the nature of electronic transitions in high-pressure hydrides.
Similar content being viewed by others
Introduction
The report of superconductivity at the critical temperature (Tc) of 203 K at 150 GPa in the sulfur-hydrogen system1 in 2015, followed by a gold rush in high-pressure sciences towards exceeding these temperatures, placed the dream of achieving room-temperature superconductivity within reach. Higher Tc were claimed to be realized in La-H2,3, Y-H4,5, and in a carbonaceous sulfur hydride6, the latter reaching a record value of 283 K at a pressure of 267 GPa. The compounds presumed to feature superconductivity in these systems could not be recovered to ambient conditions, precluding further physical properties measurements, essential for a complete understanding of the mechanisms enabling ultra-high Tc.
At the same time, the reports on high Tc in high-pressure hydrides have been heavily disputed7,8,9,10,11. The presence of phases other than the superconducting one has been considered as a potential explanation for the sudden drop of resistivity measured in some systems as they could enable a metallic conduction path to form upon temperature decrease7. The lack of a homogeneous sample would not only affect resistivity measurements but also magnetic susceptibility1,12,13 and nuclear magnetic resonance14,15,16, serving as a strong impetus to accurately determine all phases present in these superconducting hydride systems. Single-crystal X-ray diffraction (SCXRD) coupled with ab initio calculations has already been demonstrated as a very effective tool to identify the formation of novel hydrides in laser-heated diamond anvil cells (DACs) experiments. For example, this methodology allowed the synthesis and the full characterization of two sulfur hydrides (H6±xS5 (x ∼ 0.4) and H2.85±yS2 (y ∼ 0.35)17 which had not been observed despite a large number of previous, but powder XRD, studies18,19,20,21,22,23.
In this paper, we present the synthesis of seven lanthanum hydrides, as well as two carbon-containing compounds, in the range of 50–176 GPa, all characterized by employing SCXRD. The unit cell parameters, space group, and positions of non-hydrogen atoms were unambiguously experimentally determined for all compounds, deduced to be LaH3, LaH~4, LaH4+δ, La4H23, LaH6+δ, LaH9+δ, LaH10+δ, LaC, and LaCH2 through comparisons with structural analogues and their volume per lanthanum atom. Our results demonstrate the compositional and structural variety of hydrides in the La-H system and reveal regularities in the high-pressure rare-earth elements–hydrogen (RE-H) systems. Moreover, we establish that high-pressure syntheses employing high-temperature laser-heating can result in a significant sample heterogeneity that underpins difficulties in the interpretation of physical phenomena observed in the RE-H systems at low temperatures.
Results
Three DACs with anvil culets of 80 μm were loaded with small lanthanum pieces along with paraffin oil (CnH2n+2) acting as a pressure-transmitting medium and a hydrogen reservoir. As demonstrated in recent works on metal hydrides14,15,17,24,25,26,27, paraffin is an effective alternative to pure hydrogen for DAC synthesis experiments. In fact, paraffin is deemed a better choice than the more commonly used ammonia borane (NH3BH3) as it does not bring any additional elements into the experimental chamber, carbon being already present in the system due to the diamond anvils. The sample pressure was determined from the X-ray diffraction signal of the Re gaskets28—non-hydrogenated when using paraffin—and crosschecked with the diamond anvils’ Raman edge29. Further details on the experimental and theoretical methods are described in the Supplementary Materials. Lanthanum and paraffin were compressed in three DACs at ambient temperature and laser-heated above 2000 K at pressures of 96, 106, 140, 150, 155, and 176 GPa (see Supplementary Table 1 for P–T conditions and a list of the phases observed). The chemical reaction products were probed using synchrotron X-ray diffraction, and sample X-ray diffraction maps are provided in Supplementary Figs. 1–3.
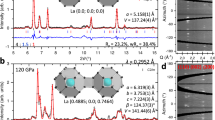
A total of nine compounds were observed: seven lanthanum hydrides and two carbides. For all of them, the determined unit cell parameters, space groups, and atomic coordinates were determined based on the arrangement formed by the non-hydrogen atoms (i.e., lanthanum and carbon). These structures, for which Pearson symbols are provided, were solved and refined exclusively from the SCXRD data obtained from microcrystals. The lanthanum atoms in the seven lanthanum hydrides, LaH3, LaH~4, LaH4+δ, La4H23, LaH6+δ, LaH9+δ, and LaH10+δ, are arranged as shown in Fig. 1—with the hydrogen content in these phases, and therefore the assigned compound stoichiometry, being discussed afterward. The structural data are also summarized in Table 1 (full crystallographic data in Supplementary Tables 2–18).
The LaH3 compound (Fig. 1a and Supplementary Table 2) was observed at 50 GPa. La atoms, forming a cubic close-packing (ccp), are located in the nodes of the fcc lattice (cF4, space group Fm−3m) with the unit cell parameter of 5.019(3) Å (V = 126.43(13) Å3).
At 140 GPa, in the LaH~4 solid (Fig. 1b and Supplementary Tables 3 and 4), the La atoms are arranged in an orthorhombic unit cell (oC4, Cmcm space group) with a = 2.949(4), b = 6.7789(19), and c = 4.7837(18) Å (V = 95.63(14) Å3). This solid was also produced after further sample compression to 155 GPa and laser-heating.
Drawn in Fig. 1c, LaH4+δ was observed after laser-heating at 140, 150, and 155 GPa (Supplementary Tables 5–7). La atoms are located in the nodes of the body-centered tetragonal unit cell (tI2, I4/mmm space group) with the lattice parameters of a = 2.9418(12) and c = 6.028(3) Å (V = 52.17(4) Å3) at 140 GPa.
The La4H23 solid was obtained after laser-heating at four different pressures: 96, 106, 140, and 150 GPa (Fig. 1d and Supplementary Tables 8–11). The structure formed by the La atoms has a cubic symmetry (cP8, space group Pm−3n). At 150 GPa, it has a lattice parameter of 6.0722(8) Å (V = 223.89(5) Å3).
The LaH6+δ compound is the only one that was solely observed at a single pressure upon laser-heating: 150 GPa (Fig. 1e and Supplementary Table 12). The cubic structure formed by La atoms located in the nodes of the body-centered lattice (cI2, Im−3m space group) has a lattice parameter of a = 3.8710(10) Å (V = 58.01(3) Å3).
Both the LaH9+δ and the LaH10+δ solids were observed at 140 and 176 GPa after laser-heating. In LaH9+δ (Fig. 1f and Supplementary Tables 13 and 14), La atoms form a hexagonal close-packing (hcp) (hP2, space group P63/mmc) with the unit cell parameters a = 3.772(2) and c = 5.634(4) Å (V = 69.41(7) Å3). In LaH10+δ (Fig. 1g and Supplementary Tables 15–16) the lanthanum atoms adopt a ccp arrangement (cF4, Fm−3m space group) with the unit cell parameters a = 5.2233(14) Å, V = 142.51(7) Å3.
Before addressing the hydrogen composition of these solids, it must be emphasized that great care was taken to verify that the seven observed La-H compounds are free of carbon; carbon atoms which could potentially originate from the diamond anvils or from the decomposed paraffin oil. Indeed, at the stage of the structure refinement the possibility to introduce carbon into the structure was always checked but led to the failure of the structure refinement. However, at 96 GPa, a previously unknown carbohydride, LaCH2, was detected by SCXRD, and its structure was solved (see Supplementary Table 17 and Supplementary Fig. 4), whereas at 150 GPa, a previously unobserved lanthanum carbide LaC was obtained and its structure was also determined (Supplementary Table 18 and Supplementary Fig. 5). The diffraction signal of polycrystalline diamond could be detected throughout the sample chamber after sample laser-heating (see Supplementary Fig. 1), suggesting it to be a decomposition product of paraffin oil.
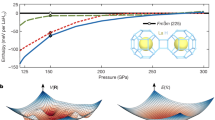
The LaH3, LaH4+δ, La4H23, LaH6+δ, LaH9+δ, and LaH10+δ solids have, respectively, metal atom arrangements like in the known LaH330 and in the predicted LaH431, RE4H23 (RE = Eu32,33, and in the Ba-H system34), REH6 (RE = Y4,35, Eu33), REH9 (RE = Y4, Ce36, Pr37,38, Nd39, Eu32,33) and the established LaH102,3,40. It is interesting to note that the unit cells of LaH~4 and LaH4+δ are very similar to some suggested for La-D compounds41, while La4H23 and LaH6+δ are likely to have been seen—but not identified as such—in previously reported powder X-ray diffraction data40. Density functional theory (DFT) calculations carried out for La hydrides assuming the hydrogen positions as in the above-mentioned prototypes predict LaH4, LaH6, LaH9, and LaH10 as dynamically (anharmonically) stable at their synthesis pressure (Supplementary Fig. 6). However, when calculating the equation of state (EoS) of these solids using DFT (Fig. 2a), the agreement with the experimental volume per lanthanum atom was found to be surprisingly poor—even when considering a ±10 GPa uncertainty in the experimental pressure. The exceptions to this were LaH3 and La4H23 for which a reasonable match is obtained, aside from one point for La4H23 at 150 GPa. Indeed, the difference between the experimental and the calculated volume per lanthanum atom (Fig. 2b) is below 1 Å3 for the LaH3 and La4H23 compounds (the 150 GPa point of La4H23 aside), but between +1.73 and +3.83 Å3 for the five other hydrides. Regarding the metal arrangement in LaH~4, to the best of our knowledge, it has neither been experimentally observed nor predicted in hydrides. However, from its volume per lanthanum atom, its hydrogen content is expected to be in between that in LaH3 and LaH4+δ, hence named LaH~4.
a Unit cell volume per La atom as a function of pressure, plotted for the seven synthesized lanthanum hydrides. The solid symbols represent the experimental data obtained in this study, for which the error bars are the largest difference observed between the rhenium and the diamond pressure gauges (±10 GPa). The colored broad bands serve as guides to the eye and are drawn based on a 2nd-order Birch–Murnaghan equation of state (see Supplementary Table 19), when sufficient datapoints are available. These have no underlying physical meaning as they suffer from two main issues: (i) the EoS parameters were obtained from very few (often two) experimental datapoints and (ii) the hydrogen content, for a given lanthanum atom arrangement, is thought to vary, which renders inaccurate the EoS parameters. The dotted lines are the calculated equation of state for LaH3 (red), LaH4 (green), La4H23 (purple), LaH6 (orange), LaH9 (dark yellow) and LaH10 (cyan), with structures based on the known RE-H compounds with an identical arrangement of metal atoms, i.e. REH330, REH431, RE4H2332,33, REH64,33,35, REH94,32,33,36,37,38,39, and REH102,3,40. The full black line represents the experimental equation of state of pure lanthanum48. b The difference in volume per lanthanum atom between the experimental datapoints and the corresponding calculated EoS of (a). The two black dashed lines are the calculated volume of one and two hydrogen atoms, based on the EoS of atomic hydrogen49. Source data are provided as a Source Data file.
Strikingly, a volume per metal atom discrepancy between the experimental and calculated data for the hypothesized stoichiometry of a hydride is common in the literature. As shown in Supplementary Fig. 7, this is especially true for LaH10—for which the largest number of independent studies were conducted—featuring a very wide range of volume per La atom with most points significantly differing from the calculated data. This is also the case for CeH336, EuH5 and EuH633, PrH4 and PrH738, UH342, and Ba4H2334, for all of which a considerable fraction of the experimental volume per metal atom datapoints lie 1.5 Å3 or more from the corresponding calculated curve.
Three hypotheses to account for the aforementioned discrepancy between experimental and calculated volume differences can be considered: (a) The experimental uncertainty on both the measured pressure and volume. The experimental error on the volume is usually very small, typically much smaller than ±0.2 Å32,3,4,38,42,. Regarding the pressure uncertainty, it is often reported to be below ±5 GPa2,3,42, even at pressures of 180 GPa. Moreover, laser-heating typically homogenizes stress within the sample chamber43. Such an uncertainty does not account for the difference with the calculated volumes. However, it is worth noting that some studies have reported a gap of up to 30 GPa between the pressure values measured by the H2 vibron and the diamond Raman edge3,4, the latter always being higher in pressure. Such a large error could indeed be responsible for the observed differences when the diamond Raman edge is employed as the sole pressure gauge. However, in all cases where pressure measurements are described and a large unit cell volume gap exists between DFT calculations and experiments33,34,38,42, at least two pressure gauges were employed—often the diamond Raman edge along with an X-ray gauge. In this study, the difference between the pressure measured from the diamond anvils Raman edge and the Re diffraction signal was always found to be equal or below 10 GPa. The use of two pressure gauges greatly diminishes the likelihood of pressure measurements being responsible for the unit cell volume discrepancy.
(b) DFT calculations of RE hydride compounds are particularly demanding as thermal effects and the quantum nature of hydrogen significantly influence key properties, e.g. the obtained pressure, and can lead to different (usually higher symmetry) structures being thermodynamically most stable at a given P, T conditions44,45. Furthermore, REs heavier than La require an advanced treatment of f-electrons (Ce, Eu, etc.) as well as taking into account spin-orbit coupling32,39. Also, the approximation employed for the exchange-correlation functional can lead to a pressure difference of the order of 10 GPa (e.g. LDA ~10 GPa lower compared to PBE for examples with lanthanum hydrides, see Supplementary Table 20). Thermal or nuclear quantum effects can also be a reason for the difference between the experimental and computational values. This is tested here using the temperature-dependent effective potential (TDEP46,47, which includes anharmonic effects) to obtain a pressure correction for pressure-volume points of some lanthanum hydrides (Supplementary Fig. 8). An average volume per La atom difference of 2.2 Å3 was found for the LaH4, LaH6, LaH9 and LaH10 compounds between the experimental data and the computed TDEP results; still insufficient to explain the volume discrepancy or the difference in the slope of the LaH9+δ and LaH10+δ datapoints (Supplementary Fig. 8).
(c) The third possibility, of physical nature, is the variability of hydrogen content for a given or mildly distorted arrangement of the metal atoms arrangement, i.e. a given arrangement of metal atoms can have a range of hydrogen compositions. This variability would likely depend on pressure, temperature, and the number of hydrogen atoms available. There are a number of established examples of this phenomenon in the literature3,36,38. Among the most striking ones is the report of the formation of LaH10 from LaH3 embedded in H2—both hydrides sharing the same ccp metal arrangement—simply by leaving the sample at ~140 GPa for two weeks3. In another study, cerium was loaded in H2 and compressed up to about 160 GPa at room temperature. Five phases were inferred to be produced based on powder X-ray diffraction measurements, sequentially forming CeH3, CeH3+x, CeH4, CeH9-x, and CeH9, each time accompanied by a mild distortion of the Ce sublattice36. This hydrogen content variability provides a straightforward explanation to discrepancies between experimentally- and DFT-derived unit cell volumes: the hydrogen content is not the same, and therefore the arrangement of hydrogen atoms can differ substantially. This underlines the inadequacy of DFT calculations to determine a hydride’s composition and full structure solely based on the arrangement of the metal atoms.
In the case of the here-synthesized lanthanum hydrides, the variability of H atoms justifies the assigned stoichiometry of LaH3, LaH4+δ, La4H23, LaH6+δ, LaH9+δ, and LaH10+δ, some of these solids containing more hydrogen compared to the stoichiometry expected based on their La atoms’ arrangement (Fig. 2). Estimates of the hydrogen content in the synthesized phases also can be proposed assuming an ideal mixing of the pure lanthanum48 and atomic hydrogen49 (Supplementary Fig. 4) as well as based on the DFT calculations with a hydrogen volume inferred from the calculated EoS of LaH3, LaH4, La4H23, LaH6, LaH9, and LaH10 (Supplementary Fig. 7). Both approaches confirm a higher-than-expected hydrogen content, although the exact stoichiometry of these hydrides remains to be determined.
The difficulties of capturing, with DFT calculations, the flexibility of a given metal atoms’ arrangement with regards to hydrogen content is especially alarming given the extreme reliance of experiments on these calculations. Indeed, these are very often used to assess the quantity and location of hydrogen atoms, crucial to determine the hydrides’ full structural model as well as to predict and interpret high-temperature superconductivity. Further emphasizing this, high-temperature superconductivity was measured on samples assumed to be LaH10 but found to have a unit cell volume 3.29 Å3 smaller than the volume expected based on the calculated EoS of LaH1040. This roughly corresponds to two fewer hydrogen atoms, based on the EoS of atomic H at 180 GPa (1.67 Å3/H, see Fig. 2b)49. Obviously, whether with more or less hydrogen atoms, the structural model of this “LaH10” compound, and therefore its critical temperature, should be significantly different.
With a total of seven solids found stable at high pressures, each with a different La:H ratio, La-H is a binary hydride system with one of the largest number of experimentally observed distinct compounds. The discovery of these solids also sheds light on regularities among synthesized hydrides of rare-earth elements Y, La, Ce, Pr, Nd, and Eu (Fig. 3) with respect to their metal atoms’ arrangement. These can be grouped as the following: LaH3, YH3 and PrH3 (cF4); LaH4+δ, YH4, CeH4, PrH4, and NdH4 (tI2); La4H23 and Eu4H23 (cP8); LaH6+δ and YH6 (cI2); LaH9+δ, YH9, CeH9, PrH9, NdH9, and EuH9 (hP2); LaH10+δ and CeH104,32,37,38,39,50 (cF4′). Considering the chemical similarities of these rare-earth elements, their propensity to forming isostructural compounds is expected. Perhaps what is more noteworthy is that not all metal atoms’ arrangement appear to be common to all RE-H systems. For example, the tI2 arrangement was observed in all systems with the exception of EuH. It is likely that it could be formed, but was missed in previous powder XRD studies32,33. In that regard, SCXRD measurements have proven, both here and previously17, to be particularly powerful compared to powder XRD. Without a structural refinement based on SCXRD data, the presence of non-hydrogen light elements, like carbon or boron and nitrogen (in experiments with ammonia borane in the sample chamber), in the structure of hydrides could hardly be ruled out. As it stands, the vast majority of rare-earth hydrides were “identified” without any sort of structural refinements, instead heavily relying on theoretical calculations, which, as here shown in the case of lanthanum hydrides, are not always capable of predicting all compounds that may be synthesized.
For clarity, the metal atoms’ arrangements are labeled by both their Pearson symbol (excluding hydrogen atoms) as well as by the chemical composition typically assumed in the literature—but likely slightly different in view of this work. For REH7, the known hP2 PrH738 and mC4 NdH739 have the same stoichiometry but distinct metal sublattices. Source data are provided as a Source Data file.
The results presented in this study have profound implications for the interpretation of the results of superconductivity measurements in RE-H systems. In the range of 140 to 155 GPa, seven La-H phases, as well as LaC, have been demonstrated to be synthesizable (see Supplementary Table 1), including all but LaH6+δ to be simultaneously present in DAC #1 at 140 GPa. The presence of multiple phases in a given sample at a given pressure hinders the quantitative interpretation of resistivity and magnetic susceptibility measurements aimed at determining the superconducting temperature. In particular, these five previously unobserved La-H compounds are likely to be the cause of the drops in resistance at temperatures other than 250 K—as well as the many unidentified diffraction peaks—found in the previous studies3. Likewise, the results of X-ray spectroscopy investigations, recently suggested for the characterization of the hydrogen atoms in hydrides6, would also be affected by a strong sample inhomogeneity. The presence of these multiple phases could even lead to the false determination of the Tc value, as it increases the probability of the formation of metallic conduction paths, as described by Hirsch and Marsiglio7. In this context, it can be pointed out that if experimental measurements and theoretical calculations for the determination of the Tc in superhydrides2,3,45 are in fact accurate, the LaH6+δ and LaH9+δ solids could prove to be promising targets as high Tc materials. Indeed, YH6 and YH9, with the same metal arrangement as in LaH6+δ and LaH9+δ, were suggested to have Tc values of 220 K and 243 K, respectively, at pressures of 183 and 201 GPa4.
The results presented here suggest a wide variability of the hydrogen content for a given structure formed by La atoms. The “LaH10” compound is a prime example, with a hydrogen composition that would be expected to vary by ±2 based on the comparison between the experimental and calculated datapoints. Moreover, we unveiled crystal-chemical regularities common for various RE-H systems: all La hydrides studied in this work, with the exception of LaH~4, were found to adopt the same La arrangements like those previously known in other RE-H systems. The detection of seven La-H compounds in the pressure range of 140–176 GPa—precisely in which superconducting samples were reported—points out the significant difficulties in having single-phase samples that are necessary for a reliable assessment of physical properties of materials, including superconductivity. Our study should promote the use of SCXRD on microcrystalline samples as an essential tool to characterize hydrides given its demonstrated ability to detect phases otherwise missed by powder XRD analysis. In particular, this approach should be employed to characterize lanthanum-compressed and laser-heated DACs along with ammonia borane to verify that no nitrides or borides other than BN are produced. Further investigations of the LaH6+δ and LaH9+δ compounds are of interest, as they potentially could be superconducting at high temperatures.
Methods
Experimental
Three BX90-type screw diamond anvil cells (DACs) were equipped with diamonds of culet sizes of 80 μm and rhenium was employed as the gasket material. The samples, composed of lanthanum embedded in paraffin oil, were prepared in one of two ways. One way was with a lanthanum ingot (99.9% purity), purchased from Sigma Aldrich, that was kept in an argon glovebox. When needed, micrometer-sized pieces of La were scratched off the lanthanum ingot in the glovebox and put in paraffin oil (CnH2n+2) immediately after being taken out of the glovebox, preventing a reaction with air, and then loaded in the DACs. For the second approach, lanthanum pieces already under paraffin oil (CxH2+x) was purchased. The lanthanum was cut down to the appropriate micrometer-size pieces in paraffin oil and directly transferred in the DACs. Paraffin was used as a pressure-transmitting media as well as a hydrogen reservoir, as it was successfully done for the synthesis of several other hydrides14,15,17,24,25,26,27. The sample pressure was determined from the X-ray diffraction signal of the Re gaskets28—never hydrogenated using paraffin—and crosschecked with the diamond anvils’ Raman edge29.
Lanthanum pieces of various sizes were loaded in the DACs so as to cover a wide lanthanum-to-hydrogen ratio. The samples were compressed at ambient temperature and laser-heated above 2000 K at pressures of 96, 106, 140, 150, 155, and 176 GPa. The double-sided YAG laser-heating of the samples was performed mainly at the GSECARS beamline of the APS and partially at the Bayerisches Geoinstitut51, with lanthanum acting as the laser absorber. Both system are quite similar and both allowed a focused (circular) laser spot of about 8 μm in diameter and enter the diamond anvil at perpendicular incidence. A flattop beam is used, which provides a roughly equal number of photons per area within that 8 μm diameter. In all cases, temperatures were measured using the samples’ thermal radiation52, although very high-temperature spikes of short during could usually not be measured. The samples were laser-heated until sample recrystallization, observed through the appearance of new sharp reflections, to a maximum measured temperature below 3200(200) K (see Supplementary Table 1).
The samples were mainly characterized by single-crystal (SCXRD) and powder X-ray diffraction (XRDp) measurements. The SCXRD was performed on very small, just few-micron size of single crystals, for which a special approach to the high-pressure XRD data acquisition and analysis was recently developed53. This approach was demonstrated on many systems54,55,56. The X-ray diffraction data were acquired at the P02.2 and GSECARS beamlines of PETRA III and the APS, respectively. At the P02.2 beamline, a Perkin Elmer XRD 1621 detector was employed with an X-ray beam of wavelength of λ = 0.2901 Å, focused down to about 2 × 2 µm2. At the GSECARS beamline, a Pilatus CdTe 1 M detector was used along with an X-ray beam focused down to 3 × 3 µm2, with a wavelength of λ = 0.2952 Å. On the polycrystalline samples, a full X-ray diffraction mapping of the experimental cavity was performed after each laser-heating in order to identify the most promising sample positions for a single-crystal data collection. On the locations where the most intense single-crystal reflections were detected, single-crystal data were acquired in step-scans of 0.5° from −38° to +38°. The CrysAlisPro software57 was utilized for the single-crystal data analysis. To calibrate an instrumental model in the CrysAlisPro software, i.e., the sample-to-detector distance, detector’s origin, offsets of goniometer angles, and rotation of both X-ray beam and the detector around the instrument axis, we used a single crystal of orthoenstatite ((Mg1.93Fe0.06)(Si1.93, Al0.06)O6), Pbca space group, a = 8.8117(2), b = 5.18320(10), and c = 18.2391(3) Å). The same calibration crystal was used at all the beamlines. The analysis procedure in the CrysAlisPro software includes the peak search, the removal of the diamond anvils’ parasitic reflections and saturated pixels of the detector, finding reflections belonging to a unique single crystal, the unit cell determination, and the data integration. The crystal structures were then solved with SHELXT structure solution program58 using intrinsic phasing and refined within the JANA2006 software59. CSD 2196053–2196069 contain the supplementary crystallographic data for this paper. These data can be obtained free of charge from FIZ Karlsruhe via www.ccdc.cam.ac.uk/structures. Powder X-ray diffraction was also performed to verify the chemical homogeneity of the samples and the data integrated with Dioptas60.
Computational details
Kohn-Sham density functional theory (DFT) based structural relaxations and electronic structure calculations were performed with the QUANTUM ESPRESSO package61,62,63 using the projector augmented wave approach64. We used the generalized gradient approximation by Perdew–Burke–Ernzerhof (PBE) for exchange and correlation65, for which the 4d and lower electrons of lanthanum are treated as scalar-relativistic core states. Convergence tests with a threshold of 1 meV per atom in energy and 1 meV/Å per atom for forces led to a Monkhorst-Pack66 k-point grid of 24 × 24 × 24, 24 × 24 × 12, 8 × 8 × 8, 24 × 24 × 24, and 24 × 24 × 12 for LaH3, LaH4, La4H23, LaH6, LaH9, and LaH10, respectively. For all phases, a cutoff for the wavefunction expansion of 80 Ry for wavefunction and 640 Ry for the density with 0.01 Ry Marzari–Vanderbilt smearing67.
We performed variable-cell relaxations (lattice parameters and atomic positions) on all experimental structures to optimize the atomic coordinates and the cell vectors until the total forces were smaller than 10−4 eV/Å per atom and the deviation from the target pressure was below 0.1 GPa.
Equation of state (EoS) calculations are performed via variable-cell structural relaxations between 75 and 200 GPa for all lanthanum hydrides with the exception of LaH~4 (see Fig. 2a), for which the complete crystal structure is unknown and LaH3 (see below). We fit a third-order Birch–Murnaghan EoS to the energy-volume points, calculate P(V), and benchmark versus the target pressure of the relaxations to ensure convergence. The crystal structure of all computationally investigated lanthanum hydrides is preserved without constraining their structures to the experimentally determined space group, even if all phases but LaH4 feature negative modes in the harmonic approximation. Calculations on LaH3 were performed between 0 and 200 GPa, and it was found that it loses symmetry transitioning from space group Fm−3m (#225) to R−3m (#166) starting from P \(\gtrsim\) 70 GPa. The resulting EoS for the high-symmetry Fm−3m LaH3 is in relatively good agreement with our experimental point at 50 GPa, while the R−3m LaH3 EoS is in good agreement with points by Drozdov et al.3.
DFT computations used as a basis for the finite-temperature calculations (see below and Supplementary Fig. 8) have been performed using the FHI-aims code68,69 in supercells with orthogonal lattice vectors of at least 5 Å length using the following DFT parameters described below.
As explained in the main text, the choice of the exchange-correlation (xc) functional when using DFT significantly affects the static calculated pressures observed in lanthanum hydrides. To estimate the effect, we computed the static pressure in a LaH4 cell using four commonly used xc-functionals, the local-density approximation (LDA) and three functionals of the generalized gradient approximation (GGA) family, with the FHI-aims code68,69. The results are listed in Supplementary Table 2. While LDA70 agrees quite well with PBEsol71 and am0572, the difference to PBE65 is about 7 to 10 GPa. While we use PBE for the rest of the calculations to match with the existing literature45, we note that it seems to yield larger pressures than the other commonly employed functionals. We also investigated the influence of the basis sets used in FHI-aims68. We checked light and tight default basis sets, which yield a difference of 0.7 GPa in the structure studied above. We, therefore, conclude that the error when using light default basis sets is negligible compared to, e.g., the choice of the xc-functional, and use light basis sets for all calculations in the following.
Finite-temperature simulations with TDEP
Finite-temperature properties have been modeled in the framework of temperature-dependent effective potentials (TDEP)46,47 using self-consistent sampling73, with expressions for the pressure similar to those described in refs. 74, 75. In TDEP, the nuclear system is described by a harmonic Hamiltonian in the canonical ensemble (NVT):
parametrized at a volume V and temperature T as described in refs. 46, 47. Here, u = (u1,…, uN) are displacements from the reference positions for N atoms, and likewise p = (p1,…, pN) are their momenta. i, j are atom indices while α, β label Cartesian coordinates. mi is the mass of atom i and U0 is the baseline energy which enforces 〈HTDEP〉T = 〈HDFT〉T with the canonical average 〈·〉T (we omit N and V in the thermodynamic average for clarity), and Φ(V, T) are the effective harmonic force constants at the V, T conditions of interest.
The harmonic force constants Φ can be used to create displacements {u} that correspond to the harmonic canonical ensemble defined by the harmonic Hamiltonian in Eq. (1) corresponding to the scheme outlined in ref. 76. These samples can be used to create new input data (forces) for parametrizing the TDEP Hamiltonian as introduced in ref. 73. This procedure can be repeated self-consistently from an initial guess as explained in detail in the appendix of ref. 77, resulting in stochastic temperature-dependent effective potentials (sTDEP). The potential pressure at finite temperature, Ppot(T), is estimated by computing the DFT pressure, PDFT in samples created from the effective harmonic model73,76,
where 〈·〉T denotes an average over the samples. To estimate the kinetic contribution to the pressure, we use that in the harmonic approximation, the kinetic pressure equals the kinetic energy, i.e., half the effective harmonic energy in the samples, modulo a volume-dependent prefactor in supercells of volume V74,75:
The total pressure, including temperature and nuclear quantum effects (through the sampling 〈·〉T), is then given by
Sampling was performed self-consistently with steps using an increasing number of samples. The convergence with respect to the number of self-consistent steps is material dependent, and can be very fast with only 16 supercells in the final step for the more harmonic LaH4, or more involved. In the current case, it was never necessary to go beyond 64 samples in the final step, even in the much more strongly anharmonic LaH9.
The chosen supercells were rectangular with at least 5 Å side length, resulting in supercell sizes up to 180 atoms. This is in line with earlier studies showing a rapid convergence of force constants with supercell size in LaH due to the short-range nature of the interatomic forces in metallic systems45.
Data availability
The details of the crystal structure investigations may be obtained from FIZ Karlsruhe, 76344 Eggenstein-Leopoldshafen, Germany (fax: +49-7247-808-666; e-mail: crysdata@fiz-karlsruhe.de) on quoting the deposition numbers CSD 2196053–2196069. All other datasets generated during and/or analyzed during the current study are available from the corresponding author upon reasonable request. Source data are provided with this paper.
References
Drozdov, A. P., Eremets, M. I., Troyan, I. A., Ksenofontov, V. & Shylin, S. I. Conventional superconductivity at 203 kelvin at high pressures in the sulfur hydride system. Nature 525, 73–76 (2015).
Somayazulu, M. et al. Evidence for superconductivity above 260 K in lanthanum superhydride at megabar pressures. Phys. Rev. Lett. 122, 27001 (2019).
Drozdov, A. P. et al. Superconductivity at 250 K in lanthanum hydride under high pressures. Nature 569, 528–531 (2019).
Kong, P. et al. Superconductivity up to 243 K in the yttrium-hydrogen system under high pressure. Nat. Commun. 12, 5075 (2021).
Snider, E. et al. Synthesis of yttrium superhydride superconductor with a transition temperature up to 262 K by catalytic hydrogenation at high pressures. Phys. Rev. Lett. 126, 117003 (2021).
Snider, E. et al. Room-temperature superconductivity in a carbonaceous sulfur hydride. Nature 586, 373–377 (2020).
Hirsch, J. E. & Marsiglio, F. Unusual width of the superconducting transition in a hydride. Nature 596, E9–E10 (2021).
Hirsch, J. E. & Marsiglio, F. Absence of magnetic evidence for superconductivity in hydrides under high pressure. Phys. C. Supercond. its Appl. 584, 1–10 (2021).
Hirsch, J. E. & Marsiglio, F. Nonstandard superconductivity or no superconductivity in hydrides under high pressure. Phys. Rev. B 103, 134505 (2021).
Hirsch, J. E. On the ac magnetic susceptibility of a room temperature superconductor: anatomy of a probable scientific fraud. Phys. C Supercond. Appl. 1353964 https://doi.org/10.1016/j.physc.2021.1353964 (2021).
Hirsch, J. E. Incompatibility of published ac magnetic susceptibility of a room temperature superconductor with measured raw data. Matter and Radiation at Extremes 7, 059901 (2022).
Huang, X. et al. High-temperature superconductivity in sulfur hydride evidenced by alternating-current magnetic susceptibility. Natl Sci. Rev. 6, 713–718 (2019).
Minkov, V. S. et al. Magnetic field screening in hydrogen-rich high-temperature superconductors. Nat. Commun. 13, 3194 (2022).
Meier, T. et al. Pressure-induced hydrogen-hydrogen interaction in metallic FeH revealed by NMR. Phys. Rev. X 9, 31008 (2019).
Meier, T. et al. Proton mobility in metallic copper hydride from high-pressure nuclear magnetic resonance. Phys. Rev. B 102, 165109 (2020).
Meier, T. et al. Nuclear spin coupling crossover in dense molecular hydrogen. Nat. Commun. 11, 6334 (2020).
Laniel, D. et al. Novel sulfur hydrides synthesized at extreme conditions. Phys. Rev. B 102, 134109 (2020).
Guigue, B., Marizy, A. & Loubeyre, P. Direct synthesis of pure H3S from S and H elements: no evidence of the cubic superconducting phase up to 160 GPa. Phys. Rev. B 95, 020104 (2017).
Goncharov, A. F. et al. Hydrogen sulfide at high pressure: change in stoichiometry. Phys. Rev. B 93, 174105 (2016).
Goncharov, A. F., Lobanov, S. S., Prakapenka, V. B. & Greenberg, E. Stable high-pressure phases in the H-S system determined by chemically reacting hydrogen and sulfur. Phys. Rev. B 95, 140101 (2017).
Einaga, M. et al. Crystal structure of the superconducting phase of sulfur hydride. Nat. Phys. 12, 835–839 (2016).
Nakao, H. et al. Superconductivity of pure H 3 S synthesized from elemental sulfur and hydrogen. J. Phys. Soc. Jpn. 88, 123701 (2019).
Minkov, V. S., Prakapenka, V. B., Greenberg, E. & Eremets, M. I. A Boosted critical temperature of 166 K in superconducting D3S synthesized from elemental sulfur and hydrogen. Angew. Chem. Int. Ed. 59, 18970–18974 (2020).
Fedotenko, T. et al. Synthesis of palladium carbides and palladium hydride in laser heated diamond anvil cells. J. Alloy. Compd. 844, 156179 (2020).
Ohta, K., Suehiro, S., Hirose, K. & Ohishi, Y. Electrical resistivity of fcc phase iron hydrides at high pressures and temperatures. Comptes Rendus Geosci. 351, 147–153 (2019).
Narygina, O. et al. X-ray diffraction and Mössbauer spectroscopy study of fcc iron hydride FeH at high pressures and implications for the composition of the Earth’s core. Earth Planet. Sci. Lett. 307, 409–414 (2011).
Thompson, E. C. et al. High‐pressure geophysical properties of Fcc phase FeH X. Geochem. Geophys. Geosystems 19, 305–314 (2018).
Anzellini, S., Dewaele, A., Occelli, F., Loubeyre, P. & Mezouar, M. Equation of state of rhenium and application for ultra high pressure calibration. J. Appl. Phys. 115, 043511 (2014).
Akahama, Y. & Kawamura, H. Pressure calibration of diamond anvil Raman gauge to 410 GPa. J. Phys. Conf. Ser. 215, 012195 (2010).
Korst, W. L. & Warf, J. C. Rare earth-hydrogen systems. I. Structural and thermodynamic properties. Inorg. Chem. 5, 1719–1726 (1966).
Liu, H., Naumov, I. I., Hoffmann, R., Ashcroft, N. W. & Hemley, R. J. Potential high- T c superconducting lanthanum and yttrium hydrides at high pressure. Proc. Natl Acad. Sci. USA 114, 6990–6995 (2017).
Semenok, D. V. et al. Novel strongly correlated europium superhydrides. J. Phys. Chem. Lett. 12, 32–40 (2021).
Ma, L. et al. Experimental clathrate superhydrides EuH6 and EuH9 at extreme pressure conditions. Phys. Rev. Res. 3, 043107 (2021).
Peña-Alvarez, M. et al. Synthesis of Weaire–Phelan barium polyhydride. J. Phys. Chem. Lett. 12, 4910–4916 (2021).
Troyan, I. A. et al. Anomalous high‐temperature superconductivity in YH6. Adv. Mater. 33, 2006832 (2021).
Li, X. et al. Polyhydride CeH9 with an atomic-like hydrogen clathrate structure. Nat. Commun. 10, 3461 (2019).
Zhou, D. et al. Superconducting praseodymium superhydrides. Sci. Adv. 6, eaax6849 (2020).
Peña-Alvarez, M. et al. Praseodymium polyhydrides synthesized at high temperatures and pressures. Phys. Rev. B 100, 184109 (2019).
Zhou, D. et al. High-pressure synthesis of magnetic neodymium polyhydrides. J. Am. Chem. Soc. 142, 2803–2811 (2020).
Geballe, Z. M. et al. Synthesis and stability of lanthanum superhydrides. Angew. Chem. Int. Ed. 57, 688–692 (2018).
Kuzovnikov, M. A. et al. Crystal structures of novel lanthanum superhydrides. in EHPRG 2019 - Abstracts 1 (2019).
Guigue, B., Marizy, A. & Loubeyre, P. Synthesis of UH7 and UH8 superhydrides: Additive-volume alloys of uranium and atomic metal hydrogen down to 35 GPa. Phys. Rev. B 102, 14107 (2020).
Uts, I., Glazyrin, K. & Lee, K. K. M. Effect of laser annealing of pressure gradients in a diamond-anvil cell using common solid pressure media. Rev. Sci. Instrum. 84, 103904 (2013).
Errea, I. et al. High-pressure hydrogen sulfide from first principles: a strongly anharmonic phonon-mediated superconductor. Phys. Rev. Lett. 114, 157004 (2015).
Errea, I. et al. Quantum crystal structure in the 250-kelvin superconducting lanthanum hydride. Nature 578, 66–69 (2020).
Hellman, O. & Abrikosov, I. A. Temperature-dependent effective third-order interatomic force constants from first principles. Phys. Rev. B 88, 144301 (2013).
Hellman, O., Abrikosov, I. A. & Simak, S. I. Lattice dynamics of anharmonic solids from first principles. Phys. Rev. B 84, 180301 (2011).
Chen, W. et al. Superconductivity and equation of state of lanthanum at megabar pressures. Phys. Rev. B 102, 134510 (2020).
Pépin, C. M., Geneste, G., Dewaele, A., Mezouar, M. & Loubeyre, P. Synthesis of FeH 5: A layered structure with atomic hydrogen slabs. Science 357, 382–385 (2017).
Chen, W. et al. High-temperature superconducting phases in cerium superhydride with a Tc up to 115 K below a pressure of 1 megabar. Phys. Rev. Lett. 127, 117001 (2021).
Fedotenko, T. et al. Laser heating setup for diamond anvil cells for in situ synchrotron and in house high and ultra-high pressure studies. Rev. Sci. Instrum. 90, 104501 (2019).
Mezouar, M. et al. Methodology for in situ synchrotron X-ray studies in the laser-heated diamond anvil cell. High. Press. Res. 37, 170–180 (2017).
Bykova, E. Single-crystal X-ray Diffraction at Extreme Conditions in Mineral Physics and Material Sciences (University of Bayreuth, 2015).
Laniel, D. et al. High pressure investigation of the S–N2 system up to the megabar range: synthesis and characterization of the SN2 solid. Inorg. Chem. 58, 9195–9204 (2019).
Laniel, D. et al. Nitrosonium nitrate (NO + NO3−) structure solution using in situ single-crystal X-ray diffraction in a diamond anvil cell. IUCrJ 8, 208–214 (2021).
Laniel, D. et al. High-pressure synthesis of the β-Zn3N2 nitride and the α-ZnN4 and β-ZnN4 polynitrogen compounds. Inorg. Chem. 60, 14594–14601 (2021).
CrysAlisPRO. Rigaku Oxford Diffraction. Agilent Technologies UK Ltd, Yarnton, England. https://www.rigaku.com/products/crystallography/crysalis (2015).
Sheldrick, G. M. A short history of SHELX. Acta Crystallogr. Sect. A Found. Crystallogr. 64, 112–122 (2008).
Petrícek, V., Dušek, M. & Palatinus, L. Crystallographic computing system JANA2006: general features. Z. fur Krist. 229, 345–352 (2014).
Prescher, C. & Prakapenka, V. B. DIOPTAS: a program for reduction of two-dimensional X-ray diffraction data and data exploration. High. Press. Res. 35, 223–230 (2015).
Giannozzi, P. et al. QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 21, 395502 (2009).
Giannozzi, P. et al. Advanced capabilities for materials modelling with quantum ESPRESSO. J. Phys. Condens. Matter 29, 465901 (2017).
Giannozzi, P. et al. Quantum ESPRESSO toward the exascale. J. Chem. Phys. 152, 154105 (2020).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Monkhorst, H. J. & Pack, J. D. Special points for Brillouin-zone integrations. Phys. Rev. B 13, 5188–5192 (1976).
Marzari, N., Vanderbilt, D., De Vita, A. & Payne, M. C. Thermal contraction and disordering of the Al(110) surface. Phys. Rev. Lett. 82, 3296–3299 (1999).
Blum, V. et al. Ab initio molecular simulations with numeric atom-centered orbitals. Comput. Phys. Commun. 180, 2175–2196 (2009).
Knuth, F., Carbogno, C., Atalla, V., Blum, V. & Scheffler, M. All-electron formalism for total energy strain derivatives and stress tensor components for numeric atom-centered orbitals. Comput. Phys. Commun. 190, 33–50 (2015).
Ceperley, D. M. & Alder, B. J. Ground state of the electron gas by a stochastic method. Phys. Rev. Lett. 45, 566–569 (1980).
Perdew, J. P. et al. Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 100, 136406 (2008).
Armiento, R. & Mattsson, A. E. Functional designed to include surface effects in self-consistent density functional theory. Phys. Rev. B - Condens. Matter Mater. Phys. 72, 1–5 (2005).
Shulumba, N., Hellman, O. & Minnich, A. J. Lattice thermal conductivity of polyethylene molecular crystals from first-principles including nuclear quantum effects. Phys. Rev. Lett. 119, 185901 (2017).
Monserrat, B., Drummond, N. D. & Needs, R. J. Anharmonic vibrational properties in periodic systems: energy, electron-phonon coupling, and stress. Phys. Rev. B 87, 144302 (2013).
Monacelli, L., Errea, I., Calandra, M. & Mauri, F. Pressure and stress tensor of complex anharmonic crystals within the stochastic self-consistent harmonic approximation. Phys. Rev. B 98, 024106 (2018).
West, D. & Estreicher, S. K. First-principles calculations of vibrational lifetimes and decay channels: hydrogen-related modes in Si. Phys. Rev. Lett. 96, 115504 (2006).
Benshalom, N., Reuveni, G., Korobko, R., Yaffe, O. & Hellman, O. Dielectric response of rock-salt crystals at finite temperatures from first principles. Phys. Rev. Mater. 6, 033607 (2022).
Acknowledgements
The authors acknowledge the Deutsches Elektronen-Synchrotron (DESY) and the Advance Photon Source (APS) for provision of beamtime at the P02.2 and GSECARS beamlines, respectively. D.L. thanks the Alexander von Humboldt Foundation, the Deutsche Forschungsgemeinschaft (DFG, project LA-4916/1-1), and the UKRI Future Leaders Fellowship (MR/V025724/1) for financial support. N.D. and L.D. thank the Federal Ministry of Education and Research, Germany (BMBF, grant no. 05K19WC1) and the DFG (projects DU 954–11/1, DU 393–9/2, and DU 393–13/1) for financial support. B.W. gratefully acknowledges funding by the DFG in the framework of the research unit DFG FOR2125 and within projects WI1232 and thanks BIOVIA for support through the Science Ambassador program. N.D. and I.A.A. also thank the Swedish Government Strategic Research Area in Materials Science on Functional Materials at Linköping University (Faculty Grant SFO-Mat-LiU No. 2009 00971). Support from the Knut and Alice Wallenberg Foundation (Wallenberg Scholar grant no. KAW-2018.0194), the Swedish e-science Research Center (SeRC), and the Swedish Research Council (VR) grant no. 2019-05600 is gratefully acknowledged. F.K. also acknowledges support from the Swedish Research Council (VR) program 2020-04630, and the Swedish e-Science Research Centre (SeRC). Computations were performed on resources provided by the Swedish National Infrastructure for Computing (SNIC) at the PDC Centre for High-Performance Computing (PDC- HPC) and the National Supercomputer Center (NSC). For the purpose of open access, the authors have applied a Creative Commons Attribution (CC BY) licence to any Author Accepted Manuscript version arising from this submission.
Author information
Authors and Affiliations
Contributions
D.L., L.D., and N.D. designed the work. D.L. and L.D. prepared the high-pressure experiments. D.L., A.A., S.K., T.F., S.C., K.G., and V.P. performed the synchrotron X-ray diffraction experiments. D.L. and L.D. processed the synchrotron X-ray diffraction data. Fl.T., B.W. F.K., V.M., and I.A.A. performed the theoretical calculations. D.L., Fl.T., T.M., and L.D. contextualized the data interpretation. D.L., Fl.T., L.D., N.D., and I.A.A. prepared the first draft of the manuscript with contributions from all other authors. All the authors commented on successive drafts and have given approval to the final version of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Jorge Hirsch, Hanyu Liu and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Source data
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Laniel, D., Trybel, F., Winkler, B. et al. High-pressure synthesis of seven lanthanum hydrides with a significant variability of hydrogen content. Nat Commun 13, 6987 (2022). https://doi.org/10.1038/s41467-022-34755-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-022-34755-y
This article is cited by
-
Electrical Resistance of Hydrides Under High Pressure: Evidence of Superconductivity or Confirmation Bias?
Journal of Superconductivity and Novel Magnetism (2023)
-
Superconductivity above 70 K observed in lutetium polyhydrides
Science China Physics, Mechanics & Astronomy (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.