Abstract
The explosive growth of deep learning applications has triggered a new era in computing hardware, targeting the efficient deployment of multiply-and-accumulate operations. In this realm, integrated photonics have come to the foreground as a promising energy efficient deep learning technology platform for enabling ultra-high compute rates. However, despite integrated photonic neural network layouts have already penetrated successfully the deep learning era, their compute rate and noise-related characteristics are still far beyond their promise for high-speed photonic engines. Herein, we demonstrate experimentally a noise-resilient deep learning coherent photonic neural network layout that operates at 10GMAC/sec/axon compute rates and follows a noise-resilient training model. The coherent photonic neural network has been fabricated as a silicon photonic chip and its MNIST classification performance was experimentally evaluated to support accuracy values of >99% and >98% at 5 and 10GMAC/sec/axon, respectively, offering 6× higher on-chip compute rates and >7% accuracy improvement over state-of-the-art coherent implementations.
Similar content being viewed by others
Introduction
The proliferation of Deep Learning (DL) workloads in today’s computational systems has triggered a new era in computing systems promoting the use of brain-inspired non-von-Neumann architectures, with the DL accelerators being currently considered as a key enabler for the efficient deployment of such workloads1. Among the researched DL accelerator technologies, neuromorphic integrated photonic circuits are constantly gaining interest due to their proven credentials to support time-of-flight latencies and THz bandwidths that may result to orders of magnitude higher computational and footprint efficiencies2,3,4. In this context, research efforts have mainly focused on the deployment and demonstration of the constituent building block technologies5 like weighting banks6,7 and activation functions8,9,10,11 as well as of complete linear neuron layouts12,13,14,15,16,17,18,19 that have so far largely relied on two broad architectural categories: (i) non-coherent setups, where typically one distinct wavelength is required per axon and optical power addition techniques are utilized for the summation functionality, leading to neuron layouts where the number of optical resource requirements scales linearly with its fan-in20, and (ii) coherent interferometric setups, where a single wavelength feeds the entire layout and the light carrier phase is employed for realizing signed weight values16,21,22,23.
The energy and area efficient promise of integrated photonic neural networks can, however, materialize only when significantly higher compute rates per axon are utilized compared to respective electronic Neural Network (NN) engines2,3,4,12,13. Recent analysis has indicated that the optimal Multiply-And-Accumulate (MAC)/sec/axon compute rates in optical setups should go well beyond the GHz regime2,3,4 in order to bring energy consumption down to the sub-pJ/MAC area. At the same time, high computational speeds have to be accommodated though on-chip elements for all constituent linear neuron functions in order to reap the benefits of low energy and low footprint integrated optics, including input vector generation, weighting and summation. Although the staggering computational power advances enabled by neuromorphic photonic circuitry, when using >10GMAC/sec/axon processing speeds, have been already witnessed through proof-of-concept demonstrations15, these have been realized through non-coherent architectures employing still non-integrated fiber-pigtailed building blocks for crucial NN functions. At the same time, their requirement for integrating and accurately controlling multiple resonant elements in high fan-in NN setups forms a significant hurdle towards their fully integrated version.
Fully on-chip optical neural networks have been so far only feasible through coherent architectural schemes, where, however, computational speeds are still far below the necessary targets and are struggling to enter the MHz regime16,22,23. On top of that, the accuracy values obtained by experimental coherent layouts reported so far have been limited to 90% and 76% for MNIST classification22 and vowel recognition16, respectively. Their rather limited performance in terms of both computational speed and accuracy is in direct relation to the overall noise that is inevitably present in any analog DL engine24,25,26,27,28,29,30,31, which is probably strengthened by the employed coherent architecture that comprises multiple cascaded Mach-Zehnder Interferometers (MZIs). Analog DL platforms have to cope by default with both deterministic and non-deterministic noise sources and the amount of noise increases significantly with operational speed. In the case of the experimental coherent-based layouts reported so far as neuromorphic platforms, their noise-resistive behavior is additionally counteracted by their circuit design that relies on Singular Value Decomposition (SVD) techniques applied over unitary optical layouts, which in turn comprise a mesh of multiple cascaded MZI following the Reck32 and Clements33 designs. In this way, the programming of multiple cascaded MZIs even for defining the weights of a single neuron is required, creating an increased sensitivity to fabrication errors that degrades the circuit fidelity and acts as an additional noise source.
In this work, we demonstrate experimentally noise-resilient deep learning at a record-high 10GMAC/sec/axon compute rate by utilizing a coherent silicon integrated circuit that combines a noise-tolerant linear neuron architectural scheme with noise-aware training methods. The silicon Coherent Photonic Neural Network (CPNN) circuit relies on the dual-IQ-modulator-based coherent linear neuron architecture recently proposed by us21,34, where a single on-chip weight value is simply defined by a phase shifting followed by an amplitude modulating element, significantly improving in this way its noise-tolerant characteristics compared to respective coherent layouts with cascaded MZIs. On-chip input vector data generation is realized by electro-optic travelling-wave Mach-Zehnder Modulators (MZM), with a single thermo-optic MZM and a single phase shifter providing the on-chip weighting per axon. Its performance has been validated within a DL layout that was trained with a noise-aware method35,36 for classifying hand-written images from the MNIST dataset, with its last two NN layers being implemented in the optical domain. Experimentally obtained accuracy values of >99% and >98% at 5 and 10GMAC/sec/axon compute rates, respectively, were obtained, even in the presence of highly noisy signals with a standard deviation of σ = 0.4. This validates the strong credentials of our integrated CPNN architectural scheme to combine its noise-tolerant design with noise-aware training models for leading to high-performance photonic DL layouts, outperforming state-of-the-art coherent-based demonstrations by 6 orders of magnitude with respect to on-chip compute rates per axon and by >7% with respect to obtained accuracy metrics.
Results
Concept and CPNN architecture
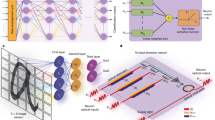
The layout of the CPNN designed for classifying MNIST images is illustrated in Fig. 1a. It comprises 2 cascaded ReLU convolutional layers (L1, L2) equipped with 32 and 64 3 × 3 kernels respectively, followed by a fully-connected ReLU feed-forward layer employed for data flattening (L3). A 4 × 2 photonic layer is employed as the L4, followed by a 2 × 1 photonic output layer denoted as L5. Both photonic layers utilize the sin2(x2) as activation function, so as to comply with respective optically implemented activations that rely on the use of a photodiode followed by a Mach-Zehnder Modulator (PD-MZM)20 at the output of an interferometric coherent architecture. A close-up view of the two photonic layers is depicted in Fig. 1b, where two identical silicon photonic chips are used for implementing the L4 and one additional chip is used for implementing the output layer L5. Each photonic neuron is identical and relies on the dual IQ architecture proposed in21, with its silicon-based deployment incorporating a 4-fan-in setup, as shown in Fig. 1c. A single CW laser source is split at the chip front-end to feed the bias branch as well as four axons. The CPNN design of Fig. 1a required the utilization of two silicon photonic axons at every chip for implementing the (x1, x2, Σ1) and (x3, x4, Σ2) layers within the L4 and the output layer L5. As shown in Fig. 1c, the input signals xa and xb of each axon are imprinted on the respective laser copies via an electro-optic MZM operating in the GHz regime. The weighting of each signal is performed individually via a thermo-optic phase shifter and a thermo-optic MZM that are responsible for the s(wi) sign and the weight absolute value |wi | , respectively, with i = a, b. Despite the low bandwidth of few MHz that thermo-optic elements can achieve, during the inference their values are static, thus the computational rate of the CPNN is dictated only by the electro-optic MZMs operating in GHz. The main advantage of using thermo-optic elements is their lower insertion loss compared to the electro-optic elements, maintaining in this way the overall insertion loss at reasonable levels. The carrier of the realized dot product xawa + xbwb interferes then with the bias signal before reaching the PD that has also a high bandwidth in the GHz regime, so that the dot product sign information imprinted on the phase of the summed signal can transform into an amplitude quantity where positive and negative values emerge as optical pulses above and optical dips below the bias signal, respectively21. The phase and the amplitude of the bias branch can be controlled by the s(wbias) and the |wbias | , respectively. Finally, the electrical output of the PD is amplified through an electrical amplifier in order to drive the next layer, realizing at the same time the sin2(x2) activation function by exploiting the non-linearity of the MZM transfer function20, as shown in the inset of Fig. 1b. The non-injective behavior of the sin2(x2) is similar to the ReLU, which is also non-injective for x < 0, while the non-linear part has similarities with the sigmoid. The appropriate training framework for such activation functions has been published in36.
a Layout of the proposed CPNN, (b) a close-up view of its integrated photonic part based on the dual-IQ coherent linear neuron architecture, with the electro-photonic activation function module being highlighted with the red-dashed box and c the layout of the integrated 4-fan-in dual-IQ coherent linear neuron.
Figure 2a illustrates a photo of the packaged Si-pho prototype, with the photonic chip mounted on an electrical Printed Circuit Board (PCB) that allows seamless electronic access to all the DC driven photonic components. A close-up microscope photo of the fabricated 4-fan-in Si-pho coherent neuron is depicted in Fig. 2b, highlighting with red lines the interferometric structures that were utilized simultaneously in the experimental implementation of the network shown in Fig. 1a (see S1). The electro-optic response of the travelling-wave MZMs used for the on-chip input vector data generation was characterized by measuring their frequency response, with an indicative measurement for one of the four MZMs depicted in Fig. 2c, revealing a 3 dB bandwidth of 7 GHz.
MNIST classification at 10GMAC/sec/axon
Figure 3 depicts the experimental results obtained when the CPNN architecture was trained for MNIST classification tasks considering a noise-free hardware and signal environment, so as to validate the noise-related characteristics of the experimental CPNN platform through the comparative analysis between the expected and obtained waveforms. The time traces of Fig. 3a–g illustrate the signals originating from the software inferenced NN and their experimentally obtained counterparts with blue and red solid lines, respectively. More specifically, the time traces in Fig. 3a, b depict the x1 and x2 signals, while Fig. 3c illustrates the weighted sum of x1 and x2, denoted as Σ1. The Mean-Squared-Error (MSE) for x1, x2 and Σ1 signals was 0.28, 0.16 and 0.63%, respectively. Figure 3d–f illustrate the respective time traces for the x3, x4 and Σ2 signals of the 2nd neuron, with the corresponding MSE values being 1.13, 0.81 and 1.93%, respectively. The time trace of Σout signal that carries the sum of the weighted Σ1 and Σ2 values utilizing the weighting stage of the last NN layer is depicted in Fig. 3g, where the MSE was equal to 1.41%. Figure 3h, i and j depict the noise distribution of Σ1, Σ2, and Σout, respectively, as well as the zero-mean best fit Gaussian distribution for each data batch, highlighted in red. Finally, the obtained classification accuracies and the calculated SNR values are depicted in Fig. 3k. The CPNN achieved an accuracy of 99.47% for the MNIST classification task when all its layers were implemented in a software environment, denoted by the dashed line as “software accuracy” in Fig. 3k. Its experimental validation with the last two layers implemented over the silicon photonic chip revealed an accuracy of 99.3% and 97.8% and a SNR of 14 and 12.4 dB at 5 and 10GMAC/sec/axon, respectively, confirming the low-noise characteristics of the proposed CPNN that allowed for only 0.17% and 1.67% degraded accuracy performance, respectively, compared to the software accuracy obtained within a noiseless environment. It is worth mentioning that the contribution of the software- and the hardware-implemented NN is analyzed in detail in supplementary note 2, where the whole NN has been implemented in software with noisy building blocks without any significant accuracy degradation.
a–g Time traces from the experimental evaluation of MNIST classification task on CPNN architecture illustrating the expected and the received signals, h–j noise distribution bar charts of each dot product Σi and the respective fitting with the Gaussian distribution and k accuracy and SNR measurements at 5 and 10GMAC/sec/axon.
Noise-resilient CPNN
Following the performance validation of the baseline CPNN model, the last two NN photonic layers were retrained following a noise-aware training model35 after introducing Additive White Gaussian Noise (AWGN). The AWGN had a mean value and a standard deviation that were set to be equal to the experimentally obtained noise characteristics of the silicon photonic circuitry. Figure 4a illustrates schematically how AWGN was inserted at every xi in the CPNN layout in both photonic layers within the NN training model, in order to emulate the signal impairments originating by the photonic hardware platform. As can be seen, AWGN noise was considered to be added on every axon, so that a signal equal to y = (x + n) × w emerges from a single axon at the neuron output. The retraining procedure was implemented in the PyTorch software model of the CPNN, for a noise with a zero mean value and a standard deviation of σ = 0.4, revealing a software accuracy of 99.3% on the MNIST classification task.
a The modified photonic part of CPNN that incorporates AWGN sources on each xi signal, b, d, f time trace and c, e, g noise distribution with the respective Gaussian fitting for : (i) the baseline model and 0 dBm at the Rx input, (ii) the baseline model and −7dBm at the Rx (iii) noise-aware model −7dBm at the Rx.
Figure 4b–e illustrates the obtained experimental results of the baseline model when used with different experimental conditions and associated noise levels on the MNIST classification task, with Fig. 4f, g depicting the respective experimental results when the noise-aware training model was enforced. Figure 4b depicts the time trace of the CPNN output layer when the baseline model is applied, with the received optical power being equal to 0 dBm. The blue solid line represents the signal expected at the CPNN output when the network performs in software, while the red solid line shows the experimentally obtained pulse trace when an optical signal power of 0 dBm reaches the PD. The difference between the two waveforms had the distribution illustrated in Fig. 4c along with its Gaussian fitting, presenting a σ = 0.21 and a MSE = 2.49%. Figure 4d shows again the software-expected and experimentally obtained pulse traces when the optical signal gets attenuated by 7 dB prior reaching the photodiode, increasing in this way the noise of the photonic system that is primarily dominated by the Rx Trans-Impendence Amplifier (TIA) thermal noise contribution. In this case, the experimentally obtained waveform deviates even more from the expected software-based pulse trace, being the result of the higher system noise within a noise-agnostic baseline training. An increased MSE of 3.85% and a σ = 0.4 are obtained, with its distribution depicted in Fig. 4e. However, enforcing the noise-aware training model over the two photonic layers can significantly improve performance for the same noise level conditions, as can be verified by the time trace captured at the CPNN output layer and shown in Fig. 4f. The same −7 dBm optical power level was retained also in this case at the PD input so as to ensure identical noise levels with the respective results of Fig. 4d, e, with the distribution of the difference between the acquired and expected signals shown in Fig. 4g and validating a significantly improved performance over the baseline model, with σ and MSE values reducing to only 0.23 and 1.58%, respectively.
A quantified comparison between the noise-aware MNIST classification model versus its baseline counterpart for different AWGN levels with a standard deviation ranging from σ = 0 up to σ = 0.6 was carried out both in software and experimental environment and the results of this analysis are illustrated in Fig. 5. The solid lines were derived from the software simulation model and the scatter points were derived from the experimentally validated DL platform, where increasing AWGN levels were obtained by attenuating the power level of the neuron output signal prior reaching the receiver. Figure 5a depict the achieved classification accuracies for the MNIST dataset at 5GMAC/sec/axon, with the blue and red points representing the experimentally obtained results from the baseline and noise-aware trained platform, respectively. As can be observed, the experimentally derived values follow closely the theoretically expected curves in both cases, validating the robustness of both the developed software framework and the effectiveness of the noise-aware model. The performance benefits of the noise-aware platform are revealed when the noise standard deviation exceeds the value of σ = 0.25, where the accuracy of the baseline model starts to degrade much faster reaching an accuracy of 95% at a σ = 0.4. At the same time, the accuracy of the noise-aware platform starts to degrade at significantly higher noise levels, remaining at >99% values even for noise standard deviations up to σ = 0.4. This implies that the performance advantages offered by the noise-aware platform can be either acquired as accuracy improvement over its baseline training model when the two schemes are evaluated for identical noise levels or as optical power savings when the same accuracy values are targeted by both schemes. More specifically, the 5GMAC/sec/axon noise-aware platform offers an accuracy improvement of 5.93% compared to the baseline model when the system noise has in both cases a standard deviation value of σ = 0.4. Alternatively, the noise-aware model can be considered as requiring a −11.7 dBm input optical power at the PD for ensuring the same 97.27% classification accuracy with the respective baseline scenario, where, however, a −7 dBm PD input optical power is needed. This highlights that the noise-aware platform can yield a power budget improvement of 4.7 dB that may translate into respective energy consumption benefits when a certain accuracy performance is targeted. Figure 5b depicts the same set of results for the case of a 10GMAC/sec/axon performing NN. Similar improvements are reported for noise values with a σ > 0.25, with the accuracy of the noise-aware platform remaining above 98% up to σ values of 0.4, revealing a best-case accuracy improvement of 2.54% or, alternatively, a power budget saving of 1.8 dB compared to the baseline scenario. It should be mentioned that the noise resiliency of the noise-aware method has been validated in detail in supplementary note 2, where the proposed training scheme enhances the noise resilience of the network using at the same time the least possible photonic hardware. This fact has been also verified on the CIFAR-10 dataset, where the usage of the noise-aware training allowed to approach the performance of traditional ReLU-based NN implementations.
Discussion
The speed and accuracy performance benefits enabled by the proposed noise-resilient silicon photonic coherent DL platform can be clearly outlined when comparing with respective state-of-the-art coherent-based experimental layouts employed so far in neuromorphic applications. Figure 6 provides a pictorial representation of the combined MAC/sec/axon compute rate and accuracy metrics reported by coherent-based demonstrations so far23,16, and22, revealing that the experimental accuracy performance accomplished so far was only 72%, 76.7% and 90.5%, with the compute rate per axon never exceeding 10 kHz. All these coherent-based deployments relied on the use of cascaded MZI meshes following the SVD-based design over the unitary optical layouts proposed by Reck32 and Clements33. Our work is the first to follow an alternative on-chip coherent neuromorphic photonic architecture where a single column of weight values required by a single neuron can be enforced via a single respective column of optical components, avoiding in this way the use of cascaded photonic stages and safeguarding higher noise tolerance. Combined with a noise-aware DL training framework, the proposed silicon coherent neuromorphic platform allowed for the first time for 10GMAC/sec/axon on-chip compute rates and >98% accuracy values, outperforming all state-of-the-art coherent neurons by ~6 orders of magnitude in terms of per axon processing rates and by >7% in terms of accuracy performance. This brings its accuracy performance very close to the standards of state-of-the-art GPU platforms, as can be revealed in Fig. 6 by the classification performance metrics accomplished by a Nvidia DGX-A100 platform that executes the baseline MNIST classification model using the same NN architecture that was followed for the CPNN layout. Taking into account that the compute rate per axon in the latest Nvidia GPU is, however, one order of magnitude lower than the 10 GHz compute rate supported by the proposed silicon photonic neuromorphic platform (Fig. 6), the proposed CPNN equipped by noise-aware training models designates a promising framework for elevating DL performance metrics beyond state-of-the-art specifications of well-established DL technologies. This dual-IQ-modulator-based architecture, demonstrated here as a rather elementary silicon integrated chip that performs dot product operation between input and weight vectors, can also scale to input vector-weight matrix multiplication functions without sacrificing its noise-resilient properties37. This can pave the way towards a highly promising coherent neuromorphic photonic layout that may lead the race towards high-speed and high-accuracy chip-scale photonic DL engines, forming a promising alternative even to current well-established DL technology platforms. In doing so, a crossbar configuration seems to be the most promising candidate to realize up to 64-by-64 photonic vector by matrix multipliers with record-low loss and unitary fidelity (see S3).
We demonstrated experimentally a noise-resilient CPNN deployed as a silicon-integrated photonic chip and trained within a noise-aware feed-forward DL training framework, demonstrating the highest classification accuracy and the fastest compute rate per axon among all coherent linear neurons reported so far. The proposed photonic neuron architecture can be extended to support on-chip vector-matrix multiplication for implementing multi-neuron layers at chip-scale37 and can be also applied to alternative DL training models supporting Convolutional Neural Network (CNN) and Recurrent Neural Network (RNNs) configurations38. Moreover, its 10GMAC/sec/axon compute rate performance can be eventually increased by replacing the silicon MZM with a higher electro-optic bandwidth on-chip input vector data generation technology.
Methods
Design and fabrication of COLN
The COLN has been designed by using explicitly designed and tested photonic building blocks that are available at CORNERSTONE’s Process Design Kit (PDK). The chip has been fabricated in Cornerstone’s Silicon Photonic 220 nm platform and wire-bonded on a custom PCB. Each electro-optic MZM responsible for the generation of xi signal relies on a push-pull asymmetric structure with 1.8 mm long phase shifters, while the heating elements are 560 um long. The insertion loss of the electro-optic MZMs is 8 dB, requiring 4.4 V on each arm to achieve a π-phase shift, while the thermo-optic MZMs has an insertion loss of 2 dB.
Software-hardware interface
An in-house software tool was developed for interfacing the software and the hardware part of the proposed CPNN. Towards the software-hardware conversion, each signal was upsampled in order to achieve the required baud rate. Then, the signal was pre-equalized by means of 11-tap Feed-Forward Equalizer (FFE) and quantized with an 8-bit format before reaching a M8195a AWG from Keysight with 65GSa/s sampling rate, 8-bit precision and 25 GHz 3 dB bandwidth. The output of the PD is sampled by means of an DSOZ634a real-time oscilloscope with 33 GHz 3 dB bandwidth, 80GSa/s sampling rate and 10-bit resolution. Afterwards, the hardware-software interface performs time recovery to the captured waveform and then a Gaussian-shaped filter is applied. The filtered signal is downsampled to 1 sample before entering the software-based NN.
Noise-aware training model
Τhe CPNN was implemented in software by means of PyTorch framework. All models were initialized using the Xavier initialization with a gain of 2 and the weights were optimized for 20 epochs using a variant of stochastic gradient descent, i.e. the Adam optimizer. Finally, the size of each batch was equal to 256 and the learning rate was set to 0.0001. For the training of noise-aware model, the experimentally measured standard deviation and the distribution of system’s noise was used to emulate the experimental conditions. The experimental measurements of noise were performed within a certain range of received optical power, resulting in different σ values ranging in [0, 0.7]. Then, the CPNN was trained by introducing noise on each axon based on the experimental findings, resulting in three different models trained with σ = 0.2, 0.4 and 0.7. The simulation and the experimental validation of three models shown that the model with σ = 0.4 has the best performance across the range of σ = [0, 1], establishing this model towards the experimental validation of noise-resilient capabilities of the CPNN. Note that the noise during the training procedure was generated by using the randn() function of PyTorch.
Data availability
The data that support the findings of this study are available from the corresponding authors on reasonable request.
Code availability
The code that used for training the ML models is available on GitHub: https://github.com/georgemourgias/noise_aware_cpnn.
References
Kendall, J. D. & Kumar, S. The building blocks of a brain-inspired computer. Appl. Phys. Rev. 7, (2020).
Nahmias, M. A. et al. Photonic multiply-accumulate operations for neural networks. IEEE J. Sel. Top. Quantum Electron. 26, 1 (2020).
Totovic, A. R., Dabos, G., Passalis, N., Tefas, A. & Pleros, N. Femtojoule per MAC neuromorphic photonics: an energy and technology roadmap. IEEE J. Sel. Top. Quantum Electron. 26, 1–15 (2020).
Stabile, R. et al. Neuromorphic photonics: 2D or not 2D? J. Appl. Phys. 129, 1–13 (2021).
Shastri, B. J. et al. Photonics for artificial intelligence and neuromorphic computing. Nat. Photonics 15, 102–114 (2021).
Tait, A. N. et al. Neuromorphic photonic networks using silicon photonic weight banks. Sci. Rep. 7, 1–10 (2017).
Tait, A. N. et al. Two-pole microring weight banks. Opt. Lett. 43, 2276 (2018).
Mourgias-Alexandris, G. et al. An all-optical neuron with sigmoid activation function. Opt. Express 27, 9620 (2019).
Huang, C. et al. Programmable silicon photonic optical thresholder. IEEE Photonics Technol. Lett. 31, 1834–1837 (2019).
Amin, R. et al. ITO-based electro-absorption modulator for photonic neural activation function. APL Mater. 7, 0–11 (2019).
Williamson, I. A. D. et al. Reprogrammable electro-optic nonlinear activation functions for optical neural networks. IEEE J. Sel. Top Quantum Electron. 26, 1–12 (2019).
Peng, H. T. et al. Neuromorphic photonic integrated circuits. IEEE J. Sel. Top. Quantum Electron. 24, 1–15 (2018).
Nahmias, M. A. et al. A TeraMAC Neuromorphic Photonic Processor. in 31st Annual Conference of the IEEE Photonics Society, IPC 2018 1–2 (IEEE, 2018). https://doi.org/10.1109/IPCon.2018.8527089.
Tait, A. N. et al. Silicon photonic modulator neuron. Phys. Rev. Appl. 11, 1–16 (2019).
Xu, X. et al. 11 TOPS photonic convolutional accelerator for optical neural networks. Nature 589, 44–51 (2021).
Shen, Y. et al. Deep learning with coherent nanophotonic circuits. Nat. Photonics 11, 441–446 (2017).
Miscuglio, M. & Sorger, V. J. Photonic tensor cores for machine learning. Appl. Phys. Rev. 7, 1–16 (2020).
Shi, B., Calabretta, N., & Stabile, R. Deep neural network through an InP SOA-based photonic integrated cross-connect. IEEE J. Sel. Top. Quantum Electron. 26, 1–1 (2019).
Feldmann, J. et al. Parallel convolutional processing using an integrated photonic tensor core. Nature 589, 52–58 (2021).
Tait, A. N., Nahmias, M. A., Shastri, B. J. & Prucnal, P. R. Broadcast and weight: an integrated network for scalable photonic spike processing. J. Light. Technol. 32, 4029–4041 (2014).
Mourgias-Alexandris, G. et al. Neuromorphic photonics with coherent linear neurons using dual-IQ modulation cells. J. Light. Technol. 38, 811–819 (2020).
Zhang, H. et al. An optical neural chip for implementing complex-valued neural network. Nat. Commun. 12, 1–11 (2021).
Shokraneh, F., Geoffroy-Gagnon, S., Nezami, M. S. & Liboiron-Ladouceur, O. A. Single layer neural network implemented by a 4×4 MZI-based optical processor. IEEE Photonics J. 11, (2019).
Lugnan, A. et al. Photonic neuromorphic information processing and reservoir computing. APL Photonics 5, (2020).
Ron, D. A., Kamalian-Kopae, M. & Turitsyn, S. Noise-Resistant Optical Implementation of Analogue Neural Networks. in 2021 Conference on Lasers and Electro-Optics Europe & European Quantum Electronics Conference (CLEO/Europe-EQEC) vol. 8 1–1 (IEEE, 2021).
Semenova, N., Larger, L. & Brunner, D. Understanding and mitigating noise in trained deep neural networks. Elsevier Neural Networks, 146, 151–160, (2022).
Semenova, N. et al. Fundamental aspects of noise in analog-hardware neural networks. Chaos 29, (2019).
Klachko, M., Mahmoodi, M. R. & Strukov, D. Improving noise tolerance of mixed-signal neural networks. arXiv:1904.01705 (2019).
Zhou, C., Kadambi, P., Mattina, M. & Whatmough, P. N. Noisy machines: understanding noisy neural networks and enhancing Robustness to analog hardware errors using distillation. arXiv:2001.04974 (2020).
Rekhi, A. S. et al. Analog/mixed-signal hardware error modeling for deep learning inference. Proc. - Des. Autom. Conf. 4–9 (2019)
Gu, J. et al. ROQ: A noise-aware quantization scheme towards Robust optical neural networks with low-bit controls. Proc. 2020 Des. Autom. Test Eur. Conf. Exhib. DATE 2020 1586–1589 (2020).
Reck, M., Zeilinger, A., Bernstein, H. J. & Bertani, P. Experimental Realization of any discrete unitary operator. Phys. Rev. Lett. 73, 58–61, (1994).
Clements, W. R., Humphreys, P. C., Metcalf, B. J., Kolthammer, W. S. & Walsmley, I. A. Optimal design for universal multiport interferometers. Optica 3, 1460 (2016).
Mourgias-Alexandris, G. A Coherent Silicon Photonic Neuron with 10GMACsec processing line-rate, 2021 Optical Fiber Communications Conference and Exhibition (OFC), 283 2021, pp. 1–3.
Passalis, N. et al. Training noise-resilient recurrent photonic networks for financial time series analysis. 28th European Signal Processing Conference (EUSIPCO), 2021, pp. 1556–1560 (2021).
Passalis, N., Mourgias-Alexandris, G., Tsakyridis, A., Pleros, N. & Tefas, A. Training Deep Photonic Convolutional Neural Networks With Sinusoidal Activations. IEEE Transactions on Emerging Topics in Computational Intelligence 1–10 (2019).
M. Moralis-Pegios et al., “Neuromorphic Silicon Photonics and Hardware-Aware Deep Learning for High-Speed Inference,” in Journal of Lightwave Technology, vol. 40, pp. 3243–3254, 15 May15, (2022).
Mourgias-Alexandris, G. et al. A photonic recurrent neuron for time-series classification. J. Light. Technol. 39, 1340–1347 (2021).
Acknowledgements
The authors would like to thank Dr. Francesco Zanetto and the Politecnico di Milano for the wirebonding of the SiPho chip. The work was in part funded by the EU-project PlasmoniAC (871391) and by Hellenic Foundation for Research and Innovation (H.F.R.I.) under the “First Call for H.F.R.I. Research Projects to support Faculty members and Researchers and the procurement of high cost research equipment grant” (Project number 4233, DeepLight).
Author information
Authors and Affiliations
Contributions
G.M.A., M.M.P., A. Tsakyridis, S.S., G.D., A. Totovic and N. Pleros conceived the experiment. G.M.A., M.M.P., A. Tsakyridis and S.S. designed the Si-Pho chip, deployed the experimental setup, performed the experiment and processed the experimental results. T.R. and F.G. fabricated the Si-Pho chip. N. Passalis, MK and A. Tefas designed and performed the training. All authors discussed the results and wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Mourgias-Alexandris, G., Moralis-Pegios, M., Tsakyridis, A. et al. Noise-resilient and high-speed deep learning with coherent silicon photonics. Nat Commun 13, 5572 (2022). https://doi.org/10.1038/s41467-022-33259-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-022-33259-z
This article is cited by
-
High-efficiency reinforcement learning with hybrid architecture photonic integrated circuit
Nature Communications (2024)
-
Partial coherence enhances parallelized photonic computing
Nature (2024)
-
Integrated photonic neuromorphic computing: opportunities and challenges
Nature Reviews Electrical Engineering (2024)
-
Multimodal deep learning using on-chip diffractive optics with in situ training capability
Nature Communications (2024)
-
Analog spatiotemporal feature extraction for cognitive radio-frequency sensing with integrated photonics
Light: Science & Applications (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.