Abstract
Deep groundwater is an important source of drinking water, and can be preferable to shallower groundwaters where they are polluted by surface-borne contaminants. Surface-borne contaminants are disproportionately common in ‘modern’ groundwaters that are made up of precipitation that fell since the ~1950s. Some local-scale studies have suggested that groundwater pumping can draw modern groundwater downward and potentially pollute deep aquifers, but the prevalence of such pumping-induced downwelling at continental scale is not known. Here we analyse thousands of US groundwater tritium measurements to show that modern groundwater tends to reach deeper depths in heavily pumped aquifer systems. These findings imply that groundwater pumping can draw mobile surface-borne pollutants to deeper depths than they would reach in the absence of pumping. We conclude that intensive groundwater pumping can draw recently recharged groundwater deeper into aquifer systems, potentially endangering deep groundwater quality.
Similar content being viewed by others
Introduction
Groundwater resources supply drinking water to billions of people1,2. However, groundwater supplies are vulnerable to pollution from surface-borne contaminants, which can accompany precipitation as it infiltrates the land surface and percolates down to the water table3. Surface-borne contaminants are disproportionately common in groundwater that is made up of relatively recent precipitation4,5,6,7,8,9,10 known as ‘modern groundwater’—defined as groundwater comprised of precipitation that fell more recently than the year 1953. Because surface-borne contaminants are disproportionately common in modern groundwater, understanding the processes that control the depth that modern groundwater reaches is important for evaluating water quality risks in shallower versus deeper wells11,12.
Several local- and regional-scale studies have demonstrated that groundwater pumping can speed up downward flow rates and enable groundwater to reach deep depths while it is still young enough to be considered ‘modern’; such pumping-induced downwelling has the potential to also draw shallow pollutants into deep wells used by municipalities and rural communities13,14,15. However, the prevalence of this pumping-induced downwelling of modern groundwater remains poorly understood, as no continent-wide study has tested if modern groundwater reaches deeper depths in places with higher groundwater withdrawal rates.
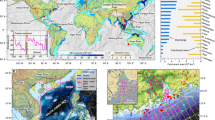
The objective of this study is to test for statistical relationships between spatial patterns of groundwater withdrawals and spatial patterns of the depth that modern groundwater reaches. To meet our objective, we analyse thousands of US groundwater tritium (3H) measurements (Fig. 1a) to calculate the depth below which modern groundwater is scarce in US aquifer systems (Methods subsection: ‘Groundwater tritium data’). Specifically, we calculated the fraction of each well water sample that is comprised of modern groundwater by comparing measured well water 3H activities to historical precipitation 3H time series16 (Methods subsection: ‘Modern groundwater calculations’). Elevated well water 3H activities indicate that modern groundwater is present in a well water sample17, because most of the precipitation that fell in the US after the year 1953 was artificially enriched in 3H by atmospheric thermonuclear testing16,18. After completing our 3H-based calculations of the proportion of individual well water samples comprised of modern groundwater, we grouped wells located within the same aquifer system (US aquifer geospatial data from ref. 19). These two-dimensional aquifer system areas are underlain by multiple geologic formations of varying hydrogeologic characteristics (for hydrogeologic cross sections for each study area, see Supplementary Figs. 99–240). Next, for each aquifer system, we calculated the depth below which modern groundwater is scarce by calculating the shallowest depth below which most samples (60%, 70% or 80%; Fig. 2) collected from deeper wells contain ‘minimal modern groundwater’ (‘minimal modern groundwater’ defined as well water samples containing <25% modern groundwater; Methods subsection: ‘Calculating the depth below which modern groundwaters are scarce’). We excluded n = 17 aquifer systems where a visual inspection of modern groundwater variations with depth suggests that our approach did not adequately capture the depth below which modern groundwater becomes scarce (Supplementary Note 1, Supplementary Figs. 1–91, and Supplementary Table 1). Last, we estimated groundwater withdrawal rates within the boundaries of each study aquifer system by downscaling county-scale groundwater withdrawal data provided by the US Geological Survey20, and tested for spatial correspondence between groundwater withdrawals and the depth below which modern groundwater becomes scarce via rank regression (Methods subsection: ‘Geospatial analyses of potential explanatory variables’; see Supplementary Note 2 for further details pertaining to our calculations of annual groundwater withdrawals).
a Light yellow shades represent lower tritium activities (below 1 tritium unit), orange shades represent mid-range tritium activities (1–10 tritium units) and red shades represent well waters with high tritium activities (exceeding 10 tritium units; 1 tritium unit is ~0.118 Bq/L). Light grey polygons underlying the yellow-red points are aquifer system boundaries published by GebreEgziabher et al. (ref. 19; data available via https://www.hydroshare.org/resource/d2260651b51044d0b5cb2d293d21af08/). b–o display hydrostratigraphy via cross-sections for n = 14 of the n = 74 aquifer systems that we studied. The presented cross-sections are based on figures and lithologic descriptions presented for the b Boise Valley and Homedale Area within the broader Snake River Plain in ref. 49, c Black Hills Uplift in ref. 50, d Williston Basin in ref. 51, e Eastern Dakota Aquifer System in ref. 52, f Michigan Basin in ref. 53, g Long Island in ref. 54, h Castle Hayne Aquifer System in ref. 55, i Lower Coastal Plain subarea of the broader Floridan Aquifer System in ref. 56, j Garber–Wellington Aquifer System in ref. 57, k Southern High Plains in ref. 58, l Mesilla Valley in ref. 59, m Santa Clara-Calleguas Basin in ref. 60, n Tulare Basin subarea of the broader California Central Valley Aquifer System in ref. 61, and the o Salt Lake Valley in ref. 62. Cross-sections for each of our n = 74 study aquifer systems are presented in Supplementary Figs. 99–240 (locations of each of the n = 74 hydrogeologic cross-sections we examined are displayed in Supplementary Note 8).
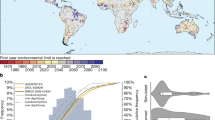
Yellow-blue shades represent the depth below which 60% (a), 70% (b) or 80% (c) of samples contain minimal modern groundwater (defined here as well water samples containing less than 25% modern groundwater). a The median depth below which >60% of samples contain minimal modern groundwater among n = 74 studied aquifer systems (with sufficient groundwater 3H data) is 38 m, and the lower–upper quartile range is 12–92 m. b The median depth below which more than 70% of samples contain minimal modern groundwater among n = 68 studied aquifer systems is 60 m, and the lower–upper quartile range is 25–113 m. c The median depth below which >80% of samples contain minimal modern groundwater among n = 61 studied aquifer systems is 75 m, and the lower-upper quartile range is 49–149 m. For a map with labels identifying aquifer systems, see Supplementary Fig. 98.
Results and discussion
Modern groundwater common at shallow depths
We identified n = 74 aquifer systems with sufficient well water 3H data to quantify the depth below which most (60%, 70% or 80%; Fig. 2a–c) groundwater samples contain minimal modern groundwater. Among our study aquifers, the median depths below which most groundwater samples contain minimal modern groundwater range from 38 to 75 m (the range of median values derives from our three different quantitative definitions of ‘most’: 60%, 70%, or 80%).
The depth below which modern groundwater is scarce is relatively shallow (less than 50 m) in portions of the Gulf Coast Regional Aquifer System (Houston-Galveston and Lafayette sub-areas) and in the Northern Great Plains Aquifer System (Williston Basin and Powder River Basin sub-areas; Fig. 2). By contrast, the depth below which modern groundwater is scarce is relatively deep (greater than 100 m) in Long Island, the Los Angeles Basin, California’s Central Valley (San Joaquin and Tulare sub-areas), and alluvial basins in Arizona (e.g., San Pedro Basin) and California (e.g., Coachella Valley; for individual plots for each aquifer system see Supplementary Figs. 1–91; for a map with labelled aquifer system titles, see Supplementary Fig. 98).
The observation that modern groundwater tends to be most common at shallow depths has important ramifications for well water quality, as surface-borne contaminants are disproportionately common in modern groundwaters4,5,6,7,8,9,10. Critically, from a water quality risk perspective, we note that most US drinking water wells are perforated at relatively shallow depths where modern groundwater is most common; 55% of domestic water wells are shallower than 50 m, and 84% are shallower than 100 m (ref. 21); however, we stress that most drinking water wells are domestic water supply wells rather than public water supply wells, and that the latter tend to be deeper than the former. Our finding that most domestic water wells are perforated at relatively shallow depths—where our 3H data suggest modern groundwaters are most common—implies that the water pumped by many domestic wells is dominated by modern groundwater, which is disproportionately likely to contain surface-borne contaminants.
Drilling domestic water wells to deeper depths may reduce the likelihood of well water contamination events in some areas11,12,22,23. However, drilling deeper wells to avoid shallow contaminated aquifers may be a stopgap21, if pumping from nearby municipal or irrigation wells draws modern groundwater downward and jeopardizes deep groundwater quality. Nevertheless, the prevalence of pumping-induced downwelling at continental scale is not known. Therefore, we calculated correlations between groundwater withdrawals and the depth below which modern groundwater is scarce (see next section entitled: ‘Deeper modern water where groundwater withdrawal rates are high’; see Methods subsection: ‘Geospatial analyses of potential explanatory variables’).
Deeper modern water where groundwater withdrawal rates are high
We find a significant (Spearman P value < 0.01) positive correlation between annual groundwater withdrawals and the depth below which modern groundwater is scarce (Fig. 3a). Spearman rank correlation coefficients (ρ) range from ρ = 0.39 to ρ = 0.42 (all statistically significant at P value < 0.01; the range of ρ values derives from three correlation coefficients, each based on the depth below which 60%, 70% or 80% of samples contain <25% modern groundwater; Supplementary Table 78). Our finding suggests that modern groundwater tends to reach deeper depths in aquifer systems that are heavily pumped.
a Relationship between estimated annual groundwater withdrawals21 and the depth below which modern groundwater is scarce. Each point represents one aquifer system. Annual groundwater withdrawals were normalized by aquifer area, such that the units (mm/year) can be interpreted as all withdrawn groundwater during the year 2015 expressed as saturated layer if it were spread evenly across the study area (for study area boundaries, see b). The Spearman rank correlation coefficient (ρ) of the data presented in panel a is ρ = 0.42 (Spearman P value <0.001). The y-axis values corresponding to each coloured point are the depth below which >70% of samples have minimal (<25%) modern groundwater; vertical error bars extend to the depth below which >60% of samples have minimal (<25%) modern groundwater (shallower depth—i.e., top of grey error bar as displayed in plot) and the depth below which >80% of samples have minimal (<25%) modern groundwater (deeper depth—i.e., bottom of grey error bar as displayed in plot; see legend in upper-left corner of plot). We only plot the n = 68 points representing the aquifer systems for which we had sufficient data to determine the depth below which >70% of samples have minimal (<25%) modern groundwater. Points are colour coded by the estimated depth to confined conditions (see legend in b). b Estimated depth to confined conditions in each of our study aquifer systems. Each polygon on the map represents one study area. Light blue colours represent shallower depths to confined conditions; darker blue shades represent deeper depths to confined conditions. Depths to confined conditions were estimated on the basis of up to three data sources: (i) US Geological Survey defined well conditions (i.e., wells defined as tapping unconfined versus confined conditions by the US Geological Survey), (ii) digitization and evaluation of hydrogeologic cross sections derived from local-scale reports, and (iii) quotes within local-scale reports pertaining to the prevalence of confined conditions (for details see Supplementary Note 3).
It is plausible that shallow low-permeability geologic formations could limit the depth below which modern groundwater is scarce and influence the effects of pumping on vertical variability in groundwater age24. We estimated the depth to confined conditions for each of our n = 74 study areas by analysing (i) vertical variations in the proportion of wells defined as tapping confined aquifers by the US Geological Survey, (ii) hydrogeologic cross sections derived from local-scale studies, and (iii) statements pertaining to confined conditions from local-scale studies (see Fig. 3b; for detailed approach for estimating depth to confined conditions for each of our n = 74 study aquifers see Supplementary Notes 3.1–3.74). We show that the depth below which modern groundwater is scarce tends to be deeper in aquifer systems characterized by thicker unconfined zones (i.e., aquifers with a relatively high (i.e., deep) depth to confined conditions; see Supplementary Note 4).
Therefore, the significant positive correlation between annual groundwater withdrawals and the depth below which modern groundwater is scarce (Fig. 3a) could arise spuriously if groundwater pumping tends to be higher in aquifer systems characterized by thick unconfined zones. To account for potential interrelationships between groundwater withdrawals and the depth to confined conditions, we completed multiple regression of the rank transforms of each explanatory variable25 (Supplementary Notes 4 and 5). The resulting partial regression coefficients (β)—that describe the statistical relationship between groundwater withdrawals and the depth below which modern groundwater is scarce—remain positive and significant (β values range 0.29 to 0.34; all significant at Spearman P value < 0.05; see Supplementary Table 79). This analysis suggests that our finding that modern groundwater tends to reach deeper depths in aquifer systems that are heavily pumped holds even after accounting for differences in the depth to confined conditions among our study aquifers.
Our pan-US statistical analyses are consistent with local-scale research in California’s Central Valley26,27, where groundwater pumping draws young and shallow groundwater deeper into the aquifer system; our results suggest that pumping-induced downwelling is not unique to California’s Central Valley and is likely occurring in other heavily pumped US aquifer systems. Though we find that modern groundwater tends to reach deeper depths in heavily pumped aquifer systems (Fig. 3a), we emphasize the moderate strength of the correlation and the high proportion of unexplained variance (see substantial scatter in points in Fig. 3a). We also emphasize that the groundwater withdrawal data that we analyse21 are highly uncertain; further, the county-scale at which these data are available limit their local relevance and complicate geospatial analyses (see Methods subsection entitled: ‘Limitations’). There is considerable room for improvement in US groundwater withdrawal data28. Should better groundwater withdrawal data become available, these data would enable a better assessment of the statistical relationship between groundwater withdrawals and the depths that modern groundwaters reach.
Potential explanations for deep modern groundwater
While our tritium data set cannot identify the specific mechanisms that transmit modern groundwater to deeper depths where groundwater withdrawal rates are high, there are a number of potential mechanisms that may help explain our main finding—that modern groundwater tends to reach deeper depths in aquifer systems that are heavily pumped (Fig. 4 and Supplementary Note 6).
Artificial groundwater recharge (left side of schematic) can increase the magnitude of downward-oriented vertical hydraulic gradients and potentially drive modern groundwater to deeper depths. Artificial recharge can derive from urban waters (e.g., Tucson Basin63), spreading basins associated with managed aquifer recharge projects (e.g., Upper Santa Ana Basin64), excess irrigation waters (e.g., San Joaquin Basin65), or leaky surface water conveyance infrastructure such as canals (e.g., Utah Lake Valley66). The construction of groundwater wells and their use via pumping (right side of schematic) may help modern waters enter deeper wells. For example, deep wells that have long perforated intervals may draw both shallow (disproportionately modern) and deep (disproportionately pre-modern) groundwater (e.g., Tulare Basin67). Further, pumping from wells can alter vertical hydraulic gradients, potentially drawing shallow modern groundwater to deeper depths (e.g., Salt Lake Valley68). The modern groundwater may move downward to deeper depths in the aquifer system via natural pore spaces (e.g., discontinuities in aquitards; e.g., Eastern Mississippi Embayment34) or via conduits created by constructed wells themselves (e.g., Northern High Plains69). For further discussion and schematics of modern groundwater distributions, see refs. 48, 70, 71. For a review of some of the studies that have posited one or more of these mechanisms as potential explanations for the distribution of modern groundwater, see Supplementary Note 6. For a more expansive version of this figure, see Supplementary Fig. 243.
First, pumping from deep aquifers can alter vertical hydraulic gradients and speed up downward flows of shallow groundwaters13,29,30,31,32; the existence of preferential flow pathways through permeable geologic structures (e.g., discontinuities in aquitards at faults or permeable intercalations33) may further enhance pumping-induced downward transport of modern groundwater34. Second, the magnitude of downward-oriented vertical hydraulic gradients—which drive modern groundwater to deep depths—may be increased by artificial groundwater recharge associated with land use and water management26 (e.g., infiltration of excess irrigation waters35,36, leakage from urban water infrastructure37 or canals38). Spreading basins and intentional flooding have been applied via ‘managed aquifer recharge’ projects for decades in several heavily pumped aquifer systems in California and Arizona39,40, potentially increasing downward groundwater flow rates in these areas. Recharge induced by such processes can sustain high-magnitude and downward-oriented vertical hydraulic gradients and may drive modern groundwaters to deeper depths. Third, modern groundwaters may be present in some deep aquifers because they were intentionally injected via aquifer storage and recovery projects, but these projects are not common in many of our study areas41; this mechanism is speculative but plausible. Fourth, modern groundwater may be transmitted relatively rapidly to deep depths in heavily pumped aquifer systems that also host poorly sealed wells, which can create conduits that enable rapid movement of shallow modern groundwater to deep aquifers33,42,43,44.
To better understand the potential for confining units to limit the depth that modern groundwater reaches, we examined the prevalence of modern groundwater in n = 1831 groundwater samples where the well has been defined by the US Geological Survey as tapping a confined aquifer (well metadata field aqfr_type_cd specifies ‘Confined single aquifer’ or ‘Confined multiple aquifers’). We find that about one-third of groundwater samples collected from a well that is perforated in a confined aquifer (n = 592) contain more than 5% modern water, highlighting that modern water can enter wells screened in confined aquifers (Supplementary Note 7 and Supplementary Fig. 244).
Differences among our study aquifers in pumping well depths, well integrity, land use activities and managed aquifer recharge practices likely contribute to the observed variability in the depth below which modern groundwater becomes scarce in our study areas. Identifying locally relevant mechanisms that may rapidly transmit shallow groundwater to deep depths is important to create strategies to protect deep groundwater quality.
Pumping-induced downwelling may impact groundwater quality
Although our tritium data cannot identify specific transport mechanisms for each of the dozens of aquifer systems we studied, our analyses demonstrate a moderately strong statistical relationship that suggests pumping may lead modern groundwaters to reach deeper depths than they would flow to naturally (Fig. 3a).
Where modern groundwater is contaminated, pumping-induced downwelling of these groundwaters can threaten deep groundwater quality; however, we stress that many contaminants flow at considerably slower rates than the groundwater itself due to, for example, retardation via adsorption. The downwelling of modern groundwater may also have indirect impacts on groundwater quality. For example, in the Red River Delta (Vietnam), intensive pumping of deep aquifers has likely increased aqueous arsenic concentrations both directly via the downwelling of shallow arsenic-rich groundwaters to deeper depths30, and also indirectly as these downward-flowing groundwaters contribute arsenic-mobilizing solutes45. Because deep aquifers tend to require millennia to flush, contamination of deep groundwaters can be especially challenging to remedy, and some groundwater remediation technologies are not well suited for deep groundwater.
Deep groundwater is a globally important water supply, and its value is expected to grow where shallower groundwater stores and qualities are declining and deteriorating. We demonstrate that modern groundwater tends to reach deeper depths in heavily pumped aquifer systems, signalling that pumping can rearrange groundwater flowpaths and impact deep groundwater quality.
Methods
Groundwater tritium data
We downloaded US well water tritium measurements from the water quality portal (https://www.waterqualitydata.us/portal accessed April 20, 2021). We excluded tritium measurements that were below analytical detection limits if the reported detection limit exceeded 0.8 tritium units (where 1 tritium unit equals 0.118 Bq/L). We excluded all measurements of media that were not categorized as ‘Groundwater’ (field code: ‘ActivityMediaSubdivisionName’). We deleted one record with a code reading ‘Systematic Contamination’. We converted negative values to zeros. We excluded one well water measurement with an unlikely ‘ActivityStartDate’ value of September 28, 1900. If more than one tritium measurement was available for a single well, we analysed only the most recent record (i.e., the measurement with the most recent date) and excluded the other measurements, to ensure each well was only counted once in our analysis.
We excluded all records that did not report a numeric well depth value (i.e., both of the following fields were blank: ‘WellDepthMeasure/MeasureValue’ and ‘WellHoleDepthMeasure/MeasureValue’) or recorded a value of zero for the well depth. If a non-zero ‘WellDepthMeasure/MeasureValue’ was available, we prioritized analysis of this well depth value; otherwise, we included the value of ‘WellHoleDepthMeasure/MeasureValue’ as the well depth. We emphasize that both values (i.e., ‘WellDepthMeasure/MeasureValue’ and ‘WellHoleDepthMeasure/MeasureValue’) are likely to be approximations because of the inherent uncertainties associated with well construction. We also highlight that our data set does not provide information about perforated intervals for all of our wells, requiring us to analyse total well depths rather than screen depth intervals and introducing uncertainty into our analyses (see (ii) in the Limitations section below).
Modern groundwater calculations
We downloaded geospatial time series of estimated precipitation tritium for the contiguous US (from https://www.sciencebase.gov/catalog/item/5af49307e4b0da30c1b44e10; see ref. 16). For each groundwater well for which we have tritium data, we identified the nearest precipitation tritium time series grid (in most cases, the well location lies within a precipitation tritium time series grid cell). Next, we decay-corrected all values in the precipitation tritium time series to determine the range of possible ‘net present’ tritium activities relevant to a given groundwater tritium measurement (following method by ref. 46). To account for the strong likelihood that at least some hydrodynamic dispersion takes place as groundwater flows within aquifer systems, we smoothed these decay-corrected precipitation tritium time series by a five-year running average (following methods by ref. 47). We then calculated the maximum and minimum decay-corrected post-1953 precipitation tritium values from these running averages; hereafter these values are used as high and low values for the term 3Hpost-1953). We then straightforwardly calculated the fraction of each groundwater sample comprised of ‘modern groundwater’ derived from precipitation that fell since the year 1953 (Fpost-1953) following ref. 46:
3Hsample represents the measured tritium activity in the well water. 3Hpost-1953 and 3Hpre-1953 represent the estimated local precipitation tritium activities16 after correcting for radioactive decay to the time of sampling. 3Hpost-1953 represents the decay-corrected precipitation tritium for years between 1953 and the date the sample was analysed (applying the aforementioned five-year running average). 3Hpre-1953 represents the decay-corrected tritium activity for precipitation that fell prior to 1953 (assumed to be zero, as most of groundwater 3H samples in our data set were analysed after multiple tritium-half-lives have elapsed since 1953, and pre-1953 precipitation tritium activities in the US were likely less than 10 tritium units48).
Calculating the depth below which modern groundwaters are scarce
We then created a binary categorization for each sample, defining each sample as either (i) containing minimal modern groundwater, defined as samples with a maximum Fpost-1953 value of <0.25 (i.e., <25% of the sample is comprised of modern water), or (ii) samples with a maximum Fpost-1953 value exceeding 0.25. The maximum Fpost-1953 values were determined for each sample using the minimum 3Hpost-1953 values in Eq. 1 (i.e., entering the minimum 3Hpost-1953 value into Eq. 1 yields the maximum Fpost-1953 value for a given groundwater sample).
First, we grouped all groundwater tritium samples by the aquifer system that the well lies within. To avoid analysing the most data-sparse aquifers, we only analysed aquifer systems with (a) at least n = 10 tritium measurements, and (b) at least a 100 m vertical offset between the total depths of the shallowest well and the deepest well for which we have groundwater tritium measurements.
Second, for each well within each study aquifer, we calculated the proportion of all samples that derive from wells that are deeper than a given depth that contain minimal modern water (i.e., categorization (i) above). We did not calculate these proportions if fewer than five wells were deeper than the depth of interest (i.e., we require a minimum of five data points to calculate a value of ‘the proportion of wells with deeper depths that contain minimal (i.e., maximum Fpost-1953 is <25%) modern water’). For each aquifer system, we determined the depth at which 60, 70, or 80% of samples derived from wells deeper than this depth contain <25% modern water (these depths presented in Fig. 2).
Third, to further scrutinize our results, we visually inspected individual plots of modern groundwater prevalence with depth for each of our study aquifers (Supplementary Figs. 1–91). We identified n = 17 aquifer systems where our approach (i.e., calculating the depth below which 60, 70 or 80% of samples contain <25% modern groundwater) provided an imperfect estimate of the depth below which modern groundwater becomes scarce due (a) a lack of groundwater tritium data at depth, or (b) a lack of a consistent decline in modern groundwater fractions with depth (Supplementary Table 1 and Supplementary Figs. 4, 6, 9, 12, 16, 19, 33, 37, 44, 52, 54, 59, 71, 79, 82, 87, 88). We excluded these n = 17 aquifer systems from our analyses.
Geospatial analyses of potential explanatory variables
For each study aquifer system with sufficient groundwater tritium data for analyses, we compared our estimates of ‘the depth below which modern groundwater is scarce’ (i.e., values in Fig. 2) to two potential explanatory variables: (a) annual groundwater withdrawals (from: https://www.sciencebase.gov/catalog/item/get/5af3311be4b0da30c1b245d8), and (b) the depth to confined conditions.
-
(a)
To estimate groundwater withdrawals within each of our study aquifers (i.e., potential explanatory variable (a)), we downscaled county-scale groundwater withdrawal data by analysing irrigated area and population density data within individual county areas, thereby providing greater statistical weight to portions of counties where groundwater withdrawal rates are more likely to be relatively high. For further details see Supplementary Note 2.
-
(b)
To estimate the depth to confined conditions within each of our study aquifers (i.e., potential explanatory variable (b)), we analysed (i) vertical variations in the proportion of wells defined as tapping confined aquifers by the USGS (depth to confined conditions estimated as the shallowest depth where both (a) the fraction of wells that tap confined conditions exceeds 80%, and (b) more than 80% of wells at deeper depths are classified as tapping confined conditions), (ii) hydrogeologic cross sections derived from local-scale studies, and (iii) statements pertaining to confined conditions from local-scale studies. For further details see Supplementary Note 3.
We then calculated rank correlation coefficients describing variability in our calculated values for the depth below which modern groundwater is scarce and these two explanatory variables (see Supplementary Note 4). Our calculations include independent correlations for each potential explanatory variable (Supplementary Table 78), and also a multiple regression of the rank transforms to account for potential interrelationships among the explanatory variables themselves25 (Supplementary Table 79).
Limitations
Our analyses have a number of limitations, five of which are described here:
-
(i)
First, the groundwater withdrawal data20 we analysed are highly uncertain and available only at county-scale. The substantial uncertainties in groundwater withdrawal data arise in part due to the lack of widespread groundwater withdrawal metering data, which limits our confidence in these withdrawal estimates (i.e., x-axis values in Fig. 3a). Further, the county-scale at which these groundwater withdrawal data are reported20 complicates our interpretation of groundwater withdrawal data and required us to downscale groundwater withdrawal data to finer spatial resolution, introducing uncertainty in the process. We emphasize that the groundwater withdrawal estimates reported in Fig. 3a and our correlation coefficients are uncertain, and that the correlation coefficients we present would differ if better groundwater withdrawal data were to become available.
-
(ii)
Second, our evaluation of the depths below which modern groundwater is scarce is limited by the lack of perforated interval data for some of the wells where groundwater tritium measurements have been made. Our calculations are thus necessarily limited to total well depth data, which are, if anything, an overestimate of the depth of the groundwater sampled by the well. Wells that are deeper than the total depths that modern groundwater penetrates may pump modern groundwater because some of these wells will be perforated at shallower depths where modern groundwater is more abundant, potentially leading to overestimations of the depth below which modern groundwaters penetrate in some wells with extensive perforated intervals.
-
(iii)
Third, we cannot evaluate the depths at which groundwater withdrawals take place, as the data we analyse20 are two-dimensional data products that do not contain information about the depths at which pumping rates are higher versus lower. However, all of our study aquifers have at least some recorded wells21 with depths that exceed the depth below which modern groundwater is scarce, implying a potential for groundwater withdrawals to play a role in determining the depth at which modern groundwater becomes scarce.
-
(iv)
Fourth, we analyse groundwater withdrawals for the year 2015 but acknowledge that groundwater pumping that took place prior to the year 2015 has also likely contributed to the depth distribution of modern groundwater.
-
(v)
Fifth, our estimate of a single value for the depth to confined conditions for a given aquifer system oversimplifies real world heterogeneous conditions. The true depth to confined conditions likely varies, possibly substantially, within each of the n = 74 aquifer systems that we study. We stress that the depths to confined conditions presented in Fig. 3b and Supplementary Note 3 are approximations.
Data availability
Aquifer system boundaries from ref. 19 are available to download via CUAHSI HydroShare: https://www.hydroshare.org/resource/d2260651b51044d0b5cb2d293d21af08/. Groundwater withdrawal estimates (county-scale) are available via https://pubs.er.usgs.gov/publication/cir1441. Well water tritium data are available via https://www.waterqualitydata.us/portal.
Code availability
The analyses presented here do not depend on specific code. Our approach can be reproduced following the procedures described in the ‘Methods’.
References
Shah, T. Groundwater and human development: challenges and opportunities in livelihoods and environment. Water Sci. Technol. 51, 27–37 (2005).
Margat, J. & van der Gun, J. Groundwater Around the World: A Geographic Synopsis (CRC Press, 2013).
Foster, S. S. D. & Chilton, P. J. Groundwater: the processes and global significance of aquifer degradation. Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci. 358, 1957–1972 (2003).
Baran, N., Mouvet, C. & Négrel, P. Hydrodynamic and geochemical constraints on pesticide concentrations in the groundwater of an agricultural catchment (Brévilles, France). Environ. Pollut. 148, 729–738 (2007).
Brown, K. B., McIntosh, J. C., Rademacher, L. K. & Lohse, K. A. Impacts of agricultural irrigation recharge on groundwater quality in a basalt aquifer system (Washington, USA): a multi-tracer approach. Hydrogeol. J. 19, 1039–1051 (2011).
Qin, D. et al. Assessing impact of irrigation water on groundwater recharge and quality in arid environment using CFCs, tritium and stable isotopes, in the Zhangye Basin, Northwest China. J. Hydrol. 405, 194–208 (2011).
Pang, Z. et al. Impacts of human activities on the occurrence of groundwater nitrate in an alluvial plain: a multiple isotopic tracers approach. J. Earth Sci. 24, 111–124 (2013).
Han, D., Cao, G., McCallum, J. & Song, X. Residence times of groundwater and nitrate transport in coastal aquifer systems: Daweijia area, northeastern China. Sci. Total Environ. 538, 539–554 (2015).
Visser, A. et al. Geostatistical analysis of tritium, groundwater age and other noble gas derived parameters in California. Water Res. 91, 314–330 (2016).
El Mountassir, O., Bahir, M., Ouazar, D., Chehbouni, A. & Carreira, P.M. Temporal and spatial assessment of groundwater contamination with nitrate using nitrate pollution index (NPI), groundwater pollution index (GPI), and GIS (case study: Essaouira basin, Morocco). Environ. Sci. Pollut. Res. 29, 17132–17149 (2021).
Zhang, X., Xu, Z., Sun, X., Dong, W. & Ballantine, D. Nitrate in shallow groundwater in typical agricultural and forest ecosystems in China, 2004–2010. J. Environ. Sci. 25, 1007–1014 (2013).
Egbueri, J. C. & Mgbenu, C. N. Chemometric analysis for pollution source identification and human health risk assessment of water resources in Ojoto Province, southeast Nigeria. Appl. Water Sci. 10, 1–18 (2020).
Kagabu, M., Shimada, J., Delinom, R., Nakamura, T. & Taniguchi, M. Groundwater age rejuvenation caused by excessive urban pumping in Jakarta area, Indonesia. Hydrol. Process. 27, 2591–2604 (2013).
Han, D. M., Song, X. F., Currell, M. J., Yang, J. L. & Xiao, G. Q. Chemical and isotopic constraints on evolution of groundwater salinization in the coastal plain aquifer of Laizhou Bay, China. J. Hydrol. 508, 12–27 (2014).
Taufiq, A. et al. Impact of excessive groundwater pumping on rejuvenation processes in the Bandung basin (Indonesia) as determined by hydrogeochemistry and modeling. Hydrogeol. J. 26, 1263–1279 (2018).
Michel, R. L., Jurgens, B. C. & Young, M. B. Tritium Deposition in Precipitation in the United States, 1953–2012. US Geological Survey Scientific Investigations Report 2018-5086 (USGS, 2018).
Gleeson, T., Befus, K. M., Jasechko, S., Luijendijk, E. & Cardenas, M. B. The global volume and distribution of modern groundwater. Nat. Geosci. 9, 161–167 (2016).
Doney, S. C., Glover, D. M. & Jenkins, W. J. A model function of the global bomb tritium distribution in precipitation, 1960–1986. J. Geophys. Res. Oceans 97, 5481–5492 (1992).
GebreEgziabher, M., Jasechko, S. & Perrone, D. Widespread and increased drilling of wells into fossil aquifers in the USA. Nat. Commun. 13, 2129 (2022).
Dieter, C. A. et al. Estimated Use of Water in the United states in 2015. US Geological Survey Circular 1441 (USGS, 2018).
Perrone, D. & Jasechko, S. Deeper well drilling an unsustainable stopgap to groundwater depletion. Nat. Sustainability 2, 773–782 (2019).
Clark, B. R., Hart, R. M. & Gurdak, J. J. Groundwater Availability of the Mississippi Embayment. US Geological Survey Professional Paper 1785 (USGS, 2011).
Wirmvem, M. J. et al. Effect of diffuse recharge and wastewater on groundwater contamination in Douala, Cameroon. Environ. Earth Sci. 76, 1–23 (2017).
Zinn, B. A. & Konikow, L. F. Potential effects of regional pumpage on groundwater age distribution. Water Resour. Res. 43, W06418 (2007).
Iman, R. L. & Conover, W. J. The use of the rank transform in regression. Technometrics 21, 499–509 (1979).
Jagucki, M. L., Jurgens, B. C., Burow, K. R. & Eberts, S. M. Assessing the vulnerability of public-supply wells to contamination—Central Valley aquifer system near Modesto, California. US Geological Survey Fact Sheet 2009–3036 (USGS, 2009).
Levy, Z. F. et al. Critical aquifer overdraft accelerates degradation of groundwater quality in California’s Central Valley during drought. Geophys. Res. Lett. 48, e2021GL094398 (2021).
Perrone, D., Hornberger, G., van Vliet, O. & van der Velde, M. A review of the United States’ past and projected water use. JAWRA J. Am. Water Resour. Assoc. 51, 1183–1191 (2015).
Lapworth, D. J. et al. Deep urban groundwater vulnerability in India revealed through the use of emerging organic contaminants and residence time tracers. Environ. Pollut. 240, 938–949 (2018).
Winkel, L. H. et al. Arsenic pollution of groundwater in Vietnam exacerbated by deep aquifer exploitation for more than a century. Proc. Natl Acad. Sci. USA 108, 1246–1251 (2011).
Khan, M. R. et al. Megacity pumping and preferential flow threaten groundwater quality. Nat. Commun. 7, 12833 (2016).
Cognac, K. E. & Ronayne, M. J. Changes to inter-aquifer exchange resulting from long-term pumping: implications for bedrock groundwater recharge. Hydrogeol. J. 28, 1359–1370 (2020).
Santi, P. M., McCray, J. E. & Martens, J. L. Investigating cross-contamination of aquifers. Hydrogeol. J. 14, 51–68 (2006).
Kingsbury, J. A., Barlow, J. R., Jurgens, B. C., McMahon, P. B. & Carmichael, J. K. Fraction of young water as an indicator of aquifer vulnerability along two regional flow paths in the Mississippi embayment aquifer system, southeastern USA. Hydrogeol. J. 25, 1661–1678 (2017).
Scanlon, B. R., Reedy, R. C., Stonestrom, D. A., Prudic, D. E. & Dennehy, K. F. Impact of land use and land cover change on groundwater recharge and quality in the southwestern US. Glob. Change Biol. 11, 1577–1593 (2005).
Ochoa, C. G., Fernald, A. G., Guldan, S. J., Tidwell, V. C. & Shukla, M. K. Shallow aquifer recharge from irrigation in a semiarid agricultural valley in New Mexico. J. Hydrologic Eng. 18, 1219–1230 (2013).
Wakode, H. B., Baier, K., Jha, R. & Azzam, R. Impact of urbanization on groundwater recharge and urban water balance for the city of Hyderabad, India. Int. Soil Water Conserv. Res. 6, 51–62 (2018).
Meredith, E. & Blais, N. Quantifying irrigation recharge sources using groundwater modeling. Agric. Water Manag. 214, 9–16 (2019).
Dillon, P. et al. Sixty years of global progress in managed aquifer recharge. Hydrogeol. J. 27, 1–30 (2019).
Scanlon, B. R., Reedy, R. C., Faunt, C. C., Pool, D. & Uhlman, K. Enhancing drought resilience with conjunctive use and managed aquifer recharge in California and Arizona. Environ. Res. Lett. 11, 035013 (2016).
Stefan, C. & Ansems, N. Web-based global inventory of managed aquifer recharge applications. Sustain. Water Resour. Manag. 4, 153–162 (2018).
Koh, E. H. et al. Hydrogeochemistry and isotopic tracing of nitrate contamination of two aquifer systems on Jeju Island, Korea. J. Environ. Qual. 41, 1835–1845 (2012).
Han, D., Currell, M. J. & Cao, G. Deep challenges for China’s war on water pollution. Environ. Pollut. 218, 1222–1233 (2016).
Shuler, C. K. et al. Isotopes, microbes, and turbidity: a multi‐tracer approach to understanding recharge dynamics and groundwater contamination in a Basaltic Island Aquifer. Groundw. Monit. Remediation 39, 20–35 (2019).
Berg, M. et al. Hydrological and sedimentary controls leading to arsenic contamination of groundwater in the Hanoi area, Vietnam: the impact of iron-arsenic ratios, peat, river bank deposits, and excessive groundwater abstraction. Chem. Geol. 249, 91–112 (2008).
Jasechko, S. Partitioning young and old groundwater with geochemical tracers. Chem. Geol. 427, 35–42 (2016).
Jasechko, S. et al. Global aquifers dominated by fossil groundwaters but wells vulnerable to modern contamination. Nat. Geosci. 10, 425–429 (2017).
Jasechko, S. Global isotope hydrogeology-review. Rev. Geophys. 57, 835–965 (2019).
Lindholm, G. F. Summary of the Snake River Plain Regional Aquifer-System Analysis in Idaho and Eastern Oregon. US Geological Survey Professional Paper 1408-A (USGS, 1996).
Driscoll, D. G., Carter, J. M., Williamson, J. E. & Putnam, L. D. Hydrology of the Black Hills area, South Dakota. US Geological Survey Water-Resources Investigations Report 2002-4094 (USGS, 2002).
Long, A. J., Thamke, J. N., Davis, K. W. & Bartos, T. T. Groundwater Availability of the Williston Basin, United States and Canada. US Geological Survey Professional Paper 1841 (USGS, 2018).
Prior, J. C., Boekhoff, J. L., Howes, M. R., Libra, R. D. & VanDorpe, P. E. Iowa’s Groundwater Basics. Iowa Department of Natural Resources Report (Iowa Department of Natural Resources, 2003).
Westjohn, D. B. & Weaver, T. L. Hydrogeologic Framework of the Michigan Basin Regional Aquifer System. US Geological Survey Professional Paper 1418 (USGS, 1998).
Smolensky, D. A., Buxton, H. T. & Shernoff, P. K. Hydrologic Framework of Long Island, New York. US Geological Survey Hydrologic Atlas 709 (USGS, 1990).
Winner Jr, M. D. & Coble, R. W. Hydrogeologic Framework of the North Carolina Coastal Plain aquifer system. US Geological Survey Report 87-690 (USGS, 1989).
Aucott, W. R. Hydrology of the Southeastern Coastal Plain Aquifer System in South Carolina and Parts of Georgia and North Carolina. US Geological Survey Professional Paper 1410-E (USGS, 1996).
Mashburn, S. L., Ryter, D. W., Neel, C. R., Smith, S. J. & Correll, J. S. Hydrogeology and Simulation of Ground-Water Flow in the Central Oklahoma (Garber-Wellington) Aquifer, Oklahoma, 1987 to 2009, and Simulation of Available Water in Storage, 2010–2059. US Geological Survey Scientific Investigations Report 2013–5219 (USGS, 2014).
Blandford, T. N. et al. Groundwater Availability Model of the Edwards-Trinity (High Plains) Aquifer in Texas and New Mexico (Texas Water Development Board, 2008).
Robertson, A. J. et al. Mesilla/Conejos-Médanos Basin: US-Mexico transboundary. Water Resour. Water 14, 134 (2022).
Hanson, R. T., Martin, P. & Koczot, K. M. Simulation of Ground-Water/Surface-Water Flow in the Santa Clara-Calleguas Ground-Water Basin, Ventura County, California. Water-Resources Investigations Report 2002-4136 (Water-Resources Investigations, 2002).
Page, R. W. & Balding, G. O. Geology and Quality of Water in the Modesto-Merced area, San Joaquin Valley, California, with a Brief Section on Hydrology. US Geological Survey Water-Resources Investigations Report 73-6 (USGS, 1973).
Manning, A. H. & Solomon, D. K. An integrated environmental tracer approach to characterizing groundwater circulation in a mountain block. Water Resour. Res. 41, W12412 (2005).
Carlson, M. A., Lohse, K. A., McIntosh, J. C. & McLain, J. E. Impacts of urbanization on groundwater quality and recharge in a semi-arid alluvial basin. J. Hydrol. 409, 196–211 (2011).
Hamlin, S. N., Belitz, K. & Johnson, T. Occurrence and Distribution of Volatile Organic Compounds and Pesticides in Ground Water in Relation to Hydrogeologic Characteristics and Land Use in the Santa Ana Basin, Southern California. US Geological Survey Scientific Investigations Report 2005-5032 (USGS, 2005).
Bennett, G. L., Fram, M. S., Belitz, K. & Jurgens, B. C. Status and Understanding of Groundwater Quality in the Northern San Joaquin Basin, 2005: California GAMA Priority Basin Project. US Geological Survey Scientific Investigations Report 2010–5175 (USGS, 2010).
Cederberg, J. R., Gardner, P. M. & Thiros, S. A. Hydrology of Northern Utah Valley, Utah County, Utah, 1975–2005. US Geological Survey Scientific Investigations Report 2008–5197 (USGS, 2008).
Hansen, J. A., Jurgens, B. C. & Fram, M. S. Quantifying anthropogenic contributions to century-scale groundwater salinity changes, San Joaquin Valley, California, USA. Sci. Total Environ. 642, 125–136 (2018).
Thiros, S. A. & Manning, A. H. Quality and Sources of Ground Water used for Public Supply in Salt Lake Valley, Salt Lake County, Utah, 2001. US Geological Survey Water-Resources Investigations Report 2003-4325 (2003).
Landon, M. K. et al. Depth-dependent sampling to identify short-circuit pathways to public-supply wells in multiple aquifer settings in the United States. Hydrogeol. J. 18, 577–593 (2010).
Ferguson, G., Cuthbert, M. O., Befus, K., Gleeson, T. & McIntosh, J. C. Rethinking groundwater age. Nat. Geosci. 13, 592–594 (2020).
Jurgens, B. C. et al. Over a third of groundwater in USA public-supply aquifers is Anthropocene-age and susceptible to surface contamination. Commun. Earth Environ. 3, 1–9 (2022).
Acknowledgements
This material is based upon work supported by the National Science Foundation under Grant No. EAR-2048227 (to S.J.). This research was supported by funding from the Zegar Family Foundation (to S.J.). This material is based upon work supported by the U.S. Geological Survey (USGS) through the California Institute for Water Resources (CIWR) under Grant/Cooperative Agreement No. G21AP10611-00 (to S.J.). The views and conclusions contained in this document are those of the authors and should not be interpreted as representing the opinions or policies of USGS/CIWR. Mention of trade names or commercial products does not constitute their endorsement by USGS/CIWR. The authors acknowledge the Jack and Laura Dangermond Preserve (https://doi.org/10.25497/D7159W), the Point Conception Institute, and the Nature Conservancy for their support of this research.
Author information
Authors and Affiliations
Contributions
M.T. and S.J. contributed equally to the manuscript. M.T. and S.J. co-generated hypotheses, co-developed methods, and co-wrote the manuscript. M.T. and S.J. calculated the depth below which modern groundwater is scarce. M.G. digitized hydrogeologic cross sections and completed the literature review to categorize geologic formations (e.g., as aquifers or as aquitards). J.Y.V-P. georeferenced maps from reviewed literature to approximate the location of each hydrogeologic cross section. S.J. estimated the depth to confined conditions for each study area.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks the anonymous reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Thaw, M., GebreEgziabher, M., Villafañe-Pagán, J.Y. et al. Modern groundwater reaches deeper depths in heavily pumped aquifer systems. Nat Commun 13, 5263 (2022). https://doi.org/10.1038/s41467-022-32954-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-022-32954-1
This article is cited by
-
Passive ecosystem services, juxtaposed with engineered processes, can democratize wastewater treatment
Nature Water (2023)
-
Variation in hydraulic structure with respect to depth and age of a large igneous province in Ethiopia
Hydrogeology Journal (2023)
-
Hydrochemical Background Levels and Threshold Values of Phreatic Groundwater in the Greater Xi’an Region, China: Spatiotemporal Distribution, Influencing Factors and Implication to Water Quality Management
Exposure and Health (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.