Abstract
The Landé or g-factors of charge carriers are decisive for the spin-dependent phenomena in solids and provide also information about the underlying electronic band structure. We present a comprehensive set of experimental data for values and anisotropies of the electron and hole Landé factors in hybrid organic-inorganic (MAPbI3, MAPb(Br0.5Cl0.5)3, MAPb(Br0.05Cl0.95)3, FAPbBr3, FA0.9Cs0.1PbI2.8Br0.2, MA=methylammonium and FA=formamidinium) and all-inorganic (CsPbBr3) lead halide perovskites, determined by pump-probe Kerr rotation and spin-flip Raman scattering in magnetic fields up to 10 T at cryogenic temperatures. Further, we use first-principles density functional theory (DFT) calculations in combination with tight-binding and k ⋅ p approaches to calculate microscopically the Landé factors. The results demonstrate their universal dependence on the band gap energy across the different perovskite material classes, which can be summarized in a universal semi-phenomenological expression, in good agreement with experiment.
Similar content being viewed by others
Introduction
Lead halide perovskite materials have attracted huge attention in recent years due to their exceptional electronic and optical characteristics, which make them highly promising for various applications in photovoltaics1,2, optoelectronics3,4,5,6,7,8, X-ray detectors9,10, etc. Their chemical formula APbX3 where the cation A = cesium (Cs), methylammonium (MA), formamidinium (FA) and the anion X = Cl, Br, I, offers a huge flexibility in composition making the band gap tunable from the infrared up to ultraviolet spectral range. Interestingly, the perovskite band structure is inverted compared to common III-V and II-VI semiconductors. As a result, the strong spin-orbit interaction influences mostly the conduction band rather than the valence band. Also strong Rashba spin splittings have been predicted both for the valence and conduction bands11.
Detailed studies of the band structure require a concerted effort of suitable experimental and theoretical approaches. The low charge carrier mobility12 hampers methods like electrical transport, also in magnetic field, and cyclotron resonance, which are usually applied to study the band structure of solids, while ion diffusion obstructs the application of capacity-based methods. Angle resolved photoemission spectroscopy13,14,15 provides promising results but, so far, with insufficient accuracy. Optics in strong magnetic fields gives access to carrier effective masses and exciton features16,17, where the parameter values can be, however, influenced by the field through band mixing.
Spin physics provides high precision tools for addressing the electronic states in the vicinity of the band gap. Namely, the Landé or g-factors of electrons and holes are inherently linked via their values and anisotropies to the band parameters, which also determine the charge carrier effective masses18,19. On the other hand, the Landé factors are the key parameters for the coupling of spins to a magnetic field and thus govern related basic phenomena and spintronics applications, which belong to a largely uncharted area for perovskites. The first concise reports show great promise demonstrating optical orientation5,20,21,22,23 and optical alignment21, polarized emission in magnetic field24,25,26, coherent spin dynamics27,28,29,30, and nuclear magnetic resonance31,32,33.
Here, we study the Landé factors of electrons and holes for representative crystals out of the class of lead halide perovskites: MAPbI3, MAPb(Br0.5Cl0.5)3, MAPb(Br0.05Cl0.95)3, FA0.9Cs0.1PbI2.8Br0.2, FAPbBr3 and CsPbBr3. Pump-probe Kerr rotation and spin-flip Raman scattering with ultimate resolution in the temporal and spectral domains, respectively, are used to measure the Landé factor tensor components in magnetic fields ranging from 20 mT up to 10 T. The discovered universal dependence of the g-factors on the band gap energy is confirmed by first-principles DFT calculations combined with tight-binding and k ⋅ p perturbation theory. Thereby we get access to the key band structure parameters and develop a reliable model to predict the Landé factors for the whole family of hybrid and inorganic lead halide perovskites, both for bulk crystals and nanostructures.
Results
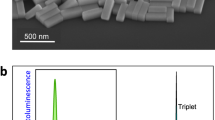
Out of the six investigated samples three representatives, namely the hybrid organic-inorganic MAPbI3 and FA0.9Cs0.1PbI2.8Br0.2 as well as the all-inorganic CsPbBr3 lead halide perovskite are chosen for discussion in detail. All samples are shown in Fig. 1b, together with photoluminescence (PL) spectra measured at the temperature of T = 1.6 − 10 K (Fig. 1a). The PL is contributed by recombination of bound excitons. The band gaps of the different materials vary from 1.527 eV up to 3.157 eV, resulting in the black to transparent colors of the studied crystals.
a Photoluminescence spectra of the crystals under study. The spectra are normalized and vertically shifted for clarity. The PL is measured at T = 1.6 − 10 K. Inset shows a sketch of the contribution of atomic orbitals to the electronic bands around the band gap in lead halide perovskites. b Photographs of representatives of the samples under study. Arrows point to the respective PL spectrum. c, d Band structure around the direct gap for the cubic and tetragonal lattices. The states at the top of the valence band (vb, holes) and the bottom of the conduction band (cb, electrons) are spin-degenerate having spin ±1/2. The degenerate heavy (he, ±3/2) and light (le, ±1/2) electron bands are split-off significantly from the cb by the spin-orbit coupling Δ. A symmetry reduction from cubic to tetragonal lifts the he-le degeneracy, leading to individual split-off energies Δhe/le. In the bottom panels the corresponding lattice structure is sketched with the [PbX6]−4 octahedra (dark red symbols show the halogen X anion) and A the inorganic/organic cation (dark blue). An octahedra twist provides the phase transition from cubic to tetragonal symmetry for the aristotype cubic structure (dashed line square)34,37.
A sketch of the atom orbitals contributing to the electronic bands in the band gap vicinity is shown in the insert of Fig. 1a. The valence band (vb) is formed by hybridization of Pb s and halogen X p orbitals and the conduction band by Pb p orbitals with some hybridization with the halogen X s orbital. The band structure around the direct band gap for cubic crystal symmetry is shown in Fig. 1c, see SI for details. The valence band is simple and has spin ± 1/2. The lowest conduction band (cb) has also spin ±1/2, while the states of the heavy (he, ±3/2) and light (le, ±1/2) electrons are split from the cb by the spin orbit coupling Δ. Commonly, perovskite crystals have cubic crystal symmetry at elevated temperatures, but at lower temperatures they undergo a phase transition by octahedral tilting (see the sketch in the bottom panel of Fig. 1d) to the tetragonal phase and, with further temperature reduction, to the orthorhomic phase34. In a nutshell, the condensation of M and R zone-boundary phonons with decreasing temperature35,36 results in reconfiguration of chemical bonds such that the densest package configuration is realized34,37. The octahedral tilting lifts the degeneracy of the light and heavy electron states, Δle > Δhe, see the upper part of Fig. 1d.
The Zeeman splitting of the carrier spin states in magnetic field B is described by the Hamiltonian
where μB is the Bohr magneton, the indices α, β = x, y, z denote the Cartesian components, gαβ are the elements of the g-factor tensor, and σα are the spin Pauli matrices. The g-factor anisotropy can reveal information on the crystal symmetry (orthorhombic in our case), while the magnitudes of gαβ are directly linked to the key band structure parameters: the band gaps and the interband momentum matrix elements18,38.
Experimentally, the g-factor can be evaluated from the measured Zeeman splitting EZ by means of
The Zeeman splitting can be measured by various techniques. In the spectral domain, spin-flip Raman scattering (SFRS) provides the required high resolution39. Here, EZ is equal to the Raman shift from the exciting laser line (Methods). In the temporal domain, time-resolved pump-probe Kerr rotation (TRKR)40 can give access to the coherent spin dynamics of carriers and therefore, the Larmor precession frequency in a transverse magnetic field, which is linked to the g-factor via
Both techniques are well established in experiments addressing the spin physics in semiconductors18,41. SFRS is applicable only in strong magnetic fields exceeding a few Tesla to obtain a sufficiently large shift from the laser for detection, but is to be preferable for identification of the involved electronic states and mechanisms via polarization analysis, while TRKR has a high precision even in weak magnetic fields and gives access to the spin dynamics. We combine the strengths of both techniques to measure the values and anisotropies of the electron and hole g-factors.
In presenting the experimental data, let us start with the FA0.9Cs0.1PbI2.8Br0.2 crystal. In the corresponding SFRS spectrum measured in the Faraday geometry at BF = 5 T, pronounced lines associated with the electron and hole spin-flips are detected, see Fig. 2a. The larger shift of the electron line corresponds to a larger Zeeman splitting, i.e. to a larger absolute value of the electron g-factor compared to the hole g-factor. Analysis of the polarization properties in the Faraday and Voigt geometries allows us to conclude that the SFRS signals are provided by the spin-flip of a resident electron or hole, interacting with a photogenerated exciton42. The resident carriers are created by photogeneration, and are localized at separate crystal sites for cryogenic temperatures28. The specific feature of lead halide perovskites is the coexistence of resident electrons and holes, which is unusual for common semiconductors. Here, we make use of this feature, as in one crystal both the electron and hole properties can be studied in the same experiment. The e+h SFRS line in Fig. 2a has a shift corresponding to ge + gh, evidencing that it is due to a combined spin-flip of an electron and a hole, interacting with the same exciton. From the linear dependence of the Raman shifts on magnetic field, using Eq. (2), we evaluate gF,h = − 1.29 and gF,e = + 3.72, Fig. 2b. Note that both shift dependencies show no offset at zero magnetic field, confirming the involvement of a resident carrier, as a finite shift would be expected due to electron-hole exchange interaction for carriers bound within an exciton18. Further we do not observe any deviations from the linear law [Eq. (2)] even at the smallest applied magnetic fields showing that the Rashba effect is negligible.
a SFRS spectrum in Faraday geometry (θ = 0∘, φ = 0∘) measured at T = 1.6 K. The excitation/detection polarization is σ+/σ−. b Magnetic field dependencies of the measured Raman shifts (symbols). Lines are linear fits. c TRKR signal (blue line) measured in the Voigt geometry (θ = 90∘, φ = 0∘). Red dashed line is fit with two oscillatory functions (see Methods) with the parameters: Se/Sh = 0.8, \({T}_{{{{{{{{\rm{2,e}}}}}}}}}^{* }(B=0.5\,{{{{{{{\rm{T}}}}}}}})=275\) ps, \({T}_{{{{{{{{\rm{2,h}}}}}}}}}^{* }(B=0.5\,{{{{{{{\rm{T}}}}}}}})=690\) ps, gh = − 1.15 and ge = + 3.48. Decomposed electron and hole components are given below. TRKR data are measured at T = 5 K. d Fast Fourier transform spectrum of the signal from c. e, f TRKR signals in magnetic fields of 0.1 T rotated in the Voigt-Voigt and Faraday-Voigt planes, respectively. g Laboratory coordinate system: blue horizontal (red vertical) plane is the Faraday-Voigt (Voigt-Voigt) plane. h Angular dependences of the electron and hole g-factors for the magnetic field rotated in the Faraday-Voigt (open symbols) and Voigt-Voigt (closed symbols) planes. Note that while gh < 0 we show ∣gh∣. Lines are guides to the eye. The indices V and F indicate the Voigt and Faraday directions of the magnetic field.
In pump-probe Kerr rotation (KR) experiments, carrier spin polarization along the light wave vector direction k is induced by the circularly polarized pump pulses, Fig. 2g and Methods. The spin polarization dynamics are detected via the Kerr rotation of the linearly-polarized probe pulses. Commonly, KR is measured in Voigt geometry where the Larmor spin precession about the magnetic field leads to an oscillating decaying signal. An example for BV = 0.5 T is shown in Fig. 2c. The signal is contributed by two frequencies corresponding to gh = − 1.15 and ge = + 3.48, as can be seen from the Fast Fourier Transformation (FFT) spectrum in Fig. 2d and also from fitting it with two oscillating functions (Methods). The decomposed spin dynamics of holes and electrons are shown in Fig. 2c.
The g-factor anisotropy is measured by tilting the magnetic field in a vector magnet. The field direction is defined by two angles: θ for rotation in the Faraday-Voigt (FV) plane (blue) and φ for rotation in the Voigt-Voigt (VV) plane (red), see Fig. 2g. For VV plane rotation (B⊥k) the TRKR signals are very similar, see Fig. 2e. For rotation from Voigt to Faraday geometry (FV plane), see Fig. 2f, the spin precession amplitude decreases while the amplitude of the monotonically decaying signal increases. The latter corresponds to the signal in Faraday geometry (θ = 0∘ or 180∘) reflecting the longitudinal spin relaxation. The g-factors evaluated from Fig. 2e, f are collected in Fig. 2h. One can see that both the electron and hole g-factors are pretty isotropic in the FA0.9Cs0.1PbI2.8Br0.2 crystals, varying in the ranges from +3.48 to +3.60 and from −1.15 to −1.22, respectively.
Let us turn to the CsPbBr3 crystal with the c-axis perpendicular to k. SFRS spectra measured in the Faraday and Voigt geometries are shown in Fig. 3a. They reveal a difference in the Raman shifts evidencing a pronounced anisotropy of the carrier g-factors: gF,e = + 2.06, gV,e = + 1.69 for the electrons and gF,h = + 0.65, gV,h = + 0.85 for the holes. The magnetic field dependencies of the Raman shifts presented in Fig. 3b together with the TRKR results for this sample published in ref. 28 allows us to conclude that in CsPbBr3, similarly to FA0.9Cs0.1PbI2.8Br0.2, the spin signals are contributed by resident carriers. The carrier spin dynamics of CsPbBr3 bulk single crystals is comparable to that of the other bulk single crystals discussed in this manuscript. For further details, we want to refer to ref. 28 containing an extended pump probe Kerr study of CsPbBr3 single crystals. The measured anisotropy in the FV plane is given in Fig. 3c. It can be well described by
a SFRS spectra measured in the Faraday (blue) and Voigt (red) geometries at T = 1.6 K. The excitation/detection polarization is σ−/σ+. Spectra are shown for the anti-Stokes spectral range where photoluminescence is suppressed. b Magnetic field dependence of the electron (purple squares) and hole (green circles) Stokes Raman shifts. Lines are linear fits with gF,e = + 2.06 and gF,h = + 0.65. c Angular dependences of the electron and hole g-factors for the magnetic field rotated in the Faraday-Voigt plane (φ = 0∘). Lines are fits using Eq. (4). The sample c-axis is oriented perpendicular to k and parallel to the x-axis, c∥B, corresponding to the Voigt geometry (θ = 90∘).
In the MAPbI3 crystal, as well as in the two other materials, the spin precession of resident electrons and holes can be also well resolved in the TRKR signals, Fig. 4a. For rotation of the field orientation in the FV plane, a strong anisotropy of the hole g-factor can be concluded from the variation of the hole precession period, e.g., following the third minimum of the hole precession as indicated by the circles. The electron g-factor is also anisotropic. The g-factor variations for rotation in the FV and VV planes are given in Fig. 4c, e. For the holes it ranges between −0.28 and −0.71, while for the electrons is varies between +2.46 and +2.98. Interestingly, the g-factor extremal values do not coincide with the main cubic axes given by the angles θ, φ = {0∘, 90∘, 180∘, 270∘}. We have recorded a large data set by measurements for further angles not falling into the FV and VV planes and found that the main axis of the electron g-tensor has the orientation θ = 33∘, φ = 54∘ and for the hole g-tensor its direction is θ = 57∘, φ = 54∘. The hole g-tensor is visualized as three-dimensional plot in Fig. 4b, for the electron see the SI. SFRS measurements are also working well for the MAPbI3 crystal, yielding the same g-factor values as we show in SI.
a TRKR signals in magnetic fields of 0.5 T rotated in the Faraday-Voigt plane (φ = 0∘). T = 7 K. The variation of the hole Larmor frequency is indicated by the open circles. b Three-dimensional presentation of the hole g-factor tensor. Stars are experimentally measured values. The contour is a fit to the data using Eq. (4). c, e Angular dependencies of the electron and hole g-factors for the magnetic field rotated in the Faraday-Voigt (open symbols) and Voigt-Voigt (closed symbols) planes. d, f Magnetic field dependencies of the electron and hole Zeeman splittings evaluated from their Larmor frequencies. Experimental data (symbols) are measured at θ = 60∘ and 150∘ (φ = 0∘). Lines are linear fits.
Discussion
Our experimental results for the Landé factors of electrons and holes are summarized in the Table 1 and plotted in Fig. 5, where the g-factor tensor components are shown as function of the band gap. The clear correlation of the g-factors and the band gap energy requires a theoretical explanation. Note, that we do not observe any deviations from the linear Zeeman term [Eq. (2)] even in the smallest applied magnetic fields, hence we neglect the Rashba term in the analysis. To that end we use atomistic approaches based on the density functional theory (DFT) and empirical tight-binding method (ETB), to calculate the band structure and Landé factors of prototypical inorganic analogues of the studied perovskites: CsPbI3, CsPbBr3, and CsPbCl343. Although these all-inorganic systems are different from organic-inorganic lead halides, resulting in somewhat different band gaps, spin-orbit couplings and Landé factors, the organic molecules are not crucial for the band structure formation, so that the study of the inorganic perovskites allows us to establish general trends and, eventually, formulate a semi-phenomenological model for the Zeeman splitting.
The details of the atomistic calculations and the k ⋅ p model description of the band structure are given in the SI. We express the components of the g-factor tensors via the matrix elements of the spin and orbital angular momenta of electrons and holes which can be further expressed via the interband momentum matrix elements and band gaps. The analysis of the influence from the different bands allows us to identify the key contributions to the electron and hole Landé factors. In particular, for the holes in the valence band the main contribution is related to the k ⋅ p mixing with the conduction band18,19,38 and, in the cubic phase one finds (see SI for details)
Here p is the interband matrix element of the momentum operator, Eg the band gap and Δ the spin-orbit splitting of the conduction band. For the electrons, the k ⋅ p mixing both with the top valence band and the remote valence states is important, resulting in (cf. ref. 19 and SI)
where Δge is the remote band contribution. Eqs. (5) and (6) with the reasonably chosen parameters Δ = 1.5 eV, ℏp/m0 = 6.8 eV ⋅ Å, and Δge = − 1 describe well the band gap dependence of the Landé factors across the studied perovskite classes, see Fig. 5. In agreement with experiment, the k ⋅ p-mixing between the conduction and valence bands decreases with increasing band gap, thus the electron g-factor decreases with increasing Eg from large positive values down to − 2/3 + Δge ≈ − 5/3, while the hole g-factor increases with increasing Eg from negative values up to +2. Note that in the studied range of band gap energies the separation from the remote bands is large, so that Δge is practically independent of the material. Also the spin-orbit interaction is about constant since it is determined by the heavy lead atoms.
Let us now address the anisotropy of the g-factors observed mainly in the experiments on MAPbI3 and CsPbBr3. Overall, the g-factor anisotropy may be expected because at low temperatures the perovskites are known to undergo phase transitions from cubic to tetragonal or orthorhombic phases, see34. In the simplest approach the tetragonal and orthorhombic phases can be considered as a cubic phase distorted along the principal cubic axes x, y, and z. In the tetragonal phase gxx = gyy ≠ gzz, where z is the C4 axis. In the orthorhombic phase, on the other hand, gxx ≠ gyy ≠ gzz. The analysis shows (see SI) that the g-factor anisotropy is caused by the conduction band crystal splitting with Δhe ≠ Δle, see Fig. 1d, and by the anisotropy of the interband momentum matrix elements. The conduction band splitting affects mainly the hole g-factor [Eq. (5)], while the anisotropy of matrix elements affects both the electron and hole Landé factors, see the SI where details of the fits are presented. This, together with the fact that ∣gh∣ < ge, results in a larger anisotropy of the hole g-factors, Ph > Pe, as observed in the experiment.
For the cubic, tetragonal and orthorhombic symmetries the main axes of the g-factor tensor are related to the cubic directions 〈001〉. We confirm this experimentally for CsPbBr3, FA0.9Cs0.1PbI2.8Br0.2 and FAPbBr3, while in MAPbI3 the main axes are found to be tilted with respect to the cubic axes. This might be a signature of the previously not reported transition to a monoclinic phase or a rotation of the crystallographic axes with respect to the lab frame44,45,46. In the former case, the reduced symmetry of the structure can be described by one of two possible point groups (both being subgroups of D2h): C1 (no non-trivial symmetry operations) or Ci (with space inversion) as symmetry operation. All other subgroups imply that at least one of the main axes of the g-factor tensor is the “cubic” axis [001], [010] or [100]. Alternatively, the explanation could be related to the formation or randomly oriented domains with different crystalline orientations. This question requires further experimental studies, particularly because X-ray diffraction for determination of the crystal structure at low temperatures is quite involved.
In conclusion, we have discovered experimentally and confirmed theoretically a universal dependence of the electron and hole g-factors on the band gap energy in the family of lead halide perovskite materials which is applicable for hybrid organic-inorganic and all-inorganic compounds. Our first-principles DFT calculations in combination with tight-binding and k ⋅ p approaches show that the universality originates from the electronic states that form the band gap being largely contributed by lead orbitals. Therefore, the g-factor dependence across the huge range of band gap energies from 1 eV up to 4 eV can be treated with the same band parameters. The derived parameters give insight into fundamental band properties, including band anisotropies caused by structural phase transitions. The selection of several halogen atoms (I, Br, Cl) and cation types (Cs, MA, FA) allows tailoring of the band gaps, which in turn leads to a correpsonding variation of the g-factor values. Our study provides a reliable relation to predict the Landé factors for the whole family of lead halide perovskites, including their nanostructures. This relation thus delivers the key parameter determining the spin physics of perovskites.
Methods
Samples
The class of lead halide perovskites possesses APbX3 composition, where the A-cation is typically Cs, methylammonium (MA, CH3NH3) or formamidinium (FA, CH(NH2)2) and the X-anion is a halogen Cl, Br, or I, giving rise of a huge flexibility. The latter is only limited by a favorable ratio of the anion to cation ion radii, named the Goldschmidt tolerance factor t, which should be close to unity47. By varying composition, the band gap of these perovskite materials can be tuned from the infrared up to the ultraviolet spectral range. All studied samples are lead halide perovskite single crystals grown out of solution with the inverse temperature crystallization (ITC) technique9,48,49. For the specific crystals the ITC protocols were modified.
FA0.9Cs0.1PbI2.8Br0.2 crystals
α-phase FA0.9Cs0.1PbI2.8Br0.2 single crystals were grown in accordance with the method sketched above, for more details see ref. 9. First, a solution of CsI, FAI (FA being formamidinium), PbI2, and PbBr2, with GBL γ-butyrolactone as solvent is mixed. This solution is then filtered and slowly heated to 130 ∘C temperature, whereby the single crystals are formed in the black phase of FA0.9Cs0.1PbI2.8Br0.2. Afterwards the crystals are separated by filtering and drying. The α-phase (black phase) exhibits a cubic crystal structure at room temperature50. In the experiment the crystal was oriented with [001] pointing along the laser wave vector k. Note that the g-factor isotropy, the small shift of the PL line with temperature and further analyses9,30 suggest the typical lead halide perovskite crystal distortion from cubic symmetry to be small at small temperatures. The size of the crystal is ≈2 × 3 × 2 mm3. The crystal shape is non-cuboid, but the crystal structure exhibits aristotype cubic symmetry. Sample code: 515a.
CsPbBr3 crystals
The CsPbBr3 crystals were grown with a slight modification of the ITC as stated above. Further information can be found in ref. 48. First, CsBr and PbBr2 were dissolved in dimethyl sulfoxide. Afterwards a cyclohexanol in N,N-dimethylformamide solution was added. The resulting mixture was heated in an oil bath to 105∘C whereby slow crystal growth appears. The obtained crystals were taken out of the solution and quickly loaded into a vessel with hot (100∘C) N,N-dimethylformamide. Once loaded, the vessel was slowly cooled down to about 50∘C. After that, the crystals were isolated, wiped with filter paper and dried. The obtained rectangular-shaped CsPbBr3 is crystallized in the orthorhombic modification. The crystals have one selected (long) direction along the c-axis [002] and two nearly identical directions along the \([\bar{1}10]\) and [110] axes51. The size of the crystal is ≈ 3 × 2 × 7 mm3. Sample code: DD4470/2.
MAPbI3 crystals
Methylammonium (MA/CH3NH3) lead tri-iodine (MAPbI3) single crystals were low temperature solution-grown in a reactive inverse temperature crystallization (RITC) process, which utilizes a mixture of γ-butyrolactone GBL precursor solvent with alcohol49. The mixed precursor solvent polarity is changed compared to pure GBL, causing a lower solubility of MAPbI3 and an optimization of nucleation rates and centers, which result in an early crystallization at low temperatures. Black MAPbI3 single crystals were obtained at a temperature of 85∘C. At room temperature a tetragonal phase with lattice constants a = 0.893 nm and c = 1.25 nm was determined by XRD49. The size of the crystal is ≈4 × 3 × 2 mm3. The crystal shape is non-cuboid, but the crystal structure exhibits aristotype cubic symmetry. The front facet was X-ray characterized to point along the a-axis49. Sample code: MAPI-SC04.
MAPb(Br0.5Cl0.5)3 & MAPb(Br0.05Cl0.95)3 crystals
In the case of MAPb(Br0.5Cl0.5)3, 0.3 mmol MACl, 0.3 mmol PbCl2, 0.7 mmol MABr and 0.7 mmol PbBr2 were dissolved in a mixture of 0.89 ml dimethylformamide (DMF) with 85 μl dimethyl sulfoxide (DMSO). In the case of MAPb(Br0.05Cl0.95)3, 2.2 mmol PbCl2, 1.2 mmol MACl and 1 mmol MABr were dissolved in 2 ml of 1:1 DMF:DMSO mixture. Both solutions were filtered through 0.45 μm polytetrafluoroethylene (PTFE) filter. The obtained solutions were slowly heated in an oil bath up to 62 ∘C. The crystals nucleate and grow in the temperature window 58–62 ∘C. The obtained crystals show a rectangular cuboid shape with sizes of 1.64 × 1.65 × 2.33 mm3 for MAPb(Br0.05Cl0.95)3 and 2 × 4 × 1 mm3 for MAPb(Br0.5Cl0.5)3. The MAPb(Br0.05Cl0.95)3 crystals are transparent and colorless, while the MAPb(Br0.5Cl0.5)3 crystals are transparent with a faint yellow appearance. Sample code: dd2924 and dd6347, respectively.
FAPbBr3 crystals
The FAPbBr3 single crystals were grown with an analogous approach as the other samples following the ITC approach. Specific extended information are given in ref. 52. The crystal is of reddish transparent appearance and shows a rectangular cuboid shape with a size of 5 × 5 × 2 mm3. Sample code: OH0071a.
Magneto-optical measurements
The samples were placed in a cryostat with the temperature variable from 1.6 K up to 300 K. For T = 1.6 K the sample is immersed in superfluid helium while for 4.2 K to 300 K the sample is in cooling helium gas. Two magnet cryostats equipped with split-coil superconducting solenoids were used. The first one is constructed to generate magnetic fields up to 10 T in a fixed direction. The second one, which is a vector magnet, has three pairs of orthogonal split coils, allowing us to apply magnetic fields up to 3 T in any direction. A sketch of the experimental geometry is shown in Fig. 2g. A magnetic field parallel to the light wave vector k is denoted here as Bz (Faraday geometry), magnetic fields perpendicular to k (Voigt geometry) are oriented in the plane spanned by the magnetic field axis Bx in the horizontal plane and By in the vertical direction. The angle θ is defined as the angle between Bx and Bz (for rotation in the Faraday-Voigt (FV) plane) with θ=0∘ corresponding to Bz∥k. The angle φ defines the rotational orientation in the vertical plane (Voigt-Voigt (VV) plane) with φ = 0∘ for the horizontal x-axis and φ = 90∘ for the vertical y-axis.
Pump-probe time-resolved Kerr rotation (TRKR)
The coherent spin dynamics were measured by a pump-probe setup, where pump and probe had the same photon energy, emitted from the same pulsed laser40. A titan-sapphire (Ti:Sa) laser emitted 1.5 ps long pulses with a spectral width of about 1 nm (1.5 meV) at a pulse repetition rate of 76 MHz (repetition period TR = 13.2 ns). The laser photon energy was tunable in the spectral range of 1.265 − 1.771 eV (700 − 980 nm). It was set to the vicinity of the exciton resonance at the maximum of the Kerr rotation signal: at 1.513 eV for FA0.9Cs0.1PbI2.8Br0.2 and at 1.637 eV for MAPbI3. The laser beam was split into two beams (pump and probe). The probe pulses were delayed with respect to the pump pulses by a mechanical delay line. Both pump and probe beams were modulated using photo-elastic modulators (PEM). The probe beam was always linearly polarized and its amplitude was modulated at a frequency of 84 kHz. The pump beam helicity was modulated between σ+ and σ− circular polarization at a frequency of 50 kHz. The polarization of the reflected probe beam was analyzed, via a lock-in technique, with respect to the rotation of its linear polarization (Kerr rotation). In finite transverse magnetic field, the Kerr rotation amplitude oscillates in time reflecting the Larmor spin precession of the carriers and decays at longer time delays. When both electrons and holes contribute to the Kerr rotation signal, which is the case for the studied perovskite crystals, the signal can be described as a superposition of two decaying oscillatory functions: \({A}_{{{{{{{{\rm{KR}}}}}}}}}={S}_{{{{{{{{\rm{e}}}}}}}}}\cos ({\omega }_{{{{{{{{\rm{L,e}}}}}}}}}t)\exp (-t/{T}_{{{{{{{{\rm{2,e}}}}}}}}}^{* })+{S}_{{{{{{{{\rm{h}}}}}}}}}\cos ({\omega }_{{{{{{{{\rm{L,h}}}}}}}}}t)\exp (-t/{T}_{{{{{{{{\rm{2,h}}}}}}}}}^{* })\). Here Se(h) are the signal amplitudes that are proportional to the spin polarization of electrons (holes). The g-factors are evaluated from the Larmor precession frequency ωL,e(h) by means of ∣ge(h)∣ = ℏωL,e(h)/(μBB). It is also important to note, that TRKR provides information on the g-factor magnitude, but not on its sign. The same is true for the SFRS technique below. Information on the sign is obtained from model calculations, e.g. for the studied perovskites ge > 0 is predicted, see SI. Also knowledge on the exciton g-factor, gX, and its sign can help to identify the hole g-factor sign using gX = ge + gh28. For standard TRKR measurements, the external magnetic field is applied in the Voigt geometry perpendicular to the light wave vector k. For measuring the g-factor anisotropy the magnetic field orientation is tuned to various angles θ, φ using the vector magnet, see Fig. 2g.
Spin-flip Raman scattering (SFRS)
The SFRS technique allows one to measure directly the Zeeman splitting of the electron and hole spins from the spectral shift of the scattered light from the laser photon energy39,42. The energy shift is provided by the spin-flip of carriers, with the required energy taken from or provided by phonons. The typical shifts do not exceed 1 meV at the magnetic field of 10 T, which demands for the high spectral resolution provided by high-end spectrometers with excellent suppression of scattered laser light. The experiments were performed for samples in contact with pumped liquid helium at T = 1.6 K. We used resonant excitation in the vicinity of the exciton resonances in order to enhance the SFRS signal, obtained for the following laser photon energies: 1.500 eV for FA0.9Cs0.1PbI2.8Br0.2, 2.330 eV for CsPbBr3, and 1.635 eV for MAPbI3. The resonant Raman spectra were measured in the backscattering geometry with the incident laser excitation density between 1 and 5 Wcm−2. The scattered light was analyzed by a Jobin-Yvon U1000 double monochromator (1 meter focal length) equipped with a cooled GaAs photomultiplier and conventional photon counting electronics. The used spectral resolution of 0.2 cm−1 (0.024 meV) allowed us to measure the SFRS signals in close vicinity of the laser line for spectral shifts ranging from 0.1 to 3 meV. The spectra were measured in co-polarized (σ+/σ+) or cross-polarized (σ+/σ− and σ−/σ+) circular polarizations of excitation and detection for the Faraday geometry (B∥k) and in crossed or parallel linear polarizations for the Voigt geometry (B⊥k), with the definition of the magnetic field axes and angles as stated above in Methods (Magneto-optical measurements). For data presentation we plot the Stokes-shifted lines (i.e. the lines shifted to lower energies from the laser) as positive shifts, while for the anti-Stokes lines negative values are taken. Note that in the anti-Stokes spectra possible contributions of photoluminescence are absent, as up-conversion at low temperatures is weak, so that spin-flip lines can be clearly identified. On the other hand, for the Stokes spectra larger Raman shifts in stronger magnetic fields can be observed.
Data availability
The data on which the plots within this paper are based and other findings of this study are available from the corresponding author upon justified request.
Code availability
The code on which the calculations within this paper are based and other findings of this study are available from the corresponding author upon justified request.
Change history
24 June 2022
The original version of this Article omitted a Supplementary Information file, which has been added after the publication of the main article.
References
Jeong, J. et al. Pseudo-halide anion engineering for α-FAPbI3 perovskite solar cells. Nature 592, 381–385 (2021).
Best Research-Cell Efficiency Chart https://www.nrel.gov/pv/cell-efficiency.html (2021).
Hansell, C. et al. Perovskites for Optoelectronics https://www.nature.com/collections/fnnxcznnbb/content/reviews (2019).
Eperon, G. E. et al. Formamidinium lead trihalide: a broadly tunable perovskite for efficient planar heterojunction solar cells. Energy Environ. Sci. 7, 982–988 (2014).
Wang, J. et al. Spin-optoelectronic devices based on hybrid organic-inorganic trihalide perovskites. Nat. Commun. 10, 129 (2019).
Fu, Y. et al. Metal halide perovskite nanostructures for optoelectronic applications and the study of physical properties. Nat. Rev. Mater. 4, 169–188 (2019).
Jena, A. K., Kulkarni, A. & Miyasaka, T. Halide perovskite photovoltaics: Background, status, and future prospects. Chem. Rev. 119, 3036–3103 (2019).
Piveteau, L., Morad, V. & Kovalenko, M. V. Solid-state NMR and NQR spectroscopy of lead-halide perovskite materials. J. Am. Chem. Soc. 142, 19413–19437 (2020).
Nazarenko, O., Yakunin, S., Morad, V., Cherniukh, I. & Kovalenko, M. V. Single crystals of caesium formamidinium lead halide perovskites: solution growth and gamma dosimetry. NPG Asia Mater. 9, e373 (2017).
Wei, H. & Huang, J. Halide lead perovskites for ionizing radiation detection. Nat. Commun. 10, 1066 (2019).
Niesner, D. et al. Giant Rashba splitting in CH3NH3PbBr3 organic-inorganic perovskite. Phys. Rev. Lett. 117, 126401 (2016).
Herz, L. M. Charge-carrier mobilities in metal halide perovskites: Fundamental mechanisms and limits. ACS Energy Lett. 2, 1539–1548 (2017).
Lee, M.-I. et al. First determination of the valence band dispersion of CH3NH3PbI3 hybrid organic–inorganic perovskite. J. Phys. D: Appl. Phys. 50, 26LT02 (2017).
Zu, F. et al. Constructing the electronic structure of CH3NH3PbI3 and CH3NH3PbBr3 perovskite thin films from single-crystal band structure measurements. J. Phys. Chem. Lett. 10, 601–609 (2019).
Yang, J. et al. Accessing the conduction band dispersion in CH3NH3PbI3 single crystals. J. Phys. Chem. Lett. 12, 3773–3778 (2021).
Miyata, A. et al. Direct measurement of the exciton binding energy and effective masses for charge carriers in organic-inorganic tri-halide perovskites. Nat. Phys. 11, 582 (2015).
Baranowski, M. & Plochocka, P. Excitons in metal-halide perovskites. Adv. Energy Mater. 10, 1903659 (2020).
Ivchenko, E. L. Optical Spectroscopy of Semiconductor Nanostructures (Alpha Science Int., Harrow, UK, 2005).
Yu, Z. G. Effective-mass model and magneto-optical properties in hybrid perovskites. Sci. Rep. 6, 28576 (2016).
Giovanni, D. et al. Highly spin-polarized carrier dynamics and ultralarge photoinduced magnetization in CH3NH3PbI3 perovskite thin films. Nano Lett. 15, 1553–1558 (2015).
Nestoklon, M. O. et al. Optical orientation and alignment of excitons in ensembles of inorganic perovskite nanocrystals. Phys. Rev. B 97, 235304 (2018).
Wang, R. et al. Circularly polarized photoluminescence and Hanle effect measurements of spin relaxation in organic-inorganic hybrid perovskite films. J. Mater. Chem. C. 6, 2989–2995 (2018).
Pan, X., Liu, H., Huynh, U. & Vardeny, Z. V. Magneto-electroluminescence response in 2d and 3d hybrid organic-inorganic perovskite light emitting diodes. J. Chem. Phys. 152, 044714 (2020).
Zhang, C. et al. Magnetic field effects in hybrid perovskite devices. Nat. Phys. 11, 427–434 (2015).
Canneson, D. et al. Negatively charged and dark excitons in CsPbBr3 perovskite nanocrystals revealed by high magnetic fields. Nano Lett. 17, 6177–6183 (2017).
Zhang, C. et al. Field-induced spin splitting and anomalous photoluminescence circular polarization in CH3NH3PbI3 films at high magnetic field. Phys. Rev. B 97, 134412 (2018).
Odenthal, P. et al. Spin-polarized exciton quantum beating in hybrid organic–inorganic perovskites. Nat. Phys. 13, 894–899 (2017).
Belykh, V. V. et al. Coherent spin dynamics of electrons and holes in CsPbBr3 perovskite crystals. Nat. Commun. 10, 673 (2019).
Garcia-Arellano, G. et al. Energy tuning of electronic spin coherent evolution in methylammonium lead iodide perovskites. J. Phys. Chem. 12, 8272–8279 (2021).
Kirstein, E. et al. Lead-dominated hyperfine interaction impacting the carrier spin dynamics in halide perovskites. Adv. Mater. 34, 2105263 (2022).
Sharma, S., Weiden, N. & Weiss, A. 207Pb and 205Tl NMR on perovskite type crystals APbX3 (A = Cs, Tl, X = Br, I). Zeitschrift für Naturforsch. A 42, 1313–1320 (1987).
Hanrahan, M. P., Men, L., Rosales, B. A., Vela, J. & Rossini, A. J. Sensitivity-enhanced 207Pb solid-state NMR spectroscopy for the rapid, non-destructive characterization of organolead halide perovskites. Chem. Mater. 30, 7005–7015 (2018).
Aebli, M. et al. Lead-halide scalar couplings in 207Pb NMR of APbX3 perovskites (A = Cs, methylammonium, formamidinium; X = Cl, Br, I). Sci. Rep. 10, 8229 (2020).
Steele, J. A. et al. Phase transitions and anion exchange in all-inorganic halide perovskites. Acc. Mater. Res. 1, 3–15 (2020).
Trendel, G. Electronic and phonon properties of the plumbates CsPbCl3, CsPbBr3 and their mixed crystals; Elektronische und phononische Eigenschaften der Plumbate CsPbCl3, CsPbBr3 und ihrer Mischkristalle. (PhD thesis, Dortmund, 1982).
Fujii, Y., Yamada, Y. & Shirane, Y. Neutron-scattering study on phase transitions of CsPbCl3. Phys. Rev. B 9, 4549–4559 (1974).
Yang, R. X., Skelton, J. M., da Silva, E. L., Frost, J. M. & Walsh, A. Assessment of dynamic structural instabilities across 24 cubic inorganic halide perovskites. J. Chem. Phys. 152, 024703 (2020).
Roth, L. M., Lax, B. & Zwerdling, S. Theory of optical magneto-absorption effects in semiconductors. Phys. Rev. 114, 90 (1959).
Häfele, H. G. Spin-Flip Raman Scattering. In Landwehr, G. & Rashba, E. I. (eds.) Landau Level Spectroscopy, vol. 27, 208–275 (Elsevier Amsterdam, 1991).
Yakovlev, D. R. & Bayer, M. Chapter 6: Coherent Spin Dynamics of Carriers. In Dyakonov, M. I. (ed.) Spin Physics in Semiconductors, 155-206 (Springer International Publishing AG, 2017).
Glazov, M. M. Electron and Nuclear Spin Dynamics in Semiconductor Nanostructures (Oxford University Press, Oxford, 2018).
Debus, J. et al. Spin-flip Raman scattering of the neutral and charged excitons confined in a CdTe/(Cd,Mg)Te quantum well. Phys. Rev. B 87, 205316 (2013).
Nestoklon, M. O. Tight-binding description of inorganic lead halide perovskites in cubic phase. Comput. Mater. Sci. 196, 110535 (2021).
Onoda-Yamamuro, N., Matsuo, T. & Suga, H. Calorimetric and IR spectroscopic studies of phase transitions in methylammonium trihalogenoplumbates (II). J. Phys. Chem. Sol. 51, 1383–1395 (1990).
Swainson, I. P., Hammond, R. P., Soulliere, C., Knop, O. & Massa, W. Phase transitions in the perovskite methylammonium lead bromide, CH3ND3PbBr3. J. Solid State Chem. 176, 97–104 (2003).
Whitfield, P. S. et al. Structures, phase transitions and tricritical behavior of the hybrid perovskite methyl ammonium lead iodide. Sci. Rep. 6, 35685 (2016).
Goldschmidt, V. M. Die Gesetze der Krystallochemie. Naturwissenschaften 14, 477–485 (1926).
Dirin, D. N., Cherniukh, I., Yakunin, S., Shynkarenko, Y. & Kovalenko, M. V. Solution-grown CsPbBr3 perovskite single crystals for photon detection. Chem. Mater. 28, 8470–8474 (2016).
Höcker, J., Brust, F., Armer, M. & Dyakonov, V. A temperature-reduced method for the rapid growth of hybrid perovskite single crystals with primary alcohols. Cryst. Eng. Comm. 23, 2202–2207 (2021).
Weller, M. T., Weber, O. J., Frost, J. M. & Walsh, A. Cubic perovskite structure of black formamidinium lead iodide, α-[HC(NH2)2]PbI3, at 298 K. J. Phys. Chem. Lett. 6, 3209–3212 (2015).
Feng, Y. et al. Low defects density CsPbBr3 single crystals grown by an additive assisted method for gamma-ray detection. J. Mater. Chem. C. 8, 11360–11368 (2020).
Saidaminov, M. I., Abdelhady, A. L., Maculan, G. & Bakr, O. M. Retrograde solubility of formamidinium and methylammonium lead halide perovskites enabling rapid single crystal growth. Chem. Comm. 54, 17658–17661 (2015).
Galkowski, K. et al. Determination of the exciton binding energy and effective masses for methylammonium and formamidinium lead tri-halide perovskite semiconductors. Energy Environ. Sci. 9, 962–970 (2016).
Acknowledgements
We acknowledge the financial support by the Deutsche Forschungsgemeinschaft in the frame of the Priority Programme SPP 2196 (Project YA65/26-1) and the International Collaboration Research Center TRR160 (project B2). It was also supported by the Russian Foundation for Basic Research (Grant No. 19-52-12038 NNIO-a, 19-52-12064 NNIO-a, and 19-02-00545). M.O.N. is grateful to the Foundation for Advancement of Theoretical Physics and Mathematics “BASIS". J.H., A.B. and V.D. acknowledge financial support from the Deutsche Forschungsgemeinschaft through the Würzburg-Dresden Cluster of Excellence on Complexity and Topology in Quantum Matter-ct.qmat (EXC 2147, project-id 39085490), DY18/15-1 and from the Bavarian State Ministry of Education and Culture, Science and Arts within the Collaborative Research Network “Solar Technologies go Hybrid". The work at ETH Zurich (O.N., D.N.D. and M.V.K.) was financially supported by the Swiss National Science Foundation (grant agreement 186406, funded in conjunction with SPP219 through DFG-SNSF bilateral program) and by ETH Zurich through ETH+ Project SynMatLab.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
E.K., E.A.Zh., D.K., I.V.K., V.F.S., G.S.D. and N.E.K built the experimental apparatus and performed the measurements. I.V.K., V.F.S., and D.R.Y. analyzed the data. M.M.G., M.A.S., M.O.N., and E.L.I. developed theoretical approach and performed model calculations. O.N., D.N.D., M.V.K., A.B., J.H., and V.D. grew the samples. All authors contributed to interpretation and analysis of the data. E.K., D.R.Y. and M.M.G. wrote the manuscript in close consultations with M.B., M.V.K., and V.D.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Linn Leppert, Yan Li and the other, anonymous, reviewers for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kirstein, E., Yakovlev, D.R., Glazov, M.M. et al. The Landé factors of electrons and holes in lead halide perovskites: universal dependence on the band gap. Nat Commun 13, 3062 (2022). https://doi.org/10.1038/s41467-022-30701-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-022-30701-0
This article is cited by
-
How spin relaxes and dephases in bulk halide perovskites
Nature Communications (2024)
-
Mode locking of hole spin coherences in CsPb(Cl, Br)3 perovskite nanocrystals
Nature Communications (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.