Abstract
The experimental study of hydrogen-bonds and their symmetrization under extreme conditions is predominantly driven by diffraction methods, despite challenges of localising or probing the hydrogen subsystems directly. Until recently, H-bond symmetrization has been addressed in terms of either nuclear quantum effects, spin crossovers or direct structural transitions; often leading to contradictory interpretations when combined. Here, we present high-resolution in-situ 1H-NMR experiments in diamond anvil cells investigating a range of systems containing linear O-H ⋯ O units at pressure ranges of up to 90 GPa covering their respective H-bond symmetrization. We found pronounced minima in the pressure dependence of the NMR resonance line-widths associated with a maximum in hydrogen mobility, precursor to a localisation of hydrogen atoms. These minima, independent of the chemical environment of the O-H ⋯ O unit, can be found in a narrow range of oxygen oxygen distances between 2.44 and 2.45 Å, leading to an average critical oxygen-oxygen distance of \({\bar{r}}_{{{{{{{{\rm{OO}}}}}}}}}^{{{{{{{{\rm{crit}}}}}}}}}=2.443(1)\) Å.
Similar content being viewed by others
Introduction
Understanding the stability and properties of hydrous minerals, possibly contributing to hydrogen transport to the lower mantle is crucial as key properties of the constituents of Earth’s mantle, e.g., melting temperatures, rheology, electrical conductivity and atomic diffusivity1,2,3,4,5 can be strongly affected by the presence of even small amounts of hydrogen. In particular, the high-pressure (P) phases of H2O ice, (Al,Fe)OOH and dense hydrous magnesium silicates are important candidates for hosting large amounts of hydrogen6. These phases have a common O-H-O sequence, with an asymmetric hydrogen-bond (O-H⋯O) at low compression, which symmetrizes under increasing P (O-H-O).
During the symmetrization, compressional (e.g. bulk modulus) as well as transport properties undergo significant modifications, but although the common O-H⋯O sequence endorses the conclusion that the phases should show very similar behaviour, significantly distinct characteristics are observed, e.g. (i) the symmetrization P has a great variation, e.g. ≃120 GPa in ice-VII7,8,9 compared to ≃15 GPa in δ-AlOOH10,11,12, (ii) proton tunnelling dominates the transition in ice-VII7,8,13,14,15, but is absent in δ-AlOOH10. (iii) The bulk modulus in ice-VII8,16,17 shows a noticeable softening, while only a minor effect is found in δ-AlOOH11.
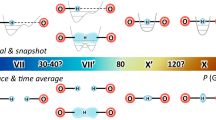
In order to shed light on the underlying mechanisms it is essential to gain a deeper understanding of the similarities and disparities between different oxide-hydroxide phases with respect to the hydrogen-bond symmetrization. Hydrogen atoms, however, have a very low X-ray cross-section and neutron techniques are typically unavailable at P ≳ 25 GPa, therefore knowledge about the hydrogen subsystem is widely limited to computational and optical studies (e.g. Raman or Infrared). Advances in high-P nuclear magnetic resonance spectroscopy in recent years18,19,20, allow for a direct investigation of the hydrogen subsystem (Fig. 1) beyond the megabar-range and enables previously unattainable experimental insight.
Schematic representation of the local hydrogen-bond environments with the hydrogen atom at the center. The energy potential of the H-bond (green graph) is determined predominantly by the nearest-neighbour atoms (e.g. oxygen atoms). Depending on initial O-O distances, hydrogen probability distributions, ∣Ψ(x)∣2, (purple schematic graph) may exhibit uni- or bi-modal characteristics. Shown here is a typical broad energy potential without barrier, leading to an uni-modal probability distribution and thermally activated hydrogen mobility. Next-nearest-neighbours may constitute metal anions, e.g., in hydrous minerals, or other hydrogen atoms in H2O ice-VII/X.
Here, we present in-situ high-P1H-NMR data on four hydrous mineral phases: (i) dense magnesium silicate phase-D with composition (Mg0.88,Fe0.12)(Si0.9, Al0.1)2O6H2, (ii) pure and (iii) iron-bearing aluminum oxide-hydroxide (δ-(Al0.3,Fe0.7)OOH) as well as (iv) high-P phases of H2O (ice-VII/X). Under compression, we find a distinct maximum in hydrogen mobility in all sampled systems at the same critical O⋯H-O in-bond oxygen-oxygen distance (\({r}_{{{{{{{{\rm{OO}}}}}}}}}^{{{{{{{{\rm{crit}}}}}}}}}\)). Being a precursor for H-bond symmetrization and under further compression localisation, this minimum was found to solely depend on the short-range local structure, i.e. rOO is independent of the nature of the further chemical surrounding, marking \({r}_{{{{{{{{\rm{OO}}}}}}}}}^{{{{{{{{\rm{crit}}}}}}}}}\) as an unifying parameter of pressure-induced hydrogen-bond symmetrization dynamics.
Results and discussion
We use the equation of state (EOS) parameters (Fig. 2a) for δ-AlOOH (V0 = 56 Å3, K0 = 183 GPa,\(K^{\prime} =3.7\)) from21, δ-(Al0.3,Fe0.7)OOH (V0 = 63.71 Å3, K0 = 164.7 GPa, \(K^{\prime} =4.04\)) and Phase-D (V0 = 84.73 Å3, K0 = 162 GPa, \(K^{\prime} =4\)), are determined from synchrotron X-ray diffraction (XRD, see Methods section). For H2O ice-VII/X we use the global EOS by22, based on DFT calculations, which was found to be in excellent agreement with recent dynamical diamond anvil cell XRD experiments8. The volume collapse in iron bearing oxide-hydroxide at P ≈ 45 GPa originates from the S = 5/2 high spin to S = 1/2 low spin transition of ferric iron23,24. Analogous transitions in dense magnesium silicate phase-D are not observable in our XRD data due to the low concentration of iron, but distinct transitions can be found in synchrotron Mössbauer spectroscopy (SMS) (see Methods section).
a Equation of state (EOS) data of the different hydrogen-bonded phases. We use the EOS for H2O ice-VII/X (gray graphs) of from22, based on ab-initio computations and the XRD based EOS of21 for δ-AlOOH (green graphs). The other curves are based on third order Birch-Murnagham EOS fits to our diffraction data for iron-bearing δ-AlOOH (brown graphs) and phase-D (blue graphs). δ-(Al0.3,Fe0.7)OOH exhibits a 7% volume collapse associated to the electron spin crossover of ferric iron (c.f. Fig. 4a). b Oxygen-oxygen distance (rOO) as a function of P. Different pressure dependencies of the Qi(i = 3, 5, 6) (red, brown and yellow graphs respectively) H-bond environments in δ-(Al,Fe)OOH20 were estimated through interpolation of rOO between endmembers δ-AlOOH10, 21 and ϵ-FeOOH25 with respect to the local iron content. We only consider the high spin state in iron bearing phases, as the spin transition occurs at significantly higher P ( ~45 GPa) than the hydrogen-bond symmetrization (~15 GPa).
In order to quantify the evolution of hydrogen NMR signals with respect to the local symmetry under compression, we calculate oxygen-oxygen distances in the H-bonds (rOO), using both diffraction data (for δ-(Al,Fe)OOH21 and phase-D) as well as DFT calculations for high-P ice-VII/X22. As shown recently in ref. 20, the hydrogen-bond manifold in δ-(Al0.3,Fe0.7)OOH can be resolved and the observed signals assigned to different local environments, Qi (i = 1−6), where the fraction i of 6 possible next-nearest-neighbour positions around the hydrogen-bond (Fig. 1) is occupied by ferric iron paramagnetic centres. We deduce the P dependence of rOO in δ-(Al0.3,Fe0.7)OOH by interpolating between the endmember δ-AlOOH10,21 and ϵ-FeOOH25 with respect to the local iron content around the hydrogen nearest-neighbours (Fig. 1). We neglect the volume collapse due to the spin transition in iron bearing phases as is at significantly higher P than the hydrogen-bond symmetrization.
We performed high-resolution 1H-Lee Goldburg (LG) NMR measurements26 for δ-(Al0.3,Fe0.7)OOH and Mg0.88,Fe0.12)(Si0.9, Al0.1)2O6H2 phase-D in order to investigate the influence of different next-nearest-neighbour configurations (Figure 1) and recorded 1H-NMR solid echos for pure δ-AlOOH as well as H2O ice-VII/X.
The electronic environment of the hydrogen nuclei should, to first approximation, be determined by their nearest-neighbours, i.e. the oxygen atoms involved in the hydrogen-bonds27. Presence of paramagnetic centres among the next-nearest-neighbours, such as in phase-D or δ-(Al0.3,Fe0.7)OOH, induces additional contributions to NMR resonance shifts and relaxation times28. These should not significantly influence dynamical effects, but instead lead to a modulation of the energy landscape of H-bonds in these systems29 and therefore a separation of the signals in the indirect LG-projection frequency domain F2 is observable.
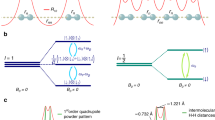
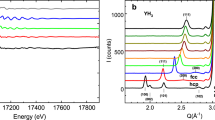
Figure 3 a shows a high-resolution 1H-LG NMR spectrum of δ-(Al0.3,Fe0.7)OOH at 15.7 GPa. As recently shown20, the 2D-LG spectrum can be separated in six different regions. Under the assumption of a stochastic distribution of ferric iron, several different H-bond environments should be present in the sample due to a modulation of the local magnetic fields at the hydrogen atoms caused by the paramagnetic centers. We associated these different regions to the different next-nearest neighbour surroundings (Qi), by matching the relative size of the regions, i.e. the 2D-signal intensities, with the probability distribution of finding a local surrounding with i of 6 possible positions being occupied by iron atoms. For further details of the signal assignment in δ-(Al0.3,Fe0.7)OOH (c.f.20). Signals associated to fully Fe3+ depleted H-bond environments (Q0) lie below the detection limit of our experiments. Interestingly, the signal associated to four ferric iron paramagnetic centres occupying next-nearest neighbour positions (Q4) was found to be much broader than to the other H-bond environments, possibly due to significant gradients in the local magnetic field stemming from an asymmetric distributions of paramagnetic centres, further hyperfine interactions or signal overlap28. The spectrum shown in Fig. 3a was recorded by oversampling in the indirect Lee-Goldburg dimension F2, other spectra were recorded using faster F2 sampling and therefore reduced resolution due to experimental time restrictions and solely intense signals Q3, Q5 and Q6 were recorded over the full pressure (see Methods section).
a High-resolution 2D-Lee Goldburg (LG) spectrum of δ-(Al0.3,Fe0.7)OOH at 15.7 GPa showing up to six distinguishable hydrogen signals in the indirect LG projection F220. Assuming a stochastic distribution of ferric iron in the sample, a comparison with signal intensities allows for the assignment of the H-bond species Qi(i = 1–6). Spectra at different pressures were recorded at reduced resolution due to experimental time restrictions and solely signals from Q3, Q5 and Q6 species were recorded over the full pressure range. The integration limits for 2D signal intensity determination were defined by 35 kHz in the direct time domain F1 and by the FWHM of each signal in the indirect LG-projection dimension F2. The colored regions are guide to the eyes and do not correspond to the integration limits. b High-resolution 2D-LG spectra of dense magnesium silicate phase-D, showing a shift towards lower chemical shifts at the HS → LS crossover (Fig. 4a). Measurements were conducted at a magnetic field of 7.04 T. 1H-NMR solid-echos of c δ-AlOOH and d H2O ice-VII/X as a function of pressure. Measurements were conducted at a magnetic field of 1.2 T. Figures a and b are reproduced from ref. 20; licensed under a Creative Commons Attribution (CC BY) license.
At ambient conditions, the resonance frequencies of these signals were found to be ω − ω0 = 80, 365 and 506 ppm for Q3, Q5 and Q6, respectively (Fig. 4a). The origin of such a pronounced proton resonance shift can reasonably be expected to be hyperfine interaction of the hydrogen nuclei with localised electron moments of Fe3+ ions, which should be modulated at the electron spin crossover around V/V0 ≈ 0.85 to 0.80. Indeed, we find a significant reduction in resonance frequency of all three signals at V/V0 ≤ 0.78, in excellent agreement with Mössbauer spectroscopy (see Methods section), evidencing the paramagnetic origin of these signals. Additionally, we observe a discontinuity in resonance shift at a relative compression of V/V0 = 0.94 (Fig. 4a) in all Qi and therefore independent of the local iron content, which we associate with the sub- to super-group phase transition from P21nm to Pnnm at P ≃ 10 GPa10,21,30.
a Top panel: Resonance shift found in 1H-NMR solid echos of H2O ice VII/X (gray). The signal shift of the resonances follows the dependence previously reported at high magnetic fields13: after an initial decrease up to 20 GPa (V/V0 ≈ 0.68), the signals are shifted downfield corresponding to the transition from a high to low barrier hydroge- bond regime. The second jump at 73 GPa (V/V0 ≈ 0.52) signifies the onset of the ice-VII → X crossover. Lower panel: Resonance shift of δ-AlOOH (green), δ-(Al,Fe)OOH (red, brown and yellow corresponding to Qi (i = 1...3) respectively) and phase-D (blue) as a function of the relative volume. Both δ-AlOOH and δ − (Al0.3,Fe0.7)OOH undergo a sub to supergroup phase transition from P21nm to Pnnm which was observed at V/V0 ≈ 0.94 by a sudden increase of the shift by about 5–10 ppm. Between V/V0 ≈ 0.83 − 0.78, both iron bearing δ-(Al0.3,Fe0.7)OOH as well as phase-D undergo an electron spin crossover, resulting in a partial reduction of the paramagnetic shift interaction as well as a volume collapse observed in Q3, Q5 and Q6. The red arrows mark the points of maximum hydrogen mobility. Error bars, center of gravity of resonance signals, are within symbol size. b Normalized FWHM line widths (same color code as in a), i.e. along F1 for the 2D-LG NMR spectra and in the direct frequency domain for the one dimensional spectra, as a function of rOO. All investigated systems go through a maximum of proton mobility (shaded area in the graph), i.e. motional narrowing of resonance lines and a consequent minimum of FWHM line widths at critical oxygen-oxygen distances between \({r}_{{{{{{{{\rm{OO}}}}}}}}}^{{{{{{{{\rm{crit}}}}}}}}}=2.44\) and 2.45, with an average value of \({\bar{r}}_{{{{{{{{\rm{OO}}}}}}}}}^{{{{{{{{\rm{crit}}}}}}}}}=2.443(1)\) Å. Error bars stem from fitting of FWHM linewidths using Voigtian lineshapes.
1H-NMR signals of dense magnesium silicate phase-D (Fig. 3b) show a narrow resonance in the indirect LG-projection frequency domain F2, indicating a single, well defined coordination of hydrogen atoms. The observed frequency shift of the signals (Fig. 4a) towards lower ppm values coincides with the electron spin crossover of ferric iron Fe3+ in δ-(Al0.3,Fe0.7)OOH. Therefore, we assume the observed signals to stem from hydrogen atoms predominantly influenced by the presence of Fe3+ ferric iron in phase-D. Signals shifted by the presence of Fe2+ ferrous iron (see Methods section) were not observed in the chosen spectral range.
One-dimensional solid echo NMR spectra of pure δ-AlOOH (Fig. 3c) at 1.2 T show a single signal at ω − ω0 ≈ 0 ppm close to the anticipated position of ferric iron depleted Qi species in the iron bearing oxide-hydroxide analogue, indicating a well defined hydrogen position in agreement with earlier NMR studies under ambient conditions31. Similar to δ-(Al0.3,Fe0.7)OOH, we associate the discontinuity at V/V0 = 0.94 (Fig. 4a) to the aforementioned sub- to super-group phase transition.
Earlier high-resolution 1H-LG NMR experiments on δ-AlOOH at similar magnetic fields and pressures10 indicated that the observed signals are comprised of only a single spectral contribution influenced by a minor chemical shift anisotropy. Influences of smaller pressure gradients might influence the shape of the presented spectra, but are expected to be marginal due to the Argon pressure transmitting medium used to ensure quasi-hydrostatic conditions. Figure 3d shows representative 1H-NMR spectra of H2O ice-VII/X recorded at 1.2 T. We observe two distinct transitions in the P dependence of the resonance frequencies (Fig. 4a): (i) At V/V0 = 0.66 (20 GPa), after a continuous shift of about 40 ppm up-field, the proton signals showed a sudden discontinuity of ≈55 ppm, indicating the transition from the high to low barrier hydrogen-bond regime in ice-VII, where the number of tunnelling protons is increasing7,8 and (ii) at V/V0 = 0.51 (73 GPa) a discontinuity of ≈20 ppm associated with the beginning of the continuous transition from ice-VII to ice-X. This behaviour is in excellent agreement with our previous study13.
In order to find a common parameter indicating the onset of the hydrogen-bond symmetrization, we calculate the full width at half maximum (FWHM) line-widths as a function of P as well as relative compression (V/V0). We analyse the change in line-width as an indicator for changes in proton mobility. The small sample sizes (10 pl) are required for our high-pressure experiments, very long data acquisition times are necessary which prohibits an analysis of other NMR parameters, such as spin-spin or spin-lattice relaxation times which would provide an even more detailed picture of hydrogen dynamics. We find a minimum in the 1H-NMR FWHM line-widths in all signals. These minima occur within a wide compression range, i.e. V/V0 ≈ 0.92 to 0.55 (red arrows in Fig. 4a), corresponding to P between 11 to 50 GPa. We furthermore calculate the FWHM as a function of the respective oxygen-oxygen distances (rOO) for all four compounds, resolving different local environments (Qi) in δ − (Al0.3,Fe0.7)OOH (Fig. 4b). Surprisingly, all signals were found to have a continuous transition through this pronounced minimum at almost identical O-O distances \({r}_{{{{{{{{\rm{OO}}}}}}}}}^{{{{{{{{\rm{crit}}}}}}}}}=2.44\) and 2.45, with an mean value of \({\bar{r}}_{{{{{{{{\rm{OO}}}}}}}}}^{{{{{{{{\rm{crit}}}}}}}}}=2.443(1)\) Å. Several possible error sources might lead to a minor modulation of this value, such as insufficient diffraction data above 40 GPa in the electronic low spin state or the interpolation of the rOO evolution of the Qi species in δ-(Al0.3,Fe0.7)OOH. Nevertheless, estimating errors based on these effects was found to not significantly alter the position of the observed minima but only the respective width and thus the spread of \({r}_{{{{{{{{\rm{OO}}}}}}}}}^{{{{{{{{\rm{crit}}}}}}}}}\) (c.f. inset in Fig. 4b). In absence of magic angle spinning32 or Lee-Goldburg derived experiments20, line narrowing in NMR mainly originates from two distinct mechanisms: (i) local structural symmetrization, leading to sharper resonance line distributions (structural narrowing) and (ii) local diffusive motion of the probed nuclei leading to an averaging of short range electromagnetic interactions (dynamic narrowing)27.
While the first effect is particularly pronounced in quadrupolar NMR as the electric nuclear quadrupole moment of any I > 1/2 nucleus is a sensitive probe of the local electronic environment and charge distribution; such an effect might not be very pronounced for I = 1/2 (e.g. 1H) nuclei. Contrarily, moderate dynamic averaging of hydrogen NMR resonances is a well established diagnostic tool to identify locally restricted low amplitude motions and has even been employed to determine hydrogen diffusivities in diamond anvil cell based research33. This minimum indicates the point of maximum hydrogen diffusivity within the H-bond, leading to a striking conclusion. At low pressures and long rOO ≈ 2.60 − 2.50 Å, hydrogen mobility continuously increases. At \({r}_{{{{{{{{\rm{OO}}}}}}}}}^{{{{{{{{\rm{crit}}}}}}}}}\), hydrogen mobility reaches a maximum, i.e. minimum in the FWHM line width, as the majority of protons de-localise.
Even more interesting is the fact that the point of maximum hydrogen de-localisation in the oxide-hydroxides and phase-D, possessing a single-well H-bond energy potential is nearly identical to the maximum found in H2O ice-VII/X characterised by a pronounced double-well character and correlated proton tunnelling7,34. This indicates that the observed effect is in a region of \({r}_{{{{{{{{\rm{OO}}}}}}}}}^{{{{{{{{\rm{crit}}}}}}}}}\) where the barrier of the double-well potential is already negligible compared to the protons energy and therefore that the high-P regime is independent of the low-P symmetry of the H-bond potential and associated tunnelling.
Being a primer for hydrogen-bond symmetrization or, more accurately, for hydrogen localisation as the diffusive motion of protons diminishes at \({r}_{{{{{{{{\rm{OO}}}}}}}}}\, < \,{r}_{{{{{{{{\rm{OO}}}}}}}}}^{{{{{{{{\rm{crit}}}}}}}}}\), this hydrogen mobility maximum is spread over a surprisingly wide range of over 40 GPa, ranging from 11 GPa in δ-AlOOH to about 50 GPa in H2O ice-VII/X. Since the FWHM linewidth dependencies are comparable in all observed samples, despite significantly different charge distributions of the respective environment (ratio of Al and Fe in Qi, O, etc.) as well as 3D (e.g. H2O ice-VII/X) and 2D (e.g. δ-AlOOH) hydrogen-bond networks, it is reasonable to assume that this effect is universal for all linear O-H ⋯ O hydrogen-bonded materials regardless of their long range atomic structure.
Furthermore, it has been argued that H-bond symmetrization or hydrogen localisation might be a primer to electron spin crossovers in iron bearing hydrous minerals like oxide-hydroxides25,35. Contrary, our NMR data clearly demonstrates that electron spin transitions and pressure induced hydrogen localisation are independent physical phenomena.
In this study, we have shown that the onset of hydrogen-bond symmetrization and therefore proton localisation as a consequence of the modulation of the H-bond energy potential is a phenomenon inherent to a wide variety of materials ranging from high-P H2O ices to (iron-bearing) oxide-hydroxides. The observed samples were found to follow identical scaling behaviour in the O-H⋯O oxygen-oxygen distance rOO, solely dependent on the short range atomic and electronic structure. We identified an average critical oxygen-oxygen distance of \({\bar{r}}_{{{{{{{{\rm{OO}}}}}}}}}^{{{{{{{{\rm{crit}}}}}}}}}=2.443(1)\) Å, where the delocalisation of hydrogen atoms in H-bonds shows a pronounced maximum.
Methods
Sample preparation and characterisation
H2O ice-VII/X & δ-AlOOH
The sample preparation and measurement of the H2O ice-VII/X and δ-AlOOH data is in detail described in refs. 36 and10,21.
δ-(Al0.3,Fe0.7)OOH
A mixture of regeant grade FeOOH and Al(OH)3 with a molar ratio of 7: 3 was used as starting material. Single crystals of ϵ-(Fe,Al)OOH were synthesized using a 1000-ton Kawai-type multi-anvil high-pressure apparatus at Bayerisches Geoinstitut, University of Bayreuth, Germany. Tungsten carbide (WC) anvils with 4-mm truncated edge lengths were used to compress the sample in combination with a 5 wt% Cr2O3-doped MgO octahedral pressure medium with a 10 mm edge length. A cylindrical LaCrO3 heater was set at the center of the pressure medium. The starting material was packed in a platinum capsule, which was welded shut. The sample capsule was inserted in an MgO capsule and put at the central part of the heater. Sample temperature was monitored at the central part of the outer surface of the Pt capsule using a W − 3%Re/W − 25%Re thermocouple, neglecting pressure effects on electromotive force of the thermocouple.
The sample was compressed to a desired press load at room temperature and then heated to a target temperature of 1200 ∘C at a rate of 100 ∘C/min. After keeping this temperature for 180 min, the sample was quenched by turning off electrical power and slowly decompressing to ambient pressure for 15 h.
Recovered single crystals with dimensions up to 200 μm were selected based on the absence of twinning and sharp optical extinction using a polarizing microscope. The crystals were mounted on a glass fibre and X-ray diffraction (XRD) data collected using a Huber Eulerian cradle single-crystal diffractometer driven by the SINGLE software37. The diffractometer was equipped with a Mo Kα X-ray source and operated at 50 kV and 40 mA. Crystals with a half-width of the diffraction peaks less than 0.1∘ were further analysed in terms of their cell parameters with the vector least-squares method38. The effect of crystal offsets and diffractometer aberrations for each crystal was eliminated using the eight-position centring method39. The crystal had the space group of P21nm and lattice parameters of a = 2.9573(1) Å, b = 4.3884(1) Å, c = 4.8873(2), V = 63.426(4) Å3.
Chemical compositions of the samples were measured using an electron microprobe analyzer (EPMA) with wavelength-dispersive spectrometers (JEOL, JXA-8200) operated at 15 kV and 10 nA, for 20 s on the peaks of Al and Fe and 10 sec on the background. Synthetic hematite and corundum were used as standard material for Fe and Al, respectively. The composition of the dark-red crystals was expressed as (Al0.305(9),Fe0.695(9))OOH, assuming that the cation number of hydrogen is one.
(Mg0.88,Fe0.12)(Si0.9,Al0.1)2O6H2 phase-D
A starting material was prepared as a powdered mixture of regent grade chemicals of Mg(OH)2 (45.11 wt.%), SiO2 (38.02 wt%), Al(OH)3 (5.48 wt.%) and 57Fe enriched Fe2O3 (11.38 wt.%). Single crystals of hydrous phase-D were synthesized using a 1200-ton Kawai-type multi-anvil high-pressure apparatus at Bayerisches Geoinstitut, University of Bayreuth, Germany . Tungsten carbide anvils with 3 mm truncated edge lengths were used in combination with a 5 wt% Cr2O3-doped MgO octahedral pressure medium with a 7-mm edge length. A cylindrical LaCrO3 heater was located at the center of the pressure medium. The starting material was packed in a welded platinum capsule. The sample capsule was inserted in an MgO capsule and put at the central part of the heater. Sample temperature was monitored at the central part of the outer surface of the Pt capsule using a W-3%Re/W-25%Re thermocouple. Pressure effect on electromotive force of the thermocouple was ignored.
The sample was compressed to a desired press load at room temperature and then heated to a target temperature of 1100 ∘C at a rate of 100 ∘C/min. After keeping this temperature for 240 min, the sample was quenched by turning electrical power off and slowly decompressed to ambient pressure for 15 h. Chemical composition of the recovered hydrous phase-D was determined using an electron microprobe analyzer (EPMA) with wavelength-dispersive spectrometers (JEOL, JXA-8200) operated at 15 kV and 10 nA, for 20 s on the peaks of Al and Fe and 10 s on the background. Natural enstatite for Mg and Si, synthetic hematite for Fe and corundum for Al were used as standard material.
Mössbauer spectroscopy
Mössbauer absorption spectra were collected at ambient temperature in a diamond anvil cell at the Nuclear Resonance beamline (ID18) at the European Synchrotron Radiation Facility (Grenoble) using Synchrotron Moessbauer (SMS) Source spectroscopy40. The experiment was conducted in transmission geometry and folded spectra contained 512 channels. The line width of the SMS was determined before and after collection of each pressure point by measuring the reference single line absorber (K2Mg57Fe(CN)6). The Mössbauer spectra were fitted using MossA software41 with the full transmission integral assuming a Lorentzian-squared line shape of the SMS. Isomer shift values are referred to that of α-Fe at 300 K.
57Fe Mössbauer spectra of phase-D measured at ambient pressure and temperature show broadened asymmetric paramagnetic doublets, indicating a superposition of several subspectra. The spectra were interpreted as a mixture of two quadrupole doublets. The value of the isomer shift δ = 0.36(1)mm/s of one subspectrum corresponds to high-spin (HS) ions Fe3+(d5, S = 5/2) located in oxygen octahedra. Sub-spectra showing high values of isomer shifts δ = 1.22(2) mm/s are characteristics of high-spin ferrous iron Fe2+(d6, S = 2)42. The high quadrupole splittings Δ of the doublets 0.81(5) mm/s and 2.19(3) mm/s showed that iron ions are located in crystal positions with a strong electric-field gradient, characteristic to a Al/Mg substitution in the phase-D crystal lattice.
Upon compression, SMS spectra change drastically: above 25 GPa, spectra can no longer be described by only two doublets. Additional sub-spectra correspond to low-spin ferrous iron, indicating the onset of a HS → LS spin crossover. The ferric to ferrous iron ratio was constant throughout the whole compression range.
Above 36 GPa, SMS signatures of HS ferric iron are lost and new sub-spectra with characteristic hyperfine parameters of LS Fe3+ appear indicating another long range spin crossover. Isomer shifts LS Fe3+ are lower than in the high-spin state and quadrupole splitting was found amplified due enhanced electric field gradients, associated with the non-uniform distribution of uncompensated 3d − t2g valence electrons. The pressure dependence of hyperfine parameters show no anomalous changes in the local environment of the iron ions.
NMR-DAC preparation
DACs for high-pressure NMR experiments were prepared following a procedure described in e.g43,44. First, rhenium gaskets were indented to the desired thickness, which depends on the size of the diamond anvil culets employed, but usually ≲ 25μm. Sample cavities were drilled using specialized laser drilling equipment. After gasket preparation, the diamond anvils were covered with a layer of 1 μm of copper or gold using chemical vapour deposition. To ensure the electrical insulation of the conductive layers from the rhenium gasket, the latter were coated by a thin layer (≈500 nm) of Al2O3 using physical vapour deposition. The Lenz lens resonators were shaped from the conductive layer on the diamonds by using focused ion beam milling.
Before the final cell assembly, radio frequency resonators were prepared accordingly to their desired operation frequency. A pair of high inductance solenoid coils (≈100 nH) for low frequency experiments of below 100 MHz or a pair of single turn printed circuit board (PCB) plated copper resonators for 1H-NMR frequencies at high fields were used as driving coil arrangements for the Lenz lens resonators’ structure and were placed around each diamond anvil. After sample loading and initial pressurisation, the driving coils were connected to form a Helmholtz coil-like arrangement.
Pressure calibration was performed using the shift of the first derivative of the first order Raman signal of the diamond edge in the center of the culet45,46. All DACs were fixed and connected to home built NMR probes equipped with customized cylindrical trimmer capacitors (dynamic range of ≈150 pF) for frequency tuning to the desired resonance frequencies and impedance matching to the spectrometer electronics (50Ω).
Proton shift referencing was conducted using the 63Cu resonances of the Lenz lenses themselves as internal references taking into account the additional shielding of B0 inherent to every DAC. These resonances were cross referenced with standard metallic copper samples at ambient conditions without a DAC. The resulting shift between both 63Cu-NMR signals are then used as a primer for the NMR signals of the samples under investigation.
Lee-Goldburg decoupling experiments were initially calibrated by quick two-dimensional nutations (~56 2D spectra) for different off resonant frequencies of the LG-pulse. Optimal pulse offset frequencies ωoff were found between 25 to 35 kHz. One dimensional LG-spectra were recorded by oversampling in the indirect time domain using previously determined values of ωoff at a pulse power of about 100 mW attenuation relative to the excitation pulse. Two dimensional LG spectra were recorded with identical direct and indirect time domains (usually 2048 points in each dimension), while matching the incrementation of the LG-pulse to the direct time domain dwell time of the spectrometer.
X-ray diffraction
Single crystal X-ray diffraction data for phase-D and δ-(Al0.3,Fe0.7)OOH were collected at the beamlines P02.2 (PETRA III, DESY, Hamburg, Germany) and ID15 (ESRF, Grenoble, France). At PETRA III the data were collected using Perkin Elmer XRD1621 flat panel detector and X-rays with the wavelength λ = 0.2887 Å. For the different experiments at ID15 the beamline was equipped with a MAR555 flat panel or a EIGER2 X 9M CdTe (340 × 370 mm) detector. Before collecting XRD data, the experimental geometry was precisely defined based on freshly collected diffraction data from enstatite (at PETRA III) or a vanadinite callibrant (ESRF). The X-ray energy at ID15 was 30 keV and the wavelength is λ = 0.4133 Å, while the beamsize was ~10 μm in FWHM. In all our experiments, at each pressure point data collection was performed in an omega range of least ± 32∘ with 0.5∘ step per frame and an exposure time of 1 to 3 s per step. Integration of the reflection intensities and absorption corrections were performed using the CrysAlisPro software. Structure solution and refinement were done in the isotropic approximation using Jana200647 with Superflip48 and SHELXT49.
Data availability
The data supporting the findings of this study are publicly available from the corresponding author upon request.
Code availability
Python code used for analysing NMR data is available from the corresponding author upon request.
References
Bercovici, D. & Karato, S.-I. Whole-mantle convection and the transition-zone water filter. Nature 425, 39–44 (2003).
Inoue, T. Effect of water on melting phase relations and melt composition in the system Mg2SiO4-MgSiO3- H2O up to 15 GPa. Phys. Earth Planet. Inter. 85, 237–263 (1994).
Karato, S.-I., Paterson, M. S. & FitzGerald, J. D. Rheology of synthetic olivine aggregates: Influence of grain size and water. J. Geophys. Res. Solid Earth 91, 8151–8176 (1986).
Yoshino, T., Matsuzaki, T., Yamashita, S. & Katsura, T. Hydrous olivine unable to account for conductivity anomaly at the top of the asthenosphere. Nature 443, 973–976 (2006).
Hu, Q. & Mao, H.-K. Role of hydrogen and proton trans portation in Earth’s deep mantle. Matter Radiat. Extremes 6, 068101 (2021).
Thompson, A. B. Water in the Earth’s upper mantle. Nature 358, 295–302 (1992).
Trybel, F., Cosacchi, M., Meier, T., Axt, V. M. & Steinle-Neumann, G. Proton dynamics in high-pressure ice-VII from density functional theory. Phys. Rev. B 102, 184310 (2020).
Méndez, A. S. J. et al. Bulk modulus of H2O across the ice VII-ice X transition measured by time-resolved x-ray diffraction in dynamic diamond anvil cell experiments. Phys. Rev. B 103, 064104 (2021).
Benoit, M., Romero, A. H. & Marx, D. Reassigning hydrogen-bond centering in dense ice. Phys. Rev. Lett. 89, 145501 (2002).
Trybel, F., Meier, T., Wang, B. & Steinle-neumann, G. Absence of proton tunneling during the hydrogen bond symmetrization in δ -AlOOH. Physical Review B, 104, 104311 (2021).
Pillai, S. B., Jha, P. K., Padmalal, A., Maurya, D. & Chamyal, L. First principles study of hydrogen bond symmetrization in δ-AlOOH. J. Appl. Phys. 123, 115901 (2018).
Cortona, P. Hydrogen bond symmetrization and elastic constants under pressure of δ-AlOOH. J. Phys.: Condens. Matter 29, 325505 (2017).
Meier, T., Petitgirard, S., Khandarkhaeva, S. & Dubrovinsky, L. Observation of nuclear quantum effects and hydrogen bond symmetrisation in high pressure ice. Nat. Commun. 9, 2766 (2018).
Lin, L., Morrone, J. A. & Car, R. Correlated tunneling in hydrogen bonds. J. Stat. Phys. 145, 365–384 (2011).
Goncharov, A. F., Struzhkin, V. V., Somayazulu, M. S. & Hemley, R. J. Compression of Ice to 210 Gigapascals : Infrared Evidence for a Symmetric Hydrogen- Bonded Phase Published by : American Association for the Advancement of Science Stable. Science 273, 218–220 (1996).
Li, X., Shi, W., Liu, X. & Mao, Z. High-pressure phase stability and elasticity of ammonia hydrate. Am. Mineralogist: J. Earth Planet. Mater. 104, 1307–1314 (2019).
Ahart, M. et al. Brillouin scattering of h2o ice to megabar pressures. J. Chem. Phys. 134, 124517 (2011).
Meier, T. & Haase, J. Anvil cell gasket design for high pressure nuclear magnetic resonance experiments beyond 30 GPa. Rev. Sci. Instrum. 86, 123906 (2015).
Meier, T. Journey to the centre of the Earth: Jules Vernes’ dream in the laboratory from an NMR perspective. Prog. Nucl. Magn. Reson. Spectrosc. 106-107, 26–36 (2018).
Meier, T. et al. In situ high-pressure nuclear magnetic resonance crystallography in one and two dimensions. Matter Radiat. Extremes 6, 068402 (2021).
Simonova, D. et al. Structural study of δ-Alooh up to 29 Gpa. Minerals 10, 1–10 (2020).
French, M. & Redmer, R. Construction of a thermodynamic potential for the water ices VII and X. Phys. Rev. B 91, 014308 (2015).
Hsieh, W.-P. et al. Spin transition of iron in δ-(Al, Fe) OOH induces thermal anomalies in Earth’s lower mantle. Geophys. Res. Lett. 47, e2020GL087036 (2020).
Thompson, E. C. et al. Phase transitions in ε-FeOOH at high pressure and ambient temperature. Am. Mineralogist: J. Earth Planet. Mater. 105, 1769–1777 (2020).
Xu, W. et al. Pressure-induced hydrogen bond symmetrization in iron oxyhydroxide. Phys. Rev. Lett. 111, 1–5 (2013).
Lee, M. & Goldburg, W. I. Nuclear-magnetic-resonance line narrowing by a rotating rf field. Phys. Rev. 140, 1261–1271 (1965).
Slichter, C. P. Principles of Magnetic Resonance. 2nd edn (Springer, Berlin, Heidelberg, 1978).
Pell, A. J., Pintacuda, G. & Grey, C. P. Paramagnetic NMR in solution and the solid state. Prog. Nucl. Magn. Reson. Spectrosc. 111, 1–271 (2019).
Levitt, M. H. Spin dynamics: basics of nuclear magnetic resonance, 2nd edition. (John Wiley & Sons., 2013).
Sano-Furukawa, A. et al. Direct observation of symmetrization of hydrogen bond in δ-AlOOH under mantle conditions using neutron diffraction. Sci. Rep. 8, 1–9 (2018).
Xue, X. & Kanzaki, M. High-Pressure δ-Al(OH) 3 and δ-AlOOH Phases and Isostructural Hydroxides/Oxyhydroxides: New Structural Insights from High-Resolution 1 H and 27 Al NMR. J. Phys. Chem. B 111, 13156–13166 (2007).
Hennel, J. W. & Klinowski, J. Magic-Angle Spinning: a Historical Perspective. In New Techniques in Solid-State NMR. Topics in Current Chemistry (ed. Klinowski, J.), 246 edn. Vol. 2, 1-14 (Springer, Berlin, Heidelberg, 2005) http://link.springer.com/10.1007/b98646.
Meier, T. et al. Proton mobility in metallic copper hydride from high-pressure nuclear magnetic resonance. Phys. Rev. B 102, 1–8 (2020).
Lin, L., Morrone, J. A. & Car, R. Correlated Tunneling in Hydrogen Bonds. J. Stat. Phys. 145, 365–384 (2011).
Gleason, A. E., Quiroga, C. E., Suzuki, A., Pentcheva, R. & Mao, W. L. Symmetrization driven spin transition in ϵ-FeOOH at high pressure. Earth Planet. Sci. Lett. 379, 49–55 (2013).
Meier, T. et al. NMR at pressures up to 90 GPa. J. Magn. Reson. 292, 44–47 (2018).
Angel, R. J. & Finger, L. W. SINGLE: A program to control single-crystal diffractometers. J. Appl. Crystallogr. 44, 247–251 (2011).
Ralph, R. L. & Finger, L. W. A computer program for refinement of crystal orientation matrix and lattice constants from diffractometer data with lattice symmetry constraints. J. Appl. Crystallogr. 15, 537–539 (1982).
King, H. E. & Finger, L. W. Diffracted beam crystal centering and its application to high-pressure crystallography. J. Appl. Crystallogr. 12, 374–378 (1979).
Potapkin, V. et al. The 57 Fe Synchrotron Mössbauer Source at the ESRF. J. Synchrotron Radiat. 19, 559–569 (2012).
Prescher, C., McCammon, C. & Dubrovinsky, L. MossA : a program for analyzing energy-domain Mössbauer spectra from conventional and synchrotron sources. J. Appl. Crystallogr. 45, 329–331 (2012).
Menil, F. Systematic trends of the 57Fe Mössbauer isomer shifts in (FeOn) and (FeFn) polyhedra. Evidence of a new correlation between the isomer shift and the inductive effect of the competing bond T-X (→Fe) (where X is O or F and T any element with a formal posit. J. Phys. Chem. Solids 46, 763–789 (1985).
Meier, T. et al. Magnetic flux tailoring through Lenz lenses for ultrasmall samples: A new pathway to high-pressure nuclear magnetic resonance. Sci. Adv. 3, eaao5242 (2017).
Meier, T. et al. Pressure-Induced Hydrogen-Hydrogen Interaction in Metallic FeH Revealed by NMR. Phys. Rev. X 9, 031008 (2019).
Akahama, Y. & Kawamura, H. High-pressure Raman spectroscopy of diamond anvils to 250 GPa: Method for pressure determination in the multimegabar pressure range. J. Appl. Phys. 96, 3748 (2004).
Akahama, Y. & Kawamura, H. Pressure calibration of diamond anvil Raman gauge to 310GPa. J. Appl. Phys. 100, 043516 (2006).
Petr^íček, V., Dušek, M. & Palatinus, L. Crystallographic computing system JANA2006: general features. Z. f.ür. Kristallographie-Crystalline Mater. 229, 345–352 (2014).
Palatinus, L. & Chapuis, G. SUPERFLIP–a computer program for the solution of crystal structures by charge flipping in arbitrary dimensions. J. Appl. Crystallogr. 40, 786–790 (2007).
Scheldrick, G. SHELXT-Integrated space-group and crystals-structure determination. Acta Crystallogr., Sect. A: Found. Adv. 71, 3–8 (2015).
Acknowledgements
We thank Nobuyoshi Miyajima for help with the FIB milling. We thank the German Research Foundation (Deutsche Forschungsgemeinschaft, DFG, Project Nos. DU 954/11-1 (L.D.), DU 393/13-1 (L.D.), DU 393/9-2 (L.D.), STE 1105/13-1 (G.S.N.) and ME 5206/3-1) (T.M.) and the Federal Ministry of Education and Research, Germany (BMBF, Grant No. 05K19WC1 (N.D.) for financial support. T.M. was supported by the Center for High Pressure Science and Technology Advance Research, Beijing, P.R. China. F.T. was supported by the Swedish Research Council (VR) Grant No. 2019-05600 (F.T.). D.L. thanks the Alexander von Humboldt Foundation for financial support. N.D. thanks the Swedish Government Strategic Research Area in Materials Science on Functional Materials at Linköping University (Faculty Grant SFO-Mat-LiU No. 2009 00971 (N.D.)).
Author information
Authors and Affiliations
Contributions
T.M. designed the experiments, prepared the DACs, conducted NMR experiments and analysed data. F.T. conducted DFT calculations and data analysis. S.K., D.L. and A.A. characterised samples using diffraction and moessbauer spectroscopy. T.I. synthesised samples. T.M., F.T., N.D. and L.D. wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Meier, T., Trybel, F., Khandarkhaeva, S. et al. Structural independence of hydrogen-bond symmetrisation dynamics at extreme pressure conditions. Nat Commun 13, 3042 (2022). https://doi.org/10.1038/s41467-022-30662-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-022-30662-4
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.