Abstract
Intermetallic compounds containing f-electron elements have been prototypical materials for investigating strong electron correlations and quantum criticality (QC). Their heavy fermion ground state evoked by the magnetic f-electrons is susceptible to the onset of quantum phases, such as magnetism or superconductivity, due to the enhanced effective mass (m*) and a corresponding decrease of the Fermi temperature. However, the presence of f-electron valence fluctuations to a non-magnetic state is regarded an anathema to QC, as it usually generates a paramagnetic Fermi-liquid state with quasiparticles of moderate m*. Such systems are typically isotropic, with a characteristic energy scale T0 of the order of hundreds of kelvins that require large magnetic fields or pressures to promote a valence or magnetic instability. Here we show the discovery of a quantum critical behaviour and a Lifshitz transition under low magnetic field in an intermediate valence compound α-YbAlB4. The QC origin is attributed to the anisotropic hybridization between the conduction and localized f-electrons. These findings suggest a new route to bypass the large valence energy scale in developing the QC.
Similar content being viewed by others
Introduction
A quantum critical point (QCP) occurs when the ground state of a system is continuously tuned between two states1,2. The strong incipient quantum fluctuations modify the system’s electronic state over large regions of its phase diagram. This has led to the notion that understanding quantum criticality (QC) is the key to understanding emergent phases in materials such as spin liquids and the high temperature superconductors.
Heavy fermion (HF) materials, mainly f-electron based intermetallics containing Ce or Yb, have been prototypical for the investigation of QC1,2,3,4: the enhanced entropy of the Fermi sea makes them susceptible to low temperature instabilities such as magnetism and superconductivity. The energy differences between these possible ground states are small, and therefore can typically be tuned by applying small magnetic field or pressure.
However, the conventional paradigm of QC in HF materials, the Doniach phase diagram and its recent extensions5, requires a stable valence of the magnetic ion, which for Yb is the 3+ state. In Yb intermetallics with fluctuating valence, such as YbAl3 or YbAgCu4, a large valence fluctuation energy scale T0 makes new phases difficult to achieve; YbAl3 is not known to order magnetically at all6, while YbAgCu4 requires extremely high pressure7.
The recently synthesized YbAlB4 is therefore remarkable because QC coexists with intermediate valence, +2.73 and +2.75 for both, α and β polymorphs8, respectively. Both materials have a valence fluctuation scale T0 ≈ 200 K8,9 and a negligible change of valence10 in magnetic fields up to 40 T. The two polymorphs of YbAlB4 are locally isostructural, with a highly anisotropic structure, atypical for intermediate valence systems, where sheets of boron separate the layers containing Yb and Al (Fig. 1a). Below the temperature T0 an expected Fermi liquid (FL) ground state should lead to a constant susceptibility (χ) and specific heat coefficient Ce/T = γ. Unusually, the Ising anisotropy along the c axis dominates9 in χ, and only for T < T* ≈ 8 K it saturates in α-YbAlB4, while in β-YbAlB4 it diverges due to QC at ambient conditions11. Nevertheless, the FL ground state of α-YbAlB4 is shown by the saturated γ value and T2-resistivity (ρ) at low temperatures. However, ρ remains very anisotropic9 with ρab/ρc ≈ 11, suggesting that the hybridization is much stronger within the ab plane than along the c axis. In this article we focus on α-YbAlB4 and show the presence of unconventional QC that can be easily tuned with a small magnetic field. We argue that the mechanism of QC is a strong hybridization anisotropy.
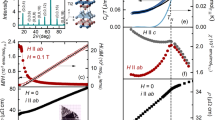
a Crystal structure of YbAlB4 formed from straight and zigzag arrangements of hexagons of Yb atoms, and the atomic neighborhood of Yb ions — the Yb site is shown in red together with the surrounding B and Al sites. B sites are colored in blue, yellow, green and orange according to their symmetry position, while Al is gray. b Thermal expansion ΔLc/Lc and thermal expansion coefficient \({\alpha }_{c}=d\left({{\Delta }}{L}_{c}/{L}_{c}\right)/dT\) along the c axis for several magnetic fields. The inset shows the field dependence of αc taken at 140 mK. c Magnetization and susceptibility χ = dM/dB vs B∥c at T = 0.08 K. d Electronic specific heat coefficient γe measured at 250 mK and Knight shift of the 11B nucleus vs B∥c measured at 142 mK. Vertical error bars in figure are least-square fit errors (1 s.d.).
In this work we use a complete set of thermodynamic, magnetotransport and microscopic experimental techniques to probe the electronic anisotropy of α-YbAlB4, as it is driven toward two electronic instabilities with a magnetic field that is small compared to T0 ≈ 200 K. Most prominently, we find that the sign of the thermal expansion, which directly probes the pressure dependence of the entropy12, changes at Bc = 3.6 T due to a change in the nature of the relevant fluctuation scale from magnetic correlations at lower fields, to the Kondo or valence correlations at higher fields – a signature of the proximity to a QCP. At a slightly lower field Bc = 2.1 T, the Shubnikov–de Haas measurements show the appearance of a new, strikingly anisotropic Fermi surface (FS), indicating a Lifshitz transition. We refer to these fields as B1 = 2.1 T and B2 = 3.6 T in what follows. At both of these fields nuclear magnetic resonance (NMR) measurements find a diverging spin lattice relaxation rate 1/T1 of 11B nuclei down to 50 mK. The magnetostriction, i.e. the rate of change of the lattice constant with magnetic field, is highly anisotropic: for the c axis the magnetostriction is maximum at B2, while for the a axis it is maximum at B1. The resistivity shows non-FL (NFL) behavior at B1 and B2 but only for current applied parallel to the c axis. The striking two dimensionality (2D) of the FS that appears at B1 is consistent with a Lifshitz transition, which was originally proposed for β-YbAlB413, while the change in energy scales at B2 indicates the proximity to a QCP. The discovery of a Lifshitz transition in an intermediate valence system at such a low field alone is remarkable, but its conjoint appearance with a QC indicates the emergence of a new physical mechanism. By combining complementary experimental techniques we propose that hybridization anisotropy, i.e. the momentum-dependent nature of the Kondo hybridization, provides the means for these phenomena to manifest at the small energy scales associated with fields B1 and B2 in contrast to the large intermediate valence energy scale. Our conclusion is supported by recent experimental verifications of anisotropic hybridization in YbAlB4 by ARPES14 and linear dichroism in core-level HAXPES15, but also by the unique properties of the thermoelectric power factor16.
Results
Ground state properties from macroscopic probes
We first describe the magnetic field dependence of the thermal expansion ΔLc/Lc, where Lc is the sample length along the c axis. At B = 0 T and low temperatures (T < 0.2 K) the linear thermal expansion coefficient αi is positive for both the i = a (not shown) and c axes (Fig. 1b), and the volume coefficient αVol > 0 already for T < T* ≈ 8 K. This is surprising since usually in Yb-based Kondo-lattice (KL) or intermediate valence systems αVol < 0, just like the magnetostriction \({\lambda }_{i}=d\left({{\Delta }}{L}_{i}/{L}_{i}\right)/dB\) (see Supplementary Note 1). However, αVol measures the pressure dependence of entropy, which in α-YbAlB4 implies that the dominant contribution does not arise from KL or intermediate valence type fluctuations, but from an energy scale that increases with pressure. In magnetic Yb-based systems this is usually (anti-)ferromagnetic (A)FM order mediated by the RKKY interaction17,18. In α-YbAlB4 the high Wilson ratio9 (χ0/γ0 ≈ 7) and αVol(B = 0) > 0 indicate the presence of FM correlations in the ground state. It has been found that pressure induces an AFM state in β-YbAlB4 through a first-order phase transition at 2.5 GPa19,20, and an AFM state emerges in α-YbAlB4 by Fe doping21,22 at 1.5%.
Under magnetic field the magnetic correlations are suppressed and the sign of αc changes between 3.3 T and 4 T, indicating a change of the relevant energy scale as expected at a crossover or a phase transition between an ordered and a disordered phase. At a QCP it is expected that αVol/T besides changing sign12 also becomes divergent. However, in α-YbAlB4 this change is rather smooth and asymmetric, similar to the QCP found in YbAgGe23, and the system remains paramagnetic (PM) on both sides of B2. This behavior is typical of metamagnetic materials, like Sr3Ru2O724 or CeRu2Si225 where the entropy is dominated by magnetic fluctuations (see Supplementary Note 1). The relatively smooth change in αVol/T suggests that α-YbAlB4 is located either close to a quantum critical endpoint, or in the proximity of a field-induced QCP. Within both scenarios a clear anomaly in magnetic susceptibility χ and specific heat coefficient γ is expected. The magnetization M and χ = dM/dB measured with B∥c are shown in Fig. 1c, with dM/dB displaying a clear enhancement at B2 before decreasing rapidly at higher magnetic field. However, compared with true metamagnetic materials the enhancement is weak and is not symmetric around B2. The same features are seen in the specific heat coefficient γ and in the NMR Knight shift 11K measured at the 11B nucleus, as shown in Fig. 1d. Since all three quantities are governed by the Fermi surface properties: γ ∝ χ ∝ 11K ∝ N(ϵF), with N(ϵF) the density of states at the Fermi level ϵF, it is clear that the anomaly at B2 involves a continuous reduction of N(ϵF) as a consequence of the suppression of the correlations by the magnetic field. This is different from a possible suppression of the HF state through a metamagnetic transition. In fact, when compared to HF metamagnetic compounds26 the value of B2 is not large enough. In α-YbAlB4 the relevant magnetic field scale, estimated from γ = 130 mJ/molK2, should exceed 20 T, and hence metamagnetism cannot account for the observed phenomena. Therefore, the QC signatures in α-YbAlB4 are unconventional. One of the ways we could confirm a QCP would be to find a diverging Güneisen parameter23 (Γ ∝ αVol/Ce). Unfortunately, a large nuclear contribution22 in specific heat upon subtraction introduces a great uncertainty in the Güneisen parameter. Hence, we turn to other techniques to check the nature of the transition at B2.
Intrinsic excitations tuned by magnetic field
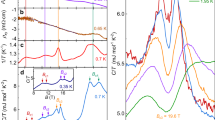
A rigorous test of the ground state properties is the character of underlying excitations. To probe them we have measured the NMR relaxation rate 1/T1 (see Methods) of the 11B nuclei (plotted in Fig. 2a, b) as a function of temperature at various magnetic fields for B∥c. The data are shown as \({({T}_{1}T)}^{-1}\) so that they can be easily contrasted to \({({T}_{1}T)}^{-1}\)= const. typical for FL state of simple metals at low temperature. Here we observe the FL state up to 1.5 T and below T*, where \({({T}_{1}T)}^{-1}\) is ≈0.7 K−1s−1. As the magnetic field approaches B2, we surprisingly find a pronounced divergence \({({T}_{1}T)}^{-1}\propto {T}^{-\delta }\) at low temperatures with exponent δ = 0.36. This power-law behavior persists down to 50 mK, two orders of magnitude lower than T*, and reveals the presence of quantum critical fluctuations that destabilize the FL and lead to a NFL ground state. Across B2 the NMR spectrum remains unchanged (Supplementary Figs. 1, 2a, b) which indicates no magnetic or charge order appears at B2, as the spectra would otherwise split due to symmetry breaking.
a (Lower panel) Density plot forming a B − T phase diagram of \({({T}_{1}T)}^{-1}\) on 11B sites showing the divergent behavior of spin fluctuations at the two critical fields B1 = 2.1 T and B2 = 3.6 T. (Upper panel) Cross section of \({({T}_{1}T)}^{-1}\) on 11B sites at T = 142 mK as indicated by the arrow in the lower panel. Vertical error bars are least-square fit errors (1 s.d.). b Temperature dependence of \({({T}_{1}T)}^{-1}\) at fields close to B1 (upper panel) and B2 (lower panel). Error bars are equal or smaller than symbol size, and they correspond to least-square fit errors (1 s.d.). The lines show a power law dependence of ∝ T−0.25 (upper panel) and ∝ T−0.36 (lower panel). The slight mismatch between the \({({T}_{1}T)}^{-1}\) values in (a) comes from a ~ 1∘ deviation in magnetic field orientation with respect to the c axis. c Density plot of the power law exponent of resistivity along the c axis and the A coefficient extracted at T = 0.1 K vs B∥c. d Magnetostriction coefficient λ vs B along both a and c- axes at T = 0.1 K and T = 4.2 K.
We have also analyzed the Knight shift behavior K = 〈bz〉/B, where 〈bz〉 is the hyperfine magnetic field at the nucleus site. While \({({T}_{1}T)}^{-1}\) is sensitive to spin excitations at q ≥ 0, the Knight shift is related to the static spin susceptibility χ(ω = 0, q ≈ 0), and for a FL it is expected to be constant against temperature and magnetic field. As seen in Fig. 1d (and Supplementary Figs. 3 and 4), for B < B2 the c-axis Knight shifts of 11B (11Kc) and 27Al (27Kc) nuclei are constant, and at B2 show a weak feature (similar to χ) confirming the absence of magnetic q = 0 mode at B1 and B2. Additionally, the NMR linewidth (Supplementary Fig. 2) is also consistent with the absence of magnetism. Across 4 T, both 11Kc and 27Kc show only a slow drop arising from N(ϵF). This lack of prominent static changes is also supported by measurements of the quadrupolar coupling of 27Al and 11B (Supplementary Fig. 5) that show only a small change.
So far, we have focused on the QC at B2 ≈ 3.6 T visible in thermodynamic and NMR measurements. In addition, the NMR measurements show the existence of another unusual behavior that suddenly appears at a lower field B1 ≈ 2.1 T. Indeed, the magnetic field dependence of the NMR relaxation rate \({({T}_{1}T)}^{-1}\) at 142 mK shows two pronounced peaks (Fig. 2a) at B1 and B2. The temperature dependence reveals another NFL power-law divergence at B1, \({({T}_{1}T)}^{-1}\propto {T}^{-\delta }\), with δ = 0.25 similar to the behavior at B2. Between B1 and B2 the system behaves as a standard metal, down to lowest temperatures, which indicates B1,2 are separate phenomena. Their qualitatively different nature is evidenced by the critical dynamics at B1 that, unlike the one at B2, shows no distinct signature in susceptibility or specific heat despite clear evidence of divergent spin fluctuations from the NMR.
Further indications about the nature of the transition at B1 are given by the magnetostriction coefficient λ, which is sensitive to structural, magnetic and electronic structure transitions, measured along the a axis (λa) and c axis (λc) with magnetic field B∥c (Fig. 2d). It can be seen that it shows a strong anisotropy: while λc(B) shows a maximum at B2 as expected from αc, λa(B) shows a maximum at the smaller field B1, which implies that it is related to a 2D effect within the ab plane.
Anisotropy in the critical behavior of α-YbAlB4 is also evidenced by resistivity measurements along the a and c axes, ρa and ρc, respectively. Low-temperature NFL behavior due to QC is quantified by observing the exponent ni and the coefficient \({A}_{i}\propto {m}_{i}^{2}\) as \({\rho }_{i}={\rho }_{0,i}+{A}_{i}{T}^{{n}_{i}}\), i = a, c (see Methods). At T = 0.1 K, Ac shows an enhancement (Fig. 2c) by ≈50% at B1 and B2 before decreasing at higher fields, and the exponent nc shows deviations (Fig. 2c) from the FL value of 2 in the vicinity of B1 and B2, where nc(B2) = 1.65 at the lowest measured temperature T = 0.04 K. Although this value is close to that expected at a FM or AFM QCP where n = 5/3 and 3/2, respectively27, since no magnetic order is observed, the QC of the pristine sample arises with the suppression of magnetic correlations. By contrast, β-YbAlB4 shows nab = 3/2 in ρab at its critical point consistent with the AFM QCP (even though fluctuations dominate28 χ(q ≈ 0)). Note that the NFL behavior in α-YbAlB4 occurs only for c-axis resistivity ρc, whereas na remains ≈2 for ρa (Supplementary Fig. 8). This shows that QC originates from specific regions of momentum space, in accordance with the anisotropic magnetostriction and the NMR data. Intrinsic electronic anisotropy is therefore a pivotal factor for understanding this system.
Properties of the Fermi surface
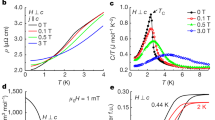
We now consider the changes in the electronic structure in the vicinity of B1 and B2 by measuring quantum oscillations (QO). Figure 3a shows ρc as a function of the magnetic field, from which we separate the slow-varying (ρMR) and the oscillatory (ρosc) component (see Methods). A clear kink in ρosc × B1/2 (Fig. 3b) is observed at 1/B1 ≈ 0.5 below which oscillations appear. The logarithmic scale is used to show that the amplitude decays linearly as expected from the Dingle relation. The amplitude is also shown against temperature in Fig. 3c, together with a fit to the Lifshitz-Kosevich (LK) relation, that describes the decay of QOs with T and gives m* = 0.55 ± 0.03. The excellent agreement to the LK relation confirms these are indeed QOs with frequency F = 10.2 T, while their sudden appearance at B1 suggests they emerge as the result of a Lifshitz transition at B1. This remarkable result makes α-YbAlB4 the first intermediate valence compound with a Lifshitz transition induced by such a low magnetic field.
a ρ, I∥c vs B∥c at T = 0.03 K, the overlaid black line is the non-oscillatory component, ρMR that is subtracted. b The oscillatory component of resistivity; ρosc × B1/2 plotted on a double logarithmic scale (values < 10−3 are plotted on a linear scale). c Temperature dependence of the Fourier transform of ρosc. d dρ/dB against B∥c at various angles of B in the [001] → [110] plane where θ = 0 ≡ B∥[001]. e (Upper panel) Hall coefficient B∥c at T = 0.06 K. (Lower panel) surface plot of Hall coefficient against field and temperature.
By rotating the sample relative to B we probe the extremal cross-section of this FS perpendicular to B. Figure 3d shows dρ/dB against the c-axis component of B, i.e. \(B\cos \theta\) where the B is rotated in the plane of [001] and [110]. The ρosc as a function of \(B\cos \theta\) remains unchanged for different field directions – indicating the FS is cylindrical and arises from 2D carriers, with a very small volume of this cylinder of 4 ⋅ 10−4 carriers per Brillouin zone. The 2D FS that emerges at B1 confirms the role of anisotropy in the electronic environment of the system. The QOs of different spin components of a 2D FS are normally split by the Zeeman interaction and interfere to produce spin zeros where the QO amplitude vanishes and the phase shifts by π. Using a g factor obtained by electron spin resonance29 and the determined value of m*, we would expect a strong angular dependence of the amplitude and a spin zero at θ = 60∘ (see Supplementary Note 3). However, no spin zeros are found, suggesting that this pocket is spin polarized. Taking mJ = 5/2, as deduced by theory30 and shown by experiment15, the magnetic moment of this pocket is 0.002μB, which is consistent with extremely small polarization increase observed in M in Fig. 1c. Therefore, considering both the primary evidence from QOs together with the consistency with macroscopic measurements, the results overwhelmingly indicate a Zeeman driven Lifshitz transition occurs at B1.
The 2D nature of the FS pocket, the divergence in \({({T}_{1}T)}^{-1}\) at the 11B site and the pronounced maximum in λa indicate that due to anisotropy the electronic properties within boron layers are most affected at B1. However, the small size of the FS pocket relative to the total number of carriers makes it difficult to account for the strong quantum critical fluctuations at B2 and suggests that larger sheets of the FS are affected. While large QO frequencies are observed at higher magnetic fields (see Supplementary Note 3), these were difficult to observe at low magnetic fields of B1 and B2, and we therefore turn to the Hall coefficient (RH) shown in Fig. 3e. RH decreases smoothly above B1, which would within a single-band model indicate a change in the carrier density by a factor of 2 with respect to the RH(B = B2) value. However, as this is not supported by the small changes in ρ, it could only be interpreted as changes in the FS velocity on larger sheets of the FS, and not as a second Lifshitz transition at B2. The \({({T}_{1}T)}^{-1}\) data, the anisotropic resistivity, sign change of thermal expansion and the gradual change in RH(H, T) therefore confirm that α-YbAlB4 is close to a QCP at the field B2.
Discussion
Intermediate valence compounds have been mainly outside the main focus of research on QC since, due to large characteristic energy scales of the valence fluctuations (e.g., T0 > 400 K in YbAl3), application of large magnetic fields or pressures is required to notably modify their properties or induce new phases31. In contrast, for both YbAlB4 polymorphs magnetic moments survive well below T0 ≈ 200 K, and become strongly correlated below T* ≈ 8 K, showing QC at low magnetic fields. Although the quantum critical behavior in the two polymorphs has different phenomenology, the pervasiveness of highly anisotropic Kondo hybridization in both compounds appears to be crucial for establishing it. In particular, the presence of a quantum critical behavior in different conditions for both, β-YbAlB4 (under ambient conditions, with doping and under increased pressure) and in α-YbAlB4 (without doping but under magnetic field, and with doping), leads to the conclusion that in YbAlB4 system, in the presence of strong electronic anisotropy, a robust physical mechanism emerges; one insensitive to the change of local symmetry and chemistry. The only energy scale that matches this description is the anisotropic Kondo hybridization, established by the crystal structure where Yb chains interpenetrate28 the sheets of B. The conventional picture of intermediate valence materials contains the hybridization energy scale Γ = πN(ϵF)∣V∣2, where V is Anderson’s coupling strength between conduction band and localized f-electrons. In the strong coupling limit Γ approaches TK. The NFL behavior and Kondo hybridization can be connected30 by appealing to the tensorial, momentum-dependent nature of the hybridization stemming from the dominant mJ = ± 5/2 nature of Yb ground state doublet in the form of \({H}_{V}={\hat{V}}_{\sigma \alpha }({{{{{{{\bf{k}}}}}}}}){c}_{{{{{{{{\bf{k}}}}}}}}\sigma }^{{{{\dagger}}} }\,{f}_{{{{{{{{\bf{k}}}}}}}}\alpha }+\,{{\mbox{h.c.}}}\,,\) expressed in terms of the creation/annihilation operators of conduction (c†) and localized (f) electrons. Subsequent theoretical work on β-YbAlB4 showed13 that the tensor \({\hat{V}}_{\sigma \alpha }({{{{{{{\bf{k}}}}}}}})\) is indeed highly anisotropic and vanishes upon approaching the Γ − Z line in the Brillouin zone as \(| {\hat{V}}_{{{{{{{{\bf{k}}}}}}}}}| \propto \sin ({k}_{z}c){k}_{\perp }^{2}\), which is also confirmed by recent ARPES14 and linear dichroism in core-level HAXPES15 measurements. In the lower symmetry polymorph α-YbAlB4, this dispersion is not expected to persist, however, the observation of a Lifshitz transition of the strikingly 2D FS pocket and the deviation from FL behavior suggest that B1 is remnant of the QCP in β-YbAlB4, but modified, as ρab in the two compounds show strikingly different behavior. In the case of α-YbAlB4, B1 is detuned from zero field by a non-zero value of the renormalized chemical potential \({\epsilon }_{F}^{* }\): \(\xi ({{{{{{{\bf{k}}}}}}}})={\epsilon }_{F}^{* }-g{\mu }_{B}B+N({\epsilon }_{F})\,{{{{{{{\rm{Tr}}}}}}}}(| \hat{V}({{{{{{{\bf{k}}}}}}}}){| }^{2})\), whereas \({\epsilon }_{F}^{* }\) is believed to be zero13 in β-YbAlB4. This is consistent with the experimental data in α-YbAlB4 if \({\epsilon }_{F}^{* }\) is gμBB1 ≈ 2 meV, such that the Lifshitz transition appears at B1 = 2.1 T, when the chemical potential reaches the bottom of the majority-spin band.
Unlike the transition at B1, the NFL behavior at B2 is a much more 3D phenomenon that drastically changes the global properties of the system. The FM fluctuations present in the ground state at zero field (shown by αVol > 0 and a high Wilson ratio) are suppressed as the magnetic field is increased to B2. Near B2, although FM (q ~ 0) fluctuations are suppressed, finite-q fluctuations get enhanced, causing power-law divergence of \({({T}_{1}T)}^{-1}\), NFL physics in resistivity and a sign change of thermal expansion coefficient, which imply the proximity to a QCP unrelated to the magnetic one in Fe-doped system. At the same time, magnetostriction, QO and Hall effect show that the transition is followed by a FS change. The QCP also differs from the one in β-YbAlB4, where the well understood FS of β-YbAlB413,14,32,33 has no small pocket like the one observed to appear at B1 in α-YbAlB4, and signatures of spin zeros were observed on larger FS sheets34 which are absent in the α-YbAlB4. Although in intermediate valence compounds magnetic field can induce a valence QCP35, our measured data exclude this for the case of α-YbAlB4 (see Supplementary Note 2). Recently36, Mössbauer spectroscopy found a change in the quadrupolar moment of Yb between 1 and 5 T. This would imply that the QC at B2 originates from a multipole-type QCP in α-YbAlB4. However, due to the low symmetry of the Yb site, its understanding will require further measurements which are beyond the scope of the current work.
It is remarkable that (coherent) critical fluctuations survive the large energy scale T0 – particularly since there has been only one reported quantum critical intermediate valence compound so far: CeRhSn37. Although it is also anisotropic, there the 2D frustrations drive the QC, while this is not likely in the case of α-YbAlB4. The unconventional nature of QC in α-YbAlB4, where a divergence is found in the dynamical quantity T1, but without observing symmetry breaking, shows that intermediate valence compounds can also offer novel types of critical phases. The tensorial nature of the Kondo hybridization and its vanishing at certain high-symmetry points in the Brillouin zone is also a central thesis of the theory of topological Kondo insulators38, and has shown promising results in a recent theoretical treatment of the quasi-1D Kondo lattice39. However, a more detailed analysis is required to encompass the richness of the phase diagram of the YbAlB4 family.
From all the data shown above we can conclude that hybridization nodes offer a new route of overcoming the high energy scale of intermediate valence compounds resulting in quantum criticality and new phases of matter.
Methods
Sample synthesis
Single crystals of α-YbAlB4 were grown from Al flux. The stoichiometric ratio of Yb:4B was heated in excess Al in an alumina crucible under an Ar atmosphere as described elsewhere40. Chemical compositions of single crystals were determined by a inductively coupled plasma - atomic emission spectrometry (ICP-AES, HORIBA JY138KH ULTRACE) at ISSP, and the analysis of both polymorphs are in good agreement with the ideal compositions of YbAlB4 within the error bars. We analyzed diffraction patterns to determine the crystal structure and lattice constant using the Rietveld analysis program PDXL (Rigaku) and found no impurity phase.
Experimental details
The thermal expansion and magnetostriction were measured with a high-resolution capacitive CuBe dilatometer in a dilution refrigerator41. Specific heat was measured using relaxation calorimetry42. Further detail and subtraction of nuclear contributions will be described elsewhere. Magnetization was measured using capacitance Faraday method43.
Resistivity and Shubnikov-de Haas measurements were performed using conventional lock-in amplifier techniques. For measurements with I∥c pristine crystals were used, while for I⊥c and for Hall effect measurements larger crystals were polished to form thin plates perpendicular to the c axis. Low temperature deviations from Fermi liquid (FL) behavior due to quantum critical fluctuations are quantified by expressing \({\rho }_{i}={\rho }_{0,i}+{A}_{i}{T}^{{n}_{i}}\). Taking n = 2 we extracted \({A}_{i}(T)\propto {m}_{i}^{2}\). Similarly, we extracted the temperature exponent by assuming A is constant in T as \({n}_{c}=d\ln \delta {\rho }_{c}/d\ln T\).
For quantum oscillations the small number of oscillation periods made the extraction of the oscillatory component of the resistance challenging; we applied two methods that gave consistent results. We assume that ρ = ρMR + ρosc where ρMR is assumed to be slowly varying. In the first method we apply a low pass filter in 1/B that subtracts a locally quadratic polynomial, this is described in detail elsewhere44. In the second we first subtract a linear component from the entire field range and then take a derivative. A comparison between the Fourier spectrum of these methods is shown in the supporting information (Supplementary Note 3 and Supplementary Fig. S-11).
The NMR measurements of 11B were performed using a pulsed spectrometer. The spectra were collected by Hahn echo sequence π/2 − τ − π with typical value of τ = 100 μs, and a π/2 pulse of 6 μs. The T1 measurements were performed using a saturation-recovery technique on a satellite NMR line determined in previous work45. Data were fitted to a magnetic relaxation function of the form: \(M(t)={M}_{0}(1-(1/10){e}^{-{(t/{T}_{1})}^{\beta }}-(5/10){e}^{-{(3t/{T}_{1})}^{\beta }}-(4/10){e}^{-{(6t/{T}_{1})}^{\beta }})\). The sample was oriented in situ by observing the quadrupolar splitting of 27Al using a two-axis goniometer for measurement temperatures 1.5–300 K, and with a single-axis goniometer for measurements at lower temperatures. In all cases the magnetic field orientation was within 2∘ of the crystal c axis.
Data availability
The datasets generated and/or analyzed during the current study are available from the corresponding author on reasonable request.
References
Coleman, P. & Schofield, A. J. Quantum criticality. Nature 433, 226 (2005).
Sachdev, S. & Keimer, B. Quantum criticality. Phys. Today 64, 29 (2011).
Gegenwart, P., Steglich, F., Geibel, C. & Brando, M. Novel types of quantum criticality in heavy-fermion systems. Eur. Phys. J. Spec. Top. 224, 975 (2015).
Wirth, S. & Steglich, F. Exploring heavy fermions from macroscopic to microscopic length scales. Nat. Rev. Mater. 1, 16051 (2016).
Custers, J. et al. The break-up of heavy electrons at a quantum critical point. Nature 424, 524–527 (2003).
Braithwaite, D. et al. (p, T, H) phase diagram of heavy fermion systems: Some systematics and some surprises from Ytterbium. J. Superconductivity Nov. Magn. 5, 1775–1780 (2013).
Graf, T., Movshovich, R., Thompson, J. D., Fisk, Z. & Canfield, P. C. Properties of YbAgCu4 at high pressures and magnetic fields. Phys. Rev. B 52, 3099 (1995).
Okawa, M. et al. Strong valence fluctuation in the quantum critical heavy fermion superconductor β-YbAlB4: A hard x-ray photoemission study. Phys. Rev. Lett. 104, 247201 (2010).
Matsumoto, Y., Kuga, K., Tomita, T., Karaki, Y. & Nakatsuji, S. Anisotropic heavy-Fermi-liquid formation in valence-fluctuating α-YbAlB4. Phys. Rev. B 84, 125126 (2011).
Terashima, T. T. et al. X-ray absorption spectroscopy in the heavy fermion compound α-YbAlB4 at high magnetic fields. J. Phys. Soc. Jpn. 84, 114715 (2015).
Nakatsuji, S. et al. Superconductivity and quantum criticality in the heavy-fermion system β-YbAlB4. Nat. Phys. 4, 603–607 (2008).
Garst, M. & Rosch, A. Sign change of the grüneisen parameter and magnetocaloric effect near quantum critical points. Phys. Rev. B 72, 205129 (2005).
Ramires, A., Coleman, P., Nevidomskyy, A. H. & Tsvelik, A. M. β-YbAlB4: a critical nodal metal. Phys. Rev. Lett. 109, 176404 (2012).
Bareille, C. et al. Kondo hybridization and quantum criticality in β-YbAlB4 by laser-ARPES. Phys. Rev. B 92, 045112 (2018).
Kuga, K. et al. Effect of anisotropic hybridization in YbAlB4 probed by linear dichroism in core-level hard X-ray photoemission spectroscopy. Phys. Rev. Lett. 123, 036404 (2019).
Kuga, K., Matsunami, M., Singh, S., Nakatsuji, S. & Takeuchi, T. Simultaneous enhancements of thermopower and electrical conductivity in quasi-onedimensional YbAlB4 single crystal. Appl. Phys. Lett. 119, 223905 (2021).
Thompson, J. D. & Lawrence, J. M. High pressure studies — physical properties of anomalous Ce, Yb and U compounds. In K. A. Gschneidner, J., Eyring, L., Lander, G. H. & Choppin, G. R. (eds.) Handbook on the Physics and Chemistry of Rare Earths, vol. 19, 383 (North-Holland, Amsterdam, 1994).
Gegenwart, P., Si, Q. & Steglich, F. Quantum criticality in heavy-fermion metals. Nat. Phys. 4, 186–197 (2008).
Tomita, T., Kuga, K., Uwatoko, Y., Coleman, P. & Nakatsuji, S. Strange metal without magnetic criticality. Science 349, 506–509 (2015).
Kuga, K., Karaki, Y., Matsumoto, Y., Machida, Y. & Nakatsuji, S. Superconducting properties of the non-Fermi-liquid system β-YbAlB4. Phys. Rev. Lett. 101, 137004 (2008).
Kuga, K., Morrison, G., Treadwell, L., Chan, J. Y. & Nakatsuji, S. Magnetic order induced by Fe substitution of Al site in the heavy-fermion systems α-YbAlB4 and β-YbAlB4. Phys. Rev. B 86, 224413 (2012).
Kuga, K. et al. Quantum valence criticality in a correlated metal. Sci. Adv. 4, eaao3547 (2018).
Gegenwart, P. Grüneisen parameter studies on heavy fermion quantum criticality. Rep. Prog. Phys. 79, 114502 (2016).
Gegenwart, P., Weickert, F., Garst, M., Perry, R. S. & Maeno, Y. Metamagnetic quantum criticality in Sr3Ru2O7 studied by thermal expansion. Phys. Rev. Lett. 96, 136402 (2006).
Weickert, F., Brando, M., Steglich, F., Gegenwart, P. & Garst, M. Universal signatures of the metamagnetic quantum critical endpoint: Application to CeRu2Si2. Phys. Rev. B 81, 134438 (2010).
Kitagawa, S. et al. Metamagnetic behavior and kondo breakdown in heavy-fermion CeFePO. Phys. Rev. Lett. 107, 277002 (2011).
Löhneysen, H. V., Rosch, A., Vojta, M. & Wölfle, P. Fermi-liquid instabilities at magnetic quantum phase transitions. Rev. Mod. Phys. 79, 1015–1075 (2007).
Matsumoto, Y. et al. Quantum criticality without tuning in the mixed valence compound β-YbAlB4. Science 331, 316–319 (2011).
Holanda, L. M. et al. Quantum critical Kondo quasiparticles probed by ESR in β-YbAlB4. Phys. Rev. Lett. 107, 026402 (2011).
Nevidomskyy, A. H. & Coleman, P. Layered Kondo lattice model for quantum critical β-YbAlB4. Phys. Rev. Lett. 102, 077202 (2009).
Lawrence, J. M., Riseborough, P. S. & Parks, R. D. Valence fluctuation phenomena. Rep. Prog. Phys. 44, 1 (1981).
O’Farrell, E. C. T. et al. Role of f electrons in the Fermi surface of the heavy fermion superconductor β-YbAlB4. Phys. Rev. Lett. 102, 216402 (2009).
O’Farrell, E. C. T., Matsumoto, Y. & Nakatsuji, S. Evolution of c−f hybridization and two-component Hall effect in β-YbAlB4. Phys. Rev. Lett. 109, 176405 (2012).
O’Farrell, E. C. T. Experimental studies of magnetic field tuned quantum criticality in β-YbAlB4 and Sr3Ru2O7, PhD Thesis (University of Cambridge, 2010).
Watanabe, S. & Miyake, K. Quantum valence criticality as an origin of unconventional critical phenomena. Phys. Rev. Lett. 105, 186403 (2010).
Oura, M. et al. Valence fluctuating compound α-YbAlB4 studied by 174Yb Mössbauer spectroscopy and X-ray diffraction using synchrotron radiation. Phys. B: Condens. Matter 536, 162 – 164 (2018).
Tokiwa, Y., Stingl, C., Kim, M.-S., Takabatake, T. & Gegenwart, P. Characteristic signatures of quantum criticality driven by geometrical frustration. Sci. Adv. 1, e1500001 (2015).
Dzero, M., Sun, K., Coleman, P. & Galitski, V. Topological Kondo insulators. Phys. Rev. Lett. 104, 106408 (2010).
Komijani, Y. & Coleman, P. Model for ferromagnetic quantum critical point in a 1D Kondo lattice. Phys. Rev. Lett. 120, 157206 (2018).
Macaluso, R. T. et al. Crystal structure and physical properties of polymorphs of LnAlB4 (Ln = Yb, Lu). Chem. Mater. 19, 1918–1922 (2007).
Küchler, R., Bauer, T., Brando, M. & Frank, S. A compact and miniaturized high resolution capacitance dilatometer for measuring thermal expansion and magnetostriction. Rev. Sci. Instrum. 83, 095102 (2012).
Matsumoto, Y. & Nakatsuji, S. Relaxation calorimetry at very low temperatures for systems with internal relaxation. Rev. Sci. Instrum. 89, 033908 (2018).
Sakakibara, T., Mitamura, H., Tayama, T. & Amitsuka, H. Faraday force magnetometer for high-sensitivity magnetization measurements at very low temperatures and high fields. Jpn. J. Appl. Phys. 33, 5067 (1994).
O’Farrell, E. C. T., Tompsett, D. A., Horie, N., Nakatsuji, S. & Sutherland, M. L. Shubnikov-de Haas oscillations in the heavy fermion α-YbAlB4. J. Phys.: Conf. Ser. 391, 012053 (2012).
Takano, S. et al. Site-selective 11B NMR studies on YbAlB4. J. Phys. Conf. Ser. 683, 012008 (2016).
Acknowledgements
We acknowledge the help of Naoki Horie. M.S.G. acknowledges the support of Croatian Science Foundation (HRZZ) under the project IP-2018-01-2970, the Unity Through Knowledge Fund (UKF Grant No. 20/15) and the support of project CeNIKS co-financed by the Croatian Government and the European Union through the European Regional Development Fund - Competitiveness and Cohesion Operational Programme (Grant No. KK.01.1.1.02.0013). The work at Rice University (A.H.N.) was supported by the U.S. National Science Foundation CAREER grant no. DMR-1350237 and the Welch Foundation grant C-1818. R.K. and M.B. are supported by the German Science Foundation through Projects No. BR 4110/1-1 and No. KU 3287/1-1, respectively. M. L. S. acknowledges the support of the EPSRC and the Royal Society. The work at the Institute for Quantum Matter, an Energy Frontier Research Center was funded by DOE, Office of Science, Basic Energy Sciences under Award # DE-SC0019331. This work was partially supported by JST-CREST (JPMJCR18T3), Japan Science and Technology Agency, and Grants-in-Aid for Scientific Research (19H00650). S.N. acknowledges support from the CIFAR as a Fellow of the CIFAR Quantum Materials Research Program. The use of the facilities of the Materials Design and Characterization Laboratory at the Institute for Solid State Physics and the Cryogenic Research Center, The University of Tokyo, is gratefully acknowledged.
Author information
Authors and Affiliations
Contributions
E.C.T.O., M.S.G. and Y.M. contributed equally to this work. E.C.T.O. performed the resistivity, Hall effect and quantum oscillations measurements, M.S.G., M.Y. and M.T. performed NMR experiments, Y.M. performed specific heat measurements. Y.M., K.K., Y.K., Y.S. and T.S. performed magnetization measurements and K.K. synthesized the samples. R.K. and Y.M. performed the thermal expansion and magnetostriction measurements. M.L.S., M.B. and A.H.N. contributed to data interpretation. M.T. and S.N. conceived the project, planed the research and contributed to data interpretation. E.C.T.O., M.S.G. and Y.M. wrote the paper. All authors took part in discussing results and editing the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Grbić, M.S., O’Farrell, E.C.T., Matsumoto, Y. et al. Anisotropy-driven quantum criticality in an intermediate valence system. Nat Commun 13, 2141 (2022). https://doi.org/10.1038/s41467-022-29757-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-022-29757-9
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.