Abstract
Heterobilayers of transition metal dichalcogenides (TMDCs) can form a moiré superlattice with flat minibands, which enables strong electron interaction and leads to various fascinating correlated states. These heterobilayers also host interlayer excitons in a type-II band alignment, in which optically excited electrons and holes reside on different layers but remain bound by the Coulomb interaction. Here we explore the unique setting of interlayer excitons interacting with strongly correlated electrons, and we show that the photoluminescence (PL) of interlayer excitons sensitively signals the onset of various correlated insulating states as the band filling is varied. When the system is in one of such states, the PL of interlayer excitons is relatively amplified at increased optical excitation power due to reduced mobility, and the valley polarization of interlayer excitons is enhanced. The moiré superlattice of the TMDC heterobilayer presents an exciting platform to engineer interlayer excitons through the periodic correlated electron states.
Similar content being viewed by others
Introduction
Bilayers of two-dimensional materials with a small twist angle or a lattice mismatch can form moiré superlattices1,2,3,4,5. Twisted bilayer graphene at the magic angle possess flat minibands that result in strong electron interactions, enabling rich, correlated states, such as Mott insulators, unconventional superconductivity, and Chern insulators6,7,8,9. The moiré superlattice of the twisted bilayer transitional metal dichalcogenides (TMDCs) can form flat minibands with less stringent requirements, with no magic angle required. In addition, due to the large effective mass10,11,12, the kinetic energy is further reduced in twisted bilayer TMDCs13. The resulting enhanced Coulomb interaction with respect to the kinetic energy leads to strong interactions that give rise to various exotic correlated insulating states13,14,15,16,17,18,19,20,21 with high transition temperatures. Very recently, Mott insulator states at fillings n = ±1 (one electron or hole per Moiré cell), generalized Wigner crystal states at filings n = ±1/3, ±2/3, and even more exotic insulating states at other fractional fillings have been reported14,15,16,17,18,19,20,21. The TMDCs moiré superlattice provides an exciting platform to investigate strongly correlated physics.
Meanwhile, stacking two different TMDC monolayers also enables the possibility for band engineering in the heterobilayer22,23. For example, a type-II alignment in the heterobilayer allows the formation of interlayer excitons, in which the optically excited electrons reside in one layer, while the holes reside in the other layer2,4,24,25. Due to their long lifetime, valley degree of freedom, and tunability, interlayer excitons are a promising candidate for quantum emitters3. Both interlayer excitons and correlated electrons are results of strong interactions, and it is natural to raise the intriguing question of how they interact with each other, which, to our best knowledge, remains an uncharted territory.
In this work, we explore the interaction of interlayer excitons with the correlated states in angle-aligned WS2/WSe2 moiré superlattice. We find that this interaction significantly modifies the photoluminescence (PL) of the interlayer exciton. Sensitive to the change in dielectric constant and the gap opening at the correlated insulating states, the interlayer exciton PL peak energy unravels the Mott insulator state at n = 1, the generalized Wigner crystal states at n = 1/3 and 2/3, as well as at n = 1/4 and 3/4 with an even longer range interaction, and a stripe phase state at n = 1/2. Interestingly, the presence of the correlated states also significantly modifies the PL intensity. At increased optical excitation power, the PL intensity of interlayer excitons brightens up at the correlated electron states, suggesting reduced mobility of interlayer excitons in the moiré cell due to their attractive interaction with the localized correlated electrons. Furthermore, the valley polarization of interlayer excitons is strongly enhanced at certain fillings. Our results inspire engineering interlayer excitons as quantum emitter arrays through moiré potential and long-range interactions, utilizing their interplay with the localized correlated electrons.
Results
Correlated states in WSe2/WS2 heterostructure
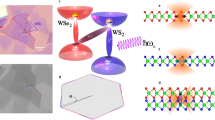
The structure of our angle-aligned WS2/WSe2 heterobilayer device is schematically shown in Fig. 1a. Due to the ~4% lattice mismatch, the angle-aligned WS2/WSe2 bilayer would form a triangular moiré superlattice with a period of ~8 nm. The strong moiré coupling1,5 will result in mini flatbands26, which could host correlated insulating state at half band filling with one carrier localized in one moiré cell (n = ±1)14,15, or even at various fractional fillings of the moiré unit cell that have been interpreted as generalized Wigner crystal states14,18,19 or stripe phases18,19,20. The filling patterns for n = 1 and 1/3 are shown schematically in Fig. 1d. These correlated states arise from the strong interaction between carriers, which localizes them in the moiré cells, and the formation of periodic filling pattern minimizes the overall interaction energy. Meanwhile, the energy bands of WS2 and WSe2 have a type-II alignment in their heterobilayer (Fig. 1b), in which the optically excited electron will reside in monolayer WS2 and the corresponding hole will reside in the WSe2 layer. Due to the strong Coulomb interaction, the electron–hole pair remain bound as the interlayer exciton.
a Schematic of the hBN encapsulated WS2/WSe2 heterobilayer. One piece of few-layer graphene (FLG) is used as the contact electrode and another piece is used as the back-gate electrode with the hBN layer working as the gate dielectric. b Schematic of the type-II alignment of the WS2/WSe2 heterobilayer moiré superlattice. c Gate-dependent PL spectra of device D1 at 4.2 K, with CW excitation centered at 1.959 eV with an excitation power of 5 µW. d Schematics of electron (red dot) configuration for fillings of n = 1 and n = 1/3 (2/3 and 1/3 are particle-hole symmetric) in the moiré superlattice.
In Fig. 1c, we show the color plot of PL intensity as a function of photon energy and gate voltage at 4.2 K, for the interlayer exciton whose emission energy is around 1.4 eV, excited by a continuous wave (CW) laser centered at 1.959 eV with an excitation power of 5 µW. The most noticeable feature is the large energy blueshift (~20 meV) at gate voltage ~2.9 V, when the Mott insulator at n = 1 (one electron per moiré cell) is formed, as confirmed by gate-dependent reflectance spectra (see Supplementary Note 2 for details) and local conductivity measurements (Fig. 2a, b). The relatively enhanced PL intensity at the gate voltage of ~0.9 V and ~1.9 V reveals the generalized Wigner crystal states at n = 1/3 and 2/3 (Fig. 2a, b), respectively, likely due to the suppressed nonradiative channels at the correlated insulating states. A closer look of Fig. 1c could even resolve the states corresponding to n = 1/4 and 3/4 (see Supplementary Fig. 2).
a PL peak position (red) extracted from Fig. 1c as a function of the gate voltage, correlated with MIM measurements of the local conductivity (blue) taken at 14 K. Dashed lines are fillings corresponding to the insulating states determined from the MIM measurements. b Zoom-in of the traces from −0.2 V to 3.2 V in a.
Microwave impedance microscopy
From Fig. 1c, we extract the PL peak energy position as a function of gate voltage and correlate it with the local conductivity measured through microwave impedance microscopy (MIM) on the same device D1 (see Fig. 2a). The various dips in the MIM signal indicate the appearance of insulating states whose filling values can be determined by matching its pattern with our prior report19. From the MIM data, we identify insulating states at fillings n = 1/4, 1/3, 1/2, 2/3, 3/4, 1, and 2 on the electron side, and n = −1/3, −2/3, and −1 on the hole side. Comparing the MIM with the PL peak position data, we find that most of these fillings also appear in the PL data. The most pronounced ones are the fillings on the electron side, which show blue shifts in the PL peak position. These observed filling values are consistent with recent reports18,19. Among them, the n = 2 corresponds to the complete filling of the first minibands and the n = ±1 correspond to the Mott insulator states at half filling of these minibands14,15,21. The n = ±1/3, ±2/3, +1/4, and +3/4 correspond to generalized Wigner crystals with a triangular lattice18,19. The n = 1/2 corresponds to a stripe phase18,19,20.
The sensitive readout of the correlated insulating states through the interlayer exciton PL energy can be understood by the larger spatial extent of the interlayer exciton, which renders it more sensitive to the dielectric environment than the intralayer exciton. Similar ideas has been utilized to use the larger 2s exciton to sensitively probe the correlated insulating states18. In addition, the background free nature makes the PL spectra a sensitive probe. At the correlated insulating states, electron interaction results in an energy gap and localizes the electrons, which subsequently modifies the dielectric constant. As a result, both the energy gap seen by the interlayer excitons and their binding energies can be modified, leading to the change in the emission energy, observed as the blueshift of the PL peak at the filling of the correlated states. This picture is consistent with our observation of the larger PL blueshift at n = 1, as the Mott insulator state has a larger gap (~10 meV) compared with other fractional fillings (~2–3 meV) according to previous reports14,15,18,19.
Power-dependent PL spectra of interlayer excitons
The interaction among the interlayer excitons and that between the excitons and the underlying electron solid can be further probed by increasing the interlayer exciton density. Figure 3a shows the color plot of the gate-dependent PL spectra of device D1 at an optical excitation power ten times (50 µW) as much as that used in Fig. 1c (5 µW). Compared with Fig. 1c, the higher excitation power data now reveals the states at n = −1/3 and −2/3, which are previously missing in the lower excitation power data. Detailed analysis of the integrated PL intensity as a function of the gate voltage shown in Fig. 3b further reveals the state corresponding to n = −1/4. We perform even more drastic excitation power dependence on another device D2, in which we increase the excitation power from 0.5 µW (Fig. 3c) to 300 µW (Fig. 3d). It is obvious that despite the increase of optical excitation by nearly three orders of magnitude, the Mott insulator states at n = ±1 remain intact. This observation is consistent with the picture that the excitons do not destroy the periodic electron solid4,27. It is worth noting that the asymmetric PL peak shift as a function of the gate voltage for the p- and n-doping sides is due to the difference in the Stark effect related to our specific device structure, which is back gated with the WSe2 layer closer to the back-gate electrode. Owing to the type-II alignment between WSe2 and WS2, the gate voltage induced holes in the p-doping side will occupy the WSe2 layer, screening the electrical field between the WSe2 and WS2 layer, and reducing the Stark effect. A detailed explanation can be found in Supplementary Note 5.
a Gate-dependent PL spectra of device D1 with the optical excitation power of 50 µW and photon energy centered at 1.959 eV. b Integrated interlayer exciton PL intensity as a function of gate voltage for device D1 with 50 µW (blue) and 5 µW (red) optical excitation power. Dashed lines are fillings determined from the insulating states from the MIM measurements. c, d Gate-dependent PL spectra for device D2 under the optical excitation power of 0.5 and 300 µW. All data are taken at 4.2 K.
One other striking observation is that, in contrast to the intense PL intensity at the charge neutral region (n = 0) under the low optical excitation power (Fig. 3c), the PL intensity at the n = 1 state is more strongly enhanced under high excitation power (Fig. 3d). The time-resolved PL spectra (TRPL) shows a lifetime of 6.5 ns for the n = 1 state (PL peak at ~1.47 eV) and 5.1 ns for the n = 0 state (PL peak at ~1.45 eV) (see Supplementary Note 3 for details). This might arise from the mobility reduction of interlayer excitons at the correlated state at n = 1, in which electrons are localized in the periodic moiré cells. Interlayer excitons can be polarized by the localized charges, inducing an attractive force between the correlated electrons and interlayer excitons that reduces the interlayer exciton mobility compared to the charge neutral scenario (n = 0). As a result, the chance of nonradiative recombination is reduced, consistent with the TRPL data. It has been shown that the moiré potential can trap interlayer excitons2,4,28,29. Our results naturally raise the question of possible localization of interlayer excitons through the additional attraction by the periodic correlated electron solid, which we will explore in future studies.
Gate-dependent valley polarization
Interlayer excitons also possess valley degree of freedom30, which can be probed through helicity-resolved PL spectroscopy measurements. Here we excite both the devices D1 and D2 using the right circularly polarized light (σ+) and detect the interlayer exciton PL of the same (σ+) or opposite (σ−) helicity. The valley polarization \(P\) is calculated by the expression \(P=\frac{I\left({\sigma }^{+}\right)-I({\sigma }^{-})}{I\left({\sigma }^{+}\right)+I({\sigma }^{-})}\), where \(I\left({\sigma }^{+}\right)\) and I\(\left({\sigma }^{-}\right)\) are interlayer exciton PL intensities with \({{\rm{\sigma }}}^{+}\) and \({{\rm{\sigma }}}^{-}\) helicity, respectively. The valley polarizations as a function of gate voltage for the devices D1 and D2 at 4.2 K are shown in Fig. 4a, b, respectively. The overall valley polarizations for these two devices have different signs due to the different alignment angles (0° for D1 and 60° for D2), and the sign of the valley polarization is consistent with the interlayer exciton at the atomic registry site of \({R}_{h}^{X}\) and \({H}_{h}^{h}\) for the devices D1 and D2, respectively31. It is noticeable that the correlated states at both integer and fractional fillings are often associated with an enhanced valley polarization, and the enhancement is most drastic at the fillings of n = 1 and 2 for device D2. This valley polarization enhancement might originate from the decreased valley scatterings due to the interaction between interlayer excitons and correlated electrons. One major valley depolarization mechanism is through Maialle–Silva–Sham mechanism32,33, which annihilates one exciton in one valley and creates another in the opposite valley. However, when interlayer excitons are attracted by the localized correlated electrons, this probability will likely be significantly suppressed. The correlated electrons, therefore, also provide a tunable platform to manipulate the valleyspin of the interlayer excitons.
Researchers have been inspired to utilize the moiré potential to control interlayer excitons to form an array of quantum emitters. Here we show that the long-range interaction of the electrons in the moiré superlattice can be further exploited for this purpose. The interaction between correlated electrons and interlayer excitons not only allows us to reveal the correlated states at different fillings through the PL spectra, more excitingly, it can be further utilized to control the mobility and valley polarization of the interlayer excitons. Our results, therefore, shed light on how to engineer the interlayer excitons in the TMDCs heterobilayer moiré superlattice for quantum optics and optoelectronics.
Methods
Heterostructure device fabrication
We use a layer-by-layer pickup method to fabricate the WS2/WSe2 heterobilayer device34. We first exfoliate monolayer WS2, monolayer WSe2, few-layer graphene and thin hBN flakes on Si substrate with 285 nm thermal oxide, respectively. We further confirm the crystal orientation of monolayer WSe2 and WS2 through second harmonic generation (SHG) measurements (see Supplementary Note 1 for details). We then mount the SiO2/Si chip on a rotational stage and use hBN as a stamp to pick up each layer sequentially. The alignment of the monolayer WS2 and WSe2 are controlled by fine adjusting the angle of the rotational stage (accuracy of 0.02°) under the microscope, ensuring a near-zero twist angle between the two flakes. The final device is annealed at 140 °C for 6 h in a vacuum chamber. The pre-patterned Au contact electrodes are fabricated through standard electron-beam lithography followed by ebeam evaporation and lift-off processes.
Optical characterization
The optical measurements are taken with a home-built confocal microscope with spectroscopy capabilities in a liquid helium-controlled optical cryostat. The PL spectra are taken with a CW laser excitation. The reflectance spectra are taken with a supercontinuum white laser source (Fianium). The SHG measurements are taken with a pulsed laser with the width ~160 fs (Ti : Sapphire, Coherent Chameleon).
MIM measurements
The MIM measurement is performed on a home-built cryogenic scanning probe microscope platform. A small microwave excitation of ~0.1 µW at a fixed frequency around 10 GHz is delivered to a chemically etched tungsten tip mounted on a quartz tuning fork35. The reflected signal is analyzed to extract the demodulated output channels, MIM-Im and MIM-Re, which are proportional to the imaginary and real parts of the admittance between the tip and the sample, respectively. The MIM-Im part characterizes the screening of the tip electric field by the sample and changes monotonically with the sample’s local conductivity. Therefore, the dips in the MIM-Im curve plotted in Fig. 2 indicate the appearance of insulating states.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Jin, C. et al. Observation of moiré excitons in WSe2/WS2 heterostructure superlattices. Nature 567, 76–80 (2019).
Seyler, K. L. et al. Signatures of moiré-trapped valley excitons in MoSe2/WSe2 heterobilayers. Nature 567, 66–70 (2019).
Yu, H., Liu, G., Tang, J., Xu, X. & Yao, W. Moiré excitons: from programmable quantum emitter arrays to spin-orbit – coupled artificial lattices. Sci. Adv. 3, e1701696 10 (2017).
Tran, K. et al. Evidence for moiré excitons in van der Waals heterostructures. Nature 567, 71–75 (2019).
Alexeev, E. M. et al. Resonantly hybridized excitons in moiré superlattices in van der Waals heterostructures. Nature 567, 81–86 (2019).
Bistritzer, R. & MacDonald, A. H. Moiré bands in twisted double-layer graphene. Proc. Natl Acad. Sci. USA 108, 12233–12237 (2011).
Cao, Y. et al. Correlated insulator behaviour at half-filling in magic-angle graphene superlattices. Nature 556, 80–84 (2018).
Cao, Y. et al. Unconventional superconductivity in magic-angle graphene superlattices. Nature 556, 43–50 (2018).
Andrei, E. Y. & MacDonald, A. H. Graphene bilayers with a twist. Nat. Mater. 19, 1265–1275 (2020).
Kono, J. et al. Magnetooptics of exciton Rydberg states in a monolayer semiconductor. Phys. Rev. Lett. 120, 1–6 (2018).
Wang, T. et al. Giant valley-polarized Rydberg excitons in monolayer WSe2 revealed by magneto-photocurrent spectroscopy. Nano Lett. 20, 7635–7641 (2020).
Li, Z. et al. Phonon-exciton Interactions in WSe2 under a quantizing magnetic field. Nat. Commun. 11, 1–7 (2020).
Wu, F., Lovorn, T., Tutuc, E. & MacDonald, A. H. Hubbard model physics in transition metal dichalcogenide moiré bands. Phys. Rev. Lett. 121, 26402 (2018).
Regan, E. C. et al. Mott and generalized Wigner crystal states in WSe2/WS2 moiré superlattices. Nature 579, 359–363 (2020).
Tang, Y. et al. Simulation of Hubbard model physics in WSe2/WS2 moiré superlattices. Nature 579, 353–358 (2020).
Shimazaki, Y. et al. Strongly correlated electrons and hybrid excitons in a moiré heterostructure. Nature 580, 472–477 (2020).
Wang, L. et al. Correlated electronic phases in twisted bilayer transition metal dichalcogenides. Nat. Mater. 19, 861–866 (2020).
Xu, Y. et al. Correlated insulating states at fractional fillings of moiré superlattices. Nature 587, 214–218 (2020).
Huang, X. et al. Correlated insulating states at fractional fillings of the WS2/WSe2 moiré lattice. Nat. Phys. https://doi.org/10.1038/s41567-021-01171-w (2021).
Jin, C. et al. Stripe phases in WSe2/WS2 moiré superlattices. Nat. Mater. https://doi.org/10.1038/s41563-021-00959-8 (2021).
Chu, Z. et al. Nanoscale conductivity imaging of correlated electronic states in WSe2/WS2 moiré superlattices. Phys. Rev. Lett. 125, 186803 (2020).
Ozcelik, V. O., Azadani, J. G., Yang, C., Koester, S. J. & Low, T. Band alignment of two-dimensional semiconductors for designing heterostructures with momentum space matching. Phys. Rev. B Condens. Matter Mater. Phys. 94, 035125 (2016).
Chiu, M. H. et al. Determination of band alignment in the single-layer MoS2/WSe2 heterojunction. Nat. Commun. 6, 1–6 (2015).
Rivera, P. et al. Observation of long-lived interlayer excitons in monolayer MoSe2/WSe2 heterostructures. Nat. Commun. 6, 6242 (2015).
Wang, T. et al. Giant valley-Zeeman splitting from spin-singlet and spin-triplet interlayer excitons in WSe2/MoSe2 heterostructure. Nano Lett. 20, 694–700 (2020).
Zhang, Z. et al. Flat bands in twisted bilayer transition metal dichalcogenides. Nat. Phys. 16, 1093–1096 (2020).
Smoleński, T. et al. Observation of Wigner crystal of electrons in a monolayer semiconductor. Preprint at https://arXiv:2010.03078 (2020).
Choi, J. et al. Moiré potential impedes interlayer exciton diffusion in van der Waals heterostructures. Sci. Adv. 6, eaba8866 (2020).
Yuan, L. et al. Twist-angle-dependent interlayer exciton diffusion in WS2/WSe2 heterobilayers. Nat. Mater. 19, 617–623 (2020).
Xu, X., Yao, W., Xiao, D. & Heinz, T. F. Spin and pseudospins in layered transition metal dichalcogenides. Nat. Phys. 10, 343 (2014).
Yu, H., Liu, G.-B. & Yao, W. Brightened spin-triplet interlayer excitons and optical selection rules in van der Waals heterobilayers. 2D Mater. 5, 35021 (2018).
Chen, S. Y. et al. Superior valley polarization and coherence of 2s excitons in monolayer WSe2. Phys. Rev. Lett. 120, 46402 (2018).
Maialle, M. Z., de Andrada e Silva, E. A. & Sham, L. J. Exciton spin dynamics in quantum wells. Phys. Rev. B 47, 15776–15788 (1993).
Wang, L. et al. One-dimensional electrical contact to a two-dimensional material. Science 342, 614–617 (2013).
Cui, Y.-T., Ma, E. Y. & Shen, Z.-X. Quartz tuning fork based microwave impedance microscopy. Rev. Sci. Instrum. 87, 063711 (2016).
Acknowledgements
We thank Dr. Chenhao Jin and Prof. Feng Wang for helpful discussions. S.M. and S.-F.S. acknowledge support by AFOSR through Grant FA9550-18-1-0312 and by NSF through Career Grant DMR-1945420. T.W. and S.-F.S. acknowledge support from ACS PRF through Grant 59957-DNI10. Z.L. and S.-F.S. acknowledge support from NYSTAR through Focus Center-NY–RPI Contract C150117. The device fabrication was supported by the Micro and Nanofabrication Clean Room (MNCR) at Rensselaer Polytechnic Institute (RPI). The optical characterization is supported by a DURIP award (AFRL FA9550-20-1-0179). D.C. and Z.W. acknowledges support from China Postdoctoral Science Foundation (Grant number 2019M653380), National Natural Science Foundation of China (Grant number 62004032, 61774029) and Sichuan Provincial Science and Technology Department (grants 21CXTD0088, 21YYJC3079, 2019JDTD0006 and 2019YFSY0007). X.H. and Y.-T.C. acknowledge support from NSF under award DMR-2004701. D.X. is supported by the Department of Energy, Basic Energy Sciences, Grant number DE-SC0012509. S.T. acknowledges support from NSF DMR-1904716, DMR-1838443, CMMI-1933214, and DOE-SC0020653. K.W. and T.T. acknowledge support from the Elemental Strategy Initiative conducted by the MEXT, Japan, Grant number JPMXP0112101001, JSPS KAKENHI Grant number JP20H00354, and the CREST(JPMJCR15F3), JST.
Author information
Authors and Affiliations
Contributions
S.M., T.W., X. H., and D.C. contribute equally to this work. S.-F.S. and Y.-T.C. conceived the project. S.M. and T.W. perform the optical measurements. D.C and Z.L. fabricated the heterostructure devices. X.H. performed the MIM measurements. M.B. and S.T. grew the TMDC crystals. T.T. and K.W. grew the hBN crystals. S.-F.S, Y.-T.C., D.X., S.M., T.W., C.W., and X.H. analyzed the data. S.-F.S., Y.-T.C., and S.M. wrote the manuscript with inputs from all authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks Yuya Shimazaki and Zhiming Zhang for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Miao, S., Wang, T., Huang, X. et al. Strong interaction between interlayer excitons and correlated electrons in WSe2/WS2 moiré superlattice. Nat Commun 12, 3608 (2021). https://doi.org/10.1038/s41467-021-23732-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-021-23732-6
This article is cited by
-
Engineering interlayer hybridization in van der Waals bilayers
Nature Reviews Materials (2024)
-
Valley-polarized excitonic Mott insulator in WS2/WSe2 moiré superlattice
Nature Physics (2024)
-
Dynamical control of nanoscale light-matter interactions in low-dimensional quantum materials
Light: Science & Applications (2024)
-
Correlation-driven nonequilibrium exciton site transition in a WSe2/WS2 moiré supercell
Nature Communications (2024)
-
Excitonic Mott insulator in a Bose-Fermi-Hubbard system of moiré WS2/WSe2 heterobilayer
Nature Communications (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.