Abstract
The nature of the actinide-actinide bonds is of fundamental importance to understand the electronic structure of the 5f elements. It has attracted considerable theoretical attention, but little is known experimentally as the synthesis of these chemical bonds remains extremely challenging. Herein, we report a strong covalent Th-Th bond formed between two rarely accessible Th3+ ions, stabilized inside a fullerene cage nanocontainer as Th2@Ih(7)-C80. This compound is synthesized using the arc-discharge method and fully characterized using several techniques. The single-crystal X-Ray diffraction analysis determines that the two Th atoms are separated by 3.816 Å. Both experimental and quantum-chemical results show that the two Th atoms have formal charges of +3 and confirm the presence of a strong covalent Th-Th bond inside Ih(7)-C80. Moreover, density functional theory and ab initio multireference calculations suggest that the overlap between the 7s/6d hybrid thorium orbitals is so large that the bond still exists at Th-Th separations larger than 6 Å. This work demonstrates the authenticity of covalent actinide metal-metal bonds in a stable compound and deepens our fundamental understanding of f element metal bonds.
Similar content being viewed by others
Introduction
Understanding the nature of chemical bonds is at the center of chemistry and is fundamental for the prediction of reactivity and consequent synthetic work. Many chemical compounds contain metal–metal bonds that are responsible for their structural and functional properties. Bonding between main group and d transition group elements have been intensively studied for many decades and significant advances have been achieved on the synthesis of f–d metal–metal bonds in recent studies1,2,3. In contrast, experimental studies of bonding between f-block metals is notably lagging behind4. Exploring the electronic structure of the 5f elements is crucial given their potential applications in different fields, such as in nuclear fuel recycling. Theory predicts that the U2 molecule should be stable in the gas phase5,6, and experimental evidence for its existence was reported in 1974 using mass spectrometry7. However, a long standing Holy Grail in inorganic chemistry is the synthesis and characterization of compounds that contain An–An bonds, and very little has been reported in this field. Most of the work concerning An–An bonds has been of a theoretical nature5,6,8,9,10,11. On the experimental side, Souter et al. reported the formation of U2H2 and U2H4 via laser ablation of U atoms in the presence of H2, stabilized in a solid argon matrix12. However, characterization was limited to infrared spectroscopy supplemented with Density Functional Theory (DFT) calculations. The authors stated in the article abstract that: ‘The molecules U(µ-H2)U and U2H4 represent the first examples of an actinide-actinide bond’. To our knowledge, there are only two other reports that claim the formation of ‘weak’ U–U bonds, one in the [U2F12]2− anion in Sr[U2F12]13 and our recent report of U2@Ih(7)-C8014,15. A molecular compound containing an An–An bond still remains highly sought after, as the synthesis of such a compound is extremely challenging, due to the fact that the actinide metals prefer to coordinate to the main group elements in the ligands instead of to other actinides. Recently, significant progress has been made with low oxidation state actinide chemistry16,17,18. Formation of a direct An–An bond between low oxidation state actinides has been theoretically proposed11. However, these low oxidation state actinides, including Th(III) and U(II), are still hardly accessible and only a very few examples have been reported17,19.
Fullerenes are known to confine metal ions within a short distance and to stabilize metal ions with usual oxidation states, which provides an ideal environment for the formation of metal–metal bonds20,21,22,23,24,25. The possible existence of an actinide metal–metal bond inside fullerene cages has also been intensively debated by theoreticians in recent years26,27. Here, we report the synthesis and characterizations of a dimetallic thorium endohedral metallofullerene (EMF), Th2@Ih(7)-C80, containing a strong covalent thorium–thorium bond between two rarely accessible Th3+ ions. This molecule represents an authentic example of an actinide metal–metal bond. Moreover, our theoretical studies show that the overlap between 7s/6d hybrid thorium orbitals is so large that the bond still exists at Th–Th separations larger than 6 Å.
Results
Synthesis and isolation of Th2@C80
Th2@C80 was synthesized by a modified Krätschmer–Huffman arc discharge method. Graphite rods, packed with ThO2 and graphite powder (molar ratio of Th/C = 1:24), were vaporized in the arcing chamber under a 200 Torr He atmosphere. The resulting soot was then extracted with CS2 for 12 h. A multistage HPLC procedure was employed to isolate and purify Th2@C80. After a four-stage HPLC separation protocol, the purified Th2@C80 was obtained (Supplementary Fig. 2). The purity of the isolated Th2@C80 was confirmed by the observation of a single peak by HPLC and by high-resolution matrix-assisted laser desorption-ionization time-of-flight positive-ion-mode mass spectrometry (MALDI-TOF/MS). The mass spectrum shows a prominent molecular ion peak with a mass-to-charge ratio of m/z = 1424.076 (Supplementary Fig. 1), corresponding to the empirical formula of [Th2C80]+and the experimental isotopic distribution agrees well with the theoretical prediction.
Molecular structure of Th2@I h(7)-C80·[NiII-OEP]
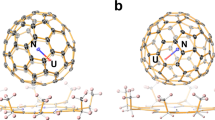
The molecular structure of Th2@C80 was determined by single-crystal X-ray diffraction analysis. Th2@C80 was co-crystallized with NiII-OEP (OEP = 2, 3, 7, 8, 12, 13, 17, 18-octaethylporphyrin dianion) by slow diffusion of a benzene solution of NiII-OEP into a CS2 solution of Th2@C80. The structure was resolved and refined in the P21/c (No. 14) space group. Fig. 1a shows Th2@Ih(7)-C80 and its relationship to the co-crystallized NiII(OEP) molecule. The crystallographic data indicate that the Ih(7)-C80 cage is fully ordered. Inside the fullerene cage, two major Th positions (Th1 and Th2) are highly ordered and have dominant occupancies of 0.783(17) and 0.748(2), respectively, with the occupancies of minor sites ranging from 0.0028(7) to 0.1299(14) (Supplementary Table 1). Most of the reported lanthanide dimetallic endohedral fullerenes as well as the recently reported U2@Ih(7)-C80 commonly display severe disorder of the metals inside the highly symmetric Ih(7)-C8014,28. The highly ordered Th positions inside this cage are very unusual for pristine dimetallic endohedral fullerenes, suggesting a hindered metal motion, possibly caused by the bonding interactions between the Th ions and the fullerene cage as well as between the two Th ions. The ordered Th positions allow us to accurately determine the distance between major Th1 and Th2 as 3.816(6) Å. This distance is slightly longer than the U–U and La–La distances reported for U2@Ih(7)-C8014 and La2@Ih-C80(C7H7)22 but is comparable to the Ce–Ce bond distance in Ce2@Ih-C8028 and even shorter than the metal–metal bond distance observed in La2@Ih-C8029, Dy2@Ih-C80(CH2Ph)21, and Tb2@C79N 20 (Supplementary Table 3). Th1 and Th2 reside under corresponding hexagons and the distances between the major thorium sites and the cage carbons all lie within the range of 2.483(9)–2.559(9) Å, with Th1 and Th2 at distances to their corresponding hexagon centroids of 2.048 and 2.066 Å, respectively. (See Fig. 1b, Supplementary Table 2, and Supplementary Fig. 4). It is noteworthy that these Th-(ring centroid) distances are shorter than those for previously reported Th3+ complexes: 2.607, 2.52, 2.53, and 2.551 Å for (C5Me5)3Th17, [C5H3(SiMe3)2]3Th30, [C5H3(SiMe2tBu)2]3Th30, and (C5Me4H)3Th31, respectively, indicating a strong interaction between the Th2 cluster and the fullerene cage.
a Th2@Ih(7)-C80·[NiII(OEP)] structure showing the relationship between the fullerene cage and the [NiII-OEP] ligands. The two Th1/Th2 sites have occupancies of 0.783(17) and 0.748(2), respectively. Other minor Th sites (Supplementary Fig. 3) and the solvent molecules are omitted here for clarity. b Fragment view showing the interaction of the major Th1–Th2 cluster with the closest aromatic ring fragments of the cage.
Electronic structure and bonding in Th2@I h(7)-C80
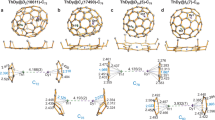
DFT and ab initio calculations were performed to determine the electronic structure of the Th2@Ih(7)-C80 EMF and to characterize the nature of the Th–Th interaction. Since no more than 6e are transferred between the guest and the host32,33, the oxidation state of the Th atoms in Th2@Ih(7)-C80 should be +3, which is a rare situation given the tendency of Th atoms to formally transfer all four valence electrons to the groups with which they coordinate17,34,35,36. Accordingly, two electrons are available to form a Th–Th bond. At the DFT level, we have computed several structures corresponding to the electronic configurations σ2, σ1π1, and π2. When the two valence electrons are localized in the σ orbital, the Th···Th separation is computed to be 3.817 Å using the hybrid functional PBE0, a value that matches the experimental distance of 3.816 Å. The nature of the HOMO, a bonding σ Th–Th orbital (Fig. 2b), suggests that despite the long Th–Th distance, the two Th atoms are linked by a direct interaction. Although the LUMO is delocalized over the carbon cage, the lowest triplet corresponds to the promotion of one electron from the HOMO to a bonding orbital with a π (6dxz,6dyz) nature and, interestingly, the Th–Th distance shortens by 0.114 Å to 3.703 Å. If both σ electrons are transferred to the π orbitals, the shortening is still larger, 0.309 Å. At the PBE0 level, the energy of the singlet (σ2) and triplet (σ1π1) are almost degenerate with the triplet being about 1 kcal mol−1 lower in energy (Fig. 2a). Using the GGA PBE functional, the energy difference reaches 4 kcal mol−1 (Supplementary Table 5).
a Th–Th distances (in Å) and relative energies (in kcal mol−1) computed for several electronic states at the DFT (PBE0) level. b Scheme containing selected DFT PBE0 frontier molecular orbitals. c Representation of CASSCF orbitals for the singlet ground state; the electron population for each orbital (in parenthesis) leads to an effective Th–Th bond order (EBO) of 0.99. d Representation of the Laplacian of the electron density distribution and electron localization function (ELF) in a plane containing the two Th atoms. Blue and red contours in the Laplacian of ρ represent negative and positive values, respectively.
To properly characterize the nature of the ground state, we have performed CASPT2 calculations using the singlet DFT-optimized structure. As shown in Table 1, the ab initio ground state is a singlet with two electrons mainly localized in a σ (7s, 6dz) orbital. The πx and πy bonding orbitals make a significant contribution (12%) to the wave function, whereas the antibonding σ* orbital has an almost null contribution (Fig. 2c). Thus, the Th–Th bond can be seen as a σ bond with some contribution of bonding π orbitals to give an effective bond order of 0.99. When one electron is promoted from the σ orbital to one of the π orbitals the relative energy increases to 11.4 kcal mol−1 (9.5 kcal mol−1 with the triplet DFT structure). The discrepancy between DFT and CASPT2 results arises from the nature of the two electronic states. Whereas the triplet state is mono configurational, the singlet ground state has an important multiconfigurational nature that cannot be correctly described at the DFT level. In all DFT and CASPT2 calculations, only two electrons reside in molecular orbitals formed mainly by valence-shell Th orbitals, which confirms the oxidation state of +3 for the Th ions in the lowest energy states.
Both DFT and CASPT2 calculations suggest that the Th–Th interaction inside the icosahedral C80 is covalent and clearly cannot be considered as a magnetic interaction. The covalent bond arises from the nature of the 7s and 6d actinide orbitals that extend their overlap over very long distances, as shown in Supplementary Fig. 6. Because the overlap between Th orbitals can extend over distances larger than 6 Å, we have analyzed the thorium–thorium interaction inside cage D2(821)-C104, which can be visualized as two hemispheres of Ih(7)-C80 with 24 additional carbon atoms located in the center of the cage (see Supplementary Fig. 7a). As for C80, the HOMO for the lowest singlet of Th2@D2(821)-C104 corresponds to a σ bonding orbital localized on Th atoms (Supplementary Fig. 7c), the Th–Th separation being significantly longer, 6.020 Å, due to the larger size of the fullerene. CASPT2 calculations were also performed for Th2@D2(821)-C104, confirming the singlet nature of the ground state. The increase of the Th–Th distance with respect to C80 necessarily reduces the covalent interaction between the two actinides. A direct consequence is the presence of a relatively small energy gap between the σ(7s/6dz2) and σ*(7s/6dz2) orbitals. A partial population of the σ* orbital is observed in the CASSCF ground-state wave function, which leads to an effective bond order of 0.76 for the Th–Th bond, still very high considering the very long separation between the two Th atoms.
Finally, the Th–Th interaction was also characterized using Baders’s Quantum Theory of Atoms in Molecules (QTAIM). This theory uses several descriptors to characterize bonds through the topology of the electron density37. Bader postulated that the presence of a bond critical point (bcp) between two atoms is a necessary and sufficient condition for the atoms to be bonded. Such a bcp was found that links the two Th atoms in Th2@Ih(7)-C80. A representation of the Laplacian of the electron density (∇2ρbcp) distribution for the singlet ground state is given in Fig. 2d, which exhibits a non-negligible negative region in the internuclear Th–Th region. A direct consequence is that the value of the Laplacian of the charge density at the bcp is negative. These results are remarkable since metal–metal bonds typically exhibit depletion of the electron density in the internuclear region, that is, positive values in the Laplacian of ρ. The ELF plot also shows that the electron density is highly localized in the internuclear Th–Th bonding region38. Indeed, when comparing the topological descriptors for Th2, U2, Lu2, and La2 bonds inside C80 and C82 (Supplementary Table 6), we have found that the thorium–thorium bond exhibits the largest values even though its bond distance is the longest. Therefore, the thorium–thorium interaction is, up to now, the strongest one among the known actinide–actinide or lanthanide–lanthanide interactions.
As one cannot dissociate the Th2 unit inside the cage, it is not easy to give an accurate value for the Th–Th bond energy in Th2@C80. A rough estimate can be obtained from the relative energy of the triplet corresponding to the σ1σ*1 configuration, as in this electronic configuration the Th–Th bond is effectively broken. However, the antibonding orbital is very high in energy and only the energies corresponding to the configurations σ1π1 and σ1cage1 could be calculated. The latter triplet is about 2 eV higher in energy than the singlet ground state at CASPT2 level (Table 1). An alternative procedure is to compare the difference in the encapsulation energies of two La atoms and two Th atoms in C80, which is 1.92 eV at the PBE0 level (1.7 eV at PBE). Assuming that the metal–cage interaction is approximately the same in both cases and that no bond is formed in the La2 case, the difference in encapsulation energy arises from the metal–metal bond in the dithorium EMF. Both procedures are rather approximate and have limitations, but it does not seem unreasonable to state that Th–Th bond energy is greater than 40 kcal mol−1. It is worth mentioning that for cage D2(821)-C104, the difference in the encapsulation energies between dithorium and dilanthanum EMFs is still 0.45 eV at the PBE0 level and 0.25 eV at PBE (Supplementary Table 7). As already mentioned above, this strong metal–metal bond interaction is a result of a high overlap between 7s6d hybrid orbitals which extend over long distances (Supplementary Fig. 6). We are persuaded that this property could also be used in more traditional chemistry to obtain long-distance interactions between actinides, for example, through the design of appropriate ligands in organometallic chemistry. It is worth mentioning that uranium–uranium interactions are not that strong over long distances, as they occur through the more contracted 5f orbitals, their overlap decreasing much more rapidly with U–U separation. Actually, according to CASPT2 calculations, two U atoms within Ih-C80 (dU-U = 3.812 Å) show magnetic coupling with an effective bond order of 0.09. A detailed analysis of under what conditions two U atoms can exhibit a covalent interaction will be reported elsewhere.
Spectroscopic properties of Th2@C80
Purified Th2@Ih(7)-C80 was characterized with UV–Vis–NIR and Raman spectroscopies as shown in Supplementary Fig. 5 and Fig. 3. The UV–Vis spectrum of Th2@ C80 shows three weak absorptions at 447, 488, and 683 nm, similar to typical Ih(7)-C80 cage based endofullerenes39. Notably, a single vibration peak at 152 cm−1 can be observed in the low energy Raman spectrum and is assigned to a metal-to-cage vibration based on previous studies40. This frequency is very close to 148 cm−1 for Th@C3v(8)-C8241, 153 cm−1 for Th@C1(11)-C8642, and 155 cm−1 for Th@C1(28324)-C8043, indicating similarly strong thorium–cage interactions. Moreover, the peaks at 220, 416 and 475 cm−1 also observed in the Raman spectra of U2@Ih(7)-C8014 and U2C@Ih(7)-C8044, can be assigned to the Ih(7)-C80 cage vibrational modes, consistent with the crystallographic analysis. The Raman peaks obtained at the DFT PBE level coincide well with the experimental ones (see Fig. 3). The computed frequencies for the optimized structure show six lower frequencies that correspond to frustrated translational and rotational modes against the cage (at 40, 47, 57, 67, and 165 cm‒1), and the internal Th–Th stretching (at 138 cm−1), which is coupled with a cage mode (Fig. 3), accounting for Th–cage and Th–Th interactions. Smaller contributions of the symmetric Th–Th stretching vibrations are found coupled with many other cage vibrations and appear at higher frequencies.
The low-energy Raman spectrum of Th2@C80 with 633 nm excitation is shown in black. Computed spectrum (in red) fits well with the experimental one if all the frequencies are shifted by 15 cm−1 to higher values. The symmetric stretching mode of Th2 (at 152 cm−1) is active in Raman and is coupled with a cage–Th vibration. The associated normal mode is also represented.
The 13C NMR spectrum of Th2@Ih(7)-C80 characterized at 298 K show four signals in the range 125–145 ppm as shown in Supplementary Fig. 9. Though there are two signals identified as contamination caused by benzene impurities, signals at 144.05 and 129.27 ppm could be assigned to characteristic signals for a C80 cage with Ih symmetry. In particular, there is no paramagnetic broadening effect found in the 13C NMR spectrum of Th2@Ih(7)-C80, further proving that Th2@Ih(7)-C80 displays diamagnetic features and two electrons are available to form a Th–Th bond, agreeing well with the above computational results.
To determine the valence state of thorium inside the Ih(7)-C80 cage, the X-ray absorption near edge structure (XANES) spectroscopy of Th2@Ih(7)-C80 was conducted along with the ThO2 (Th4+) as the reference species. The oxidation state of the metal in a statistical nature can be analyzed from the XANES region based on the edge position and the inflection point of the edge absorption. In terms of the edge position, the Th L3-edge spectrum of Th2@C80 is shifted to lower energy side compared to that of the ThO2 as shown in Fig. 4a. In addition, the maximum peak position in the first derivative of normalized μ(E) spectra is defined as E0, namely the inflection point energies. In particular, the E0 found for Th2@C80, 16306.7 eV, is shifted to lower energy by 4.7 eV compared with that of ThO2, 16311.4 eV (see Fig. 4a inset and Supplementary Fig. 8), indicating that the two Th atoms encapsulated in the Ih(7)-C80 cage have a lower charge state and agrees well with the theoretical predictions that the two Th ions exist in +3 oxidation state.
a L3−edge normalized μ(E) spectra of Th in Th2@Ih(7)-C80 (purple) and ThO2 (green). The inset shows an enlarged spectral range (16280–16360 eV) and the diamonds indicate the absorption edges E0. b Radial distribution function obtained by Fourier transform of k2-weighted Th L3-edge EXAFS spectrum of Th2@Ih(7)-C80 measured at room temperature. c χ(k) space (blue) and fitting curve (orange) of Th2@Ih(7)-C80. d Radial distribution function of k2-weighted Th L3-edge EXAFS spectrum and fitting curves of Th2@Ih(7)-C80, including the magnitude (R-mag in purple) and real part (R-re in blue) of the Fourier transform of the EXAFS data of Th2@Ih(7)-C80 along with their fitting curves (R-mag fitting in green and R-re fitting in orange).
Moreover, the extended X-ray absorption fine structure (EXAFS) spectroscopy further provides information of the coordination environment of Th atoms. The radial distance space spectrum χ(R), obtained by the Fourier transform of the Th L3-edge EXAFS oscillation, χ(k) of Th2@Ih(7)-C80 (k range 2.54–10.42 Å−1), is presented as the radial distribution function including the phase shift (+0.41 Å). This shift is determined by the difference between the first shell Th–C distance from single crystal structure (2.48 Å) and the first scattering path (2.07 Å). As shown in Fig. 4b, the predominant peak located around 2.47 Å can be assigned as the scattering path of Th–C interaction from the first coordination shell in Th2@Ih(7)-C80, which is consistent with the ferrocene like Th–C bonds observed in single crystal structure shown in Fig. 1b. Besides the relative strong first Th–C interactions, the observation of the second and third Th–C interaction suggests that Th ions may also have weaker but non-negligible interaction with carbon atoms in wider region. As shown in Supplementary Figs. 12 and 13, the Th–C distances of 2.90 Å and 3.35 Å (average values) can be found in the crystal structure of Th2@C80, which correspond to the second and third Th–C interaction peaks at 3.11 and 3.54 Å, respectively. Note that the differences between Th–C distances found in SCXRD and EXAFS might be ascribed to different methodologies as well as the different measure temperatures, as the single crystal X-ray data were collected at 113 K and the XAS experiment was carried out at room temperature (ca. 298 K).
Interestingly, the prominent peak located around 4.24 Å can be attributed to the scattering path of Th–Th bond in fourth coordination shell in Th2@Ih(7)-C80. Noteworthy that due to the obvious attenuation in higher χ(R), the strength of Th–Th bond with long distance in fourth coordination is not as strong as the typical metallic bond like Fe–Fe bond in first coordination of Fe foil45. However, it still can be recognized since there is no scattering path signal of Th–C bond at this distance. Note that the scattering path of Th–Th interaction is a little longer than the bond distance (3.816 Å) observed from single crystal structure due to the phase shift.
Finally, quantitative χ(R) space spectra fitting with the k range from 0 to 11.06 Å-1 were also performed to validate local atomic structure and further obtain the bonding type and coordination numbers of Th in Th2@Ih(7)-C80 (Fig. 4c). The single crystal structure of Th2@Ih(7)-C80 shows that there is no bond existing under 2 Å, thus all the scattering path signals from 2 to 6 Å have been taken into the fitting consideration. The χ(R) space spectrum of Th2@Ih(7)-C80 displays Th–C bond with coordination number (CN) approaching 6.0 at 2.477 Å, 6.0 at 3.100 Å, and 8.0 at 3.563 Å, respectively (Supplementary Table 8), from first to third coordination shell which can be connected to Fig. 1b, Supplementary Figs. 12 and 13, respectively. Moreover, the obvious Th–Th metallic bond with coordination number (CN) approaching 1.0 at 4.24 Å from fourth coordination shell can be also observed. The good fitting results of χ(k), χ(R), and real χ(R) space spectra, as shown in Fig. 4d, with reasonable R-factor (0.0218%, Supplementary Table 8) and the obtained fitting parameters quantitatively confirms the coexistence of Th–C and Th–Th bonds. Thus, the two Th3+ ions confined in C80 with Th–Th metallic bonding formation and the ferrocene like Th–C bonds can be confirmed by the combination of single crystal X-ray diffraction and XAFS characterization results, which agree well with the above discussed theoretical calculation results.
Discussion
In summary, we report the formation and characterization of a strong bond between actinides with low oxidation states inside a fullerene cage, namely, Th2@Ih(7)-C80. This compound was synthesized by the arc-discharge method. The single-crystal X-ray diffraction unambiguously determined that the two encapsulated Th atoms are separated by 3.816 Å inside an Ih(7)-C80. The overall agreement between the crystallographic, XAS, and quantum-computational results conclusively shows that the two encapsulated Th ions have formal charges of +3 and confirm the presence of a strong covalent Th–Th bond inside Ih(7)-C80, estimated to be ≥40 kcal mol−1. The computational studies reveal that the overlap between 7s/6d hybrid thorium orbitals is so large that the bond still prevails at Th–Th separations larger than 6 Å, suggesting that this thorium–thorium bond is, up to now, the strongest one among the known actinide–actinide or lanthanide–lanthanide interactions.
This study presents an isolated compound with a strong covalent actinide metal-metal bond, paving the way for future experimental studies of these fundamentally important yet far from fully understood bonding motifs. Moreover, this study proves that the unique bonding environment inside fullerene cages make actinide endohedral fullerenes unique prototype molecules to study actinide–actinide bonding in detail. Because encapsulation always restricts the number of electrons that are transferred from the guest to the fullerene at ≤6, diactinide endohedral fullerenes always have two or more electrons that are available to form single or multiple An–An bonds. Such bonds remain inaccessible by conventional synthetic procedures. These metal–metal bonds may help in the formation mechanisms of dimetallic endohedral fullerenes and it is conceivable that stronger An–An bonds could be formed inside smaller fullerene cages. Further studies are under way to better understand the multiple factors involved in the formation of encapsulated actinide–actinide clusters and the stabilization of the corresponding endohedral fullerenes.
Methods
Synthesis, separation, and purification of Th2@C80
The carbon soot containing thorium EMFs was synthesized by the direct-current arc discharge method. The graphite rods, packed with ThO2 and graphite powder (molar ratio of Th/C = 1:24), were annealed in a tube furnace at 1000 °C for 20 h under an Ar atmosphere and then vaporized in the arcing chamber under 200 Torr He atmosphere. In total 1.87 g of graphite powder and 1.73 g of ThO2 were packed in each rod. The resulting soot was refluxed in CS2 under an argon atmosphere for 12 h. On average ca. 210 mg of crude fullerene mixture per rod was obtained. In total, 100 carbon rods were vaporized in this work. The separation and purification of Th2@C80 was achieved by a multistage HPLC procedure (Supplementary Fig. 2). Multiple HPLC columns, including Buckyprep M (25 × 250 mm, Cosmosil, Nacalai Tesque Inc.), Buckyprep-D (10 × 250 mm, Cosmosil, Nacalai Tesque, Japan), and Buckyprep (10 × 250 mm, Cosmosil, Nacalai Tesque, Japan), were utilized in this procedure. Toluene was used as the mobile phase and the UV detector was adjusted to 310 nm for fullerene detection. The HPLC traces and corresponding MALDI-TOF spectra for the isolated fractions are shown in Supplementary Fig. 2. In total, ca. 1 mg of highly purified Th2@C80 was obtained for characterization.
X-ray crystallographic study
The black block crystals of Th2@Ih(7)-C80·[NiII·(OEP)] were obtained by slow diffusion of a carbon disulfide solution of Th2@C80 into a benzene solution of [NiII·(OEP)]. X-ray data were collected at 113 K using a diffractometer (Bruker D8 Venture) equipped with a CCD detector. The multi-scan method was used for absorption correction. The structure was solved using direct methods46 and refined on F2 using full-matrix least-squares using SHELXL201547. Hydrogen atoms were inserted at calculated positions and constrained with isotropic thermal parameters.
Crystal data for Th2@Ih(7)-C80·[NiII(OEP)]·1.5C6H6·CS2: Mr = 2209.63, 0.2 × 0.2 × 0.2 mm, monoclinic, P21/c (No. 14), a = 17.7202(14) Å, b = 17.0187(13) Å, c = 26.800(2) Å, α = 90°, β = 106.811(2)°, γ = 90°, V = 7736.7(10) Å3, Z = 4, ρcalcd = 1.897 g cm−3, μ(Cu Kα) = 13.585 mm−1, θ = 3.12 − 68.26, T = 113(2) K, R1 = 0.0591, wR2 = 0.1682 for all data; R1 = 0.0587, wR2 = 0.1678 for 13898 reflections (I > 2.0σ(I)) with 1284 parameters. Goodness-of-fit indicator 1.048. Maximum residual electron density 3.590 e Å−3.
XAFS measurements
The X-ray absorption structure spectroscopy (Th L3−edge) were collected at BL11B in Shanghai Synchrotron Radiation Facility (SSRF). The samples were filled into the hole with 1.5 mm diameter on PTFE films (film thickness ca. 0.2 mm) for test. Presented data were produced as an average of three consecutive scans for Th2@C80 while two consecutive scans for ThO2.
Computational methods
DFT calculations for Th2@C2n EMFs were carried out with the ADF 2017 package48 using PBE and PBE0 exchange-correlation functionals in combination with Slater TZP basis sets to describe the valence electrons of Th and C49,50. Frozen cores were described by means of single Slater functions, consisting of the 1 s shell for C and the 1 s to 5d shells for Th. Scalar relativistic corrections were included by means of the ZORA formalism. Dispersion corrections by Grimme were also included51. Relatives energies were computed with GGA PBE and BP86 functionals reoptimizing the structures with each functional.
CASPT2 calculations were performed with OpenMolcas52. The active space contains six orbitals and two electrons in all cases. Test calculations with larger active spaces do not alter the results; Th-carbon bonding and anti-bonding orbitals enter the active space with occupation numbers close to 2 and 0, respectively. The computational costs were reduced by imposing the symmetry restrictions of the D2h group in the case of Th2@C80 and D2 for Th2@C104. Furthermore, we have used the Cholesky decomposition of the two-electron integrals with a 10−4 threshold. Scalar relativistic effects were taken into account with the Douglas–Kroll–Hess Hamiltonian53. We have used the standard IPEA = 0.25 zeroth-order Hamiltonian in the CASPT2 calculations and applied an imaginary level shift of 0.15 eV to avoid intruder states. CASPT2 calculations were performed using PBE0 geometries obtained under the symmetry constraints.
Data availability
The X-ray crystallographic coordinates for the structure reported in this article are available free of charge from the Cambridge Crystallographic Data Centre (CCDC) under deposition number 1961861. The data can be obtained free of charge from The Cambridge Crystallographic Data Centre via www.ccdc.cam.ac.uk/data_request/cif. A data set collection of computational results is available in the ioChem-BD repository and can be accessed via https://doi.org/10.19061/iochem-bd-2-4154. All other data supporting the findings of this study are available from the corresponding authors on request.
References
Hlina, J. A., Pankhurst, J. R., Kaltsoyannis, N. & Arnold, P. L. Metal–metal bonding in Uranium–group 10 complexes. J. Am. Chem. Soc. 138, 3333–3345 (2016).
Lu, E., Wooles, A. J., Gregson, M., Cobb, P. J. & Liddle, S. T. A very short Uranium(IV)-Rhodium(I) bond with net double-dative bonding character. Angew. Chem. 57, 6587–6591 (2018).
Feng, G. et al. Identification of a uranium-rhodium triple bond in a heterometallic cluster. PNAS 116, 17654–17658 (2019).
Wagner, F. R., Noor, A. & Kempe, R. Ultrashort metal–metal distances and extreme bond orders. Nat. Chem. 1, 529–536 (2009).
Knecht, S., Jensen, H. J. A. & Saue, T. Relativistic quantum chemical calculations show that the uranium molecule U2 has a quadruple bond. Nat. Chem. 11, 40–44 (2019).
Roos, B. O., Malmqvist, P.-Å. & Gagliardi, L. Exploring the actinide−actinide bond: theoretical studies of the chemical bond in Ac2, Th2, Pa2, and U2. J. Am. Chem. Soc. 128, 17000–17006 (2006).
Gorokhov, L. N., Emelyanov, A. M. & Khodeev, Yu. S. Mass-spectroscopic investigation of stability of gaseous molecules of U2O2 and U2. High. Temp. 12, 1156–1158 (1974).
Wang, C. Z. et al. Actinide (An = Th-Pu) dimetallocenes: promising candidates for metal–metal multiple bonds. Dalton Trans. 44, 17045–17053 (2015).
Gagliardi, L. & Roos, B. O. Quantum chemical calculations show that the uranium molecule U2 has a quintuple bond. Nature 433, 848–851 (2005).
Roos, B. O., Borin, A. C. & Gagliardi, L. Reaching the maximum multiplicity of the covalent chemical bond. Angew. Chem. 119, 1491–1494 (2007).
Hu, H. S. & Kaltsoyannis, N. The shortest Th-Th distance from a new type of quadruple bond. Phys. Chem. Chem. Phys. 19, 5070–5076 (2017).
Souter, P. F., Kushto, G. P., Andrews, L. & Neurock, M. Experimental and theoretical evidence for the formation of several uranium hydride molecules. J. Am. Chem. Soc. 119, 1682–1687 (1997).
Scheibe, B. et al. The [U2F12]2− anion of Sr[U2F12]. Angew. Chem. Int. Ed. 57, 2914–2918 (2018).
Zhang, X. et al. U2@Ih(7)-C80: crystallographic characterization of a long-sought dimetallic actinide endohedral fullerene. J. Am. Chem. Soc. 140, 3907–3915 (2018).
Cai, W., Chen, C. H., Chen, N. & Echegoyen, L. Fullerenes as nanocontainers that stabilize unique actinide species inside: structures, formation, and reactivity. Acc. Chem. Res. 52, 1824–1833 (2019).
Langeslay, R. R., Fieser, M. E., Ziller, J. W., Furche, F. & Evans, W. J. Expanding thorium hydride chemistry through Th2+, including the synthesis of a mixed-valent Th4+/Th3+ hydride complex. J. Am. Chem. Soc. 138, 4036–4045 (2016).
Langeslay, R. R. et al. Synthesis, structure, and reactivity of the sterically crowded Th3+ complex (C5Me5)3Th including formation of the thorium carbonyl, [(C5Me5)3Th(CO)][BPh4]. J. Am. Chem. Soc. 139, 3387–3398 (2017).
Langeslay, R. R., Fieser, M. E., Ziller, J. W., Furche, F. & Evans, W. J. Synthesis, structure, and reactivity of crystalline molecular complexes of the {[C5H3(SiMe3)2]3Th}1- anion containing thorium in the formal +2 oxidation state. Chem. Sci. 6, 517–521 (2015).
La Pierre, H. S., Scheurer, A., Heinemann, F. W., Hieringer, W. & Meyer, K. Synthesis and characterization of a uranium(II) monoarene complex supported by delta backbonding. Angew. Chem. 53, 7158–7162 (2014).
Zuo, T. et al. M2@C79N (M = Y, Tb): isolation and characterization of stable endohedral metallofullerenes exhibiting M−M bonding interactions inside Aza[80]fullerene cages. J. Am. Chem. Soc. 130, 12992–12997 (2008).
Liu, F. et al. Single molecule magnet with an unpaired electron trapped between two lanthanide ions inside a fullerene. Nat. Commun. 8, 16098 (2017).
Bao, L. et al. Crystallographic evidence for direct metal-metal bonding in a stable open-shell La2 @Ih-C80 derivative. Angew. Chem. 55, 4242–4246 (2016).
Shen, W. et al. Lu2@C2n (2n = 82, 84, 86): crystallographic evidence of direct Lu-Lu bonding between two divalent lutetium ions inside fullerene cages. J. Am. Chem. Soc. 139, 9979–9984 (2017).
Liu, F. et al. Air-stable redox-active nanomagnets with lanthanide spins radical-bridged by a metal-metal bond. Nat. Commun. 10, 571 (2019).
Yao, Y.-R. et al. Atomically precise insights into metal-metal bond by comparable endo-units of Sc2 and Sc2C2. CCS Chem. 3, 294–302 (2021).
Infante, I., Gagliardi, L. & Scuseria, G. E. Is fullerene C60 large enough to host a multiply bonded dimetal? J. Am. Chem. Soc. 130, 7459–7465 (2008).
Foroutan-Nejad, C., Vicha, J., Marek, R., Patzschke, M. & Straka, M. Unwilling U-U bonding in U2@C80: cage-driven metal-metal bonds in di-uranium fullerenes. Phys. Chem. Chem. Phys. 17, 24182–24192 (2015).
Feng, L. et al. Mapping the metal positions inside spherical C80 cages: crystallographic and theoretical studies of Ce2@D5h-C80 and Ce2@Ih-C80. Chem. -Eur. J. 19, 988–993 (2013).
Nishibori, E., Takata, M., Sakata, M., Taninaka, A. & Shinohara, H. Pentagonal-dodecahedral La2 charge density in [80-Ih]fullerene: La2@C80. Angew. Chem. Int. Ed. 40, 2998–2999 (2001).
Blake, P. C. et al. Synthesis, properties and structures of the tris(cyclopentadienyl)thorium(III) complexes [Th{η5-C5H3(SiMe2R)2-1,3}3] (R=Me or tBu).J. Organomet. Chem. 636, 124–129 (2001).
Siladke, N. A. et al. Actinide Metallocene Hydride Chemistry: C–H Activation in Tetramethylcyclopentadienyl Ligands to Form [μ-η5-C5Me3H(CH2)-κC]2– Tuck-over Ligands in a Tetrathorium Octahydride Complex.Organometallics 32, 6522–6531 (2013).
Campanera, J. M., Bo, C. & Poblet, J. M. General rule for the stabilization of fullerene cages encapsulating trimetallic nitride templates. Angew. Chem. Int. Ed. 44, 7230–7233 (2005).
Rodriguez-Fortea, A., Alegret, N., Balch, A. L. & Poblet, J. M. The maximum pentagon separation rule provides a guideline for the structures of endohedral metallofullerenes. Nat. Chem. 2, 955–961 (2010).
Bratsch, S. G. & Lagowski, J. J. Actinide thermodynamic predictions. 3. Thermodynamics of compounds and aquo-ions of the 2+, 3+, and 4+ oxidation states and standard electrode potentials at 298.15 K. J. Phys. Chem. 90, 307–312 (1986).
Ionova, G., Madic, C. & Guillaumont, R. About the existence of Th(III) in aqueous solution. Polyhedron 17, 1991–1995 (1998).
Nugent, L. J., Baybarz, R. D., Burnett, J. L. & Ryan, J. L. Electron-transfer and f-d absorption bands of some lanthanide and actinide complexes and the standard (II-III) oxidation potential for each member of the lanthanide and actinide series. J. Phys. Chem. 77, 1528–1539 (1973).
Bader, R. F. W. Atoms in Molecules—A Quantum Theory. (Oxford Univ. Press, 1990).
Savin, A. et al. Electron localization in solid-state structures of the elements: the diamond. Struct. Angew. Chem. Int. Ed. Engl. 31, 187–188 (1992).
Popov, A. A., Yang, S. & Dunsch, L. Endohedral fullerenes. Chem. Rev. 113, 5989–6113 (2013).
Lebedkin, S., Renker, B., Heid, R., Schober, H. & Rietschel, H. A spectroscopic study of M@C82 metallofullerenes: Raman, far-infrared, and neutron scattering results. Appl. Phys. A 66, 273–280 (1998).
Wang, Y. et al. Unique four-electron metal-to-cage charge transfer of Th to a C82 fullerene cage: complete structural characterization of Th@C3v(8)-C82. J. Am. Chem. Soc. 139, 5110–5116 (2017).
Wang, Y. et al. Th@C1(11)-C86: an actinide encapsulated in an unexpected C86 fullerene cage. Chem. Commun. 55, 9271–9274 (2019).
Cai, W. et al. Synthesis and characterization of non-isolated-pentagon-rule actinide endohedral metallofullerenes U@C1(17418)-C76, U@C1(28324)-C80, and Th@C1(28324)-C80: low-symmetry cage selection directed by a tetravalent ion. J. Am. Chem. Soc. 140, 18039–18050 (2018).
Zhang, X. et al. A diuranium carbide cluster stabilized inside a C80 fullerene cage. Nat. Commun. 9, 2753 (2018).
Hu, J. et al. Melt-salt-assisted direct transformation of solid oxide into atomically dispersed FeN4 sites on nitrogen-doped porous carbon. Nano Energy 72, 104670 (2020).
Dolomanov, O. V., Bourhis, L. J., Gildea, R. J., Howard, J. A. K. & Puschmann, H. OLEX2: a complete structure solution, refinement and analysis program. J. Appl. Crystallogr. 42, 339–341 (2009).
Sheldrick, G. Crystal structure refinement with SHELXL. Acta Crystallogr. C. 71, 3–8 (2015).
te Velde, G. et al. Chemistry with ADF. J. Comput. Chem. 22, 931–967 (2001).
Becke, A. D. Density functional calculations of molecular bond energies. J. Chem. Phys. 84, 4524–4529 (1986).
Perdew, J. P. Density-functional approximation for the correlation energy of the inhomogeneous electron gas. Phys. Rev. B 33, 8822–8824 (1986).
Grimme, S., Ehrlich, S. & Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 32, 1456–1465 (2011).
Aquilante, F. et al. Molcas 8: new capabilities for multiconfigurational quantum chemical calculations across the periodic table. J. Comput. Chem. 37, 506–541 (2016).
Hess, B. A. Relativistic electronic-structure calculations employing a two-component no-pair formalism with external-field projection operators. Phys. Rev. A 33, 3742–3748 (1986).
Álvarez-Moreno, M. et al. Managing the computational chemistry big data problem: the ioChem-BD platform. J. Chem. Inf. Model. 55, 95–103 (2015).
Acknowledgements
We cordially thank beamline BL11B of the Shanghai Synchrotron Radiation Facility (SSRF) for XAS test and Dr. Duo Zhang (Soochow University) for the kind technique support. C.N. thanks the National Science Foundation China (NSFC 91961109, 51302178), the Natural Science Foundation of Jiangsu Province (BK20200041), and Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD). J.M.P. and C.d.G. thank the Spanish Ministry of Science (grants CTQ2017-87269-P and CTQ2017-83566-P), the Generalitat de Catalunya (grant 2017SGR629) and the URV for support. J.M.P. also thanks ICREA foundation for an ICREA ACADEMIA award. R.M.M. thanks Spanish Ministry of Science for a PhD fellowship. Z.J.W. thanks the National Natural Science Foundation of China (grant 21701168). L.E. thanks the US National Science Foundation (NSF) for generous support of this work under grant CHE-1801317, the Robert A. Welch Foundation is also gratefully acknowledged for an endowed chair to L.E. (grant AH-0033).
Author information
Authors and Affiliations
Contributions
N.C. conceived and designed the experiments. Z.J.X. and W.Y.F. synthesized and isolated all the compounds. R.M.M., A.R.F., C.d.G., and J.M.P. performed the computations and theoretical analyses. Y.Y.R and Z.J.X. performed the crystallographic analysis. Z.J.X. and P.C.Y. performed the XAS measurements and Z.J.W. performed the XAS analyses. N.C., J.M.P., Z.J.X., C.d.G., Z.J.W., R.M.M., A.R.F., L.E., and W.S.A. co-wrote the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks Weiqun Shi, Koichiro Takao, and other anonymous reviewers for their contributions to the peer review of this work. Peer review reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhuang, J., Morales-Martínez, R., Zhang, J. et al. Characterization of a strong covalent Th3+–Th3+ bond inside an Ih(7)-C80 fullerene cage. Nat Commun 12, 2372 (2021). https://doi.org/10.1038/s41467-021-22659-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-021-22659-2
This article is cited by
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.