Abstract
Mechanical systems are one of the promising platforms for classical and quantum information processing and are already widely-used in electronics and photonics. Cavity optomechanics offers many new possibilities for information processing using mechanical degrees of freedom; one of them is storing optical signals in long-lived mechanical vibrations by means of optomechanically induced transparency. However, the memory storage time is limited by intrinsic mechanical dissipation. More over, in-situ control and manipulation of the stored signals processing has not been demonstrated. Here, we address both of these limitations using a multi-mode cavity optomechanical memory. An additional optical field coupled to the memory modifies its dynamics through time-varying parametric feedback. We demonstrate that this can extend the memory decay time by an order of magnitude, decrease its effective mechanical dissipation rate by two orders of magnitude, and deterministically shift the phase of a stored field by over 2π. This further expands the information processing toolkit provided by cavity optomechanics.
Similar content being viewed by others
Introduction
Information processing devices exhibit dissipation due to their coupling to external degrees of freedom. This permits energy to leave and fluctuations to enter the system1, and typically degrades the performance of components such as memories. Within the field of optomechanics2,3, this has motivated tremendous progress in reducing intrinsic dissipation through precise tailoring of device geometry and materials4,5,6,7. A complementary approach, sometimes referred to as reservoir engineering8, uses dissipation channels to enhance system properties, typically via an auxiliary coherent source that couples to the system. Here, we show that when reservoir engineering is generalized to incorporate dynamic control of this external coupling, a system’s steady state can be adiabatically manipulated. By dynamically varying the coupling of an optomechanical memory to an auxiliary control field–a reservoir mode–we demonstrate that stored light can be coherently modified. This is a crucial step towards realizing the optical processing of light stored in the mechanical motion of a nanoscale device.
The concept of using an external field to manipulate optical information via coupling to a mechanical degree of freedom has been previously explored in Brillouin scattering optomechanics9, where powerful functionality including pulse storage10,11, all optical signal processing12, and coherently refreshed memory13 have been demonstrated in cm-long waveguides. Cavity optomechanical devices, in which optical and mechanical modes can be confined and spatially overlapped within wavelength-scale volumes, allow the nearly complete transfer of an optical excitation to low dissipation mechanical resonances. These devices operate with relatively low power and occupy micron-scale footprints, and have been used for information storage14,15. However, manipulating this stored information has not been demonstrated.
In this work, we use a diamond optomechanical microdisk cavity to realize a memory based on optomechanically induced transparency16,17 that converts a weak optical input to a long-lived mechanical excitation. We then show that by adjusting the frequency of a field input to a reservoir mode, we can effectively reduce the mechanical dissipation of the device through parametric feedback until it is just below the self-oscillation threshold, allowing the memory lifetime to be extended. Through precise tuning of the reservoir-field frequency, we directly observe a memory lifetime enhancement of over seven times, and realize an over 150 times reduction in the resonator’s effective mechanical dissipation rate. Finally, we demonstrate that by dynamically varying the reservoir-field frequency the phase of the stored signal can be manipulated.
Results
Diamond microdisks can operate as multimode cavity optomechanical systems whose optical whispering gallery modes are coupled by radiation pressure to the motion of the device’s mechanical resonances18. Coherent multimode optomechanical coupling is possible in these devices even at room-temperature and ambient conditions19 thanks to the low-energy dissipation rates, κ and Γ, of their optical and mechanical modes, respectively, combined with diamond’s ability to support high-intensity fields without suffering from nonlinear absorption and heating. This latter property increases the maximum number (n) of photons that can be supported by the microdisk, which enhances the photon-assisted optomechanical coupling rate \(g=\sqrt{n}{g}_{0}\). These devices have a high single-photon optomechanical coupling rate g0 due to their wavelength-scale dimensions and strong spatial overlap of the microdisk’s whispering gallery modes with its mechanical radial breathing mode.
The condition for coherent optomechanical coupling in both classical and quantum devices is cooperativity C = 4g2/κΓ > 1, and can be achieved simultaneously by using multiple modes of a diamond microdisk. Multimode cavity optomechanics enables optical wavelength conversion20,21,22,23, photon entanglement24,25, and low-noise frequency conversion in the microwave domain26. We show in this paper that multimode diamond microdisks are excellent platforms for implementing memories whose stored information can be manipulated via dynamic reservoir engineering27,28.
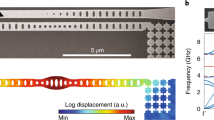
The system used in this work is illustrated schematically in Fig. 1. Information input to an optical “signal” mode (a) of a diamond microdisk cavity is transferred via optomechanical coupling to the device’s mechanical mode (b). Simultaneously, the mechanical mode dynamics are modified through its coupling to an optical “reservoir” mode (r). The optical and mechanical modes are characterized by their frequencies (ωa,r, ωb) and energy decay rates (κa,r, Γb), respectively. The reservoir mode is driven by a control laser whose detuning from resonance, Δr, sets the phase lag of its optomechanical coupling to the mechanical resonator, and whose power, Pr (defined here as the power input to the fiber taper waveguide), sets the coupling strength. This tunable resonator–reservoir interaction induces additional mechanical dissipation \({{{\Gamma }}}_{{\rm{r}}}^{{\rm{opt}}}\) and shifts the mechanical resonator frequency by \({\omega }_{{\rm{r}}}^{{\rm{opt}}}\), two effects widely studied in single-mode optomechanical systems, for example in demonstration of mechanical ground-state cooling29,30.
a Annotated scanning electron micrograph of the diamond microdisk optomechanical cavity. A tapered optical fiber is utilized to couple light into two of the microdisk whispering gallery modes which in turn are coupled to mechanical vibrations of the radial breathing mode of the microdisk. b Schematic of the system under study where the mechanical mode b is coupled to the environment (red bath), an optical reservoir mode, r, and the optical mode a used for writing and reading the information, at the indicated rates. While coupling of the mechanical mode to the surrounding environment is an intrinsic property of the device and environment, the coupling to r may be manipulated through the use of a control laser. c, d Density of states (DOS) picture showing the detuning of the control and probe laser fields for (c) mode a and (d) mode r. Here, ωc,a and ωc,r are the frequencies of the control lasers for the signal and reservoir modes, respectively.
To process information stored in the mechanical resonator, we dynamically adjust the power and detuning of the reservoir input field. The resonator evolution is governed by (Supplementary Note 1):
where \(\hat{b}\) is the phonon annihilation operator, \({\hat{e}}_{{\rm{in}}}\) is the thermal bath input field, \({\hat{r}}_{{\rm{in}}}\) is the optical reservoir input field, \({g}_{{\rm{r}}}\propto \sqrt{{P}_{r}}\) is the photon-assisted optomechanical coupling rate between the reservoir mode and the resonator, and χr is the reservoir mode’s optical response in the frame of the reservoir mode control laser. The key feature that we test and exploit is the ability to dynamically control the memory’s effective mechanical frequency, \({\omega }_{{\rm{b}}}^{{\rm{eff}}}={\omega }_{{\rm{b}}}+{\omega }_{{\rm{r}}}^{{\rm{opt}}}(t)\), and effective damping rate, \({{{\Gamma }}}_{{\rm{b}}}^{{\rm{eff}}}={{{\Gamma }}}_{{\rm{b}}}+{{{\Gamma }}}_{{\rm{r}}}^{{\rm{opt}}}(t)\), by adjusting the reservoir-mode parameters gr(t) and Δr(t) as a function of time. Notably, we find that when we input a field to mode a to this system, the memory operates as if it is a conventional single-mode cavity optomechanical device whose mechanical resonator dynamics have been renormalized. This regime is valid if Γb ≪ κr.
Equation (1) shows that the reservoir-mode coupling acts as a dissipative process, and not a direct drive. Since we alter the effective dissipation of the system, we use the descriptor reservoir engineering, in analogy to the work that introduced this term8. Note that although the effects demonstrated below can be described classically, the quantum formalism used here allows the analysis of noise processes, including photon-phonon scattering, that will ultimately limit memory performance.
Below we test the validity of this description and demonstrate applications of dynamic reservoir coupling through three experiments. First, we show an enhancement of the system’s optomechanical cooperativity due to its renormalized mechanical dissipation and switch the dynamics of the system from overall loss to the overall gain. Second, we increase the optomechanical memory storage time through control of \({{{\Gamma }}}_{{\rm{b}}}^{{\rm{eff}}}\). Finally, we control the phase of a stored mechanical signal through manipulation of \({\omega }_{{\rm{b}}}^{{\rm{opt}}}\) as a function of time.
Engineering the system dynamics
We first probe how the dynamics of the mechanical resonator, and its resulting coupling to light, are affected by the resonator–reservoir interaction. This is accomplished using optomechanically induced transparency (OMIT) spectroscopy16,17. OMIT creates a transparency window in the cavity lineshape whose properties depend on the dynamics of the optomechanical system. By coherently coupling a probe field in a to the mechanical resonator for varying reservoir control laser settings, we can learn about the influence of the reservoir on the resonator. These measurements are shown in Fig. 2a, which were obtained using a fiber taper waveguide to evanescently couple the reservoir control laser to mode r (ωr/2π = 192 THz, κr/2π = 1.13 GHz) for varying Δr, while performing OMIT spectroscopy on mode a (ωa/2π = 197 THz, κa/2π = 0.856 GHz) using a weak resonant probe laser and a control laser red detuned by ωb. Note that in all measurements presented below the probe field is generated by modulating the control laser and is typically in the μW range (see “Methods”). The device used here has ωb/2π ~ 2.14 GHz and Γb/2π = 190 kHz for the radial breathing mode and operates in the resolved sideband regime for modes a and r(ωb/κa = 2.5, ωb/κr = 1.9). Coupling to other mechanical modes of the microdisk was not observed. Note that the optical reservoir mode is a standing wave doublet (see “Methods” and Supplementary Note 1) formed from backscattering in the microdisk31,32, whose most apparent effect is the two sets of minima and maxima in Fig. 2a. In all measurements, the mode a control field detuning was set relative to the lowest frequency doublet resonance.
a Normalized OMIT scans as a function of mode a probe-cavity detuning, δa, and control-reservoir detuning, Δr, and S21 is the probe laser reflection measured using a vector network analyzer. The changes in the transparency window as a function of Δr are indicative of reservoir interactions. Optomechanically manipulated effective (b) mechanical frequency and (c) damping as a function of Δr and the reservoir-mode input power, Pr. (d) Illustration of effective cooperativity, Ceff, for varying \({{{\Gamma }}}_{{\rm{b}}}^{{\rm{eff}}}\) controlled by the reservoir mode, when \({{{\Gamma }}}_{{\rm{a}}}^{{\rm{opt}}}={{{\Gamma }}}_{{\rm{b}}}\) due to the presence of the mode a control field. Three different regimes of operation are shown: OMIT OMIA, and self-oscillation (SO). The yellow star indicates the operating point when the reservoir field is off.
This measurement was repeated for three different values of Pr, with the probe control laser fixed at input power Pa ~ 0.26 mW (intracavity photon number na ~ 3.2 × 104). At each reservoir setting \({{{\Gamma }}}_{{\rm{b}}}^{{\rm{eff}}}\) and \({\omega }_{{\rm{b}}}^{{\rm{eff}}}\) were extracted from the OMIT window shape (see Supplementary Note 2), and are plotted along with fits to the data in Fig. 2b, c. The fits, which show excellent agreement with measurements, were obtained with gr as the only fitting parameter. This confirms that optomechanical renormalization of the mechanical resonator dynamics by the reservoir field affect mode a’s optomechanical response as if \({{{\Gamma }}}_{{\rm{b}}}^{{\rm{eff}}}\) and \({\omega }_{{\rm{b}}}^{{\rm{eff}}}\) were the mechanical resonator’s intrinsic mechanical properties.
The system dynamics are most dramatically affected when \({{{\Gamma }}}_{{\rm{b}}}^{{\rm{eff}}}\) approaches zero and becomes negative. In a conventional OMIT system, the depth and width of the transparency window is parameterized by the optomechanical cooperativity, \(C=\frac{4| {g}_{{\rm{a}}}{| }^{2}}{{\kappa }_{{\rm{a}}}{{{\Gamma }}}_{{\rm{b}}}}={n}_{\text{a}}\frac{4| {g}_{0}{| }^{2}}{{\kappa }_{{\rm{a}}}{{{\Gamma }}}_{{\rm{b}}}}\), where ga is the photon-assisted optomechanical coupling rate for mode a. For the microdisk used here, g0/2π ~ 25 kHz23. Note that the optomechanical cooperativity differs from the single-photon cooperativity by a factor of na. However, in our multimode system, OMIT is governed by an effective cooperativity \({C}_{{\rm{eff}}}=C\times {{{\Gamma }}}_{{\rm{b}}}/{{{\Gamma }}}_{{\rm{b}}}^{{\rm{eff}}}\). In the measurement presented here, we achieve a maximum Ceff = 83, which represents an enhancement of 158 × the bare C = 0.52 experienced by the mode a probe in absence of the reservoir field. This allows our system to act as though it has large cooperativity, enabling large light delays and narrow transparency windows (see Supplementary Note 2). This enhancement is limited only by how close to zero \({{{\Gamma }}}_{{\rm{b}}}^{{\rm{eff}}}\) can be tuned through adjustment of Δr. Hence, it is not limited by available laser power since the regime of \({{{\Gamma }}}_{{\rm{b}}}^{{\rm{eff}}}<0\) can be reached for the powers used here (see below).
As \({{{\Gamma }}}_{{\rm{b}}}^{{\rm{eff}}}\) becomes negative, the mechanical resonator motion changes from experiencing an overall loss to an overall gain. Consequently, by adjusting our reservoir coupling, we are able to tune the system dynamics between OMIT and the regime of optomechanically induced amplification (OMIA). This gain would normally cause optomechanically induced self-oscillation to occur33,34. However, this instability is repressed in our multimode measurements by the optomechanical damping \({{{\Gamma }}}_{{\rm{a}}}^{{\rm{opt}}}\) induced by mode a’s OMIT process, provided \({{{\Gamma }}}_{{\rm{a}}}^{{\rm{opt}}}+{{{\Gamma }}}_{{\rm{b}}}^{{\rm{eff}}}\,> \,0\). The ability of the reservoir mode to tune the system dynamics between OMIT, OMIA, and self-oscillation regimes is illustrated in Fig. 2d for the special case that \({{{\Gamma }}}_{{\rm{a}}}^{{\rm{opt}}}={{{\Gamma }}}_{{\rm{b}}}\). In our measurements, the OMIA regime was entered for both the Pr = 3.3 mW and Pr = 4.1 mW settings when the control laser was blue detuned from the reservoir mode’s lowest frequency doublet feature by approximately ωb. This regime was not accessed during the storage measurements described in the following sections, and can only be measured due to the damping provided by the mode a fields.
Pulse-storage manipulation
Pioneering experiments with Λ-type atomic systems have demonstrated that a strong control field can dramatically alter the optical response of a material, including rendering otherwise opaque materials transparent35, enhancing nonlinear processes36,37, and slowing the group velocity of a pulse of light38,39. Furthermore, by dynamically altering the transparency of a material, a pulse of light may be trapped and deterministically released at a later time40,41,42. Such schemes have been used to store light pulses for over a minute43, and have been proven to work at a single-photon level44,45.
Cavity optomechanical systems have similar capabilities. In OMIT, the interaction between optical mode a and the mechanical resonator is described by the beamsplitter Hamiltonian \({\hat{H}}_{\text{bs}}=\hslash {g}_{\text{a}}({\hat{a}}^{\dagger }\hat{b}+\hat{a}{\hat{b}}^{\dagger })\) when the mode a control field is red detuned by ωb from resonance2. Here, \(\hat{a}\)\(\left({\hat{a}}^{\dagger }\right)\) and \(\hat{b}\)\(({\hat{b}}^{\dagger })\) are annihilation (creation) operators for optical mode a and mechanical resonator mode b, respectively. This Hamiltonian allows for coherent exchange of excitations between modes a and b. By adjusting the control field amplitude, which in turn controls ga, a field input to a can be coherently and reversibly stored in the mechanical resonator14,15,46,47.
Here, we show that an optical field stored in the motion of an optomechanical memory can be dynamically modified by varying the resonator’s coupling to a reservoir mode. Our memory protocol is illustrated using mass-on-spring systems in Fig. 3a. During the writing stage, the red-detuned mode a control laser couples a weak signal field resonant with mode \(\hat{a}\) to mode \(\hat{b}\) at rate ga. Following the write stage, the control laser is removed, decoupling modes a and b. Finally, during the read stage, the reservoir control laser is removed and the signal control laser is turned back on, reconverting the stored mechanical signal to the optical domain. Our scheme deviates from a conventional optomechanical memory15,46,47 in two ways: not only does coupling to the reservoir modify the mechanical resonator dynamics as described above, the reservoir coupling can also be varied temporally. This both modifies the stored information and the rate at which it dissipates.
a Outline of the storage protocol where the optomechanical coupling between optical mode a and the mechanical mode facilitates storage of an optical pulse as a mechanical excitation. Mode r is used to manipulate the mechanical damping rate, \({{{\Gamma }}}_{{\rm{b}}}^{{\rm{eff}}}\)(t), and frequency, \({\omega }_{{\rm{b}}}^{{\rm{eff}}}\)(t) which can be carried out concurrently with the storage process. b Normalized read pulse amplitude, \(\bar{A}\) for the off-resonant, Δr ≫ ωm, case (cyan) and for Δr ~ ωm (orange) as a function of τd. These are fit to an exponential decay (dashed lines) to extract \({{{\Gamma }}}_{\,\text{b}}^{\text{eff}\,}\). c, d Zoom-in of of the read data shown in (b) for τd = (0.14, 0.93) μs, illustrating the enhancement in \(\bar{A}\) when Δr ~ ωm. e Complete data set from which (b) was taken showing both an enhancement and reduction in storage time as a function of Δr, which is compared to the expected behavior (f).
Through continuous amplification of the stored mechanical signal by the reservoir mode, the pulse-storage lifetime of the mechanical resonator can be extended. This is in a similar spirit to previous demonstrations of optomechanical amplification in waveguides13. In cavity optomechanics, amplification is achieved by setting Δr to +ωb, so that the reservoir-resonator interaction is governed by the parametric amplifier Hamiltonian \({\hat{H}}_{\text{amp}}=\hslash {g}_{\text{r}}(\hat{r}\hat{b}+{\hat{r}}^{\dagger }{\hat{b}}^{\dagger })\), where \(\hat{r}\)\(({\hat{r}}^{\dagger })\) is the annihilation (creation) operator for optical mode r. In the experiments, Δr is tuned until \({{{\Gamma }}}_{{\rm{b}}}^{{\rm{eff}}}\) nearly vanishes, as in Fig. 2c. Note that in contrast to Brillouin scattering, the mechanical mode amplitude can grow exponentially during this interaction2,48.
To measure the storage time for a given reservoir setting, we varied the delay τd between the write and read pulses. The measured amplitude output during the read pulse encodes the temporal envelope of the mechanical signal, which decays exponentially at a rate \({{{\Gamma }}}_{{\rm{b}}}^{{\rm{eff}}}\). An example of this decay is plotted in Fig. 3b for two cases: when the reservoir control is optimally detuned for enhanced storage time (Δr ≈ −ωb and \({{{\Gamma }}}_{{\rm{b}}}^{{\rm{eff}}}\ll {{{\Gamma }}}_{{\rm{b}}}\)), and when the reservoir is far detuned (Δr ≫ ωb and \({{{\Gamma }}}_{{\rm{b}}}^{{\rm{eff}}} \sim {{{\Gamma }}}_{{\rm{b}}}\)).
Comparing the observed decay rates for each configuration indicates a 7 × enhancement in 1/e time from 1.1 μs to 7.7 μs due to the reservoir coupling. Examples of the signal extracted at two values of τd are shown in Fig. 3c, d, demonstrating the dramatic increase in the amplitude of the enhanced signal at longer timescales. Full measurement of the readout amplitude decay for varying Δr was also acquired, the results of which are plotted in Fig. 3e. This shows qualitative agreement to the theoretical amplitudes obtained from an analytic fit of \({{{\Gamma }}}_{{\rm{b}}}^{{\rm{eff}}}({{{\Delta }}}_{{\rm{r}}})\) and plotted in Fig. 3f. Note the doublet nature of the reservoir mode is again evident in the measurement. Differences between theory and experiment are understood to be a consequence of thermal drifts in the resonance frequencies of the modes, as well as wavelength drifts in the readout laser used in the experiment. These imperfections lead to a deviation of the readout signal from a sinusoid in Fig. 3c and will reduce the fidelity of the reamplified memory. They can be mitigated by an active stabilization of Δr but further measurements with shaped input pulses are required to fully characterize their effect.
The optomechanical memory’s storage time depends on dephasing governed by \(1/{{{\Gamma }}}_{\,\text{b}}^{\text{eff}\,}\) and on added noise. The latter is created by the optical field, which can amplify thermal phonons and spontaneously generate phonons, in addition to amplifying desirable signal phonons. Ignoring spontaneous processes, given a stored signal with an initial signal-to-noise ratio (SNR0) defined by the ratio of the signal and thermal phonon populations, for large SNR0 the thermal and signal phonon populations become equal at time \({t}_{s} \sim 1/{{{\Gamma }}}_{\,\text{b}}^{\text{eff}\,}\mathrm{ln}\,\left({\text{SNR}}_{0}\right)\). This storage time exceeds the 1/e decay time, as it is defined by the minimum acceptable SNR of the retrieved signal. It ignores the reduction to the initial thermal population from the OMIT write step, which will further extend ts; a more general expression is given together with an analysis of storage time in Supplementary Note 4. The maximum SNR0 is set by the device’s temperature combined with its maximum achievable oscillation amplitude. From previous measurements an SNR0 of 1000 at room temperature should be achievable18. Together with a realistic value of \({{{\Gamma }}}_{\,\text{b}}^{\text{eff}\,}=2\pi \times 1\) kHz, a memory time of ≈ 5 ms is predicted. Finally, note that the ultimate limit on storage time will be set by generation and amplification of Stokes phonons, which were not considered in this analysis but will become important when operating in the quantum regime.
We also emphasize that thermal phonons from the environment preclude storage of quantum states when operating at room temperature, due to the persistent thermal occupation of the memory. Even in the absence of thermal noise, phonons introduced by the reservoir laser, e.g., through spontaneous Stokes scattering, will degrade the device’s ability to store quantum states. These effects could potentially be mitigated by utilizing phononic shielding29,49, and by further increasing the optomechanical cooperativity through reducing the device’s optical loss (which is limited by surface roughness50), its mechanical dissipation, and its optical mode volume.
However, in the measurements of decay time presented here, technical noise dominated over amplified mechanical noise. In particular, drifts in control and probe laser detunings required operating at a lower Pr compared to the cooperativity enhancement measurements in Fig. 2, to ensure that the system did not enter the unstable regime (\({{{\Gamma }}}_{\,\text{b}}^{\text{eff}\,}<\,0\)). This lower power explains the modest observed decease in the decay time compared to the 158 × cooperativity enhancement reported above. By operating more closely to the self-oscillation threshold through stabilization of Δr, reductions in decay time similar to or exceeding the cooperativity enhancement will be possible.
Another important characteristic of a memory is its time–bandwidth product (TBP). A conservative measure of this for our system can be obtained from the product of the 1/e decay time and the mechanical linewidth. For CW excitation of the reservoir, this product will not change with \({{{\Gamma }}}_{{\rm{b}}}^{{\rm{eff}}}\) as any increase in decay time will be accompanied by a reduction in linewidth; it is 1.38 for our device which is typical for OMIT-based memories14,46 and is an order of magnitude smaller than in Brillouin waveguide memories13. However, note that in waveguide systems storage time is often defined by SNR, as discussed above, resulting in a TBP \(\propto \mathrm{ln}\,\left({\text{SNR}}_{0}\right)\) dependent on the initial signal strength. Increasing the bandwidth can be realized by using multiple mechanical modes or cascaded resonators51, which is predicted to provide a maximum bandwidth ~ ΓbC. Alternatively, by operating with a reservoir field that is turned on adiabatically during the storage phase, one could combine enhanced storage times and the intrinsic bandwidth of the mechanical resonator.
We next show that the phase of the stored pulse can be controlled by dynamically varying the reservoir-mode input. By changing \({\omega }_{{\rm{b}}}^{{\rm{eff}}}\) adiabatically and hence the frequency of the stored pulse, we can complete a trajectory that moves away from and then returns to the original frequency. Over the course of this trajectory, the mechanical oscillator acquires a dynamical phase \(\varphi ({t}_{2})=\varphi ({t}_{1})+\mathop{\int}\nolimits_{{t}_{1}}^{{t}_{2}}\delta \omega (t)dt\), assuming that we return to the original mechanical frequency. This is analogous to a pendulum whose length is adjusted in time52. In our experiment, we varied the amplitude of the reservoir mode in time using an amplitude electro-optic modulator driven by a symmetric RF ramp pulse (see “Methods”) for various Δr as shown in Fig. 4a. Here, the ramp pulse was 3.5 μs long and was situated 1.5 μs after the write, and before the read pulse. By fitting the beat note detected at the fiber output for each of the write, ramp, and read pulse segments, we can plot the phase as referenced to the well-defined write pulse, as shown in shown in Fig. 4b. Here, we have removed the phase shift associated with the spring effect induced by the write pulse, which added a linear slope to the ramp and read pulse segments. This allows us to isolate the shift due to the spring effect associated with the reservoir-mode ramp pulse (see Supplementary Note 5). From the read pulse segments, we extract the phase relative to the write pulse, demonstrating a reservoir controlled phase shift, Δφ > 2π as shown in Fig. 4c. Further studies of quantum noise generated by the reservoir mode during the frequency tuning process are required to assess the performance of this technique in the quantum domain.
a Amplitude of the acquired signals vs. time and reservoir detuning for the phase-manipulation experiment. In this experiment, no optical filtering was used, so that the write, ramp, and read pulses may all be detected. b Phase of the mechanical oscillator vs. time as inferred from the optical output of the device. c Final phase as a function of Δr along with a fit to the data based on the predicted temporally varying optical spring effect associated with the ramp pulse.
Discussion
In this work, we have demonstrated in-situ control of an optomechanical memory, bypassing the usual limitations imposed by the intrinsic damping rate and generating controllable phase shifts in the stored information. The diamond microdisk platform benefits from the diamond’s superior optical and mechanical properties. Low optical absorption, high thermal conductivity, and a cavity-based design minimize the necessary control and probe lasers powers, compared to waveguide optomechanics, by creating high intracavity light intensities. Low mechanical dissipation ensures that high effective cooperativity and vanishing effective mechanical dissipation can be achieved at the modest power levels used here, resulting in an increased memory lifetime that is primarily limited by the stability of the system not available optical power. Together with a small footprint, this allows for compact, fully integrated optical memories whose multimode nature allows stored information to be coherently manipulated.
In the future, the performance of the demonstrated optomechanical memory can be improved by cooling and cascading devices to enhance the memory time and memory-bandwidth product. By virtue of operating in the sideband resolved regime, \({{{\Gamma }}}_{{\rm{b}}}^{{\rm{eff}}}\) and \({\omega }_{{\rm{b}}}^{{\rm{eff}}}\) for our device are linearly independent of gr and Δr53. As a result, it should be possible to incorporate dynamical control of the damping rate, enabling pulse compression by the realization of a time lens54,55 (see Supplementary Note 6) as well as other processing functionality inspired by Brillouin scattering based signal processing12. Operating the device in the OMIA regime will allow demonstration of narrow spectral filters. Furthermore, spatially confined and optically-induced mechanical oscillations can be coupled, for example, to spin qubits and electromagnetic fields, facilitating the development of next-generation hybrid quantum systems.
Methods
Fabrication
The microdisks studied here were fabricated from an optical grade, chemical vapor deposition (CVD) grown 〈100〉-oriented single-crystal diamond substrate supplied by Element Six, according the process outlined in detail in ref. 50. The polished substrates were first cleaned in boiling piranha, and coated with ~400 nm of PECVD Si3N4 as a hard mask. To avoid charging effects during electron beam lithography (EBL), ~5 nm of Ti was deposited before the ZEP 520A EBL resist. The developed pattern was transferred to the hard mask via inductively coupled reactive ion etching (ICPRIE) with C4F8/SF6 chemistry. The anisotropic ICPRIE diamond etch was performed using O2, followed by deposition of ~250 nm of conformal PECVD Si3N4 as a sidewall protection layer. The bottom of the etch windows were then cleared of Si3N4 using a short ICPRIE etch with C4F8/SF6. This was followed by a zero RF power O2 RIE diamond undercut etch to partially release the devices. The undercutting process was interrupted and an ~100 nm layer of SiO2 is deposited via electron beam evaporation to alter the microdisk pedestal profile before finishing the undercut. Lastly, the Si3N4 layer was removed using a wet etch in 49% HF, and the devices were cleaned again in boiling piranha.
Apparatus
The measurement apparatus for the results described in the main text is shown in Fig. 5, where the optical components added for each measurement described in the main text are outlined in the legend. Mode a was driven by a tunable diode laser at 1560 nm (Newport TLB-6700) while the reservoir mode, r, was also driven by a tunable diode laser at 1520 nm (Newport TLB-6700) whose output was connected to a variable attenuator (VA: Exfo FVA-3100). For the verification of mutual coherence, the mode a laser was passed through a phase electro-optic modulator (φ(t): EOSpace PM-5S5-20-PFA-PFA-UV-UL) to generate a weak probe field from the control field, which was swept across the resonance using a vector network analyzer (VNA: Keysight E5063A) allowing the measurement of OMIT. The mode r laser was combined with the mode a laser on a fiber coupled 50/50 beamsplitter (BS: Newport F-CPL-L22355-A) where one output was sent to an erbium doped fiber amplifier (EDFA: Pritel LNHPFA-30-IO) and the other to an optical spectrum analyzer (OSA: Ando AQ6317B) such that the laser wavelengths could be tracked during the experiment. The output of the EDFA was sent to a fiber polarization unit followed by the fiber taper waveguide coupled to the diamond microdisk. The output of the fiber taper was then split on another 50/50 beamsplitter where one output is sent to a power meter (PM: Newport 1936-R) and one to a 1510/1550 nm wavelength division multiplexer (WDM: Montclair MFT-MC-51-30 AFC/AFC-1) to separate the light from modes a and r. The output of the WDM was then measured on a high-speed photodetector (New Focus 1554-B) whose output is high-pass filtered and electronically amplified before being sent to the VNA for measuring OMIT or a digital serial analyzer (DSA:Tektronix DSA70804B) for the pulse-storage measurements.
In the pulse-storage enhancement measurement an amplitude modulator (A(t): EOSpace AZ-0K5-10-PFA-SFA) was added to the mode a laser to generate the optical pulses, while the phase modulator was used to generate the signal to be written. The signal to be written was a sine wave at ωb generated by an arbitrary waveform generator (AWG: Tektronix AWG70002A) which was superimposed on the optical pulses generated by a low pass filtered pulse generator (PG: Stanford Research Systems DG535), triggered by the AWG. Here, the reservoir-mode control laser was operated in c.w. mode, however, during the phase-manipulation measurement an amplitude modulator (A(t): Lucent Technologies 2623CS) is added to the output of the laser, which was driven by a separate function generator to generate the phase-manipulation pulses, as shown in Fig. 6. A thermoelectric heater/cooler was also placed under the sample and controlled with a PID for thermal stability during the measurement.
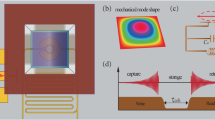
a Timing diagram for optomechanical pulse storage, along with an example of a typical measure signal (purple). b Detail of a short section of the write (left panel) and read pulse (right panel). c Timing diagram for the storage enhancement and phase-manipulation experiments described in the main text.
Mode characterization
The power spectral density for the radial breathing mode was measured using a high-speed photodetector and real time spectrum analyzer (Tektronix RSA5106A), and is shown in Fig. 7b, which was carried out at low input power (Pin ~ 50 μW) to avoid optomechanical backaction. By fitting the power spectral density to a Lorentzian, we extract a mechanical quality factor, Qm ~ 1.1 × 104, at room temperature and pressure. Optical transmission scans are shown in Fig. 7c, d, with intrinsic quality factors labeled for each of the doublet modes. The per-photon optomechanical coupling rates were measured in a separate experiment, yielding gr/αr, ga/αa ~ 2π × 25 kHz, where αr and αa are the strong control laser amplitudes for mode r, and a, respectively (see Supplementary Note 1).
a Scanning electron micrograph of the diamond microdisk used in this work. b Measured power spectral density of radial breathing mode at room temperature and pressure (inset: COMSOL simulated displacement profile). c, d Fiber taper transmission scans for both optical modes used in this work, revealing the doublet nature of the modes. Intrinsic optical quality factors are labeled.
In the limit that surface scattering effects are smaller than all other optical loss mechanisms (gss ≪ κ), microdisks will possess degenerate clockwise and anticlockwise propagating modes, with negligible coupling between them. However, when the surface scattering approaches or exceeds the optical linewidth (gss ≥ κ), the clockwise and counter clockwise modes couple and will form pairs of modes known as optical doublets. These are simply symmetric and antisymmetric combinations of the traveling wave modes. The orthogonality of the doublet modes allow us to calculate the overall mechanical frequency shift, or damping rate induced by a strong control laser by taking the sum of the contributions from the symmetric and antisymmetric mode.
Data availability
The datasets generated during and/or analyzed during this study are available from the corresponding author on reasonable request.
References
Callen, H. B. & Welton, T. A. Irreversibility and generalized noise. Phys. Rev. 83, 34–40 (1951).
Aspelmeyer, M., Kippenberg, T. J. & Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 86, 1391–1452 (2014).
Safavi-Naeini, A. H., Thourhout, D. V., Baets, R. & Laer, R. V. Controlling phonons and photons at the wavelength scale: integrated photonics meets integrated phononics. Optica 6, 213–232 (2019).
Ghadimi, A. H. et al. Elastic strain engineering for ultralow mechanical dissipation. Science 360, 764–768 (2018).
MacCabe, G. S. et al. Nano-acoustic resonator with ultralong phonon lifetime. Science 370, 840–843 (2020).
Otterstrom, N. T., Behunin, R. O., Kittlaus, E. A., Wang, Z. & Rakich, P. T. A silicon brillouin laser. Science 360, 1113–1116 (2018).
Tsaturyan, Y., Barg, A., Polzik, E. S. & Schliesser, A. Ultracoherent nanomechanical resonators via soft clamping and dissipation dilution. Nat. Nanotechnol. 12, 776 (2017).
Poyatos, J. F., Cirac, J. I. & Zoller, P. Quantum reservoir engineering with laser cooled trapped ions. Phys. Rev. Lett. 77, 4728–4731 (1996).
Eggleton, B. J., Poulton, C. G., Rakich, P. T., Steel, M. J. & Bahl, G. Brillouin integrated photonics. Nat. Photonics 13, 664–677 (2019).
Zhu, Z., Gauthier, D. J. & Boyd, R. W. Stored light in an optical fiber via stimulated brillouin scattering. Science 318, 1748–1750 (2007).
Merklein, M., Stiller, B., Vu, K., Madden, S. J. & Eggleton, B. J. A chip-integrated coherent photonic-phononic memory. Nat. Commun. 8, 574 (2017).
Santagiustina, M., Chin, S., Primerov, N., Ursini, L. & Thévenaz, L. All-optical signal processing using dynamic brillouin gratings. Sci. Rep. 3, 1594 (2013).
Stiller, B. et al. Coherently refreshing hypersonic phonons for light storage. Optica 7, 492–497 (2020).
Fiore, V. et al. Storing optical information as a mechanical excitation in a silica optomechanical resonator. Phys. Rev. Lett. 107, 133601 (2011).
Wallucks, A., Marinković, I., Hensen, B., Stockill, R. & Gröblacher, S. A quantum memory at telecom wavelengths. Nat. Phys. 16, 772–777 (2020).
Weis, S. et al. Optomechanically induced transparency. Science 330, 1520–1523 (2010).
Safavi-Naeini, A. H. et al. Electromagnetically induced transparency and slow light with optomechanics. Nature 472, 69–73 (2011).
Mitchell, M. et al. Single-crystal diamond low-dissipation cavity optomechanics. Optica 3, 963–970 (2016).
Lake, D. P., Mitchell, M., Kamaliddin, Y. & Barclay, P. E. Optomechanically induced transparency and cooling in thermally stable diamond microcavities. ACS Photonics 5, 782 (2018).
Hill, J. T., Safavi-Naeini, A. H., Chan, J. & Painter, O. Coherent optical wavelength conversion via cavity optomechanics. Nat. Commun. 3, 1196 (2012).
Dong, C., Fiore, V., Kuzyk, M. C. & Wang, H. Optomechanical dark mode. Science 338, 1609–1613 (2012).
Liu, Y., Davanço, M., Aksyuk, V. & Srinivasan, K. Electromagnetically induced transparency and wideband wavelength conversion in silicon nitride microdisk optomechanical resonators. Phys. Rev. Lett. 110, 223603 (2013).
Mitchell, M., Lake, D. P. & Barclay, P. E. Optomechanically amplified wavelength conversion in diamond microcavities. Optica 6, 832–838 (2019).
Barzanjeh, S. et al. Stationary entangled radiation from micromechanical motion. Nature 570, 480–483 (2019).
Chen, J., Rossi, M., Mason, D. & Schliesser, A. Entanglement of propagating optical modes via a mechanical interface. Nat. Commun. 11, 943 (2020).
Ockeloen-Korppi, C. et al. Low-noise amplification and frequency conversion with a multiport microwave optomechanical device. Phys. Rev. X 6, 041024 (2016).
Tóth, L. D., Bernier, N. R., Nunnenkamp, A., Feofanov, A. K. & Kippenberg, T. J. A dissipative quantum reservoir for microwave light using a mechanical oscillator. Nat. Phys. 13, 787–793 (2017).
Fang, K. et al. Generalized non-reciprocity in an optomechanical circuit via synthetic magnetism and reservoir engineering. Nat. Phys. 13, 465–471 (2017).
Chan, J. et al. Laser cooling of a nanomechanical oscillator into its quantum ground state. Nature 478, 89–92 (2011).
Teufel, J. et al. Sideband cooling of micromechanical motion to the quantum ground state. Nature 475, 359–363 (2011).
Kippenberg, T. J., Spillane, S. M. & Vahala, K. J. Modal coupling in traveling-wave resonators. Opt. Lett. 7, 1669–1671 (2002).
Borselli, M., Johnson, T. J. & Painter, O. beyond the rayleigh scattering limit in high-q silicon microdisks: theory and experiment. Opt. Express 13, 1515–1530 (2005).
Rokhsari, H., Kippenberg, T. J., Carmon, T. & Vahala, K. J. Radiation-pressure-driven micro-mechanical oscillator. Opt. Express 13, 5293 (2005).
Poot, M., Fong, K., Bagheri, M., Pernice, W. & Tang, H. Backaction limits on self-sustained optomechanical oscillations. Phys. Rev. A. 86, 053826 (2012).
Boller, K.-J., Imamoğlu, A. & Harris, S. E. Observation of electromagnetically induced transparency. Phys. Rev. Lett. 66, 2593–2596 (1991).
Jain, M., Merriam, A., Kasapi, A., Yin, G. & Harris, S. Elimination of optical self-focusing by population trapping. Phys. Rev. Lett. 75, 4385 (1995).
Hakuta, K., Suzuki, M., Katsuragawa, M. & Li, J. Z. Self-induced phase matching in parametric anti-stokes stimulated raman scattering. Phys. Rev. Lett. 79, 209 (1997).
Kasapi, A., Jain, M., Yin, G. & Harris, S. E. Electromagnetically induced transparency: propagation dynamics. Phys. Rev. Lett. 74, 2447 (1995).
Hau, L. V., Harris, S. E., Dutton, Z. & Behroozi, C. H. Light speed reduction to 17 metres per second in an ultracold atomic gas. Nature 397, 594–598 (1999).
Liu, C., Dutton, A., Behroozi, C. H. & Hau, L. V. Oberservation of coherent optical information storage in an atomic medium using halted light pulses. Nature 409, 490 (2001).
Phillips, D. F., Fleischhauer, A., Mair, A., Walsworth, R. L. & Lukin, M. D. Storage of light in atomic vapor. Phys. Rev. Lett. 86, 783–786 (2001).
Sprague, M. R. et al. Broadband single-photon-level memory in a hollow-core photonic crystal fibre. Nat. Photonics 8, 287–291 (2014).
Heinze, G., Hubrich, C. & Halfmann, T. Stopped light and image storage by electromagnetically induced transparency up to the regime of one minute. Phys. Rev. Lett. 111, 033601 (2013).
Chaneliere, T. et al. Storage and retrieval of single photons transmitted between remote quantum memories. Nature 438, 833 (2005).
Eisaman, M. D. et al. Electromagnetically induced transparency with tunable single-photon pulses. Nature 438, 837 (2005).
Fiore, V., Dong, C., Kuzyk, M. C. & Wang, H. Optomechanical light storage in a silica microresonator. Phys. Rev. A. 87, 023812 (2013).
Palomaki, T., Harlow, J., Teufel, J., Simmonds, R. & Lehnert, K. Coherent state transfer between itinerant microwave fields and a mechanical oscillator. Nature 495, 210 (2013).
Van Laer, R., Baets, R. & Van Thourhout, D. Unifying brillouin scattering and cavity optomechanics. Phys. Rev. A. 93, 053828 (2016).
Nguyen, D. T. et al. Improved optomechanical disk resonator sitting on a pedestal mechanical shield. N. J. Phys. 17, 023016 (2015).
Mitchell, M., Lake, D. P. & Barclay, P. E. Realizing Q > 300 000 in diamond microdisks for optomechanics via etch optimization. APL Photonics 4, 016101 (2019).
Chang, D. E., Safavi-Naeini, A. H., Hafezi, M. & Painter, O. Slowing and stopping light using an optomechanical crystal array. N. J. Phys. 13, 023003 (2011).
Goldstein, H. Classical Mechanics (Addison Wesley, San Francisco, 2002).
Xu, H., Mason, D., Jiang, L. & Harris, J. G. E. Topological energy transfer in an optomechanical system with exceptional points. Nature 537, 80–83 (2016).
Kolner, B. & Nazarathy, M. Temporal imaging with a time lens. Opt. Lett. 14, 630–632 (1989).
Patera, G., Shi, J., Horoshko, D. B. & Kolobov, M. I. Quantum temporal imaging: application of a time lens to quantum optics. J. Opt. 19, 054001 (2017).
Acknowledgements
The authors would like to thank Daniel Oblak and the QCloudLab for their generosity in lending us some of the components required to obtain these results. This work was supported by the National Research Council, Canadian Foundation for Innovation, Alberta Innovates, and the Natural Sciences and Engineering Research Council of Canada.
Author information
Authors and Affiliations
Contributions
D.P.L. and M.M. fabricated the device, performed the experiments, and analyzed the data. D.P.L. and D.D.S. developed the theory. P.E.B. supervised the project. All authors contributed to writing the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks Mahdi Hosseini and the other, anonymous reviewer∣(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lake, D.P., Mitchell, M., Sukachev, D.D. et al. Processing light with an optically tunable mechanical memory. Nat Commun 12, 663 (2021). https://doi.org/10.1038/s41467-021-20899-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-021-20899-w
This article is cited by
-
High-fidelity and robust optomechanical state transfer based on pulse control
Applied Physics B (2023)
-
Long-lifetime coherent storage for microwave photons in the magnomechanical resonator
Quantum Frontiers (2023)
-
Recent Advances in Triplet–Triplet Annihilation Upconversion for Bioimaging and Biosensing
Journal of Analysis and Testing (2023)
-
Optomechanical interface between telecom photons and spin quantum memory
Nature Physics (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.