Abstract
The segregation of solute atoms at grain boundaries (GBs) can profoundly impact the structural properties of metallic alloys, and induce effects that range from strengthening to embrittlement. And, though known to be anisotropic, there is a limited understanding of the variation of solute segregation tendencies across the full, multidimensional GB space, which is critically important in polycrystals where much of that space is represented. Here we develop a machine learning framework that can accurately predict the segregation tendency—quantified by the segregation enthalpy spectrum—of solute atoms at GB sites in polycrystals, based solely on the undecorated (pre-segregation) local atomic environment of such sites. We proceed to use the learning framework to scan across the alloy space, and build an extensive database of segregation energy spectra for more than 250 metal-based binary alloys. The resulting machine learning models and segregation database are key to unlocking the full potential of GB segregation as an alloy design tool, and enable the design of microstructures that maximize the useful impacts of segregation.
Similar content being viewed by others
Introduction
In alloys, the segregation of solute atoms at grain boundaries (GBs) induces structural effects1,2 that include strengthening3,4,5, embrittlement6,7, corrosion resistance8,9, and GB phase transitions10,11. As such, controlling GB segregation is an essential tool for many engineering applications12, including, e.g., the thermodynamic stabilization of nanocrystalline alloys against grain growth13,14,15. And, though most technically relevant alloys are used in a polycrystalline form, there is a very limited understanding of GB segregation in polycrystals16, and a general lack of databases of segregation information relevant to them.
In a polycrystal, the GB network has a variety of site-types that can either promote or inhibit segregation to different degrees, depending on their unique local atomic environments. The drive for a solute atom to segregate to a GB site-type (i) is quantified by the segregation enthalpy \({\Delta}H_i^{{\rm{seg}}}\), which, in solids17, is equivalent to the internal energy difference between the solute atom occupying the GB site, and a bulk (intra-grain) site, \({\Delta}H_i^{{\rm{seg}}} \approx {\Delta}E_i^{{\rm{seg}}} = E_{{\rm{gb}},i}^{{\rm{solute}}} - E_{\rm{c}}^{{\rm{solute}}}\); a negative \({\Delta}E_i^{{\rm{seg}}}\) (i.e. the system reduces energy upon segregation) promotes segregation and vice versa. The spectrum of \({\Delta}E_i^{{\rm{seg}}}\) in a polycrystal will determine the extent of equilibrium GB segregation in an alloy18,19,20. Recently, we have shown this spectrum to be captured by a skew-normal distribution for an Mg solute segregation in an Al polycrystal20. However, the computation of these segregation spectra is a resource-intensive task. For example, a (50 nm)3 Al polycrystal with an average grain size of 10 nm has roughly one million GB sites, which translates to a million atomistic calculations, where a solute atom is placed substitutionally at each GB site independently and allowed to relax. This makes the task of investigating different microstructures (i.e. multiple polycrystalline samples) cost-prohibitive for a given alloy.
Here, we propose a machine learning (ML) framework that can accurately predict the relaxed segregation energy of a solute atom in a GB site, solely based on its undecorated (pre-segregation) atomic environment. Our approach is tiered and offers two models. The first is a high-fidelity model that is trained to accurately capture the variation of segregation energy across a large swath of the GB space, and thus can be used to study an alloy system in detail and instantaneously evaluate segregation for different microstructures. The second is an accelerated model that uses dimensionality reduction to reproduce the high-fidelity model—with a minimal loss in accuracy—using three orders of magnitude fewer data-points for training (only 100 sites). We use the accelerated approach to scan across the alloy space, and build an extensive database giving GB segregation spectra for all aluminum, magnesium, and transition metals-based binary alloys for which an interatomic potential exists in the Interatomic Potentials Repository21,22 of the National Institute of Standards and Technology (NIST) - a total of 259 binary alloys. This database allows us to identify alloys of interest with minimal computational cost, for which high-fidelity models can be trained and used. The proposed ML framework and the resulting spectral segregation database should provide a general and broadly applicable alloy design toolbox relevant to all material properties impacted by solute segregation.
Results
High-Fidelity ML model for GB segregation
If a solute atom is substitutionally placed at a GB site and is allowed to relax, its local neighboring atoms will be affected (and possibly displaced) by the introduced elastic and chemical interactions. Hence it follows that the local atomic environment (LAE) of a GB site will influence its favorability for solute segregation, and thus this environment should be accurately captured in any learning model that aims to correlate the undecorated (pre-segregation) GB site to its final decorated (post-segregation) relaxed state. So far, the state-of-the-art learning models in the literature use simple well-known structural features23,24, such as atomic volume, coordination, and Voronoi parameters, which mostly limit the description of the LAE to its first nearest-neighbor atoms. Instead, we propose using an atom-centered feature extraction method “descriptor” that encodes the local atomic environment around an atom within a cutoff radius25,26. Such descriptors—also known as “fingerprints”—are developed and widely used to construct ML-based interatomic potentials; examples include the atom-centered symmetry functions27, bispectrum components28,29, and smooth overlap of atomic positions (SOAP)30. There are two main advantages to using such atom-centered descriptors. The first is that no a priori knowledge or selection of what constitutes an important structural feature of the LAE (such as volume, coordination, etc.) is required, but rather, by using a complete description of the LAE within a cutoff radius, we relegate the decision of learning the most important features to the ML model. The second is that the use of a large cutoff radius ensures that the most dominant interactions between the solute atom and its LAE are captured. As these descriptors are borrowed from the interatomic potential fitting literature, we can think of our approach as fitting a “pseudo interatomic potential” for solute segregation at GBs.
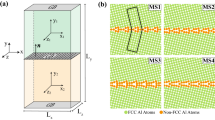
The proposed high-fidelity ML model is summarized in Fig. 1, which shows two main steps: (a) feature extraction and (b) a learning algorithm. For feature extraction, we use the SOAP method30, as it was recently shown to perform well in describing GB environments (albeit for the different problem of predicting GB energies)31. The SOAP method produces for a given GB site and its LAE within a cutoff radius, a feature vector (descriptor) that is invariant under all physical symmetries (permutation, translation, rotation, etc.). The size of the feature vector is controlled by the SOAP hyperparameters (detailed in the methods section), which, in essence, determines the resolution of the vector and its sensitivity to changes in the LAE. In this work, the SOAP feature vector for each GB site has FSOAP=1,015 features. For the cutoff radius, we use 6 Å, which is a conservative cutoff used in constructing interatomic potentials, as it captures the most dominant atomic interactions for an atom with its LAE25,32. We note that, though we opted to use the same FSOAP and a radial cutoff of 6 Å for all binary alloys (as optimal parameters that require minimal input from the user), this procedure is flexible, and one could, by further optimizing the SOAP hyperparameters to the specific alloy of interest, improve the accuracy of the ML model. (For example, a solute atom that has a large size mismatch with solvent atoms could benefit from a larger radial cutoff.)
For the (a) 20x20x20 nm3 thermally annealed Al polycrystal with 16 grains (colored by the centro-symmetry parameter74), (b) the LAE of every identified GB atom is transformed into a feature vector, using the SOAP method30 with rcutoff = 6 Å, to construct a feature matrix for the full GB network (NGB atoms x FSOAP features), which is used as the input to the (c) learning algorithm (linear regression) to learn Mg GB segregation energies, using a 50/50 training/testing split. d Predictive performance—mean absolute error (MAE)—of the trained ML model across the full GB network.
The product of the first step of the ML framework, feature extraction, is a feature matrix of size (NGB atoms x FSOAP features), which is used as the input to the second step, the learning algorithm, which learns to map the input SOAP features to the target property (segregation energy). For the learning algorithm, we use linear regression for three reasons: first, it is a simple inexpensive model to train and use for predictions; second, it can be automated as it does not require any hyperparameter optimization; and third, it inherently ensures regularization (i.e. is less prone to overfitting)—by simply using a sample size of >10xFSOAP GB sites (following the “one in ten” rule of thumb33, which we further validate in Supplementary Fig. 21) to fit the F + 1 coefficients of the model (F coefficients + intercept), we guard against model overfitting, and selection bias towards a small subset of the population (randomly sampling as few as ~400 points from an infinite population gives a 95% confidence level and 5% margin of error34). We note that although more elaborate learning algorithms could be used, such as support vector machines31, Gaussian process regression28 or neural networks32, our proposed ML framework prioritizes simplicity and minimal input from the user, so that other researchers can adopt it easily. We use this approach to showcase the utility of using atom-centered descriptors for learning GB site segregation energies, without getting lost in the intricate details of fine-tuning more advanced learning algorithms. We note that though the proposed learning framework focuses on segregation spectra in substitutional alloys, it is extensible in principle to interstitial alloys by defining interstitial sites35 at the GB and bulk regions.
Using the high-fidelity approach, we train a model, in Fig. 1c, for Mg solute36 segregation in a thermally annealed 20 × 20 × 20 nm3 Al polycrystal that has 16 grains and ~105 GB sites, using a randomized 50/50 split for training/testing. This simple holdout method is easy/cheap to train and use, and its conservative test ratio will guard against a high variance model in most cases. The trained model is highly accurate, with a mean absolute error (MAE) of 2.4(2.5) kJ/mol for the train(test) datasets, respectively, and a root-mean-square error of RMSE=3.8(4.1) kJ/mol. The model faithfully reproduces the distribution of segregation enthalpies in the polycrystal and has a well-behaved error with normally distributed residuals. This result compares favorably with a more sophisticated ML model by Huber et al.23, which used 19 structural features (volume, coordination, Voronoi analysis parameters, and Steinhardt bond-order parameters) with gradient boosted decision trees, and had a 9-fold cross-validation RMSE=7.7 kJ/mol for Mg solute segregation in a database of 38 low and high-symmetry boundaries in Al. The comparison is not direct, of course, since that work focused on bi-crystals whereas we use polycrystals, but it is also encouraging that the present error is also much lower than the reported error of the interatomic potential as compared to DFT GB segregation energies, which has an RMSE of 8.7 kJ/mol24.
We further validate the efficacy of the high-fidelity ML model for GB solute segregation across the alloy space by training to six more 20 × 20 × 20 nm3 polycrystalline volumes for different alloys: Ag(Ni)37, Cu(Zr)38, Fe(Al)39, Ni(Cu)40, Pt(Au)41, and Zr(Ni)42. As shown in Fig. 2, the ML model accurately reproduces the segregation spectra for the six binary alloys, and has a low MAE typically below ~6 kJ/mol and often below 1 kJ/mol. Alloys with higher absolute values (wider distribution) for the segregation energy will correspondingly have a higher MAE, and the worst of these seen here is MAE = 12.8 kJ/mol for the Zr(Ni) system, but here the segregation spectrum spans about 250 kJ/mol; as a fraction of the total spread of the segregation spectrum, the MAE is uniformly below about 5%. To test the extrapolability of the high-fidelity framework, we report the mean (and standard deviation) absolute errors using 5-fold cross-validation in Supplementary Table 1, which shows that the fitted models are able to generalize well to the unseen folds of the dataset (with similar errors as reported in Fig. 2 for the 50/50 holdout method, and low standard deviation across the folds). We note that although most of the surveyed base-metals have fcc lattice structure, the ML framework seems to be insensitive to the lattice structure, as it similarly performs well for bcc (Fe), and hcp (Zr) metals. Therefore, we conclude that the high-fidelity ML model can be used to accurately model GB segregation across the GB and alloy spaces.
Accelerated ML model for GB segregation
In alloy design, it is of interest to be able to quickly scan across the alloy space for interesting combinations. In the context of GB segregation, for example, significant efforts have been conducted to screen for nanocrystalline stabilizing elemental combinations15,43, complexion forming combinations44, or GB embrittling solute additions45,46,47. Though the high-fidelity ML model is highly accurate, it still requires ~104 data points for training and fitting its ~103 coefficients (features). To reduce the training cost and permit a broader scan across the full alloy space, it is appropriate to reduce the dimensions of the input features. We propose the use of unsupervised dimensionality reduction algorithms, which map a high dimensional feature vector into a low-dimensional embedding that captures its main characteristics; “unsupervised” signifies that such mapping is done without a priori knowledge the of the target value (segregation energies). As an illustration, we adopt the simplest of these algorithms, namely principal component analysis48, which we use to transform the FSOAP = 1015 into 10 principal components (PSOAP) that maximize the captured variance of the feature space. We can think of this process as compressing the 1,015 features into 10 components; such compression captures >99% of the variance of the SOAP feature matrix of the Al polycrystal, as shown in Fig. 3.
For the Al(Mg) alloy, shown in Fig. 1, (a) principal component analysis is used to reduce the dimensionality of the feature matrix by projecting the FSOAP features into P = 10 components that capture >99% of the variance. b k-means clustering is then used to divide the 10-d transformed feature space into P × 10 = 100 similar clusters; the closest GB sites to the cluster centers (shortest Euclidean distance) are used as training data-points for the learning algorithm (linear regression). c Predictive performance—mean absolute error (MAE)—of the accelerated model across the full Al GB network.
For an accelerated option of the ML framework, we propose using the 10 principal components obtained from PCA as the input for the linear regression algorithm49,50. As the problem is now reduced to fitting PSOAP + 1 coefficients (instead of FSOAP + 1), we conservatively only need ~P × 10 = 100 data-points for training; 100 molecular statics computations involving the substitution of a single solute atom at a grain boundary site in a polycrystal give insight on the entire segregation spectrum. As for the selection of the 100 training data points, though random selection can be used, this could be a biased approach due to the low number of points accessing only a prevalent subset of the GB feature space in a given polycrystalline structure. Instead, we propose using k-means clustering51,52 to partition the reduced feature space into k=100 clusters that minimize within-cluster variances. We then use the cluster centroids to identify optimal training data-points (i.e., shortest Euclidean distance to the centroids), as shown in Fig. 3, for which GB segregation is computed, and use it to train the accelerated model. Such an approach is computationally inexpensive and ensures the full coverage of the feature space in our training dataset.
Similar to the high-fidelity model, the accelerated one can be fully automated and requires minimal input from the user. To compare the performance of both approaches, an accelerated model for Al(Mg), trained with only 100 GB sites, results in an MAE of 4.2 kJ/mol for predictions of the full ~105 GB sites, compared to an MAE of 2.5 kJ/mol from the high-fidelity model trained with 50% of GB sites. This reduction (two orders of magnitude) in the required training data points, with minimal loss of accuracy, is significant, and showcases the power of the accelerated model to quickly, and accurately, predict the segregation spectra in binary alloys. It also signifies that the full GB space could possibly be reduced to a small number of key GB environments—also known as GB “building blocks”31—that decipher the features of the full space. We expect this to be a significant direction of future work in the context of grain boundary segregation.
Using the accelerated approach, we build ML models to predict solute segregation spectra in polycrystals for every aluminum, and magnesium, and transition metal-based binary alloys (Supplementary Figs. 2–20) that have interatomic potentials in the NIST Interatomic Potentials Repository—a total of 259 alloys (see Supplementary Fig. 1). This segregation database not only allows us to screen the alloy space for segregation “hot-spots” or regions of interest, but also to compare the variation of the spectrum with different interatomic potentials (for alloys where more than one potential exists). To illustrate the utility of the database, we plot in Fig. 4 all solute segregation spectra in a nickel-based alloy; Ni(Ag)37 is predicted to be highly segregating, and the opposite for Ni(Al)53.
Using the accelerated ML model outlined in Fig. 3, we compute GB segregation energy spectra for 18 solutes37,40,42,53,58,75,76,77,78,79,80,81 in a 20x20x20 nm3 Ni polycrystal of grain size 10 nm; the anti-segregation region (\({\Delta}E_i^{{\rm{seg}}} > 0\)) is shaded. The spectra are fitted to the skew-normal function Eq. (3) (solid line), and the value of the characteristic energy μ (kJ/mol), width σ (kJ/mol), and shape α of the function are listed. Also, the spectra are compared to the “average” segregation energy (dashed vertical line) used to charecterize these alloys in the database of Murdoch and Schuh55.
Discussion
There are three key findings to the spectral segregation database (Fig. 4 and Supplementary Figs. 2–20). The first is that all segregation spectra in all binary alloys surveyed, as hypothesized earlier in our study of the Al(Mg) system20, are captured well by a skew-normal function (the fitted probability density function has an R2 > 0.95 in all but one alloy with an R2=0.80; see Supplementary Figs. 2–20). This function involves three parameters—the characteristic energy μ, width σ and shape α of the distribution:
These parameters are provided in the corresponding figure for each alloy considered. The second key finding is that using a McLean “average”54 segregation energy to characterize a binary alloy, which is the segregation literature norm55,56, misses key information about the accessible segregation states at the GB network. For example, the Ni(Ag) system that has a reported “average” segregation energy of −50 kJ/mol55, has approximately 15% of its GB network with segregation energies more than twice that, below −100 kJ/mol, as shown in the first panel of Fig. 4. GB segregation occurs first in the lowest energy states, and before a grain boundary in Ni(Ag) would experience the McLean average segregation energy, it would lie at an extremely high composition of approximately 50 atom% Ag. The knowledge of the full spectrum is thus essential to enable the design of microstructures57 that maximize the desired tail of the segregation spectrum (i.e. either promote or inhibit segregation). The third key finding is that, for alloys with more than one available interatomic potential, the computed segregation spectra can be sensitive to the choice of the potential. For example, potentials for the Al(Ni) system produce completely different segregation spectra, as shown in Supplementary Fig. 3, which range from having almost all GB sites being unfavorable to segregation58 to the complete opposite59; such variation can result in an order of magnitude difference in predictions for GB solute concentration even at low total solute concentrations in the system (see Supplementary Fig. 23). Further work is needed in the future to quantify the accuracy of such potentials for GB segregation studies60, and as always with atomistic models, it is important to remember that the present framework will only return physically reasonable results if the potential is specifically suitable for the problem at hand. For now, we report all of them, and leave the selection step to the judgment of the user.
Though the analysis in Figs. 1–3 shows that the ML models faithfully reproduce most of the details of the GB segregation spectrum, this is not the most critical test for their practical viability; these models are only useful to the extent that they correctly capture GB segregation in some realistic situation. Thus, the most important metric is the prediction for the equilibrium GB segregation state (i.e. extent of segregation). For a spectrum of segregation energies at the GB network, the equilibrium solute distribution among the different sites follows Fermi-Dirac statistics18,19,20. In a closed system with finite grain sizes, the total solute concentration Xtot is fixed and shared by the bulk (intra-grain) and GB solute concentrations, Xc and \(\bar X^{gb}\), respectively, according to the GB site fraction fgb:
The equilibrium Xc and \(\bar X^{{\rm{gb}}}\) are a function of the temperature T, the distribution of GB segregation energies \(F_i^{{\rm{gb}}}\)(\({\mathrm{{\Delta}}}E_i^{{\rm{seg}}}\)), and are obtained by numerically solving for Xc that satisfies the expanded form of Eq. (2)20:
In Fig. 5, we compare the equilibrium GB segregation state obtained using the true computed spectrum versus the ML predicted ones with both high-fidelity and accelerated models, for all seven alloys from Figs. 1 and 2, in a polycrystal of average grain size 15 nm (\(f^{{\rm{gb}}} \approx 10\%\)) at T = 600 K. The predictions of the ML models closely match those of the true spectrum, indicating that the ML models capture the necessary information to correctly predict the equilibrium segregation state. Also, as briefly discussed earlier, though the value of the MAE differs from one system to another, a higher MAE does not necessarily translate to a worse result, when one normalizes to the scale of the segregation energy distribution, e.g. the Zr(Ni) system in Fig. 5. Finally, we note that the difference (deviation) in predictions of the equilibrium segregation state could be even less of an issue if the skew-normal approximation Eq. (1) is used, instead of the full discrete spectra, to quantify GB segregation using the continuous form of the segregation isotherm Eq. (3)20:
as the three fitted parameters (μ, σ, and α) of the skew-normal function for the true and ML predicted spectra should closely match, even for systems with high MAE, as the residuals are well-behaved and normally distributed (with a zero mean, as shown in Figs. 1 and 3).
To motivate further analysis of the spectral segregation database, and visually summarize the segregation tendency across the alloy space, we plot a two-dimensional Pettifor61 map in Fig. 6 (for most alloys in the database) using the 25th percentile value (energy) for the segregation spectra (i.e. 25% of GB sites have lower segregation energies). As the lower tail is the most enthalpically favorable, it will disproportionately influence the segregation tendency in any given alloy, especially at low or dilute solute concentration. The choice of the Pettifor chemical scale (which preserves the Mendeleev-type features of the elements61) is based on its success in pattern clustering (separation) for miscibility62, ordering tendency63,64, and crystal structures of intermetallics61 in binary alloys. Though Fig. 6 shows some clustering, it is not enough to draw concrete conclusions on the segregation tendency across the alloy space; the same finding applies to another two routinely used parameters to characterize the chemical and physical nature of the elements—electronegativity65, and metallic radius66—(see Supplementary Figs. 24–27). It is evident that more effort is needed to formulate (or extract from ML) simple phenomenological parameters (preferably derived from atomic features e.g. Miedema-style parameters67) that better explain these trends. We hope that this preliminary exploration of the data will promote further work on this front.
The value of the first quartile of the segregation spectra (i.e. 25% of GB sites have lower segregation energies) as predicted using the accelerated model for 210 alloys (we removed columns with empty entries for compact viewing); the elements are arranged by their order on the Pettifor chemical scale61. For alloys with multiple interatomic potentials (see Supplementary Fig. 1), we report the least segregating spectra as a conservative choice (see Supplementary Fig. 25 for an alternative version of the figure with the most segregating spectra).
In summary, our proposed ML framework, inspired by methods developed for fitting ML-based interatomic potentials, aims to fit a “pseudo interatomic potential” for GB segregation energies in polycrystalline alloys. The framework is designed to require minimal input from the user, and as such, is automatable. As the ML literature is constantly evolving, we look forward to new developments and tools that can further improve the framework. We offered two model options. The first is a high-fidelity model that uses a large SOAP vector (>103 features), a conservative radial cutoff (6 Å), and linear regression. The second, is an accelerated model that uses PCA to transform the original features into a few (10) principal components (which are then used as input features to linear regression); this reduces the dimension of the learning problem to just 100 key GB environments, which are selected by k-means clustering to ensure coverage of the GB space. The accelerated model is used to build an extensive database for segregation spectra in 259 binary alloys, which is included the Supplementary Information. We look forward to applications of this database in alloy design, and hope it motivates more widespread use of spectral approaches to GB segregation in polycrystalline materials.
Methods
GB segregation enthalpies
The atomistic simulation package LAMMPS68,69 is used for all molecular statics and dynamics simulations; OVITO70 is used for visualization and identification of atomic structures.
To generate the base-metal polycrystal, we fill a 20x20x20 nm3 volume with 16 randomly oriented grains using Voronoi tesselations with Atomsk71. The polycrystal is thermally annealed at 0.3–0.5 of the melting temperature under a Nose-Hoover thermostat/barostat for 250 ps using a time step of 1 fs, which relaxes the grain structure and boundaries without permitting exaggerated grain growth; this is followed by slow cooling to 0 K at a cooling rate of 3 K/ps, and a final conjugate gradient energy minimization.
To compute the spectrum of segregation enthalpies in a binary alloy, we follow the procedure in ref. 20. We first relax the base-metal polycrystal using the interatomic potential of that alloy, by applying an external pressure of zero in a conjugate gradient minimization, followed by a second conjugate gradient minimization (with no applied pressure). This is necessary to scale the cell, and correct for minor differences in the equilibrium lattice parameter of the base-metal across the different interatomic potentials (for example, the Ni polycrystal is thermally annealed using an interatomic potential42 that is fitted to Ni lattice parameter of 3.518 Å, but the Ni(Al)53 is fitted to 3.520 Å). Then, every GB site in the annealed polycrystal is identified using adaptive-common neighbor analysis method72; all atoms that have a different atomic structure than the base metal are assumed to be GB atoms. For every GB site (i), its \({\mathrm{{\Delta}}}E_i^{{\rm{seg}}}\) is calculated as the relaxed energy difference between the solute atom occupying the GB site, versus a bulk (intra-grain) site: \({\mathrm{{\Delta}}}E_i^{{\rm{seg}}} = E_{{\rm{gb}},i}^{{\rm{solute}}} - E_{\rm{c}}^{{\rm{solute}}}\); the relaxation of each state is achieved using a conjugate gradient minimization, and the reference bulk site for \(E_c^{solute}\) is chosen as the center of a 6 nm sphere of the pure solvent (in the polycrystal), to avoid any long-range interactions with GB atoms. All calculations are at 0 K, isolating the enthalpic portion of the segregation energy for each site.
Machine Learning
For feature extraction, the LAE of every GB site within a cutoff radius of 6 Å is described using the SOAP method, as implemented in the QUIP/GAP software package28,30. SOAP fits a set of radial basis functions and spherical harmonics to Gaussian particle density functions placed over all neighboring atoms in the LAE. The maximum number of radial basis functions (nmax), degree of spherical harmonics (lmax), and the width of Gaussian functions (σat) control the size and resolution of the SOAP feature vector. We use nmax = lmax = 12 and σat = 1 Å for all alloys, which gives a SOAP vector with 1015 features. As for the other components of the ML framework: linear regression, principal component analysis, and k-means clustering are used as implemented in the Scikit-learn73 python package.
Data availability
The database for segregation spectra of all 250+ binary alloys, in the form of LAMMPS text dump files of solvent polycrystals with predicted GB solute segregation energies, is available at https://doi.org/10.5281/zenodo.4107058. Additional data related to this work are available from the authors upon request.
Code availability
An example Jupyter Notebook with all necessary code to train and use the high-fidelty and accelerated machine learning models is also available at https://doi.org/10.5281/zenodo.4107058.
References
Lejček, P. & Hofmann, S. Thermodynamics and structural aspects of grain boundary segregation. Crit. Rev. Solid State Mater. Sci. 20, 1–85 (1995).
Seah, M. P. Chemistry of solid–solid interfaces — A review of its characterization, theory, and relevance to materials science. J. Vac. Sci. Technol. 17, 16–24 (1980).
Liu, C. T., White, C. L. & Horton, J. A. Effect of boron on grain-boundaries in Ni3Al†. Acta Met. 33, 213–229 (1985).
Wu, R., Freeman, A. J. & Olson, G. B. First principles determination of the effects of phosphorus and boron on iron grain boundary cohesion. Science 265, 376–380 (1994).
Yang, T. et al. Ultrahigh-strength and ductile superlattice alloys with nanoscale disordered interfaces. Science 369, 427–432 (2020).
Rogers, H. C. Hydrogen Embrittlement of Metals. Science 159, 1057–1064 (1968).
Schweinfest, R., Paxton, A. T. & Finnis, M. W. Bismuth embrittlement of copper is an atomic size effect. Nature 432, 1008–1011 (2004).
Briant, C. L. & Andresen, P. L. Grain boundary segregation in austenitic stainless steels and its effect on intergranular corrosion and stress corrosion cracking. Metall. Trans. A 19, 495–504 (1988).
Duarte, M. J. et al. Element-resolved corrosion analysis of stainless-type glass-forming steels. Science 341, 372–376 (2013).
Harmer, M. P. The phase behavior of interfaces. Science 332, 182–183 (2011).
Frolov, T., Olmsted, D. L., Asta, M. & Mishin, Y. Structural phase transformations in metallic grain boundaries. Nat. Commun. 4, 1899 (2013).
Raabe, D. et al. Grain boundary segregation engineering in metallic alloys: A pathway to the design of interfaces. Curr. Opin. Solid State Mater. Sci. 18, 253–261 (2014).
Kirchheim, R. Grain coarsening inhibited by solute segregation. Acta Mater. 50, 413–419 (2002).
Koch, C. C., Scattergood, R. O., Darling, K. A. & Semones, J. E. Stabilization of nanocrystalline grain sizes by solute additions. J. Mater. Sci. 43, 7264–7272 (2008).
Chookajorn, T., Murdoch, H. A. & Schuh, C. A. Design of stable nanocrystalline alloys. Science 337, 951–954 (2012).
Herbig, M. et al. Atomic-scale quantification of grain boundary segregation in nanocrystalline material. Phys. Rev. Lett. 112, 126103 (2013).
Steigerwald, D. A. & Wynblatt, P. Calculation of the anisotropy of equilibrium surface composition in metallic solid solutions using the embedded atom method. Surf. Sci. 193, 287–303 (1988).
White, C. L. & Stein, D. F. Sulfur segregation to grain boundaries in Ni3Al and Ni3(AI,Ti) alloys. Metall. Trans. A 9, 13–22 (1978).
Kirchheim, R. Hydrogen solubility and diffusivity in defective and amorphous metals. Prog. Mater. Sci. 32, 261–325 (1988).
Wagih, M. & Schuh, C. A. Spectrum of grain boundary segregation energies in a polycrystal. Acta Mater. 181, 228–237 (2019).
Becker, C. A., Tavazza, F., Trautt, Z. T. & Buarque De Macedo, R. A. Considerations for choosing and using force fields and interatomic potentials in materials science and engineering. Curr. Opin. Solid State Mater. Sci. 17, 277–283 (2013).
Hale, L. M., Trautt, Z. T. & Becker, C. A. Evaluating variability with atomistic simulations: the effect of potential and calculation methodology on the modeling of lattice and elastic constants. Model. Simul. Mater. Sci. Eng. 26, 055003 (2018).
Huber, L., Hadian, R., Grabowski, B. & Neugebauer, J. A machine learning approach to model solute grain boundary segregation. npj Comput. Mater. 4, 64 (2018).
Huber, L., Grabowski, B., Militzer, M., Neugebauer, J. & Rottler, J. Ab initio modelling of solute segregation energies to a general grain boundary. Acta Mater. 132, 138–148 (2017).
Mueller, T., Hernandez, A. & Wang, C. Machine learning for interatomic potential models. J. Chem. Phys. 152, 241722 (2020).
Behler, J. Perspective: Machine learning potentials for atomistic simulations. J. Chem. Phys. 145, 170901 (2016).
Behler, J. & Parrinello, M. Generalized neural-network representation of high-dimensional potential-energy surfaces. Phys. Rev. Lett. 98, 146401 (2007).
Bartók, A. P., Payne, M. C., Kondor, R. & Csányi, G. Gaussian Approximation Potentials: The Accuracy of Quantum Mechanics, without the Electrons. Phys. Rev. Lett. 104, 136403 (2010).
Thompson, A. P., Swiler, L. P., Trott, C. R., Foiles, S. M. & Tucker, G. J. Spectral neighbor analysis method for automated generation of quantum-accurate interatomic potentials. J. Comput. Phys. 285, 316–330 (2015).
Bartók, A. P., Kondor, R. & Csányi, G. On representing chemical environments. Phys. Rev. B 87, 184115 (2013).
Rosenbrock, C. W., Homer, E. R., Csányi, G. & Hart, G. L. W. Discovering the building blocks of atomic systems using machine learning: application to grain boundaries. npj Comput. Mater. 3, 29 (2017).
Deringer, V. L., Caro, M. A. & Csányi, G. Machine Learning Interatomic Potentials as Emerging Tools for Materials Science. Adv. Mater. 31, 1902765 (2019).
Harrell, F. E. Jr Regression Modeling Strategies: With Applications to Linear Models, Logistic and Ordinal Regression, and Survival Analysis (Springer, 2015).
Cochran, W. Sampling Techniques (John Wiley, 2006).
Rhodes, N. R., Tschopp, M. A. & Solanki, K. N. Quantifying the energetics and length scales of carbon segregation to α -Fe symmetric tilt grain boundaries using atomistic simulations. Model. Simul. Mater. Sci. Eng. 21, 035009 (2013).
Mendelev, M. I., Asta, M., Rahman, M. J. & Hoyt, J. J. Development of interatomic potentials appropriate for simulation of solid–liquid interface properties in Al–Mg alloys. Philos. Mag. 89, 3269–3285 (2009).
Pan, Z., Borovikov, V., Mendelev, M. I. & Sansoz, F. Development of a semi-empirical potential for simulation of Ni solute segregation into grain boundaries in Ag. Model. Simul. Mater. Sci. Eng. 26, 075004 (2018).
Borovikov, V., Mendelev, M. I. & King, A. H. Effects of stable and unstable stacking fault energy on dislocation nucleation in nano-crystalline metals. Model. Simul. Mater. Sci. Eng. 24, 085017 (2016).
Mendelev, M. I., Srolovitz, D. J., Ackland, G. J. & Han, S. Effect of Fe segregation on the migration of a non-symmetric ∑5 tilt grain boundary in Al. J. Mater. Res. 20, 208–218 (2005).
Onat, B. & Durukanoǧlu, S. An optimized interatomic potential for Cu-Ni alloys with the embedded-atom method. J. Phys. Condens. Matter 26, 035404 (2014).
O’Brien, C. J., Barr, C. M., Price, P. M., Hattar, K. & Foiles, S. M. Grain boundary phase transformations in PtAu and relevance to thermal stabilization of bulk nanocrystalline metals. J. Mater. Sci. 53, 2911–2927 (2018).
Wilson, S. R. & Mendelev, M. I. Anisotropy of the solid-liquid interface properties of the Ni-Zr B33 phase from molecular dynamics simulation. Philos. Mag. 95, 224–241 (2015).
Darling, K. A. et al. Stabilized nanocrystalline iron-based alloys: Guiding efforts in alloy selection. Mater. Sci. Eng. A 528, 4365–4371 (2011).
Schuler, J. D. & Rupert, T. J. Materials selection rules for amorphous complexion formation in binary metallic alloys. Acta Mater. 140, 196–205 (2017).
Lejček, P., Šob, M. & Paidar, V. Interfacial segregation and grain boundary embrittlement: An overview and critical assessment of experimental data and calculated results. Prog. Mater. Sci. 87, 83–139 (2017).
Gibson, M. A. & Schuh, C. A. Segregation-induced changes in grain boundary cohesion and embrittlement in binary alloys. Acta Mater. 95, 145–155 (2015).
Gibson, M. A. & Schuh, C. A. A compilation of ab-initio calculations of embrittling potencies in binary metallic alloys. Data Br. 6, 143–148 (2016).
Tipping M. E., M. E. & Bishop CMBishop, C. M. Probabilistic Principal Component Analysis (TensorFlow, 1997).
Jolliffe, I. T. A Note on the Use of Principal Components in Regression. Appl. Stat. 31, 300 (1982).
Helfrecht, B. A., Semino, R., Pireddu, G., Auerbach, S. M. & Ceriotti, M. A new kind of atlas of zeolite building blocks. J. Chem. Phys. 151, 154112 (2019).
Lloyd, S. P. Least squares quantization in PCM. IEEE Trans. Inf. Theory 28, 129–137 (1982).
Elkan, C. Using the Triangle Inequality to Accelerate-Means. ACM 147–153 (2003).
Purja Pun, G. P. & Mishin, Y. Development of an interatomic potential for the Ni-Al system. Philos. Mag. 89, 3245–3267 (2009).
McLean, D. Grain Boundaries in Metals (Clarendon Press, 1957).
Murdoch, H. A. & Schuh, C. A. Estimation of grain boundary segregation enthalpy and its role in stable nanocrystalline alloy design. J. Mater. Res. 28, 2154–2163 (2013).
Lejcek, P. Grain Boundary Segregation in Metals Vol. 136 (Springer, Berlin, Heidelberg, 2010).
Watanabe, T. & Tsurekawa, S. Control of brittleness and development of desirable mechanical properties in polycrystalline systems by grain boundary engineering. Acta Mater. 47, 4171–4185 (1999).
Zhou, X. W., Johnson, R. A. & Wadley, H. N. G. Misfit-energy-increasing dislocations in vapor-deposited CoFe/NiFe multilayers. Phys. Rev. B - Condens. Matter Mater. Phys. 69, 144113 (2004).
Mishin, Y., Mehl, M. J. & Papaconstantopoulos, D. A. Embedded-atom potential for B2-NiAl. Phys. Rev. B 65, 1–14 (2002).
Hu, Y., Schuler, J. D. & Rupert, T. J. Identifying interatomic potentials for the accurate modeling of interfacial segregation and structural transitions. Comput. Mater. Sci. 148, 10–20 (2018).
Pettifor, D. G. The structures of binary compounds: I. phenomenological structure maps. J. Phys. C. Solid State Phys. 19, 285–313 (1986).
Zhang, R. F. et al. An informatics guided classification of miscible and immiscible binary alloy systems. Sci. Rep. 7, 1–12 (2017).
Hart, G. L. W., Curtarolo, S., Massalski, T. B. & Levy, O. Comprehensive search for new phases and compounds in binary alloy systems based on platinum-group metals, using a computational first-principles approach. Phys. Rev. X 3, 041035 (2014).
Curtarolo, S. et al. The high-throughput highway to computational materials design. Nat. Mater. 12, 191–201 (2013).
Allred, A. L. Electronegativity values from thermochemical data. J. Inorg. Nucl. Chem. 17, 215–221 (1961).
Teatum, E. T., Gschneidner, K. A. Jr & Waber, J. T. Compilation of Calculated Data Useful in Predicting Metallurgical Behavior of the Elements in Binary Alloy Systems, https://doi.org/10.2172/4789465 (1968).
Miedema, A. R. Simple model for alloys. Philips Tech. Rev. 33, 149–160 (1973).
Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 117, 1–19 (1995).
Brown, W. M., Kohlmeyer, A., Plimpton, S. J. & Tharrington, A. N. Implementing molecular dynamics on hybrid high performance computers - Particle-particle particle-mesh. Comput. Phys. Commun. 183, 449–459 (2012).
Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 18, 015012 (2010).
Hirel, P. Atomsk: A tool for manipulating and converting atomic data files. Comput. Phys. Commun. 197, 212–219 (2015).
Stukowski, A. Structure identification methods for atomistic simulations of crystalline materials. Model. Simul. Mater. Sci. Eng. 20, 045021 (2012).
Pedregosa, F. et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 12, 2825–2830 (2011).
Kelchner, C. L. & Plimpton, S. Dislocation nucleation and defect structure during surface indentation. Phys. Rev. B - Condens. Matter Mater. Phys. 58, 11085–11088 (1998).
Samolyuk, G. D., Béland, L. K., Stocks, G. M. & Stoller, R. E. Electron-phonon coupling in Ni-based binary alloys with application to displacement cascade modeling. J. Phys. Condens. Matter 28, 175501 (2016).
Maisel, S. B., Ko, W. S., Zhang, J. L., Grabowski, B. & Neugebauer, J. Thermomechanical response of NiTi shape-memory nanoprecipitates in TiV alloys. Phys. Rev. Mater. 1, 33610 (2017).
Adams, J. B., Foiles, S. M. & Wolfer, W. G. Self-diffusion and impurity diffusion of fcc metals using the five-frequency model and the Embedded Atom Method. J. Mater. Res. 4, 102–112 (1989).
Béland, L. K. et al. Features of primary damage by high energy displacement cascades in concentrated Ni-based alloys. J. Appl. Phys. 119, 085901 (2016).
Howells, C. A. & Mishin, Y. Angular-dependent interatomic potential for the binary Ni–Cr system. Model. Simul. Mater. Sci. Eng. 26, 085008 (2018).
Zhou, X. W., Foster, M. E. & Sills, R. B. An Fe-Ni-Cr embedded atom method potential for austenitic and ferritic systems. J. Comput. Chem. 39, 2420–2431 (2018).
Zhang, Y., Ashcraft, R., Mendelev, M. I., Wang, C. Z. & Kelton, K. F. Experimental and molecular dynamics simulation study of structure of liquid and amorphous Ni62Nb38 alloy. J. Chem. Phys. 145, 204505 (2016).
Acknowledgements
This work was supported by the US Department of Energy, Office of Basic Energy Sciences under grant DE-SC0020180.
Author information
Authors and Affiliations
Contributions
M.W., P.M.L, and C.A.S. proposed the research idea and designed the workflow. M.W. wrote all code, performed all calculations, and applied machine learning. P.M.L advised on setting up the machine learning framework. C.A.S. provided overall guidance. All the authors analyzed the data, discussed the results, and contributed to writing and reviewing the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks Yuri Mishin and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wagih, M., Larsen, P.M. & Schuh, C.A. Learning grain boundary segregation energy spectra in polycrystals. Nat Commun 11, 6376 (2020). https://doi.org/10.1038/s41467-020-20083-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-020-20083-6
This article is cited by
-
Virtual node graph neural network for full phonon prediction
Nature Computational Science (2024)
-
Learning grain boundary segregation behavior through fingerprinting complex atomic environments
Communications Materials (2024)
-
Computed entropy spectra for grain boundary segregation in polycrystals
npj Computational Materials (2024)
-
Accelerating the design of compositionally complex materials via physics-informed artificial intelligence
Nature Computational Science (2023)
-
Efficient machine learning of solute segregation energy based on physics-informed features
Scientific Reports (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.