Abstract
Crystalline solids exhibiting glass-like thermal conductivity have attracted substantial attention both for fundamental interest and applications such as thermoelectrics. In most crystals, the competition of phonon scattering by anharmonic interactions and crystalline imperfections leads to a non-monotonic trend of thermal conductivity with temperature. Defect-free crystals that exhibit the glassy trend of low thermal conductivity with a monotonic increase with temperature are desirable because they are intrinsically thermally insulating while retaining useful properties of perfect crystals. However, this behavior is rare, and its microscopic origin remains unclear. Here, we report the observation of ultralow and glass-like thermal conductivity in a hexagonal perovskite chalcogenide single crystal, BaTiS3, despite its highly symmetric and simple primitive cell. Elastic and inelastic scattering measurements reveal the quantum mechanical origin of this unusual trend. A two-level atomic tunneling system exists in a shallow double-well potential of the Ti atom and is of sufficiently high frequency to scatter heat-carrying phonons up to room temperature. While atomic tunneling has been invoked to explain the low-temperature thermal conductivity of solids for decades, our study establishes the presence of sub-THz frequency tunneling systems even in high-quality, electrically insulating single crystals, leading to anomalous transport properties well above cryogenic temperatures.
Similar content being viewed by others
Introduction
Low thermal conductivity crystals have been extensively researched for applications such as thermoelectrics1,2,3,4,5,6 and are typically realized by introducing crystalline defects that scatter phonons7,8,9. This strategy has been demonstrated in diverse classes of materials including multilayers10,11, polycrystalline semiconductors12,13, and solids containing nanoprecipitates14,15, among many others. Crystalline materials that exhibit intrinsically low thermal conductivity typically possess large anharmonic force constants, as in SnSe16 and Tl3VSe44; a complex crystal structure leading to a large phonon scattering phase space7,17; or a naturally occurring inhomogeneous nanoscale structure, as in AgSbTe22, otherwise remaining free of structural defects. Such homogeneous single crystals with low defect concentrations usually exhibit the familiar trend of decreasing thermal conductivity with increasing temperature above the Debye temperature18. Within the perovskite material family, the thermal conductivity varies from 1 to 20 W m−1 K−1 for the simplest ABO3-type perovskite oxides19,20,21 and chalcogenides22, and <1 W m−1 K−1 for organic–inorganic hybrid perovskites23 and inorganic halides24, although all of these materials follow the crystalline trend of thermal conductivity with temperature.
Only a few compounds have been reported to deviate from this trend. While a material with a complex or low-symmetry crystal structure does not necessarily possess a glassy thermal conductivity, most materials exhibiting the trend are structurally complex. Examples include NaNbO321 with a low-symmetry monoclinic or orthorhombic crystal structure at room temperature25, orthorhombic CsBiNb2O7 with 22 atoms per primitive cell26, polydiacetylene single crystals27, Yb-based zintls28, and clathrates5,6,29. The glassy thermal conductivity of clathrates, in particular, have been extensively investigated30,31,32. However, unambiguously identifying the origin of the glassy trend has proved challenging. For instance, while early works on clathrates hypothesized that two-level systems were responsible29,30, later works suggested that charge carrier scattering could play a role33 as the samples were electrically conducting. Further, direct detection of tunneling of heavy structural atoms is generally not possible with scattering methods as the tunneling splitting energies are expected to be sub GHz34, which is too low to affect thermal conduction except at temperatures less than around 1 K. As a result, the mechanism underlying the glassy thermal conductivity of single crystals remains unclear.
Here, we report measurements of the thermal conductivity of single crystals of electrically insulating hexagonal perovskite chalcogenide BaTiS3 with a highly symmetric and simple primitive unit cell. We find that the thermal conductivity of this material is among the lowest ever reported for single crystals, and further exhibits a glass-like temperature dependence with ultralow thermal conductivity extending down to cryogenic temperatures. Elastic and inelastic scattering measurements reveal the origin of this unusual trend as scattering from an atomic tunneling two-level system formed by the Ti atom residing in a shallow double-well potential. Our study provides the first direct observation of a two-level system of sufficiently high frequency to disrupt thermal conduction in high-quality, electrically insulating single-crystalline materials over an extended temperature range, a result that is of both fundamental and practical interest.
Results
Crystal structure of BaTiS3
We synthesized needle-like single crystals of BaTiS3 with dimensions up to ~2 cm × 100 μm × 50 μm using chemical vapor transport35,36. BaTiS3 has a BaNiO3-type hexagonal perovskite structure in which the octahedra of Ti coordinated by S atoms share common faces, resulting in chain-like structures along the c axis. These parallel chains possess strong intra-chain bonding and weak electrostatic interactions along a/b-axes, as shown in Fig. 1a, b. From the X-ray diffraction (XRD) measurement (Fig. 1c) and a rotational XRD map (see Supplementary Information Fig. S1), the crystallographic orientation of the BaTiS3 single crystal was determined. The termination plane was the bc-plane with the c axis as the long edge, as depicted in the scanning electron microscopy (SEM) image in the inset of Fig. 1c. The rocking curve of the 200 reflections is also shown in the inset of Fig. 1c. The sharp full-width-at-half-maximum (FWHM) of 0.024° indicates high crystalline quality. We also performed refinements of the single-crystal XRD measurements, which yielded a structure of P63mc, in agreement with a previous report37. The refinements on multiple single-crystal samples showed that the crystals were stoichiometric within the limits of the measurement technique.
Illustration of the BaTiS3 structure in perspective view along c axis (a) and projected down a axis (b). Blue and orange spheres denote Ba and S atoms, respectively. Octahedra formed by Ti and six surrounding S atoms are highlighted in green. c XRD measurement of a crystal to identify the crystallographic directions. The left inset panel of c is an SEM image of the sample for which thermal conductivity was measured using TDTR. The right inset panel of c is the rocking curve for the 200 reflections. STEM HAADF images showing c axis (d) and a axis (e) projection of BaTiS3. The bottom panels show the high-resolution HAADF images with overlaid atomic models. f Measured thermal conductivity versus temperature for BaTiS3 (green) and other materials from literature. First-principles calculations using temperature-dependent effective potential (TDEP) method are also shown (black dashed line). Data for BaTiO3 and SrTiO3, amorphous silica (a-SiO2), Bi2Te3, CsBiNb2O7, CsPbI3, NaNbO3, Tl3VSe4, AgSbSe2, SnSe and (SnS)1.2(TiS2)2 are from refs. 4,16,18,19,21,26,41,69,70, respectively. The estimation of error bars is detailed in Supplementary Information.
To further ascertain the quality of the BaTiS3 crystals, we performed atomic-scale imaging using scanning transmission electron microscopy (STEM). Figure 1d, e shows wide field-of-view high-angle annular dark-field (HAADF) images of a BaTiS3 crystal along with c and a axis projections, respectively. The zoomed-in view of atomic resolution HAADF images overlaid with corresponding atomic models are also shown. In this imaging mode, the intensity of an atomic column is approximately proportional to the squared atomic number (~Z2) of the elements in the column38. The corresponding selected area electron diffraction (SAED) patterns are available in Supplementary Information (Supplementary Fig. S2). We did not observe any line or planar defects, confirming the high quality of the BaTiS3 crystals. These STEM images provide a detailed view of the atomic positions compared to our past investigation35 and help rule out the presence of any extended defects or large concentrations of point defects.
Glass-like and ultralow thermal conductivity
We measured the thermal conductivity of BaTiS3 using time-domain thermoreflectance (TDTR)39,40. Owing to the sample geometry and the low thermal conductivity, we can only measure the cross-plane thermal conductivity or thermal conductivity perpendicular to the c axis. We determined the thermal conductivity by fitting the measured TDTR signal using a standard thermal diffusion model39. (See Supplementary Information for details of the implementation, raw data, analysis, and uncertainty estimation of the TDTR measurements). The measured thermal conductivity of BaTiS3 from 70 to 400 K is shown in Fig. 1f. The measured thermal conductivity κ of BaTiS3 at room temperature is only 0.39 W m−1 K−1. This value is more than an order of magnitude smaller than that of BaTiO319 and is comparable to the lowest thermal conductivity reported for single crystals such as Tl3VSe44, CsBiNb2O726, and CsPbI341. Further, the measurements show an anomalous trend of increasing thermal conductivity with increasing temperature over the entire measured temperature range that is unexpected for a single crystal. Below ~100 K, the thermal conductivity is lower than that of any other crystalline solid to the best of our knowledge.
To identify the origin of this unusual behavior, we performed a number of additional characterizations on the BaTiS3 crystal. We first verified that the crystal is indeed an electrical insulator and possesses the expected stoichiometry; these properties were confirmed using electrical resistivity measurements and Rutherford backscattering (Supplementary Information). In particular, the Rutherford backscattering and refinements of the single-crystal XRD patterns indicate that the sulfur vacancy concentration cannot exceed a few percent. At these low vacancy concentrations, the scattering due to vacancies is well approximated by the Tamura formula42, and such a scattering rate cannot yield the observed temperature dependence and low values of thermal conductivity.
Next, we examined whether anharmonic damping could explain the observed trend using first-principles anharmonic phonon calculations based on the structure determined by single-crystal XRD. In this method, known as the temperature-dependent effective potential (TDEP) method, the renormalized harmonic force constants are determined at each temperature by fitting the force-displacement data sets obtained from density functional theory to a model Hamiltonian43,44,45. This method is capable of incorporating anharmonicity beyond the perturbative limits of conventional phonon calculations. As shown in Fig. 1f, this calculation matches the value of thermal conductivity at room temperature but predicts the opposite temperature trend of thermal conductivity. This result suggests that the anomalous thermal conductivity of BaTiS3 has a different origin.
Local structure of BaTiS3
To quantitatively characterize the local structure of BaTiS3, we measured neutron powder diffraction patterns on the NOMAD instrument at the Spallation Neutron Source (see “Methods” section) and performed a pair distribution function (PDF) analysis using the PDFgui computer program46. Figure 2a shows the PDF (G(r)) for pair distances up to 10 Å. Significant peak anisotropy exists in the negative Ti-S peaks (note that because Ti has a negative neutron scattering length Ti-S and Ti-Ba peaks in the PDF appear negative). Typically, pair–pair correlation peaks decrease in intensity with increasing temperature because of thermal motion; this trend is observed for the Ba-S and S-S peaks but not for the Ti-S and Ti-Ba peaks. The absence of temperature dependence in these PDF peaks suggests a more complex site potential for the Ti atoms. Note that although other peaks such as the Ba-Ba and S-S peak near 4.84 Å also appear to show weak temperature dependence, this trend is due to the presence of other negative peaks. A breakdown of the PDF by atomic pairs determined from a refinement of the 100 K data is shown in the bottom panel of Fig. 2a (see Supplementary Information for details). Refinements of the PDFs were performed using both the P63/mmc and P63mc37 structures, but this choice of structure did not change the resulting local structure pair distributions.
a Measured PDF (G(r)) for several temperatures (top) and a breakdown of the pair distribution function (PDF) by atomic pairs for the 100 K refinement (bottom). The first few nearest neighbor distances are indicated. Since Ti has a negative neutron scattering length, the Ti-X peaks are negative. The nearest neighbor Ti-S peak is asymmetric and lacks temperature dependence. Note that other peaks that appear to lack temperature dependence actually consist of both positive and negative peaks as shown in the bottom panel, in contrast to the first Ti-S peak. b Measured PDF (blue circles) and best fit (red line) at 300 K. The residual difference between the measurements and fit is also shown (green line). Anisotropic distribution ellipsoids for 90 percent probability from the fit to PDF at c 100 K and d 300 K from different perspectives. The Ti distributions along the c axis (stretched blue ellipsoids) decrease in size with increasing temperature, the opposite of what is expected for thermal vibrations. e Derived atomic displacement parameters versus temperature. Note that the Ti-U33 parameter decreases with increasing temperature. The inset shows a schematic for the bimodal distribution of Ti atoms residing in shallow potential wells.
Figure 2b shows a representative fit to the PDF at 300 K using the P63mc space group from 1.5 to 30 Å. The resulting anisotropic displacement parameters at 90% probability are illustrated in Fig. 2c, d. At 100 K (Fig. 2c) the anisotropic displacements of the Ti atoms are elongated along the c axis with a large (≫0.01 Å2) atomic displacement parameter Ti-U33 = 0.2(0.07) Å2, compared to Ti-U22 = 0.03(0.005) Å2, which is more consistent with typical thermal amplitudes. The S atoms are similarly elongated along the c axis with S-U33 = 0.07(0.01) Å2 compared to S-U22 = 0.014(0.002) Å2. On heating, however, these large U33 values decrease to 0.15(0.05) and 0.055(0.01) Å2 for Ti and S atoms, respectively, as shown in Fig. 2e. This behavior is opposite to that expected for thermal vibrations. The U33 and U22 parameters for the Ba atoms, on the other hand, are smaller and show the expected increase in heating from 100 to 300 K (Fig. 2e).
All of these results suggest the presence of increasingly large-amplitude displacements of one or both of the Ti and S atoms along the c axis as temperature decreases. We find that splitting the Ti position into two sites displaced by 0.15 Å along the c axis improves the fit at 100 K. A schematic illustrating such a bimodal distribution of the Ti atoms is shown in the inset of Fig. 2e. Given that the fits at higher temperatures are not improved by the bimodal model, it seems likely that above 100 K thermal vibrations in a soft potential are sufficient to explain the distributions. This observation may explain why the anharmonic phonon calculations agree well with experiments for 200 K and above (Fig. 1f) but qualitatively differ from the experiments at lower temperatures as the bimodal distribution develops.
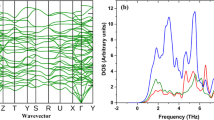
To assess the accuracy of our anharmonic phonon calculations and identify the origin of the dynamic displacements at 300 K, we measured the phonon dispersion of BaTiS3 using inelastic X-ray scattering on the HERIX-3 instrument at the Advanced Photon Source (see “Methods” section). As shown in Fig. 3a, the calculations agree with the measured dispersions (see Supplementary Information Fig. S10) with the exception of the LA and TA2 phonons along the Γ to K direction, in which case the measured dispersions are steeper than predicted. The largest displacements come from the low-energy (2 meV) TA1 phonon branch extending along Γ-M-K-Γ, which shows excellent agreement between theory and experiment. This phonon branch has large displacements polarized along the c axis and explains the large thermal displacements along this direction in Fig. 2e. However, the tendency for the Ti sites to develop bimodal distributions on cooling suggests that the Ti atoms are in shallow double-well potentials. On the other hand, static diffuse elastic scattering between the Bragg peaks in the IXS measurements was smaller by order 10−8 compared to the (200) Bragg intensity outside of the tails of this Bragg peak (see Supplementary Information Fig. S13). Hence, we can exclude any static diffuse scattering with high confidence, and the diffuse scattering observed by electron, X-ray, and neutron diffraction must be dynamic in origin.
a Phonon dispersion measured using inelastic X-ray scattering for longitudinal (circles) and transverse (triangles) polarization, along with first-principles simulations (peach lines). The low-energy transverse acoustic phonon (TA1) is polarized along the c axis and is responsible for large-amplitude thermal displacements along this direction. b High-energy resolution inelastic neutron scattering spectra measured on BaTiS3 powder at 2.4 K. An excitation is observed at 0.46 meV. The top right panel shows the spectrum integrated over momentum, Q. The bottom left panel shows the tunneling peak intensity versus Q, and the bottom right panel shows the momentum-integrated spectrum at different temperatures. c Tunneling splitting energy, ΔE, versus oscillator energy (ℏω) from an analytical model for three double-well separation distances. The inset shows the double-well parameters and the symmetric and antisymmetric wave functions. The well separation predicted from the tunneling splitting (intersection of the red curve and pink horizontal bar) agrees with that inferred from the TA1 phonon energy (intersection of the red curve and blue vertical bar).
Phonons and an atomic tunneling system
Quantum mechanics predicts that a particle in double-well potential may tunnel through the potential barrier, leading to a tunneling splitting between the ground state and excited states47. A prominent example of atomic tunneling is the tunneling umbrella inversion of ammonia, which was used in the first MASER48,49. Translational tunneling of atoms other than hydrogen is rare in solids34 and has so far never been observed by scattering methods. Tunneling systems may scatter other phonons and have long been used to explain the thermal conductivity of solids at sub-1 K temperatures29,50,51,52,53. To obtain direct evidence of tunneling splitting, we performed high-energy resolution inelastic neutron scattering measurements on BaTiS3 powders using the HYSPEC instrument at the Spallation Neutron Source (see “Methods” section). As shown in Fig. 3b, a sharp low-energy excitation appears at 0.46 meV at a temperature of 2.4 K. That the intensity of the excitation peaks occurs above the Bragg peaks, the first of which is located at Q = 2π/c (c = c axis lattice parameter), indicates that it follows the crystal symmetry and that spatial correlations exist. The excitation energy remains constant to within error up to at least 200 K, as shown in the bottom right panel of Fig. 3b. This trend is consistent with atomic tunneling and rules out a thermally activated Arrhenius process.
We provide further evidence for the presence of the tunneling system by comparing the well separation distance inferred from the tunneling splitting energy and the TA1 phonon energy using a textbook model for tunneling in a double-harmonic well47. The tunneling splitting, ΔE, can be expressed in terms of the oscillator energy, ℏω, and the potential barrier, V0, as:
For the double-harmonic well illustrated in Fig. 3c, the barrier potential can be written in terms of the oscillator frequency, ω, the atomic mass of Ti m, and separation distance a, using 2V0 = mω2a2. Figure 3c shows the expected tunneling splitting ΔE versus ℏω for several atomic separations. Since the low-energy TA1 phonon (Fig. 3a) contributes the large amplitudes to the Ti atomic motion for T > 100 K, we take its energy as representative of the oscillator splitting energy for the Ti atom, highlighted in the blue region in Fig. 3c. The 0.46 meV tunneling energy in red intersects this oscillator splitting at the curve corresponding to a separation distance of 0.28 Å. From the PDF analysis of Fig. 2, the mean square displacement parameter for Ti along the c axis in the double well at 100 K is U33 = 0.2 Å2 so that half the peak distance is \(\sqrt{2{U}_{33}}/2=0.31\) Å. Therefore, the expected separation distance a is about half of the maximum extent of the thermal ellipsoid for Ti in Fig. 2c, a reasonable agreement given the simplicity of this model.
The Ti tunneling provides a natural explanation for the temperature dependence of the Ti-U33 displacement parameter. At sufficiently high temperatures, the atom is free to explore all positions allowed by a harmonic potential, which, by symmetry results in a distribution centered at the equilibrium position. As the temperature is decreased, when the occupation of the ground state and first excited tunneling state dominates, the central position is a local minimum for the wavefunction (Fig. 3c) and the maximum of probability ∣ψ2∣ to find the atom is split into both of the two off-center positions, which leads to an apparent large atomic displacement parameter (ADP) with respect to the average position (center of the well), even if the ADP within each well is minimal, in the zero-point motion limit. More generally, this behavior is a consequence of the dynamic instability encountered when a double-well potential develops54,55.
The origin of the unusual thermal conductivity trend can also be identified from this analysis. The calculation above yields an estimate of the potential barrier height as V0 = 2.3 meV, which is only about twice the ground state energy ℏω/2 of the oscillator. It is the low barrier potential arising from the softness of the TA1 phonon that results in a sufficiently high tunneling frequency to scatter thermal phonons transporting heat above cryogenic temperatures. Evidence of strong scattering of these thermal phonons can also be seen in the quasielastic scattering that appears just beneath the tunneling peak in Fig. 3b (broad inelastic intensity extending from elastic peak). This observation is consistent with the phonons being overdamped by resonant scattering with the tunneling states and naturally explains the low and glassy thermal conductivity.
Atomic two-level tunneling systems have been invoked to explain the low-temperature thermal properties of solids for over 40 years29,52. The model postulates that there exist atoms or groups of atoms that have available two nearly degenerate configurations between which they may tunnel50,51; thermal conductivity is then reduced because propagating vibrations are scattered by the two-level systems53. The low energy of the two-level systems in typical glasses confined their effects on thermal conductivity to sub-1 K temperatures. In contrast, our results show that sub-THz frequency atomic tunneling states can exist in high-quality single crystals, resulting in glass-like ultralow thermal conductivity well above cryogenic temperatures. The soft, symmetric double-well potential responsible for the high-frequency atomic tunneling provides a guide for identifying crystalline solids with intrinsically low thermal conductivity.
Methods
Growth of BaTiS3 single crystals
Single-crystal needles were grown using chemical vapor transport, similar to methods employed for other perovskite sulfides reported elsewhere35,36. The precursors, barium sulfide (Sigma-Aldrich, 99.9%), titanium (Alfa Aesar, 99.9%), and sulfur (Alfa Aesar, 99.999%) were mixed stoichiometrically and loaded in a quartz ampoule with the transporting agent iodine (Alfa Aesar 99.99%) in an argon-filled glove box. The tube was then evacuated and flame sealed using a blowtorch. The sealed ampoule was about 12 cm in length and 2 cm in diameter. The samples were heated to 1000 °C with a 0.3 °C/min ramp rate, held at 1000 °C for 60 h, and then quenched to room temperature using a sliding furnace setup with a cooling rate of 100 °C/min.
Single-crystal XRD
The single-crystal X-ray diffraction was conducted on a Bruker SMART APEX DUO 3-circle platform diffractometer using monochromatic Mo Kα radiation (λ = 0.71073 Å) with a fixed χ axis. For low-temperature measurements, APEX II CCD detector and Oxford Cryosystems Cryostream 700 apparatus were employed. A black needle-like specimen of BaTiS3 crystal, ~0.044 mm × 0.060 mm × 0.512 mm, was used as the sample for single-crystal XRD analysis. Paratone oil was used to help mount the sample in a Cryo-Loop. We scanned a complete hemisphere of points on omega (0.5°) with a 50 mm detector distance and 512 × 512 pixels resolution. A total of 2520 frames were collected.
c-axis identification
The c-axis direction of the needle-like crystal was confirmed by rotating the BaTiS3 crystal along an in-plane direction to identify the six-fold rotational axis of the crystal (see Supplementary Fig. S1). The XRD map with sample tilt and the rocking curve measurements were carried out in a Bruker D8 Advance X-ray diffractometer with parallel beam configuration and a Ge (440) 2-bounce monochromator for Cu Kα1 radiation.
Time-domain thermoreflectance
A thin Al layer (~40 nm) was deposited onto the BaTiS3 single crystal using electron-beam evaporation for TDTR measurements. TDTR splits an ultrafast laser pulse train into two beams, a pump and a probe beam. The pump beam is modulated at radio frequency and heats the sample. The surface temperature of the sample is monitored by the probe beam via the change of reflectance with temperature. The thermal conductivity of BaTiS3 is extracted by fitting a model to the measured signal, where the magnitude and phase depend on the thermal properties of each layer. Here we used a 1/e2 laser radius of 10 μm and a modulation frequency of 4.6 MHz. Both pump power and probe power were maintained at 2.5 mW to limit the steady-state temperature rise to less than 20 K while still providing a signal to noise ratio of more than 50. More details can be found in the Supplementary Information.
Ab initio calculations
We carried out first-principles simulations using the projector augmented wave (PAW) method56 as implemented in the Vienna Ab initio Simulation Package (VASP)57,58,59,60. Exchange-correlation was treated using the AM05 functional61,62, and the plane wave energy cutoff was set to 800 eV. We performed calculations on a temperature-volume grid consisting of 6 temperatures and 5 volumes sampled using 3 × 3 × 3 Monkhorst-Pack63 mesh of k-points. We employed a near-cubic non-diagonal supercell containing 240 atoms. We fully relaxed the structure for each volume until forces act on the atoms were less than 10−7 eV/Å. We calculated forces and displacements using a self-consistent procedure, consisting of four iterations, where an iteration consists of calculating normal modes, generating snapshots, calculating forces, and fitting force constants. For each iteration, a total of 250 snapshots were used to achieve sufficient constraints to the IFCs and their convergence. Then, we minimized Helmholtz free energy F(T, V) at each temperature to find the equilibrium volume at each temperature. The phonon dispersions and thermal conductivity were calculated and analyzed with the temperature-dependent effective potential method (TDEP)43,44,45 by extracting second and third-order force constants.
Neutron powder diffraction measurements
Approximately 200 mg of BaTiS3 powder was loaded in a 3-mm-diameter quartz capillary and sealed with a nut and ferrule lid. The capillary was loaded in the sample shifter carousel at the Nanoscale Order Materials Diffractometer (NOMAD) instrument64 at the Spallation Neutron Source. Data were collected at 100, 150, 200, and 300 K (controlled by an Argon cryostream) for a total of 4 h per temperature at 60 Hz setting. The NOMAD data reduction programs64 were used to normalize collected spectra against a vanadium rod, subtract background and container scattering signals, and produce data appropriate for Rietveld and pair distribution function (PDF) analyses. PDF data G(r) were produced by Sine Fourier transformation of the total scattering structure factor S(Q) data with the Q range of 0.2 to 31 Å−1. The resulting PDF was analyzed using the PDFgui computer program46.
Inelastic X-ray scattering measurements
Phonon dispersion curves were measured using inelastic X-ray scattering (IXS) rather than neutron scattering because the crystal dimensions were too small for neutron scattering but well matched to IXS. Dispersion curves were measured from single crystals of BaTiS3 using the HERIX-3 X-ray spectrometer at the Advanced Photon Source (APS)65,66,67 with 21.657 keV (λ = 0.5725 Å) X-rays focused to a beam size of 20 μm. The energy resolution for the IXS scans was 2.1 meV FWHM. The X-ray attenuation length is about 190 μm for BaTiS3 with 21.6 keV X-rays, and we used crystals near this thickness (160 μm) to optimize the signal.
Inelastic neutron scattering measurements
To determine the tunneling energy, high-energy-resolution measurements were performed on 10 g of BaTiS3 powder loaded in an aluminum sample that can use the HYSPEC time-of-flight cold neutron spectrometer at the Spallation Neutron Source of Oak Ridge National Laboratory68. Measurements were performed at T = 2, 100, 200, and 300 K with an incident neutron energy of Ei = 3.8 meV and an energy resolution of 0.06 meV (FWHM) at a neutron energy transfer of 0.46 meV, the energy of the tunneling splitting. Empty cans were also measured at each temperature and used to make background subtractions.
Data availability
The authors declare that the data supporting the findings of this study are available within the paper and its Supplementary Information files.
References
Morelli, D. T., Jovovic, V. & Heremans, J. P. Intrinsically minimal thermal conductivity in cubic I-V-VI2 semiconductors. Phys. Rev. Lett. 101, 035901 (2008).
Ma, J. et al. Glass-like phonon scattering from a spontaneous nanostructure in AgSbTe2. Nat. Nanotechnol. 8, 445 (2013).
Beekman, M., Morelli, D. T. & Nolas, G. S. Better thermoelectrics through glass-like crystals. Nat. Mater. 14, 1182 (2015).
Mukhopadhyay, S. et al. Two-channel model for ultralow thermal conductivity of crystalline Tl3VSe4. Science 360, 1455–1458 (2018).
Takabatake, T., Suekuni, K., Nakayama, T. & Kaneshita, E. Phonon-glass electron-crystal thermoelectric clathrates: experiments and theory. Rev. Mod. Phys. 86, 669–716 (2014).
Keppens, V., Sales, B., Mandrus, D., Chakoumakos, B. & Laermans, C. When does a crystal conduct heat like a glass? Philos. Mag. Lett. 80, 807–812 (2000).
Snyder, G. J. & Toberer, E. S. Complex thermoelectric materials. Nat. Mater. 7, 105 (2008).
Minnich, A. J., Dresselhaus, M. S., Ren, Z. F. & Chen, G. Bulk nanostructured thermoelectric materials: current research and future prospects. Energy Environ. Sci. 2, 466–479 (2009).
Cahill, D. G. et al. Nanoscale thermal transport. II. 2003–2012. Appl. Phys. Rev. 1, 011305 (2014).
Costescu, R. M., Cahill, D. G., Fabreguette, F. H., Sechrist, Z. A. & George, S. M. Ultra-low thermal conductivity in W/Al2O3 nanolaminates. Science 303, 989–990 (2004).
Ravichandran, J. et al. Crossover from incoherent to coherent phonon scattering in epitaxial oxide superlattices. Nat. Mater. 13, 168 (2014).
Chiritescu, C. et al. Ultralow thermal conductivity in disordered, layered WSe2 crystals. Science 315, 351–353 (2007).
Poudel, B. et al. High-thermoelectric performance of nanostructured bismuth antimony telluride bulk alloys. Science 320, 634–638 (2008).
Kim, W. et al. Thermal conductivity reduction and thermoelectric figure of merit increase by embedding nanoparticles in crystalline semiconductors. Phys. Rev. Lett. 96, 045901 (2006).
Biswas, K. et al. Strained endotaxial nanostructures with high thermoelectric figure of merit. Nat. Chem. 3, 160 (2011).
Zhao, L.-D. et al. Ultralow thermal conductivity and high thermoelectric figure of merit in Sn Se crystals. Nature 508, 373 (2014).
Lu, X. et al. High performance thermoelectricity in earth-abundant compounds based on natural mineral tetrahedrites. Adv. Energy Mater. 3, 342–348 (2012).
Beekman, M. & Cahill, D. G. Inorganic crystals with glass-like and ultralow thermal conductivities. Cryst. Res. Technol. 52, 1700114 (2017).
Suemune, Y. Thermal conductivity of Ba TiO3 and Sr TiO3 from 4.5∘ to 300∘ K. J. Phys. Soc. Jpn. 20, 174–175 (1965).
De Yoreo, J. J., Pohl, R. O. & Burns, G. Low-temperature thermal properties of ferroelectrics. Phys. Rev. B 32, 5780–5784 (1985).
Tachibana, M., Kolodiazhnyi, T. & Takayama-Muromachi, E. Thermal conductivity of perovskite ferroelectrics. Appl. Phys. Lett. 93, 092902 (2008).
Osei-Agyemang, E. & Balasubramanian, G. Understanding the extremely poor Lattice thermal transport in chalcogenide perovskite BaZrS3. ACS Appl. Energy Mater. 3, 1139–1144 (2019).
Pisoni, A. et al. Ultra-low thermal conductivity in organic-inorganic hybrid perovskite CH3NH3 PbI3. J. Phys. Chem. Lett. 5, 2488–2492 (2014).
Lee, W. et al. Ultralow thermal conductivity in all-inorganic halide perovskites. Proc. Natl Acad. Sci. USA 46, 201711744 (2017).
Mishra, S. K., Choudhury, N., Chaplot, S. L., Krishna, P. S. R. & Mittal, R. Competing antiferroelectric and ferroelectric interactions in NaNbO3: neutron diffraction and theoretical studies. Phys. Rev. B 76, 024110 (2007).
Cahill, D. G., Melville, A., Schlom, D. G. & Zurbuchen, M. A. Low thermal conductivity of CsBiNb2O7 epitaxial layers. Appl. Phys. Lett. 96, 121903 (2010).
Wybourne, M. N., Kiff, B. J. & Batchelder, D. N. Anomalous thermal conduction in polydiacetylene single crystals. Phys. Rev. Lett. 53, 580–583 (1984).
Bux, S. K. et al. Glass-like lattice thermal conductivity and high thermoelectric efficiency in Yb9Mn4.2Sb9. J. Mater. Chem. A 2, 215–220 (2014).
Cohn, J. L., Nolas, G. S., Fessatidis, V., Metcalf, T. H. & Slack, G. A. Glasslike heat conduction in high-mobility crystalline semiconductors. Phys. Rev. Lett. 82, 779–782 (1999).
Sales, B. C., Chakoumakos, B. C., Jin, R., Thompson, J. R. & Mandrus, D. Structural, magnetic, thermal, and transport properties of X8Ga16Ge30 (x=Eu,Sr,Ba) single crystals. Phys. Rev. B 63, 245113 (2001).
Nolas, G. S., Weakley, T. J. R., Cohn, J. L. & Sharma, R. Structural properties and thermal conductivity of crystalline Ge clathrates. Phys. Rev. B 61, 3845–3850 (2000).
Avila, M. A. et al. Glasslike versus crystalline thermal conductivity in carrier-tuned Ba8Ga16X30 clathrates (x=Ge,Sn). Phys. Rev. B 74, 125109 (2006).
Bentien, A. et al. Thermal conductivity of thermoelectric clathrates. Phys. Rev. B 69, 045107 (2004).
Hermann, R. P. et al. Direct experimental evidence for atomic tunneling of europium in crystalline Eu8Ga16Ge30. Phys. Rev. Lett. 97, 017401 (2006).
Niu, S. et al. Giant optical anisotropy in a quasi-one-dimensional crystal. Nat. Photonics 12, 392–396 (2018).
Niu, S. et al. Mid-wave and long-wave infrared linear dichroism in a hexagonal perovskite chalcogenide. Chem. Mater. 30, 4897–4901 (2018).
Tilley, R. J. D. Perovskites: Structure-Property Relationships (Wiley, 2016).
Pennycook, S. J. & Jesson, D. E. High-resolution Z-contrast imaging of crystals. Ultramicroscopy 37, 14–38 (1991).
Cahill, D. G. Analysis of heat flow in layered structures for time-domain thermoreflectance. Rev. Sci. Instrum. 75, 5119–5122 (2004).
Sun, B. & Koh, Y. K. Understanding and eliminating artifact signals from diffusely scattered pump beam in measurements of rough samples by time-domain thermoreflectance (TDTR). Rev. Sci. Instrum. 87, 064901 (2016).
Lee, W. et al. Ultralow thermal conductivity in all-inorganic halide perovskites. Proc. Natl Acad. Sci. USA 114, 8693–8697 (2017).
Mendoza, J., Esfarjani, K. & Chen, G. An ab initio study of multiple phonon scattering resonances in silicon germanium alloys. J. Appl. Phys. 117, 174301 (2015).
Hellman, O., Abrikosov, I. A. & Simak, S. I. Lattice dynamics of anharmonic solids from first principles. Phys. Rev. B 84, 180301 (2011).
Hellman, O., Steneteg, P., Abrikosov, I. A. & Simak, S. I. Temperature dependent effective potential method for accurate free energy calculations of solids. Phys. Rev. B 87, 104111 (2013).
Hellman, O. & Abrikosov, I. A. Temperature-dependent effective third-order interatomic force constants from first principles. Phys. Rev. B 88, 144301 (2013).
Farrow, C. L. et al. PDFfit2 and PDFgui: computer programs for studying nanostructure in crystals. J. Phys. Condens. Matter 19, 335219 (2007).
Merzbacher, E. Quantum Mechanics 3rd edn (Wiley, 1998).
Cleeton, C. E. & Williams, N. H. Electromagnetic waves of 1.1 cm wave-length and the absorption spectrum of ammonia. Phys. Rev. 45, 234–237 (1934).
Feynman, R., Leighton, R. & Sands, M. The Feynman Lectures on Physics. (Addison-Wesley Publishing Co., Inc. in Reading Massachusetts, 1965).
Phillips, W. A. Tunneling states in amorphous solids. J. Low. Temp. Phys. 7, 351–360 (1972).
Anderson, P. W., Halperin, B. I. & Varma, C. M. Anomalous low-temperature thermal properties of glasses and spin glasses. Philos. Mag. 25, 1–9 (1972).
Leggett, A. J. & Vural, D. C. Tunneling two-level systems model of the low-temperature properties of glasses: are smoking-gun tests possible? J. Phys. Chem. B 117, 12966–12971 (2013).
Feldman, J. L., Kluge, M. D., Allen, P. B. & Wooten, F. Thermal conductivity and localization in glasses: Numerical study of a model of amorphous silicon. Phys. Rev. B 48, 12589–12602 (1993).
Itoh, K. & Fujihara, K. Mean position and thermal displacement of the atom in the double-quadratic well potential associated with structural phase transitions. Ferroelectrics 120, 175–183 (1991).
Singh, A., Moriyoshi, C., Kuroiwa, Y. & Pandey, D. Anomalous atomic displacement parameters and local dynamics in the curie range of a Pb-free relaxor ferroelectric system (Bi1−xBax)(Fe1−xTix)O3(0.36≤x≤0.50). J. Appl. Phys. 123, 164103 (2018).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994).
Kresse, G. & Hafner, J. Ab initio molecular dynamics for open-shell transition metals. Phys. Rev. B 48, 13115–13118 (1993).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Kresse, G. & Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50 (1996).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999).
Armiento, R. & Mattsson, A. E. Functional designed to include surface effects in self-consistent density functional theory. Phys. Rev. B 72, 085108 (2005).
Mattsson, A. E. & Armiento, R. Implementing and testing the AM05 spin density functional. Phys. Rev. B 79, 155101 (2009).
Monkhorst, H. J. & Pack, J. D. Special points for brillouin-zone integrations. Phys. Rev. B 13, 5188–5192 (1976).
Neuefeind, J., Feygenson, M., Carruth, J., Hoffmann, R. & Chipley, K. K. The Nanoscale ordered materials diffractometer NOMAD at the spallation neutron source SNS. Nucl. Inst. Methods Phys. Res. B 287, 68–75 (2012).
Toellner, T. S., Alatas, A. & Said, A. H. Six-reflection meV-monochromator for synchrotron radiation. J. Synchrotron Radiat. 18, 605–611 (2011).
Sinn, H. et al. An inelastic X-ray spectrometer with 2.2 mev energy resolution. Nucl. Instrum. Methods Phys. Res. Sect. A 467-468, 1545–1548 (2001).
Alatas, A. et al. Improved focusing capability for inelastic X-ray spectrometer at 3-ID of the APS: a combination of toroidal and Kirkpatrick-Baez (KB) mirrors. Nucl. Instrum. Methods Phys. Res. Sect. A 649, 166–168 (2011).
Stone, M. B. et al. A comparison of four direct geometry time-of-flight spectrometers at the spallation neutron source. Rev. Sci. Instrum. 85, 045113 (2014).
Jeon, H. W., Ha, H. P., Hyun, D. B. & Shim, J. D. Electrical and thermoelectrical properties of undoped Bi2Te3-Sb2Te3 and Bi2Te3-Sb2Te3-Sb2Se3 single crystals. J. Phys. Chem. Solids 52, 579–585 (1991).
Nielsen, M. D., Ozolins, V. & Heremans, J. P. Lone pair electrons minimize lattice thermal conductivity. Energy Environ. Sci. 6, 570–578 (2013).
Acknowledgements
N.S. and A.J.M. acknowledge the support of the DARPA MATRIX program under Grant No. HR0011-15-2-0039. B.S., Y.J., and A.J.M. acknowledge the support of the GIST-Caltech Research Collaboration in 2018. J.R. and S.N. acknowledge the support from the Air Force Office of Scientific Research under award no. FA9550-16-1-0335 and Army Research Office under award no. W911NF-19-1-0137. Neutron and X-ray scattering research (R.P.H. and M.E.M.) and STEM characterization (A.S.T. and R.M.) are sponsored by the U.S. Department of Energy (DOE), Office of Basic Energy Sciences, Materials Sciences and Engineering Division. J.M.-G. and B.C.M. gratefully acknowledge support from the Office of Naval Research Grant No. N00014-15-1-2411. A.S.T. and R.M. acknowledge support through the National Science Foundation grant DMR-1806147. S.N. acknowledges Link Foundation Energy Fellowship. This research used resources at the Spallation Neutron Source and the Center for Nanophase Materials Sciences, DOE Office of Science User Facility operated by the Oak Ridge National Laboratory, and resources of the Advanced Photon Source, a U.S. DOE Office of Science User Facility operated by Argonne National Laboratory under Contract No. DE-AC02-06CH11357. We thank Dr. Rakesh Singh and Cameron Kopas for performing the RBS experiments. M.E.M. and R.P.H. acknowledge encouraging discussions with Brian Sales.
Author information
Authors and Affiliations
Contributions
A.J.M. and J.R. conceived the project and supervised the research. B.S. performed TDTR measurements with help from Y.-D.J. on thin film deposition. S.N. grew the crystals and performed structural characterizations and electrical measurements with B.Z. N.S. contributed to the first-principle calculations. K.L.P. and M.E.M. conducted the neutron diffraction measurements. A.S.T., R.M., K.M., B.M.H., and M.M. performed STEM imaging studies. R.H. contributed to single-crystal XRD measurements. J.M.-G. and B.C.M. contributed to heat capacity studies. R.P.H., J.M., A.A., and M.E.M. conducted the inelastic X-ray scattering measurements and analysis. M.E.M. and B.W. conducted the inelastic neutron scattering measurements to identify the tunneling mechanism proposed by R.P.H. All authors discussed the results. B.S., A.J.M., and M.E.M. wrote the manuscript with contributions from all authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks Jie Ma, Nuo Yang and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sun, B., Niu, S., Hermann, R.P. et al. High frequency atomic tunneling yields ultralow and glass-like thermal conductivity in chalcogenide single crystals. Nat Commun 11, 6039 (2020). https://doi.org/10.1038/s41467-020-19872-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-020-19872-w
This article is cited by
-
Optical characterization of (TlInS2)0.5(TlInSe2)0.5 crystal by ellipsometry: linear and optical constants for optoelectronic devices
Journal of Materials Science: Materials in Electronics (2023)
-
Glassy thermal conductivity in Cs3Bi2I6Cl3 single crystal
Nature Communications (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.