Abstract
The ground state of a fermionic condensate is well protected against perturbations in the presence of an isotropic gap. Regions of gap suppression, surfaces and vortex cores which host Andreev-bound states, seemingly lift that strict protection. Here we show that in superfluid 3He the role of bound states is more subtle: when a macroscopic object moves in the superfluid at velocities exceeding the Landau critical velocity, little to no bulk pair breaking takes place, while the damping observed originates from the bound states covering the moving object. We identify two separate timescales that govern the bound state dynamics, one of them much longer than theoretically anticipated, and show that the bound states do not interact with bulk excitations.
Similar content being viewed by others
Introduction
Interfaces in fermionic condensates and the bound states hosted by them have recently attracted research focus in numerous condensed matter systems. Contemporary superfluid research is moving towards nanoscale probes1,2, nanoconfinement3,4,5 and microscopic dissipation mechanisms related to quantum turbulence6,7. Unconventional superconductivity in various materials8 and the dynamics of certain atomic BECs9 is characterised by the physics of bound excitations. Nanofabrication of superconducting hybrid structures has enabled tailoring bound states with desired properties. For instance, engineered superconducting systems containing Andreev-bound states (ABS) are used in studies of Majorana fermions10,11 aimed at producing components of, say, a quantum computer12. Understanding the dynamics of bound states is of central importance for these research directions.
A recent experiment showed, contrary to the classic textbook picture, that a macroscopic object moving quasi-uniformly in superfluid 3He-B can exceed the predicted Landau velocity 13 in the zero-temperature limit without destroying the condensate14. Phenomenologically, the dissipation experienced by objects moving rapidly can be explained in terms of the Lambert picture15. This scenario is based on assuming that there is a well-defined two-dimensional (2D) gapless spectrum of bound states available within roughly a coherence length of all surfaces, and that the fermions occupying these states can escape to the bulk promoted by macroscopic flow fields, thereby providing dissipation. This is clearly a simplification, but the model captures the main features of the experiment well enough for the presentation of the results. Simultaneously, the surface layer shields the bulk condensate from interacting with the moving object, preventing pair breaking even if the object’s velocity exceeds the Landau velocity. Therefore the bound states covering the surface of a fermionic condensate not only determine the properties of its surfaces, but ABS dynamics are also central in understanding one of the most elementary of bulk phenomena: the drag an object experiences when moving at constant velocity through the fermionic superfluid.
The existence of a gapless spectrum covering all surfaces in superfluid 3He is well-motivated by theoretical studies16,17,18,19, and supported by independent experimental evidence18,20,21. In terms of dynamics, however, the above picture still lacks rigorous theoretical justification. In particular, its critics have pointed out that thermalisation of the surface-bound states should be so fast, of the order of nanoseconds, that the equilibrium cannot be disturbed by the relatively slow motion (typically milliseconds) of a macroscopic moving object22. In this article, we provide experimental evidence to end the controversy. We show that such criticism correctly identifies only one of the two timescales that govern the dynamics of surface-bound states, and that this process is very fast as theoretically anticipated. Crucially, we also observe a second, much slower process, which allows for the surface states’ contribution to dissipation. Our experiment demonstrates, remarkably, that the observed dissipation is independent of the density of thermal bulk excitations, which justifies the assumption that surface-bound states are involved in the process in the first place.
Results
An ideal experiment aimed at probing ABS-originating dissipation in superfluid 3He-B would be carried out at a temperature so low that thermal bulk excitations vanish completely. Otherwise, trivial collisions with them provide a thermal dissipation background. In our experiments, the sample temperature was between 140 μK and 240 μK. The superfluid transition temperature is Tc = 929 μK. Therefore the density of thermal bulk quasiparticles is not negligible, but it is low enough that they propagate ballistically, and their contribution to observed dissipation can be confidently subtracted.
In these conditions at saturated vapour pressure, the Landau critical velocity is vL = Δ/pF = 27 mm s−1 (Δ is the superfluid gap and pF the Fermi momentum). We can reach and exceed this velocity in both oscillatory and constant-speed measurements by driving alternating (AC) or direct (DC) current through a goalpost-shaped superconducting wire (legs 25 mm, crossbar 9 mm, thickness 135 μm). An external magnetic field is oriented parallel to the legs of the wire, and the resulting Lorentz force on the crossbar moves the wire. In an AC measurement, the wire is moved by a sinusoidal current at the mechanical resonance frequency of the wire. This is how mechanical probes are traditionally operated in order to probe the dissipation in a liquid23,24,25. In a DC measurement, the drive current changes at a constant rate, resulting in a sweep of the probe wire from one side to the other at a (quasi) constant speed14. The wire is surrounded by a bolometric volume of superfluid 3He-B, and the drag force experienced by the wire is inferred from the number of emitted quasiparticles, seen as a heat pulse measured by the thermometers.
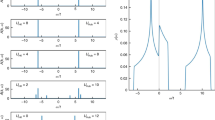
Let us study the consequences of a gapless spectrum of bound states covering the surface of the moving wire crossbar at a temperature so low that there are no thermal bulk excitations. The spectrum has an approximately direction-independent density of states and a relatively flat dispersion relation assuming the surface scatters quasiparticles diffusively, and a more Dirac-like dispersion relation with partial specularity18. For the purposes of the experiments presented here, the details of the dispersion relation are irrelevant. By default, the wire surface is diffusive, and tuning the scattering conditions using 4He preplating is discussed later. For the sake of simplicity, we have illustrated the measurement with Dirac dispersion curves in Fig. 1.
(Centre) The crossbar of the wire is moved in two phases along direction labelled x. All ramps begin by accelerating the wire from zero to a constant velocity (here v = 40 mm s−1, gray line) and then back to zero. The magnitude of the resulting flow field, vfl, in the coordinate system of the wire is shown with contour lines in the inset. The ramp is then either repeated in the same direction (up ramp, blue line) or in the opposite direction (down ramp, red line). Bound-state dynamics are probed by varying the waiting time Δt between the two phases. a The flow shifts both the bound-state energy spectrum, E(p), and the available bulk states as explained in the main text. After the acceleration, the population of bound quasiparticles (red circles) and quasiholes (blue circles) on the wire surface reaches a steady-state (point a along the wire trajectory). The schematic dispersion curves (black dash line at the surface, blue dash line in bulk) are drawn for the top (or bottom) generatrices of the wire, where the flow velocity is maximal. b During Δt, momentum exchange with the wire surface allows the exchange of bound quasiparticle populations between the branches (τ1). Within a branch, the population relaxes with τ2. c During an up ramp, if Δt ≲ τ1, the population imbalance results in less dissipation from quasiparticles escaping to bulk as compared with the first phase of motion. d In a down ramp, if Δt ≲ τ1, the dissipation will be enhanced. Note that the bound-state dispersion depends on surface specularity, and the Dirac dispersion illustrated here is chosen for simplicity.
In the presence of macroscopic flow, both bulk and gapless surface dispersion curves for quasiparticles (and holes) shift according to ±vflpF (in one dimension). Here, vfl is the local flow velocity of the superfluid. In the frame of the crossbar, the bulk far away from the wire flows at vfl = −v, where v is the velocity of the crossbar in the laboratory frame. Near the cylindrical crossbar, the flow is enhanced and reaches a maximum of vfl = −2 v, assuming perfect potential flow. These two contributions narrow down the energy mismatch Δ between available bulk states and populated ABS states by 3 vpF, and the flow, therefore, enables ABS escape from the surface of the wire to the bulk when the wire moves faster than vc = 1/3 ⋅ Δ/pF = 9 mm s−1, the well-known critical velocity in AC measurements26. Strikingly, if v is held constant, the ABS spectrum finds equilibrium and the drag force disappears14.
The above-described difference between oscillatory and uniform motion must arise from the time constants that govern the ABS escape process. Basically, the repeating reversal of direction in oscillatory motion replenishes the reserve of quasiparticles that can escape to bulk when the velocity exceeds the critical velocity, while in uniform motion such replenishment is not available. If we compare equally long and otherwise identical trajectories where velocity is either reversed or not, the reversal should increase the observed dissipation. In the absence of the bound-state contribution, such directional dependence is not expected14.
In order to experimentally substantiate this picture, and to remove the effect of the finite density of thermal bulk excitations that cannot be avoided in experiments, we move the wire crossbar in two phases (Fig. 1). Each measurement starts from standstill long enough to remove any history dependence. The wire is then quickly accelerated to v, the velocity is kept constant for 0.5 mm distance, before reducing the velocity back to zero27. The acceleration time was varied from 3 ms to 5 ms, and the obtained results were independent of it. After time Δt, the ramp is repeated from this new starting location with either v (“up ramp”) or −v (“down ramp”). This allows subtracting the dissipation measured for up ramps Qup from that measured for down ramps Qdown, ΔQ = Qdown − Qup. As described in detail in “Methods”, the dissipation due to ambient bulk quasiparticles in ΔQ is cancelled assuming the up and down trajectories are equally long.
The above measurement shows that bound-state dissipation is characterised by two regimes: First, the difference in the measured dissipation, ΔQ, is zero when v ≤ 9 mm s−1 (see “Methods”). This implies that, in the zero-temperature limit, dissipation vanishes below the critical velocity vc = 9 mm s−1. Second, for velocities higher than 9 mm s−1 at Δt = 0, up ramps experience less dissipation than down ramps. Phenomenologically we find that \(\Delta Q\propto {((v-{v}_{{\rm{c}}})/{v}_{{\rm{c}}})}^{2.5}\). We can only measure this velocity dependence in detail when the sample is preplated with 4He. This could in principle limit applying the obtained results on the quasiparticle dynamics where no 4He is present. However, we emphasise that vc = 9 mm s−1 is the AC critical velocity, observed here both with and without 4He, confirming that the results of the DC measurement directly apply to dissipation experienced by moving objects in superfluid 3He-B in general. This shows that direct bulk pair breaking is replaced by a much weaker drag force originating from surface-bound quasiparticles, as speculated earlier14. The velocity dependence is discussed in more detail in “Methods”.
We can now vary Δt to measure the dynamics of bound states on the wire surface (Fig. 2). The difference in dissipation, ΔQ, disappears exponentially as \(\exp (-\Delta t/\tau )\), where τ ≈ 6 ms in the measured temperature range of 160–230 μK. Within this range of temperatures, the thermal bulk quasiparticle density varies by almost two orders of magnitude, while measured τ is constant. Together with the above observations, this justifies the assumption that bound quasiparticles are responsible for the dissipation. It also rules out any direct interaction between surface-bound and bulk quasiparticles as the source of thermalisation.
a Measured dissipation as a function of Δt for up ramps (blue upward triangles) and down ramps (red downward triangles) reveals the characteristic time of bound-state dynamics on the wire surface. The solid lines are exponential fits to the data. At large waiting times ΔQ ≈ − 2.6 pJ, as expected due to the hysteretic contribution analysed in Fig. 4. b The fitted time constants with 4He preplating (magenta squares) and without it (black circles) are independent of temperature, τ = 6 ± 3 ms. The relative change in thermal quasiparticle density is shown on the top axis. All data in this figure were measured at H = 130 mT and v = 45 mm s−1. Error bars indicate the 68% confidence interval for the exponential fits.
The dynamics of bound quasiparticles on the wire surface can be described by two time constants in our toy model. The first one, τ1, gives the probability of the inter-branch process where a quasiparticle scatters from the wire exchanging momentum going from, say, p to −p. This process enables drag, as the exit channel to bulk is open only in the direction of wire motion while only quasiparticles with the momentum in the opposite direction gain energy due to the flow. That is, drag is produced by those quasiparticles that escape to bulk right after scattering with the wire, removing momentum from the wire. The second time constant, τ2, describes the rate at which quasiparticles that did not escape to bulk relax within each dispersion branch to the thermal equilibrium distribution distorted by process one. If τ2 = ∞, then the imbalance produced by moving the wire and stopping in the middle, measured by comparing up and down ramps, disappears diffusively as determined by τ1. Assuming τ2 = 0, the imbalance still disappears at the rate given by τ1, but this time the process is deterministic. Therefore, regardless of τ2, we have measured τ1 ≈ τ = 6 ms.
It is also possible to set an experimental upper bound for τ2. We have measured the AC critical velocity of a set of probes with resonance frequencies f0 ranging from 350 Hz to 158 kHz (Fig. 3). The critical velocity is seen as kink in the velocity of the probe measured as a function of force. It corresponds to a sudden increase in the force required to increase the velocity by a given amount. As speculated by Lambert15, when f0 > 1/τ2, one should see a clear reduction in the observed AC critical velocity as quasiparticles would be able to “climb up” the dispersion curves diffusively by scattering back and forth between p and −p. For instance, by a two-step process, one would get escape to bulk starting at 4.5 mm s−1, and so on.
In AC measurements, critical velocity vc is seen as a sharp increase in the force needed to increase peak oscillation velocity above the critical velocity. The exact critical velocity depends on details of the flow field around the probe, and therefore on the shape of the object. The measured probes are in order from left to right: a 1-μm thick vibrating wire operating at 843 Hz (red points, measured at 110 μK), a 4.5-μm thick vibrating wire at 355 Hz (green points, 110 μK), a custom-made quartz tuning fork at 25.7 kHz with prong length 1.75 mm and prong cross-section 50 × 90 μm (blue points, 120 μK), and an overtone of the same fork at 158 kHz (magenta points, 110 μK). The inset shows critical velocities extracted from the main figure. Error bars correspond to the uncertainty in locating the critical velocity in the main figure. Black dash line is a guide to the eye that corresponds to \({v}_{{\rm{c}}}\propto {f}_{0}^{0.1}\), illustrating the increase of vc with frequency.
We observe no critical velocity reduction up to f0 = 158 kHz. In fact, the observed critical velocity slowly and smoothly increases as a function of the resonance frequency. This happens despite the varying geometries of the four probes used: the two low-frequency probes are vibrating superconducting wires, while the two kHz probes are the first harmonic and an overtone of a custom-made quartz tuning fork with smooth surfaces. While studying the reason for the observed slow increase of vc systematically remains a task for the future, this result implies that τ2 ≲ 1/f0 ≈10 μs. We believe that τ2 describes the fast thermalisation process anticipated in ref. 22.
Surface specularity may play an important role in the bound-state escape process. In particular, the critical velocity vc predicted by the phenomenological toy model depends on the bound-state gap for quasiparticles with in-plane momentum, Δ∥, which is zero for a diffusively scattering surface and obtains the bulk value when the surface becomes fully specular18. In the one-dimensional picture, the flow couples to bound quasiparticles with momentum in the plane of the surface. The predicted vc therefore eventually approaches vL = 27 mm s−1 with increasing specularity. Also, one would expect that τ1 depends on specularity as it describes the process of quasiparticle scattering with the wire.
The surface scattering can be tuned from diffuse to specular continuously by preplating the sample with slightly over two monolayers of 4He28. It is possible that 4He coverage also changes the scattering qualitatively by removing magnetic spin exchange with the surface layer29. However, reaching fully specular scattering requires a two-dimensional superfluid layer of 4He, which flows to the coldest part of the sample container (the heat sink) and cannot therefore be stabilised on the wire in our experiment5. We have resorted to measuring the effect of adding ~2.5 monolayers of solid 4He on the wire surface (and all other surfaces in the sample container). The amount of 4He to be added was estimated based on the dimensions of the sample container, the known surface area of the heat exchanger sinters30, and the known density of 4He monolayers31. This estimate was then favourably compared with the amount of 4He needed to be added to the originally-empty sample container at 4 K temperature to create a small equilibrium pressure, corresponding to saturated solidification on the surfaces.
While adding 4He causes the heat exchangers to become less efficient by a factor of two32, we observe very little change in the bound-state dynamics or dissipation. First, τ1 remains ≈5 ms within the scatter of the data. This shows that the quasiparticle escape process is robust against at least small changes in the scattering conditions. Second, the measured AC critical velocity is 9 mm s−1 with and without 4He. This implies that the bound-state dispersion does not change dramatically. Based on Fig. 4 in ref. 18, this suggests that the surface specularity S obtained was smaller than S = 0.8, and probably between S = 0.2 and S = 0.5. We therefore conclude that the observed DC velocity dependence is (qualitatively) universal at least up to the obtained specularity. Measuring the precise amount of 4He on the surfaces is possible indirectly using nuclear magnetic resonance techniques as 4He replaces the paramagnetic layers of solid 3He otherwise covering all surfaces5,33,34,35, but building a new experiment with the necessary instruments for that remains a task for the future.
a The measured hysteretic difference in dissipation with Δt = 50 ms (cyan circles) follows the empirical power law \(\Delta Q=a{(v/{v}_{{\rm{c}}})}^{1/2}\) (solid line), as clearly seen in log scale. b When Δt = 0 (cyan circles), the hysteretic contribution can be removed by fitting the data at v ≤ 9 mm s−1 with the above power law (solid black line). After subtracting this fit, the data (blue circles) follows \(\Delta Q=b{((v-{v}_{{\rm{c}}})/{v}_{{\rm{c}}})}^{2.5}\) (solid blue line) above vc = 9 mm s−1, and ΔQ = 0 for v < vc, as explained in the text. The sum of the two fits is shown by the cyan line. The fitted values of a are shown in panel (c): Fits to data where Δt = 0 are shown with black circles, Δt = 50 ms corresponds to blue squares, and Δt = 100 ms is shown as red triangles. The dashed line is a guide to the eye that corresponds to a = −5.0/H2nJ mT2. Panel (d) shows fitted values of b (black circles), which within the scatter of the data are independent of H as expected. The temperature varied from 150 μK to 190 μK in these measurements. All data in this figure were obtained with 4He preplating. Selected error bars in panel c correspond to one standard deviation of the fits to illustrate the point-wise scatter (omitted error estimates are similar and can be found in the data container, see the data availability statement), and in panel d to the 68% confidence interval of the fits.
Discussion
In conclusion, our experiments confirm that quasiparticles (and holes) bound to the region of gap suppression near solid surfaces in the B phase of superfluid 3He are responsible for the zero-temperature dissipation experienced by macroscopic objects moving in the superfluid. The dissipation begins when the flow velocity is sufficient for releasing the bound quasiparticles to the bulk of the superfluid. We have demonstrated experimentally that the bound states re-equilibrate through a two-stage process involving a fast thermalisation step with τ2 < 10 μs, but importantly also a theoretically unforeseen slow scattering step characterised by τ1 = 6 ms. To be clear, τ1 is the effective time constant describing the process where the quasiparticle momentum is changed from pF to −pF. In a proper two-dimensional treatment of the process that τ1 emerges from, this may involve a large number of scattering events which collectively allow the quasiparticle to eventually find the very opposite momentum. We speculate that this process is potentially the underlying reason as to why τ1 is not of the order of nanoseconds. Furthermore, we vary the bulk quasiparticle concentration to show that the bulk states do not contribute to bound-state dynamics on any observable timescale. Therefore our results can be readily generalised to the description of transient phenomena in 2-dimensional Dirac systems such as graphene36, if the escape process to bulk is neglected. It is worth emphasising that the bulk escape process is temperature independent at low temperatures and, hence, provides dissipation even in the zero-temperature limit.
We acknowledge the preliminary nature of the bound-state model presented above. In particular, it remains an open question how exactly bound-state dynamics should be described in a full two-dimensional model of the wire surface with a flow velocity distribution, a theoretically justifiable bound state spectrum (not fully gapless), diffusion or transport between various parts of the surface etc. Competing theoretical suggestions are sparse, but there have been some discussions related to a layer of vortices covering the wire acting as a buffer and therefore masking the Landau velocity22. On the other hand, theoretical work on superflows exceeding the Landau velocity has recently been published studying other systems, such as polaron–polaritons37 and graphene38. For these reasons, it remains of interest to provide additional experimental insight. For example, one could change the Landau velocity by studying flow in a confined geometry, say, in the recently-discovered polar phase of superfluid 3He3. The gap spectrum of the polar phase contains a nodal line, meaning that the Landau speed limit is zero in that plane. On the other hand, it seems essential to enhance the experiment presented in this article by building a detector or spectrometer fast enough to distinguish the dissipation associated with the separate phases of the wire motion. This requires designing and devising nano-sized instruments1,2.
Methods
An ideal experiment aimed at probing bound-state-originating dissipation in superfluid 3He-B would be carried out at a temperature so low that thermal bulk excitations are rare enough to be neglected completely. Otherwise, trivial collisions with them provide a thermal dissipation background. In our experiments, we used a nested nuclear demagnetisation cryostat39, capable of holding the sample temperature anywhere between 140 μK and 240 μK for several days. The temperature was measured with a quartz tuning fork23, and a vibrating wire thermometer24,25. Pressure in all measurements was the saturated vapour pressure, corresponding to superfluid transition temperature Tc = 929 μK. Therefore the density of thermal bulk quasiparticles is not negligible, but it is low enough so that they propagate ballistically, and their contribution to the observed dissipation can be subtracted. We can vary the thermal quasiparticle density by two orders of magnitude within the ballistic regime. Subtracting the thermal quasiparticle contribution is robust and reliable because the gap spectrum of the B phase is isotropic in zero magnetic field, and only slightly distorted in the small external magnetic field.
The main probe used in the experiment is the goalpost-shaped wire. The bolometric volume that surrounds the wire is calibrated by resonant AC measurements40 by fitting the measured calibration data to known BCS heat capacity using the effective volume of the sample as a fitting parameter. The fitted volume is 16 cm3, which falls between the free volume of the sample container, 15 cm3 and the total volume of the sample container, including the volume within the heat exchangers, 32 cm3.
We simultaneously monitor the position of the wire by picking up a high-frequency signal mixed in with the driving current using nearby coils. This method is not sensitive enough for measuring the drag force41, but together with the known wall-to-wall distance (≈10 mm) it calibrates the range of motion. Finally, we record the induced voltage across the wire with a four-point measurement. The induced voltage reveals whether the main AC resonance or some higher mode of oscillation is excited by the DC drive, allowing us to ensure that dissipation due to these modes was minimised during all measurements.
We access zero-temperature dissipation by moving the wire crossbar in two phases (Fig. 1). Each measurement starts from standstill long enough to remove any history dependence. The wire is then quickly accelerated to v, the velocity is kept constant for 0.5 mm distance, before decelerating back to zero. After time Δt, the ramp is repeated from this new starting location with either v (up ramp) or −v (down ramp). This allows subtracting the dissipation measured for up ramps Qup from that measured for down ramps Qdown, ΔQ = Qdown − Qup.
Ideally, both the trajectories would meet identical dissipation from the scattering of thermal quasiparticles in bulk. Subtracting the dissipation measured for up ramps Qup from that measured for down ramps Qdown would leave only the ABS contribution ΔQ = Qdown − Qup, which for long enough Δt is expected to be zero. In practice, the motion of the goalpost-shaped superconducting wire is hysteretic27 due to the motion of flux lines or some other dissipation in the superconducting wire. Flux line motion, for example, would be driven by variation of the current used for moving the wire in the magnetic field, or by the effective change of direction of the external magnetic field when the legs of the wire are bent42,43,44.
This dissipation is not seen in the temperature of the surrounding bolometer because the coupling of the phonons in the metallic wire to the superfluid is very weak due to the Kapitza resistance. However, the hysteretic motion has an indirect consequence for our measurements: the crossbar travels a shorter distance with down ramps than with up ramps, and as a result, scatters a different amount of ambient quasiparticles. Therefore, in the absence of other contributions, ΔQ < 0. Phenomenologically, the hysteretic contribution follows \(\Delta Q=a{(v/{v}_{{\rm{c}}})}^{1/2}\) (Fig. 4a, b), where a ∝ (ΔI)2 (Fig. 4c). That is, the force moving the wire is kept constant in all the measurements (for a given velocity v), and measurements were carried out in varying magnetic fields H. Fixing the force means that the change in the current passed through the wire ΔI ∝ 1/H, and therefore a ∝ (H)−2. A detailed study of the origin of this effect is beyond the scope of the present work.
Once the hysteretic contribution is subtracted, ΔQ = 0 when v ≤ 9 mm s−1 (Fig. 4b), corresponding to zero dissipation from the bound states. For velocities higher than 9 mm s−1 at Δt = 0, up ramps experience less dissipation than down ramps. In this region, we find that \(\Delta Q=b{((v-{v}_{{\rm{c}}})/{v}_{{\rm{c}}})}^{p}\) with p = 2.5 ± 0.5 and b ≈ 1.0 pJ. The data in Fig. 4d are fitted with fixed p = 2.5 in order to show that b has no magnetic field dependence. That is, all the field dependence is contained in parameter a, as expected. Lambert15 predicts that, in a planar geometry, the instantaneous flux of energy follows p = 5 when (v − vc)/vc is small, and p = 2 when (v − vc)/vc is large. Our measured value falls in the predicted range, but this calculation neglects the possibility that the bound quasiparticle reserve is completely exhausted, and is therefore not directly applicable to the DC measurements presented here.
Note that the measurement shown in Fig. 4 was obtained with 4He preplating, which changes the surface specularity and therefore, the bound-state spectrum. While this does not increase the obtained critical velocity, it is possible that p is different with no 4He. Detailed analysis of the velocity-dependence data obtained in DC measurements without 4He preplating is hindered by the coincidence that without 4He the signal becomes too small to resolve at low velocities. That is, 4He preplating makes the heat exchangers less efficient, which increases the signal. This allows us to access also velocities below vc, which is crucial for the above analysis owing to the hysteresis effect.
Data availability
All the data in this paper are available at https://doi.org/10.17635/lancaster/researchdata/356, including descriptions of the data sets.
References
Guénault, A. M. et al. Probing superfluid 4He with high-frequency nanomechanical resonators down to millikelvin temperatures. Phys. Rev. B 100, 020506 (2019).
Guénault, A. M. et al. Detecting a phonon flux in superfluid 4He by a nanomechanical resonator. Phys. Rev. B 101, 060503 (2020).
Dmitriev, V. V., Senin, A. A., Soldatov, A. A. & Yudin, A. N. Polar phase of superfluid 3He in anisotropic aerogel. Phys. Rev. Lett. 115, 165304 (2015).
Autti, S. et al. Observation of half-quantum vortices in topological superfluid 3He. Phys. Rev. Lett. 117, 255301 (2016).
Levitin, L. V. et al. Phase diagram of the topological superfluid 3He confined in a nanoscale slab geometry. Science 340, 841–844 (2013).
Silaev, M. A. Universal mechanism of dissipation in Fermi superfluids at ultralow temperatures. Phys. Rev. Lett. 108, 045303 (2012).
Mäkinen, J. T. & Eltsov, V. B. Mutual friction in superfluid 3He − B in the low-temperature regime. Phys. Rev. B 97, 014527 (2018).
Sauls, J. A. Andreev bound states and their signatures. Philos. Trans. R. Soc. A: Math., Phys. Eng. Sci. 376, 20180140 (2018).
Yefsah, T. et al. Heavy solitons in a fermionic superfluid. Nature 499, 426–430 (2013).
Wilczek, Frank Majorana returns. Nat. Phys. 5, 614–618 (2009).
Li, C. et al. 4π-periodic Andreev bound states in a Dirac semimetal. Nat. Mater. 17, 875–880 (2018).
Mourik, V., Zuo, K., Frolov, S. M., Plissard, S. R., Bakkers, E. P. A. M. & Kouwenhoven, L. P. Signatures of Majorana fermions in hybrid superconductor-semiconductor nanowire devices. Science 336, 1003–1007 (2012).
Landau, L. Theory of the superfluidity of helium II. Phys. Rev. 60, 356–358 (1941).
Bradley, D. I. et al. Breaking the superfluid speed limit in a fermionic condensate. Nat. Phys. 12, 1017–1021 (2016).
Lambert, C. J. Theory of pair breaking by vibrating macroscopic objects in superfluid 3He. Phys. B: Condens. Matter 178, 294–303 (1992).
Nagato, Y., Yamamoto, M. & Nagai, K. Rough surface effects on the p-wave Fermi superfluids. J. Low. Temp. Phys. 110, 1135–1171 (1998).
Nagai, K., Nagato, Y., Yamamoto, M. & Higashitani, S. Surface bound states in superfluid 3He. J. Phys. Soc. Jpn. 77, 111003 (2008).
Murakawa, S. et al. Surface Majorana cone of the superfluid 3He B phase. J. Phys. Soc. Jpn. 80, 013602 (2011).
Okuda, Y. & Nomura, R. Surface Andreev bound states of superfluid 3He and Majorana fermions. J. Phys. Condens. Matter 24, 343201 (2012).
Aoki, Y. et al. Observation of surface Andreev bound states of superfluid 3He by transverse acoustic impedance measurements. Phys. Rev. Lett. 95, 075301 (2005).
Zheng, P., Jiang, W. G., Barquist, C. S., Lee, Y. & Chan, H. B. Anomalous damping of a microelectromechanical oscillator in superfluid 3He-B. Phys. Rev. Lett. 117, 195301 (2016).
Kuorelahti, J. A., Laine, S. M. & Thuneberg, E. V. Models for supercritical motion in a superfluid Fermi liquid. Phys. Rev. B 98, 144512 (2018).
Blaauwgeers, R. et al. Quartz tuning fork: thermometer, pressure- and viscometer for helium liquids. J. Low. Temp. Phys. 146, 537–562 (2007).
Bäuerle, C., Bunkov, Y. M., Fisher, S. N. & Godfrin, H. Temperature scale and heat capacity of superfluid 3He-B in the 100μK range. Phys. Rev. B 57, 14381–14386 (1998).
Guénault, A. M., Keith, V., Kennedy, C. J., Mussett, S. G. & Pickett, G. R. The mechanical behavior of a vibrating wire in superfluid 3He-B in the ballistic limit. J. Low. Temp. Phys. 62, 511–523 (1986).
Castelijns, C. A. M., Coates, K. F., Guénault, A. M., Mussett, S. G. & Pickett, G. R. Landau critical velocity for a macroscopic object moving in superfluid 3He-B: evidence for gap suppression at a moving surface. Phys. Rev. Lett. 56, 69–72 (1986).
Zmeev, D. E. A method for driving an oscillator at a quasi-uniform velocity. J. Low. Temp. Phys. 175, 480–485 (2014).
Tholen, S. M. & Parpia, J. M. Effect of 4He on the surface scattering of 3He. Phys. Rev. B 47, 319–329 (1993).
Fomin, I. A. Analog of the Anderson theorem for the polar phase of liquid 3He in a nematic aerogel. J. Exp. Theor. Phys. 127, 933–938 (2018).
Keith, V. & Ward, M. G. A recipe for sintering submicron silver powders. Cryogenics 24, 249–250 (1984).
Carneiro, K., Passell, L., Thomlinson, W. & Taub, H. Neutron-diffraction study of the solid layers at the liquid-solid boundary in 4He films adsorbed on graphite. Phys. Rev. B 24, 1170–1176 (1981).
Autti, S. et al. Effect of boundary condition on Kapitza resistance between superfluid 3He-B and sintered metal. Phys. Rev. B 102, 064508 (2020).
Dmitriev, V. V., Soldatov, A. A. & Yudin, A. N. Effect of magnetic boundary conditions on superfluid 3He in nematic aerogel. Phys. Rev. Lett. 120, 075301 (2018).
Heikkinen, P. J. et al. Fragility of surface states in topological superfluid 3He. Preprint at http://arxiv.org/abs/1909.04210 (2019).
Ahonen, A. I. et al. Boundary magnetism in liquid 3He at very low temperatures. J. Phys. C: Solid State Phys. 9, 1665–1672 (1976).
Korniyenko, Y., Shevtsov, O. & Löfwander, T. Nonlinear response of a ballistic graphene transistor with an AC-driven gate: high harmonic generation and terahertz detection. Phys. Rev. B 94, 125445 (2016).
Nielsen, K. K., Camacho-Guardian, A., Bruun, G. M. & Pohl, T. Superfluid flow of polaron polaritons above Landau’s critical velocity. Phys. Rev. Lett. 125, 035301 (2020).
Yang, W. et al. Landau velocity for collective quantum Hall breakdown in bilayer graphene. Phys. Rev. Lett. 121, 136804 (2018).
Pickett, G. R. & Fisher, S. N. Superfluid 3He in the zero-temperature limit. Phys. B: Condens. Matter 329, 75–79 (2003).
Skyba, M. Critical Flow Velocity in Superfluid 3He-B PhD thesis, Lancaster Univ. (2016).
Bradley, D. I. et al. A new device for studying low or zero frequency mechanical motion at very low temperatures. J. Low. Temp. Phys. 165, 114–131 (2011).
Esquinazi, P., Setzer, A., Fuchs, D., Kopelevich, Y., Zeldov, E. & Assmann, C. Vortex avalanches in Nb thin films: global and local magnetization measurements. Phys. Rev. B 60, 12454–12461 (1999).
Kopelevich, Y. & Esquinazi, P. Second magnetization peak at low fields due to thermomagnetic flux-jump instability. J. Low. Temp. Phys. 113, 1–9 (1998).
Golovchanskiy, I. A. et al. Origin of magnetic flux-jumps in Nb films subject to mechanical vibrations and corresponding magnetic perturbations. Phys. Rev. B 97, 014524 (2018).
Acknowledgements
We thank Erkki Thuneberg and colleagues in Lancaster for stimulating discussions. This work was funded by UK EPSRC (Grant No. EP/P024203/1) and EU H2020 European Microkelvin Platform (Grant Agreement 824109). We acknowledge M.G. Ward and A. Stokes for their excellent technical support. S.A. acknowledges financial support from the Jenny and Antti Wihuri Foundation.
Author information
Authors and Affiliations
Contributions
The measurements and data analysis were carried out by S.A., S.L.A., A.J., M.P., R.S., V.T., J.V., A.A.S., T.W., A.J.W. and D.E.Z. Theoretical work, interpretation of the results, and background investigations were made by S.A., R.P.H., G.R.P., V.T. and D.E.Z. This paper was prepared by S.A., A.J. and D.E.Z., while all authors provided comments and clarifications.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks Mihail Silaev and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Autti, S., Ahlstrom, S.L., Haley, R.P. et al. Fundamental dissipation due to bound fermions in the zero-temperature limit. Nat Commun 11, 4742 (2020). https://doi.org/10.1038/s41467-020-18499-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-020-18499-1
This article is cited by
-
Kelvin–Helmholtz Instability in \(^3\)He Superfluids in Zero-Temperature Limit
Journal of Low Temperature Physics (2024)
-
Drag on Cylinders Moving in Superfluid \(^3\)He-B as the Dimension Spans the Coherence Length
Journal of Low Temperature Physics (2024)
-
Observation of suppressed viscosity in the normal state of 3He due to superfluid fluctuations
Nature Communications (2023)
-
Transport of bound quasiparticle states in a two-dimensional boundary superfluid
Nature Communications (2023)
-
Progress on Levitating a Sphere in Cryogenic Fluids
Journal of Low Temperature Physics (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.