Abstract
Practical quantum networks require low-loss and noise-resilient optical interconnects as well as non-Gaussian resources for entanglement distillation and distributed quantum computation. The latter could be provided by superconducting circuits but existing solutions to interface the microwave and optical domains lack either scalability or efficiency, and in most cases the conversion noise is not known. In this work we utilize the unique opportunities of silicon photonics, cavity optomechanics and superconducting circuits to demonstrate a fully integrated, coherent transducer interfacing the microwave X and the telecom S bands with a total (internal) bidirectional transduction efficiency of 1.2% (135%) at millikelvin temperatures. The coupling relies solely on the radiation pressure interaction mediated by the femtometer-scale motion of two silicon nanobeams reaching a Vπ as low as 16 μV for sub-nanowatt pump powers. Without the associated optomechanical gain, we achieve a total (internal) pure conversion efficiency of up to 0.019% (1.6%), relevant for future noise-free operation on this qubit-compatible platform.
Similar content being viewed by others
Introduction
Large scale quantum networks will facilitate the next level in quantum information technology, such as the internet did for classical communication, enabling, e.g., secure communication and distributed quantum computation1. Some of the most promising platforms to process quantum information locally, such as superconducting circuits2, spins in solids3, and quantum dots4, operate naturally in the gigahertz frequency range, but the long-distance transmission of gigahertz radiation is relatively lossy and not resilient to ambient noise. This limits the length of supercooled microwave waveguides in a realistic scenario to tens of meters5. In contrast, the transport of quantum information over distances of about 100 km is nowadays routinely achieved by sending optical photons at telecom frequency through optical fibers.
There is a variety of platforms, which in principle have shown to be able to merge the advantages of both worlds ranging from mechanical, piezoelectric, electro-optic, magneto-optic, rare-earth, and Rydberg atom implementations6,7. So far, the optomechanical approach8 has been proven to be most efficient, reaching a record high photon conversion efficiency of up to 47% with an added noise photon number of only 389. But this composite device is based on a Fabry–Perot cavity that has to be hand assembled and utilizes a membrane mode that is restricted to relatively low mechanical frequencies. Using piezo-electricity, coherent conversion between microwave and optical frequencies has been shown uni- and bidirectional at room temperature10,11, and at low temperatures12,13 with integrated devices, so far with either low efficiency or unspecified conversion noise properties. The electro-optic platform has shown promising photon conversion efficiencies14, recently up to 2% at 2 K15, but generally requires very large pump powers in the milliwatt range16.
In this work we present a device that converts coherent signals between 10.5 GHz and 198 THz at millikelvin temperatures via the radiation pressure interaction. Due to the need of only picowatt range pump powers, both the heat load to the cryostat and local heating of the integrated device is minimized. The chip-scale device is fabricated from CMOS compatible materials on a commercial silicon-on-insulator wafer over an area of ~200 μm × 120 μm. It is compact, versatile and fully compatible with silicon photonics17 and superconducting qubits18. The unique electro-opto-mechanical design is optimized for very strong field confinements and radiation pressure couplings, which enable internal efficiencies exceeding unity for ultra-low pump powers. We find that the conversion noise so far precludes a quantum limited operation and we present a comprehensive theoretical and experimental noise analysis to evaluate the potential for scalable and noise-free conversion in the future. Such a power-efficient, ultra-sensitive, and highly integrated hybrid interconnect might find applications ranging from quantum communication8 and RF receivers19 to magnetic resonance imaging20.
Results
Transducer theory
The transducer consists of one microwave resonator and one optical cavity, both parametrically coupled via the vacuum coupling rates g0,j with j = e, o to the same mechanical oscillator as shown in Fig. 1a and b. The intrinsic decay rate of the optical (microwave) resonator is κin,o (κin,e), while the optical (microwave) waveguide–resonator coupling is given by κex,o (κex,e) resulting in a total damping rate of κj = κin,j + κex,j and coupling ratios ηj = κex,j/κj. The mechanical oscillator with intrinsic decoherence rate γm and frequency ωm is shared between the optical cavity and the microwave resonator and acts as a bidirectional coherent pathway to convert the photons between the two different frequencies8,21,22,23. In the interaction frame, the Hamiltonian describing the conversion process is (see Supplementary Note 1):
where \({\hat{a}}_{\mathrm{j}}\), \((\hat{b})\) with j = e, o is the annihilator operator of the electromagnetic (mechanical) mode, and \({\hat{H}}_{{\rm{CR}},\mathrm{j}}=\hslash {G}_{\mathrm{j}}({\hat{a}}_{\mathrm{j}}\hat{b}\ {e}^{2i{\omega }_{{\rm{m}}}t}+\,\text{h.c.})\) describes the counter-rotating terms which are responsible for the coherent amplification of the signal. \({G}_{\mathrm{j}}=\sqrt{{n}_{{\rm{d}},\mathrm{j}}}{g}_{0,\mathrm{j}}\) is the parametrically enhanced electro- or optomechanical coupling rate where nd,j is the intracavity photon number due to the corresponding microwave and optical pump tones. For a red-detuned drive in the resolved-sideband regime 4ωm > κj we neglect \({\hat{H}}_{{\rm{CR}},\mathrm{j}}\) under the rotating-wave approximation and the Hamiltonian (1) represents a beam-splitter like interaction in which the mechanical resonator mediates noiseless photon conversion between microwave and optical modes. Note that near-unity photon conversion \({\zeta }_{{\rm{RS}}}=4{\eta }_{{\rm{e}}}{\eta }_{{\rm{o}}}{{\mathcal{C}}}_{{\rm{e}}}{{\mathcal{C}}}_{{\rm{o}}}/{(1+{{\mathcal{C}}}_{{\rm{e}}}+{{\mathcal{C}}}_{{\rm{o}}})}^{2}\) can be achieved in the limit of \({{\mathcal{C}}}_{{\rm{e}}}={{\mathcal{C}}}_{{\rm{o}}}\gg 1\) with \({{\mathcal{C}}}_{\mathrm{j}}=4{G}_{\mathrm{j}}^{2}/({\kappa }_{\mathrm{j}}{\gamma }_{{\rm{m}}})\) being the electro- or optomechanical cooperativity, as demonstrated between two optical24 and two microwave modes25,26, respectively.
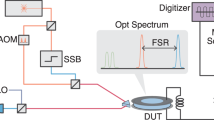
a Diagram showing the microwave \(({\hat{a}}_{{\rm{e}}})\), mechanical \((\hat{b})\), and optical \(({\hat{a}}_{{\rm{o}}})\) mode, and the relevant coupling and loss rates of the device. Scattering parameters Sij characterizing the transducer performance are indicated. b Schematic showing the frequencies of the coherent signals involved in the conversion process (green arrows). On the left an optical input signal (IS) is converted to an upper sideband (US) of the microwave pump signal, whereas in the microwave-to-optics conversion on the right also the lower sideband (LS) is created. The bidirectional transduction ζ is only evaluated between the upper sidebands at ωd,j + ωm. c Scanning electron micrograph of the device showing the microwave lumped element resonator with an inductively coupled feed line, the photonic crystal cavity, and the optical coupling waveguide fabricated on a fully suspended 220 nm thick silicon-on-insulator device layer. White scale bar, 10 μm. The inset shows an enlarged view of the central part (green boxed area) comprising the mechanically compliant vacuum gap capacitors of size ~70 nm and two optomechancial zipper cavities (top one unused) with a central tapered photonic crystal mirror coupled optical waveguide. White scale bar, 1 μm. d Finite-element method (FEM) simulation of the mechanical displacement ∣u∣ of the utilized mechanical resonance. e FEM simulation of the electric in-plane-field Ey(x, y) for the relevant optical mode. f Simplified experimental setup. The device is mounted on the mixing chamber plate of a cryogen-free dilution refrigerator at a temperature of Tfridge = 50 mK. A microwave switch selects between the incoming microwave and optical signal to be analyzed by the ESA. Optical heterodyning is used to detect the low power levels used in the experiment. SG microwave signal generator; ESA electronic spectrum analyzer; VOA variable optical attenuator; SSB EOM single-sideband electro-optic modulator; AOM acousto-optic modulator.
Transducer design
We realize conversion by connecting an optomechanical photonic crystal zipper cavity27 with two aluminum coated and mechanically compliant silicon nanostrings28 as shown in Fig. 1c. The mechanical coupling between these two components is carefully designed (see Supplementary Note 2), leading to a hybridization of their in-plane vibrational modes into symmetric and antisymmetric supermodes. In case of the antisymmetric mode that is used in this experiment, the strings and the photonic crystal beams vibrate 180° out of phase as shown by the finite-element method simulation in Fig. 1d. The photonic crystal cavity features two resonances at telecom frequencies with similar optomechanical coupling strength. The simulated spatial distribution of the electric field component Ey(x, y) of the higher frequency mode with lower loss rate used in the experiment is shown in Fig. 1e. The lumped element microwave resonator consists of an ultra-low stray capacitance planar spiral coil inductor29 and two mechanically compliant capacitors with a vacuum gap of size of ~70 nm. This resonator is inductively coupled to a shorted coplanar waveguide, which is used to send and retrieve microwave signals from the device. The sample is fabricated using a robust multi-step recipe including electron beam lithography, silicon etching, aluminum thin-film deposition, and hydrofluoric vapor acid etching, as described in detail in ref. 30.
Transducer characterization
Standard sample characterization (see Supplementary Notes 3 and 4) reveals an optical resonance frequency of ωo/(2π) = 198.081 THz with total loss rate κo/(2π) = 1.6 GHz and waveguide coupling rate κex,o/(2π) = 0.18 GHz leading to a coupling efficiency of ηo = 0.11. When the optical light is turned off, the microwave resonance frequency is ωe/(2π) = 10.5 GHz with coupling efficiency ηe = 0.4 and κex,e/(2π) = 1.15 MHz. The mechanical resonator frequency has a value of ωm/(2π) = 11.843 MHz with an intrinsic decoherence rate γm/(2π) = 15 Hz at a mode temperature of 150 mK. The achieved single-photon-phonon coupling rates are as high as g0,e/(2π) = 67 Hz and g0,o/(2π) = 0.66 MHz.
Conversion measurements
To perform coherent photon conversion, red-detuned microwave and optical tones with powers Pe(o) are applied to the microwave and the optical resonator. These drive tones establish the linearized electro- and optomechanical interactions, which results in the conversion of a weak microwave (optical) signal tone to the optical (microwave) domain measured in our setup as shown in Fig. 1f. We experimentally characterize the transducer efficiency by measuring the normalized reflection ∣Sjj∣2 (j = e, o) and the bidirectional transmission ζ : = ∣Seo∣∣Soe∣ coefficients as a function of signal detuning δj. As shown in Fig. 2a, for drive powers Pe = 601 pW and Po = 625 pW with drive frequencies ωd,j and detunings Δj = ωj − ωd,j of Δe = ωm and Δo/(2π) = 126 MHz leading to intracavity photon numbers of nd,e \(\approx\) 9 × 105 and nd,o \(\approx\) 0.2 with cooperativities \({{\mathcal{C}}}_{{\rm{e}}}\approx 0.57\) and \({{\mathcal{C}}}_{{\rm{o}}}\approx 0.9\), the measured total (waveguide to waveguide) photon transduction efficiency is \(\approx\)1.1% corresponding to 96.7% internal (resonator to resonator) photon transduction efficiency over the total bandwidth of Γconv/(2π) \(\approx\) 0.37 kHz. In the case of κo > 4ωm and κe < 4ωm, the bandwidth is given by \({\Gamma }_{{\rm{conv}}}\approx ({{\mathcal{C}}}_{{\rm{e}}}+1){\gamma }_{{\rm{m}}}\) because the nonsideband resolved optomechanical cavity does not induce mechanical broadening. The signal tone adds 17(10−3) photons to the microwave resonator (optical cavity).
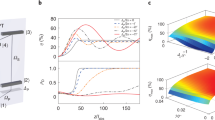
a The reflection ∣Sjj∣2 (j = e, o) and bidirectional transduction ζ: = ∣Seo∣∣Soe∣ parameters as a function of signal tone detuning δj = ω − (ωd,j + ωm) for fixed pump powers Pe = 601 pW and Po = 625 pW. The dots represent the experimental data while the solid lines show the theoretical prediction with γm as the only fit parameter. b Measured photon number transduction efficiency as a function of microwave and optical pump powers. c Measured transduction efficiency with respect to optical pump power for fixed Pe = 601 pW. d Measured transduction efficiency with respect to microwave pump power for fixed Po = 625 pW. In (c) and (d), the error bars are the standard deviation of three independent measurement runs and solid lines are theory with interpolated γm (from (f)) and no other free parameters. e The coupling efficiency of the microwave resonator to the waveguide ηe = κex,e/κe, extracted from broadband reflection measurements, as a function of optical (blue, Pe = 601 pW) and microwave (red, Po = 625 pW) pump tones. f Intrinsic mechanical decoherence rate γm versus optical (blue, Pe = 601 pW) and microwave (red, Po = 625 pW) pump powers extracted from (c) and (d) with Eq. (3) and γm as only fit parameter. Solid lines in (f) are linear fits to the data.
Here we use a self-calibrated measurement scheme that is independent of the gain and loss of the measurement lines as described in ref. 31 and we only take into account transduction between the upper two sidebands at ωd,j + ωm as shown in Fig. 1b. Neglecting the lower optical sideband that is generated due to the nonsideband resolved situation κo/4ωm \(\approx\) 30 reduces the reported mean bidirectional efficiencies by \(\sqrt{2}\) compared to the actually achieved total transduction efficiency between microwave and optical fields. The observed reflection peaks indicate that both resonators are undercoupled, equivalent to an impedance mismatch for incoming signal light. All scattering parameters are obtained from measured coherent tones whose linewidths are given by the chosen resolution bandwidth and the stability of the heterodyne setup. While this does not explicitly show long term phase stability of the conversion we find that these results are in excellent agreement with our coherent conversion theory model (solid lines) with γm as the only free fit parameter.
Figure 2b shows the total transduction efficiency for different pump power combinations with microwave and optical pump powers ranging from 30 to 953 pW and 48 to 1561 pW, respectively. Figure 2c, d shows the efficiency versus Po (Pe) for fixed microwave (optical) pump power Pe = 601 (Po = 625) pW. As expected, the transduction efficiency rises with increasing pump powers and reaches a maximum of ζ = 1.2%. The internal transduction efficiency is significantly higher (ζ/(ηoηe) ≤ 135%) because both the microwave resonator as well as the optical cavity are highly undercoupled with coupling ratios of ηo = 0.11 and ηe ranging between 0.07 and 0.18 when both pumps are on. The increase in the intrinsic loss rate of microwave κin,e and mechanical resonator γm at higher pump powers are shown in Fig. 2e and f caused by considerable heating related to (especially optical) photon absorption. This results in the degradation of the microwave and mechanical quality factors and consequently reduces the waveguide coupling efficiency, the cooperativities and the total transduction efficiency (see Supplementary Note 5).
Sideband resolution and amplification
In the nonsideband resolved limit the contribution of the counter-rotating term of the Hamiltonian \({\hat{H}}_{{\rm{CR}},{\rm{o}}}\) is nonnegligible, resulting in a transduction process that cannot be fully noise- free. This interesting effect can be correctly described by introducing an amplification of the signal tone with (in the absence of thermal noise) quantum limited gain \({{\mathcal{G}}}_{{\rm{o}}}\) (see Supplementary Note 1). In contrast, the microwave resonator is in the resolved-sideband condition 4ωm > κe, so that the signal tone amplification due to electromechanical interaction is negligible \({{\mathcal{G}}}_{{\rm{e}}}\simeq 1\). This results in the total, power independent, bidirectional conversion gain of \({\mathcal{G}}={{\mathcal{G}}}_{{\rm{e}}}{{\mathcal{G}}}_{{\rm{o}}}\simeq {{\mathcal{G}}}_{{\rm{o}}}\), which turns out to be directly related to the minimum reachable phonon occupation:
induced by optomechanical quantum backaction when the mechanical resonator is decoupled from its thermal bath32. Due to this amplification process the measured transduction efficiency in Fig. 2a is about 110 times larger than one would expect from a model that does not include gain effects for the chosen detuning, and adds the equivalent of at least one half of a vacuum noise photon to the input of the transducer in our case of heterodyne detection (for ηj = 1 and \({\mathcal{G}}\gg 1\)). However, it turns out that this noise limitation, which might in principle be overcome with efficient feedforward9, sideband suppression33,34, or sideband resolution35, accounts for only about 0.1% of the total conversion noise observed in our system. The total transduction (including gain) can be written in terms of the susceptibilities of the electromagnetic modes \({\chi }_{\mathrm{j}}^{-1}(\omega )=i({\Delta }_{\mathrm{j}}-\omega )+{\kappa }_{\mathrm{j}}/2\) and the mechanical resonator \({\chi }_{{\rm{m}}}^{-1}(\omega )=i({\omega }_{{\rm{m}}}-\omega )+{\gamma }_{{\rm{m}}}/2\) as:
where \(\tilde{{\chi }_{\mathrm{j}}}(\omega )={\chi }_{\mathrm{j}}{(-\omega )}^{* }\).
Equation (3) can be decomposed into a product of the conversion gain \({\mathcal{G}}\) and the pure conversion efficiency θ, i.e., \(\zeta :={\mathcal{G}}\times \theta\), for frequencies in the vicinity of ωm (see Supplementary Note 1). Equation (2) shows that the signal amplification depends only on the resonator linewidth and the detuning and is not directly related to the \(\propto {\hat{a}}^{\dagger }{\hat{b}}^{\dagger }\) interaction term or the pump power31. This can be understood by the alternative interpretation that the gain represents the ratio of the transduced upper sideband to the difference between upper and lower sideband at each cavity. Therefore, it is instructive to measure the transducer parameters as a function of optical pump detuning as shown in Fig. 3a. While changing the optical detuning, we also vary the pump power in order to keep the optical intracavity photon number constant at nd,o = 0.185 ± 0.015. This way it is possible to investigate the influence of Δo at a constant optomechanical coupling \({G}_{{\rm{o}}}={g}_{{\rm{0,o}}}\sqrt{{n}_{{\rm{d}},{\rm{o}}}}\). The measured total transduction efficiency is shown in Fig. 3a and reaches ζ\(\,\approx\,\)1% at Δo \(\approx\) 0 for the chosen pump powers in agreement with Fig. 2c, d. We can now separate the measured transduction (Eq. (3)) into conversion gain and pure conversion, as shown in Fig. 3b. The gain shows the expected steep increase at Δo → 0 where the pure conversion θ approaches zero for equal cooling and amplification rates. Around Δo = κo/2 on the other hand, where \({\langle n\rangle }_{\min }\) reaches its minimum of roughly κo/4ωm \(\approx\) 30, also the gain reaches its minimum and the noiseless part (at zero temperature) of the total (internal) conversion process shows its highest efficiency of θ = 0.019% (θ/(ηeηo) = 1.6%).
a Measured total transduction efficiency ζ: = ∣Seo∣∣Soe∣ with respect to pump detuning Δo of the nonsideband resolved optical cavity for a constant intracavity photon number nd,o = 0.185. b Pure and—in the absence of thermal noise—noiseless conversion θ (green dots) as well as the total conversion gain \({\mathcal{G}}\) (blue dots) that gives rise to amplified vacuum noise. θ is extracted from (a) by dividing the measured total transduction by the calculated gain using Supplementary Eqs. (16) and (17). While \({{\mathcal{G}}}_{{\rm{o}}}\) diverges for Δo → 0, the optomechanical damping rate drops to zero and leads to a vanishing pure conversion θ. The arrows in both panels indicate the detuning used in Figs. 2 and 4.
Added noise
Another important figure of merit, not only for quantum applications, is the amount of added noise quanta36, usually an effective number referenced to the input of the device. For clarity with regards to the physical origin and the actual measurement of the noise power, in the following we define the total amount of added noise quanta nadd,j added to the input signal Sin,j after the transduction process as Sout,j = ζSin,j + nadd,j. Figure 4a, b shows the measured conversion noise nadd,j as a function of frequency δj for the same powers and detunings as in Fig. 2a. At these powers our device adds nadd,o(e) = 224(145) noise quanta to the output of the microwave resonator (optical cavity), corresponding to an effective input noise of nadd,j/ζ. The noise floor originates from the calibrated measurement system and in case of the microwave port to a small part also from an additional broadband resonator noise, cf. Fig. 4b. The solid lines are fits to the theory with the mechanical bath occupation \({\bar{n}}_{{\rm{m}}}\) as the only fit parameter (see Supplementary Note 4).
The fitted effective mechanical bath temperature as a function of pump powers is shown in Fig. 4c. It reveals the strong optical pump dependent mechanical mode heating (blue), while the microwave pump (red) has a negligible influence on the mechanical bath. Fig. 4d shows the measured total added noise at the output of the microwave resonator and optical cavity as a function of optical pump power. The noise added to the optical output (blue) increases with pump power due to absorption heating and increasing optomechanical coupling rate Go, while the degradation of the resonator-waveguide coupling efficiency ηe explains the decreasing nadd,e at higher optical powers for the microwave output noise (red), see Fig. 2e. The intersection of the two noise curves occurs at \({{\mathcal{C}}}_{{\rm{e}}}\simeq {{\mathcal{C}}}_{{\rm{o}}}\) with cooperativities Cj as defined above, and shows that the optical and microwave resonators share the same mechanical thermal bath. The power dependence is in full agreement with theory (solid lines) and demonstrates that the thermal mechanical population is the dominating origin of the added transducer noise.
Measured noise spectra at the device output for the optical cavity (a) and the microwave resonator (b) as a function of the signal tone detuning δj = ω − (ωd,j + ωm) at fixed pump powers Pe = 601 pW and Po = 625 pW in units of added noise quanta. a The dark blue region represents the two-quadrature noise added by the optical measurement chain; the light blue region indicates the thermal mechanical noise added to the converted optical output signal. b Bottom light red region represents the two-quadrature background noise from the microwave measurement chain. The central dark red region indicates a small amount of broadband resonator noise and the light blue region the transduction noise due to the thermal population of the mechanical mode. In both panels, fits to one common mechanical bath nm are shown in black. c Mechanical bath temperature Tm,bath extracted as only fit parameter from fits to the measured output noise as in (a) and (b) with respect to optical (blue dots, Pe = 601 pW) and microwave (red dots, Po = 625 ± 19 pW) pump power. Black lines show fits to the data with the logarithmic growth function \(T_{\mathrm{m,bath}}=0.18\ {\mathrm{log}\,}_{{\rm{e}}}({P}_{{\rm{o}}})-0.47\) and Tm,bath = 0.70 K respectively. The dashed line indicates the thermalized mechanical mode temperature Tsample when both pumps are off. d Microwave (red, nadd,e) and optical (blue, nadd,o) added noise photons at the output with respect to optical pump power (Pe = 601 pW). The full theory based on an interpolation of Tm,bath from (c) is shown as black lines.
Discussion
In conclusion, we demonstrated an efficient bidirectional and chip-scale microwave-to-optics transducer using pump powers orders of magnitude lower than comparable all-integrated11,13,15 approaches. Low pump powers are desired to limit the heat load of the cryostat and to minimize on-chip heating, which is particularly important for integrated devices because of their limited heat dissipation at millikelvin temperatures. Due to the standard material choice involving only silicon and aluminum, our device can be easily integrated with other elements of superconducting circuits as well as silicon photonic and phononic devices in the future.
The two main challenges ahead are the reduced pure conversion efficiency and the optical heating that adds incoherent noise to the converted signal. We expect that both can be solved with design improvements in combination with new measurement techniques. Specifically, starting from the observed pure efficiency of 0.019% a factor of up to nearly two orders of magnitude could be gained with better waveguide coupling geometries in combination with fabrication optimization, e.g., by using surface cleaning and the reduction of humidity37. Improving the sideband resolution by increasing the mechanical frequency35 could yield another factor of up to 25 assuming the same cooperativities can be achieved. Going to the high cooperativity limit would then yield the remaining fraction needed for unity total conversion efficiency. This will certainly require a very effective mitigation of the optical pump power dependent mechanical heating and the associated linewidth degradation that is also required for noise-free conversion. Nevertheless, with better chip thermalization, reduced optical absorption and low duty cycle pulsed measurements this should be feasible. Moreover, it has already been shown that pulsed pump-probe type experiments together with high efficiency heralding measurements can be used for postselecting rare successful conversion or entanglement generation events for low-noise low-efficiency devices12,38.
In terms of near-term classical receiver and modulation applications, an important figure of merit is the voltage required to induce an optical phase shift of π. We are able to reach a value as low as Vπ = 16 μV (see Supplementary Note 6), comparable with typical zero point fluctuations in superconducting circuits, nearly a factor 9 lower than the previously reported record19, and almost 1012 times more power efficient than commercial passive and wide-band unidirectional electro-optic modulators at X band gigahertz frequencies.
Data availability
The data and code used to produce the results of this paper are available at https://doi.org/10.5281/zenodo.3961562.
Change history
01 October 2020
An amendment to this paper has been published and can be accessed via a link at the top of the paper.
09 October 2020
The original version of this Article was updated shortly after publication following an error that resulted in the ORCID ID of A. Rueda being incorrectly assigned to F Hassani.
References
Kimble, H. J. The quantum internet. Nature 453, 1023–1030 (2008).
Blais, A., Huang, R.-S., Wallraff, A., Girvin, S. M. & Schoelkopf, R. J. Cavity quantum electrodynamics for superconducting electrical circuits: an architecture for quantum computation. Phys. Rev. A 69, 062320 (2004).
Awschalom, D. D., Hanson, R., Wrachtrup, J. & Zhou, B. B. Quantum technologies with optically interfaced solid-state spins. Nat. Photon. 12, 516–527 (2018).
Burkard, G., Gullans, M. J., Mi, X. & Petta, J. R. Superconductor-semiconductor hybrid-circuit quantum electrodynamics. Nat. Rev. Phys. 2, 129–140 (2020).
Kurpiers, P., Walter, T., Magnard, P., Salathe, Y. & Wallraff, A. Characterizing the attenuation of coaxial and rectangular microwave-frequency waveguides at cryogenic temperatures. EPJ Quantum Technol. 4, 8 (2017).
Lambert, N. J., Rueda, A., Sedlmeir, F. & Schwefel, H. G. L. Quantum information technologies: coherent conversion between microwave and optical photons—an overview of physical implementations. Adv. Quantum Technol. 3, 2070011 (2020).
Lauk, N. et al. Perspectives on quantum transduction. Quantum Sci. Technol. 5, 020501 (2020).
Stannigel, K., Rabl, P., Sørensen, A. S., Zoller, P. & Lukin, M. D. Optomechanical transducers for long-distance quantum communication. Phys. Rev. Lett. 105, 220501 (2010).
Higginbotham, A. P. et al. Harnessing electro-optic correlations in an efficient mechanical converter. Nat. Phys. 14, 1038–1042 (2018).
Vainsencher, A., Satzinger, K. J., Peairs, G. A. & Cleland, A. N. Bi-directional conversion between microwave and optical frequencies in a piezoelectric optomechanical device. Appl. Phys. Lett. 109, 033107 (2016).
Jiang, W. et al. Efficient bidirectional piezo-optomechanical transduction between microwave and optical frequency. Nat. Commun. 11, 1166 (2020).
Forsch, M. et al. Microwave-to-optics conversion using a mechanical oscillator in its quantum ground state. Nat. Phys. 16, 69–74 (2020).
Han, X. et al. Cavity piezo-mechanics for superconducting-nanophotonic quantum interface. Nat. Commun. 11, 3237 (2020).
Rueda, A. et al. Efficient microwave to optical photon conversion: an electro-optical realization. Optica 3, 597–604 (2016).
Fan, L. et al. Superconducting cavity electro-optics: a platform for coherent photon conversion between superconducting and photonic circuits. Sci. Adv. 4, eaar4994 (2018).
Hease, W. et al. Cavity quantum electro-optics: microwave-telecom conversion in the quantum ground state. arXiv (2020). https://arxiv.org/abs/2005.12763v1.
Safavi-Naeini, A. H., Van Thourhout, D., Baets, R. & Van Laer, R. Controlling phonons and photons at the wavelength scale: integrated photonics meets integrated phononics. Optica 6, 213–232 (2019).
Keller, A. J. et al. Al transmon qubits on silicon-on-insulator for quantum device integration. Appl. Phys. Lett. 111, 042603 (2017).
Bagci, T. et al. Optical detection of radio waves through a nanomechanical transducer. Nature 507, 81–85 (2014).
Simonsen, A. et al. Magnetic resonance imaging with optical preamplification and detection. Sci. Rep. 9, 18173 (2019).
Regal, C. A. & Lehnert, K. W. From cavity electromechanics to cavity optomechanics. J. Phys.: Conf. Ser. 264, 012025 (2011).
Safavi-Naeini, A. H. & Painter, O. Proposal for an optomechanical traveling wave phonon-photon translator. New J. Phys. 13, 013017 (2011).
Barzanjeh, S., Abdi, M., Milburn, G. J., Tombesi, P. & Vitali, D. Reversible optical-to-microwave quantum interface. Phys. Rev. Lett. 109, 130503 (2012).
Hill, J. T., Safavi-Naeini, A. H., Chan, J. & Painter, O. Coherent optical wavelength conversion via cavity optomechanics. Nat. Commun. 3, 1196 (2012).
Lecocq, F., Clark, J. B., Simmonds, R. W., Aumentado, J. & Teufel, J. D. Mechanically mediated microwave frequency conversion in the quantum regime. Phys. Rev. Lett. 116, 043601 (2016).
Fink, J. M., Kalaee, M., Norte, R., Pitanti, A. & Painter, O. Efficient microwave frequency conversion mediated by a photonics compatible silicon nitride nanobeam oscillator. Quantum Sci. Technol. 5, 034011 (2020).
Safavi-Naeini, A. H. et al. Squeezed light from a silicon micromechanical resonator. Nature 500, 185–189 (2013).
Barzanjeh, S. et al. Stationary entangled radiation from micromechanical motion. Nature 570, 480–483 (2019).
Peruzzo, M., Trioni, A., Hassani, F., Zemlicka, M. & Fink, J. M. Surpassing the resistance quantum with a geometric superinductor. arXiv (2020). https://arxiv.org/abs/2007.01644.
Dieterle, P. B., Kalaee, M., Fink, J. M. & Painter, O. Superconducting cavity electromechanics on a silicon-on-insulator platform. Phys. Rev. Appl. 6, 014013 (2016).
Andrews, R. W. et al. Bidirectional and efficient conversion between microwave and optical light. Nat. Phys. 10, 321–326 (2014).
Aspelmeyer, M., Kippenberg, T. J. & Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 86, 1391–1452 (2014).
Asjad, M., Zippilli, S. & Vitali, D. Suppression of stokes scattering and improved optomechanical cooling with squeezed light. Phys. Rev. A 94, 051801 (2016).
Lau, H.-K. & Clerk, A. A. Ground-state cooling and high-fidelity quantum transduction via parametrically driven bad-cavity optomechanics. Phys. Rev. Lett. 124, 103602 (2020).
Kalaee, M. et al. Quantum electromechanics of a hypersonic crystal. Nat. Nanotechnol. 14, 334–339 (2019).
Zeuthen, E., Schliesser, A., Sørensen, A. S. & Taylor, J. M. Figures of merit for quantum transducers. Quantum Sci. Technol. 5, 034009 (2020).
Sekoguchi, H., Takahashi, Y., Asano, T. & Noda, S. Photonic crystal nanocavity with a Q-factor of 9 million. Opt. Express 22, 916–924 (2014).
Zhong, C. et al. Proposal for heralded generation and detection of entangled microwave–optical-photon pairs. Phys. Rev. Lett. 124, 010511 (2020).
Acknowledgements
We thank Yuan Chen for performing supplementary FEM simulations and Andrew Higginbotham, Ralf Riedinger, Sungkun Hong, and Lorenzo Magrini for valuable discussions. This work was supported by IST Austria, the IST nanofabrication facility (NFF), the European Union’s Horizon 2020 research and innovation program under grant agreement no. 732894 (FET Proactive HOT) and the European Research Council under grant agreement no. 758053 (ERC StG QUNNECT). G.A. is the recipient of a DOC fellowship of the Austrian Academy of Sciences at IST Austria. W.H. is the recipient of an ISTplus postdoctoral fellowship with funding from the European Union’s Horizon 2020 research and innovation program under the Marie Sklodowska-Curie grant agreement no. 754411. J.M.F. acknowledges support from the Austrian Science Fund (FWF) through BeyondC (F71), a NOMIS foundation research grant, and the EU’s Horizon 2020 research and innovation program under grant agreement no. 862644 (FET Open QUARTET).
Author information
Authors and Affiliations
Contributions
G.A., M.W., and S.B. performed and analyzed the measurements. S.B. and G.A. contributed to the theoretical model. G.A. designed the transducer device. M.W., G.A., A.R., and W.H. built the experimental setup. M.W., E.R., and G.A. contributed to sample fabrication. F.H. tapered optical fibers used for optomechanical characterization tests. G.A., M.W., S.B., and J.M.F. wrote the paper. J.M.F. supervised the research.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Arnold, G., Wulf, M., Barzanjeh, S. et al. Converting microwave and telecom photons with a silicon photonic nanomechanical interface. Nat Commun 11, 4460 (2020). https://doi.org/10.1038/s41467-020-18269-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-020-18269-z
This article is cited by
-
Wideband coherent microwave conversion via magnon nonlinearity in a hybrid quantum system
npj Spintronics (2024)
-
An integrated microwave-to-optics interface for scalable quantum computing
Nature Nanotechnology (2024)
-
Coherent optical coupling to surface acoustic wave devices
Nature Communications (2024)
-
Active-feedback quantum control of an integrated low-frequency mechanical resonator
Nature Communications (2023)
-
Quantum-enabled operation of a microwave-optical interface
Nature Communications (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.