Abstract
The optical properties of monolayer and bilayer transition metal dichalcogenide semiconductors are governed by excitons in different spin and valley configurations, providing versatile aspects for van der Waals heterostructures and devices. Here, we present experimental and theoretical studies of exciton energy splittings in external magnetic field in neutral and charged WSe2 monolayer and bilayer crystals embedded in a field effect device for active doping control. We develop theoretical methods to calculate the exciton g-factors from first principles for all possible spin-valley configurations of excitons in monolayer and bilayer WSe2 including valley-indirect excitons. Our theoretical and experimental findings shed light on some of the characteristic photoluminescence peaks observed for monolayer and bilayer WSe2. In more general terms, the theoretical aspects of our work provide additional means for the characterization of single and few-layer transition metal dichalcogenides, as well as their heterostructures, in the presence of external magnetic fields.
Similar content being viewed by others
Introduction
Monolayer (ML) and bilayer (BL) transition metal dichalcogenides (TMDs) such as WSe2 represent semiconductor building blocks for novel van der Waals heterostructures. By virtue of sizable light–matter coupling governed by excitons1, they exhibit versatile potential for applications in photonics and optoelectronics2,3, opto-valleytronics4,5, and polaritonics6. Most recently, the optical interface to TMDs has been instrumental for the observation of strongly correlated electron phenomena in twisted homobilayer and heterobilayer moiré systems7,8,9.
The key to further developments of van der Waals heterostructures for fundamental studies and practical devices using TMD MLs and BLs is the detailed understanding of their optical properties. While substantial understanding of zero-momentum excitons in ML and BL WSe2 has been established1, some important aspects remain subject of debate10. This holds, in particular, for valley-dark excitons with finite center-of-mass momentum that escape direct optical probes by virtue of momentum mismatch with photons. In MLs, they complement the notion of intravalley spin-bright and spin-dark excitons1, and they entirely dominate the photoluminescence (PL) from the lowest-energy states in native homobilayers of WSe2 (ref. 11).
Within the realm of optical spectroscopy techniques, magneto-spectroscopy provides means for studying the exciton spin and valley degrees of freedom. Magneto-luminescence experiments on ML WSe2 in the presence of out-of-plane and in-plane magnetic fields, for instance, have been used to quantify the valley Zeeman splitting of bright excitons12,13,14,15,16,17 or to brighten spin-dark excitons18,19,20, respectively. To date, however, a rigorous assignment of exciton g-factors to intervalley excitons with finite momentum falls short mainly due to the lack of theoretical predictions10.
In this work, we develop theoretical methods to evaluate g-factors for excitons in different spin and valley configurations, and provide explicit values for WSe2 ML and BL excitons composed from electron and hole states away from high symmetry points of the first Brillouin zone. Our calculations go beyond the existing tight-binding models by employing the density functional theory (DFT). We compare our theoretical results with experimentally determined g-factors of intravalley excitons and use them to interpret ambiguous peaks in the PL spectra of ML and BL WSe2 attributed to intervalley excitons. The technique can be expanded to other materials like WS2 with similarly complex spectra21 and large g-factors of ML17 and BL22 excitons.
Results
Magneto-luminescence spectroscopy of charge-controlled ML and BL WSe2
In our experiments, we used a field-effect heterostructure based on an exfoliated WSe2 crystal with extended ML and BL regions encapsulated in hexagonal boron nitride (hBN). The device layout is shown schematically in Fig. 1a (see the Methods section for details) and the first Brillouin zone of ML and BL WSe2 with most relevant points in Fig. 1b. The sample was cooled down to 3.2 K, and the PL was probed as a function of voltage-controlled doping with laser excitation at 1.85 eV and powers below the regimes of neutral and charged biexcitons23,24,25,26. Magneto-luminescence experiments were performed in Faraday configuration with a bi-directional solenoid at magnetic fields of up to 9 T (see the Methods section for experimental details).
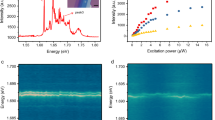
a Schematics of the field-effect device with monolayer and bilayer WSe2 encapsulated in hBN. b First Brillouin zone with high symmetry points. c, d Logarithmic false-color plots of the photoluminescence as a function of the gate voltage, recorded at representative positions of monolayer and bilayer WSe2, respectively. The monolayer features characteristic photoluminescence of neutral bright (X0) and dark (D0) excitons, as well as the negatively charged bright trion doublet (\({X}_{1}^{-}\) and \({X}_{2}^{-}\)) and dark trion (D−). All other peaks of monolayer (M) and bilayer (B) photoluminescence are labeled according to their charge state in the superscript and an increasing subscript number.
The evolution of the PL with the gate voltage is shown in Fig. 1c, d for representative spots of ML and BL regions, respectively. In Fig. 1c, the ML reaches the intrinsic limit at gate voltages <−5 V consistent with residual n-doping of the exfoliated crystal27,28. The neutral regime is characterized by the bright exciton PL (X0) at 1.72 eV and a series of red-shifted peaks that we label as \({M}_{1}^{0}\), \({M}_{2}^{0}\), and \({M}_{3}^{0}\). None of these peaks with respective red-shifts of 35, 60 and 75 meV from the bright exciton peak is to be attributed to the PL of dark excitons (D0) with 42 meV red-shift20,29,30. In our sample, this feature is a rather weak shoulder at the low-energy side of \({M}_{1}^{0}\). At positive gate voltages, the ML is charged with electrons and thus exhibits the characteristic signatures of a bright trion doublet (\({X}_{1}^{-}\) and \({X}_{2}^{-}\)) split by the exchange energy of ~6 meV (ref. 28), the dark trion (D−) at 28 meV red-shift from \({X}_{1}^{-}\) (refs. 31,32,33,34), and a series of low-energy peaks dominated by the peak \({M}_{1}^{-}\) at 44 meV red-shift33,34.
The PL from the BL region in Fig. 1d is characterized by a multi-peak structure, >100 meV below X0. It exhibits the same limits of charge neutrality and electron doping as a function of the gate voltage, consistent with the charging behavior of the ML in Fig. 1c. The BL peaks, labeled by an increasing subscript number with decreasing peak energy as \({B}_{1}^{0}\) through \({B}_{3}^{0}\) and \({B}_{1}^{-}\) through \({B}_{3}^{-}\) in the neutral and negative regime, respectively, correspond to phonon sidebands of neutral and charged momentum-indirect excitons with a global red-shift of 22 meV at about −7 V (ref. 11) in Fig. 1d. According to the single-particle band structure of BL WSe2 (refs. 35,36), the field-induced electron concentration is accommodated at the conduction band edge by the six inequivalent Q-valleys. However, the nature of the hole states that constitute the lowest-energy momentum-dark excitons as long-lived reservoirs of phonon-assisted PL remains ambiguous. The energetic proximity of the valance band edge states at K and Γ in BL WSe2 (ref. 37) renders QK and QΓ excitons and trions (composed from electrons at Q and holes at K or Γ) nearly degenerate, which in turn complicates their energetic ordering11.
To examine the origin of the BL peaks and to shed light on the nature of ML peaks with ambiguous or partly controversial interpretation, we performed magneto-spectroscopy in the two well-defined limits of charge neutrality and negative doping. The external magnetic field B was applied along the z-axis perpendicular to the sample. It removes the valley degeneracy and splits the exciton reservoirs by their characteristic Zeeman energies proportional to the exciton g-factor in WSe2 (refs. 12,13,14,15,16,17). The respective polarization-contrasting spectra recorded at −8 T under linearly polarized excitation (π) and circularly polarized detection (σ+ and σ−) for the neutral (negatively charged) ML and BL are shown in the top (bottom) panel of Fig. 2a, b.
a, b Photoluminescence spectra of monolayer and bilayer WSe2, respectively, in a perpendicular magnetic field of −8 T. The neutral and negatively charged regimes are shown in the top and bottom panels, respectively. The spectra were recorded with linearly polarized excitation (π) and circularly polarized detection (σ+ and σ−).
At each magnetic field, we quantified the experimental Zeeman splitting for every PL peak as the energy difference Δ = E+ − E− between the peak energies E+ and E− recorded under σ+ and σ− polarized detection. The left and right panels of Fig. 3a, b show Δ as a function of the magnetic field for all peaks of the neutral and negatively charged ML and BL, respectively. The set of data derived from magneto-PL measurements was complemented for X0, \({X}_{1}^{-}\), and \({X}_{2}^{-}\) by performing magneto-reflectivity under circular excitation and detection. The corresponding experimental exciton g-factors, obtained from Δ = gμBB as the slopes of best linear fits to the data in Fig. 3 scaled by the Bohr magneton μB, are summarized in Table 1. The negative sign of the g-factors reflects the energy ordering of exciton states that exhibit higher (lower) energy for σ− (σ+) polarized PL peaks at positive magnetic fields.
a, b Valley Zeeman splitting Δ as a function of the magnetic field for the photoluminescence peaks (closed circles) of monolayer and bilayer WSe2 in the neutral (left panel) and negatively charged (right panel) regimes. Complementary data (open circles) were obtained from polarization-resolved reflectivity.
In ML WSe2, the g-factors of both neutral and negatively charged excitons with the corresponding PL peaks X0, D0, \({X}_{1}^{-}\), \({X}_{2}^{-}\), and D− have been established in previous experiments on a wide range of different samples12,13,14,15,16,17,18,19,20,31,32,33,34. Our results for the bright exciton and the trion doublet in Table 1 agree well with these reports if we discard the magneto-luminescence result for \({X}_{1}^{-}\) that is compromised by both a vanishingly small PL intensity at high magnetic fields and the relatively broad linewidth of 6 meV in our sample. Due to this inhomogeneous broadening, we are unable to track the dispersion of the relatively weak spin-dark exciton peak D0, with g-factors ranging between 9.1 and 9.9 in previous reports20,31,33,34 nor its chiral-phonon replicum with the same g-factor at 65 meV red-shift from X0 (refs. 33,34,38). The signature of the latter is overwhelmed in our spectra by the peak \({M}_{2}^{0}\) with 60 meV red-shift and a g-factor of −12.9 ± 0.7 in agreement with values reported from samples with spectrally narrow PL33,34. The red-most peak \({M}_{3}^{0}\) features the same g-factor within the experimental error bars as \({M}_{1}^{0}\), suggesting a joint reservoir as their origin. The negatively charged trion D− was reported to have the same g-factor as its neutral counterpart31,32,33,34, whereas we determine −12.2 ± 0.1. The agreement with previous reports is better for the peak \({M}_{1}^{-}\) with a g-factor of −9.0 ± 0.1 that is supposed to be a phonon sideband of D− (refs. 33,34). The latter studies also reported an intense PL peak between \({M}_{1}^{-}\) and D− with a remarkably small g-factor of −4.1 (ref. 33) and −3.4 (ref. 34). This peak of unidentified origin is missing in our spectra from the negative doping regime.
There are other peaks in ML WSe2 without conclusive assignment, and in particular \({M}_{1}^{0}\) has received controversial interpretation as phonon-assisted PL from virtual trions39, phonon sidebands of momentum-dark Q-excitons21, or zero-phonon PL of finite-momentum excitons in spin-like configuration34 that we denote as \({K}_{L}^{\prime}\). Due to the lack of theory for the g-factors of excitons with finite center-of-mass momentum, the task of confronting the competing hypotheses with the characteristic valley Zeeman splittings of controversial ML peaks has remained elusive. The same shortcoming holds for both neutral and charged BL excitons with finite center-of-mass momentum. To shed additional light on the nature of PL peaks in both ML and BL WSe2, we calculate in the following the g-factors for excitons in different spin and valley configurations from DFT.
Ab initio calculations of exciton g-factors
We consider a crystal electron in a Bloch state \({\psi }_{n{\bf{k}}}({\bf{r}})={S}^{-1/2}\exp ({\rm{i}}{\bf{kr}}){u}_{n{\bf{k}}}({\bf{r}})\) with energy Enk, where n is the band number, k is the wave vector, unk(r) is the periodic Bloch amplitude, and S is the normalization area. In the presence of a weak perturbation by a static magnetic field B, the first-order correction to the electron energy is proportional to B and given by40:
where μB = ∣e∣ℏ/(2m0c) is the Bohr magneton, e and m0 are the charge and mass of the free electron, ℏ is the Planck constant, and c is the speed of light. The expression in square brackets is usually called the effective magnetic moment41,42, which contains both spin and orbital contributions. In particular, the first term is proportional to the free electron Landé factor g0 ≃ 2 and the spin angular momentum s = σ/2, where σ denotes the Pauli matrix.
The second term, \({{\bf{L}}}_{n}({\bf{k}})=\left\langle {\psi }_{n{\bf{k}}}({\bf{r}})\right|{\bf{L}}\left|{\psi }_{n{\bf{k}}}({\bf{r}})\right\rangle\), is the orbital angular momentum with the operator L = ℏ−1[r × p]. To obtain its matrix elements, one can reduce the calculation to the interband matrix elements of the space coordinate operator r14,41,42,43:
where m is the sum over all bands with energy Enk but the band of interest, and \({{\boldsymbol{\xi }}}_{nm}({\bf{k}})={\rm{i}}\left\langle {u}_{n{\bf{k}}}({\bf{r}})\right|\partial /\partial {\bf{k}}\left|{u}_{m{\bf{k}}}({\bf{r}})\right\rangle\) is the interband matrix element of the crystal coordinate operator.
In the following, we restrict our analysis to the orientation of the magnetic field along the z-axis and define the electron Zeeman splitting as the difference between the energy of the electron state with wave vector +k and spin projection +s along the z-axis and the state with −k and −s as:
Thus the electron g-factor of Bloch electrons in the nth band can be written as:
with +(−) for s = +1/2 (−1/2) corresponding to spin up (down) projections along z denoted as ↑ (↓), and the explicit expression for the z-component of the orbital angular momentum:
where \({\xi }_{mn}^{(\pm )}=({\xi }_{mn}^{(x)}\pm {\rm{i}}{\xi }_{mn}^{(y)})/\sqrt{2}\).
To calculate the contributions of the conduction (c) band electron with kc, sc and the hole (h) with kh, sh to the exciton g-factor, we neglect electron–hole Coulomb interactions14,44. In this case, the exciton Zeeman splitting simplifies to the sum of the Zeeman splittings of the electron and the hole. Using time reversal symmetry that relates the spin and wave vector of the hole to the corresponding spin and wave vector of the empty electron state in the valence (v) band (sh = −sv and kh =−kv), we obtain the exciton g-factor as
Finally, by reference to the valence band electron with kv = K or Γ with spin-up projection sv = +1/2, we discriminate spin-like (L) excitons (with sc = sv) from spin-unlike (U) excitons (with sc = −sv). Their respective exciton g-factors are given by:
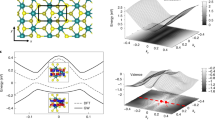
Using Eqs. (7) and (8), we calculate in the following the exciton g-factors from the orbital angular momenta Lc(kc) and Lv(kv) of conduction and valence bands obtained from Eq. (5) within DFT calculations on the Γ-centered \(\overrightarrow{k}\) grid of 12 × 12 divisions with 300 (600) bands (see the Methods section for details of DFT calculations). In Fig. 4a, b, we show the convergence of the orbital angular momenta Ln(k) within our ML and BL calculations as a function of the number of bands taken into account in the sum of Eq. (5). For the ML, Fig. 4a shows the results for the top-most valence band state v at K (blue solid line) and the highest valence band state v at Γ (gray solid line), as well as the two lowest conduction band states c and c + 1 at K and Q (red and black solid and dashed lines). As the BL bands are doubly degenerate, each k-point of the Brillouin zone has at least two bands with Ln(k) = Ln+1(k) or Ln(k) = Ln−1(k). For the BL in Fig. 4b, we consider the same k-points as for the ML and show the corresponding bands where the orbital angular momenta have the same sign as in the ML case of Fig. 4a.
For the orbital angular momenta of these states, convergence is observed above 275 and 550 bands in the case of ML and BL in Fig. 4a, b, respectively, with the factor of two difference related to the doubled number of atoms in BL calculations. We note that the values for the valence band states at Γ must vanish by symmetry arguments, whereas our numerical calculations yield ±0.01 for both ML and BL. This marginal discrepancy is due to a finite number of bands taken into account and can be used to estimate the precision of our numerical calculations. The corresponding bound on the absolute error of the exciton g-factors from DFT, given explicitly in Table 2 for selected exciton configurations, is thus in the order of ±0.05.
As evident from Fig. 4a, particular bands make decisive contributions to the g-factor. To discuss this behavior for the ML case in more detail, we consider the 24th and 26th bands that correspond to the highest valence band (v) and the second conduction band (c + 1), respectively, and give rise to largest mutual contributions in the g-factors. This is expected according to Eq. (5), where the orbital angular momentum is proportional to the product of the interband matrix elements, which in turn are largest for the fundamental A-exciton transition X0 between the 24th and 26th bands. Similar arguments apply for the mutual contributions of the 23rd and 25th bands to the g-factor of B-excitons. It is also instructive to note the different dependencies of the orbital momenta for the two lowest conduction bands (Lc and Lc+1) and the top valence band (Lv) on the number of bands included. In Fig. 4a, Lc and Lc+1 exhibit jumps at 23rd and 24th bands, respectively, and then increase only marginally. In contrast, Lv in Fig. 4a increases nearly monotonously beginning from m ~ 30 on. A closer inspection shows that for m > 26, the sign of the square bracket in Eq. (5) alternates with increasing m, and the terms of comparable absolute values therefore cancel each other for both Lc and Lc+1. For Lv, on the other hand, the absolute values of the positive terms systematically exceed the negative terms and thus Lv continues to grow with increasing band number. Further analysis will be required to understand this behavior in more detail.
The DFT results for Ln(k) within the first Brillouin zone are shown in Fig. 5. Since spin–orbit effects were included at the DFT level, it is instructive to show both spin–orbit split highest valence bands (v and v − 1) and lowest conduction bands (c and c + 1). With the matrix elements of the orbital angular momenta of the valence and conduction bands in Fig. 5, it is straight forward to calculate the g-factors of the lowest-energy ML excitons in various configurations. In Table 2, we list the g-factors obtained from our DFT results for excitons in different configurations of valleys (kc, kv) and spins (sc, sv, with ↑ or ↓ projection along z).
In the top block of Table 2, we list excitons with the hole at K and the electron at K or \(K^{\prime}\) in spin-like and spin-unlike configurations with short exciton notation for zero-momentum bright and dark neutral excitons X0 and D0 and their finite-momentum counterparts \({K}_{L}^{\prime}\) and \({K}_{U}^{\prime}\). The block below shows the results for the spin-like and spin-unlike Q-excitons with the electron in Q and the hole in K, followed by two blocks without short exciton notation for momentum-indirect excitons composed from electrons in K or Q and holes in Γ. Note that the sign of the g-factor can be determined without further assumptions only for X0 with established valley-contrasting dipolar selection rules. For Zeeman-split momentum-indirect excitons, on the other hand, the sign will depend on the symmetry of the actual phonons involved in phonon-assisted PL34. This is analogous to the case of spin-dark excitons D0 with linearly polarized in-plane zero-phonon emission30 contrasted by circularly polarized PL sidebands of the same reservoir mediated by chiral phonons33,45. In principle, not only the g-factor signs but also the absolute values of the respective PL peaks should be distinct due to different exciton–phonon coupling not accounted for in our model. However, we expect such higher-order corrections to be well below the resolution of our measurements.
Discussion
First, we discuss the results of our calculations for excitons in ML WSe2. The g-factor of −4.0 from our DFT model is in excellent agreement with the experimental value of −4.1 for X0 (refs. 12,13,14,15,16,17). The good agreement in the g-factor of spin-dark excitons with g ≃ 9.4 in experiment20 and 10.1 in DFT provides further confidence in our model. According to our calculations, the states \({K}_{L}^{\prime}\) and \({K}_{U}^{\prime}\), which are the momentum-indirect counterparts of X0 and D0, exhibit different g-factors with large values of 13.6 and 19.6, respectively. The g-factors of Q-momentum excitons (9.2–14.5) are similar to those of D0 and \({K}_{L}^{\prime}\), whereas excitons with the hole at Γ are predicted to have rather small g-factors (<5.8) except for the spin-unlike configuration with \(K^{\prime}\) electron (9.8). As expected, the g-factors of intralayer excitons in BL WSe2 are close to the values of the corresponding ML excitons46. In addition to intralayer excitons, the BL hosts interlayer counterparts (e.g., intralayer QL and interlayer \({Q}_{L}^{\prime}\), intralayer QU and interlayer \({Q}_{U}^{\prime}\), so on) that exhibit the same g-factors within our model, which neglects Coulomb corrections for intralayer and interlayer excitons.
By providing explicit g-factor values for momentum-indirect excitons, our DFT results complement the experimental observations in ML and BL WSe2. In the framework of neutral MLs, however, they do not resolve the ambiguity between the two competing explanations of the peak \({M}_{1}^{0}\). The assignment of the peak as a phonon sideband of Q-momentum excitons21, on the one hand, is consistent with the g-factors of 9.2 and 14.5 for QL and \({Q}_{U}^{\prime}\) states in Table 2 (note that QU and \({Q}_{L}^{\prime}\) excitons, 250 meV above degenerate QL and \({Q}_{U}^{\prime}\) states47, are irrelevant in this context) and the structured peak \({M}_{1}^{0}\) in Fig. 2 with a g-factor of 11.5. On the other hand, the interpretation of the peak as direct PL emission by momentum-dark \({K}_{L}^{\prime}\) excitons34 is also consistent with the theoretical g-factor of 13.6 from DFT. Our DFT results also identify KΓ and QΓ with small g-factors as potential candidates to explain the bright PL peak between \({M}_{1}^{-}\) and D− in the negatively charged regime of high-quality samples with narrow spectra33,34.
For the neutral BL, our results help to rule out QΓ excitons and suggest spin-unlike interlayer QK and intralayer \(Q^{\prime} K\) exciton reservoirs rather than \(K^{\prime} \Gamma\) as a joint origin of phonon sidebands \({B}_{1}^{0}\), \({B}_{2}^{0}\), and \({B}_{3}^{0}\) (ref. 11). Whereas a detailed assignment of the neutral BL peaks to the specific reservoirs and phonon sidebands is yet to be developed, the values of the exciton g-factors in the charged regime can be understood, as in the ML case, by regarding the additional electron in the charged complex simply as a spectator to the Zeeman effect of the neutral finite-momentum exciton reservoir.
In summary, our work provides exciton g-factors for neutral and charged ML and BL WSe2 from both experiment and DFT. For ML WSe2, the g-factors obtained from first-principles calculations are in excellent quantitative agreement with previous reports and complement these studies by providing theoretical g-factors for momentum-indirect excitons in different configurations of spins and valleys. For BL WSe2, our work adds insight into the origin of PL peaks on the basis of theoretical g-factor values. In the broad context of research on layered semiconductors and their applications, the theoretical aspects of our work provide guidelines for magneto-optical studies of single-layer TMDs, homobilayer or heterobilayer systems, and other realizations of TMD-based van der Waals heterostructures.
Note: During the submission of our manuscript, we became aware of three related works on the theory of exciton g-factors in TMD MLs and heterostructures from first principles48,49,50.
Methods
Experimental methods
The field-effect heterostructure consisted of an exfoliated WSe2 crystal (HQ Graphene) with extended ML and BL regions encapsulated in hBN (NIMS). To control the charge doping, the crystal was contacted by a gold electrode deposited on a 50-nm-thick thermal silicon oxide layer of a p-doped silicon substrate. With the electrode grounded, a gate voltage applied to the highly doped silicon was used to control the doping level in ML and BL WSe2. The sample was mounted in a cryogenic confocal microscope and cooled down in a closed-cycle magneto-cryostat (attocube systems, attoDRY1000) with a base temperature of 3.2 K. The PL was excited at 1.85 eV with a few μW power of a continuous-wave laser diode focused to the diffraction-limited confocal excitation and detection spot of a low-temperature apochromatic objective (attocube systems, LT-APO/VISIR/0.82), dispersed with a monochromator (Roper Scientific, Acton SP2500), and detected with a nitrogen-cooled CCD (Roper Scientific, Spec 10:100BR/LN). Magneto-luminescence experiments were performed in Faraday configuration with a bi-directional solenoid at magnetic fields of up to 9 T.
DFT calculations
DFT calculations were performed within the generalized gradient approximation with the PBEsol exchange-correlation functional51 as implemented in the Vienna ab initio simulation package. The van der Waals interactions were considered with the DFT-D3 method with Becke–Johnson damping52,53; the spin–orbit interaction was included at all stages. Elementary cells with a vacuum thickness of 30 Å were used in order to minimize interactions between periodic images. The atomic positions were relaxed with a cut-off energy of 400 eV until the change in the total energy was <10−6 eV. The band structure of ML (BL) was calculated on the Γ-centered \(\overrightarrow{k}\) grid of 12 × 12 divisions with 300 (600) bands.
Data availability
The data that support the findings of this study are available from the corresponding authors upon reasonable request.
References
Wang, G. et al. Excitons in atomically thin transition metal dichalcogenides. Rev. Mod. Phys. 90, 3721 (2018).
Wang, Q. H., Kalantar-Zadeh, K., Kis, A., Coleman, J. N. & Strano, M. S. Electronics and optoelectronics of two-dimensional transition metal dichalcogenides. Nat. Nanotechnol. 7, 699 (2012).
Mak, K. F. & Shan, J. Photonics and optoelectronics of 2D semiconductor transition metal dichalcogenides. Nat. Photonics 10, 216 (2016).
Neumann, A. et al. Opto-valleytronic imaging of atomically thin semiconductors. Nat. Nanotechnol. 12, 329 (2017).
Schaibley, J. R. et al. Valleytronics in 2D materials. Nat. Rev. Mater. 1, 16055 (2016).
Schneider, C., Glazov, M. M., Korn, T., Höfling, S. & Urbaszek, B. Two-dimensional semiconductors in the regime of strong light-matter coupling. Nat. Commun. 9, 2695 (2018).
Tang, Y. et al. Simulation of Hubbard model physics in WSe2/WS2 moiré superlattices. Nature 579, 353 (2020).
Regan, E. C. et al. Mott and generalized Wigner crystal states in WSe2/WS2 moiré superlattices. Nature 579, 359 (2020).
Shimazaki, Y. et al. Strongly correlated electrons and hybrid excitons in a moiré heterostructure. Nature 580, 472 (2020).
Koperski, M. et al. Optical properties of atomically thin transition metal dichalcogenides: observations and puzzles. Nanophotonics 6, 1289 (2017).
Lindlau, J. et al. The role of momentum-dark excitons in the elementary optical response of bilayer WSe2. Nat. Commun. 9, 2586 (2018).
Srivastava, A. et al. Valley Zeeman effect in elementary optical excitations of monolayer WSe2. Nat. Phys. 11, 141 (2015).
Aivazian, G. et al. Magnetic control of valley pseudospin in monolayer WSe2. Nat. Phys. 11, 148 (2015).
Wang, G., Bouet, L., Glazov, M. M., Amand, T. & Ivchenko, E. L. Magneto-optics in transition metal diselenide monolayers. 2D Mater. 2, 034002 (2015).
Mitioglu, A. A. et al. Optical investigation of monolayer and bulk tungsten diselenide WSe2 in high magnetic fields. Nano Lett. 15, 4387 (2015).
Stier, A. V. et al. Magnetooptics of exciton Rydberg states in a monolayer semiconductor. Phys. Rev. Lett. 120, 057405 (2018).
Koperski, M. et al. Orbital, spin and valley contributions to Zeeman splitting of excitonic resonances in MoSe2, WSe2 and WS2 monolayers. 2D Mater. 6, 015001 (2018).
Zhang, X.-X. et al. Magnetic brightening and control of dark excitons in monolayer WSe2. Nat. Nanotechnol. 12, 883 (2017).
Molas, M. R. et al. Brightening of dark excitons in monolayers of semiconducting transition metal dichalcogenides. 2D Mater. 4, 021003 (2017).
Robert, C. et al. Fine structure and lifetime of dark excitons in transition metal dichalcogenide monolayers. Phys. Rev. B 96, 155423 (2017).
Lindlau, J. et al. Identifying optical signatures of momentum-dark excitons in monolayer transition metal dichalcogenides. Preprint at arXiv https://arxiv.org/abs/1710.00988 (2017).
Sun, S. et al. Large g factor in bilayer WS2 flakes. Appl. Phys. Lett. 114, 113104 (2019).
You, Y. et al. Observation of biexcitons in monolayer WSe2. Nat. Phys. 11, 477 (2015).
Barbone, M. et al. Charge-tuneable biexciton complexes in monolayer WSe2. Nat. Commun. 9, 3721 (2018).
Steinhoff, A. et al. Biexciton fine structure in monolayer transition metal dichalcogenides. Nat. Phys. 14, 1199 (2018).
Li, Z. et al. Revealing the biexciton and trion-exciton complexes in BN encapsulated WSe2. Nat. Commun. 9, 3719 (2018).
Mak, K. F. et al. Tightly bound trions in monolayer MoS2. Nat. Mater. 12, 207 (2013).
Courtade, E. et al. Charged excitons in monolayer WSe2: experiment and theory. Phy. Rev. B 96, 085302 (2017).
Zhou, Y. et al. Probing dark excitons in atomically thin semiconductors via near-field coupling to surface plasmon polaritons. Nat. Nanotechnol. 12, 856 (2017).
Wang, G. et al. In-plane propagation of light in transition metal dichalcogenide monolayers: optical selection rules. Phys. Rev. Lett. 119, 047401 (2017).
Liu, E. et al. Gate tunable dark trions in monolayer WSe2. Phys. Rev. Lett. 123, 027401 (2019a).
Li, Z. et al. Direct observation of gate-tunable dark trions in monolayer WSe2. Nano Lett. 19, 6886 (2019a).
Liu, E. et al. Valley-selective chiral phonon replicas of dark excitons and trions in monolayer WSe2. Phys. Rev. Res. 1, 032007 (2019b).
He, M. et al. Valley phonons and exciton complexes in a monolayer semiconductor. Nat. Commun. 11, 618 (2020).
Wickramaratne, D., Zahid, F. & Lake, R. K. Electronic and thermoelectric properties of few-layer transition metal dichalcogenides. J. Chem. Phys. 140, 124710 (2014).
Terrones, H. & Terrones, M. Bilayers of transition metal dichalcogenides: different stackings and heterostructures. J. Mater. Res. 29, 373 (2014).
Wilson, N. R. et al. Determination of band offsets, hybridization, and exciton binding in 2D semiconductor heterostructures. Sci. Adv. 3, 1601832 (2017).
Li, Z. et al. Emerging photoluminescence from the dark-exciton phonon replica in monolayer WSe2. Nat. Commun. 10, 2469 (2019b).
Van Tuan, D., Jones, A. M., Yang, M., Xu, X. & Dery, H. Virtual trions in the photoluminescence of monolayer transition-metal dichalcogenides. Phys. Rev. Lett. 122, 217401 (2019).
Landau, L. D. & Lifshitz, E. M. Quantum Mechanics: Non-Relativistic Theory 3rd edn Vol. 3 (Elsevier, 2013).
Roth, L. M., Lax, B. & Zwerdling, S. Theory of optical magneto-absorption effects in semiconductors. Phys. Rev. 114, 90 (1959).
Bir, G. L. & Pikus, G. E. Symmetry and Strain-Induced Effects in Semiconductors (Wiley, 1974).
Xiao, D., Chang, M.-C. & Niu, Q. Berry phase effects on electronic properties. Rev. Mod. Phys. 82, 1959 (2010).
Kormányos, A., Rakyta, P. & Burkard, G. Landau levels and Shubnikov-de Haas oscillations in monolayer transition metal dichalcogenide semiconductors. New J. Phys. 17, 103006 (2015).
Chen, X. et al. Entanglement of single-photons and chiral phonons in atomically thin WSe2. Nat. Phys. 15, 221 (2019).
Arora, A. et al. Zeeman spectroscopy of excitons and hybridization of electronic states in few-layer WSe2, MoSe2 and MoTe2. 2D Mater. 6, 015010 (2018).
Deilmann, T. & Thygesen, K. S. Finite-momentum exciton landscape in mono- and bilayer transition metal dichalcogenides. 2D Mater. 6, 035003 (2019).
Wozniak, T., Faria Junior, P. E., Seifert, G., Chaves, A. & Kunstmann, J. Exciton g factors of van der Waals heterostructures from first-principles calculations. Phys. Rev. B 101, 235408 (2020).
Deilmann, T., Krüger, P. & Rohlfing, M. Ab initio studies of exciton g factors: monolayer transition metal dichalcogenides in magnetic fields. Phys. Rev. Lett. 124, 226402 (2020).
Xuan, F. & Quek, S. Y. Valley Zeeman effect and Landau levels in two-dimensional transition metal dichalcogenides. Phys. Rev. Res. 2, 033256 (2020).
Csonka, G. I. et al. Assessing the performance of recent density functionals for bulk solids. Phys. Rev. B 79, 155107 (2009).
Grimme, S., Antony, J., Ehrlich, S. & Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 132, 154104 (2010).
Grimme, S., Ehrlich, S. & Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comp. Chem. 32, 1456 (2011).
Acknowledgements
The authors thank M. M. Glazov, T. Deilmann, and P. Hawrylak for fruitful discussions. This research was funded by the European Research Council (ERC) under the Grant Agreement No. 772195 and the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy EXC-2111-390814868. N.V.T. acknowledges support from the Federal Target Program for Research and Development of the Ministry of Science and Higher Education of the Russian Federation (No. 14.587.21.0047, identifier RFMEFI58718X0047). S.Y.K. acknowledges support from the Austrian Science Fund (FWF) within the Lise Meitner Project No. M 2198-N30. A.S.B. has received funding from the European Union’s Framework Programme for Research and Innovation Horizon 2020 (2014–2020) under the Marie Skłodowska-Curie Grant Agreement No. 754388 and from LMU Munich’s Institutional Strategy LMUexcellent within the framework of the German Excellence Initiative (No. ZUK22). A.H. acknowledges support from the Center for NanoScience (CeNS) and the LMUinnovativ project Functional Nanosystems (FuNS). K.W. and T.T. acknowledge support from the Elemental Strategy Initiative conducted by the MEXT, Japan, Grant Number JPMXP0112101001, JSPS KAKENHI Grant Numbers JP20H00354 and the CREST (JPMJCR15F3), JST. Open access funding provided by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
J.F., J.L., V.F., and M.F. performed experiments on samples with high-quality hBN provided by K.W. and T.T.; J.F., J.L., A.S.B., and A.H. analyzed the data; A.S.B. developed the theory of exciton g-factors from first principles; N.V.T., S.Y.K., and A.S.B. performed numerical calculations; J.F., A.S.B., and A.H. prepared the figures and wrote the manuscript. All authors commented on the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Förste, J., Tepliakov, N.V., Kruchinin, S.Y. et al. Exciton g-factors in monolayer and bilayer WSe2 from experiment and theory. Nat Commun 11, 4539 (2020). https://doi.org/10.1038/s41467-020-18019-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-020-18019-1
This article is cited by
-
Cavity Floquet engineering
Nature Communications (2024)
-
Amplification of interlayer exciton emission in twisted WSe2/WSe2/MoSe2 heterotrilayers
npj 2D Materials and Applications (2024)
-
Electrically tunable layer-hybridized trions in doped WSe2 bilayers
Nature Communications (2024)
-
Excitonic devices based on two-dimensional transition metal dichalcogenides van der Waals heterostructures
Frontiers of Chemical Science and Engineering (2024)
-
Enhanced valley polarization in WSe2/YIG heterostructures via interfacial magnetic exchange effect
Nano Research (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.