Abstract
The discovery of borospherenes unveiled the capacity of boron to form fullerene-like cage structures. While fullerenes are known to entrap metal atoms to form endohedral metallofullerenes, few metal atoms have been observed to be part of the fullerene cages. Here we report the observation of a class of remarkable metallo-borospherenes, where metal atoms are integral parts of the cage surface. We have produced La3B18– and Tb3B18– and probed their structures and bonding using photoelectron spectroscopy and theoretical calculations. Global minimum searches revealed that the most stable structures of Ln3B18– are hollow cages with D3h symmetry. The B18-framework in the Ln3B18– cages can be viewed as consisting of two triangular B6 motifs connected by three B2 units, forming three shared B10 rings which are coordinated to the three Ln atoms on the cage surface. These metallo-borospherenes represent a new class of unusual geometry that has not been observed in chemistry heretofore.
Similar content being viewed by others
Introduction
The electron deficiency of boron often leads to electron delocalization and the violation of the octet rule in boron compounds and three-dimensional (3D) cage units in different bulk boron allotropes1,2,3. Because of the strong boron–boron bonding, there were speculations about the formation of boron nanotubes composed of a triangular boron lattice4,5, after the discovery of carbon nanotubes. The triangular boron lattice can be viewed as a graphene-like sheet with the filling of a boron atom in each B6 hexagon. Further theoretical calculations revealed, however, that triangular lattices with hexagonal vacancies were more stable and more suitable to construct boron nanotubes6,7. In the meantime, combined spectroscopic and theoretical studies have shown that size-selected boron clusters all have 2D structures with delocalized multi-center bonding within the cluster plane8,9,10,11. The discovery of the hexagonal 2D B36 clusters provided the first experimental evidence of the viability of atom-thin boron nanostructures with hexagonal vacancies, named as borophene akin to graphene12. Borophenes have been recently synthesized using atomic vapor deposition on Ag(111) substrates13,14, forming a new class of synthetic 2D nanomaterials15. The analogy between nanostructures made of boron and carbon has been further extended when the B40 and B39– clusters were found to have global minimum cage structures16,17, i.e. borospherenes analogous to the fullerenes. Fullerenes are known to form endohedral metallofullerenes for alkali, alkali earth, lanthanide, and actinide elements18,19, albeit not for transitions metals. Heterofullerenes in which one carbon atom is substituted by a transition metal atom have been observed in the gas phase, but the metal substitution induces large local structural distortions and such heterofullerenes have not been synthesized in the bulk20,21,22. The first cage cluster made of multiple metal atoms and carbons was proposed to be Ti8C12+ (metallocarbohedrene)23. However, subsequent theoretical calculations showed that the metallocarbohedrene is not stable and the global minimum of Ti8C12+ consisted of a tetrahedral, close-packed Ti8 clusters coordinated by six C2 units on the cluster surface24. In the present article, we report the first observation of a class of metallo-borospherenes, hollow cage clusters consisting of three lanthanide (Ln) atoms and 18 boron atoms (Ln3B18–).
Transition-metal-doped boron clusters were first found to form aromatic borometallic molecular wheels, M©Bn− (n = 8–10)25,26, as well as metal-centered nanotubular structures27. More interestingly, it has been shown that transition metals can be an integral part of larger 2D boron clusters28, leading to the possibility of metallo-borophenes29. Lanthanide-doped boron clusters, however, have been found recently to form very different structures, due to both charge transfer interactions and strong (d–p)π bonding30. For example, lanthanide-doped boron clusters do not form similar borometallic molecular wheels as the transition metals. Instead, they form inverse-sandwich-type structures for Ln2Bn– clusters (n = 7–9)31,32. The most recent study indicates that the inverse-sandwich structure may extend to form lanthanide-boron nanowires33.
Here we report a joint photoelectron spectroscopy (PES) and quantum chemistry study of two tri-lanthanide-doped B18 clusters (La3B18– and Tb3B18–), which are found to possess unprecedented D3h cage structures with the Ln atoms being integral parts of the cage surface. These D3h metallo-borospherenes belong to an unusual class of geometry known as spherical trihedron. The B18 framework consists of two B6 triangles connected by three B2 units, forming three shared B10 rings. The high stability of the spherical trihedral structures is derived from the strong interactions between the Ln atoms and the B10 rings via charge transfer interactions and d–p covalent bonding. Theoretical calculations show that the entire series of lanthanide elements (Ln = La–Lu) can form spherical trihedral Ln3B18– metallo-borospherenes with tunable magnetic properties, making them a fascinating series of building blocks for new types of magnetic materials.
Results and discussion
Photoelectron spectroscopy
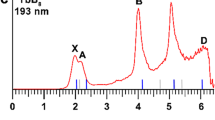
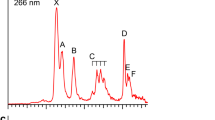
The PE spectrum at 193 nm was first measured for the La3B18– cluster (Fig. 1a), which was found to exhibit a relatively simple pattern compared with that of the recently reported La3B14– cluster33. This observation suggested that La3B18– should possess a highly symmetric structure. Subsequently, we also obtained the spectrum of a late-Ln cluster Tb3B18– (Fig. 2a) and observed a spectral pattern, exhibiting some similarities to that of La3B18– and suggesting that these two Ln-doped boron clusters should have similar structures and chemical bonding. The well-resolved PES features of the Ln3B18– clusters serve as electronic fingerprints to allow analyses of their structures and chemical bonding by comparing with theoretical calculations, as shown in Figs. 1b, 2b, and Supplementary Tables S1 and S2 for Ln = La and Tb, respectively.
The spectrum of La3B18– displayed five well-resolved bands labeled as X, A, B, C, and D (Fig. 1a). The X band yielded the first vertical detachment energy (VDE) of 2.97 eV for La3B18–. The adiabatic detachment energy (ADE) for band X was evaluated from its onset to be 2.80 eV, which also represents the electron affinity (EA) of neutral La3B18. The higher binding energy bands (A, B, C, and D) correspond to detachment transitions to the excited states of neutral La3B18. The A band at 3.64 eV was broad and not well resolved at 193 nm, but it was slightly better resolved in the 266 nm spectrum (Supplementary Fig. 1). This broad spectral feature could be due to geometry changes upon electron detachment or overlapping detachment transitions. Band B at 4.01 eV is sharper compared with band A (Fig. 1a). An intense and sharp band C at 4.43 eV was clearly resolved in the 193 nm spectrum. Following a large energy gap, a broad band (D) was observed above ~5.5 eV. Due to the poor signal-to-noise ratio, band D was tentatively assigned for the sake of discussion.
The PE spectrum of Tb3B18– showed five well-resolved peaks assigned as X, A, B, C, D (Fig. 2a). The X band gave rise to a VDE of 3.26 eV for Tb3B18– and an ADE of 3.13 eV, which is also the EA of neutral Tb3B18. Band A was observed at a VDE of 3.84 eV, followed by three closely-lying bands (B, C, D). Band B at 4.28 eV and band C at 4.52 eV were relatively weak and closely spaced, whereas band D at 4.77 eV was much more intense. Beyond ~5 eV, the signal-to-noise ratio was poor and no obvious spectral bands were observed. Band E close to the threshold at a VDE of ~6.2 eV was tentatively labeled. The overall spectral pattern for Tb3B18– exhibits some similarity to that of La3B18–. In particular, the strong X and D bands in Tb3B18– are similar to the strong X and C bands in La3B18–. There is a large energy gap on the high binding energy side in both spectra. Similar spectral patterns could be an indication of similar structures, as have been observed for a series of dilanthanide clusters (Ln2B8–)31.
Global minimum structural searches
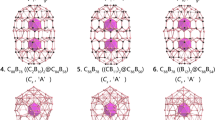
The low-lying isomers within 55 kcal mol−1 of the global minimum at the levels of PBE/TZP and PBE0/TZP are presented in Supplementary Fig. 2. The global minimum of La3B18– is a hollow cage with a closed-shell ground state (1A1) and D3h symmetry. This is a hetero-metallo-borospherene, in which the three La atoms are integral parts of the cage surface, as shown in Fig. 3. All the other low-lying isomers are low-symmetry 3D structures, many of which are distorted cages. The highly symmetric global minimum D3h metallo-borospherene exhibits overwhelming stability relative to the other low-lying isomers: it is more stable than the nearest isomer with Cs symmetry by ~19 kcal mol−1 at the PBE/TZP and PBE0/TZP levels of theory. The B18 framework in the La3B18– cage can be viewed as consisting of two B6 triangles linked together at their three corners by three B2 units, creating three shared B10 rings along the C3 axis. The three La atoms are coordinated by the three B10 rings, giving rise to the closed cage structure. The La3B18– metallo-borospherene has an oblate shape with a diameter of 4.62 Å along the C3 axis (between the two B6 triangles) and 5.09 Å encompassed by the three equatorial La atoms. The relevant bond lengths of the La3B18– metallo-borospherene are shown in Supplementary Fig. 3a.
The hollow cage structure of La3B18– was totally unexpected and the geometry is highly unusual. To further examine its stability and robustness, we performed ab initio molecular dynamics (AIMD) simulations at different temperatures, 300, 500, 700, and 1000 K (see Supplementary Fig. 4). We found that even at 1000 K the La3B18– metallo-borospherene is dynamically stable for the 13 ps duration of the simulations. At 1000 K, the structure displayed a root-mean-square-deviation of 0.199 Å and a maximum bond length deviation of 0.260 Å during the simulations.
The similarity in their PE spectra suggested that the global minima of Tb3B18– and La3B18– should be similar. Because of the localized and nonbonding nature of the 4f orbitals in Tb, we optimized the D3h structure for Tb3B18– using the 4f-in-core pseudopotential34. The structural parameters of the Tb3B18– metallo-borospherene are similar to those for La3B18– (Supplementary Fig. 3), except that the Tb–B and B–B bond lengths are all slightly shorter due to the smaller atomic radius of Tb as a result of the lanthanide contraction. Because of the use of the 4f-in-core pseudopotential, the spin state of the Tb3B18– metallo-borospherene was not determined from the geometry optimization. We performed broken symmetry calculations and compared the relative energies between the ferromagnetic and antiferromagnetic couplings of the 4f electrons, as shown in Supplementary Table 3 for Tb3B18–, as well as for Pr3B18–. The relative energies due to the inter-atomic spin couplings of the unpaired 4f electrons are relatively small, although the high spin ferromagnetic coupling seems to give the lowest energy in both cases. Hence, the spin multiplicity of the Tb3B18– metallo-borospherene should be 19 (with 18 unpaired 4f electrons).
Comparison between the experimental and theoretical results
To validate the D3h cage structure for La3B18– and Tb3B18–, we calculated their ADEs and VDEs using the ΔSCF–TDDFT formalism. Figures 1b, 2b present the simulated spectra for the D3h global minimum structures, in comparison with the experimental data. The computed ADE/VDE1 at the CCSD(T) level are 2.828/2.972 eV for La3B18– (Supplementary Table 4), in excellent agreement with the experimental data of 2.80/2.97 eV. As shown in Fig. 4, the valence MOs of La3B18– are mainly of La-B d–p and B sp characters. Because La3B18– has a closed-shell configuration, single-electron removal from each molecular orbital (MO) yields one detachment channel, as shown in Supplementary Table 1. The computed VDEs for detachment from the 5e′′ HOMO (2.972 eV) and 8a1′ HOMO-1 (2.987 eV) are very close to each other, in excellent agreement with the experimental VDE of the X band (2.97 eV). In fact, each of the observed PES band corresponds to two detachment channels, as given in Supplementary Table 1, where the electron configurations and final state symmetries are also presented. The simulated spectral patterns and the experimental spectra are in excellent agreement, providing considerable credence for the D3h cage global minimum for La3B18–. We have also simulated the PE spectra for the next nine higher-lying isomers of La3B18–, as shown in Supplementary Fig. 5. None of these spectra fits the experimental spectrum, giving additional support for the D3h global minimum structure.
The computed ADE/VDE for Tb3B18– are 2.901/3.017 eV at the CCSD(T) level (Supplementary Table 4), slightly underestimated relative to the experimental data of 3.13/3.26 eV probably due to the use of the 4f-in-core approximation as well as the incomplete account of electron correlations. Nevertheless, the theoretical results by not considering the 4f electrons and detachment channels are still in very good agreement with the experimental data, as can be seen in Fig. 2 and Supplementary Table 2. These results are consistent with our previous observations that the detachment cross sections of the 4f electrons are much weaker and the PE spectra of Ln–B binary clusters are dominated by the Ln–B d–p and B sp detachment channels31,32.
Stabilities of the first metallo-borospherenes
The observation of the La3B18– and Tb3B18– cage clusters, in which the three Ln atoms are integral parts of the cage surface, is unprecedented. The two B6 triangles in the D3h structure are reminiscent of the B40 borospherene16, which consists of eight fused B6 triangles on a spherical surface. Hence, the Ln3B18– cage clusters can be viewed as a new class of metallo-borospherenes. Networked metallo-fullerenes usually involve a single transition-metal atom substituting one carbon atom on the fullerene surface20,21,22. The incorporation of multiple metal atoms on the borospherene surface is due to the flexibility of the 2D boron network, which is a direct result of the electron deficiency of boron. It is interesting to note that the crystal structure of a Ni–Zn boride (Ni21Zn2B24) was shown to contain characteristic cages of B20 units, with an octahedral Ni6 cluster nested inside35. Our observation of the Ln3B18– metallo-borospherenes represents the first isolated molecules of Ln–B cages in the gas phase.
To understand the stability of these remarkable cage structures, we carried out fragment MO analyses by first considering the construction of the B18 framework in two different pathways and then its bonding with the three La atoms, as schematically shown in Fig. 5. Figure 5a shows one possible path to construct the B18 framework by the fusion of three B10 rings. Four of the boron atoms in each B10 ring are shared with the other B10 rings, which each coordinate to a La atom to form three shared La©B10 units. This hypothetical formation pathway of La3B18– can be expressed by the following steps:
The energetics were calculated from single-point energy differences of the reactants and products, using the geometries directly taken from the optimized La3B18– cage at the PBE/TZP level of theory. The interactions between the B18 framework and the three La atoms are extremely strong (steps 2 and 3), which underlies the stability of the La3B18– cage. It should be noted that in platonic solids four surfaces are the minimum number to form a 3D object, i.e., the tetrahedron. However, Fig. 5a shows that three La©B10 surfaces are fused together to form the D3h La3B18– cage. This is because the La©B10 surface is curved. It turns out that the Ln3B18– metallo-borospherenes belong to a class of geometry mathematically known as n-gonal hosohedron, which is basically a tessellation of lunes on a spherical surface, such that each lune shares the same two vertices. Thus, the D3h La3B18– cage is a trigonal hosohedron, also known as spherical trihedron, where the two vertices consist of the triangular B6 units. To the best of our knowledge, such a geometry has not been observed in any cluster or molecular systems heretofore.
Figure 5b shows another pathway to construct the La3B18– cage, in which the B18 framework is formed by two triangular B6 motifs linked by three B2 bridges, such that three B10 rings are created. This hypothetical pathway can be represented by the following steps:
The interactions between the B18 framework and the three La atoms to form the La3B18– cage are represented by steps 2/3 or 6/7 with an estimated binding energy of 724.6 kcal mol-1, i.e., 241.5 kcal mol−1 for the binding energy between each La atom and the B10 ring. This huge La-B10 binding energy underlies the extraordinary stability of the La3B18– metallo-borospherene. Compared with the pathway in Fig. 5a, the pathway in Fig. 5b is more favorable energetically since each step is exothermic. We should emphasize, though, that these exercises provide different views of the unprecedented hollow cage structures. The two pathways to construct the La3B18– cage depicted in Fig. 5 certainly do not represent the mechanisms about how it is formed.
The nature of the bonding between B18 and the La atoms
Since the global minimum of B18 is a planar structure36, the stabilization of the 3D B18 framework is entirely due to its strong bonding with the three La atoms, as discussed above. We have analyzed the nature of the La–B10 bonding in the La3B18– metallo-borospherene using several different methods. The MO energy-level diagram and the relevant MOs of La3B18– derived from the La3– and B18 moieties are shown in Fig. 4. The 5e′′, 9e′, and 1a1′′ MOs of La3B18– (red-colored) represent the bonding orbitals between the three La atoms and the B18 moiety, mainly corresponding to the interactions between the irreducible representations, 4e′′, 6e′, and 1a1′′ on the B18 moiety and 6e′′, 12e′, and 2a1′′ on the La3– moiety (the red highlighted MOs). Supplementary Table S5 gives the compositions of the 5e′′, 9e′, and 1a1′′ MOs, which are dominated by contributions from the B18 moiety. Hence, there is a strong charge transfer from La to B18, resulting in a closed-shell La3B18– with a large HOMO-LUMO gap of 1.51 eV computed at the PBE/TZP level. The La atoms are in their favorite +III oxidation state in La3B18–, which can be viewed approximately as (La3+)3[B1810–]. As shown in Fig. 4, the 6e′′, 12e′, and 2a1′′ irreducible representations on the La3– moiety are of La 5d characters, while the 4e′′, 6e′, and 1a1′′ irreducible representations on the B18 framework are of B 2p characters. Hence, the 5e′′, 9e′, and 1a1′′ MOs also represent significant La 5d and B18 2p covalent bonding. It is the strong covalent and ionic bonding between the La atoms and the B10 rings that gives rise to the extraordinary stability of the La3B18– cage structure. These bonding characteristics are found in all lanthanide boride compounds due to the low electronegativity of the lanthanide elements and their diffuse 5d orbitals37.
The La–B10 interactions can be further characterized using the EDA-NOCV method with B18 (…6a1′21a1′′06e′04e′′0) and La3– (…6e′′42a1′′212e′4) fragments, a powerful energy decomposition tool to give insight into chemical bonding38. We analyzed the B18…La3– interaction by the decomposition of the orbital terms into pairwise contributions, as shown in Supplementary Fig. 6. There are three major terms ΔE1, ΔE2, and ΔE3 associated with the deformation densities Δρ1, Δρ3, and Δρ3, respectively. The remaining terms contribute <10% to the total orbital interactions. The color code of the deformation densities indicates the direction of the charge flow from red → blue. It is interesting to see that the 1a1′′ orbital of La3B18–, which is analogous to the (d–p)δ bonding MO in the Ln2B8– inverse sandwich complexes31,32, contributes significantly (25.7% from the EDA-NOCV analyses, Supplementary Fig. 6) to the stability of the orbital interaction. The other two stronger Δρ2 (34.8%) and Δρ3 (28.9%) deformation densities correspond to the degenerate 9e′ and 5e′′ MOs, respectively. The direction of the charge flow is from the La3– to the B18 moiety, consistent with the fragment MO analyses discussed above (Fig. 4).
We further analyzed the chemical bonding in the La3B18– metallo-borospherene using the adaptive natural density partitioning (AdNDP) approach39, as shown in Fig. 6. The first row displays nine localized two-center two-electron (2c–2e) σ bonds formed within the three B2 units and between the B2 units and the three apexes of the two B6 triangles. The second row reveals the delocalized bonds in the B6 triangles, with four three-center two-electron (3c–2e) σ bonds within each B6 unit. The multi-center 12c–2e and 18c–2e delocalized bonds can be viewed as π bonds within the B6 units. The third row represents totally delocalized σ and π bonds within the B18 framework. The last row shows five totally delocalized 21c–2e bonds between the La atoms and the B18 framework, corresponding to the 5e′′, 9e′, and 1a1′′ MOs in Fig. 4. We also found that the La3B18– metallo-borospherene possesses both 3D aromaticity with calculated nucleus-independent chemical shifts (NICS)40 of −47.87 ppm at the cage center, and planar aromaticity on each B6 triangles with NICS(0) of −31.44 ppm and NICS(1) of −2.16 above the plane center, as shown in Supplementary Table 6, where the aromaticity in the metallo-borospherene is compared with that of the recently synthesized cubic [ZnI]8 compound41.
The analyses were done using the AdNDP method29. ON stands for occupation number.
We also performed bond-order index analyses for the B–B and La–B interactions, as presented in Supplementary Table 7. The B2 bridges have shorter bond lengths and higher bond orders than those of the B6 triangles. In terms of the La–B interactions, the distances and bond order indices are similar to those in the lanthanide–boron complexes reported previously30,31,32,33.
A new class of spherical trihedron metallo-borospherenes
The discoveries of the La3B18– and Tb3B18– metallo-borospherenes suggest that other lanthanide elements could also form similar structures because of the similarity in the chemical properties of the whole series of lanthanides. We have calculated the D3h cage structures for all the lanthanide elements, Ln3B18– (Ln = Ce–Lu). The coordinates obtained at the PBE0 level are given as Supplementary Data 1, whereas those of La3B18– and La3B18 are provided in Supplementary Table 8. All these structures are indeed minima on their potential energy surfaces. Hence, we conclude that there indeed exist a whole class of Ln3B18– metallo-borospherenes. While borospherenes have not been observed beyond the B40 cluster42, the unique bonding characteristics between lanthanide and boron suggest that other lanthanide metallo-borospherenes with different sizes and LnxBy– stoichiometries may exist. Recent studies of transition-metal borides showed that the metal–boron interactions have major influences on their magnetic properties43,44. Hence, the understanding of Ln–B interactions in the metallo-borospherene systems may provide insights for the design of lanthanide borides with tunable magnetic or catalytic properties.
In conclusion, we report the observation of the first tri-lanthanide-doped boron cage clusters (metallo-borospherenes), in which the metal atoms are integral parts of the cage surface. Photoelectron spectra of two representative systems, Ln3B18– (Ln = La, Tb), show similar and relatively simple spectral patterns, suggesting that they have similar highly symmetric structures. Theoretical calculations reveal that the Ln3B18– anions have cage-like structures with D3h symmetry: two planar B6 triangular units linked by three B2 bridges to form the B18 framework consisting of three shared B10 rings coordinated to the three Ln atoms. Strong ionic and covalent chemical bonding is found between the Ln atoms and the B18 framework. The extraordinary stabilities of the metallo-borospherenes are understood by various theoretical analyses. La3B18– is found to have a closed-shell electron configuration with a large HOMO-LUMO gap and possesses 3D aromaticity. The Ln3B18– cage complexes are expected to exist for all lanthanide elements, suggesting the possibility that there may exist a large class of lanthanide metallo-borospherenes with different Ln/B stoichiometries and tunable properties.
Methods
Experimental details
The experiments were carried out using a magnetic-bottle PES apparatus equipped with a laser vaporization supersonic cluster source, details of which have been published elsewhere11. The La3B18– and Tb3B18– clusters were produced by laser vaporization of a La/11B or Tb/11B mixed target, respectively. The laser-induced plasma was cooled by a He carrier gas seeded with 5% Ar, initiating nucleation between the boron and lanthanide atoms. The nascent clusters were entrained in the carrier gas and underwent a supersonic expansion. Negatively-charged clusters were extracted from the collimated cluster beam and analyzed by a time-of-flight mass spectrometer. Both pure (Bn–) and mixed (LnxBy–) clusters were produced from the cluster source. The La3B18– and Tb3B18– clusters of current interest were mass-selected and photodetached by the 193 nm (6.424 eV) radiation from an ArF excimer laser or the fourth harmonics from a Nd:YAG laser (266 nm, 4.661 eV). Photoelectrons were collected and analyzed in a 3.5-m-long electron flight tube at nearly 100% efficiency. The photoelectron spectra were calibrated by the known transitions of Au– and Bi–. The resolution of the PES apparatus (ΔKE/KE) was around 2.5%, that is, about 25 meV for photoelectrons with 1 eV kinetic energy (KE).
Computational methods
Unbiased global-minimum structural searches for the La3B18– cluster were performed using the TGMin 2.0 code45. The global minimum structure of Tb3B18– was not searched separately. More than 2000 structures were evaluated for La3B18– using the constrained Basin–Hopping algorithm at the PBE/DZP46,47 level from the ADF 2017 software48. A D3h cage structure was found to be the global minimum, which was significantly lower in energy in comparison to the next lowest-lying isomer (Supplementary Fig. 2). To confirm the stability of the global minimum, we conducted another 500 structural searches, using the D3h cage as the seed structure. No structures with lower energies were found. All the local minima were verified via harmonic vibrational frequency calculations. The frozen-core approximation was employed for the inner shells of [1s2] for B and [1s2−4d10] for the La atoms. The zero-order regular approximation49 was applied, to account for the scalar relativistic effects. Low-lying isomers were subsequently optimized using the PBE and PBE0 density functionals50 along with the TZP basis sets. Born–Oppenheimer molecular dynamic simulations were further carried out on La3B18– for 13 ps using the CP2K code51 at different temperatures, from 300 to 1000 K (Supplementary Fig. 4). To minimize the 4f-electron induced complexity (i.e. spin multiplicity) and considering the negligible geometry change due to the occupations of the localized 4f orbitals (radial-density maximum probability radii <0.5 Å), we used the 4f-in-core pseudopotentials34 for the lanthanide elements to optimize the geometric parameters in the other Ln3B18– (Ln = Ce–Lu) species.
The simulation of the PE spectra was done using the ΔSCF-TDDFT method52 with the SAOP exchange-correlation functional53 to account for the long-range interactions. The ground state adiabatic and vertical detachment energies were calculated at the DFT levels, as well as the more accurate DLPNO-CCSD(T) level54 with the Def2-TZVP basis sets55 and the Def2-TZVPP pseudopotential for La34, utilizing the AutoAux generation procedure55. We also used the 4f-in-core pseudopotential34 for the simulation of the PE spectrum of Tb3B18– without consideration of the 4f electron detachment channels. Previous studies showed that such detachment channels carried very low detachment cross sections at the low detachment photon energies used and the main PES features of Ln–B binary clusters were dominated by MOs with Ln sd or B sp characters31,32,33. Chemical bonding and electronic structure analyses were carried out by canonical molecular orbital (MO) theory and the semi-localized AdNDP method39. We also performed calculations using the energy decomposition analysis–natural orbitals for chemical valence (EDA–NOCV) approach38 to quantitatively elucidate the bonding mechanisms between the B18 and La3– moieties. The bond order indexes of different interatomic interactions were calculated using the Mayer56, Gopinathan–Jug (G–J)57, and Nalewajski–Mrozek schemes58.
Data availability
The data that support the findings of this study are available within the article and the associated Supplementary information. Any other data are available from the corresponding authors upon request.
Code availability
The TGMin code used for the global minimum search is available from the corresponding author (J.L.) upon request and signing a license.
References
Lipscomb, W. N. The boranes and their relatives. Science 196, 1047–1055 (1977).
Oganov, A. R. et al. Ionic high-pressure form of elemental boron. Nature 457, 863–866 (2009).
Albert, B. & Hillebrecht, H. Boron: elementary challenge for experimenters and theoreticians. Angew. Chem. Int. Ed. 48, 8640–8668 (2009).
Gindulytė, A., Lipscomb, W. N. & Massa, L. Proposed boron nanotubes. Inorg. Chem. 37, 6544–6545 (1998).
Boustani, I., Quandt, A., Hernández, E. & Rubio, A. New boron based nanostructured materials. J. Chem. Phys. 110, 3176–3185 (1999).
Tang, H. & Ismail-Beigi, S. Novel precursors for boron nanotubes: the competition of two-center and three-center bonding in boron sheets. Phys. Rev. Lett. 99, 115501 (2007).
Yang, X., Ding, Y. & Ni, J. Ab initio prediction of stable boron sheets and boron nanotubes: structure, stability, and electronic properties. Phys. Rev. B 77, 041402 (2008).
Zhai, H. J., Kiran, B., Li, J. & Wang, L. S. Hydrocarbon analogs of boron clusters: Planarity, aromaticity, and antiaromaticity. Nat. Mater. 2, 827–833 (2003).
Alexandrova, A. N., Boldyrev, A. I., Zhai, H. J. & Wang, L. S. All-boron aromatic clusters as potential new inorganic ligands and building blocks in chemistry. Coord. Chem. Rev. 250, 2811–2866 (2006).
Sergeeva, A. P. et al. Understanding boron through size-selected clusters: structure, chemical bonding, and fluxionality. Acc. Chem. Res. 47, 1349–1358 (2014).
Wang, L. S. Photoelectron spectroscopy of size-selected boron clusters: from planar structures to borophenes and borospherenes. Int. Rev. Phys. Chem. 35, 69–142 (2016).
Piazza, Z. A. et al. Planar hexagonal B36 as a potential basis for extended single-atom layer boron sheets. Nat. Commun. 5, 3113 (2014).
Mannix, A. J. et al. Synthesis of borophenes: anisotropic, two-dimensional boron polymorphs. Science 350, 1513–1516 (2015).
Feng, B. et al. Experimental realization of two-dimensional boron sheets. Nat. Chem. 8, 563 (2016).
Mannix, A. J., Zhang, Z., Guisinger, N. P., Yakobson, B. I. & Hersam, M. C. Borophene as a prototype for synthetic 2D materials development. Nat. Nanotechnol. 13, 444 (2018).
Zhai, H. J. et al. Observation of an all-boron fullerene. Nat. Chem. 6, 727 (2014).
Chen, Q. et al. Experimental and theoretical evidence of an axially chiral borospherene. ACS Nano 9, 754–760 (2014).
Lu, X., Feng, L., Akasaka, T. & Nagase, S. Current status and future developments of endohedral metallofullerenes. Chem. Soc. Rev. 41, 7723–7760 (2012).
Zhang, X. et al. A diuranium carbide cluster stabilized inside a C80 fullerene cage. Nat. Commun. 9, 2753 (2018).
Clemmer, D. E., Hunter, J. M., Shelimov, K. B. & Jarrold, M. F. Physical and chemical evidence for metallofullerenes with metal atoms as part of the cage. Nature 372, 248–250 (1994).
Branz, W. et al. Cage substitution in metal–fullerene clusters. J. Chem. Phys. 109, 3425–3430 (1998).
Vostrowsky, O. & Hirsch, A. Heterofullerenes. Chem. Rev. 106, 5191–5207 (2006).
Guo, B., Kerns, K. & Castleman, A. Ti8C12 +-metallo-carbohedrenes: a new class of molecular clusters? Science 255, 1411–1413 (1992).
Dance, I. Ti8C12: barrierless transformation of the T h Isomer to the T d isomer. J. Am. Chem. Soc. 118, 6309–6310 (1996).
Romanescu, C., Galeev, T. R., Li, W. L., Boldyrev, A. I. & Wang, L. S. Aromatic metal‐centered monocyclic boron rings: Co©B8 − and Ru©B9 −. Angew. Chem. Int. Ed. 50, 9334–9337 (2011).
Romanescu, C., Galeev, T. R., Li, W. L., Boldyrev, A. I. & Wang, L. S. Transition-metal-centered monocyclic boron wheel clusters (M©Bn): a new class of aromatic borometallic compounds. Acc. Chem. Res. 46, 350–358 (2012).
Popov, I. A., Jian, T., Lopez, G. V., Boldyrev, A. I. & Wang, L. S. Cobalt-centred boron molecular drums with the highest coordination number in the CoB16 − cluster. Nat. Commun. 6, 8654 (2015).
Li, W. L. et al. The planar CoB18 − cluster as a motif for metallo‐borophenes. Angew. Chem. Int. Ed. 55, 7358–7363 (2016).
Li, W. L. et al. From planar boron clusters to borophenes and metalloborophenes. Nat. Rev. Chem. 1, 0071 (2017).
Jian, T. et al. Probing the structures and bonding of size-selected boron and doped-boron clusters. Chem. Soc. Rev. 48, 3550–3591 (2019).
Li, W. L. et al. Observation of highly stable and symmetric lanthanide octa-boron inverse sandwich clusters. Proc. Natl Acad. Sci. USA 115, E6972–E6977 (2018).
Chen, T. T., Li, W. L., Li, J. & Wang, L. S. La (ηx-Bx)La]−(x = 7–9): a new class of inverse sandwich complexes.Chem. Sci. 10, 2534–2542 (2019).
Chen, T. T., Li, W. L., Chen, W. J., Li, J. & Wang, L. S. La3B14 –: an inverse triple-decker lanthanide boron cluster. Chem. Commun. 55, 7864–7867 (2019).
Dolg, M., Stoll, H. & Preuss, H. A combination of quasi-relativistic pseudopotential and ligand field calculations for lanthanoid compounds. Theor. Chim. Acta 85, 441–450 (1993).
Malik, Z. P., Sologub, O., Grytsiv, A., Giester, G. & Rogl, P. F. Crystal structure of novel Ni–Zn borides: first observation of a boron–metal nested cage unit: B20Ni6. Inorg. Chem. 50, 7669–7675 (2011).
Sergeeva, A. P., Averkiev, B. B., Zhai, H. J., Boldyrev, A. I. & Wang, L. S. All-boron analogues of aromatic hydrocarbons: B17 − and B18 −. J. Chem. Phys. 134, 224304 (2011).
Scheifers, J. P., Zhang, Y. & Fokwa, B. P. Boron: Enabling exciting metal-rich structures and magnetic properties. Acc. Chem. Res. 50, 2317–2325 (2017).
Mitoraj, M. P., Michalak, A. & Ziegler, T. A combined charge and energy decomposition scheme for bond analysis. J. Chem. Theory Comput. 5, 962–975 (2009).
Zubarev, D. Y. & Boldyrev, A. I. Developing paradigms of chemical bonding: adaptive natural density partitioning. Phys. Chem. Chem. Phys. 10, 5207–5217 (2008).
Schleyer, Pv. R., Maerker, C., Dransfeld, A., Jiao, H. & van Eikema Hommes, N. J. Nucleus-independent chemical shifts: a simple and efficient aromaticity probe. J. Am. Chem. Soc. 118, 6317–6318 (1996).
Cui, P. et al. A multicentre-bonded [ZnI]8 cluster with cubic aromaticity. Nat. Commun. 6, 6331 (2015).
Bai, H. et al. Planar B41 − and B42 − clusters with double-hexagonal vacancies. Nanoscale 11, 23286–23295 (2019).
Mbarki, M., St. Touzani, R. & Fokwa, B. P. Unexpected synergy between magnetic iron chains and stacked B6 rings in Nb6Fe1−xIr6+xB8. Angew. Chem. Int. Ed. 53, 13174–13177 (2014).
Sharma, N., Zhang, Y., Fokwa, B., Mbarki, M. & Huq, A. Structural-distortion-driven magnetic transformation from ferro-to ferrimagnetic iron chains in B6-based Nb6FeIr6B8. Angew. Chem. Int. Ed. 57, 10323–10327 (2018).
Zhao, Y., Chen, X. & Li, J. TGMin: a global-minimum structure search program based on a constrained basin-hopping algorithm. Nano Res. 10, 3407–3420 (2017).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Van Lenthe, E. & Baerends, E. J. Optimized Slater‐type basis sets for the elements 1–118. J. Comput. Chem. 24, 1142–1156 (2003).
ADF, SCM, Theoretical Chemistry, Vrijie Universiteit, (Amsterdam, The Netherlands, 2017). http://www.scm.com.
Lenthe, E. V., Baerends, E.-J. & Snijders, J. G. Relativistic regular two‐component Hamiltonians. J. Chem. Phys. 99, 4597–4610 (1993).
Adamo, C. & Barone, V. Toward reliable density functional methods without adjustable parameters: the PBE0 model. J. Chem. Phys. 110, 6158–6170 (1999).
VandeVondele, J. et al. Quickstep: fast and accurate density functional calculations using a mixed Gaussian and plane waves approach. Comput. Phys. Commun. 167, 103–128 (2005).
Li, J., Li, X., Zhai, H. J. & Wang, L. S. Au20: a tetrahedral cluster. Science 299, 864–867 (2003).
Schipper, P. R., Gritsenko, O. V., van Gisbergen, S. J. & Baerends, E. J. Molecular calculations of excitation energies and (hyper) polarizabilities with a statistical average of orbital model exchange-correlation potentials. J. Chem. Phys. 112, 1344–1352 (2000).
Neese, F., Hansen, A. & Liakos, D. G. Efficient and accurate approximations to the local coupled cluster singles doubles method using a truncated pair natural orbital basis. J. Chem. Phys. 131, 064103 (2009).
Weigend, F. & Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: design and assessment of accuracy. Phys. Chem. Chem. Phys. 7, 3297–3305 (2005).
Mayer, I. Bond orders and valences from ab initio wave functions. Int. J. Quantum Chem. 29, 477–483 (1986).
Gopinathan, M. & Jug, K. Valency. I. A quantum chemical definition and properties. Theor. Chim. Acta 63, 497–509 (1983).
Michalak, A., DeKock, R. L. & Ziegler, T. Bond multiplicity in transition-metal complexes: applications of two-electron valence indices. J. Phys. Chem. A 112, 7256–7263 (2008).
Acknowledgements
The experiment done at Brown University was supported by the National Science Foundation (CHE-1763380). The theoretical work done at Tsinghua University was supported by the National Natural Science Foundation of China (21590792, 91426302, and 21433005). The calculations were done using supercomputers at the Southern University of Science and Technology (SUSTech), Tsinghua National Laboratory for Information Science and Technology, and the Computational Chemistry Laboratory of the Department of Chemistry under the Tsinghua Xuetang Talents Program.
Author information
Authors and Affiliations
Contributions
T-T.C. and W-J.C. conducted the experiment; W-L.L. did the calculations with assistance from X-H.Y. and X-R.D.; J.L. and L-S.W. guided the work. T-T.C., W-L.L., J.L., and L-S.W. co-wrote the manuscript. All the authors read and commented on the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks Boniface Fokwa, Panaghiotis Karamanis and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Chen, TT., Li, WL., Chen, WJ. et al. Spherical trihedral metallo-borospherenes. Nat Commun 11, 2766 (2020). https://doi.org/10.1038/s41467-020-16532-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-020-16532-x
This article is cited by
-
Perfect Tetrahedral B16X4 (X = P, As) as Non-metal-stabilized Borospherenes with a Truncated B16 Cage at the Center
Journal of Cluster Science (2024)
-
Half-Sandwich LaBn−/0 (n = 14–17): π Dually Aromatic Lanthanide Boride Complexes with Multicenter Fluxional Bonds
Journal of Cluster Science (2022)
-
Monovalent lanthanide(I) in borozene complexes
Nature Communications (2021)
-
Cage-like La4B24 and Core-Shell La4B290/+/− : perfect spherically aromatic tetrahedral metallo-borospherenes
Journal of Molecular Modeling (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.