Abstract
Genome-wide association studies (GWAS) have led to the identification of hundreds of susceptibility loci across cancers, but the impact of further studies remains uncertain. Here we analyse summary-level data from GWAS of European ancestry across fourteen cancer sites to estimate the number of common susceptibility variants (polygenicity) and underlying effect-size distribution. All cancers show a high degree of polygenicity, involving at a minimum of thousands of loci. We project that sample sizes required to explain 80% of GWAS heritability vary from 60,000 cases for testicular to over 1,000,000 cases for lung cancer. The maximum relative risk achievable for subjects at the 99th risk percentile of underlying polygenic risk scores (PRS), compared to average risk, ranges from 12 for testicular to 2.5 for ovarian cancer. We show that PRS have potential for risk stratification for cancers of breast, colon and prostate, but less so for others because of modest heritability and lower incidence.
Similar content being viewed by others
Introduction
Genome-wide association studies (GWASs) have led to the identification of hundreds of independent cancer susceptibility loci containing common, low-risk variants1,2. The number of discoveries varies widely across cancers, largely driven by available sample size, which reflects, in part, disease incidence in the general population. However, specific cancers, e.g., chronic lymphoid leukemia (CLL)3 and testicular cancer4, are notable for unexpectedly high numbers of genome-wide significant discoveries from GWASs of relatively small sample size. Previous studies have also reported that these two cancers have high heritability5. Across cancer types, polygenic risk scores (PRSs) show varying levels of risk stratification depending on the heritability explained by the identified variants and the disease incidence rates in the population6,7,8,9,10,11,12. Their potential clinical utility would depend not only on the level of risk stratification but also on other factors such as the availability of appropriate risk-reducing interventions for those identified as at high risk.
Estimation of heritability due to additive effects of all single-nucleotide polymorphisms (SNPs) included in GWAS arrays13, referred to as GWAS heritability in this article, have shown that common variants have substantial potential to identify individuals at different levels of risk for many cancer types14. It remains, however, unclear how large the sample sizes of GWAS need to be to reap the full potential of PRS-based risk prediction. Herein we apply our recently published method15 to estimate the degree of polygenicity and the effect-size distribution associated with common variants (minor allele frequency (MAF) > 0.05) across 14 different cancer types, based on summary-level association statistics from available GWASs16,17,18,19,20,21,22,23,24,25,26,27,28 from populations of European ancestry (Supplementary Table 1). From these inferred parameters, we then provide projections of the expected number of common variants to be discovered and predictive performance of associated PRS as a function of increasing sample size for future GWASs. Finally, by incorporating age-specific incidence29 from population-based cancer registries, we explore the magnitude of absolute risk stratification potentially achievable by PRS.
Results
Cancer polygenicity
We found that cancers are highly polygenic, like other complex traits15,30,31. Estimates of the number of susceptibility variants with independent risk associations vary from ~1000 to 7500 between the 14 cancer sites (Table 1). For comparability, effect-size distributions are shown in groups of similarly sized GWASs with similar power for detecting associations (Fig. 1). For GWASs with <10,000 cancer cases (group 1), CLL and testicular cancer are each associated with 2000–2500 variants and characterized by a much larger proportion of variants with larger estimated effect sizes than for the other group 1 cancers, as reflected by wider effect-size distribution with heavier tails (Fig. 1, Table 1). GWAS heritability estimates indicate that, in aggregate, common variants explain a high degree of variation of risk for these two cancers. In contrast, in group 1, esophageal and oropharyngeal cancers are associated with a larger proportion of variants with substantially smaller effect sizes, compared with CLL and testicular cancers in group 1.
Effect-size distribution of susceptibility SNPs is modeled using a two-component normal mixture model for all sites, except esophageal and oropharyngeal cancers. For these sites, effect sizes are modeled using a single normal distribution that provided similar fit as the two-component normal mixture model (see Supplementary Figs. 1 and 2). SNPs with extremely large effects are excluded for effect-size distribution estimation (see “Methods”). Plots are stratified by sample size of the GWAS for comparability. Distributions with fatter tails imply the underlying traits have relatively greater number of susceptibility SNPs with larger effects. Note here that the effect-size distribution is plotted on the log scale of odds ratio (x-axis). CLL chronic lymphocytic leukemia.
For GWASs with 10,000–25,000 cases (group 2), melanoma is noteworthy because it is associated with a wider effect size distribution than other group 2 cancers. The estimated number of susceptibility variants in this group ranges from 1000 to 2000. GWAS heritability estimates indicate that aggregated common variants make a relatively small contribution to ovarian and endometrial cancer susceptibility. Finally, for the 3 GWAS with >25,000 cases each (group 3), prostate cancer is remarkable for having more variants with large effect sizes, namely, the underlying effect-size distribution has a heavier tail, compared with cancers of the breast and lung (Fig. 1). In this group, all three cancer types tend to have large numbers of associated variants (>4500) compared with cancer sites in other groups, but this pattern could partially be due to the very large sample sizes of group 3 GWAS15.
For a large majority of the 14 cancer sites, a two-component normal-mixture model for non-null effects provides a substantially better fit to observed summary statistics than a single normal distribution; this indicates the presence of a fraction of variants with distinctly larger effect sizes than the remaining (Supplementary Figs. 1 and 2). In contrast, a single normal distribution appears to be adequate for esophageal and oropharyngeal cancer, indicating the presence of a large number of variants with a continuum of small effects, similar to our previous findings for traits related to mental health and abilities15. Across all 14 cancers, the predicted number of discoveries and their associated genetic variance explained for current GWAS sample sizes match well to those observed empirically (Supplementary Table 2), indicating good fit of our model to the observed data.
Future GWAS projections
GWAS heritability estimates indicate that the potential of PRS for risk discrimination in the population varies widely among cancer types (Table 1). The area under the curve (AUC) statistics associated with the best achievable PRS varies from 64% (endometrial and ovarian cancer) to 88% (testicular cancer) and in the range of 70–80% for most cancers. The percentage of GWAS heritability explained by known variants varies widely, depending on study sample size and the underlying trait genetic architecture (Fig. 2). Known variants explain more than a quarter of heritability for cancer sites based on very large sample sizes (e.g., breast and prostate cancer) or for cancer sites that have susceptibility variants with relatively large effect sizes (e.g., CLL, melanoma, and testicular cancer). Oropharyngeal cancer, in contrast, has both a small sample size and small effect sizes; its percentage heritability currently explained is almost zero.
Results are shown for projections including SNPs at the optimized p value threshold (solid curve) and at genome-wide significance (p < \(5 \times 10^{ - 8}\)) level (dashed curve). Colored dots correspond to sample size for the largest published GWAS and those for doubled and quadruped sizes. For oropharyngeal cancer, the projections at the “current sample size” are based on a sample size of 25K cases and 25K controls. For breast and esophageal cancer, the projections at the “current sample size” are based on the current largest GWAS sample sizes: 123K cases and 106K controls and 10K cases and 17K controls, respectively. For all other cancer sites, the projections at the “current sample size” are based on the GWAS sample sizes in Supplementary Table 1. CLL chronic lymphocytic leukemia.
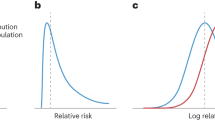
The sample size needed to identify common variants that could explain approximately 80% of the total GWAS heritability for the cancers evaluated is generally very large, requiring 200,000–1,000,000 cancer cases, with a comparable number of controls (Fig. 2). However, for three sites, namely, testicular cancer, CLL, and melanoma, the required sample size is smaller, 60,000, 80,000, and 110,000 cases, respectively, due to the large effect sizes of their associated variants. By quadrupling the sample sizes of currently published GWASs, the percentage of GWAS heritability explained would rise to >40% across all cancers, except for oropharyngeal cancer. Such sample size increases would also lead to appreciable improvements in PRS discriminatory power across all these sites (Figs. 3 and 4). For cancers that were found to be the most polygenic and that had small effect sizes (e.g., cancers of breast, lung, and oropharynx), improvement would occur at a slower rates as sample sizes increase, and these sites would require the largest sample sizes to generate PRSs with discriminatory power close to theoretical limits. Of note, for a number of cancers, the achievable relative risks for subjects at the 99th percentile of PRS distribution compared with those at average risk, are comparable to those for monogenic disorders32 (e.g., relative-risk >3–4-fold) (Fig. 4). Across all 14 cancer types, inclusion of SNPs using more liberal but optimized p value thresholds (see “Methods”) would improve performance of PRS-based risk prediction versus using the stringent genome-wide significance level, but the anticipated gains would be generally modest (Supplementary Figs. 3 and 4).
Results are shown for PRS including SNPs at the optimized p value threshold. The dotted horizontal red line indicates the maximum AUC achievable according to the estimate of GWAS heritability. Colored dots correspond to sample size for largest published GWAS and those for doubled and quadruped sizes. For oropharyngeal cancer, the projections at the “current sample size” are based on a sample size of 25K cases and 25K controls. For breast and esophageal cancer, the projections at the “current sample size” are based on the current largest GWAS sample sizes: 123K cases and 106K controls and 10K cases and 17K controls, respectively. For all other cancer sites, the projections at the “current sample size” are based on the GWAS sample sizes in Supplementary Table 1. CLL chronic lymphocytic leukemia.
Results are shown where PRS is built based on SNPs at optimized p value threshold. The dotted horizontal red line indicates the maximum relative risk achievable according to estimate of GWAS heritability. Colored dots correspond to sample size for the largest published GWAS and those for doubled and quadruped sizes. y-Axis is presented in log10 scale. For oropharyngeal cancer, the projections at the “current sample size” are based on a sample size of 25K cases and 25K controls. For breast and esophageal cancer, the projections at the “current sample size” are based on the current largest GWAS sample sizes: 123K cases and 106K controls and 10K cases and 17K controls, respectively. For all other cancer sites, the projections at the “current sample size” are based on the GWAS sample sizes in Supplementary Table 1. CLL chronic lymphocytic leukemia.
Projections of residual lifetime cancer risks for the US non-Hispanic white population show that the discriminatory power of PRS built from current or foreseeable studies will depend heavily on the underlying cancer incidence in the population (Fig. 5, Supplementary Figs. 5–7). The potential clinical utility of PRS depends on the degree of risk stratification and specific prevention or early detection strategies for a given cancer, should they exist. For common cancers, such as breast, colorectal, and prostate, a PRS with even modest discriminatory power (maximum AUC of approximately 70%, Fig. 3) can provide substantial stratification of absolute risk in the population. In contrast, for CLL and testicular cancer, even though its PRS could achieve a higher AUC (e.g. in the range 80–90%, Fig. 3), the degree of absolute risk stratification will be modest because of the infrequency of these cancers. Thus a PRS by itself has the least impact on risk stratification for cancer sites that are infrequent or/and that have low heritability. However, it is possible that PRS could have clinical utility for some of these cancers in the presence or in combination with other risk factors and biomarkers. For example, a PRS for lung cancer may provide larger stratification for absolute risk among smokers than never smokers because of the higher baseline risk in smokers.
The risk is obtained according to variation of polygenic risk scores. The projections are shown for PRS built based on GWAS with current, doubled and quadrupled sample sizes and the best PRS that corresponds to limits defined by heritability. The projections are obtained by combining information on projected population variance of PRS, age-specific population incidence rate, competing risk of mortality and current distribution of age according to US 2016 census. For oropharyngeal cancer, the projections at the “current sample size” are based on a sample size of 25K cases and 25K controls. For breast and esophageal cancer, the projections at the “current sample size” are based on the current largest GWAS sample sizes: 123K cases and 106K controls and 10K cases and 17K controls, respectively. For all other cancer sites, the projections at the “current sample size” are based on the GWAS sample sizes in Supplementary Table 1. CLL chronic lymphocytic leukemia.
Discussion
Our study is subject to several limitations. We may have underestimated the number of underlying common susceptibility loci, especially for those cancers for which current GWAS have small sample sizes15. Thus the interpretation of comparisons of the underlying genetic architecture across cancer types with very different sample sizes requires caution. Nevertheless, the major patterns are unlikely to be due to differences in sample size. For example, we estimated oropharyngeal and esophageal cancers to be two of the most polygenic sites, though the GWAS sample sizes for these two sites were relatively small. Further, Q–Q plots of observed and expected p values indicate that the inferred models for effect-size distributions explain observed GWAS summary statistics well, regardless of GWAS sample size. Another important limitation is that we only included data from subjects of European ancestry, since GWAS data for other ancestries are currently too small to permit reliable projections for most cancer sites. In addition, several cancers (e.g., lung, ovary, glioma, and breast) consist of etiologically heterogeneous subtypes that were not considered in our analyses due to lack of adequate sample sizes for appropriate subtypes for most of these cancer sites. Further studies of ancestry- and subtype-specific genetic architectures are needed to address these limitations.
In our projections, we assume standard agnostic association analysis of SNPs without incorporating any external information on population genetics or functional characteristics of SNPs. It is, however, possible to incorporate various types of external information to improve power for discovery of associations33,34,35,36 and genetic risk prediction37. We have evaluated the merit of future GWAS only in terms of their ability to explain heritability and improve risk prediction. However, current and future discoveries have other major implications, including provident insights to biological pathways and mechanisms, potential gene–environment interactions, and understanding causal relationships through Mendelian Randomization analyses38. A number of these cancers are known to have rare high-penetrant risk variants, but for this study we have focused on estimating effect-size distribution associated with common variants. Furthermore, heritability analysis indicate that uncommon and rare variants could explain a substantial fraction of the variation of complex traits39, and thus it is likely that there are many unknown uncommon and rare variants associated with these cancers as well. In the future, characterization of heritability and effect-size distribution associated with the full spectrum of allele frequencies will require individual-level sequencing data on a substantially larger number of cases and controls.
The observed differences in the underlying genetic architecture of susceptibility across cancers could be due to various factors, including the effect of negative selection30,40, tissue-specific genetic regulation of gene expression41, cell of origin42, the number of biological steps needed to transition from normal to malignant tissue43, mediation of genetic effects by underlying environmental exposures44, and the presence of heterogeneous cancer-specific subtypes21,25,27,28. A number of cancer types, including those of lung, oropharynx, and esophagus, which were associated with large numbers of SNPs with small average effect sizes, have known strong environmental risk factors and distinct etiologic subtypes. It is also noteworthy that testicular cancer also stands out for a large number of discoveries in cross-tissue expression quantitative trait loci analyses, likely indicating a stronger association of SNPs on gene expression levels for this tissue compared to others41.
In conclusion, our comprehensive analysis of 14 cancer sites in adults of European ancestry reveals that, while all sites have polygenic influences, there is substantial diversity observed in their underlying genetic architectures, which reflects important biology and also influences the utility of polygenic risk prediction for individual cancers. Our projections for future yields of GWAS across these cancers provide a roadmap for important returns from future investment in research, including the potential clinical utility of polygenic risk prediction for stratification of absolute risks in the population.
Methods
Description of GWAS studies
We analyzed summary data from GWAS studies across 14 cancer types. For select cancer sites26,28, we downloaded publicly available genome-wide summary-level statistics from the latest consortium-based analyses. For others, we obtained access to data through collaborative efforts with individual consortia. Details about individual studies, including the number of cases and controls, are provided in Supplementary Table 1.
Linkage disequilibrium (LD) reference panel selection
We consider a reference panel with ~1.07 million SNPs included in the HapMap3 and that had MAF > 0.05 in the 1000 Genome European Ancestry sample. Based on known LD among common variants, we expect these set of variants to provide high coverage for all common variants for European ancestry population and thus loss of information due to imperfect tagging of causal variants to be fairly minimal.
Quality control for summary GWAS data
Across all cancers, we applied several filtering steps analogous to those used earlier for estimation of heritability45,46 and effect-size distribution using summary-level data15. First, we restricted analysis to SNPs within a set of reference ~1.07 million SNPs included in the HapMap3 and that had MAF > 0.05 in the 1000 Genome European Ancestry sample. Second, we excluded SNPs having substantial amounts of missing genotype data: sample sizes <0.67 times the 90th percentile of the distribution of sample sizes across all SNPs. Third, we excluded SNPs within the major histocompatibility complex region (i.e., SNPs between 26,000,000 and 34,000,000 base pairs on chromosome six), which is known to have very complex allelic architecture and can have uncharacteristically large effects on some traits. Fourth, we removed regions that have SNPs with extremely large effect sizes to reduce possible undue influence of them on estimation of parameters associated with overall effect-size distributions. Using PLINK --clump, we identify all top SNPs that have associated chi-square statistics >80 (i.e., odds ratio (in standardized scale) >2.19) and removed all SNPs that were within 1-MB distance of or had an estimated squared LD >0.1 with those top SNPs. We added back the contribution of these top independent SNPs in the final reporting of the total number of susceptibility SNPs, estimates of total heritability, and various projections we made as a function of sample size of the GWAS.
Statistical model
We inferred common variant genetic architecture of the different cancers using GENESIS15, a method we recently developed to characterize underlying effect-size distributions in terms of the total number of susceptibility SNPs (polygenicity) and a normal mixture model for the distribution of their effects. Specifically, it is assumed that standardized effects of common SNPs in an underlying logistic regression model on the risk of a cancer can be specified in the mixture distribution in the form \(\beta _m \sim \left( {1 - \pi _{\mathrm{c}}} \right)\delta _0 + \pi _{\mathrm{c}}N(0,\sigma ^2)\) (two-component model) or \(\beta _m \sim \left( {1 - \pi _{\mathrm{c}}} \right)\delta _0 + \pi _{\mathrm{c}}\left[ {p_1N\left( {0,\sigma _1^2} \right) + p_2N\left( {0,\sigma _2^2} \right)} \right]\) (three-component model) where \(\delta _0\) is the Dirac delta function indicating that a fraction, \(1 - \pi _{\mathrm{c}}\), of the SNPs have null effects and remaining \(\pi _{\mathrm{c}}\) fraction of SNPs have non-null effects. Under the three-component model, \(p_2 = 1 - p_1\) denotes the proportion of SNPs allocated to mixture component with larger variance component (assuming \(\sigma _2^2\) > \(\sigma _1^2\)) models. Under these models, \(M\pi _{\mathrm{c}}\) characterizes the degree of polygenicity, i.e., the number of susceptibility SNPs with independent effects on disease risk. Under both models, we defined “GWAS heritability” of a disease as \(h^2 = M\pi _{\mathrm{c}}{\mathrm{E}}\left( {\beta ^2} \right)\), where \({\mathrm{E}}\left( {\beta ^2} \right)\) denotes the average variance size of the non-null SNPs. We observed that, under the above model, \(h^2\) is also the population variance of the underlying “true” PRS, defined as \({\mathrm{PRS}} = \mathop {\sum }\nolimits_{m = 1}^M \beta _mG_m\), where \(G_m\) denotes the standardized genotype associated with the \(m\)th SNP. Under the two-component model, which assumes a single normal distribution for the effect of all susceptibility SNPs, \(E\left( {\beta ^2} \right) = \sigma ^2\). Under the three-component model, which allows mixture of two normal distributions with distinct variance components and thus can better accommodate the presence of a group of susceptibility SNPs with much larger effects than others, we have \(p_1\sigma _1^2 + p_2\sigma _2^2\). Under the three-component model, we use the fraction \(\upsilon = p_2\sigma _2^2/(p_1\sigma _1^2 + p_2\sigma _2^2)\) to characterize the proportion of heritability explained by SNPs associated with the larger variance component parameter. As we removed SNPs with extremely large effects (\(\chi _i^2\;> \;80\)) and the associated regions from the analysis, in reporting the final heritability estimates, we added back the contribution of the independent top SNPs from these excluded regions as \(\mathop {\sum }\nolimits_i (\hat \beta _i^2 - \tau _i^2)\) where \(\hat \beta_i\) is the estimate of log odds ratio (in standardized scale) and \(\tau _i\) is the corresponding standard error for the \(i\)th SNP.
Genetic variance projection
Given the estimated effect-size distribution, we calculated expected discoveries and genetic variance explained using \({\mathrm{ED}} = M\hat \pi _{\mathrm{c}}\mathop {\smallint }\limits_\beta {\mathrm{pow}}_{\alpha ,n}\left( \beta \right)\mathop {\sum }\nolimits_{h = 1}^H \hat p_hN\left( {0,\hat \sigma _h^2} \right)d\beta\) and \({\mathrm{EV}} = M\hat \pi _{\mathrm{c}}\mathop {\smallint }\limits_\beta \beta ^2{\mathrm{pow}}_{\alpha ,n}\left( \beta \right)\mathop {\sum }\nolimits_{h = 1}^H \hat p_hN\left( {0,\hat \sigma _h^2} \right)d\beta\), respectively, at \(\alpha = 5 \times 10^{ - 8}\) for a GWAS of sample size \(n\), where \({\mathrm{pow}}_{\alpha ,n}\left( \beta \right) = 1 - \Phi \left( {c_{\frac{\alpha }{2}} - \sqrt n \beta } \right) + \Phi ( - c_{\frac{\alpha }{2}} - \sqrt n \beta )\) with \(\Phi \left( \cdot \right)\) the standard normal cumulative density function and \(c_\alpha = \Phi ^{ - 1}\left( {1 - \alpha } \right)\) the αth quantile for the standard normal distribution. Similar to heritability calculations, we added back the contributions of independent top SNPs with very large effects to the number of expected discoveries and associated variances explained by the quantities \(\mathop {\sum }\nolimits_i {\mathrm{pow}}_{\alpha ,n}(\hat \beta _i)\) and \(h^{ - 2}\mathop {\sum }\nolimits_i (\hat \beta _i^2 - \tau _i^2){\mathrm{pow}}_{\alpha ,n}(\hat \beta _i)\). We observed that for projections involving sample sizes bigger than the current study \({\mathrm{pow}}_{\alpha ,n}\left( {\hat \beta _i} \right)\) for the large effect SNPs will all be very close to 1.0.
Projection for AUC and relative risk at top 1%
As we quantify heritability in terms of the variability of the underlying “true” PRS, we used the formula12,47,48 \({\mathrm{AUC}} = \Phi (\sqrt {\frac{{h^2}}{2}} )\) to characterize the best discriminatory power achievable in limiting using common variant PRS. We used the same formula to calculate the AUC associated with PRSs that could be built using SNPs either reaching genome-wide significance (p value <5\(\times 10^{ - 8}\)) or a weaker but optimized threshold for a GWAS of given sample size based on the projected variance of the respective PRS. Given sample size of GWAS and an effect-size distribution for the underlying cancer, an optimal threshold for SNP selection that will maximize the expected predictive performance of PRS is calculated using analytic formula we have derived earlier48. The relative risk for those estimated to be at the 99th percentile or higher of the distribution of a PRS (compared to the average risk of the population) was calculated using the formula12 \({\mathrm{exp}}( - \frac{{h^2}}{2} + \Phi ^{ - 1}\left( {0.99} \right)\sqrt {h^2} )\), where \(h^2\) is the population variance of the PRS.
Absolute risk projection
For each cancer site, we projected the distribution of residual lifetime risk (up to age 80 years) for non-Hispanic white individuals in the general US population according to PRSs, which could be built from GWASs of different sample sizes. For any given age, we first obtain the distribution of residual lifetime risks based on a model for absolute risks developed using the iCARE tool that we have described earlier12,29. The iCARE tool uses projected standard deviations of PRS at different GWAS sample sizes and age-specific cancer incidence rates available from the US National Cancer Institute-Surveillance, Epidemiology, and End Results Program (NCI-SEER) (2015) to obtain absolute risk distributions. In deriving absolute risks, we adjusted for competing risk of mortality due to other causes using the age-specific mortality rates from the Center for Disease Control WONDER database (2016). We then weighted the projected residual lifetime risk distribution at different baseline ages (in 5-year categories) based on the US population distribution of ages within 30–75 years, as observed in the estimated 2016 US Census. For cancers of the reproductive system, weights were based on the age distributions among males or females, as appropriate.
Reporting summary
Further information on research design is available in the Nature Research Reporting Summary linked to this article.
Data availability
The data that support the findings of this study are available by application from the participating consortia: BCAC (bcac@medschl.cam.ac.uk), BEACON (P Gharahkhani), ColonCFR (M Jenkins), GECCO/CORECT (U Peters), ECAC (TA O’Mara), GenoMEL (M Iles), GICC (R Houlston), ILLCO/INTEGRAL (C Amos), InterLymph (S Berndt), OCAC (PDP Pharoah), Oral Cancer GWAS (P Brennan), PanC4/PanScan (LT Amundadottir), PRACTICAL (Data Access Committee/http://practical.icr.ac.uk/), Renal Cancer GWAS (MP Purdue, P Brennan), and TECAC (KA McGlynn). For breast and prostate cancers, summary GWAS data can also be downloaded from http://bcac.ccge.medschl.cam.ac.uk/bcacdata/oncoarray/gwas-icogs-and-oncoarray-summary-results/ and http://practical.icr.ac.uk/blog/?page_id=8164.
Code availability
The code for running the analysis in the paper is freely available from the CancerEffectSize GitHub repository (https://github.com/yandorazhang/CancerEffectSize).
References
Sud, A., Kinnersley, B. & Houlston, R. S. Genome-wide association studies of cancer: current insights and future perspectives. Nat. Rev. Cancer 17, 692–704 (2017).
Tam, V. et al. Benefits and limitations of genome-wide association studies. Nat. Rev. Genet. 20, 467–484 (2019).
Law, P. J. et al. Genome-wide association analysis implicates dysregulation of immunity genes in chronic lymphocytic leukaemia. Nat. Commun. 8, 14175 (2017).
Litchfield, K. et al. Identification of 19 new risk loci and potential regulatory mechanisms influencing susceptibility to testicular germ cell tumor. Nat. Genet. 49, 1133–1140 (2017).
Mucci, L. A. et al. Familial risk and heritability of cancer among twins in Nordic countries. JAMA 315, 68–76 (2016).
Maas, P. et al. Breast cancer risk from modifiable and nonmodifiable risk factors among white women in the United States. JAMA Oncol. 2, 1295–1302 (2016).
Mavaddat, N. et al. Polygenic risk scores for prediction of breast cancer and breast cancer subtypes. Am. J. Hum. Genet. 104, 21–34 (2019).
Jeon, J. et al. Determining risk of colorectal cancer and starting age of screening based on lifestyle, environmental, and genetic factors. Gastroenterology 154, 2152.e19–2164.e19 (2018).
Seibert, T. M. et al. Polygenic hazard score to guide screening for aggressive prostate cancer: development and validation in large scale cohorts. BMJ 360, j5757 (2018).
Garcia-Closas, M. et al. Common genetic polymorphisms modify the effect of smoking on absolute risk of bladder cancer. Cancer Res. 73, 2211–2220 (2013).
Turnbull, C., Sud, A. & Houlston, R. S. Cancer genetics, precision prevention and a call to action. Nat. Genet. 50, 1212–1218 (2018).
Chatterjee, N., Shi, J. & García-Closas, M. Developing and evaluating polygenic risk prediction models for stratified disease prevention. Nat. Rev. Genet. 17, 392–406 (2016).
Yang, J. et al. Common SNPs explain a large proportion of the heritability for human height. Nat. Genet. 42, 565–569 (2010).
Sampson, J. N. et al. Analysis of heritability and shared heritability based on genome-wide association studies for thirteen cancer types. J. Natl Cancer Inst. 107, djv279 (2015).
Zhang, Y., Qi, G., Park, J. H. & Chatterjee, N. Estimation of complex effect-size distributions using summary-level statistics from genome-wide association studies across 32 complex traits. Nat. Genet. 50, 1318–1326 (2018).
Berndt, S. I. et al. Meta-analysis of genome-wide association studies discovers multiple loci for chronic lymphocytic leukemia. Nat. Commun. 7, 10933 (2016).
Wang, Z. et al. Meta-analysis of five genome-wide association studies identifies multiple new loci associated with testicular germ cell tumor. Nat. Genet. 49, 1141–1147 (2017).
Lesseur, C. et al. Genome-wide association analyses identify new susceptibility loci for oral cavity and pharyngeal cancer. Nat. Genet. 48, 1544–1550 (2016).
Klein, A. P. et al. Genome-wide meta-analysis identifies five new susceptibility loci for pancreatic cancer. Nat. Commun. 9, 556 (2018).
Scelo, G. et al. Genome-wide association study identifies multiple risk loci for renal cell carcinoma. Nat. Commun. 8, 15724 (2017).
Melin, B. S. et al. Genome-wide association study of glioma subtypes identifies specific differences in genetic susceptibility to glioblastoma and non-glioblastoma tumors. Nat. Genet. 49, 789–794 (2017).
Law, M. H. et al. Genome-wide meta-analysis identifies five new susceptibility loci for cutaneous malignant melanoma. Nat. Genet. 47, 987–995 (2015).
O’Mara, T. A. et al. Identification of nine new susceptibility loci for endometrial cancer. Nat. Commun. 9, 3166 (2018).
Schumacher, F. R. et al. Genome-wide association study of colorectal cancer identifies six new susceptibility loci. Nat. Commun. 6, 7138 (2015).
Phelan, C. M. et al. Identification of 12 new susceptibility loci for different histotypes of epithelial ovarian cancer. Nat. Genet. 49, 680–691 (2017).
Schumacher, F. R. et al. Association analyses of more than 140,000 men identify 63 new prostate cancer susceptibility loci. Nat. Genet. 50, 928–936 (2018).
McKay, J. D. et al. Large-scale association analysis identifies new lung cancer susceptibility loci and heterogeneity in genetic susceptibility across histological subtypes. Nat. Genet. 49, 1126–1132 (2017).
Michailidou, K. et al. Association analysis identifies 65 new breast cancer risk loci. Nature 551, 92–94 (2017).
Choudhury, P. P. et al. iCARE: an R package to build, validate and apply absolute risk models. PLoS ONE 15, e0228198 (2020).
Zeng, J. et al. Signatures of negative selection in the genetic architecture of human complex traits. Nat. Genet. 50, 746–753 (2018).
Stahl, E. A. et al. Bayesian inference analyses of the polygenic architecture of rheumatoid arthritis. Nat. Genet. 44, 483–489 (2012).
Khera, A. V. et al. Genome-wide polygenic scores for common diseases identify individuals with risk equivalent to monogenic mutations. Nat. Genet. 50, 1219–1224 (2018).
Schork, A. J. et al. All SNPs are not created equal: genome-wide association studies reveal a consistent pattern of enrichment among functionally annotated SNPs. PLoS Genet. 9, e1003449 (2013).
Pickrell, J. K. Joint analysis of functional genomic data and genome-wide association studies of 18 human traits. Am. J. Hum. Genet. 94, 559–573 (2014).
Andreassen, O. A. et al. Improved detection of common variants associated with schizophrenia by leveraging pleiotropy with cardiovascular-disease risk factors. Am. J. Hum. Genet. 92, 197–209 (2013).
Andreassen, O. A. et al. Improved detection of common variants associated with schizophrenia and bipolar disorder using pleiotropy-informed conditional false discovery rate. PLoS Genet. 9, e1003455 (2013).
Hu, Y. et al. Leveraging functional annotations in genetic risk prediction for human complex diseases. PLoS Comput. Biol. 13, e1005589 (2017).
Davey Smith, G. & Hemani, G. Mendelian randomization: genetic anchors for causal inference in epidemiological studies. Hum. Mol. Genet. 23, R89–R98 (2014).
Wainschtein, P. et al. Recovery of trait heritability from whole genome sequence data. Preprint at https://www.biorxiv.org/content/10.1101/588020v1 (2019).
O’Connor, L. J. et al. Extreme polygenicity of complex traits is explained by negative selection. Am. J. Hum. Genet. 105, 456–476 (2019).
GTEx, C. The Genotype-Tissue Expression (GTEx) project. Nat. Genet. 45, 580–585 (2013).
Visvader, J. E. Cells of origin in cancer. Nature 469, 314–322 (2011).
Rizzo, A. A., Strickland, D. & Bouchard, S. The challenge of using virtual reality in telerehabilitation. Telemed. J. E Health 10, 184–195 (2004).
Hutter, C. M. et al. Gene-environment interactions in cancer epidemiology: a National Cancer Institute Think Tank report. Genet. Epidemiol. 37, 643–657 (2013).
Bulik-Sullivan, B. K. et al. LD score regression distinguishes confounding from polygenicity in genome-wide association studies. Nat. Genet. 47, 291–295 (2015).
Zheng, J. et al. LD Hub: a centralized database and web interface to perform LD score regression that maximizes the potential of summary level GWAS data for SNP heritability and genetic correlation analysis. Bioinformatics 33, 272–279 (2017).
Pharoah, P. D. et al. Polygenic susceptibility to breast cancer and implications for prevention. Nat. Genet. 31, 33–36 (2002).
Chatterjee, N. et al. Projecting the performance of risk prediction based on polygenic analyses of genome-wide association studies. Nat. Genet. 45, 400–405 (2013).
Acknowledgements
The research was supported by an RO1 grant from NHGRI (1 R01 HG010480-01) and the intramural program of the National Cancer Institute.
Author information
Authors and Affiliations
Consortia
Contributions
N.C. and M.G.-C. conceived the project. Y.Z. and A.W. performed main analyses. Y.Z., N.C., and M.G.-C. wrote the first draft of the manuscript. BCAC, BEACON, CCFR, CORECT, ECAC, GECCO, GenoMEL, GICC, ILCCO, Integral, InterLymph, OCAC, Oral Cancer GWAS, PANC4, PanScan, PRACTICAL, Renal Cancer GWAS, and TECAC contributed data. P.P.C., R.L.M., M.K.S., M.J., U.P., L.H., S.L. Schmit., T.A.O., A.B.S., D.J.T., M.H.L., M.M.I., F.D., S.M., S.V.W., M.R.W., C.I.A., S.I.B., B.M.B., N.J.C., P.D.P.P., T.A.S., L.T.A., E.J.J., H.A.R., R.Z.S.-S., M.P.P., M.H.G., K.A.M., and S.J.C. commented on earlier drafts of the manuscript. H.Z., D.F.E., J.S., P.H., K.M., J.D., J.C.-C., P.G., D.W., P.T.C., M.H., S.B.G., G.C., I.T., I.D.V., M.T.L., R.K., D.T.B., M.L.B., R.H., J.K.W., B.M., J.B.-S., B.K., R.J.H., P.B., J.M., N.E.C., P.K., N.R., S.L. Slager., A.B., S.A.G., C.L.P., E.L.G., J.M.S., K.B.M., A.P.K., G.M.P., B.M.W., D.L., R.A.E., C.A.H., Z.K.-J., F.R.S., A.A.A.O., G.S., M.D.D., T.G., P.A.K., K.L.N., C.T., and F.W. reviewed the manuscript. All authors reviewed and approved the final draft of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhang, Y.D., Hurson, A.N., Zhang, H. et al. Assessment of polygenic architecture and risk prediction based on common variants across fourteen cancers. Nat Commun 11, 3353 (2020). https://doi.org/10.1038/s41467-020-16483-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-020-16483-3
This article is cited by
-
Genetic variation across and within individuals
Nature Reviews Genetics (2024)
-
Germline determinants of aberrant signaling pathways in cancer
npj Precision Oncology (2024)
-
Polymorphisms in transcription factor binding sites and enhancer regions and pancreatic ductal adenocarcinoma risk
Human Genomics (2024)
-
Polygenic scores in cancer
Nature Reviews Cancer (2023)
-
Biobank-scale methods and projections for sparse polygenic prediction from machine learning
Scientific Reports (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.