Abstract
Defects can induce drastic changes of the electronic properties of two-dimensional transition metal dichalcogenides and influence their applications. It is still a great challenge to characterize small defects and correlate their structures with properties. Here, we show that tip-enhanced Raman spectroscopy (TERS) can obtain distinctly different Raman features of edge defects in atomically thin MoS2, which allows us to probe their unique electronic properties and identify defect types (e.g., armchair and zigzag edges) in ambient. We observed an edge-induced Raman peak (396 cm−1) activated by the double resonance Raman scattering (DRRS) process and revealed electron–phonon interaction in edges. We further visualize the edge-induced band bending region by using this DRRS peak and electronic transition region using the electron density-sensitive Raman peak at 406 cm−1. The power of TERS demonstrated in MoS2 can also be extended to other 2D materials, which may guide the defect engineering for desired properties.
Similar content being viewed by others
Introduction
Two-dimensional (2D) transition metal dichalcogenides (TMDCs) have emerged as promising materials with remarkable physicochemical properties1,2,3,4. Almost all TMDCs inevitably contain structure defects generated from the fabrication process. Though these defects are small (few nanometers and even single atom), they can break the lattice symmetry, create a quantum-confined environment, and modify the electronic band structures. These heterogeneities affect the electron excitation, electron scattering, and also energy transfer between phonons and electrons5,6,7. Therefore, defects introduce unique electronic properties in TMDCs and in turn dictate their electrical, optical, and chemical behaviors5,6,7. Moreover, defect effect leads to the band bending and the varied carrier density results in a gradual change of electronic properties of the nearby pristine materials. The formed electronic property variation regions between defect and pristine material have significant but different impacts on the electronic and chemical properties of 2D materials6,7,8. It was found that the electron transfer rate of graphene decreased in the lattice disordered region, whereas increased in the electronic transition region (ETR)8. Therefore, quantitative measurement of the lengths of these two regions may guide the effective defect engineering. The electronic properties of 2D materials can be impressively influenced by the edge defects5,7, e.g., the zigzag edge is metallic, whereas the armchair edge is semiconducting for MoS29. The identification of defect types may in turn help correlate defects and their electronic properties, and guide the effective defect engineering.
Up to now, considerable efforts have been devoted to characterizing and understanding the electronic properties of defects. However, it is still a great challenge because defects are so small that their signals may be obscured by the strong signals of the surrounding pristine materials. Although scanning tunneling spectroscopy is able to characterize the electronic properties of defects at nanometer or even atomic scale6,10,11, it has to work under ultrahigh vacuum and ultralow temperature, which is much different from the real application environment of TMDCs.
In this work, we employed tip-enhanced Raman spectroscopy (TERS), which can simultaneously obtain the morphologic and chemical fingerprint information with a nanometer spatial resolution and even single-molecule sensitivity assisted by the huge electromagnetic field enhancement of the plasmonic Au or Ag tip12,13, to probe the edge-related lattice structure and corresponding electronic properties of atomically thin MoS2. We showed that TERS can spatially obtain distinctly different Raman features of the edge defects in mono- and bilayer MoS2, and investigate their unique lattice vibration and electronic properties. We observed an edge-induced Raman peak (396 cm−1) activated by the double resonance Raman scattering (DRRS) process, and revealed the interaction of electron and phonon, which was significantly affected by the electronic band structures at the edge.
We further visualize the defect-induced band-bending region of the conduction band at K and Q states which are involved in the DRRS process by using the DRRS-related Raman peak at 396 cm−1 and the ETR using the electron density-sensitive Raman peak at 406 cm−1. Notably, we spatially distinguished zigzag and armchair edges by using their spectral features, which can hardly be realized with conventional spectroscopic techniques. The power of TERS demonstrated in MoS2 can also be extended to other TMDCs materials, which may provide a deep understanding of the fundamental electronic properties and guide the defect engineering for desired properties.
Results
Raman features of different 1D defects in 1 L and 2 L MoS2
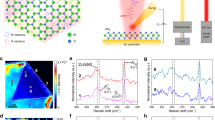
The scheme to measure the TERS signals on edge defects in MoS2 materials is shown in Fig. 1a. We first measured the far-field Raman spectra of the sample followed by topological imaging by an atomic force microscope (AFM) to identify the interested defects. Finally, we measured the TERS signal (in either single point or imaging manner). In this work, we used the mechanically exfoliated14,15 monolayer (1 L) and bilayer (2 L) MoS2 with different one-dimensional (1D) defects (1 L wrinkle, 1 L edge, 1–2 L step, and 2 L edge) transferred onto an atomically smooth Au substrate as the sample, and the AFM image of the sample was shown in Fig. 1b. The far-field Raman spectra on 1 and 2 L pristine MoS2, and TERS spectra obtained on different types of defects are shown in Fig. 1c. The TERS signals from these defects are clearly different from the far-field signal of 1 and 2 L pristine MoS2, and the different types of defects also show strikingly different Raman features in both the peak position and peak intensity. Most interestingly, the two peaks at 220 and 396 cm−1 marked in the Raman spectra selectively present on the defect. Such fine features are not induced by TERS tips (as shown in the near-field spectra of the basal plane in Fig. 1c, upper two spectra) and will not be possible to observe without the help of the high spatial resolution of TERS.
TERS study of edge defects in the atomically thin MoS2. a Schematic of a TERS configuration using an Au-coated AFM tip and an atomically smooth Au film with monolayer (1 L) or bilayer (2 L) MoS2 on the surface. b AFM image of the mechanically exfoliated MoS2 with different types of 1D defect on an Au substrate. c Raman spectra of four 1D defects and the basal plane in MoS2 marked in b, when the tip was approached and retracted. Note that these spectra are the near-field spectra and have been subtracted with the far-field signal, as well as the tip-enhanced photoluminescence background from MoS2 and surface plasmon resonance (SPR) from the TERS tip. The intensity is normalized to the A1g peak for comparison.
The broad Raman peak at ~220 cm−1 can only be observed in defects with dangling bonds (unsaturated coordination, such as edges and step), and absent in wrinkle and pristine MoS2, as shown in Fig. 1c. This peak has been assigned to the defect-induced longitudinal acoustic phonons (LA mode) with a DRRS feature5,7,16,17, similar to that of the D-band in graphene18. For the DRRS process of LA mode to occur, it requires one phonon and a defect for the momentum conservation18,19,20,21,22. The defect of the edge and step with dangling bonds will participate in the DRRS through the elastic scattering of the excited electron. However, the investigated wrinkle induces small lattice strain (≤0.4%; Supplementary Fig. 7), which exhibits little influence on lattice vibration23. Consequently, the wrinkle-assisted elastic scattering can be neglected, and the LA mode in wrinkle with a small curvature is absent according to the Raman selection rule.
In comparison, the 396 cm−1 peak was observed in the defects in the multilayer MoS2 (2 L edge and 1–2 L step in Fig. 1c) and was absent in the defects of monolayer MoS2 (1 L edge and 1 L wrinkle in Fig. 1c). This peak was only explicitly observed and studied in the bulk MoS2 at an ultralow temperature24,25,26 and has not yet been observed experimentally in the defect at room temperature. It has been assigned to the combination of the LA and transverse acoustic (TA) phonons at the M point (LA(M) + TA(M)) of the Brillouin zone27. In addition, our wavelength-dependent measurement on the bulk MoS2 at room temperature further reveals that this mode can only be activated under the resonance condition (Supplementary Fig. 15a; red and blue spectra) and the frequency of this peak shifts with the change of the laser excitation energy (Supplementary Fig. 15a; inset). The latter phenomenon is a signature of a DRRS, which requires photons with different energies to select electrons and phonons with different wave vectors in the Brillouin zone to satisfy the energy and momentum conservation21. This peak (396 cm−1) is found to be related to the DRRS process between K and Q valleys and involves two phonons, i.e., LA(M) and TA(M) with wave vectors qM (Fig. 2a and Supplementary Fig. 15b). This DRRS process starts with an incoming photon (660 nm laser), whose energy matches the bandgap near K point, creating an electron–hole pair near K point. The electron can be excited by a resonant transition from the state in the valence band to the state in the conduction band. Then the excited electron can be resonantly scattered by emitting a phonon with wave vector qM to the electron state in the conduction band near Q point, when the energy of the K conduction band (ECK) is larger than that of the Q conduction band (ECQ). Afterward, the electron is inelastically scattered back to the virtual electron state near the K valley by emitting a second phonon with wave vector −qM, where the electron–hole pair recombines and emits a photon with energy Elaser − ħωLA(M)+TA(M) in valence band near K points. Therefore, the Raman intensity of this phonon can be greatly enhanced. Hence, when the energy of the K conduction band (ECK) is higher than that of the Q conduction band (ECQ; Fig. 2a), the probability of the DRRS process increases and thus enhances the corresponding Raman mode at 396 cm−1. This peak is weak and even absent in the mono- and bilayer MoS2 (Supplementary Fig. 15d) because ECK is smaller than ECQ (Supplementary Fig. 15b) in these two cases and the DRRS can hardly be activated. However, if there are defects in the mono- and bilayer MoS2, they will lead to bending of the electronic band structure of MoS2, resulting in a considerable change of ECK and ECQ (Fig. 2b, see Supplementary Note 3.3 for details about the electronic band structures of nanoribbon with different widths). As a result, the DRRS can be activated and the intensity of this peak can be greatly enhanced in the 1–2 L step and 2 L edge, since ECK becomes larger than ECQ (Fig. 2b; right two panels). Whereas, the possibility of DRRS is low in the 1 L wrinkle and 1 L edge due to the smaller ECK compared to ECQ (Fig. 2b; left two panels). This DRRS-involved mode opens up an opportunity to further study the intervalley scattering of electrons by acoustic phonons in the defect. It should be pointed out that it is almost impossible to observe this peak in the defect without the high spatial resolution provided by TERS.
DRRS in the defect. a Representation of DRRS process of the LA(M) + TA(M) mode. b Electronic band structures of monolayer wrinkle (monolayer nanoribbon with 0.4% strain (Supplementary Figs. 6 and 7), for more details see Supplementary Note 3), monolayer armchair nanoribbon (1 L edge), monolayer armchair nanoribbon on the monolayer basal plane (1–2 L step), and bilayer armchair nanoribbon (2 L edge). Blue and green dots are K and Q points of conduction bands, respectively. The solid horizontal red arrows indicate the DRRS can occur and the dash arrows cannot occur. Note that the width armchair nanoribbon employed here is ~2.4 nm. See Supplementary Note 3.3 for details about the electronic band structures of nanoribbon with different widths (1–3 nm).
Nanoscale characterization of the edge in the bilayer MoS2
With the observed distinctive spectral features related to the defects, we further explored the different Raman features at the edge and basal plane of MoS2. Figure 3a shows the topographic height profile (left panel) and the corresponding color-coded intensity map of the line-trace TERS image (right panel) of the bilayer edge marked in Supplementary Fig. 16b, inset. The larger height of the bilayer MoS2 (~1.8 nm) compared with the typical bilayer thickness (1.4–1.6 nm)28,29 is the result of a thin water layer existing between MoS2 and the substrate30,31,32 (Supplementary Figs. 1 and 2), which can block the doping effect from the Au substrate (Supplementary Note 1). The line-trace TERS image of the edge matches well with the height profile. When the tip was positioned on the Au substrate, only the far-field Raman signal of the pristine bilayer MoS2 was observed. When the tip was moved gradually from the Au substrate to MoS2, both the TERS spectral background contributed by tip-enhanced photoluminescence (TEPL) of the bilayer MoS2 and the Raman signal are enhanced and reach the maximum values at the edge. Interestingly, the TEPL spectra can be deconvoluted into a short wavelength part contributed by the neutral electron–hole pair (A-exciton) and a long wavelength part by the charged complex (A−-trion; Supplementary Fig. 16c, d), and A exciton PL dominates in the TEPL spectra at both edge and basal plane MoS2. It has been reported that the carrier density can be estimated from the exciton and trion PL spectral weight10,11,33. We observed an increased A integrated intensity and a decreased A− integrated intensity near the edge site, indicating that part of A− trions have lost electrons and transformed into A excitons. Therefore, electron density near the edge is lower than that of the basal plane. A depletion of electrons weakens the charge screening effect, leading to a higher intensity of all the Raman modes at the edge34,35 (Supplementary Fig. 17 shows that as the potential shifts positively, the intensity of all the Raman modes increases). Similarly, we can conclude that the other three types of 1D defects also have a lower electron density than the basal plane from the line-trace TERS image (Supplementary Fig. 18).
TERS characterization of a bilayer edge in MoS2. a TERS line image across the edge of a bilayer MoS2. Left panel: topographic height profile of the edge of bilayer MoS2 marked in Supplementary Fig. 16b inset. Right panel: a line-trace TERS image of the edge. Note that these are original TERS experimental spectra without any processing. See Supplementary Fig. 16a for more data sets for the corresponding line-trace TERS spectra. b Two typical TERS spectra of a bilayer MoS2 at the basal plane and the edge. c Plots of normalized intensities of two TERS peaks (396 and 406 cm−1) with the tip position. The solid lines are the fitted results. Note that these spectra are the pure near-field signals and have been subtracted with the far-field signals. Inset is the enhanced TERS intensity profile of the ETR in the 2 L edge after the deconvolution of the EM field the intensity distribution (see Supplementary Note 2 for more details). d Schematic diagram of band reconstruction and ETR of MoS2 near the edge. De is the electron density.
To clearly identify the difference in the spectral features at the edge and basal plane, we present two representative Raman spectra in Fig. 3b. It is clear that distinctly different Raman features, including the two new Raman peaks at 220 and 396 cm−1, show up at the edge and disappear on the basal plane, indicating a significant difference in physicochemical properties (such as the lattice structure and electronic property) between the edge and basal plane10,11,36. As a result, transitional space forms between the edge and pristine MoS2. Therefore, a precise measurement of this space is vital to the understanding of defect and to the defect engineering. As discussed above, the intensity of LA(M) + TA(M) mode is sensitive to ECK − ECQ. Thus, the intensity variation region of LA(M) + TA(M) mode at the edge can reflect the band-bending region of DRRS involved states (i.e., K and Q states in the conduction band; see Supplementary Note 3.3 for more details). We plot its intensity as a function of tip position as the red curve in Fig. 3c. The intensity becomes higher when the tip was moved closer to the edge, indicating a stronger DRRS-involved band bending at the edge. The full width at half maximum (FWHM) of the 396 cm−1 intensity profile is 7 nm (Supplementary Fig. 5, and see Supplementary Note 2 for more details). It should be pointed out that the measured TERS intensity profile is a convolution of the DRRS-involved band-bending region (dLA(M)+TA(M)) and the spatial resolution of TERS. Considering the typical spatial resolution of AFM-based TERS obtained in our lab of ~7 nm12, which is equal to the experimentally measured TERS intensity profile, we expect the length of the DRRS-involved band-bending region to be much smaller than 7 nm. Indeed, theoretical calculation reveals that dLA(M)+TA(M) of bilayer MoS2 induced by the edge only involves several lattice with a length of ~1.8 nm (shown in Supplementary Fig. 12; see Supplementary Note 3 and Supplementary Figs. 9–11 for more details). This DRRS-involved mode sheds light on the influence of defect on the band structure and energy bending for the involved electronic states.
Different from the 396 cm−1 peak, the A1g peak (406 cm−1) is sensitive to the electron density and its intensity becomes stronger when the tip is moved closer to the edge (Fig. 3c). Here, we neglect the phonon confinement at the edge because the phonon confinement region is small and it would decrease the intensity of A1g peak17,35,37,38. The stronger signal at the edge is attributed to a lower electron density35, which is also supported by a lower TEPL intensity of the A− trion (Supplementary Fig. 16c, d). Two factors may account for the different electron densities at the edge and basal plane. First, the Fermi level at the edge is higher than that on the basal plane (Supplementary Fig. 13b), leading to a charge transfer from the edge to the basal plane. Second, the active edge site can be easily chemisorbed by O2 or H2O in air (Supplementary Fig. 16e), which leads to the p-type doping induced by the oxygen species and a decreased electron density33,34,39. From this A1g intensity profile, we further obtained an ~10 nm ETR from the edge to the basal plane after deconvoluting the spatial distribution of the electromagnetic field (Supplementary Figs. 3 and 4)10,11. Very interestingly, different from the maximum intensity of LA(M) + TA(M) mode (the largest DRRS scattering) located at the edge site, the maximum intensity of A1g mode (the lowest electron density) appears inside the pristine MoS2 and is located just a few nanometers away from the edge (Fig. 3c inset and Supplementary Fig. 19). The reason for this is unclear yet at this moment, which may come from the confined edge state (a few lattice spacings)40 (Supplementary Fig. 8e) and the depletion of the electron by the chemisorbed oxygen species near the edge rather than at the edge.
We further used TERS to investigate ETRs induced by the monolayer edge and the step between monolayer and bilayer (1–2 L) MoS2. As shown in Fig. 4a, b, no 396 cm−1 signal can be detected at the monolayer edge, and the 396 cm−1 intensity fluctuates in a narrow region (FWHM ~6.9 nm) across the 1–2 L step, indicating a high TERS spatial resolution in these measurements. Similar to the bilayer edge, the electron density becomes smaller when the tip is moved closer to the edge and the step. The lowest electron density (i.e., the maximum A1g intensity) appears inside the pristine MoS2, and is located in just a few nanometers away from the edge (Fig. 4c) and the step (Fig. 4d). In addition, we can obtain a larger ETR of ~18 nm induced by the monolayer edge (Fig. 4c) than that of 10 nm induced by the bilayer edge (Fig. 3c inset). This may be a result of a larger Fermi energy difference between the monolayer edge and the basal plane (Supplementary Fig. 13b), as well as a deeper oxygen p-type doping due to the higher chemical activity compared with that of 2 L MoS241. Interestingly, we observed two obviously different ETRs near the 1–2 L step (Fig. 4d). The step is doped by oxygen and acts as a narrow quantum wire40, and thus induces ETRs near the step in both monolayer (~16 nm) and bilayer (~19 nm). The above study clearly reveals the defect-induced ETR of MoS2 in the real application environment, which guides better engineering of the defect density to achieve the desired properties.
ETRs induced by 1 L edge and 1–2 L step. a, b Plots of normalized intensities of TERS peaks with the tip positions across the 1 L edge (a) and 1–2 L step (b). The solid lines are the fitted results. See Supplementary Note 2 for details about the data fitting. Note that these spectra are the pure near-field signals and have been subtracted with the far-field signals. Supplementary Fig. 20b, cshows more data sets for the corresponding line-trace TERS spectra. Enhanced TERS intensity profiles of the ETR in 1 L edge (c) and 1–2 L step (d) after the deconvolution of the EM field intensity distribution (see Supplementary Note 2 for more details).
Determination of different edge structures
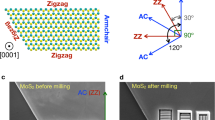
We have demonstrated the incredible ability of TERS to spatially investigate the edge-related lattice structure and electronic properties of atomically thin MoS2 flakes previously. It would be very interesting to determine the periodic arrangement of different atoms (zigzag or armchair) of MoS2 as it has a significant impact on the band gap, magnetic, optical, and electronic properties5,42,43,44. In the graphene case, the D peak has been used to identify different edge structures because it is inactive at the zigzag edge but active at the armchair edge42,45. Unfortunately, no such clear conclusion has been made to allow the identification of different edge structures of TMDCs, to the best of our knowledge. Interestingly, during our line-trace TERS study, in addition to the increased intensity of the A1g mode (406 cm−1), we often found two opposite changing trends of its peak position when the tip was moved from the basal plane to the edge: downshift (Fig. 5a, b; left panels) and upshift (Fig. 5a, b; right panels). The A1g frequency may change with the relaxation of momentum conservation induced by the phonon confinement effect and the weak electron–phonon coupling due to the reduced electron density at the edge. However, these two effects should only lead to the small upshift of the A1g frequency17,35,37,38, which cannot fully illustrate the two opposite directions of the frequency shift at the edge. We then consider the influence of local strains introduced by different edge structures on the A1g frequency with density functional theory (DFT) calculation. The calculation result given in Fig. 5c shows that the frequency of the A1g mode at the armchair edge would upshift compared with that on the basal plane, whereas there is a significant downshift in the A1g frequency at the zigzag edge for both S-terminated and Mo-terminated. As a result, the A1g frequency downshifts at the zigzag edge compared with the basal plane (Fig. 5a). In addition, the FWHM of the A1g peak increases at both the zigzag and armchair edges (Supplementary Fig. 21) due to the disorder of the structure at the edge.
Effect of the edge structure on the peak position of the Raman A1g mode. (a) Typical line-trace TERS spectra of the zigzag edge (left panel) and armchair edge (right panel) in the spectral range of the A1g mode. Note that the spectra have been normalized with the intensity of A1g peak for a better comparison. (b) Plots of peak position with the tip position. The corresponding line-trace TERS spectra are shown in Supplementary Fig. 16a and Supplementary Fig. 20a, respectively. The dash red lines are guides for the eye. (c) Calculated Raman spectra and lattice vibration of the basal plane, zigzag nanoribbon (ZNR, with a width of 3.59 nm) localized at the Mo and S edges, and armchair nanoribbon (ANR, with a width of 2.05 nm). The envelope of each Raman spectrum is evaluated by smearing the peaks with half width 5 cm−1. Note that the displacements of A1g or A1g-like mode with out-of-plane vibration are side viewed. See Supplementary Note 3.4 for details. (d) AFM image of a mechanically exfoliated 1 L MoS2 with different edge angles on an Au substrate. (e) Illustration of the relationship between angles and edge structures of zigzag (ZZ) and armchair (AC) in 2 H MoS2. (f) TERS spectra of four edges in the spectral range of the A1g mode marked in d. Note that the spectra have been normalized with the intensity of A1g peak for a better comparison. The corresponding line-trace TERS spectra of these edges are shown in Supplementary Fig. 22.
To further verify the conclusion drawn above, we mechanically exfoliated 1 L MoS2 with different edge angles (60° and 90°) on the Au substrate, as indicated by the dotted lines in Fig. 5d. These special angles would provide the structure information of the two adjacent edges42,46,47. For an angle of 60° (Fig. 5e), both edges have the same structure (either zigzag or armchair). The frequency shift direction of the A1g mode at both edges should be either downshift or upshift. On the other hand, for an angle of 90° (Fig. 5e), the two edges have different structures, i.e., one armchair and the other zigzag (Mo- or S-terminated). The A1g frequency at these two edges should shift to different directions, i.e., one upshift and the other downshift. Therefore, for a sample containing both 60° and 90° edge angles, the four edges should contain either three AC and one ZZ or one AC and three ZZ. Indeed, on TERS spectra of these edge (Fig. 5f), we detected three upshifted edge and one downshifted edge, which can be convincingly assigned to AC and ZZ edges following the conclusion of our rigorous theoretical calculation, respectively. Therefore, we demonstrate here that TERS can conveniently identify the edge type of TMDC materials under the ambient condition, which will be very important for the practical application of TMDCs.
Discussion
We have spatially resolved the unique electronic property of the defects in atomically thin MoS2, as well as the influence of defects on the nearby pristine material, by using TERS with 7 nm spatial resolution. We observed a Raman peak at 396 cm−1 in the defect of bilayer MoS2 that is rather difficult to observe and obscured by conventional Raman microscopy. We assigned it to the phonon vibration activated by two-phonon DRR intervalley scattering, and subsequently unveiled the interaction of electron and phonon during the electron excitation and scattering, which was significantly affected by the electronic band structures in different defects. We successfully determined the lengths of edge-induced band-bending region (~1.8 nm) of DRRS involved conduction band at K and Q states (~1.8 nm) and the ETR (~18 nm near 1 L edge, ~10 nm near 2 L edge, and ~16 nm (monolayer) and ~19 nm (bilayer) near the step) in the real space by taking the advantage of the high spatial resolution (7 nm) of TERS. We further demonstrated that TERS can be effectively used to identify edge structures using the frequency shift direction of the A1g mode at 406 cm−1, with an upshift at the armchair edge and downshift at the zigzag edge. This work provides a general approach to investigate the defect-related electronic properties in 2D materials by TERS, which may assist in revealing the structure–function relationship of the defect and subsequently guide the effective defect engineering and promote the applications of TMDC materials.
Methods
Sample preparation
An atomically smooth Au substrate was prepared following a template-stripping method proposed by Hegner et al.48. First, Au (Zhongnuo Advanced Material Technology Co., Ltd. 99.999%) was vapor-coated onto a Si wafer in a vacuum chamber at a pressure of 5 × 10−7 torr at a slow deposition rate of 0.35 nm s−1 to form a layer with a thickness of 200 nm. Afterward, small glass slides were glued to the Au film using UV adhesive (Norland Optical Adhesive, Norland Products Inc., NJ). The glue was then exposed to UV light for 10 min; the slide can be saved for use. Before use, the glass slide is to be peeled off to reveal the atomically smooth Au surface.
MoS2 samples were obtained by mechanical exfoliation14,15. In brief, freshly cleaved MoS2 was fabricated on the Nitto tape and then pasted onto the viscoelastic polydimethylsiloxane stamp (Gel-park, WF-20-X4) to produce plenty of thin MoS2 flake. The stamp was inspected under the optical microscope to select the interested MoS2 flakes and finally pressed against the exposed Au surface to transfer MoS2. No doping effect from the Au substrate on MoS2 was observed (see Supplementary Note 1 for more details).
AFM and TERS measurements
An upright Raman microscope (NTEGRA Spectra, NT-MDT) was employed for the TERS measurement49. The system is equipped with a confocal laser microscope, an AFM, and a white-light video microscope for rough observation/alignment of the sample and tip. A 100 × long working-distance objective with a numerical aperture of 0.7 was used for both excitation and collection of the backscattered light from the sample. A 660 nm laser was used for TERS measurements in a p-polarized configuration. Au-coated AFM tips used in TERS experiments were produced by electrodeposition of Au onto silicon AFM tips (VIT_P/IR, NT-MDT)49. The radii of the as-prepared tips were ~65 nm. The sample topography was measured using a tapping mode AFM and TERS spectra were obtained using a contact mode AFM. The doping effect induced by the Au tip on the edge and the basal plane is the same, which will not influence the conclusion (see Supplementary Note 1 for more details). In the TERS line-trace imaging experiment, the tip was scanned at a velocity of 2 nm s–1 and TERS spectra were acquired simultaneously. Note that all the TERS data are the pure near-field spectra and have been subtracted from the far-field signal otherwise mentioned.
TEPL measurements were conducted on the same microscope (NTEGRA Spectra, NT-MDT) combined with a scanning tunneling microscope. The Ag metallic tip and the p-polarized laser beam (with a wavelength of 632.8 nm) were used. The constant current mode (300 pA tunneling current and 600 mV tip to sample bias) was employed to maintain the same electron tunneling to the basal plane and defects of MoS2.
Raman measurements of bulk MoS2 excited by different laser lines were conducted on the same Raman microscope (NTEGRA Spectra, NT-MDT) as mentioned above. The p-polarized laser beams (with wavelengths of 594, 632.8, 660, and 691 nm) were used for investigations.
Theoretical simulations
The DFT calculations were performed using the Vienna Ab Initio Simulation Package (VASP)50. The electron–ion interaction was described by the Projector Augmented Wave (PAW) pseudopotentials51 and the plane–wave basis set with a kinetic energy cutoff of 500 eV. The exchange–correlation function is described by Perderw, Burke, and Ernzerhof (PBE) version of the generalized gradient approximation (GGA)52. The conjugated gradient method was performed for geometry optimization. The convergence condition for the energy was 10−8 eV. The influence of edge defect on pristine electronic and vibrational properties is estimated by zigzag and armchair nanoribbon with different widths (1–3 nm). The details of employed structures and Raman intensity calculations are presented in Supplementary Note 3. Unit cell and nanoribbon structures were relaxed until the force on each atom was less than 10−2 eV Å−1. The Monkhorst–Pack special k-point meshes of the unit cell and nanoribbon structures were 11 × 11 × 1 and 1 × 5 × 1, respectively. The phonon dispersion of nanoribbons was calculated by using 1 × 3 × 1 supercell and based on DFT implemented in VASP software in connection with the Phonopy software53.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Code availability
The code that used in this study are available from the corresponding author upon reasonable request.
References
Li, X. & Zhu, H. Two-dimensional MoS2: properties, preparation, and applications. J. Materiomics 1, 33–44 (2015).
Zhang, G., Liu, H., Qu, J. & Li, J. Two-dimensional layered MoS2: rational design, properties and electrochemical applications. Energy Environ. Sci. 9, 1190–1209 (2016).
Butler, S. Z. et al. Progress, challenges, and opportunities in two-dimensional materials beyond graphene. ACS Nano 7, 2898–2926 (2013).
Duan, X., Wang, C., Pan, A., Yu, R. & Duan, X. Two-dimensional transition metal dichalcogenides as atomically thin semiconductors: opportunities and challenges. Chem. Soc. Rev. 44, 8859–8876 (2015).
Wu, Z. & Ni, Z. Spectroscopic investigation of defects in two-dimensional materials. Nanophotonics 6, 1219–1237 (2017).
Hus, S. M. & Li, A.-P. Spatially-resolved studies on the role of defects and boundaries in electronic behavior of 2D materials. Prog. Surf. Sci. 92, 176–201 (2017).
Zhong, L. et al. Defect engineering of two-dimensional transition metal dichalcogenides. 2D Mater. 3, 022002 (2016).
Zhong, J.-H. et al. Quantitative correlation between defect density and heterogeneous electron transfer rate of single layer graphene. J. Am. Chem. Soc. 136, 16609–16617 (2014).
Li, Y., Zhou, Z., Zhang, S. & Chen, Z. MoS2 nanoribbons: high stability and unusual electronic and magnetic properties. J. Am. Chem. Soc. 130, 16739–16744 (2008).
Zhang, C., Johnson, A., Hsu, C.-L., Li, L.-J. & Shih, C.-K. Direct imaging of band profile in single layer MoS2 on graphite: quasiparticle energy gap, metallic edge states, and edge band bending. Nano Lett. 14, 2443–2447 (2014).
Huang, Y. L. et al. Bandgap tunability at single-layer molybdenum disulphide grain boundaries. Nat. Commun. 6, 6298 (2015).
Wang, X. et al. Tip-enhanced Raman spectroscopy for surfaces and interfaces. Chem. Soc. Rev. 46, 4020–4041 (2017).
Huang, T.-X. et al. Tip-enhanced Raman spectroscopy: tip-related issues. Anal. Bioanal. Chem. 407, 8177–8195 (2015).
Novoselov, K. S. et al. Two-dimensional gas of massless Dirac fermions in graphene. Nature 438, 197 (2005).
Castellanos-Gomez, A. et al. Deterministic transfer of two-dimensional materials by all-dry viscoelastic stamping. 2D Mater. 1, 011002 (2013).
Frey, G. L., Tenne, R., Matthews, M. J., Dresselhaus, M. S. & Dresselhaus, G. Raman and resonance Raman investigation of MoS2 nanoparticles. Phys. Rev. B 60, 2883–2892 (1999).
Mignuzzi, S. et al. Effect of disorder on Raman scattering of single-layer MoS2. Phys. Rev. B 91, 195411 (2015).
Thomsen, C. & Reich, S. Double resonant Raman scattering in graphite. Phys. Rev. Lett. 85, 5214–5217 (2000).
Saito, R. et al. Probing phonon dispersion relations of graphite by double resonance Raman scattering. Phys. Rev. Lett. 88, 027401 (2001).
Pimenta, M. A. et al. Studying disorder in graphite-based systems by Raman spectroscopy. Phys. Chem. Chem. Phys. 9, 1276–1290 (2007).
Carvalho, B. R. et al. Intervalley scattering by acoustic phonons in two-dimensional MoS2 revealed by double-resonance Raman spectroscopy. Nat. Commun. 8, 14670 (2017).
Malard, L. M., Pimenta, M. A., Dresselhaus, G. & Dresselhaus, M. S. Raman spectroscopy in graphene. Phys. Rep. 473, 51–87 (2009).
Lee, J.-U. et al. Strain-shear coupling in bilayer MoS2. Nat. Commun. 8, 1370 (2017).
Gołasa, K. et al. Multiphonon resonant Raman scattering in MoS2. Appl. Phys. Lett. 104, 092106 (2014).
Livneh, T. & Sterer, E. Resonant Raman scattering at exciton states tuned by pressure and temperature in 2H-MoS2. Phys. Rev. B 81, 195209 (2010).
Fan, J.-H. et al. Resonance Raman scattering in bulk 2H-MX2 (M = Mo, W; X = S, Se) and monolayer MoS2. J. Appl. Phys. 115, 053527 (2014).
Tsachi, L. & Jonathan, E. S. A comprehensive multiphonon spectral analysis in MoS2. 2D Mater. 2, 035003 (2015).
Lee, C. et al. Anomalous lattice vibrations of single- and few-layer MoS2. ACS Nano 4, 2695–2700 (2010).
Wang, X., Feng, H., Wu, Y. & Jiao, L. Controlled synthesis of highly crystalline MoS2 flakes by chemical vapor deposition. J. Am. Chem. Soc. 135, 5304–5307 (2013).
Xu, K., Cao, P. & Heath, J. R. Graphene visualizes the first water adlayers on mica at ambient conditions. Science 329, 1188–1191 (2010).
Bampoulis, P. et al. Latent heat induced rotation limited aggregation in 2D ice nanocrystals. J. Chem. Phys. 143, 19–23 (2015).
Varghese, J. O. et al. The influence of water on the optical properties of single-layer molybdenum disulfide. Adv. Mater. 27, 2734–2740 (2015).
Oh, H. M. et al. Photochemical reaction in monolayer MoS2 via correlated photoluminescence, Raman spectroscopy, and atomic force microscopy. ACS Nano 10, 5230–5236 (2016).
Bera, A., Muthu, D. V. S. & Sood, A. K. Enhanced Raman and photoluminescence response in monolayer MoS2 due to laser healing of defects. J. Raman. Spectrosc. 49, 100–105 (2018).
Chakraborty, B. et al. Symmetry-dependent phonon renormalization in monolayer MoS2 transistor. Phys. Rev. B 85, 161403 (2012).
Zhou, W. et al. Intrinsic structural defects in monolayer molybdenum disulfide. Nano Lett. 13, 2615–2622 (2013).
Wu, J.-B. et al. Monolayer molybdenum disulfide nanoribbons with high optical anisotropy. Adv. Opt. Mater. 4, 756–762 (2016).
Shi, W. et al. Phonon confinement tffect in two-dimensional nanocrystallites of monolayer MoS2 to probe phonon dispersion trends away from Brillouin-zone center. Chin. Phys. Lett. 33, 057801 (2016).
Nan, H. et al. Strong photoluminescence enhancement of MoS2 through defect engineering and oxygen bonding. ACS Nano 8, 5738–5745 (2014).
Zhang, C. et al. Visualizing band offsets and edge states in bilayer–monolayer transition metal dichalcogenides lateral heterojunction. Nat. Commun. 7, 10349 (2016).
Tan, Y. et al. Monolayer MoS2 films supported by 3D nanoporous metals for high-efficiency electrocatalytic hydrogen production. Adv. Mater. 26, 8023–8028 (2014).
You, Y., Ni, Z., Yu, T. & Shen, Z. Edge chirality determination of graphene by Raman spectroscopy. Appl. Phys. Lett. 93, 163112 (2008).
Ritter, K. A. & Lyding, J. W. The influence of edge structure on the electronic properties of graphene quantum dots and nanoribbons. Nat. Mater. 8, 235 (2009).
Nagai, H. et al. Theoretical study on third-order nonlinear optical properties in hexagonal graphene nanoflakes: edge shape effect. Chem. Phys. Lett. 477, 355–359 (2009).
Casiraghi, C. et al. Raman spectroscopy of graphene edges. Nano Lett. 9, 1433–1441 (2009).
Tinoco, M., Maduro, L., Masaki, M., Okunishi, E. & Conesa-Boj, S. Strain-dependent edge structures in MoS2 layers. Nano Lett. 17, 7021–7026 (2017).
Guo, Y. et al. Distinctive in-plane cleavage behaviors of two-dimensional layered materials. ACS Nano 10, 8980–8988 (2016).
Hegner, M., Wagner, P. & Semenza, G. Ultralarge atomically flat template-stripped Au surfaces for scanning probe microscopy. Surf. Sci. 291, 39–46 (1993).
Yang, L.-K. et al. Rational fabrication of a gold-coated AFM TERS tip by pulsed electrodeposition. Nanoscale 7, 18225–18231 (2015).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Togo, A. & Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 108, 1–5 (2015).
Acknowledgements
The authors acknowledge the final supports from MOST of China (2016YFA0200601 and 2016YFA0301204), NSFC (21633005, 21790354, 21503181, 21711530704, 21621091, 11874350, 11474277, and 11434010), Natural Science Foundation of Fujian Province (2016J05046), and China Postdoctoral Science Foundation (2017M622062).
Author information
Authors and Affiliations
Contributions
B.R., P.-H.T. and X. W. supervised the project. T.-X.H., X.W. and B.R. conceived the ideas. T.-X.H., S.-S.W., K.-Q.L. and Y.-F.B. performed the experiments. X.Y. fabricated the Au substrate. X.C., J.-B.W. and P.-H.T. performed the DFT calculations. Y.-H.H. and S.-C.H. helped with experiments and analysis. All authors contributed to data interpretation and writing of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks Emanuele Poliani and the other, anonymous, reviewers for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Huang, TX., Cong, X., Wu, SS. et al. Probing the edge-related properties of atomically thin MoS2 at nanoscale. Nat Commun 10, 5544 (2019). https://doi.org/10.1038/s41467-019-13486-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-019-13486-7
This article is cited by
-
Tip-enhanced Raman scattering
Nature Reviews Methods Primers (2024)
-
Plasmonic trimers designed as SERS-active chemical traps for subtyping of lung tumors
Nature Communications (2024)
-
Visualizing the structural evolution of individual active sites in MoS2 during electrocatalytic hydrogen evolution reaction
Nature Catalysis (2024)
-
Recent advances in tip-enhanced Raman spectroscopy probe designs
Nano Research (2023)
-
Thickness Effect on Electro-Optical Characteristics of RF Magnetron Sputtered MoS2/p-Si heterojunction Devices Fabricated by Aerosol Jet Printing
Silicon (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.