Abstract
Strongly correlated quantum solids are characterized by an inherently granular electronic fabric, with spatial patterns that can span multiple length scales in proximity to a critical point. Here, we use a resonant magnetic X-ray scattering nanoprobe with sub-100 nm spatial resolution to directly visualize the texture of antiferromagnetic domains in NdNiO3. Surprisingly, our measurements reveal a highly textured magnetic fabric, which we show to be robust and nonvolatile even after thermal erasure across its ordering temperature. The scale-free distribution of antiferromagnetic domains and its non-integral dimensionality point to a hitherto-unobserved magnetic fractal geometry in this system. These scale-invariant textures directly reflect the continuous nature of the magnetic transition and the proximity of this system to a critical point. The present study not only exposes the near-critical behavior in rare earth nickelates but also underscores the potential for X-ray scattering nanoprobes to image the multiscale signatures of criticality near a critical point.
Similar content being viewed by others
Introduction
Transition metal oxides (TMOs) are characterized by rich phase diagrams where different collective electron phases (metal, insulator, superconductor) cohabit in proximity to one another1,2,3. When these electronic phases compete, they segregate at nano- or mesoscopic length scales, giving rise to complex, multiscale domain textures4,5,6. Nowadays, there is overwhelming evidence of domain pattern formation for an array of emergent phenomena, including metal-insulator transitions7,8,9,10,11, charge/magnetic ordering12,13,14, and unconventional superconductivity15,16,17. Several studies have identified these spatial textures as essential underpinnings for phenomena in TMOs and other correlated electron systems5,13,18,19,20,21.
Rare earth nickelates are a fertile platform to realize and explore the emergent physics brewing in proximity to electronic symmetry-breaking phenomena, thanks to the cooperative action of the coupled charge, spin, and lattice degrees of freedom. In this family of compounds, the dominant structural/electronic instability sets the stage for a first-order transition (P21/n to Pbnm) to a bond-disproportionated phase, which is accompanied by a concurrent insulator-to-metal transition (IMT). The low-temperature electronic phase then undergoes a second transition to an antiferromagnetic (AFM) ground state22,23,24. The nature of the AFM transition ostensibly changes from second-order for smaller cations (Sm, Eu, Y) to first-order for larger ones (Nd and Pr)22,23. This abrupt change in the nature of the magnetic transition has been a long-standing puzzle, one that has been obfuscated by the dominance of the structural/electronic transition and by the imprinting of its hysteretic signatures onto the secondary magnetic order parameter. For this latter reason, a conventional temperature scaling analysis of the AFM transition is not applicable for NdNiO3 and PrNiO3, hindering a full elucidation of the magnetic transition. Whether the nature and universality class of the magnetic transition truly changes with the rare earth cation size across the bifurcation point, and whether the IMT and AFM transition lines meet at a tricritical point, are only a few of the outstanding questions that have hindered a full understanding of the electronic phase diagram of rare earth nickelates.
Recent studies have aimed at these scientific questions by examining the spatial organization of electronically ordered domains. This intense activity has exposed a remarkably textured nanoscale fabric manifested by the coexistence of electronic (metal/insulator) nanoregions across the IMT7,11. Even more recently, nanoscale evidence has been reported of a continuous temperature evolution of conductive one-dimensional domain walls in NdNiO3, despite this system nominally undergoes a first-order transition10. These observations reignited the debate on the nature of the phase transition in nickelates and on whether the charge and spin degrees of freedom are coupled or decoupled across the IMT. These matters have remained pending owing to the lack of direct nanoscale visualization of the AFM domains in these systems, and have here motivated the development of experimental tools to provide a comprehensive view of these phenomena in inherently phase-separated materials.
In the present work, we examined the spatial organization of AFM domains in an epitaxial bulk-like (26 nm) NdNiO3 thin film grown on NdGaO3 (110)ortho substrate with TIMT = TNéel ~ 180 K (Supplementary Fig. 1). Our experimental strategy relies on phase transition theory that second-order transitions are characterized by critical behavior whereby various physical quantities exhibit power-law scaling. Criticality generically implies power-law correlations, which are dynamic in time. However, when the critical point involves random field disorder25, barriers to equilibration grow exponentially with proximity to the critical point26, and the power-law distribution becomes frozen in time, manifesting itself as a static, fractal domain structure27. Recently, nanoscale probes have been developed and applied to visualize scale-invariant electronic domain patterns in various correlated systems, directly exposing their proximity to critical behavior12,21,28. At the same time, AFM domain patterns have evaded conventional magnetic imaging techniques, including scanning probes of the local magnetization, which are insensitive to antiferromagnetism29,30, or electron microscopy techniques, which are exquisitely sensitive to surface phenomena31,32,33,34. To date, a bulk-sensitive, submicron-level nanoprobe of AFM domain textures has been lacking.
Results
Scanning resonant magnetic X-ray scattering nanoprobe
For this study, we combined resonant magnetic soft X-ray scattering (RMXS) with special X-ray focusing optics (Fresnel zone plate) to visualize AFM order at the 100 nm scale35. RMXS has been extensively used to probe magnetic ordering in TMOs, especially in thin film materials that fall below the detection limit of neutron scattering36. When the incident photon energy is tuned to the Ni 2p-3d core level transition (852.5 eV), the atomic scattering amplitudes become spin-dependent, enabling detection of periodic AFM ordering of the Ni spins37,38,39,40. However, conventional RMXS measurements have been historically performed with macroscopic X-ray beam footprints (⪆ 100 microns), which average out over spatial inhomogeneities in the magnetic domain distribution. Here, we used this scanning RMXS nanoprobe (hereafter, nano-RMXS) to visualize symmetry-breaking electronic orders in reciprocal and real space simultaneously, in a unique combination of scattering and microscopy. The X-ray probing depth at resonance (⪆ 100 nm) guarantees access to bulk AFM textures.
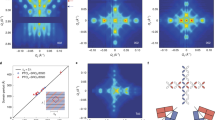
The nano-RMXS setup is illustrated in Fig. 1. The macroscopic X-ray beam is focused by the zone plate lens, which produces a series of focal spots along the optical axis41. An order sorting aperture is used to propagate only the first-order beam and filter out all other diffraction orders. During the entire experiment, soft X-rays are focused on the sample surface with a lateral beam waist of ~ 100 nm (Fig. 1a). The NdNiO3 sample and the charge-coupled detector are positioned to collect photons scattered at the AFM ordering vector QAFM = [¼, ¼, ¼]pc (in reciprocal lattice units and pseudocubic notation), as shown in Fig. 1b37,38,39,40. The AFM domain maps are obtained upon scanning the X-ray beam by a synchronized translation of the focusing optics to within a ~5 nm accuracy. The integrated scattering intensity is subsequently extracted at each beam position, yielding the AFM domain maps shown in Fig. 1c. The magnetic scattering intensity, which is proportional to the squared amplitude of the AFM order parameter, exhibits multiscale inhomogeneities even at a temperature (130 K) far below the ordering transition. The AFM domains tend to coalesce into interconnected submicron clusters but, at the same time, smaller spatial structures can be observed, reflecting a broad distribution of length scales.
Experimental setup and nanoscale antiferromagnetic landscape in NdNiO3. The combined use of a Fresnel zone plate and an order sorting aperture delivers a ~ 100 nm focused soft X-ray spot at the sample. The magnetic Bragg diffraction patterns are visualized with a fast area detector. a Knife edge scan, demonstrating a spot size of around 100 nm at 852.5 eV (Ni-L3 resonance). b The sample was oriented to intercept the antiferromagnetic diffraction peak at QAFM = [¼, ¼, ¼]pc (reciprocal lattice units in pseudocubic notation) arising from ordering within the Ni spin sublattice38,39. c The spatial map of magnetic scattering intensity exposes a highly inhomogeneous electronic landscape at the nanoscale. Arrows indicate the local pseudocubic crystallographic orientation. Each arrow length spans 1 μm in the sample frame of reference. Notice that in this scattering geometry, owing to the sample surface not being normal to the incident X-ray beam, additional geometric factors need to be accounted for when converting lateral beam translation footprint (defined in lab frame) onto the sample surface (sample frame)
It is crucial to understand the origin of this apparent inhomogeneity in the magnetic domain distribution. One possible scenario is that we are observing the phase separation of AFM-insulating and paramagnetic-metallic domains that persists below TIMT7. To elucidate the electronic texture of the “weak AFM” region where the magnetic scattering intensity is low, we imaged the X-ray absorption spectral signature at the Ni-L3 resonance using X-ray photoemission electron microscopy (XPEEM), where the Ni valence state properties can be visualized down to 50 nm spatial resolution. At 100 K, far below TIMT (TNéel), the XPEEM map provides direct evidence that there are no metallic domains within the whole field of view as shown in Supplementary Fig. 3c. Therefore, the textured AFM domain landscape we observe is not owing to the coexistence of metal and insulator domains.
The presence of AFM spatial textures in a homogeneous insulating state can be understood to originate from a distribution of different magnetic domains. As the ordering vector QAFM = (¼, ¼, ¼)pc has eight equivalent direction in the pseudocubic cell, the spiral magnetic configuration shown in Fig. 1b lifts the eightfold degeneracy in such a way that a specific magnetic domain only generates scattering intensity along two out of eight directions. The structure factor of the spin spiral magnetic structure along (1/4, 1/4, 1/4) only become nonzero when measuring at Q1 = (¼, ¼, ¼)pc and Q2 = (−¼, −¼, −¼)pc and is zero for the other ordering vectors. With only two out of eight equivalent QAFM ordering direction can be accessed in the current geometry, we effectively probe a fraction of 2/8 = 25% of magnetic patches, assuming an equal population of the symmetry-equivalent AFM Q-domains.
Memory effect
To investigate the evolution of the AFM domain patterns across the Néel transition, the sample was thermally cycled from 130 K to 210 K (above TNéel) and back. Figure 2 displays the nanoscale AFM order parameter within the same field of view before the hysteresis region (Fig. 2a), within the Néel transition (Fig. 2b), and after completion of a full hysteresis cycle back at 130 K (Fig. 2c). The corresponding temperatures of the maps in Fig. 2a–c are marked onto the intensity-temperature curve in Fig. 2d. The scattering intensity decreases during the warming cycle, and no scattering intensity is detected above the transition even with a macroscopic X-ray beam (200 μm), indicating a complete erasure of AFM order. Interestingly, the domain distribution remains largely similar between 130 K and 180 K, despite a substantial metal/insulator phase separation being expected near TIMT ~ 180 K7.
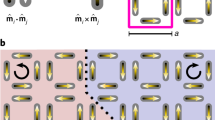
Magnetic texture vs. temperature. a–c Evolution of the spatial AFM order parameter (square root of scattering intensity) during a thermal cycle across TNéel at temperatures corresponding to the plot markers in (d). Min/max color scales are specific to each map. Black dashed contours outline the AFM domains at 130 K (warming cycle (a) and are also overlaid in (b) and (c) to highlight the evolution. The apc and bpc crystallographic axes are indicated in (c); the arrow length corresponds to 1 μm in the sample frame. d Temperature dependence of the [¼, ¼, ¼]pc AFM Bragg peak intensity, measured using a macroscopic X-ray beam, shows a typical first-order like hysteresis [red (blue) curve is the warming (cooling) cycle]. The temperatures of maps a–c are marked out as well. e The projected AFM landscape map on the sample surface. Note that the measured sample area is not square, and the projected shape, size, and orientation of the AFM domain landscape are shown in the top right inset
As the sample is cooled back down to 130 K, the full thermal cycle does not appear to reset the domain morphology, as hinted by the overlaid domain contours of Fig. 2a (130 K) onto the other maps. This observation reflects a reminiscence of the spin degrees of freedom even after full quenching above TNéel, suggesting a sizeable memory effect during the reentrance into the AFM phase (for a more-quantitative analysis of this memory effect, see Supplementary Fig. 4 and supplementary discussion). This apparent resilience against temperature variations suggests the occurrence of domain pinning which is robust across the magnetic ordering transition. This memory effect, which to the best of our knowledge has never been studied at the nanoscale across a Néel transition, has also been observed in other strongly correlated electron systems42.
The temperature-dependent spatial maps of AFM domains offer further insights onto the origin of the hysteretic, first-order-like behavior of the magnetic scattering intensity, as apparent from Fig. 2d38,43. The observed sixfold suppression of the global order parameter between 130 K and 180 K (Fig. 2d) is found to arise not out of shrinking magnetic domains, but rather from a reduction in the order parameter within each domain (see Supplementary Fig. 6 and corresponding supplementary discussion for additional details on the analysis). This local reduction is of the same order as that of the spatially averaged order parameter—suggesting that, although the domain structure remains largely unchanged, the order parameter is uniformly suppressed across the transition. In other words, the magnetic order parameter develops via a continuous transition inside the static AFM domains, and not by means of a nucleation and growth mechanism. The latter are, in turn, constrained within the insulating domains which themselves behave hysteretically (following a first-order metal-insulator transition). We note that the continuous evolution of the AFM order parameter in the interior of the domains cannot be directly compared with similar findings of smoothly evolving metallicity in 1D conducting channels as visualized in ref. 10, as the latter were proposed to represent regions where antiferromagnetism is locally suppressed.
Scale-invariant domains textures
The availability of nanoscale spatial maps of the AFM order parameter also allows for higher-level statistical analysis of the anatomy of the domain distribution. In Fig. 3a, we binarized the 130 K scattering map (warming cycle) using an intensity threshold point designed to select a coverage fraction of 25% of the total area. Correspondingly, we separate the magnetic domains (yellow, 25% of the total probed area) probed in the current geometry from all other domains (blue, the other 75% of the total probed area). From the binarized maps (Fig. 3a), various descriptors of the domain morphology can be inferred via statistical analysis. Figure 3b shows the domain area distribution histogram. We employ logarithmic binning, a standard technique for power-law distribution analysis44. Most of the points fall onto a single line for the three maps, without the use of any cross-normalization. Quantitatively, these distribution functions exhibit power-law scaling spanning two decades in the domain area with an average critical exponent τ = 1.25. A similar form of power-law scaling behavior in the charge degrees of freedom has been previously observed in strongly correlated oxides with various techniques12,21,27. Figure 3c, summarizes the relationship between the perimeter (area) and the gyration radius for all domains. The domain perimeter (P) and area (A) scale as a power of the gyration radius Rg (\(P = R_{\mathrm{g}}^{d_h}\), \(A = R_{\mathrm{g}}^{d_v}\)) across two decades of scaling. The gyration radius of an individual domain is defined as \(R_{\mathrm{g}} = \sqrt {\left( {r - r} \right)^2}\). The fitting analysis returns the averaged exponents dh = 1.23 and dv = 1.78, known as the hull and volume fractal dimensions45. These fractal dimensions cannot be trivially explained by an uncorrelated (i.e., non-interacting) percolation model, in which local quenched disorder is the sole determiner of the local magnetic order parameter at each spot in space. The fact that the critical exponents of uncorrelated percolation (dh = 7/4 = 1.75, dv = 91/48 = 1.8958, and η = 5/24 = 0.20845) are inconsistent with our data-extracted exponents (Fig. 3e and Supplementary Table 1) is an indication that Coulomb interactions play a crucial role in the pattern formation. Furthermore, our 25% single QAFM domain coverage is far from the 2d critical uncorrelated percolation threshold on a square lattice pc = 0.59. Therefore, the scale-free distribution of the AFM domains in our NdNiO3 thin film cannot be attributed to 2d uncorrelated percolation effect45. Domains either touching the boundary of the maps or with the size close to single pixel size are excluded from the analysis (hollow markers). The smallest domains are subjected to non-universal, short-distance physics, whereas spanning clusters are left out as their dimension can be affected by the finite spatial field of view. Most of the excluded points still fall near the scaling curve, possibly suggesting a larger scaling range that could be accessed with higher resolution or larger fields of view. Details of the fitting results for each map are described in the Supplementary Table 1. These observations of non-integral exponents and scale-free distribution altogether point to an unexpected fractal nature of AFM domains in NdNiO38,21,27,31,46.
Fractal magnetic patterns. a The AFM domain map at 130 K (warming cycle) is binarized to highlight the AFM domains at the ordering vector probed here (yellow), vs. other, symmetry-equivalent ones to which we are not sensitive in the present geometry (blue). b The logarithmically binned AFM domain area distributions follow a scale-free power-law distribution (D~A−τ) with the critical exponent τ = 1.25 ± 0.04. Dashed lines are power-law fits to the experimental data points. Hollow markers represent points excluded from the fit. c, d Domain perimeter (P) and area (A) vs. gyration radius (Rg) with logarithmic binning. Dashed lines are power-law fits of \(P\sim R_{\mathrm{g}}^{d_h}\) and \(A\sim R_{\mathrm{g}}^{d_v}\)with the critical exponents dh = 1.23 ± 0.03 and dh = 1.78 ± 0.07. The power-law scaling and corresponding critical exponents (dh, dv) reveal a robust scale-invariant texture at all temperatures. e Pair connectivity function vs. distance (r) with logarithmic binning. The dash lines are fits to a power-law function with an exponential cutoff\(g_{{\mathrm{conn}}}\sim r^{ - \eta }e^{ - x/\xi }\) where ξ is the correlation length and η = 0.32 ± 0.13 is the exponent for the connectivity function. f Overlay of the temperature dependence of the [¼, ¼, ¼]pc AFM Bragg peak intensity with the correlation lengths extracted from the pair connectivity function. The error bars for correlation lengths at 130 K are smaller than marker size
The formation of static fractal electronic patterns hints at nearby criticality. By tuning the temperature, we can locate the system in the vicinity of the critical point. In Fig. 3e, we extracted the pair connectivity function gconn(r) for each map. The pair connectivity gconn(r) is defined as the probability that two sites separated by a distance r belong to the same connected finite cluster45,47. The pair connectivity function was fitted by a power-law function with an exponential cutoff r−nexp(−r/ξ) where ξ is the correlation length, expected to diverge near criticality. The fitting result indicates that the correlation length at 180 K is the largest among the three maps. Moreover, the scaling exponent of the pair connectivity function is also far from the uncorrelated disorder model (Supplementary Table 1). Figure 3f shows the ξ(T) data points overlaid onto the temperature dependence of the AFM Bragg peak intensity. The correlation length exhibits a clear enhancement (3 × ) near TNéel, as expected in the critical theory.
To explain the observed scaling behavior, we note that when the system undergoes a phase transition near a critical point, its fluctuations become long-ranged, and multiple physical properties display power-law scaling with characteristic critical exponents27,28. Here, owing to domain pinning, potentially arising from quenched disorder, we can recover and visualize scale-invariant spatial correlations even down to 130 K, well below the critical temperature. The power-law scaling in the domain area distribution, the hull fractal dimension, the volume fractal dimension, and the pair connectivity function are all indicators of near-critical behavior, which has been previously discussed in the case of rare earth nickelates48,49,50. Μoreover, these critical exponents satisfies the hyperscaling relation d − 2 + η = 2 (d − dv), corroborating the validity of our analysis45. Furthermore, while the correlation length diverges at a critical point, it is expected to decrease away from a critical point as ξ ~ |T − TNéel|ν, providing a cutoff to the power-law scaling. This effect is evident in the 130 K cooling and 130 K warming datasets, where the correlation length of the pair connectivity function is about three times smaller than it is in the 180 K warming case (Fig. 3f).
Discussion
The present results shed light on the complex mechanisms underlying the electronic and magnetic phase transition in nickelate compound NdNiO3, conclusively demonstrating the near-critical nature of the AFM ordering transition. The direct visualization of magnetic domains presented here provides key complementary information to a series of previous studies of the nanoscale organization of the charge degrees of freedom, completing a body of experimental evidence from which we can now conclude that, in the rare earth nickelates: (i) the electronic domains form by nucleation and growth across a hysteretic, first-order IMT7,11; (ii) the magnetic domains are subordinated to the insulating regions within which they form, thus forcing the global order parameter to exhibit hysteresis (Fig. 2d); (iii) the AFM domains manifest the spatial signatures of scale invariance and critical behavior (Fig. 3), here rendered static by the pinning action of quenched disorder (the same pinning potential that likely underlies the observed memory effect); (iv) the critical behavior observed here is purely associated to the spin degree of freedom, which points to a different type of universality class as the continuous transition reported in ref. 10, which is only defined in spatial regions of vanishing magnetic order.
The methods and outcomes of the present study reach beyond the platform of rare earth nickelates. On the verge of criticality, the close interplay between competing phases triggers new organizing principles, with the underlying electronic fabric exhibiting spatial textures across all length scales. We have shown that nano-RMXS is a powerful imaging technique to visualize multiscale electronic textures in complex oxides and diagnose critical behavior from a different perspective, and one that is complementary to temperature scaling analysis. In this context, we find unexpected scale-invariant AFM domain patterns in NdNiO3 thin films, which directly demonstrate the continuous nature of the magnetic phase transition in this system and extend the paradigm of nanoscale phase inhomogeneity to correlated electron systems with an AFM ground state. Together with prior studies, the reported observations reaffirm the critical need for nanoscale probes of local order parameters to examine electronic symmetry-breaking phenomena, whose true nature may evade conventional approaches based on macroscopic measurements. These methods have important implications for the experimental protocols aimed at assessing the nature and symmetry of electronic phase transitions in the presence of inhomogeneity and coupled degrees of freedom. In light of these aspects, the present work paves the way for future explorations of emergent electronic and magnetic phases in strongly correlated quantum materials near criticality.
Methods
Samples
The NdNiO3 (001)pc film was grown epitaxially on a commercial NdGaO3 (110) substrate by off-axis radio-frequency magnetron sputtering. The film showed a hysteresis loop in the metal-to-insulator transition (MIT) as shown in Supplementary Fig. 1a. The MIT temperature is 178.4 K and 168.7 K for the warming and cooling cycle respectively, determined from where dR/dT changes sign. The inset shows an atomic force microscopy image of the atomic terraces at the film surface. The X-ray reflectivity (Supplementary Fig. 1b) measurements indicate a film thickness of 26 nm, corresponding to 69 unit cells, which is thick enough to exhibit bulk properties. Prior to the experiment, a semitransparent Cr fiducial mask was deposited onto the sample surface for position registration purpose during the scanning X-ray scattering measurements. The grid layout, as well as an optical microscope view of the Cr fiducial mask, are shown in Supplementary Fig. 1c and d. The thickness of the Cr grid line is 143 nm as measured by atomic force microscopy.
Nano-RMXS
The resonant soft X-ray scattering nanoprobe (nano-RMXS) experiment was performed at beamline CSX (23-ID-1) of the National Synchrotron Light Source II, where a bright and almost fully coherent soft X-ray photon beam is delivered at the sample. A 20 μm pinhole was used to magnify the X-ray beam to around 200 μm diameter at the zone plate location (1 m downstream of the pinhole). The focusing setup includes a gold Fresnel zone plate (FZP) and an order sorting aperture (OSA), mounted on two independent nanopositioning stages. The FZP has a diameter of 240 μm and a 95 μm central beam stop to block the 0th order transmission. The FZP outer zone width is 35 nm, which gives a focal length of 5.7 mm for the first diffraction order, at the Ni-L3 resonant edge (852 eV). The combination of FZP, central beam stop, and OSA, is used to select the first diffraction order.
XPEEM
XPEEM was measured at beamline ESM (21-ID-2) of the National Synchrotron Light Source II.
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.
References
Fradkin, E., Kivelson, S. A. & Tranquada, J. M. Colloquium: theory of intertwined orders in high temperature superconductors. Rev. Mod. Phys. 87, 457–482 (2015).
Milward, G. C., Calderón, M. J. & Littlewood, P. B. Electronically soft phases in manganites. Nature 433, 607–610 (2005).
Keimer, B., Kivelson, S. A., Norman, M. R., Uchida, S. & Zaanen, J. From quantum matter to high-temperature superconductivity in copper oxides. Nature 518, 179–186 (2015).
Dagotto, E. Complexity in strongly correlated electronic systems. Science 309, 257–262 (2005).
Shenoy, V. B. & Rao, C. N. Electronic phase separation and other novel phenomena and properties exhibited by mixed-valent rare-earth manganites and related materials. Philos. Trans. R. Soc. A 366, 63–82 (2008).
Moler, K. A. Imaging quantum materials. Nat. Mater. 16, 1049–1052 (2017).
Mattoni, G. et al. Striped nanoscale phase separation at the metal-insulator transition of heteroepitaxial nickelates. Nat. Commun. 7, 13141 (2016).
Sohn, A., Kanki, T., Sakai, K., Tanaka, H. & Kim, D.-W. Fractal nature of metallic and insulating domain configurations in a VO2 thin film revealed by kelvin probe force microscopy. Sci. Rep. 5, 10417 (2015).
Mcleod, A. S. et al. Nanotextured phase coexistence in the correlated insulator V2O3. Nat. Phys. 13, 80 (2016).
Post, K. W. et al. Coexisting first- and second-order electronic phase transitions in a correlated oxide. Nat. Phys. 14, 1056–1061 (2018).
Preziosi, D. et al. Direct mapping of phase separation across the metal–insulator transition of NdNiO3. Nano Lett. 18, 2226–2232 (2018).
Campi, G. et al. Inhomogeneity of charge-density-wave order and quenched disorder in a high-T c superconductor. Nature 525, 359–362 (2015).
Loudon, J. C., Mathur, N. D. & Midgley, P. A. Charge-ordered ferromagnetic phase in La0.5Ca0.5MnO3. Nature 420, 797–800 (2002).
Uehara, M., Mori, S., Chen, C. H. & Cheong, S.-W. Percolative phase separation underlies colossal magnetoresistance in mixed-valent manganites. Nature 399, 560–563 (1999).
McElroy, K. et al. Atomic-scale sources and mechanism of nanoscale electronic disorder in Bi2Sr2CaCu2O8. Science 309, 1048–1052 (2005).
Pasupathy, A. N. et al. Electronic origin of the inhomogeneous pairing interaction in the high-Tcsuperconductor Bi2Sr2CaCu2O8. Science 320, 196–201 (2008).
Poccia, N. et al. Percolative superconductivity in La2CuO4.06 by lattice granularity patterns with scanning micro x-ray absorption near edge structure. Appl. Phys. Lett. 104, 221903 (2014).
Zhang, L., Israel, C., Biswas, A., Greene, R. L. & De Lozanne, A. Direct observation of percolation in a manganite thin film. Science 298, 805–807 (2002).
Phillips, J. C. Percolative theories of strongly disordered ceramic high-temperature superconductors. Proc. Natl Acad. Sci. USA 107, 1307–1310 (2010).
Pelc, D. et al. Emergence of superconductivity in the cuprates via a universal percolation process. Nat. Commun. 9, 4327 (2018).
Fratini, M. et al. Scale-free structural organization of oxygen interstitials in La2CuO4+y. Nature 466, 841–844 (2010).
Catalano, S. et al. Rare-earth nickelates RNiO3: thin films and heterostructures. Rep. Prog. Phys. 81, 046501 (2018).
Torrance, J. B., Lacorre, P., Nazzal, A. I., Ansaldo, E. J. & Niedermayer, C. Systematic study of insulator-metal transitions in perovskites RNiO3 (R=Pr,Nd,Sm,Eu) due to closing of charge-transfer gap. Phys. Rev. B 45, 8209–8212 (1992).
Middey, S. et al. Physics of ultrathin films and heterostructures of rare earth nickelates. Annu. Rev. Mater. Res. 46, 305–334 (2016).
Tarjus, G., Balog, I. & Tissier, M. Critical scaling in random-field systems: 2 or 3 independent exponents? Europhys. Lett. 103, 6 (2013).
Fisher, D. S. Scaling and critical slowing down in random-field Ising systems. Phys. Rev. Lett. 56, 416–419 (1986).
Phillabaum, B., Carlson, E. W. & Dahmen, K. A. Spatial complexity due to bulk electronic nematicity in a superconducting underdoped cuprate. Nat. Commun. 3, 915 (2012).
Richardella, A. et al. Visualizing critical correlations near the metal-insulator transition in Ga1-xMnxAs. Science 327, 665–669 (2010).
Bert, J. A. et al. Direct imaging of the coexistence of ferromagnetism and superconductivity at the LaAlO3/SrTiO3 interface. Nat. Phys. 7, 767–771 (2011).
Kalisky, B. et al. Locally enhanced conductivity due to the tetragonal domain structure in LaAlO3/SrTiO3 heterointerfaces. Nat. Mater. 12, 1091–1095 (2013).
Bezencenet, O., Bonamy, D., Belkhou, R., Ohresser, P. & Barbier, A. Origin and tailoring of the antiferromagnetic domain structure in α-Fe2O3 thin films unraveled by statistical analysis of dichroic spectromicroscopy (X-ray photoemission electron microscopy) images. Phys. Rev. Lett. 106, 107201 (2011).
Baldasseroni, C. et al. Temperature-driven growth of antiferromagnetic domains in thin-film FeRh. J. Phys. Condens. Matter 27, 256001 (2015).
Scholl, A. Observation of antiferromagnetic domains in epitaxial thin films. Science 287, 1014–1016 (2000).
Nolting, F. et al. Direct observation of the alignment of ferromagnetic spins by antiferromagnetic spins. Nature 405, 767–769 (2000).
Chao, W., Harteneck, B. D., Liddle, J. A., Anderson, E. H. & Attwood, D. T. Soft X-ray microscopy at a spatial resolution better than 15 nm. Nature 435, 1210–1213 (2005).
Fink, J., Schierle, E., Weschke, E. & Geck, J. Resonant elastic soft x-ray scattering. Rep. Prog. Phys. 76, 056502 (2013).
Frano, A. et al. Orbital control of noncollinear magnetic order in nickel oxide heteroctures. Phys. Rev. Lett. 111, 106804 (2013).
Scagnoli, V. et al. Role of magnetic and orbital ordering at the metal-insulator transition in NdNiO3. Phys. Rev. B 73, 100409 (2006).
Scagnoli, V. et al. Induced noncollinear magnetic order of Nd3+ in NdNiO3 observed by resonant soft x-ray diffraction. Phys. Rev. B 77, 115138 (2008).
Först, M. et al. Spatially resolved ultrafast magnetic dynamics initiated at a complex oxide heterointerface. Nat. Mater. 14, 883–888 (2015).
Born, M. et al. Principles of Optics. (Cambridge University Press, 1999).
García-Fernández, M. et al. Antiferromagnetic domain structure in bilayer manganite. Phys. Rev. B 88, 075134 (2013).
Gaecía-Muñoz, J. L., Rodríguez-Carvajal, J. & Lacorre, P. Sudden appearance of an unusual spin density wave at the metal-insulator transition in the perovskites RNiO3 (R = Pr, Nd). Europhys. Lett. 20, 241–247 (1992).
Newman, M. E. J. Power laws, Pareto distributions and Zipf’s law. Contemp. Phys. 46, 323–351 (2005).
Stauffer, D. & Aharony, A. Introduction to Percolation Theory (Taylor & Francis, 1992).
Catalan, G. et al. Fractal dimension and size scaling of domains in thin films of multiferroic BiFeO3. Phys. Rev. Lett. 100, 027602 (2008).
Liu, S., Carlson, E. W. & Dahmen, K. A. Connecting complex electronic pattern formation to critical exponents. Preprint at (2018).
Liu, J. et al. Heterointerface engineered electronic and magnetic phases of NdNiO3 thin films. Nat. Commun. 4, 2714 (2013).
Allen, S. J. et al. Gaps and pseudogaps in perovskite rare earth nickelates. APL Mater. 3, 062503 (2015).
Zhou, J. S., Goodenough, J. B. & Dabrowski, B. Pressure-induced non-fermi-liquid behavior of PrNiO3. Phys. Rev. Lett. 94, 226602 (2005).
Acknowledgements
The authors would like to thank B. Keimer, E. Benckiser, M. Bluschke, D. Basov, S. Ramanathan, G. Mattoni, A. Caviglia, G. Sawatzky, R. Green, P. Evans, and I. Schuller for insightful discussions. This material is based upon work supported by the National Science Foundation under Grant No. 1751739. This research used resources of the National Synchrotron Light Source II and the Center for Functional Nanomaterials, which are US Department of Energy (DOE) Office of Science facilities at Brookhaven National Laboratory, under Contract No. DE-SC0012704. This work was supported by the Swiss National Science Foundation through Division II. The research leading to these results has received funding from the European Research Council under the European Union’s Seventh Framework Program (FP7/2007-2013)/ERC Grant Agreement no. 319286 (Q-MAC). E.W.C. and F.S. acknowledge support from NSF DMR-1508236, Depasrtment of Education Grant No. P116F140459, and the Purdue Research Foundation. J.P. acknowledges financial support by the Swiss National Science Foundation Early Postdoc Mobility fellowship project number P2FRP2_171824 and PostDoc Mobility project number P400P2_180744.
Author information
Authors and Affiliations
Contributions
J.L., C.M., and R.C. conceived the research study, especially with sample and setup design. S.C., M.G., and J.M.T. synthesized the samples, and carried out materials analysis and characterization. J.L., J.P., C.M., A.L., S.W., and R.C. contributed to the nano-RMXS experiment. J.L. and J.T.S carried out XPEEM measurements. J.L., F.S., E.C., and R.C. performed data analysis and interpretation. J.L. and R.C. wrote the manuscript, with input and edits from all co-authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Li, J., Pelliciari, J., Mazzoli, C. et al. Scale-invariant magnetic textures in the strongly correlated oxide NdNiO3. Nat Commun 10, 4568 (2019). https://doi.org/10.1038/s41467-019-12502-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-019-12502-0
This article is cited by
-
Multiquanta flux jumps in superconducting fractal
Scientific Reports (2023)
-
From hidden metal-insulator transition to Planckian-like dissipation by tuning the oxygen content in a nickelate
npj Quantum Materials (2021)
-
Inhomogeneous Kondo-lattice in geometrically frustrated Pr2Ir2O7
Nature Communications (2021)
-
Coexistence of Spin Density Wave and Metallic Phases Under Pressure
Journal of Superconductivity and Novel Magnetism (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.