Abstract
The nature of the Verwey transition occurring at TV ≈ 125 K in magnetite (Fe3O4) has been an outstanding problem over many decades. A complex low temperature electronic order was recently discovered and associated structural fluctuations persisting above TV are widely reported, but the origin of the underlying correlations and hence of the Verwey transition remains unclear. Here we show that local structural fluctuations in magnetite emerge below the Curie transition at TC ≈ 850 K, through X-ray pair distribution function analysis. Around 80% of the low temperature correlations emerge in proportion to magnetization below TC. This confirms that fluctuations in Fe-Fe bonding arising from magnetic order are the primary electronic instability and hence the origin of the Verwey transition. Such hidden instabilities may be important to other spin-polarised conductors and orbitally degenerate materials.
Similar content being viewed by others
Introduction
Short-range structural correlations above the Verwey transition1,2,3,4 were reported in early diffuse scattering studies of magnetite5, and their persistence up to at least room temperature has been studied recently6 and corroborated by observations of anomalous phonon broadening7, a charge gap from optical and photoelectron spectroscopies8,9, and magnetic excitations driven by polaronic distortions in resonant inelastic X-ray scattering data10. Analysis of the interatomic pair distribution function (PDF)11 derived from total X-ray scattering data is a simple method for exploring local structure that is highly sensitive to the displacements of metal atoms associated with the formation of orbital molecules, metal–metal-bonded clusters such as the trimerons observed in magnetite12. Persistence of orbital molecules far above their long-range electronic ordering transitions has been discovered from X-ray PDF studies of Li2RhO413, Li2RuO314, AlV2O415, and GaV2O416.
The thermal variation of local structure in magnetite has been explored here over a wide temperature range encompassing both the Verwey and Curie transitions through synchrotron X-ray PDF analysis.
Results
Variable temperature PDF analysis of magnetite
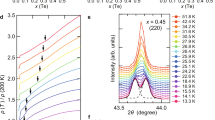
Experimental details are in the “Methods” section. Total X-ray scattering data from a highly stoichiometric sample of magnetite were recorded from 90 to 923 K. Representative scattering intensity S(Q) plots and the derived PDFs G(r) are shown in Fig. 1. The monoclinic superstructure adopted by magnetite below TV is very complex with 168 small (<0.24 Å) displacements of atoms from their positions in the high temperature cubic spinel structure3. To fit the PDFs over all temperatures, we have used this monoclinic supercell with lattice parameters adjusted to a cubic metric and with each of the 168 atomic coordinates given by p = pu + fV(pd − pu) where pu is the coordinate from an undistorted high-temperature cubic crystal structure refinement and pd is the coordinate in the distorted 90 K structure reported previously3. fV is a Verwey shift parameter that describes the set of constrained structural displacements, such that fV = 0 corresponds to the cubic spinel structure without any local distortions and fV = 1 describes the full magnitude of distortions in the 90 K magnetite superstructure3. Comparative views of the fV = 0 and fV = 1 structures are shown in ref. 4. Three values of fV were determined at each temperature by fitting the structural model to three successive regions of the PDF corresponding approximately to distances from atoms to their neighbours in the same unit cell (First Unit Cell range, covering all interatomic distances for r < 9.36 Å) and similarly to atoms in the Second and Third Unit Cell regions. The structural models and fitting procedure are further described in “Methods”, and fits to data and their sensitivity to changing fV are shown in Fig. 2.
Fitting of magnetite pair distribution functions (PDFs). a, b Comparison of fits of a the cubic (residual Rw = 15.6%) and b the monoclinic superstructure (Rw = 11.6%) models to the 90 K PDF. The visible improvement of the fit to the r ≈ 3 Å peak measuring nearest neighbour Fe–Fe (and O–O) distances and lowering of Rw demonstrates sensitivity to the monoclinic Verwey superstructure distortions. PDF data are open blue circles, fits are red curves and the difference is below in green. c Rw as a function of the Verwey shift parameter fV from fits to the First Unit Cell region of the high-temperature PDFs. The well-defined minimum seen at fV ≈ 0.8 for the 498 K fits becomes more shallow and moves to zero at the highest temperatures, as plotted in Fig. 3b. This subtle change of local structure can be seen in the shift in the maximum of the 3 Å peak to slightly longer r (inset), consistent with the loss of Fe–Fe distances shortened through trimeron bonding
Thermal variations of refined structural quantities from the PDF fits are shown in Fig. 3. The cubic cell parameter and isotropic atomic temperature factors Uisos in Fig. 3a show a slight anomaly at the Verwey transition (previously found to be TV = 123.4 K for this highly pure magnetite sample)17 but increase monotonically from 150 up to 923 K. The Verwey shift fV measures an averaged local structural distortion due to electronic fluctuations. The thermal variation of fV when fitted to the Third Unit Cell separations (between atoms 16.8 to 24.6 Å apart) in Fig. 3b is a typical order-parameter behaviour at a first-order phase transition, with a sharp fall to fV = 0 on warming through TV. Second Unit Cell correlations have a qualitatively similar variation although critical fluctuations decay more gradually above TV and are estimated to persist up to 250–300 K. However, structural correlations between atoms in the First Unit Cell range (<9.4 Å apart) show a strikingly different behaviour. fV falls a little on warming though the Verwey transition, but around 80% of the structural fluctuations remain in the cubic phase of magnetite up to 500 K. At higher temperatures, fV decreases rapidly to zero close to the Curie transition at TC ≈ 850 K and so behaves like an order parameter for the magnetic ordering transition with a very similar temperature dependence to the bulk magnetisation reported for a similar synthetic microcrystalline magnetite18. This is the key discovery of the present study as it demonstrates that the structural fluctuations responsible for the Verwey transition emerge directly with the long-range magnetic order below the Curie transition and scale with the magnetisation.
Thermal variations of parameters from magnetite pair distribution function (PDF) fits. a Isotropic temperature factors Uisos for tetrahedral FeA, octahedral FeB, and oxygen sites and the cubic cell parameter from fits to the First Unit Cell PDF range. b Verwey shifts fV fitted to First, Second and Third Unit Cell PDF ranges. fV represents the magnitude of structural distortions due to electronic fluctuations in the cubic phase of magnetite above TV. The First Unit Cell values show that substantial local structural distortions persist up to TC and closely match the variation of bulk magnetisation data taken from ref. 18. This demonstrates that the structural and electronic fluctuations responsible for the Verwey transition are a direct result of the long-range magnetic order. c Comparison of the atomic displacements due to electronic fluctuations dV, calculated from atomic coordinates for the First Unit Cell fV values, and those due to thermal motion taken as dT = √Uiso from values shown in a. Error bars are estimated standard deviations from the refinements
The thermal variations of the unit cell parameter and isotropic atomic temperature factors of magnetite plotted in Fig. 3a do not show any discontinuity at TC ≈ 850 K, in keeping with previous high-temperature structural studies19,20. This demonstrates that our PDF fitting method is robust in decorrelating the overall lattice expansion and phonon motion, quantified by the latter parameters, from the local structural distortions due to electronic fluctuations described by fV. The magnitudes of the displacements of atoms from their ideal positions due to phonon motion and due to First Unit Cell electronic distortions are compared in Fig. 3c. The electronic distortion displacements are smaller than those due to thermal motion in the disordered high-temperature region, but they increase to a comparable magnitude below TV. Although the timescale for these structural fluctuations is not directly measured, their lack of correlation with phonon motions suggests that they are essentially static or slowly diffusing. A recent quasi-elastic neutron scattering study of GaV2O4 spinel above the 415-K charge-ordering transition found that structurally disordered orbital molecules remain well defined and without measurable dynamics up to 1100 K16.
Trimeron fluctuations in cubic magnetite
The complex monoclinic superstructure of magnetite below TV was previously found to exhibit trimerons (Fig. 4a), small polarons surrounding three Fe units that share corners with each other to build up a long-range ordered network as shown in Fig. 4b. The end-to-end Fe–Fe distance in a trimeron is 6 Å, so their local lattice distortion lies within the First Unit Cell range (< 9.4Å) and hence arises below the Curie transition as demonstrated in Fig. 3b. Persistence of a disordered glassy network of trimerons in the cubic phase of magnetite up to TC provides a mechanism for the coupling of the high-temperature structural fluctuations to the magnetism and hence for the origin of the Verwey transition as follows.
Trimeron bonding driven by magnetic order in magnetite. Charge-ordered Fe2+/Fe3+ states are shown as blue/yellow spheres, trimerons are green, and oxide ions are red. a A single trimeron unit consisting of three Fe sites with parallel S = 5/2 spins as shown by the brown–green arrows. Orbital order at the central Fe2+ site localises an antiparallel spin electron in one of the t2g orbitals, which distorts the local structure through elongation of four Fe–O bonds and shortening of the distances through weak bonding to two Fe neighbours in the same plane, as indicated by the purple arrows. The minority spin electron density is approximated by the ellipsoid shown. b Long-range order of trimerons in the monoclinic superstructure formed below the Verwey transition. Corner-sharing of trimerons results in a complex pattern of atomic displacements that has been used to model the local structure in the pair distribution functions
Trimerons result from coupled Fe2+/Fe3+ charge ordering, Fe2+ orbital ordering, and weak Fe–Fe bonding effects driven by ferromagnetism within three Fe atom units as described in the caption of Fig. 4a3. Comparison with other mixed valent Fe2+/Fe3+ oxides shows that neither the charge nor orbital orders require long-range spin order, as evidenced by Fe2OBO321,22 and LuFe2O423, both of which have charge and orbital ordering transitions at higher temperatures than their magnetic transitions. However, the weak bonding interactions that shorten Fe–Fe distances in the trimerons do require ferromagnetic alignment of the three core S = 5/2 spins, as demonstrated recently in CaFe3O5 where phase-separated trimeron and non-trimeron ground states are observed24. Hence, the rapid emergence of structural fluctuations in proportion to magnetisation on cooling below the long-range magnetic ordering temperature confirms that the direct Fe–Fe bonding interactions are the primary driver of the local distortions in magnetite. As suggested previously, the Fe–Fe interactions induce associated charge and orbital fluctuations that become ordered as trimeron units below the Verwey transition3. The regular cubic spinel arrangement in which all nearest-neighbour Fe–Fe distances are equivalent is thus unstable with respect to local variations in Fe–Fe separations in the magnetically ordered state of magnetite. There are many degenerate arrangements for linking trimerons with similar connectivities to the observed low-temperature network shown in Fig. 4b3, so the long-range electronic order is frustrated. The ratio of energy scales for formation (TC) and long-range order (TV) of the electronic distortions serves as a measure of the degree of electronic frustration, analogous to the Weiss to Néel temperature ratio used for frustrated antiferromagnets. The value of TC/TV ≈ 7 confirms that electronic order in magnetite is strongly frustrated.
Discussion
Analysis of the PDF derived from X-ray scattering data reveals that local structural distortions due to electronic fluctuations emerge at the Curie transition of magnetite. This confirms that fluctuations in Fe–Fe bonding are the dominant electronic instability that couples charge and orbital fluctuations to the magnetic order and hence are the origin of the Verwey transition. Although many experimental studies of magnetite have been carried out at temperatures around TV, changes near TC are much less investigated and will be important to explore the incipient electronic fluctuations further. Such ‘hidden’ local instabilities may also be important to the physics of other spin-polarised conductors and orbitally degenerate materials, and the assumed uniformity of their high temperature structures may require critical reassessment.
Methods
Powder X-ray scattering experiments
The same highly pure magnetite powder (Fe3-δO4 with δ < 0.0001) as used in previous studies3,25,26,27 was packed in a 0.5-mm diameter quartz capillary and sealed under Ar atmosphere in a glove bag. Preliminary measurements were performed on beam line ID15B at ESRF, Grenoble and full data were collected on ESRF instrument ID11 with wavelength λ = 0.15720(1) Å using a FReLoN camera for diffraction pattern acquisition. A nitrogen cryostream was used to collect patterns between 90 and 400 K in 10 K steps. Small anomalies seen in several refined quantities around 250–300 K in Fig. 3 most likely reflect ice in the sample vicinity leading to additional scattering contributions, as magnetite does not have an intrinsic lattice anomaly in this temperature region. A hot air blower was used to collect data between 498 and 923 K in 50 K steps. Empty capillary data were collected at 90, 200, 473, 573, 673, 773, and 873 K. For each data set, the temperature was stabilised for 10 min and then data were collected for 10 min using the accumulation mode of the detector for 10-s exposure frames. Data were also collected from CeO2 and Si standards at 300 K to calibrate the instruments and determine instrumental parameters.
Instrument calibration and image integration was performed with the pyFAI software28. The instrument model was recalibrated for every temperature in the cryostat data sets in order to allow for slight detector shifts. A fixed instrument model was used for the hot air blower data. Data sets were converted to scattering intensities S(Q) as a function of scattering vector Q and these were transformed to PDFs G(r), where r is interatomic distance, using the pdfgetx3 suite29. Parameters values Qmin = 1 Å−1, Qmax = 31 Å−1, and rpoly = 0.9 Å were applied to all data sets to enable structural changes in G(r) to be analysed consistently across the full temperature range. Representative S(Q) and G(r) plots are shown in Fig. 1 and Supplementary Fig. 1.
Structural models for PDF analysis
Structural models used to fit magnetite PDFs at all temperatures were based on the supercell of the low-temperature structure with monoclinic space group Cc symmetry, which contains 56 unique atoms with 168 variable coordinates. A cubic model previously refined against 130 K powder X-ray and neutron data25,26 was used as the reference undistorted structure. The VESTA software30 was used to generate a supercell of the cubic structure with metric a = b = √2ac, c = 2ac, α = β = γ = 90°, where ac is the cubic spinel cell parameter, and atomic coordinates pu in Cc space group symmetry are shown in Supplementary Table 1. This model has fV = 0. The previously reported 90 K monoclinic Cc structure3 was transformed to the same cell metric (from a = 11.88881(3) Å, b = 11.84940(3) Å, c = 16.77515(1) Å, β = 90.2363(2)° to a = b = 11.86182(3) Å, c = 16.77515(1) Å, β = 90°). Atomic positions were shifted slightly in order to preserve the magnitude of the distortions as generated by the ISODISTORT program31. This approximation was found to have little effect on fits of the Cc model to the 90 K PDF (Rw = 11.5% for monoclinic cell parameters vs. Rw = 11.6% with metric constraints). Coordinates pd for this fully distorted reference structure (fV = 1) are shown in Supplementary Table 2. To vary the magnitude of the structural distortion, seven structural models were constructed by taking linear combinations of the undistorted and distorted coordinates p = pu + fV(pd − pu) for values of the Verwey shift fV from 0 to 1.2 in increments of 0.2.
PDF fits
Refinements of structural models including simulation of termination ripples were performed with the PDFgui software32. A fit to the CeO2 PDF with a fixed structural model was used to extract the instrument-sensitive parameters Qdamp = 0.0475(4) Å−1 and Qbroad = 0.0186(3) Å−1. It was not possible to minimise the value of fV directly in the refinements and so the best-fit value was found by comparing Rws for the seven structural models with varying fixed fV values.
A ‘box-car’ refinement procedure was followed where, at each temperature, each of the seven structural models were fitted to three regions of the PDF; r = 1.50–9.36, 9.30–16.85, and 16.80–24.60 Å, to fit correlations between atoms separated by approximate First, Second, and Third Unit Cell distances, respectively. The cubic cell parameter ac, separate isotropic thermal parameters Uiso for tetrahedrally coordinated FeA, octahedral FeB, and O sites, and the peak width correlation parameter δ1 were refined during fits to data in the First Unit Cell range. Second and Third Unit Cell fits used ac values from the First Unit Cell fits, and δ1 was set to 0. A further constraint of equal FeA and FeB Uisos was needed to fit Third Unit Cell data sets for temperatures >150 K. Fits to 90 K First Unit Cell data are shown in Fig. 3a.
The best-fit value of fV for each temperature and data range was found from the position of the minimum in the Rw vs. fV curve fitted by the arbitrary function:
where A, B, C, and D are refined parameters. Fits to Rw vs. fV points are shown in Fig. 2c and Supplementary Fig. 2. Estimated standard deviations (esds) in the best-fit fV values were calculated from those in A, B, C, and D in Eq. (1). The esds on fV values <0.3 are large so these fV values were set to zero. The best-fit First Unit Cell’s cell parameters and Uisos and their errors were calculated by linear interpolation between values at the two fV increments closest to the minimum value. Lattice parameters were also fitted to the diffraction data using the Rietveld method and are shown in Supplementary Fig. 3. An approximate correlation length for the structural distortions was calculated from the First Unit Cell fV values and is shown in Supplementary Fig. 4.
Data availability
Data that support the findings of this study have been deposited at https://doi.org/10.7488/ds/2574.
References
Verwey, E. J. W. Electronic conduction of magnetite (Fe3O4) and its transition point at low temperatures. Nature 144, 327–328 (1939).
Walz, F. The Verwey transition—a topical review. J. Phys.Condens. Matter 14, R285–R340 (2002).
Senn, M. S., Wright, J. P. & Attfield, J. P. Charge order and three-site distortions in the Verwey structure of magnetite. Nature 481, 173–176 (2012).
Senn, M. S., Wright, J. P. & Attfield, J. P. The Verwey phase of magnetite—a long-running mystery in magnetism. J. Korean Phys. Soc. 62, 1372–1375 (2013).
Shapiro, S. M., Iizumi, M. & Shirane, G. Neutron scattering study of the diffuse critical scattering associated with the Verwey transition in magnetite (Fe3O4). Phys. Rev. B 14, 200–207 (1976).
Bosak, A. et al. Short-range correlations in magnetite above the Verwey temperature. Phys. Rev. X 4, 011040 (2014).
Hoesch, M. et al. Anharmonicity due to electron-phonon coupling in magnetite. Phys. Rev. Lett. 110, 207204 (2013).
Park, S. K., Ishikawa, T. & Tokura, Y. Charge-gap formation upon the Verwey transition in Fe3O4. Phys. Rev. B 58, 3717 (1998).
Taguchi, M. et al. Temperature dependence of magnetically active charge excitations in magnetite across the Verwey transition. Phys. Rev. Lett. 115, 256405 (2015).
Huang, H. Y. et al. Jahn-Teller distortion driven magnetic polarons in magnetite. Nat. Commun. 8, 15929 (2017).
Egami, T. & Billinge, S. J. L. Underneath the Bragg Peaks: Structural Analysis of Complex Materials, Vol. 16 (Pergamon Materials Series, Pergamon Press, Oxford, 2012).
Attfield, J. P. Orbital molecules in electronic materials. APL Mater. 3, 041510 (2015).
Knox, K. R. et al. Local structural evidence for strong electronic correlations in spinel LiRh2O4. Phys. Rev. B 88, 174114 (2013).
Kimber, S. A. et al. Valence bond liquid phase in the honeycomb lattice material Li2RuO3. Phys. Rev. B 89, 081408 (2014).
Browne, A. J., Kimber, S. A. J. & Attfield, J. P. Persistent three-and four-atom orbital molecules in the spinel AlV2O4. Phys. Rev. Mater. 1, 052003 (2017).
Browne, A. J., Lithgow, C., Kimber, S. A. J. & Attfield, J. P. Orbital molecules in the new spinel GaV2O4. Inorg. Chem. 57, 2815–2822 (2018).
Senn, M. S., Wright, J. P., Cumby, J. & Attfield, J. P. Charge localization in the Verwey structure of magnetite. Phys. Rev. B 92, 024104 (2015).
Ponomar, V. P., Dudchenko, N. O. & Brik, A. B. Thermal stability of micro- and nanoscale magnetite by thermomagnetic analysis data. In 2017 IEEE 7th International Conference Nanomaterials: Application & Properties (NAP), Odessa, 02MFPM03, Ed. Pogrebnjak, Alexander D., IEEE, Piscataway, NJ, USA (2017).
Okudera, H., Kihara, K. & Matsumoto, T. Temperature dependence of structure parameters in natural magnetite: single crystal X-ray studies from 126 to 773 K. Acta Cryst. B 52, 450–457 (1996).
Levy, D., Giustetto, R. & Hoser, A. Structure of magnetite (Fe3O4) above the Curie temperature: a cation ordering study. Phys. Chem. Miner. 39, 169–176 (2012).
Attfield, J. P. et al. Electrostatically driven charge-ordering in Fe2OBO3. Nature 396, 655–658 (1998).
Angst, M. et al. Charge order superstructure with integer iron valence in Fe2OBO3. Phys. Rev. Lett. 99, 086403 (2007).
de Groot, J. et al. Charge order in LuFe2O4: an unlikely route to ferroelectricity. Phys. Rev. Lett. 108, 187601 (2012).
Hong, K. H., Arevalo-Lopez, A. M., Cumby, J., Ritter, C. & Attfield, J. P. Long range electronic phase separation in CaFe3O5. Nat. Commun. 9, 2975 (2018).
Wright, J. P., Attfield, J. P. & Radaelli, P. G. Long range charge ordering in magnetite below the Verwey transition. Phys. Rev. Lett. 87, 266401 (2001).
Wright, J. P., Attfield, J. P. & Radaelli, P. G. Charge ordered structure of magnetite Fe3O4 below the Verwey transition. Phys. Rev. B 66, 214422 (2002).
Goff, R. J., Wright, J. P., Attfield, J. P. & Radaelli, P. G. Resonant x-ray diffraction study of the charge ordering in magnetite. J. Phys. Condens. Matter 17, 7633–7642 (2005).
Kieffer, J. & Wright, J. P. PyFAI: a Python library for high performance azimuthal integration on GPU. Powder Diffr. 28, S339–S350 (2013).
Juhás, P., Davis, T., Farrow, C. L. & Billinge, S. J. PDFgetX3: a rapid and highly automatable program for processing powder diffraction data into total scattering pair distribution functions. J. Appl. Crystallogr. 46, 560–566 (2013).
Momma, K. & Izumi, F. VESTA: a three-dimensional visualization system for electronic and structural analysis. J. Appl. Crystallogr. 41, 653–658 (2008).
Campbell, B. J., Stokes, H. T., Tanner, D. E. & Hatch, D. M. ISODISPLACE: an internet tool for exploring structural distortions. J. Appl. Cryst. 39, 607–614 (2006).
Farrow, C. L. et al. PDFfit2 and PDFgui: computer programs for studying nanostructure in crystals. J. Phys. Condens. Matter 19, 335219 (2007).
Acknowledgements
We acknowledge financial support from European Research Council (ERC) and Science and Technology Facilities Council (STFC) for provision of beam time at ESRF. This work was also supported by the French "Investissements d'Avenir" program, project ISITE-BFC (contract ANR-15-IDEX-0003). We thank Professor J.M. Honig (Purdue University) for provision of the high-quality magnetite sample.
Author information
Authors and Affiliations
Contributions
G.P., E.P., J.C., S.A.J.K. and J.P.A. designed the concept for this study. G.P., E.P., J.C., J.M.H., J.P.W. and S.A.J.K., performed the experimental work and data analysis. G.P. and J.P.A. wrote the manuscript with inputs from all the authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information: Nature Communications thanks Sverre Selbach for his contribution to the peer review of this work.
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Perversi, G., Pachoud, E., Cumby, J. et al. Co-emergence of magnetic order and structural fluctuations in magnetite. Nat Commun 10, 2857 (2019). https://doi.org/10.1038/s41467-019-10949-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-019-10949-9
This article is cited by
-
Quantitative three-dimensional local order analysis of nanomaterials through electron diffraction
Nature Communications (2023)
-
Slow dynamics of disordered zigzag chain molecules in layered LiVS2 under electron irradiation
npj Quantum Materials (2021)
-
Designing disorder into crystalline materials
Nature Reviews Chemistry (2020)
-
Heat capacity signature of frustrated trimerons in magnetite
Scientific Reports (2020)
-
Discovery of the soft electronic modes of the trimeron order in magnetite
Nature Physics (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.