Abstract
The electronic nematic phase is an unconventional state of matter that spontaneously breaks the rotational symmetry of electrons. In iron-pnictides/chalcogenides and cuprates, the nematic ordering and fluctuations have been suggested to have as-yet-unconfirmed roles in superconductivity. However, most studies have been conducted in thermal equilibrium, where the dynamical property and excitation can be masked by the coupling with the lattice. Here we use femtosecond optical pulse to perturb the electronic nematic order in FeSe. Through time-, energy-, momentum- and orbital-resolved photo-emission spectroscopy, we detect the ultrafast dynamics of electronic nematicity. In the strong-excitation regime, through the observation of Fermi surface anisotropy, we find a quick disappearance of the nematicity followed by a heavily-damped oscillation. This short-life nematicity oscillation is seemingly related to the imbalance of Fe 3dxz and dyz orbitals. These phenomena show critical behavior as a function of pump fluence. Our real-time observations reveal the nature of the electronic nematic excitation instantly decoupled from the underlying lattice.
Similar content being viewed by others
Introduction
Iron-based superconductors exhibit attractive properties such as high-transition-temperature (Tc) superconductivity and complex competing phases1. Their electronic structures consist of multiple iron 3d orbitals, thus giving rise to a variety of antiferroic and ferroic ordering phenomena involving spin and orbital profiles2,3,4. Among these mysterious phases, there has been increasing interest in nematic order5,6,7,8,9,10,11,12,13, which spontaneously breaks the rotational symmetry of electrons and triggers a lattice instability8. Recent investigations by electronic Raman scattering14,15 and elastoresistivity measurements11 unveiled the fluctation of electronic nematicity and its critical behavior commonly in the optimally doped regimes of different material families11.
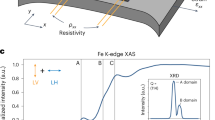
FeSe exhibits superconductivity (Tc = 9 K) and a nematic order accompanied by the tetragonal-to-orthorhombic lattice deformation (Ts = 90 K) without any magnetic order16. Its electronic structure is given in Fig. 1 (see also Supplementary Note 1). In the tetragonal phase, FeSe exhibits a circular Fermi surface around the Γ point (Fig. 1a). Along kx (ky), the hole band forming the Fermi surface has the yz (xz) orbital component. Note that such momentum (k)-dependent orbital characters keep the four-fold (C4) symmetry (Fig. 1b). In the orthorhombic (nematic) phase, the k-dependent orbital polarization17 modifies the Fermi surface shape into an elliptical one (nematic Fermi surface) as shown in Fig. 1c, resulting in inequivalent Fermi momenta (kF) along kx and ky (kFx < kFy). At the same time, the orbital components at the kF’s are mixed, especially along kx as shown in Fig. 1d (Supplementary Note 2). While these characteristics associated with the nematic order have been verified through intensive angle-resolved photoemission spectroscopy (ARPES) studies17,18,19,20, the understanding of dynamics and excitations peculiar to this condensed state remain lacking.
Electronic structure of FeSe and experimental setup for TARPES. a Schematic Fe lattice and Fermi surface around the Γ point in the tetragonal phase. x and y are coordinates along the crystal axes of the orthorhombic setting a and b (a > b), respectively. b Band dispersions and orbital characters in the tetragonal phase obtained by a band calculation including the spin–orbit coupling17. α, β, and γ denote the outer, middle, and inner hole band, respectively. c, d, The same as a and b but for the orthorhombic phase. For reproducing the ARPES results (Supplementary Note 1), the spin–orbit coupling and orbital polarization were included in the band calculations in d (ref. 17). e Schematic experimental geometry of TARPES on detwinned bulk FeSe
Time-resolved ARPES (TARPES) has the potential impact to resolve electron dynamics not only in energy and momentum but also into spin and orbital degrees of freedom. A wide range of materials have been investigated for clarifying their electronic dynamics, such as the recombination of the superconducting quasiparticles21,22, fluctuating charge density waves23, collapse of long-range order24,25, and coupling with optical phonons25,26,27. These results, which are inaccessible from equilibrium state, contributed to the deeper understanding of exotic quantum states, especially those with short lifetimes.
Here, we use TARPES to track the ultrafast dynamics of electronic nematicity in FeSe. By combining detwinned crystals with a linear-polarized probe laser, we can selectively obtain the electrons of xz and yz orbitals (Supplementary Note 3). With this TARPES setup28 (Fig. 1e), the ultrafast dynamics of the nematic Fermi surface and the orbital-dependent carrier dynamics can be visualized.
Results
Ultrafast dynamics of nematic Fermi surface
Immediately after photo-excitation (t = 120 fs), the hole bands around the Γ point along kx and ky exhibit remarkable momentum shifts with the opposite signs, and take comparable kF values as indicated by the red and blue arrows in Fig. 2a, b. This observation suggests that the elliptical Fermi surface quickly changes to circular by the photo-excitation, thus indicating the melting of the nematic order. Fig. 2c displays the fluence (F)-dependence, where the shift of kFy (ΔkFy) at t = 120 fs gradually increases as a function of F (weak-excitation regime), and saturates at F > Fc = ∼200 μJ cm−2 where the isotropic Fermi surface is attained (strong-excitation regime).
Ultrafast transformation of the nematic Fermi surface. a E–k images in a logarithmic color scale obtained by p-polarized probe laser of hν = 5.9 eV along kx (left panel) and ky (right panel) axes at 20 K, before photo-excitation of F = 220 μJ cm−2 (t = −1700 fs). Black curves represent the momentum-distribution curves (MDCs) at the EF and the broken black lines indicate their peak positions. White markers show the band dispersions obtained from the MDC peaks. b The same as a but after photo-excitation (t = 120 fs). c F dependence of the kF shift along ky (ΔkFy) at t = 120 fs. Fc represents the F where the C4 symmetric Fermi surface is attained after the photo-excitation. d F dependence of ΔkFy(t). The data set was obtained at 20 K from five single crystals as indicated by the different markers in c. e Schematics of the Fermi surface around the Γ point for t < 0 ps, t = 0 ps, and t = 4 ps deduced from the transient kFx and kFy, and the width of the MDCs at the EF. f Transient kFy (blue open circles) and kFx (red open circles) as a function of delay time with the fitting functions (black curves). Damped oscillation in kFy was extracted by subtracting the exponential decay components, as shown in the bottom
Here we track the time dependence of ΔkFy(t) for respective F (Fig. 2d). As shown in Fig. 2c, ΔkFy(t) indicates the sudden decrease at t ≈ 120 fs representing the melting of nematicity, followed by the subsequent recovery in ~1 ps. The overall picture of this transient Fermi surface for F > Fc is shown in Fig. 2e. We further find that the recovery clearly becomes faster for F > Fc, and some modulated feature appears. The time dependences of kFx and kFy for 220 μJ cm−2, where the modulation appears most strongly, are presented in Fig. 2f. These data indicate that the C2 anisotropy in kF is completely suppressed (kFx ≈ kFy) within the time resolution (250 fs), followed by an anomalous hump in the recovery. These behaviors of kFx and kFy can be reproduced by the functions including the damped oscillation term in the form of kF(t) = kF0 + kF1exp(−t/τ1) + kF2exp(−t/τ2) + kF3exp(−t/τ3)cos(2πt/tp) convoluted by the Gaussian of the time resolution, with common values of τ1 = 830 ± 50 fs, τ2 > 80 ps, τ3 = 550 ± 50 fs, and tp = 1.4 ± 0.05 ps. The observed anti-phase oscillation of kFx and kFy directly represents the Pomeranchuk-type oscillation of Fermi surface29, being intensively discussed as the fundamental excitation in the electronic nematic state. The time scale of the oscillatory response (1.4 ps, 3.1 meV) is considerably slow as compared to the coherent A1g optical phonon (190 fs, 22 meV), which is known to strongly couple to the electronic state in this system25,26,27. Their possible interplay is unfortunately hidden in the present TARPES data, possibly due to the duration of the pump pulse (170 fs) comparable to the time period of A1g mode (190 fs) that tends to vanish the coherent oscillation.
Orbital-dependent carrier dynamics
Based on the behavior of transient Fermi surface, we focus on the orbital-dependent carrier dynamics. With p-polarized probe pulse, we obtain the energy-distribution curves (EDCs) for xz and yz electrons around the Γ point by integrating ky and kx in 0.00 ± 0.04 Å−1, respectively (see Supplementary Note 3 for experimental settings). The main peak of EDC around −18 meV in Fig. 3a, b, e, f corresponds to the top of the middle (β) hole band sinking below EF, predominantly of yz orbital character (Fig. 1d). In the weak-excitation regime of F = 40 μJ cm−2 (Fig. 3a, b), the main peak gets rapidly suppressed, and electrons are excited toward the unoccupied state. Here we track the evolution of the corresponding photo-electron intensities ΔI(t) at E – EF = 7.5 ± 2.5 meV and k = 0.00 ± 0.04 Å−1, i.e. black rectangles in Fig. 1b, d. Figure 3c, d shows that ΔI(t) for xz and yz exhibit the similar exponential decay function with two time constants 850 fs and >80 ps, thus indicating the mostly equivalent relaxation processes of both orbitals. However, we note that the excited tail intensity of EDCs at E > EF is very low for yz, being consistent with the predominantly xz character of the outer (α) hole band top at Γ (Fig. 1d). Substantial spectral weight depletion in the yz states after pumping might be attributed to the photoexcited yz electrons which are partly trapped at the M point. Because of the semi-metallic electronic structure, some part of electrons excited by 1.5 eV photons at Γ may quickly gather around the electron bands at M. The momentum-dependent sign-inversion of orbital polarization17 realizes the yz dominated electron pocket near EF at M, which may work as the reservoir for photoexcited yz electrons. To fully understand these dynamics, the TARPES covering the whole Brillouin zone is desired.
Orbital-dependent dynamics of the photoexcited electrons at the Γ point. a EDCs around the Γ point (k = 0.0 ± 0.04 Å−1) obtained from the E–k images at 20 K along ky at t = −1700, 120, 700, and 2000 fs, in the p-polarized setting. The fluence of the photo-excitation was F = 40 μJ cm−2. b The same as a but obtained along kx axis. xz (yz) electrons are dominantly observed in a (b). c The photo-electron intensities normalized by that before photo-excitation, ΔI(t), at the α band top (E−EF = 7.5 ± 2.5 meV) around the Γ point (ky = 0.0 ± 0.04 Å−1), obtained by the p-polarized probe laser and the pump fluence of F = 40 μJ cm−2. The black curve represents the fitting function assuming the double exponential components with the time constants of 850 fs and 80 ps. d The same as c but at kx = 0.0 ± 0.04 Å−1. e–h The same as a–d but with the pump fluence of F = 220 μJ cm−2. The light blue markers in g represent the ΔI(t) of xz obtained by an s-polarized probe laser (Supplementary Note 4). i F dependence of the normalized ΔI(t) for xz. The black arrows represent the time of the retarded maxima tret for F > Fc
In the strong-excitation regime, the photo-response changes drastically. The EDCs in Fig. 3e, f show that the photoexcited states at E > EF also appear in yz, indicating that the C4 isotropic state (Fig. 1b) is achieved by the strong photo-excitation (F = 220 μJ cm−2). On the other hand, the excited intensity of xz shows a nonmonotonic relaxation which keeps increasing from t = 120 to 700 fs as indicated by the black arrow in Fig. 3e, being markedly different from yz. As shown in Fig. 3g, h, ΔI(t) of xz exhibits the retarded maximum at tret = ∼700 fs, whereas the yz electrons show the exponential decay more or less similar to the weak-excitation regime, with the initial maximum at ~250 fs. These contrastive behaviors solely depend on the orbital characters, not on experimental configuration (Supplementary Notes 4 and 5). To discuss the retardation behavior, the F dependence of ΔI(t) for xz is shown in Fig. 3i. In the weak-excitation regime (F < Fc), ΔI(t) curves commonly show the simple relaxation with the maximum around 250 fs. With increasing F, the retardation suddenly shows up at F ≈ Fc. Its time scale estimated by tret is 700 fs at F ≈ Fc and gradually decreases to 350 fs by increasing F to 430 μJ cm−2.
Fluence-dependent dynamics of electronic nematicity
Here we summarize the dynamics of the electronic nematicity in Fig. 4b. By fitting ΔkFy(t) curves in Fig. 2d (Supplementary Note 6), we plot τ1 and tp/2 for respective F. τ1 is the exponential decay time indicating the quick recovery of nematicity. It shows a constant value (∼800 fs) in the weak-excitation regime and a rapid decrease above F > Fc. The time scale of the Fermi surface oscillation indicated by tp/2, which only appears in F > Fc, also rapidly decreases from 700 to 300 fs as increasing F. It shows that the oscillation gets more severely damped and hard to observe at high F. We also overlay the time scale of the retarded maximum in xz component tret. As a result, τ1, tp/2, and tret similarly show the maximum values at Fc = 220 μJ cm−2 that monotonically decrease with increasing F, while keeping the common relation τ1 ≈ tret ≈ tp/2. The relation tret ≈ tp/2 implies that the orbital-dependent carrier dynamics is synchronized with the short-life nematic Fermi surface oscillation. We note that the transient Fermi surface at tp/2 (≈ tret) is more elliptical than that expected without the oscillatory response. Such an overshoot of the nematicity in Fermi surface should also appear in the orbital-dependent carrier dynamics. In the process relaxing back from C4 isotropic to C2 nematic ground state, the electrons at the band top (black rectangle in Fig. 1b, d) change their orbital characters from “(nearly) xz/yz degenerate” to “predominantly xz”. The retarded maximum in I(t) for xz can be thus regarded as an indication of the orbital redistribution from yz to xz (Fig. 4a). The synchronized responses in the Pomenranchuk Fermi surface oscillation and orbital-dependent carrier dynamics thus represent the nematic-orbital excitation.
Pump-fluence dependence of the time scales for the orbital and nematicity dynamics. a Illustration of the orbital excitation in FeSe. b F dependences of tret (open green circles), tp/2 (filled black circles) and τ1 (filled red diamonds). c tp−1 (filled black circles) and τ1−1 (filled red diamonds) plotted as functions of F. The dotted line is a linear function derived from the data at F > Fc
Discussion
Now we discuss the nematic-orbital excitation obtained in the present TARPES results by comparing with the nematic dynamics in thermal equilibrium as probed by recent Raman scattering measurements15,30. The electronic Raman spectra of XY symmetry (X and Y are coordinates along the crystal axes of the tetragonal setting) show the characteristic quasi-elastic peak (QEP) evolving toward Ts on cooling the temperature (T), discussed in terms of nematic susceptibility enhancement15,30. The QEP rapidly diminishes at T < Ts, on the other hand, and a gap opens in the XY Raman spectra, thus indicating the suppression of low-energy nematic excitations30. These behaviors are reminiscent of the nematic-orbital excitation observed by TARPES, where the peculiar slowing down behavior shows up in F > Fc, and the excitation itself suddenly disappears in F < Fc. The nematic fluctuation is incoherent in nature, however, by instantaneously triggering the dissolution of the nematic state, it may be appearing as the heavily damped oscillatory response in the time domain.
Further insight of the peculiar F dependence can be obtained by plotting tp−1 and τ1−1 (Fig. 4c). These values show a more or less F-linear behavior at F > Fc, indicating the critical slowing down. At F = Fc, tp−1 decreases down to 3.1 meV. In F < Fc, as already mentioned, the kF oscillation as well as the anomaly in the xz orbital response disappear, and τ1−1 becomes constant. In the XY Raman spectrum, the T-linear behavior was found in the inverse of the QEP intensity above Ts (ref. 15), indicative of the Gaussian fluctuation evolving in this regime. Similarly, the elastoresistivity measurement had also revealed the existence of electronic nematic fluctuation at T > Ts interpreted as the Curie–Weiss-like nematic susceptibility30. Through the analysis of the T-dependent nematic susceptibility in the form of |T – T0|−1, the authors discuss the mean-field transition temperature T0 in terms of the ideal nematic transition purely driven by electrons without any influence of lattice15,30. For FeSe, T0 was estimated to be far below Ts, i.e. 8, 20 (ref. 15), and 30 K (ref. 31). The Curie–Weiss-like behavior of tp−1 and τ1−1 toward F ≈ 40 ± 20 μJ cm−2, i.e. much smaller than Fc = 220 μJ cm−2, may be reflecting that the base temperature of the TARPES measurements (20 K) is close to T0. This scenario is also consistent with the initial photo-response of ΔkFy with small threshold (<30 μJ cm−2, see Fig. 2c). These results indicate that the electronic nematiciy in the initial ultrafast regime (~120 fs) shows the flexible photo-reaction by decoupling from the lattice. Our analysis on the transient electronic temperature (Te) (Supplementary Note 7) indeed shows that Te immediately reaches 88 ± 2 K at 120 fs and then decreases in less than 1 ps (Supplementary Fig. 6). For t > 3 ps, it becomes nearly constant at ~45 K, indicating the realization of quasi-equilibrium state where the temperatures of electrons and lattice become equivalent through the electron–lattice coupling32. The maximum lattice temperature is thus much lower than Ts (= 90 K), showing that the lattice stays orthorhombic. We also note that the reduction of the lattice orthorhombicity is known to occur in a much slower time scale (e.g. ~30 ps) with a much higher pump fluence (e.g. 3.3 mJ cm−2) for BaFe2As2 (ref. 33).
The present results show that the femtosecond photon pulse can perturb the electronic nematic order and instantly decouple it from the lattice. Only in the strong-excitation regime where the nematic state is completely destroyed, there appears the peculiar dynamical process involving the orbital redistribution and short-life Pomenranchuk-type Fermi surface oscillation. This behavior is seemingly related to the critical nematic fluctuation; nevertheless, future theoretical studies on non-equilibrium critical phenomena are highly necessary. The recovery time scale of the nematic Fermi surface is strongly correlated with the short-life kF oscillation (τ1 ≈ tp/2), which also awaits investigations on the dynamics of fluctuation and dissipation in non-equilibrium states. Experimentally, further studies on the nematic dynamics around the quantum critical point in the FeSe1−xSx system31 and the coherent nematic resonance mode in the superconducting state is highly desired. Systematic time-resolved diffraction measurements will also help understanding the possible interplay among the nematic excitation and the optical/acoustic phonons26,34. Ultrafast photo-excitation adds to the possibilities for understanding and manipulating the large-amplitude electronic fluctuations associated with phenomena such as unconventional superconductivity, exotic magnetism, thermopower enhancement, and so on.
Methods
Sample preparations
High-quality single crystals of FeSe were grown by the vapor transport method. A mixture of Fe and Se powders was sealed in an evacuated SiO2 ampoule together with KCl and AlCl3 powders16. The transition temperatures of the single crystals were estimated to be Ts = 90 K and Tc = 9 K from the electrical resistivity measurements. We showed the data obtained from five single crystals of FeSe which were synthesized less than 2 months before the TARPES measurements.
Time and angle-resolved photoemission measurements
The TARPES measurements were done at ISSP, the University of Tokyo28. The laser pulse (1.5 eV and 170 fs duration) delivered from a Ti:Sapphire laser system operating at 250 kHz repetition (Coherent RegA 9000) was split into two branches: one is used as a pump and the other was up-converted into 5.9 eV and used as a probe to generate photoelectrons. The delay origin t = 0 ps and time resolution (250 fs) were determined from the pump-probe photoemission signal of graphite attached near the sample. The photoelectrons were collected by a VG Scienta R4000 electron analyzer. The EF and the energy resolution (20 meV) were determined by recording the Fermi cutoff of gold in electrical contact to the sample. To detwin the single crystals, we applied an in-plane uniaxial tensile strain17,19, which brings the orthorhombic a axis (a > b) along its direction below Ts. We chose s and p polarizations to separately observe the xz and yz orbital electrons (see Supplementary Note 3 for the details of experimental geometry and selection rule). Samples were cleaved in situ at room temperature in an ultrahigh vacuum of 5 × 10−11 Torr.
Data availability
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
References
Paglione, J. & Greene, R. L. High-temperature superconductivity in iron-based materials. Nat. Phys. 6, 645–658 (2010).
Liu, C. et al. Evidence for a Lifshitz transition in electron-doped iron arsenic superconductors at the onset of superconductivity. Nat. Phys. 6, 419–423 (2010).
Yi, M. et al. Symmetry-breaking orbital anisotropy observed for detwinned Ba(Fe1-xCox)2As2 above the spin density wave transition. Proc. Natl Acad. Sci. USA 108, 6878–6883 (2011).
Shimojima, T. et al. Antiferroic electronic structure in the nonmagnetic superconducting state of the iron-based superconductors. Sci. Adv. 3, e1700466 (2017).
Borzi, R. A. et al. Formation of a nematic fluid at high fields in Sr3Ru2O7. Science 315, 214–217 (2007).
Daou, R. et al. Broken rotational symmetry in the pseudogap phase of a high-T c superconductor. Nature 463, 519–522 (2010).
Fradkin, E. et al. Nematic fermi fluids in condensed matter physics. Annu. Rev. Condens. Matter Phys. 1, 153–178 (2010).
Fernandes, R. M., Chubukov, A. V. & Schmalian, J. What drives nematic order in iron-based superconductors? Nat. Phys. 10, 97–104 (2014).
Shibauchi, T., Ikeda, H. & Matsuda, Y. Broken symmetries in URu2Si2. Philos. Mag. 94, 3747–3759 (2014).
Lederer, S., Schattner, Y., Berg, E. & Kivelson, S. A. Enhancement of superconductivity near a nematic quantum critical point. Phys. Rev. Lett. 114, 097001 (2015).
Kuo, H.-H. et al. Ubiquitous signatures of nematic quantum criticality in optimally doped Fe-based superconductors. Science 352, 958–962 (2016).
Yonezawa, S. et al. Thermodynamic evidence for nematic superconductivity in CuxBi2Se3. Nat. Phys. 13, 123–126 (2017).
Sato, Y. et al. Thermodynamic evidence for a nematic phase transition at the onset of the pseudgap in YBa2Cu3Oy. Nat. Phys. 13, 1074–1078 (2017).
Gallais, Y. & Paul, I. Charge nematicity and electronic Raman scattering in iron-based superconductors. Comptes Rendus Phys. 17, 113–139 (2016).
Massat, P. et al. Charge-induced nematicity in FeSe. Proc. Natl Acad. Sci. USA 113, 9177–9181 (2016).
Böhmer, A. E. et al. Lack of coupling between superconductivity and orthorhombic distortion in stoichiometric single-crystalline FeSe. Phys. Rev. B 87, 180505 (2013).
Suzuki, Y. et al. Momentum-dependent sign inversion of orbital order in superconducting FeSe. Phys. Rev. B 92, 205117 (2015).
Nakayama, K. et al. Reconstruction of band structure induced by electronic nematicity in an FeSe superconductor. Phys. Rev. Lett. 113, 237001 (2014).
Shimojima, T. et al. Lifting of xz/yz orbital degeneracy at the structural transition in detwinned FeSe. Phys. Rev. B 90, 121111(R) (2014).
Borisenko, S. V. et al. Direct observation of spin–orbit coupling in iron-based superconductors. Nat. Phys. 12, 311–317 (2016).
Smallwood, C. L. et al. Tracking Cooper pairs in a cuprate superconductor by ultrafast angle-resolved photoemission. Science 336, 1137–1139 (2012).
Ishida, Y. et al. Quasi-particles ultrafastly releasing kink bosons to form Fermi arcs in a cuprate superconductor. Sci. Rep. 6, 18747 (2016).
Schmitt, F. et al. Transient electronic structure and melting of a charge density wave in TbTe3. Science 321, 1649–1652 (2008).
Rohwer, T. et al. Collapse of long-range charge order tracked by time-resolved photoemission at high momenta. Nature 471, 490–493 (2011).
Rettig, L. et al. Ultrafast momentum-dependent response of electrons in antiferromagnetic EuFe2As2 driven by optical excitation. Phys. Rev. Lett. 108, 097002 (2012).
Gerber, S. et al. Femtosecond electron-phonon lock-in by photoemission and x-ray free-electron laser. Science 357, 71–75 (2017).
Okazaki, K. et al. Antiphase Fermi-surface modulations accompanying displacement excitation in a parent compound of iron-based superconductors. Phys. Rev. B 97, 121107 (2018).
Ishida, Y. et al. Time-resolved photoemission apparatus achieving sub-20-meV energy resolution and high stability. Rev. Sci. Instrum. 85, 123904 (2014).
Pomeranchuk, I. Ia On the stability of a Fermi liquid. J. Exp. Theor. Phys. 8, 361 (1959).
Zhang, W.-L. et al. Stripe quadrupole order in the nematic phase of FeSe1−xSx. Preprint at https://arxiv.org/abs/1710.09892 (2018).
Hosoi, S. et al. Nematic quantum critical point without magnetism in FeSe1−xSx superconductors. Proc. Natl Acad. Sci. USA 113, 8139–8143 (2016).
Anisimov, S. I. et al. Electron emission from metal surfaces exposed to ultrashort laser pulses. J. Exp. Theor. Phys. 66, 375–377 (1974).
Rettig, L. et al. Ultrafast structural dynamics of the orthorhombic distortion in the Fe-pnictide parent compound BaFe2As2. Struct. Dyn. 3, 023611 (2016).
Nakamura, A. et al. Evaluation of photo-induced shear strain in monoclinic VTe2 by ultrafast electron diffraction. Appl. Phys. Exp. 11, 092601 (2018).
Acknowledgements
We thank M. Imada, Y. Yamaji, Y. Gallais and I. Paul for valuable discussions. We acknowledge H. Kontani and Y. Yamakawa for valuable discussions and band calculations. This research was supported by the Photon Frontier Network Program of the MEXT, the CREST project of the JST (Grant Number JPMJCR16F2), Grant-in-Aid for Scientific Research (KAKENHI) (Grant Nos. 15H03687, 15H02106, 15KK0160, 18H01177, 18H05227 and 18H01148) and on Innovative Areas ''Topological Material Science" (No. 15H05852) from Japan Society for the Promotion of Science (JSPS).
Author information
Authors and Affiliations
Contributions
T. Shimojima and K.I. designed the research. T. Shimojima, Y.S., A.N., N.M. and Y.I. performed the TARPES measurements and analyzed the data. S.K., T. Shibauchi, and Y.M. synthesized the single crystals. Y.I. and S.S. set up the TARPES apparatus. T. Shimojima wrote the paper with inputs from S.K., T. Shibauchi, Y.M., Y.I., S.S. and K.I.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Journal peer review information: Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Shimojima, T., Suzuki, Y., Nakamura, A. et al. Ultrafast nematic-orbital excitation in FeSe. Nat Commun 10, 1946 (2019). https://doi.org/10.1038/s41467-019-09869-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-019-09869-5
This article is cited by
-
Nematicity and nematic fluctuations in iron-based superconductors
Nature Physics (2022)
-
High-resolution time- and angle-resolved photoemission studies on quantum materials
Quantum Frontiers (2022)
-
Pressure-induced reconstitution of Fermi surfaces and spin fluctuations in S-substituted FeSe
Scientific Reports (2021)
-
Light-induced enhancement of superconductivity in iron-based superconductor FeSe0.5Te0.5
Communications Physics (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.