Introduction

Electron valley degree of freedom emerges as local extrema in the electronic band structures. Inequivalent valleys, well separated in the Brillouin zone, can be energetically degenerate due to symmetry and serve as novel information carriers controllable via external fields1,2,3,4,5,6. A feasible means to manipulate such a valley degree of freedom is through a valley Hall effect (VHE)5,6,7,8,9. Analogous to an ordinary Hall effect, in which a transverse charge current is driven by a uniform magnetic field in real space, a transverse valley current in the VHE is produced by valley-contrasting Berry curvatures in momentum space. Upon the application of an external electric field, the curvatures drive carriers from different valleys to traverse in opposite directions. Therefore, the VHE has been a major theme in the study of valleytronics, particularly in those 2D materials featuring K and K’ valleys in their hexagonal Brillouin zones10,11,12,13,14,15,16,17,18,19.

As Berry curvature is even under spatial inversion (P) and odd under time reversal (T), the VHE cannot survive when both P and T symmetries are present. To achieve VHEs in monolayer and bilayer graphene, an elaborately aligned h-BN substrate10 and a strong dual gating field11,12 were respectively utilized to break the P symmetry. To excite VHEs in specific valleys17,18, circularly polarized lights20,21,22 were used for breaking the T symmetry in atomically thin transition-metal dichalcogenides (TMDC). Monolayer TMDCs have direct band gaps of optical frequencies at two inequivalent K-valleys23,24, due to the intrinsic P asymmetry in their unit cells depicted in Fig. 1a. Thus, Berry curvatures with opposite signs naturally emerge at the two K-valleys. Moreover, the T and mirror symmetries lock the spin and valley indices of the sub-bands split by the spin-orbit couplings, both of which are flipped under T; the spin conservation suppresses the inter-valley scattering. Therefore, monolayer TMDCs have been deemed an ideal platform for realizing intrinsic VHE without extrinsic symmetry breaking15,16.

Fig. 1
figure 1

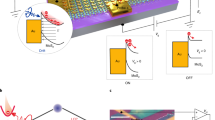
Valley Hall transport induced nonlocal resistance in monolayer MoS2. a Top view and side view of the crystal structure of 2H-MoS2; an odd- (even-) layer is inversion asymmetric (symmetric). b Schematic of the h-BN encapsulated MoS2 field-effect transistor. c High-resolution bright-field STEM image showing details of the edge-contacted monolayer MoS2 device structure (scale bar 10 nm). The expanded region shows that the BN-MoS2-BN interface is pristine and free of impurities down to the atomic scale (scale bar 3 nm). d Schematic of the nonlocal resistance measurement and the VHE-mediated nonlocal transport. The applied charge current in the left circuit generates a pure valley current in the transverse direction via a VHE. This valley current induces opposite chemical potential gradients for the two valleys over the inter-valley scattering length, which, in turn, generates a voltage drop measured by probes 3 and 4 in the right circuit via an inverse VHE. e Nonlocal resistance RNL (upper panel) and the classical ohmic contribution RCL (lower panel) as functions of gate voltage Vg at varied temperatures. Inset: optical image of a typical monolayer MoS2 device (scale bar 2 μm). A MoS2 Hall bar is sandwiched between the top and bottom h-BN flakes

Full size image

However, the quantum transport in atomically thin TMDCs has been a long-standing challenge due to the low carrier mobility and the large contact resistance in their field-effect devices prepared by an exfoliation method. Recent breakthroughs in the fabrication of low-temperature ohmic contacts for high-mobility 2D TMDC devices25,26,27,28 have already facilitated the observation of transport hallmarks of Q-valley electrons28,29, K-valley electrons30,31, K-valley holes32,33,34, and Γ-valley holes35. These discoveries have revealed the rich and unique valley physics in the platform of atomically thin TMDCs.

In this work, we design nonlocal, layer-dependent, transport measurements to systematically examine the intrinsic VHEs in n-type 2H-MoS2. For the first time, we observe nonlocal resistances that exhibit cubic power-law scaling with the local resistances in the monolayers and trilayers, evidencing intrinsic VHEs. Because of the large intrinsic bandgaps and spin-valley locking of TMDCs, such VHEs can even be observed at room temperature in our monolayer devices. Beyond critical carrier densities (∼4.0 × 1011 cm−2 for monolayers and trilayers), the cubic scaling turns into linear scaling. Notably, only linear scaling is observed in bilayer MoS2, where the P symmetry is restored. Intriguingly, although the monolayer and trilayer feature respectively K- and Q-valleys near their conduction-band edges, they display comparable valence-band Berry curvatures, valley Hall signatures, and micron-sized valley diffusion lengths. Our results not only offer the first experimental evidence for the intrinsic VHE but also help elucidate its topological origin6 in odd-layer TMDCs and pave the way for realizing room-temperature low-dissipation valleytronics by purely electronic means.

Results

Devices for nonlocal measurements

The structure of a monolayer MoS2 field-effect transistor is sketched in Fig. 1b. Its bright-field cross-sectional scanning transmission electron microscopy (STEM) image in Fig. 1c clearly shows the layered BN-MoS2-BN structure without any impurities in the interfaces down to the atomic scale. The device fabrication process includes a dry transfer step followed by a reactive ion etching step27,28,35 (see Methods and Supplementary Fig. 1 for details). A low contact barrier formed on the n-type MoS2 is evidenced by the I-V curves, contact resistances (Supplementary Fig. 2), and the field-effect mobilities μ varied from 500–4000 cm2 V−1 s−1 for monolayers, 4000–23000 cm2 V−1 s−1 for bilayers, and 10000–25000 cm2 V−1 s−1 for trilayers at T = 2 K (Supplementary Figs. 3 and 4). The impurity-free STEM images and the high mobilities coincide well with the low residue carrier densities (n∗ = 4 × 1010 cm−2, see Supplementary Fig. 5).

As for the electronic measurement, an inverse VHE is exploited to detect a valley current, as sketched in Fig. 1d. An applied current I12 through probes 1 and 2 induces charge imbalance in a remote region, as measured by the voltage drop V34 between probes 3 and 4 (Supplementary Fig. 6). The nonlocal resistance RNL = V34/I12 mediated by the valley Hall current was predicted36 to present cubic power-law dependence on the local resistance RL = V24/I13.

Nonlocal transport in monolayer MoS2

Nonlocal resistance RNL in an n-type monolayer MoS2 (sample B of length L = 6 μm and width W = 1.5 μm illustrated in the inset of Fig. 1e), measured as a function of gate voltage Vg at varied temperatures, is shown in Fig. 1e. A giant RNL is observed in the range of Vg ∼ −15 to −25 V that amounts to the electron density n ∼ 1010 to 1011 cm−2. In particular, the observed RNL ∼ 106 Ω exceeds the classical ohmic contribution \(R_{{\mathrm{CL}}} = R_{\mathrm{L}}\frac{W}{{{\mathrm{\pi }}L}}{\mathrm{e}}^{ - {\mathrm{\pi }}L/W} \sim 10^4\,\Omega\) by two orders of magnitude in the range of Vg ∼ −15 to −18 V at 2 K and Vg ∼ −22 to −25 V at 300 K. Another unexpected feature of RNL is its Vg dependence. In sharp contrast to the classical contribution RCL, which decreases gradually with increasing Vg, the observed RNL drops by at least one order of magnitude within an increase of several volts in Vg. Both the pronounced nonlocal signal and its unusual sensitivity to Vg suggest that the observed RNL has a physical origin different from the classical ohmic contribution RCL.

The temperature dependence of RL and RNL uncovers the mesoscopic mechanism of both the local and nonlocal transport. The conduction can be separated into three regimes: the thermal activation (TA) at 250 K > T > 130 K, the nearest-neighbor hopping (NNH) at 130 K > T > 60 K, and the variable-range hopping (VRH) below 60 K (sample A of L = 3.6 μm and W = 1.5 μm, see Fig. 2f and Supplementary Fig. 7a and 7b). These transport regimes are consistent with previous studies37,38. Since pronounced nonlocal signals are observed in all three transport regimes, there appears no clear connection between the transport regimes and the onset of strong nonlocal signals. Interestingly, the characteristic temperatures of both NNH and VRH for RNL are much larger than those for RL in the range of Vg ∼ −60 to −58 V (Supplementary Fig. 7d and 7e). This indicates a higher energy barrier in the nonlocal transport and an anomalous origin of the nonlocal signal.

Fig. 2
figure 2

Local and nonlocal resistances of monolayer MoS2. a, b Semilog plots of RL and RNL as a function of Vg measured at varied temperatures. Inset of b: optical micrograph of our typical h-BN/MoS2/h-BN device with multi-terminal Hall Bar configurations. Scale bar: 5 μm. c Scaling relations between ln RL and ln RNL at Vg ranging from −50 V to −60 V. When the electron density is relatively high, i.e., RL and RNL are small, RNL is linearly proportional to RL. When the electron density is relatively low, a crossover from linear to cubic scaling is observed. The critical density nc = 4 × 1011 cm−2, with the gate voltage Vg = −57 V. d Crossover phenomenon by considering classical diffusion (RNL ∝ RL) and valley Hall transport (RNL ∝ RL3). The experimental data (solid circles, Vg = −60 V) clearly show two different regimes which are fitted by two linear curves (orange dashed line with slope 1 and blue dashed line with slope 3). The critical temperature is around 160 K~200 K, as marked by the blue arrow. e RNL plotted as a function of Vg at low temperatures. The ohmic contribution, calculated according to RL and device geometry, is deducted from the measured RNL at different temperatures. f 1/RNL (orange circles) and 1/RL (blue circles) in log scale plotted as functions of 1/T at Vg = −60 V. Three distinct transport regimes were observed: the thermal activation (TA) transport, nearest neighbor hopping (NNH) transport, and the variable range hopping (VRH) transport. g Semilog plot of RNL as a function of L at n = 2 × 1011 cm−2 (orange squares). Nonlocal signal decays exponentially with increasing L. The dashed line yields a valley diffusion length of ∼1 μm

Full size image

To determine the origin of the observed RNL, we investigate the scaling relation between RNL and RL as functions of Vg at different temperatures for both sample A (Fig. 2) and sample B (Supplementary Fig. 8). For a fixed Vg, both RL and RNL increase when the temperature is lowered. In sample A, two regimes with distinct scaling behaviors become clearly visible in Fig. 2c, d, the logarithmic plot of RL and RNL at different Vg. Above 160 K, the slopes of the lnRNL versus lnRL curves are 1, indicating that RNL ∝ RL. Below 160 K, the slopes turn to 3 in the low electron density regime (RL ≈ 108 to 109 Ω), which amounts to \(R_{{\mathrm{NL}}} \propto R_{\mathrm{L}}^3\). Indeed, a diffusive model has predicted such power-law relations36, in which a cubic scaling holds for a spin or valley Hall effect36. As introduced above and calculated later, the massive Dirac band structure of monolayer MoS2 produces large valley Hall conductivity \(\sigma _{{\mathrm{xy}}}^{\mathrm{V}}\) (see below) but much weaker spin Hall conductivity36 (see Supplementary Note 1), Therefore, it is natural to attribute the observed nonlocal signal to the VHE, and the obtained cubic scaling may be analyzed by the predicted formula36

$$R_{{\mathrm{NL}}} = \frac{1}{2}\left( {\frac{{\sigma _{{\mathrm{xy}}}^{\mathrm{V}}}}{{\sigma _{{\mathrm{xx}}}}}} \right)^{{\hskip -2.5pt}2}\frac{W}{{\sigma _{{\mathrm{xx}}}l_{\mathrm{V}}}}{\mathrm{e}}^{ - \frac{L}{{l_{\mathrm{V}}}}} \propto \left( {\sigma _{{\mathrm{xy}}}^{\mathrm{V}}} \right)^{\hskip -2pt 2}R_{\mathrm{L}}^3.$$
(1)

where lV is the valley diffusion length (or inter-valley scattering length), and σXX and RL have the simple relation of \(\sigma _{{\mathrm{xx}}} = \frac{L}{{R_{\mathrm{L}}W}}\). We will focus on such a VHE-based hypothesis now and elaborate more on the exclude of spin Hall effect in Discussion.

The RNL and RL data measured at different temperatures for the case of Vg = −60 V are plotted in Fig. 2d. The cubic law is not applicable above 160 K, due to the enhancement of inter-valley scattering by the smear of the lowest conduction sub-band spin splitting (estimated as Es/kB ∼ 169 K, see Supplementary Fig. 9) at high temperatures. Below 160 K, Eq. (1) can be employed to estimate lV. For the case of intermediate inter-valley scattering and edge roughness, lV ∼ 0.36 μm if we assume \(\sigma _{{\mathrm{xy}}}^{\mathrm{V}}\sim 1e^2/h\). In the limit of strong inter-valley scattering and edge roughness, lV ∼ 0.43 μm if we assume \(\sigma _{{\mathrm{xy}}}^{\mathrm{V}}\sim 0.1e^2/h\). These values of lV are comparable to those obtained in graphene systems10,11,12,13,14,17,18.

We further investigated the length dependence of the nonlocal valley transport. Apart from sample A (L = 3.6 μm) and sample B (L = 6 μm), two more samples (L = 11 μm and 16 μm) are investigated (Supplementary Fig. 8). The semilog plot of RNL at n = 4 × 1011 cm−2 (extracted from the Hall measurement, see Supplementary Fig. 10) versus the sample length yields an estimate of lV ∼ 1 μm (Fig. 2g). This value is very close to W and much larger than the electron mean-free path lm ∼ 20 nm (estimated from the sample mobility μ for the range of n where the cubic scaling appears) and the localization length ξ ∼ 50 nm (see Supplementary Fig. 11). Nevertheless, these estimates based on the observed nonlocal signals are suggestive of lv in the order of micron. In sample B, the cubic scaling remains even at room temperature, attributed to the dominant valence-band contribution to \(\sigma _{{\mathrm{xy}}}^{\mathrm{V}}\) and particularly the large intrinsic bandgap that is impossible for graphene systems.

Nonlocal transport in bilayer and trilayer MoS2

For bilayer MoS2, the measured RL and RNL as functions of Vg at different temperatures are plotted in Fig. 3a, b. As the carrier density increases, RL and RNL decrease in a similar fashion in the temperature range of 5–50 K. This yields a linear scaling behavior between RL and RNL, as analyzed in Fig. 3c, d, and no cubic scaling is detected. We note that extrinsic P symmetry breaking can be introduced into atomically thin bilayers via external gating, as achieved in bilayer graphene11,12, and that detecting a nonlocal signal in gated bilayer graphene requires a threshold gating strength11,12. In our devices, however, Vg is too low to reach the threshold estimated by an recent optical experiment18, the estimated potential difference between the top and bottom layers is ∼ 9.2 meV at Vg = −60 V. This weak symmetry breaking produces little change in the total Berry curvature as compared with the pristine case (Supplementary Fig. 12), given the facts that the induced potential is much smaller than the bandgap and that the valence-band contribution to \(\sigma _{{\mathrm{xy}}}^{\mathrm{V}}\) is dominant. In light of this analysis, the gating-induced P symmetry breaking is negligible in our bilayer MoS2. Therefore, we conclude that the absence of cubic scaling in bilayer MoS2 indicates the crucial role of strong P symmetry breaking in generating VHE. This is consistent with the theoretical understanding of VHE5,6,7,8,9, as aforementioned in Introduction.

Fig. 3
figure 3

Local and nonlocal resistances of bilayer and trilayer MoS2. a, b, e, f Gate-dependence of RL and RNL at different temperatures in bilayer a, b and trilayer e, f samples. c, g Scaling relation between ln RL and ln RNL is obtained at different temperatures in bilayer c and trilayer g samples. For the trilayer case, RNL scales linearly with RL in the high electron density regime, whereas the cubic scaling law RNL ∝ RL3 is observed in the low electron density regime (nc = 4 × 1011 cm−2 or Vg = −18.4 V). d lnRL v.s. lnRNL for bilayer MoS2. In the full range of gate voltages, RNL scales linearly with RL, and the experimental data (black dots, Vg = −60 V) is fitted by a linear curve (red solid line). h lnRL v.s. lnRNL for trilayer MoS2. The experimental data (black dots, Vg = −20 V) clearly show two different regimes which are fitted by two linear curves (red solid line with slope 1 and blue solid line with slope 3). Evidently, a crossover exists from linear (RNL ∝ RL) to cubic scaling behaviors (RNL ∝ RL3)

Full size image

This key conclusion can be immediately tested in thicker MoS2 samples. Given that P symmetry is broken (respected) in pristine odd-layer (even-layer) MoS2, one might wonder whether the intrinsic VHE and its cubic scaling could be detected in trilayer MoS2. Figure 3e, f display our RL and RNL data measured in trilayer MoS2 as functions of Vg at different temperatures. Evidently, the measured RNL rapidly decreases as Vg increases in the narrow range of −20 V < Vg < −18.4 V, which is reminiscent of the behavior of RNL in our monolayer devices in the low density regime. Similar to the monolayer case, the logarithmic plots of RL and RNL in Fig. 3g exhibit clear changes in slop from 1 to 3 near Vg = −18.4 V, further confirming the observation of the nonlocal signal of VHE in trilayer MoS2. To illustrate the temperature dependence, Fig. 3h plots the scaling relation between RL and RNL at different temperatures for the case of Vg = −20 V. Again, there is a clear change in slop from 1 to 3 near 30 K. Moreover, the valley diffusion length can be extracted based on Fig. 3h and Eq. (1). We obtain lV ∼ 0.5 μm and ∼1 μm, respectively, for the aforementioned two limits \(\sigma _{{\mathrm{xy}}}^{\mathrm{V}}\sim 1e^2/h\;{\mathrm{and}}\sim \hskip -2pt 0.1\;e^2/h\). Both the observed amplitude of nonlocal signal and the estimated valley diffusion length in the trilayer MoS2 devices are comparable to those in the monolayer case. In addition to the crucial role of P symmetry breaking, significantly, these observations are suggestive of a universal physical origin of VHEs in odd-layer TMDCs, as discussed below.

Layer-dependent Berry curvatures

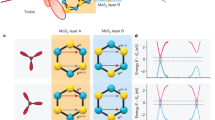
To better understand the thickness dependent observations, we calculate the electronic band structures and Berry curvatures15,16 for monolayer, bilayer, and trilayer MoS2. The band structures in Fig. 4a, c are indeed thickness dependent. In particular, the conduction-band minima lie at the K-valleys for the monolayer, whereas they shift to the Q-valleys for the bilayer and trilayer. Given the low electron densities in our samples (∼4 × 1011 cm−2 in monolayers and trilayers, ∼1 × 1012 cm−2 in bilayers), the Fermi levels only cross the lowest conduction sub-bands, as indicated by the green lines in Fig. 4a, c. As bilayer MoS2 has a restored P symmetry that is intrinsically broken in odd-layer MoS2, the sub-bands are spin degenerate in the bilayer yet spin split in the monolayer and trilayer. With these band structures, we further compute the Berry curvatures that drive the VHEs. Berry curvature vanishes if both P and T are present. As plotted in Fig. 4d, f, our calculations reveal that the curvatures are indeed trivial in the bilayer yet substantial in the monolayer and trilayer. This explains the reason why no cubic scaling is observed in bilayer MoS2 and highlights the role of P symmetry breaking in producing VHEs.

Fig. 4
figure 4

Band structures and Berry curvatures of atomically thin MoS2. a–c Band structure of (a) monolayer, (b) bilayer, and (c) trilayer MoS2. The conduction band edges lie at the K-valleys in the monolayer but at the Q-valleys in the bilayer and trilayer. Insets of a–c: The Fermi levels only cross the lowest sub-bands, which are spin degenerate in b but spin split in a and c. d–f Berry curvatures of d monolayer, e bilayer, and f trilayer MoS2. The blue curves are the total curvatures of all occupied states below the Fermi levels (~2 meV from the conduction band bottom), whereas the orange curves are the total curvatures of all valence-band states. The red arrow in f points out a tiny bump at a Q-valley. Insets of d–f 2D mapping of Berry curvatures in the 2D Brillouin zone (white dashed lines)

Full size image

It is puzzling to understand and compare the nonlocal signals of VHEs in monolayer and trilayer MoS2. Similar cubic scaling behaviors and their transitions to linear ones above the critical densities or temperatures are observed in both cases. However, the conduction-band Berry curvatures (the difference between the blue and orange curves in Fig. 4d, f) are large in the monolayer K-valleys yet negligibly small in the trilayer Q-valleys. This implies that the geometric explanation of VHE requiring finite doping5 should not be the origin11, which is further evidenced by the fact that the cubic scaling behaviors weaken rapidly with increasing the electron densities.

On the other hand, these facts appear to be in harmony with the topological VHE6,7,8,9 that arises from the valley Hall conductivity (see Supplementary Note 1). This conductivity amounts to the total valley-contrasting Berry curvature contributed from all occupied states, i.e., all the states below the Fermi level if at zero temperature. In our case, the monolayer and trilayer share almost identical substantial valence-band Berry curvatures (the orange curves in Fig. 4d, f), due to the extremely weak interlayer couplings. By contrast, the conduction-band contributions are different but very minor (the difference between the blue and orange curves in Fig. 4d, f) because of the low electron densities. Therefore, the valence-band contributions dominate the valley Hall conductivities, leading to similar nonlocal signals of VHEs in monolayer and trilayer. Recently, nearly quantized edge transports have been observed along the designed or selected domain walls in graphene systems13,14 and even in artificial crystals19. In our case, the roughness of natural edges can cause edge inter-valley scattering8 and remove any possible edge state39. This also partly reduces the valence-band contributions4 which in principle would result in a quantized valley Hall conductivity (valley Chern number6,8) in the massive Dirac model.

Discussion

Finally, we note that the VHE and spin Hall effects are distinct in TMDCs, in spite of the spin-valley locking. The spin-valley locking is a property at Fermi level only when it lies in the lowest conduction or highest valence sub-band. Yet, all states below Fermi level contribute to the spin and valley Hall conductivities6 (see Supplementary Note 1). Although a similar line of analysis based on Eq. (1) can be done for a theoretical hypothesis of spin Hall effect as well, it appears that this is not the case for three reasons. First, the spin Hall conductivities are predicted to be very small for pristine odd-layer TMDCs when the valence bands are fully filled16 (see Supplementary Note 1). Second, the observed nonlocal resistances have little response to a magnetic field up to 9 T (Supplementary Fig. 13). Third, the spin diffusion length in TMDCs is at the scale of several tens of nanometers40,41, which is 1–2 orders smaller than the extracted diffusion lengths based on our experimental data or Eq. (1).

In conclusion, the pronounced nonlocal signals are observed in our MoS2 samples with length up to 16 μm and at temperature up to 300 K. The valley diffusion lengths are also estimated to be in the order of micron. The low carrier concentration ensures the low possibility of bulk inter-valley scattering and maintains a long valley diffusion length. In addition, the mirror and T symmetries lock the spin and valley indices of the lowest sub-bands, preventing bulk inter-valley scattering via spin conservation. Our observed intrinsic VHEs and their long valley diffusion lengths are promising for realizing room-temperature low-dissipation valleytronics. To better elucidate the outstanding problems of both geometric5 and topological6,7,8,9 VHEs, our observations and analyses call for future efforts, particularly complementary experiments in p-type TMDCs (where spin Hall conductivities are predicted to be much larger16) such as the one42 that we became aware of during the peer review process.

Methods

Van der Waals structures

MoS2 bulk crystals are bought from 2D semiconductors (website: http://www.2dsemiconductors.com/), and the h-BN sources (grade A1) are bought from HQ graphene (website: http://www.hqgraphene.com/). To fabricate van der Waals heterostructures, a selected MoS2 sample is picked from the SiO2/Si substrate by a thin h-BN flake (5–15 nm thick) on PMMA (950 A7, 500 nm) via van der Waals interactions. The h-BN/MoS2 flake is then transferred onto a fresh thick h-BN flake lying on another SiO2/Si substrate, to form a BN-MoS2-BN heterostructure (step 1 in Supplementary Fig. 1).

Layer numbers and stacking orders

To determine the number of layers for a MoS2 sample, we carried out micro-Raman and photoluminescence measurements before making a device (Supplementary Fig. 14). We also took cross-sectional STEM (JEOL JEM-ARM200F Cs-corrected TEM, operating at 60 kV) images after the electronic measurement. The STEM image can clearly determine the number of MoS2 layers (Supplementary Fig. 14) and distinguishes the 2H stacking order from other stacking orders such as 1T and 3R (Supplementary Fig. 15).

Selective etching process

A hard mask is patterned on the heterostructure by the standard e-beam lithography technique using PMMA (step 2 in Supplementary Fig. 1). The exposed top BN layer and MoS2 are then etched via reactive ion etching (RIE), forming a Hall bar geometry (steps 3 & 4 in Supplementary Fig. 1). Then a second-round e-beam lithography and RIE is carried out to expose the MoS2 layer (steps 5 & 6 in Supplementary Fig. 1). The electrodes are then patterned by a third-round e-beam lithography followed by a standard e-beam evaporation (steps 7 & 8 in Supplementary Fig. 1). To access the conduction band edges of MoS2, we choose Titanium as the contact metal, as the work function of Titanium (∼4.3 eV) matches the band-edge energy of MoS2 (∼4.0–4.4 eV depending on the layer numbers).

Electronic measurement

The I–V curves are measured by Keithley 6430. Other transport measurements are carried out by using: (i) low-frequency lock-in technique (SR 830 with SR550 as the preamplifier and DS 360 as the function generator, or (ii) Keithley 6430 source meter (>1016 Ω input resistance on voltage measurements). The cryogenic system provides stable temperatures ranging from 1.4 to 300 K. A detailed discussion of the nonlocal measurement is presented in Supplementary Fig. 6.