Abstract
Manganese based layered oxides have received increasing attention as cathode materials for sodium ion batteries due to their high theoretical capacities and good sodium ion conductivities. However, the Jahn–Teller distortion arising from the manganese (III) centers destabilizes the host structure and deteriorates the cycling life. Herein, we report that zinc-doped Na0.833[Li0.25Mn0.75]O2 can not only suppress the Jahn–Teller effect but also reduce the inherent phase separations. The reduction of manganese (III) amount in the zinc-doped sample, as predicted by first-principles calculations, has been confirmed by its high binding energies and the reduced octahedral structural variations. In the viewpoint of thermodynamics, the zinc-doped sample has lower formation energy, more stable ground states, and fewer spinodal decomposition regions than those of the undoped sample, all of which make it charge or discharge without any phase transition. Hence, the zinc-doped sample shows superior cycling performance, demonstrating that zinc doping is an effective strategy for developing high-performance layered cathode materials.
Similar content being viewed by others
Introduction
The gradual depletion of fossil fuels, together with environmental concerns over their use, has led to a rapidly increasing demand for high performance electrochemical energy storage and conversion (EESC) technologies, driving the development of secondary batteries1,2,3,4,5. Among various EESC devices, lithium-ion batteries (LIBs) have the widest applications in various fields6,7,8,9. However, limited lithium availability makes it difficult to meet the forecast growth in market demand for LIBs. In contrast, Na is widely distributed around the world and is inexpensive, making sodium-ion batteries (SIBs) a promising alternative for LIBs10,11,12,13,14,15,16,17,18.
As cathode materials are the key determinant for the performance of SIBs, various compounds have been investigated as SIB cathodes, including sodium transition-metal oxides, polyanions, and alkali-metal hexacyanometalates19,20,21,22. Among these materials, sodium-based layered transition-metal oxides (abbreviated as NaxMO2 where M is a first row transition-metal) have gained significant attention because of their unique structural advantages and high theoretical capacities23. To date, O3-type and P2-type layered structures have been intensely studied among various sodium-based layered transition-metal oxides, although there is greater interest in the latter. This is because P2-type NaxMO2 generally performs better electrochemically due to its lower Na+ diffusion barrier and higher ionic conductivity than its O3 phase23,24. In addition, O3-phase samples are too hygroscopic to be stored at ambient atmosphere25, while P2-phase has sufficient stability to be stored at ambient condition.
Mn-based layered oxides have been extensively studied for SIBs due to their low costs, elemental availability and environmental friendliness13,26,27. However, these materials tend to undergo large Jahn–Teller distortions induced by Mn3+ ions (t2g3eg1), leading to severe cyclic degradations during charge or discharge. Unlike Mn3+ ions, Mn4+ ions (t2g3eg0) occupy the octahedral sites and stabilize their electronic structures based on energetics28,29. In order to suppress the Jahn–Teller distortion for cyclic improvement, several research groups focused on doping different metal ions (e.g., Mg, Al, and Li) into Mn-based layered oxides30,31,32,33,34. Even though such metal doping helped to enhance capacity retention, their capacity retentions are still insufficient for the practical application of Mn-based layered oxides as conventional cathode materials. Furthermore, due to the larger ionic radius of Na+ ion, NaxMO2 generally undergoes more drastic phase transformations during desodiation than LiMO2 during delithiation, which makes its degradation more disastrous35,36,37.
Hence, reducing the Jahn–Teller distortion and controlling the phase transformations in NaxMO2 during repeated charge/discharge look critical for its use as a conventional cathode material. Some studies attempted to understand their electronic structure and thermodynamic phase stability upon Na extraction using both theoretical and experimental approaches, because this stability is directly associated with the capacity retention of NaxMO238,39,40. In this regard, reducing the amount of Mn3+ and suppressing the phase separation during desodiation may be essential for improving the capacity retention of Mn-based layered oxides.
Considering that Jahn–Teller distortion is primarily induced by trivalent Mn ions and the inherent phase transformations of Mn-based layered oxides are closely linked to their thermodynamic instability, divalent Zn has been doped into P2-type Na0.833[Li0.25Mn0.75]O2 (NLMO) to investigate its structural and thermodynamic contributions in this study. The reason to choose P2-type NLMO is because introduction of Li into the transition-metal layer can increase the Na content and thus enhance its capacity32,41. Specifically, (Na0.833Zn0.0375)[Li0.25Mn0.7125]O2 (NLMO-Zn) has been obtained via Zn doping by a sol–gel process combined with a subsequent heat treatment. Such doping not only alleviates Jahn–Teller distortion by increasing the average oxidation state of Mn but also reduces the inherent phase separation or instability. This approach has been rationalized using first-principles calculation and has been verified using several analytical techniques, such as X-ray photoelectron spectroscopy (XPS), X-ray absorption spectroscopy (XAS), and in situ X-ray diffraction (XRD). In comparison with bare NLMO, Zn-doped samples have superior capacity retention. These findings can be used to formulate rational strategies to improve the phase stabilities and electrochemical performances of manganese-based cathode materials in both LIBs and SIBs.
Results
Theoretical prediction of electronic and thermodynamic stability
The material we targeted for the Zn doping strategy, Na[Li0.25Mn0.75]O2, is expected to have a mixed Mn valence of 3+ and 4+ to meet the charge balance. We first verified this mixed valence by computationally modelling the structure of Na[Li0.25Mn0.75]O2 and calculating the partial density of states (PDOS) of Mn. As expected, Mn in these oxidation states is present with the Mn3+ occupying the sites identified by the purple octahedra (Fig. 1a) and Mn4+ by the purple octahedra (Fig. 1b).
Theoretical calculations regarding the effects of Zn doping in the fully sodiated Na[Li0.25Mn0.75]O2. a Shows the Mn3+ sites as purple octahedra in the relaxed crystal structure of Na[Li0.25Mn0.75]O2 together with its corresponding PDOS. Likewise, the Mn4+ sites are shown as purple octahedra in b together with its corresponding PDOS. c Shows PDOS of the Mn3+ sites in the Zn-doped Na[Li0.25Mn0.75]O2. Likewise, PDOSs of the Zn2+ and the Mn4+ sites in the Zn-doped Na[Li0.25Mn0.75]O2 are shown in d, e, respectively
We then modelled the Zn-doped Na[Li0.25Mn0.75]O2 structure, and the structure was fully relaxed using first-principles method (Fig. 1c−e). The PDOSs of the Mn3+, Zn2+, and Mn4+ centers are illustrated in Fig. 1c–e, respectively. It is found that the Mn3+ centers are oxidized (Fig. 1c), leading to the increased density of states of the Mn4+ centers in the Zn-doped model compared to the undoped model. This indicates that Zn-doped Na[Li0.25Mn0.75]O2, which includes more Mn4+, would experience less Jahn–Teller distortion and hence better capacity retention compared to the undoped Na[Li0.25Mn0.75]O2.
Because the capacity retention of cathode material is closely associated with its thermodynamic phase stability which is mainly changed during the extraction of charge carriers, the formation energies of mixing enthalpy (∆Hmix) for Na[Li0.25Mn0.75]O2 and Zn-doped Na[Li0.25Mn0.75]O2 were calculated with Na content and shown in Fig. 2a, b. The calculated thermodynamic energy values have been utilized for plenty of battery materials to predict their phase stability as a function of charge carrier content. In these calculations, we have considered all possible combinations of Na ions and their vacancies in Na1−x[Li0.25Mn0.75]O2 and Zn-doped Na1−x[Li0.25Mn0.75]O2 when their sodium contents are in the range of x = 0.0−1.0. From these energy diagrams, Na1−x[Li0.25Mn0.75]O2 exhibits five ground states, while Zn-doped Na1−x[Li0.25Mn0.75]O2 includes seven ground states. In details, both of Fig. 2a, b are composed of four regions with the inverse Na content. In the first region from x = 0 to x = 0.25, the Zn-doped Na[Li0.25Mn0.75]O2 has a ∆Hmix difference (notated as ∆H1 in Fig. 2a, b, i.e., ∆H1 = ∆Hmix(x = 0.25) − ∆Hmix(x = 0.0)) of −0.2709 eV, which is lower than that of Na[Li0.25Mn0.75]O2 (−0.3256 eV), implying that a volumetric strain (εV = ΔV/Vx=0 where ΔV is the volumetric change and Vx=0 is its unit cell volume at x = 0) for the Zn-doped structure (εV = −0.027) is smaller than that for the undoped structure (εV = −0.044) during the initial desodiation. In the second region, the ground states of Zn-doped Na[Li0.25Mn0.75]O2 as marked by the red circles in Fig. 2b lie on the tie line between x = 0.25 and x = 0.5, indicative of desodiation occurring in the same phase. This is in contrast to its undoped counterpart, where the appearance of a pseudo ground state (grey circle) at x = 0.38 suggests the formation of a new phase, that is, desodiation involves a two-phase reaction in Na[Li0.25Mn0.75]O2. In the third region (x = 0.50–0.88), the two pseudo ground states are shown as grey circle above the tie line at x = 0.63 and at x = 0.75 are present for Na[Li0.25Mn0.75]O2 and is indicative of phase separation when desodiated to this extent. By contrast, Zn-doped Na[Li0.25Mn0.75]O2 only has one pseudo ground state as illustrated by the grey circle at x = 0.63, indicating that phase separation may occur only within the narrow region of x = 0.5 and x = 0.75. The additional ground states in Zn-doped Na[Li0.25Mn0.75]O2 can contribute to suppressing the inherent phase separation or transition which can occur in Na[Li0.25Mn0.75]O242.
The phase stability of Na[Li0.25Mn0.75]O2 and Zn-doped Na[Li0.25Mn0.75]O2 with different Na contents. The mixing enthalpy (∆Hmix) values were calculated considering all possible Na and their vacancy configurations and the results are shown for Na[Li0.25Mn0.75]O2 (a) and Zn-doped Na[Li0.25Mn0.75]O2 (b). Here, the two atomic models contain 8 Na atoms in each unit cell structure. Based on statistical thermodynamics, many unit cell structures can be generated based on the combinations of Na and its vacancy sites in the unit cell structure. Among them, one should have the lowest mixing enthalpy value as marked with the red or grey circles in a and b, while the other structures must have higher enthalpy values (marked with white circles). Above the tie lines (blue solid lines), grey filled circles are notated as pseudo ground states that are not preferential to exist in certain compositions. In the cases where the ground state as indicated by the red circles lie on the tie lines, these are true ground states as their structures are thermodynamically favourable at the specified compositions. ∆H1 indicates the difference between the lowest energy values at x = 0.25 and x = 0.0. Homogeneous bulk free energies are shown for Na[Li0.25Mn0.75]O2 (c) and Zn-doped Na[Li0.25Mn0.75]O2 (d) at 300 K. In both panels, the range between the dotted lines indicate the spinodal decomposition regions satisfying the condition of \(\frac{{\partial \Delta G_{\hom }}}{{\partial x^2}} < 0\)
To investigate the detailed phase separations in the third region of the two samples, minimum ∆Hmix values were fitted using a double-well function. Then, the homogeneous bulk free energies (∆Ghom), which can predict spinodal decomposition region and the related phase separation behaviour43, were calculated at 300 K and shown in Fig. 2c, d. For Na[Li0.25Mn0.75]O2, the range of inverse Na content (x value) where spinodal decomposition would occur looks broad, suggesting that the pristine sample continues to suffer from a couple of phase separations when charged above x = 0.57. Meanwhile, due to the additional ground states accompanied by Zn doping, the doped sample tends to have a spinodal decomposition just within a much narrower range of inverse Na content and thereby remarkably reduces the degree of phase separation when charged above x = 0.54. The calculated thermodynamic phase stability predicts that Zn-doped Na[Li0.25Mn0.75]O2 has lower ∆H1 and more stable intermediate phases, and smaller spinodal decomposition region, finally enhancing its cyclic stability compared to Na[Li0.25Mn0.75]O2.
Following these computational findings, we also investigated the phase stability of NLMO and NLMO-Zn at different temperatures and compositions by calculating their bulk free energies. NLMO-Zn has a lower free energy than NLMO at all temperatures and at all extent of sodium extraction (Supplementary Fig. 1), indicating that the doped sample exhibits higher stability than its undoped counterpart.
Preparation and structural analysis of materials
Following computational verification of our hypothesis, we proceeded to synthesize undoped NLMO and NLMO-Zn using a sol–gel method combined with a subsequent heat treatment. The precursor solution was evaporated at 80 °C for 12 h and was then heated in a vacuum oven at 60 °C for 4 h, yielding a viscous white mixture (Supplementary Fig. 2). This mixture was pre-calcined first for 2 h at 400 °C, the temperature at which all volatiles have been removed according to thermal gravimetric analysis (TGA) (Supplementary Fig. 3), and then re-ground and pelletized for a final calcination at 700 °C for 6 h in air.
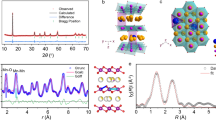
Figure 3a shows the XRD patterns of NLMO and NLMO-Zn. All peaks in both samples agree well with the pattern having the P2-phase from previous studies (Supplementary Fig. 4)32, demonstrating that the P2-type structure is constructed without any impurity phase. For more accurate structure determination of the doped and undoped NLMO, high resolution powder diffraction (HRPD) patterns were collected using synchrotron X-ray with a wavelength of 0.7749 Å. Figure 3b, c each show the Rietveld refinement results for pristine NLMO and NLMO-Zn. The patterns of both samples have high peak intensities, which indicate their high crystallinity. The detailed cell parameters for NLMO and NLMO-Zn are listed in Table 1 and Supplementary Tables 1, 2. NLMO and NLMO-Zn have a hexagonal structure in the P63 space group; no other phase is found, confirming the phase purity of both samples. The corresponding P2-type crystal structure of NLMO or NLMO-Zn is shown in Fig. 3d, e. When viewed along the y-axis, the layered structure of P2-NLMO where O-layers are stacked in ABBAAB sequence is clearly visible. Therein, Li and Mn ions occupy the same positions (2a and 2b sites) but with different occupancies. When viewed along the z-axis, some Na ions seem to surround O ions, while other Na ions are observed to surround Li and Mn ions. After doping Zn, Zn ions occupy 6c positions in the Na layer. The detailed description of crystal structure of NLMO or NLMO-Zn is placed in Supplementary Note.
Structural analyses of NLMO and NLMO-Zn. a Shows the XRD patterns of NLMO and NLMO-Zn. b, c Show the Rietveld refinement results for high-resolution diffraction patterns (HRPD) of NLMO and NLMO-Zn, respectively. Crystal structure of P2-type NLMO (or NLMO-Zn) viewed along the y-axis (d) and the z-axis (e). f Shows the XPS spectra in the Mn 2p3/2 region of NLMO and NLMO-Zn
The electronic structures of NLMO and NLMO-Zn were characterized by XPS, and their spectra in the Mn 2p3/2 region are shown in Fig. 2f. The Mn in NLMO-Zn has a higher binding energy, which suggests that the oxidation state of Mn in this sample is closer to 4+ than that in NLMO. Furthermore, the higher binding energy of Zn in NLMO-Zn indicates that the Mn−O bonds in NLMO-Zn are more robust than those in NLMO, which may contribute to improving the phase stability and thereby the capacity retention. These XPS results experimentally confirm our hypothesis and computational design of employing Zn dopant to reduce the amount of the Jahn–Teller distorted Mn3+ centers. For completeness, the Zn 2p partial spectrum is provided in Supplementary Fig. 5. Here, the Zn 2p3/2 and 2p1/2 peaks are located at 1023.13 and 1046.14 eV, respectively, coinciding with those of ZnCl2 and ZnSO4 (from the National Institute of Standards and Technology (NIST) database) and demonstrating that the doped Zn in NLMO-Zn has a valence very close to +2.
In order to directly validate the location of the doped Zn, we conducted scanning transmission electron microscopy (STEM) and solid-state nuclear magnetic resonance (NMR) analyses together. Bright-field TEM image of the NLMO-Zn particle along the [010] projection with the corresponding selected area diffraction pattern (SAED) is shown in Fig. 4a. The P2-type layered structure is verified again, which is consistent with the HRPD refinement results. HAADF-STEM images of NLMO-Zn are displayed in Fig. 4b, and bright contrasts exist in between two adjacent transition-metal layers, which are marked by the red arrows in the magnified images on the right side of panel b. It demonstrates that Zn dopants exist in the Na layers. To further understand the Zn position, a series of HAADF-STEM image simulations were done. As shown in Fig. 4c, Zn located at the Na layer causes a bright contrast, while no significant difference can be observed compared to the undoped case, demonstrating that Zn2+ ions are likely to occupy in Na layer. Figure 4d shows that the contrast caused by Zn at the Na layer varied depending on its occupancy. These simulation results indicate that the occupancy of Zn in the Na-atomic columns is less than 10%. The Zn2+ ions in the Na layers would stabilize the diffusion channels during charge/discharge processes44. HAADF-STEM can thus visualize the Zn dopants located at the Na sites. We then performed 23Na solid-state nuclear magnetic resonance (NMR) spectroscopy for NLMO and NLMO-Zn to compare their sodium chemical environments, and the results reveal that the doped Zn2+ ions do not exist in the transition-metal layer (Supplementary Fig. 6)45. Altogether, these analyses provide strong evidences that the doped Zn preferentially occupies the Na layer rather than the transition-metal layer.
Microscopy structure investigation of NLMO-Zn. a Bright-field TEM image of the particle along the [010] projection. Inset shows the selected area diffraction pattern from the particle. b HAADF-STEM image of NLMO-Zn. c Simulated HAADF images in the [010] projection of the three cases: undoped NLMO, 5%-Zn occupying the Na site in NLMO-Zn, and 5%-Zn occupying the Mn site in NLMO-Zn. d Simulated HAADF images showing the different contrasts by the variation of Zn-occupancy (3%, 5%, 7%, and 9% Zn in the Na layer)
The morphologies and structures of both samples were further corroborated by scanning electron microscopy (SEM) images and elemental analyses using energy dispersive X-ray spectroscopy (EDS) and inductively coupled plasma optical atomic emission spectroscopy (ICP-AES). Both NLMO and NLMO-Zn are predominantly particles of several microns in dimensions (Supplementary Fig. 7), and all elements are homogeneously distributed in both samples (Supplementary Fig. 8). All atomic ratios are similar to their calculated values based on their crystal structures (Supplementary Fig. 9 and Supplementary Table 3, 4). Although the sodium content in NaxMnO2 is usually in the range of x = 0.68−0.76, the introduction of Li into the transition-metal layer can extend the upper limit of this range to 0.8 or 0.83332,46. Unfortunately, our attempts to increase the amount of Zn dopant was unsuccessful; when attempting to increase the atomic percent of Zn from 0.98% to 1.96% to obtain a stoichiometry of (Na0.833Zn0.075)[Li0.25Mn0.675]O2, an impure phase (i.e., LiMn2O4) emerges in its XRD pattern (Supplementary Fig. 10). Thus, substituting Zn ions for 5% Mn is found to be the optimum condition in terms of phase purity.
As an experimental indicator of thermal stability, we characterized NLMO and NLMO-Zn by TGA and DSC (Supplementary Fig. 11). Both samples exhibit two exothermic events as marked by the arrows in Supplementary Fig. 11b, but these occur at higher temperatures for NLMO-Zn than for NLMO, corroborating the computational finding that the Zn-doped compound possesses higher thermal stability as shown in Supplementary Fig. 1.
Experimental validation of electronic and thermodynamic stability
To verify the computational results regarding Jahn–Teller distortion experimentally, we performed ex situ X-ray adsorption near-edge structure (XANES) and extended X-ray adsorption fine structure (EXAFS) analyses for the two samples in the as-prepared, fully charged, and fully discharged states during the 1st cycle. The XANES spectra at Mn K-edge region are shown in Fig. 5a, and its magnified pre-edge region is shown in its figure inset. In the pre-edge region, two peaks are observable, which is consistent with previous reports47,48. However, these Mn pre-edge peaks look similar for both pristine NLMO and NLMO-Zn owing to their weak intensities. After full discharge to 1.5 V, these two pre-edge peaks, as well as the main absorption edge in both samples, shift to lower energies because of the decreased oxidation state of Mn. However, two pre-edge peaks and the main edge of NLMO are positioned at lower energies than those of NLMO-Zn, which implies that the Mn in NLMO has a lower average oxidation state (i.e. closer to the Jahn–Teller active Mn3+), and thus NLMO would suffer more severe Jahn–Teller distortion than NLMO-Zn.
Observation of Jahn–Teller distortion in NLMO and NLMO-Zn during the first cycle. a Shows the XANES spectra at the Mn-K edge for NLMO and NLMO-Zn before cycling as well as in the fully charged and discharged states. b Shows Fourier-transformed (FT) magnitude of Mn K-edge EXAFS spectra for NLMO and NLMO-Zn before cycling as well as in the fully charged and discharged states
From the Fourier-transformed (FT) magnitude plot of the Mn K-edge EXAFS spectra shown in Fig. 5b, two main peaks are observable in all cases. The peak at about 1.5 Å corresponds to the single scattering paths of adjacent oxygen atoms (i.e., Mn-O), while the peak at approximately 2.5 Å is attributed to the interactions between Mn ions and their neighbouring metal ions (i.e., Mn, Zn, or Li)46,47. Note that these distances are not the actual bond lengths because these FT spectra were not phase-corrected. For NLMO in the fully discharged state, an additional peak at 0.98 Å (circled in dashed lines) resulting from Jahn–Teller distortion can be clearly resolved, but this peak is not observed in NLMO-Zn in the fully charged and discharged states evidencing our hypothesis and computational calculations regarding the suppression of Jahn–Teller distortion by the doped Zn.
To figure out the structural changes of NLMO and NLMO-Zn during charge/discharge, in situ XRD analysis was carried out during the 1st cycle, as shown in Fig. 6. For pristine NLMO, the (002) peak splits into two peaks when the sample was charged to 4.12 V (purple line in Fig. 6a), which indicates that two phases coexisted in this high voltage region. Because the (002) peak of the O2 phase is located at around 20°, the newly emerged phase has nothing to do with the O2 phase49. However, any peak assigned to the O2 phase does not emerge in both samples (Supplementary Fig. 12), but the (002) peak splits into two adjacent peaks for pristine NLMO, demonstrating that a phase transformation occurs to form a new phase. Because the new phase is similar to the P2 phase in the structural viewpoint, it is named P2’ phase. During charge, the (002) peak of the P2 phase keeps decreasing gradually and finally almost vanishes in the fully charged state. The phase transformation and two-phase behaviour of pristine NLMO are induced by the phase separation stemming from thermodynamic phase instability as predicted by our first-principles calculations above. The (002) peak of the P2’ phase gradually shifts to high angles during the charging process from 4.12 V to 4.4 V, which is indicative of the decrease of layer spacing. The (010) and (012) peaks also shift to high angles during charge because of their reduced lattice parameters as well. Figure 6b shows the in situ XRD patterns of pristine NLMO during discharge. As Na ions are inserted back into interlayers, the (002) peak of P2’ phase gradually shifts to lower angles, and its intensity simultaneously decreases. Then, it completely disappears when discharged to 2.08 V. On the other hand, the (002) peak of the P2 phase reappears, and its intensity gradually becomes higher during discharge. Likewise, the (010) and (012) peaks gradually return to the original angles in the initial state during discharge.
Supplementary Fig. 13 shows how the cycling performance of pristine NLMO changes depending on the voltage window. When charged or discharged between 1.5 and 4.6 V, the P2 phase completely transforms into P2’ phase with a drastic capacity decay for the initial three cycles. Between 1.5 and 4.2 V, the P2–P2’ transition is avoided, thereby enhancing the capacity retention. However, with this condition, the initial capacities and coulombic efficiencies are relatively low. When the charge terminal voltage is increased to 4.7 V, the electrolyte is completely decomposed (Supplementary Fig. 14). Both high capacity and decent capacity retention could be achieved via the improved thermodynamic phase stability only when the charging voltage is set to 4.4 V.
Figure 6c shows the in situ XRD patterns of NLMO-Zn when charged to 4.4 V. Interestingly, any peak assigned to the P2’ phase is not detected, and the (002) peak of the P2 phase just broadens during charge, substantiating the argument that the phase transition or separation into the P2’ phase is suppressed thanks to the presence of a ground state at x = 0.75 in the mixing enthalpy diagram (Fig. 2b). The (010) and (012) peaks of NLMO-Zn shift in a similar manner to pristine NLMO, but less compared with the pristine sample, proving that NLMO-Zn undergoes less lattice parameter change during charge. The (002) peak of the P2 phase slightly shifts to lower angles (Fig. 6d), indicating that the interlayer spacing of NLMO-Zn is a little increased during discharge. Just like the pristine sample, the (010) and (012) peaks return back to their original positions before cycling. Hence, it is completely verified that NLMO-Zn does not undergo P2 to P2’ phase transition unlike the pristine NLMO, which well agrees with the thermodynamic phase stability results from first-principles calculation. Hence, Zn doping may well contribute to improving the cycling performance of NLMO-Zn over the undoped counterpart.
The (002) peak of the P2 phase in NLMO and NLMO-Zn was also observed after the 2nd and 100th cycles (Supplementary Fig. 15). The (002) peak of NLMO-Zn has no obvious change even after the 2nd and 100th cycles, whereas the undoped NLMO has a new peak located beside the (002) peak, which is assigned to the P2’ phase. The intensity of this peak becomes higher as the cycle number increases because the P2’ phase cannot completely revert to the P2 phase every cycle, demonstrating that the phase separation of undoped NLMO becomes more serious with the cycle number.
Electrochemical performance
Based on the computational and experimental results above regarding the reduction of the Jahn–Teller distorted Mn3+ centers and the improved phase stability, Zn doping must enhance the capacity retention of NLMO. We verified this by comparatively evaluating the electrochemical performances of NLMO and NLMO-Zn in coin cells using Na as the anode. In the 1st cycle of the cyclic voltammogram (CV) in Fig. 7a, NLMO exhibits two oxidative peaks at 4.15 V and 4.38 V. Herein, the peak at 4.15 V can be assigned to the oxidation of Mn3+ and O2−, while the peak at 4.38 V may be attributed to the phase transformation as previously reported26,28,29,35. We nonetheless also considered the possibility of anion redox-based on some recent literature findings29,32,41 as well as ex situ XPS characterisation for the charged or discharged electrodes (Supplementary Fig. 16). In the CV of NLMO-Zn, only one oxidation peak at 4.20 V is present, which is assigned to the oxidation of O2− and Mn3+ ions. Herein, the absence of the second oxidation peak may indicate that this material does not undergo phase change as previously demonstrated. The reductive sweep during the 1st cycle shows the cationic reduction of Mn4+ as well as anionic reduction of O2n−. The redox peaks appear asymmetric because the reaction process during desodiation is different from that during sodiation in the 1st cycle as reported in previous papers32,41. In addition, all redox peaks have sizeable magnitude of current densities, indicating the involvement of significant amount of redox-active centers.
As shown in the charge/discharge curves of NLMO (Fig. 7b) and NLMO-Zn (Fig. 7c) for the 1st, 2nd and 100th cycle, both samples exhibit similar changes in electrochemical behaviours upon repeated cycling in spite of the apparent superiority of NLMO-Zn. The charge curves of both samples look similar during the whole cycling in that there is a sloping region between 2.2 and 3.8 V and thereafter a plateau region. Actually, as the cycle number increases, the capacity contribution of the sloping region becomes larger, whereas that of the plateau region keeps falling down. The changes are the most prominent up to the 2nd cycle, but get less from the 3rd cycle onward. These changes have been observed in previous studies as well and attributed to the activation of Mn4+ to Mn3+32,41. This plateau region decreases from the 1st to the 100th cycle more rapidly in NLMO than in NLMO-Zn, which is attributed to their different desodiation pathways as shown in the CV curves (Fig. 7a) and in the in situ XRD patterns. Although the charge and discharge curves of both NLMO and NLMO-Zn undergo continuous shape change as the cycling proceeds, the capacity contribution above 3.9 V is a bit higher for NLMO-Zn than for NLMO after the 1st cycle (Supplementary Fig. 17). While discharge proceeds, both samples show similar discharge curves in which the continuous slope is maintained down to the cut-off voltage, 1.5 V, but the discharge capacity of NLMO displays much faster decay than that of NLMO-Zn up to the 100th cycle.
Figure 7d shows the cycling performance of NLMO and NLMO-Zn. Because the redox-active Mn centers are partially substituted by the redox-inactive Zn dopant in NLMO-Zn, the doped sample exhibits lower initial capacity than that of NLMO. However, with repeated charge/discharge cycles, NLMO-Zn maintains very stable capacity retention, while the capacity of NLMO gradually decays up to the 60th cycle, finally rendering the capacity of NLMO-Zn to surpass that of NLMO. In the 1st cycle, the charge and discharge capacities of the doped sample respectively correspond to 0.241 Ah g−1 and 0.166 Ah g−1, which are a little lower than those of its undoped counterpart (0.252 Ah g−1 and 0.179 Ah g−1, respectively). However, NLMO-Zn exhibits a discharge capacity of 0.162 Ah g−1 in the 100th cycle, which is similar to its 1st cycle discharge capacity and exceeds that of NLMO that has dropped down to 0.139 Ah g−1. Up to the 200th cycle, NLMO-Zn still maintains the same discharge capacity reaching 0.161 Ah g−1, which is two times higher than that of NLMO (0.074 Ah g−1), and a coulombic efficiency (CE) of 100.06%, which is superior to that of the undoped sample at 98.20% (Supplementary Fig. 18). Hence, these results clearly demonstrate that Zn doping in NLMO enables superior capacity retention, which can be attributed to the suppression of Jahn–Teller distortion and phase separation as consistent with our hypothesis and computational predictions above. From the morphological observation of the electrodes before and after cycling (Supplementary Fig. 19), the particle sizes of both samples are well maintained even after 100 cycles. In addition, the reproducibility of these electrochemical results was confirmed (Supplementary Figs. 20−22).
Discussion
Figure 8 shows the changes in the electronic and crystal structures of NLMO and NLMO-Zn during the 1st cycle. The initial valences of Mn ions in pristine NLMO and NLMO-Zn are commonly close to +4, even if that of NLMO-Zn is quite higher than that of pristine NLMO, thus suppressing Jahn–Teller distortion. Hence, the charge capacities of NLMO and NLMO-Zn may significantly depend on the oxygen redox reaction (O2− → O2n−), as evidenced by XPS spectra in the O 1s region in the fully charge/discharged states (Supplementary Fig. 16). During the 1st charge, the phase transition from P2 to P2’ takes place in NLMO, but this is not observed in NLMO-Zn. The phase transition in NLMO results from higher O 2p than Mn 3dt2g50, which makes an irreversible oxygen loss inevitable. During the 1st discharge, the P2’ phase reverts to the P2 phase, and the reduction reactions of O2n− and Mn4+ occur simultaneously. During discharge, the phase reversion from P2’ to P2 is accompanied by the reduction of both O2n− and Mn4+ in NLMO. During recharge, the reduction from Mn4+ to Mn3+ becomes higher in NLMO than in NLMO-Zn because of the oxygen loss resulting from the phase transition from P2 to P2’.
As the activation process of Mn4+ ions occurs for both samples, the change of Mn valence in NLMO and NLMO-Zn was also observed after 50 cycles, and the ratios of Mn3+ to Mn4+ in NLMO and NLMO-Zn are 1:7.2 and 1:15.2, respectively (Supplementary Fig. 23). The poor phase stability of NLMO leads to the phase transition from P2 to P2’ and significant oxygen loss, which is accompanied by more reduction of Mn ions, thereby continuously increasing the amount of Mn3+ during the repeated cycling. After 50 cycles, the differences in capacity retention between NLMO and NLMO-Zn become larger and larger with the cycle number.
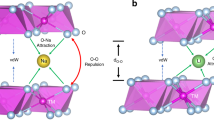
Due to the difference in electronegativity, the doped Zn likely occupies the original Mn3+ sites in NLMO, and thereby reduces the amount of Mn3+ through modulating the electron density in NLMO-Zn. Considering this positive and advantageous effect of the Zn dopant, other non-transition metals were screened computationally as well to figure out whether they have similar benefits (Supplementary Fig. 24, 25). Interestingly, Mg-doped Na[Li0.25Mn0.75]O2 is predicted to show significantly reduced Jahn–Teller distortion because its Mn electronic structure is similar to that of Zn-doped Na[Li0.25Mn0.75]O2. In good agreement with our predictions, a recent paper showed the improved structural stability of Na2/3Mn1−yMgyO2 (y = 0.05 and 0.1)51.
In addition, Zn doping significantly contributes to improving the thermodynamic phase stability of the Mn-based layered oxide. The influence of Zn doping on the electrochemical performance of other Mn-based cathode materials were also investigated, and P2-type Na2/3MnO2, O3-type NaMnO2, and their Zn-doped counterparts were synthesized. As demonstrated by the capacity retention results (Supplementary Fig. 26, 27), both P2-type and O3-type Mn-based cathode materials clearly exhibit enhanced cyclic retention after Zn doping.
Here, all experimental results agree well with the predictions from our first-principles calculations. Based on our empirical and computational findings, it seems that Zn doping has two positive effects on NLMO. First, Zn2+ would primarily results in Jahn–Teller distortion of Mn3+. Secondly, and Zn2+ doping makes the phase stability of the P2 structure robust during charge/discharge and thus helps to prevent its phase transition to the P2’ structure. Consequently, NLMO-Zn could exhibit significantly improved phase stability and capacity retention in comparison with NLMO. Even if the content of Zn in NLMO-Zn is not that high, it looks sufficient for stabilizing the crystal structure of NLMO, as similar to the previous reports with small amount of doping31,52. Thus, Zn doping may be an effective and broadly applicable strategy for Mn-based cathode materials.
Methods
Material preparations
NLMO and NLMO-Zn were prepared using a sol–gel method with a subsequent heat treatment. For NLMO-Zn, LiCH3COO (49.5 mg, 0.750 mmol), NaCH3COO (211.2 mg, 2.575 mmol), Mn(CH3COO)2∙4H2O (523.9 mg, 2.138 mmol) and Zn(NO3)2 (33.5 mg, 0.113 mmol) were dissolved in deionized water. Citric acid (1.73 g) and PEG400 (2 mL) were added to the solution and continuously stirred for 30 min. The transparent solution was evaporated at 80 °C for 12 h and then heated in a vacuum oven at 60 °C for 4 h, yielding a viscous white precursor. This precursor was calcined at 400 °C for 2 h and then annealed at 700 °C for 6 h in air. After cooling to room temperature, the product NLMO-Zn was obtained as a purple powder. For NLMO, the amount of Mn precursor, Mn(CH3COO)2∙4H2O, was changed to 551.5 mg (2.25 mmol); the Zn precursor was not added.
Calculation methods
Densities of states and thermodynamic values were calculated using the density functional theory (DFT) and implemented using a Vienna ab initio simulation package (VASP), which was based on a plane-wave set with the pseudopotentials of a projector-augmented wave (PAW). A generalized gradient approximation (GGA) of a Perdew–Burke–Ernzerhof (PBE) was used for a functional exchange-correlation parameterization. A Li pseudopotential was treated with one 2s electron and two 1s electrons, and one 3s electron and six 2p electrons for Na, to achieve their valence states. Standard potentials were used for Mn and Zn.
To find a strong correlation between transition-metal 3d bands, a Hubbard-type U correction was used in the GGA and PBE with spin-polarized calculations. For standard computational parameters, a kinetic energy cut-off of 400 eV and a k-point mesh in a reciprocal space of 4 × 4 × 2 were applied to all calculations. For all DFT calculations, cell parameters and atomic positions were fully relaxed to achieve optimized electronic structures.
The homogeneous bulk free energy (∆Ghom) was calculated by the thermodynamic mixing enthalpies using a double-well function with the enthalpy coefficient, Ω, as follows:43,53
where ΔHhom indicates the homogeneous mixing enthalpy from xi to xf. \(\Delta G_{\hom }^c\) can be obtained using a theoretical model including the configurational entropy, ΔShom, with temperature (T) as follows:
where kB refers to the Boltzmann constant.
Material characterizations
The crystal structures of the samples were analyzed by powder X-ray diffraction (Rigaku Ulyima IV, Cu Kα, operating at a current of 30 mA and a voltage of 40 kV). The morphologies and microstructures of the samples were characterised using a field emission-scanning electron microscopy (FESEM, JEOL, JSM-6700F) and a transmission-electron microscopy (TEM, JEOL, JEM-2100F). Elemental analyses were performed using energy dispersive X-ray spectrometer (EDS, X-MaxN, Oxford Instruments) and an inductively coupled plasma-optical emission spectrometer (ICP-OES, OPTIMA 8300, Perkin-Elmer). The oxidation states of the elements in the samples were characterised by XPS (Perkin Elmer PHI 1600 ESCA system). Thermogravimetric analysis (TGA) and differential scanning calorimetry (DSC) were conducted using a thermal gravimetric analyzer (TA instruments, SDT Q600) and a DSC analyzer (DSC 200 F3 Maia, NETZSCH), respectively. 23Na solid-state nuclear magnetic resonance (NMR) experiments were performed at 132.3 MHz on a Bruker Avance II spectrometer using a 4 mm MAS probe at rotor spinning speed of 60 kHz.
HAADF-STEM images were collected by a transmission electron microscope (JEM-2100F, JEOL, Japan) at 200 kV with spherical-aberration correction (CEOS GmbH, Germany). The powder was pre-treated by grinding and ion-milling and was then transferred onto a TEM grid. HAADF-STEM image simulations were performed via QSTEM [Christioph Koch, Determination of Core Structure Periodicity and Point Defect Density along Dislocations, PhD thesis, Arizona State University (2002)].
Mn-K edge X-ray adsorption near edge structure (XANES) spectra of the samples were collected at the 10 C beam line at Pohang Accelerator Laboratory (PAL) in Pohang, South Korea,. All spectra were normalized to the main-edge jump. Additionally, high-resolution powder diffraction (HRPD) patterns were collected at National Synchrotron Radiation Research Center (NSRRC) in Taiwan. Synchrotron X-ray was monochromated to a wavelength of 0.7749 Å using a double-crystal Si (111) monochromator. The Rietveld refinement was performed by utilizing the GSAS software54,55.
In situ synchrotron powder XRD data were recorded in a powder diffraction beamline at the Australian Synchrotron with a wavelength of 0.6888 Å. The wavelength was calibrated according to the standard reference material (LaB6 660b) of the National Institute of Standards and Technology (NIST). The cell used for the data collection was charged at a rate of 0.3 C, and the voltage window was 1.5 V–4.4 V. All in-situ XRD patterns were transferred based on Cu Kα standard.
Electrochemical characterizations
All electrochemical tests were conducted in CR2032 coin-type cells. The working electrode consisted of 80 wt.% active materials, 10 wt.% conductive carbon (super P) and 10 wt.% polyvinylidene fluoride (PVdF) binder. The mixture was dispersed in N-methyl pyrrolidone (NMP) and then hand-ground for 30 min. The slurry was cast onto a Cu foil and dried at 110 °C for 12 h under vacuum. The loading of the undoped NLMO and NLMO-Zn was between 1.9 mg cm−2 and 3.2 mg cm−2. The coin cells were assembled using glass-fibre filter paper as separator, Na disc as both counter and reference electrode, and 80 μL of 1 M NaPF6 in ethylene carbonate/diethyl carbonate (EC/DEC, 1:1 v/v) as electrolyte. All cell assembly was performed in an argon-filled glove box. Galvanostatic charge/discharge tests and cyclic voltammetry (CV) were conducted using a WBCS battery cycler (WonATech). For charge/discharge tests, 0.25 A g−1 was used as 1 C.
Data availability
The data that support the findings of this study are available from the corresponding author upon request.
References
Bruce, P. G., Freunberger, S. A., Hardwick, L. J. & Tarascon, J. M. Li-O2 and Li-S batteries with high energy storage. Nat. Mater. 11, 19–29 (2012).
Dunn, B., Kamath, H. & Tarascon, J. M. Electrical energy storage for the grid: a battery of choices. Science 334, 928–935 (2011).
Liu, C., Li, F., Ma, L. P. & Cheng, H. M. Advanced materials for energy storage. Adv. Mater. 22, E28–E62 (2010).
Yang, J. et al. In situ analyses for ion storage materials. Chem. Soc. Rev. 45, 5717–5770 (2016).
Zhang, K. et al. Nanostructured Mn-based oxides for electrochemical energy storage and conversion. Chem. Soc. Rev. 44, 699–728 (2015).
Etacheri, V., Marom, R., Elazari, R., Salitra, G. & Aurbach, D. Challenges in the development of advanced Li-ion batteries: a review. Energy Environ. Sci. 4, 3243–3262 (2011).
Lu, J., Wu, T. & Amine, K. State-of-the-art characterization techniques for advanced lithium-ion batteries. Nat. Energy 2, 17011 (2017).
Jiang, J. et al. Recent advances in metal oxide-based electrode architecture design for electrochemical energy storage. Adv. Mater. 24, 5166–5180 (2012).
Chen, J. S. & Lou, X. W. SnO2-based nanomaterials: synthesis and application in lithium-ion batteries. Small 9, 1877–1893 (2013).
Luo, W. et al. Na-ion battery anodes: materials and electrochemistry. Acc. Chem. Res. 49, 231–240 (2016).
Palomares, V., Casas-Cabanas, M., Castillo-Martinez, E., Han, M. H. & Rojo, T. Update on Na-based battery materials. A growing research path. Energy Environ. Sci. 6, 2312–2337 (2013).
Kim, H. et al. Recent progress in electrode materials for sodium-ion batteries. Adv. Energy Mater. 6, 1600943 (2016).
Yabuuchi, N., Kubota, K., Dahbi, M. & Komaba, S. Research development on sodium-ion batteries. Chem. Rev. 114, 11636–11682 (2014).
Pan, H., Hu, Y. S. & Chen, L. Room-temperature stationary sodium-ion batteries for large-scale electric energy storage. Energy Environ. Sci. 6, 2338–2360 (2013).
Islam, M. S. & Fisher, C. A. J. Lithium and sodium battery cathode materials: computational insights into voltage, diffusion and nanostructural properties. Chem. Soc. Rev. 43, 185–204 (2014).
Kim, S. W., Seo, D. H., Ma, X., Ceder, G. & Kang, K. Electrode materials for rechargeable sodium-ion batteries: potential alternatives to current lithium-ion batteries. Adv. Energy Mater. 2, 710–721 (2012).
Peng, S. et al. Unique cobalt sulfide/reduced graphene oxide composite as an anode for sodium-ion batteries with superior rate capability and long cycling stability. Small 12, 1359–1368 (2016).
Wen, Y. et al. Expanded graphite as superior anode for sodium-ion batteries. Nat. Commun. 5, 5033 (2014).
Xiang, X., Zhang, K. & Chen, J. Recent advances and prospects of cathode materials for sodium-ion batteries. Adv. Mater. 27, 5343–5364 (2015).
Park, Y. U. et al. A new high-energy cathode for a Na-ion battery with ultrahigh stability. J. Am. Chem. Soc. 135, 13870–13878 (2013).
Lee, H. W. et al. Manganese hexacyanomanganate open framework as a high-capacity positive electrode material for sodium-ion batteries. Nat. Commun. 5, 5280 (2014).
Wang, Y., Xiao, R., Hu, Y. S., Avdeev, M. & Chen, L. P2-Na0.6[Cr0.6Ti0.4]O2 cation-disordered electrode for high-rate symmetric rechargeable sodium-ion batteries. Nat. Commun. 6, 6954 (2015).
Han, M. H., Gonzalo, E., Singh, G. & Rojo, T. A comprehensive review of sodium layered oxides: powerful cathodes for Na-ion batteries. Energy Environ. Sci. 8, 81–102 (2015).
Yabuuchi, N. et al. P2-type Nax[Fe1/2Mn1/2]O2 made from earth-abundant elements for rechargeable Na batteries. Nat. Mater. 11, 512–517 (2012).
Billaud, J. et al. β-NaMnO2: A high-performance cathode for sodium-ion batteries. J. Am. Chem. Soc. 136, 17243–17248 (2014).
Ortiz-Vitoriano, N., Drewett, N. E., Gonzalo, E. & Rojo, T. High performance manganese-based layered oxide cathodes: overcoming the challenges of sodium ion batteries. Energy Environ. Sci. 10, 1051–1074 (2017).
Clément, R. J., Bruce, P. G. & Grey, C. P. Review−manganese-based P2-type transition metal oxides as sodium-ion battery cathode materials. J. Electrochem. Soc. 162, A2589–A2604 (2015).
Li, X. et al. Direct visualization of the Jahn-Teller effect coupled to Na ordering in Na5/8MnO2. Nat. Mater. 13, 586–592 (2014).
Kim, D., Cho, M. & Cho, K. Rational design of Na(Li1/3Mn2/3)O2 operated by anionic redox reactions for advanced sodium-ion batteries. Adv. Mater. 29, 1701788 (2017).
Hasa, I., Buchholz, D., Passerini, S. & Hassoun, J. A comparative study of layered transition metal oxide cathodes for application in sodium-ion batteries. ACS Appl. Mater. Interfaces 7, 5206–5212 (2015).
Billaud, J. et al. Na0.67Mn1−xMgxO2 (0 ≤ x ≤ 0.2): a high capacity cathode for sodium-ion batteries. Energy Environ. Sci. 7, 1387–1391 (2014).
Yabuuchi, N. et al. New O2/P2-type Li-excess layered manganese oxides as promising multi-functional electrode materials for rechargeable Li/Na batteries. Adv. Energy Mater. 4, 1301453 (2014).
de Boisse, B. M., Carlier, D., Guignard, M., Bourgeois, L. & Delmas, C. P2-NaxMn1/2Fe1/2O2 phase used as positive electrode in Na batteries: structural changes induced by the electrochemical (de)intercalation process. Inorg. Chem. 53, 11197–11205 (2014).
Thorne, J. S., Dunlap, R. A. & Obrovac, M. N. Structure and electrochemistry of NaxFexMn1−xO2 (1.0 ≤ x ≤ 0.5) for Na-Ion Battery Positive Electrodes. J. Electrochem. Soc. 160, A361–A367 (2012).
Wang, P. F., You, Y., Yin, Y. X. & Guo, Y. G. Layered oxide cathodes for sodium-ion batteries: phase transition, air stability and performance. Adv. Energy Mater. 8, 1701912 (2018).
Bo, S. H., Li, X., Toumar, A. J. & Ceder, G. Layered-to-rock-salt transformation in desodiated NaxCrO2 (x < 0.4). Chem. Mater. 28, 1419–1429 (2016).
Kubota, K. et al. Understanding the structural evolution and redox mechanism of a NaFeO2-NaCoO2 solid solution for sodium-ion batteries. Adv. Funct. Mater. 26, 6047–6059 (2016).
Singh, G. et al. High voltage Mg-doped Na0.67Ni0.3–xMgxMn0.7O2 (x = 0.05, 0.1) Na-ion cathodes with enhanced stability and rate capability. Chem. Mater. 28, 5087–5094 (2016).
Xu, G. L. et al. Insights into the structural effects of layered cathode materials for high voltage sodium-ion batteries. Energy Environ. Sci. 10, 1677–1693 (2017).
Talaie, E., Duffort, V., Smith, H. L., Fultz, B. & Nazar, L. F. Structure of the high voltage phase of layered P2-Na2/3−z[Mn1/2Fe1/2]O2 and the positive effect of Ni substitution on its stability. Energy Environ. Sci. 8, 2512–2523 (2015).
de la Llave, E. et al. Improving energy density and structural stability of manganese oxide cathodes for Na-ion batteries by structural lithium substitution. Chem. Mater. 28, 9064–9076 (2016).
Kim, D., Lim, J.-M., Park, M.-S., Cho, K. & Cho, M. Phase separation and d electronic orbitals on cyclic degradation in Li−Mn−O compounds: first-principles multiscale modeling and experimental observations. ACS Appl. Mater. Interfaces 8, 16631–16639 (2016).
Bai, P., Cogswell, D. A. & Bazant, M. Z. Suppression of phase separation in LiFePO4 nanoparticles during battery discharge. Nano. Lett. 11, 4890–4896 (2011).
Pouillerie, C., Croguennec, L., Biensan, P., Willmann, P. & Delmas, C. Synthesis and characterization of new LiNi1−yMgyO2 positive electrode materials for lithium-ion batteries. J. Electrochem. Soc. 147, 2061–2069 (2000).
Han, M. H. et al. High-performance P2-phase Na2/3Mn0.8Fe0.1Ti0.1O2 cathode material for ambient-temperature sodium-ion batteries. Chem. Mater. 28, 106–116 (2016).
Xu, J. et al. Identifying the critical role of Li substitution in P2–Nax[LiyNizMn1–y–z]O2 (0 < x, y, z < 1) intercalation cathode materials for high-energy Na-ion batteries. Chem. Mater. 26, 1260–1269 (2014).
Nam, K. W. et al. Combining in situ synchrotron X-ray diffraction and absorption techniques with transmission electron microscopy to study the origin of thermal instability in overcharged cathode materials for lithium-ion batteries. Adv. Funct. Mater. 23, 1047–1063 (2013).
Koga, H. et al. Operando X-ray absorption study of the redox processes involved upon cycling of the Li-rich layered oxide Li1.20Mn0.54Co0.13Ni0.13O2 in Li ion batteries. J. Phys. Chem. C. 118, 5700–5709 (2014).
Wang, P.-F. et al. Suppressing the P2−O2 phase transition of Na0.67Mn0.67Ni0.33O2 by magnesium substitution for improved sodium-ion batteries. Angew. Chem. Int. Ed. 55, 7445–7449 (2016).
Xie, Y., Saubanere, M. & Doublet, M. L. Requirements for reversible extra-capacity in Li-rich layered oxides for Li-ion batteries. Energy Environ. Sci. 10, 266–274 (2017).
Clement, R. J. et al. Structurally stable Mg-doped P2-Na2/3Mn1-yMgyO2 sodium-ion battery cathodes with high rate performance: insights from electrochemical, NMR and diffraction studies. Energy Environ. Sci. 9, 3240–3251 (2016).
Ramasamy, H. V. et al. Efficient method of designing stable layered cathode material for sodium ion batteries using aluminum doping. J. Phys. Chem. Lett. 8, 5021–5030 (2017).
Lim, J.-M. et al. Intrinsic origins of crack generation in Ni-rich LiNi0.8Co0.1Mn0.1O2 layered oxide cathode material. Sci. Rep. 7, 39669 (2017).
Larson, A. C. & Von Dreele, R. B. General structure analysis system (GSAS). Los Alamos National Laboratory Report LAUR 86−748 (1994).
Toby, B. H. E. X. P. G. U. I. a graphical user interface for GSAS. J. Appl. Crystallogr. 34, 210–213 (2001).
Acknowledgements
Y.-M. Kang and M. Cho would like to thank the National Research Foundation of Korea (NRF) grants through the Korean government (MSIP) for funding this work. The grant numbers are NRF-2017R1A2B3004383, NRF-2017M3D1A1039553, NRF-2017R1A5A1015365 and 2012R1A3A2048841. Y. -M. Kang would also like to thank the Korea Institute of Energy Technology Evaluation and Planning (KETEP) and the Ministry of Trade, Industry and Energy (MOTIE) in South Korea; the number for the grant is 20152020105420. Additionally, the authors are grateful for the assistance of PAL, the Australian Synchrotron, and Dr. Qinfen Gu regarding synchrotron XAS and XRD data for the samples. Finally, K. Zhang would like to thank the Korea Research Fellowship Program of the NRF, which was funded by the Ministry of Science and ICT; the number for this grant is 2016H1D3A1906790.
Author information
Authors and Affiliations
Contributions
K. Z., D. K., M. C. and Y-M. K. jointly conceived the project and designed the experiments. K. Z performed the material fabrications, most of the material characterizations and the electrochemical tests. D. K. and M. C. carried out all theoretical calculations. Z. H. and S-L. C. performed the in situ XRD analyses. M. P. and J. Z. assisted with partial material characterizations, such as TEM and XPS characterizations. G. N., Y. Y., and S.-Y. C. supported us to perform STEM tests. Finally, K. Z., D. K., and Y.-M. K. wrote the manuscript. V. W. L. revised and polished up the manuscript. All authors assisted with the discussion and reviewed the manuscript before it was submitted for publication.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhang, K., Kim, D., Hu, Z. et al. Manganese based layered oxides with modulated electronic and thermodynamic properties for sodium ion batteries. Nat Commun 10, 5203 (2019). https://doi.org/10.1038/s41467-018-07646-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-018-07646-4
This article is cited by
-
Layered oxide cathodes for sodium-ion batteries: microstructure design, local chemistry and structural unit
Science China Chemistry (2024)
-
Entropy and crystal-facet modulation of P2-type layered cathodes for long-lasting sodium-based batteries
Nature Communications (2022)
-
Enabling high energy lithium metal batteries via single-crystal Ni-rich cathode material co-doping strategy
Nature Communications (2022)
-
Boron-doped sodium layered oxide for reversible oxygen redox reaction in Na-ion battery cathodes
Nature Communications (2021)
-
Tuning local chemistry of P2 layered-oxide cathode for high energy and long cycles of sodium-ion battery
Nature Communications (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.