Abstract
Current enhancement without increasing the input power is a critical issue to be pursued for electronic circuits. However, drivability of metal-oxide-semiconductor (MOS) transistors is limited by the source-injection current, and electrons that have passed through the source unavoidably waste their momentum to the phonon bath. Here, we propose the Si electron-aspirator, a nanometer-scaled MOS device with a T-shaped branch, to go beyond this limit. The device utilizes the hydrodynamic nature of electrons due to the electron–electron scattering, by which the injected hot electrons transfer their momentum to cold electrons before they relax with the phonon bath. This momentum transfer induces an electron flow from the grounded side terminal without additional power sources. The operation is demonstrated by observing the output-current enhancement by a factor of about 3 at 8 K, which reveals that the electron–electron scattering can govern the electron transport in nanometer-scaled MOS devices, and increase their effective drivability.
Similar content being viewed by others
Introduction
Electron–electron (e-e) scattering1 conserves the total momentum of the electron system in semiconductors, and thus influences only indirectly the mobility and ON-state current of the transistors2,3. In fact, in state-of-the-art nano-transistors, the drivability is limited by the source injection current, which in turn is dominated by the momentum-nonconserving (MN) scattering processes involving interface roughness, impurities and phonons4,5.
The e-e scattering, however, plays a crucial role in some particular conditions (and/or materials) when the e-e scattering length is shorter than that of the MN scattering. In such a case, hydrodynamic effects become apparent and some unusual phenomena, such as the absolute negative resistance6 and higher-than-ballistic conduction7, are observable.
Research studies of the e-e scattering and related hydrodynamic phenomena have been intensively performed at low temperatures in GaAs/AlGaAs heterostructures8,9,10,11,12,13,14 and recently extended to other materials such as PdCoO2 and graphene15,16,17. On the other hand, the research of the e-e scattering in Si MOS transistors is rather restricted to the magnetoconductance measurements18,19,20 from the viewpoint of the carrier localization. Only one group has so far pointed out its importance for nano-scaled MOS transistors in their hot-electron experiments21,22. This stagnation may be because the MN processes, such as interface roughness scattering, have been believed to predominate in the electron transport in Si MOS channels23,24,25. However, since the e-e scattering itself is a momentum-conserving and energy-conserving process, the devices based on this process will guide us to a new concept for high-speed and low-power circuits, and thus research on this issue with Si, in particular on nanometer scale, is important. Actually, previous studies have investigated the hydrodynamic effects on micrometer-scale or larger, while the nano-scale hydrodynamics remains a frontier to be researched.
We thus propose a MOS device with a T-shaped branch to shed light on the role of the e-e scattering in nanometer-scale Si. We show that the device works as an “electron aspirator”, in which energetic electrons from the inlet (emitter) induce a net electron flow from the grounded base terminal, resulting in the current enhancement at the outlet (collector).
The present result reveals that the e-e scattering has a crucial impact on the transport of nano-scaled Si devices, and that the hydrodynamic effects can be observed in such small devices. Most importantly, this is a key demonstration that one can increase the drivability of the MOS devices with negligibly small additional power dissipation. We also show that the interface roughness scattering, or what we call “the collision with the wall” in hydrodynamics, plays a significant role as a competing MN scattering against the e-e scattering.
Results
Device structure
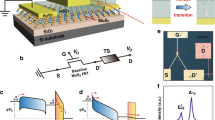
The device was fabricated on a silicon-on-insulator (SOI) substrate, and composed of emitter, collector and base. Figure 1a, b shows the schematic view of the device and a scanning electron microscope image. The emitter and collector have their own gates so that we can control the electrostatic potentials independently. The device also has a broad gate, referred here to as upper gate, which covers the emitter/collector gates and the T-branch region. By applying a positive voltage to it, electron inversion layers are formed beneath, which work as the electrical leads for the emitter-gate and collector-gate of the MOS transistors. The fabrication process26,27 and the basic characteristics of the device can be found in the Method section and in Supplementary Fig. 1, respectively.
Structure and enhancement characteristics of the device. a Schematic top and cross-sectional views of the device. The front and back (buried) oxides, and the SOI are 20-nm, 390-nm, and 18-nm thick, respectively. The Si channel width W in the T-branch region is about 30 nm. The length of the emitter and collector gates are about 60 nm and the spacing between the two gates L, which is an important parameter in the present study, is about 90 nm. b Scanning electron microscope image of a sample device with the same structure26,27 as those measured here (before the upper-gate formation). Note that the Si channel and the gates are covered by oxide, and thus their actual widths are narrower than the appearance in the image. c Energy diagram of the device. EF and EC are the Fermi energy and the conduction band edge, respectively. Open blue dots represent holes. d Electron flow at small |VE| (left) and large |VE| (right). The arrows indicate the direction of the electron flow. e RI ( = |IC/IE|) as a function of the collector gate voltage VCG measured at 8 K. Inset shows the log-scale plot of the RI. f RI as a function of VCG for the emitter-gate voltage VEG = – 1.8 V using the temperature T as a parameter
Device characterization
The experiments were performed at low temperatures (mainly at the substrate temperature T = 8 K), in which electrons were injected from the emitter to the T-branch region (Fig. 1c). In the experiments, the upper-gate voltage VUG and the substrate (or the back-gate) voltage VSG were fixed at positive and negative values (mainly 3.87 and –15 V), respectively, which ensures that the electron channels are formed only at the front interface of the SOI layer. With the above values for VUG and VSG, the electron density N and the Fermi energy EF at the T-branch region were estimated to be 5.7 × 1012 cm−2 and 36 meV, respectively. Except for the experiments for the last figure, the emitter was constant-current biased with the emitter current IE of –10 nA. Therefore, when we change the emitter gate voltage VEG, the emitter voltage VE follows it and is auto-adjusted in order to keep IE constant. Unless otherwise mentioned, the collector and base currents, IC and IB, were measured while keeping the collector and base terminals grounded.
Figure 1e shows RI as a function of the collector gate voltage VCG, where RI = |IC/IE|. We also show the log-scale plot of the RI in the inset of the figure. The voltage VEG was set at 0.7 to –1.8 V. These VEG values resulted in VE of –0.21 mV to –1.34 V, respectively. Note that these RI curves are identical to those of IC since IE is constant in the measurements. As one can see, when VEG = 0.7 V, or |VE| is small (black curve), RI starts to increase at the threshold voltage of the collector gate VCG-TH (≃ 0 V) and then becomes nearly constant at RI ≃ 0.35–0.4. This strongly suggests that the collector and base are nearly equivalent from the viewpoint of the ‘resistor’ and the current flows diffusively (Fig. 1d left).
We should mention that this result for low |VE| is in striking contrast to the results of GaAs/AlGaAs lateral hot-electron transistors, where electrons travel to the collector nearly ballistically, which causes the current to flow below the threshold28,29,30,31. The present results indicate that the MN scattering is dominant for low |VE|. Previous reports on the low-temperature transport of Si MOS transistors have revealed that the interface roughness and impurity (Coulomb) scatterings limit the mobility. (The phonon scattering has only a minor effect on the mobility at low temperatures.)23,24,25 In fact, the low-temperature transport measurements of the present (undoped) SOI layer showed that the mobility was indeed limited by the interface roughness scattering for the front interface32. Therefore, we expect that the transport at the low-|VE| region is dominated by the interface roughness scattering.
When VE is negatively large (green to red curves), on the other hand, RI was found to significantly deviate from the low-|VE| case. RI exceeds unity (IB turns to negative, Fig. 1d right) and becomes as high as 3 for VEG = –1.8 V. This is in effect the aspirator operation because the injection of energetic particles induces the net flow from the side channel. As shown in the inset of Fig. 1e, we observed a very small current below the threshold voltage of the collector gate, VCG ≲ 0 V. This is the current of hot electrons, i.e., of electrons whose energy is much larger than the EF. As one can see, the hot-electron current is more than three orders of magnitude smaller than the main current above the threshold voltage. This indicates that the present current enhancement is not due to the hot electrons quasi-ballistically passing beneath the collector gate, but rather the small hot-electron current indicates the strong carrier scattering at the T-branch region.
Figure 1f shows the temperature dependence of the RI. One can see that the RI enhancement is observed at temperatures up to about 100 K. Notice that we measured more than ten devices and found that all of them showed the enhancement effects though the maximum value of RI was scattered between about 1.5 and 3.5. (Notice that the performance improvement, in particular for the room-temperature operation, is discussed at the end of the main text and in Supplementary Note 5.)
Figure 2a shows the color plot of RI in the plane defined by VCG and VEG. We also performed a different type of measurements, in which the base voltage VB was measured with the base terminal constant-current biased at IB = 0 A. (The collector terminal was grounded.) In this case, IC + IE = 0 holds. (Note that, in this paper, the polarity of the current is defined by the direction of the electron flow in terms of the terminal, i.e., we define the current to be positive (negative) if electrons flow in (out of) the corresponding terminal.) Fig. 2b shows the color plot of VB in the plane defined by VCG and VEG. One can see that, in spite of negative VE, VB becomes positive, i.e., the resistance at the collector gate becomes negative. In other words, electrons flow towards the collector against the reversed bias. This is in effect the pumping operation, and the energy for the pumping is supplied from the emitter electrons. One can also see that the contour map of VB nearly coincides with that of RI in Fig. 2a.
What happens here is that, due to the e-e collisions, the cold electrons at the T-branch region gain forward momentum, forming an electron stream directed to the collector. The escape of electrons from the T-branch region leaves holes behind, which lowers the electrostatic potential there. (We mean by ‘holes’ positive charges created in the conduction band.) This potential drop attracts electrons, resulting in the electron flow from the base (Figs. 1e, 2a). When the base is current-biased at IB = 0 A, this hole accumulation generates a positive VB. In other words, this hole accumulation is compensated by a positive VB in order to hold IB = 0 A (Fig. 2b). (In order for readers to understand how electrons move, we show expected potential profiles in the device in Supplementary Figs. 2, 3 of Supplementary Note 2.)
The phenomena can be observed when the scattering length lee of the e-e scattering is shorter than the device size (the spacing L between the emitter and collector gates in the present case), lee < L. If the length lMN of the MN scattering is longer than the device size, lMN > L, as well, the electron system can be treated as a “fluid” and the effect similar to the Venturi effect in hydrodynamics becomes effective6,11,12,13. As lMN becomes shorter, the directions of the momentum of each electron become more random (the total momentum of the electron system decreases), resulting in a reduced enhancement33.
The presence of the electron fluid in the T-branch region can be claimed from the RI value for the large-VCG region. As shown in Fig. 1e, RI for large |VE| (e.g., the red curve) is larger than that for small |VE| (black) for the condition VCG ≥ VUG (= 3.87 V). This indicates that the total momentum of the electron system at the T-branch region is non-zero and directed to the collector. This is because, under this VCG condition, the potential hump at the collector gate disappears, and thus the collector and base channels are equivalent from the viewpoint of the ‘resistor’. Therefore, if the direction of the momentum is completely random in the T-branch region, RI should be equal to the low-|VE| value (≃ 0.35–0.4), independent of VE (and thus of VEG). This is not what we observed. (See also discussion around Fig. 5 for the claim that the directional momentum is present.)
If VCG is set at an appropriate value, the potential hump is formed (Fig. 1c) and it blocks the backflow of the low-energy (≲ EF) collector electrons to be recombined with holes, making the aspirator more efficient (Figs. 1e and 2a). In other words, the collector gate works as a “check valve”. Thus, we expect that the gradual decrease of RI as a function of VCG reflects the hole-density distribution below EF.
The theory34 based on the random phase approximation predicts that the e-e scattering rate τee−1 due to the single particle excitation is given by
where Δ = E – EF is the electron energy with respect to EF, and kF and kTF are Fermi and Thomas-Fermi wave numbers, respectively. This equation is applicable for kT << Δ << 2(kTF/kF)EF, which corresponds to 0.7 meV << |eVE| << 4 eV, covering the present experimental conditions.
From the above formula, lee can be estimated as lee = vINτee, where vIN is the initial forward velocity of electrons injected into the T-branch region. Figure 3a shows the calculated lee as a function of |VE|. (Details of the calculation can be found in Supplementary Note 3.) As indicated by the horizontal and vertical dotted lines, we obtain lee = L (≃ 90 nm) with |VE| ≃ 11 mV. Larger |VE| makes lee shorter, e.g., lee ≃ 1 nm at |VE| = 0.2 V. For such a high |VE|, the e-e scattering is expected to overwhelm the MN scattering due to the short lee. Thus, the injected electrons will experience multiple e-e scatterings immediately after entering the T-branch region, and transfer their forward momentum to many cold electrons until encountering the MN scattering.
Calculated scattering length lee and measured RI as a function of |VE|. a Calculated scattering length lee. The vertical dotted line indicates the |VE| value ( = 11 mV) that gives lee = 90 nm (≃ L). b RI as a function of |VE| using VCG as a parameter. The dotted circle shows the broad threshold at which the RI starts to increase. The arrow indicates the accidental drop of RI
Figure 3b shows RI as a function of |VE| using VCG as a parameter. A broad threshold indicated by the dotted circle can be seen at |VE| ~ 0.01 V. This agrees with the calculated result, lee = L at |VE| ≃ 11 mV. Note that the dip indicated by the arrow was attributed to the trapping/detrapping of an electron to/from a localized state located near the emitter. This is not a common feature of the fabricated devices and its appearance is device-dependent. However, this is a strong implication that the momentum transfer property is drastically deteriorated by the Coulomb scattering, and that the present devices contain very few Coulomb scattering centers. Beside this accidental drop, RI monotonically increases with |VE|.
We here notice that the previous Si MOS devices with similar structure did not provide the increase in the collector current, and the ratio of the collector to emitter currents was less than unity21,22. The critical difference between the previous and present devices is the channel doping concentration; undoped for the present devices, while boron-doped with a concentration on the order of 1018 cm−3 for the previous ones. This implies that eliminating the impurity scattering is crucial for the present observations.
Then, the interface roughness scattering35,36 is the most plausible candidate for the competing MN scattering process, if any. We therefore investigated the dependence of RI on the vertical electric field. Figure 4a shows RI as a function of VSG. For these measurements, VSG and VUG were simultaneously varied so that the electron density N at the T-branch region was kept constant (= 5.7 × 1012 cm−2). Note that the vertical electric field is proportional to VSG for the triangular confinement potential of the SOI32.
Figure 4b shows the maximum value RI-MAX of RI as a function of VSG using VE as a parameter. One can see that RI-MAX decreases with VSG (except when VSG is close to 0 V), supporting the idea that the interface roughness scattering plays a role. (A slight reduction observed at VSG close to zero may be due to the onset of the back channel at the buried interface which causes the inter-channel scattering37,38.) Therefore, separating the channel from the interface by employing, e.g., the SOI volume conduction39 and the use of the atomically flat Si/SiO2 interfaces40,41 will increase the enhancement capability.
From the viewpoint of hydrodynamics, the interface roughness scattering is nothing but the collision with the wall, whose strength determines the properties of the fluid9,42. In this sense, the electron fluid at the Si/SiO2 interface will be an interesting experimental host for investigating how the friction with the wall affects the electron fluid.
In nano-scaled MOS transistors, a fraction of injected electrons turns back to the source due to the MN (back-) scattering, the amount of which determines the transferable momentum and thus the transistor drivability4,5. This means that any (MN or e-e) scatterings in the drain region play insignificant roles for the transistor ON-current2,43, and electrons that have passed through the source merely waste their energy to the phonon bath. This energy dissipation process is unavoidable in the transistor. In the electron aspirator, on the other hand, the channel electrons do work more efficiently than those in the transistor. They transfer their momentum to other electrons via the e-e scattering before they relax with the phonon bath, and this momentum transfer induces the base current, which flows between two grounded terminals, the base and the collector. This means that the electron aspirator enhances the transistor current with negligibly small additional power dissipation, which corresponds to the increase in the effective drivability of the device.
Figure 5a shows the transistor (gate-voltage) characteristics of the emitter, operating in the aspirator mode (the base is grounded) and in the transistor mode (the base is constant-current biased at IB = 0 A). The voltage setup is shown in Fig. 5b. In these measurements, the emitter voltage VE (corresponding to the source voltage of the transistor) was kept at –1.0 V, while the collector (corresponding to the drain terminal of the transistor) was grounded. The voltage VCG was kept at 0.36 V. One can see that the aspirator-mode current (red solid curve) is larger than the transistor-mode current (red dotted curve) owing to the negative base current (blue solid curve) in the aspirator mode. This demonstrates that the present device can enhance the MOS transistor current with negligibly small additional power dissipation.
Comparison between the transistor-mode and aspirator-mode characteristics. The collector current IC and the base current IB as a function of the emitter gate voltage VEG. The solid and dotted lines show the current curves in the aspirator-mode and transistor-mode, respectively. The collector (corresponding to the drain of the transistor) and the base currents are shown in red and blue, respectively. The RA/T is shown in black. The measurement setup for the aspirator- and transistor-modes are also shown. The arrows show the direction of the electron flow. a Measurement data with the collector and the substrate (back) gates being biased at VCG = 0.36 V and VSG = − 15 V. b Voltage setup for data shown in a. c Measurement data with the collector and the substrate gates being grounded. d Voltage setup for data shown in c
The ratio RA/T of the IC in the aspirator mode to IC in the transistor mode is also shown (black curve). Note that the RA/T is in effect the RI. One can see that it is nearly constant at about 3 when VEG ≲ –1.35 V, or the IC in the transistor mode (corresponding to |IE| for other figures) is less than about 3 nA (see dashed black lines in the figure). This is another evidence that the electron system at the T-branch region has a directional momentum. This is because the RA/T (i.e., RI) is uniquely determined by VE, not by IE or the injected power (= |IEVE|)11,33.
In order to confirm that the device can operate with simpler voltage configuration, we also show in Fig. 5c the results for the case where the collector-gates and substrate-gates (back-gates) were both grounded. The voltage setup is shown in Fig. 5d. With this voltage setup, the device operates with only one supplemental gate (the upper gate) whose voltage is kept constant. One can see that the results are basically the same as those shown in Fig. 5a. (Note that the figures that include IE can be found in Supplementary Fig. 4 of the Supplementary Note 4.)
However, Figs. 5a, c reveal that the RA/T decreases when IC becomes larger than about 2–3 nA. We ascribed that the main cause of this degradation is the interface roughness scattering, which randomizes the direction of the momentum vector. Therefore, this problem will be relevant to the fact that the present aspirator works only at low temperatures. That is, another MN scattering, the phonon scattering, should be the cause of the momentum randomization at high temperatures.
Discussion
Because of the above-mentioned problem, we systematically investigated the origin of the performance degradation (RI reduction) due to the high injection current and high temperature. Detailed arguments can be found in Supplementary Note 5, but here we briefly summarize the results. We investigated the temperature dependence of RI for various injection currents IE. As a result, we found that the RI degradation at 8 K is not due to the increase in the lattice temperature T caused by the high injection power, which in turn indicates that the cause is the other MN scattering, i.e., the interface roughness scattering. On the other hand, RI was found to decrease with the lattice temperature in a similar manner irrespective of the IE value, which strongly suggests that RI is limited by the phonon scattering at high temperatures (see Supplementary Figs. 5–7).
Based on the above analysis, we propose here that the device is made smaller in order to satisfy the inequality lee << L < lPH (the phonon scattering length) for higher temperature operation. According to numerical simulations (Fig. 9 of ref.44.), the electron-phonon scattering rate τPH−1 at room temperature is about 1 and 3 × 1013 s−1 for the electron kinetic energy of 0.1 and 0.3 eV, respectively. The electron-phonon scattering length lPH can then be estimated by using lPH = vINτPH, which results in lPH = 20 and 30 nm for the electron kinetic energy of 0.1 and 0.3 eV, respectively. Therefore, the requirement for the room temperature operation will be L ≲ 20–30 nm for the input voltage range |VE| = 0.1–0.3 V. The state-of-the-art nanotechnology has already enabled the fabrication of such small transistors, which we expect to raise the operation temperature of the present devices, as well.
We will finally estimate the maximum achievable value of RI. In a scaled MOS transistor, the level of the current is determined by the source injection current4,5, or by the forward momentum of an incident electron, pIN, which can be expressed in the most simplified form as pIN = (2 mkT)1/2 at room temperature (and as pIN = (2 mEF)1/2 at low temperatures), where m is the effective mass. The injected electron is accelerated by the electric field in the channel and its momentum could reach p = (2m(kT + |eVE|))1/2. However, the momentum gained by the electric field, pEL ≃ (2m|eVE|)1/2 (for pEL >> pIN) is unavoidably wasted to the phonon bath in MOS transistors. On the other hand, the aspirator uses the pEL for generating the base current, resulting in the output-current enhancement. If we could take a full use of it, the enhancement factor will reach RI ~ p/pIN ≃ (|eVE|/kT)1/2, or RI ≃ 3.5 with |VE| = 0.3 V at room temperature. Furthermore, if the injected electrons could scatter selectively with cold electrons with a forward momentum11, further increase in RI may be possible. The estimation is encouraging, but detailed analysis about the dependence of RI on the device structure and the influence of the MN scattering will be called for to make any decisive conclusions. Exploring circuit architectures suitable for the device will also be needed.
There are several preceding reports regarding the electron hydrodynamic effects in solid-state devices and materials8,9,10,11,12,13,14,15,16. However, the device- and/or material-dimension was on the order of micrometer or larger. What we have demonstrated here is that the hydrodynamic effect can be observed and even predominate in the device characteristics on a nanometer-scale regime, where the energy dissipation issue is critical. The observation of the nano-hydrodynamic effect is mainly thanks to the heavy effective mass of electrons in Si, which gives us a short e-e scattering length. A strong gate effect of Si MOS transistors, which enables us to generate a steep electric field, or a large voltage difference in a tiny area, will also be beneficial for the appearance of the hydrodynamic effect on nanometer-scale. Because of these material properties and well-developed Si nanotechnology, Si will be a suitable material for the research of the hydrodynamic effect on nano-scale.
In summary, the present results reveal that the e-e scattering could govern the electron transport of nano-scaled Si MOS devices, and that the hydrodynamic effects can be observed in such small structures. In particular, we have shown that the Si electron nano-aspirator enhances the output current by a factor of about 3 at 8 K with negligibly small additional power dissipation, and thus increases the drivability of the MOS devices.
Methods
Device fabrication
The device was fabricated on a (100) SIMOX (separation by implanted oxygen) substrate, a type of SOI, using the standard CMOS process, except for the use of electron-beam lithography for the Si wire formation. The SOI layer is undoped. All the gates are made of n++ poly-Si. The fabrication was finalized with the annealing in H2/N2 ambient at 400 °C. This annealing effectively reduced the interface state density down to less than 1 × 1010 cm−2, which was confirmed by the charge-pumping current using large-area MOSFETs fabricated on the same wafer.
The fabrication process is the same as reported in refs. 26 and 27. However, we employed thicker (18-nm thick) SOI layer and thinner (20-nm thick) gate oxide to minimize unwanted formation of Coulomb (single electron) islands due to potential fluctuation at the interface. Note that the stacked gate structure is an important feature of our device because the upper-gate driven electrical-lead formation prevents electrons from encountering the unwanted impurity scattering in the heavily-doped source/drain regions, allowing us to enhance the effects of the e-e scattering process.
The channel width W of the T-branch region and the spacing L between the emitter and collector gates are, respectively, about 30 and 90 nm, as shown in Fig. 1(a).
Electrical measurements
The device was measured on a low-temperature probe station with the source monitor units (SMUs) of the semiconductor parameter analyzer Keysight B1500A. Special care has been taken for the offset of the input voltages generated by the SMUs. We measured the current flowing between the grounded base and collector terminals with the input emitter current IE = 0 A, and confirmed that the offsets and fluctuation of the voltage between the base and collector terminals were negligibly small. Details of the measurements are shown in the Supplementary Note 6, with data shown in Supplementary Figs. 8, 9.
In this study, we mean by temperature T the substrate (lattice) temperature, which was measured and calibrated by using a commercially available Si diode thermometer.
Data availability
The authors declare that the data supporting the findings of this study are available within the paper and its supplementary information file.
References
Lifshitz, E. M. & Pitaevskii, L. P. Statistical Physics Pt. 2 (Pergamon Press, New York, 1980).
Fischetti, M. V. et al. Theoretical study of some physical aspects of electronic transport in nMOSFETs at the 10-nm gate-length. IEEE Trans. Electron Dev. 54, 2116–2136 (2007).
Knezevic, I., Ramayya, E. B., Vasileska, D. & Goodnick, S. M. Diffusive transport in quasi-2D and quasi-1D electron systems. J. Comput. Theor. Nanosci. 6, 1725–1753 (2009).
Lundstrom, M. Elementary scattering theory of the Si MOSFET. IEEE Electron Dev. Lett. 18, 361–363 (1997).
Lundstrom, M. & Ren, Z. Essential physics of carrier transport in nanoscale MOSFETs. IEEE Trans. Electron Dev. 49, 133–141 (2002).
Govorov, A. O. & Heremans, J. J. Hydrodynamic effects in interacting Fermi electron jets. Phys. Rev. Lett. 92, 026803 (2004).
Guo, H. et al. Higher-than-ballistic conduction of viscous electron flows. Proc. Natl Acad. Sci. USA 114, 3068–3073 (2017).
Dyakonov, M. & Shur, M. Shallow water analogy for a ballistic field effect transistor: new mechanism of plasma wave generation by dc current. Phys. Rev. Lett. 71, 2465–2468 (1993).
de Jong, M. J. M. & Molenkamp, L. W. Hydrodynamic electron flow in high-mobility wires. Phys. Rev. B 51, 13389–13402 (1995).
Predel, H. et al. Effects of electron-electron scattering on electron-beam propagation in a two-dimensional electron gas. Phys. Rev. B 62, 2057–2064 (2000).
Kaya, I. I. & Eberl, K. Absolute negative resistance induced by directional electron-electron scattering in a two-dimensional electron gas. Phys. Rev. Lett. 98, 186801 (2007).
Taubert, D. et al. Electron-avalanche amplifier based on the electronic Venturi effect. Phys. Rev. B 82, 161416 (R) (2010).
Taubert, D. et al. An electron jet pump: the Venturi effect of a Fermi liquid. J. Appl. Phys. 109, 102412 (2011).
Taubert, D. et al. Relaxation of hot electrons in a degenerate two-dimensional electron system: transition to one-dimensional scattering. Phys. Rev. B 83, 235404 (2011).
Moll, P. J. W. et al. Evidence for hydrodynamic electron flow in PdCoO2. Science 351, 1061–1064 (2016).
Bandurin, D. A. et al. Negative local resistance caused by viscous electron backflow in graphene. Science 351, 1055–1058 (2016).
Kumar, R. K. et al. Superballistic flow of viscous electron fluid through graphene constrictions. Nat. Phys. 13, 1182–1186 (2017).
Wheeler, R. G. Magnetoconductance and weak localization in silicon inversion layers. Phys. Rev. B 24, 4645–4651 (1981).
Choi, K. K. Inelastic electron-electron scattering in silicon (100) inversion layers. Phys. Rev. B 28, 5774–5780 (1983).
Abrahams, E., Kravchenko, S. V. & Sarachik, M. P. Metallic behavior and related phenomena in two dimensions. Rev. Mod. Phys. 73, 251–266 (2001).
Sakamoto, T. et al. Direct observation of hot-electron energy distribution in silicon metal–oxide–semiconductor field-effect transistors. Appl. Phys. Lett. 75, 1113–1115 (1999).
Sakamoto, T. et al. Characteristic length of hot-electron transport in silicon metal–oxide–semiconductor field-effect transistors. Appl. Phys. Lett. 76, 2618–2620 (2000).
Stern, F. Calculated temperature dependence of mobility in silicon inversion layers. Phys. Rev. Lett. 44, 1469–1472 (1980).
Ando, T., Fowler, A. B. & Stern, F. Electronic properties of two-dimensional systems. Rev. Mod. Phys. 54, 437–672 (1982).
Cham, K. M. & Wheeler, R. G. Temperature-dependent resistivities in silicon inversion layers at low temperatures. Phys. Rev. Lett. 44, 1472–1475 (1980).
Fujiwara, A. et al. Double-island single-electron devices–a useful unit device for single-electron logic LSI’s. IEEE Trans. Electron Dev. 46, 954–959 (1999).
Fujiwara, A. & Takahashi, Y. Manipulation of elementary charge in a silicon charge-coupled device. Nature 410, 560–562 (2001).
Palevski, A. et al. Lateral tunneling, ballistic transport, and spectroscopy in a two-dimensional electron gas. Phys. Rev. Lett. 62, 1776–1779 (1989).
Sivan, U., Heiblum, M. & Umbach, C. P. Hot ballistic transport and phonon emission in a two-dimensional electron gas. Phys. Rev. Lett. 63, 992–995 (1989).
Laikhtman, U. et al. Long mean free path of hot electrons selectively injected to higher subbands. Phys. Rev. Lett. 65, 2181–2184 (1990).
Dzurak, A. S. et al. Two-dimensional electron-gas heating and phonon emission by hot ballistic electrons. Phys. Rev. B 45, 6309–6312 (1992).
Niida, Y. et al. Electron and hole mobilities at a Si/SiO2 interface with giant valley splitting. Appl. Phys. Lett. 102, 191603 (2013).
Brill, B. & Heiblum, M. Electron heating in GaAs due to electron-electron interactions. Phys. Rev. B 49, 14762–14765 (1994).
Giuliani, G. F. & Quinn, J. J. Lifetime of a quasiparticle in a two-dimensional electron gas. Phys. Rev. B 26, 4421–4428 (1982).
Matsumoto, Y. & Uemura, Y. Scattering mechanism and low temperature mobility of MOS inversion layers. Jpn. J. Appl. Phys., 13(Suppl. 2–2), 367–370 (1974).
Goodnick, S. M. et al. Surface roughness at the Si(100)-SiO2 interface. Phys. Rev. B 32, 8171–8186 (1985).
Palevski, A. et al. Resistance resonance in coupled potential wells. Phys. Rev. Lett. 65, 1929–1932 (1990).
Takashina, K. et al. Intersubband scattering in double-gate MOSFETs. IEEE Trans. Nanotechnol. 5, 430–435 (2006).
Balestra, F. et al. Double-gate silicon-on-insulator transistor with volume inversion: a new device with greatly enhanced performance. IEEE Electron Dev. Lett. 8, 410–412 (1987).
Kuroda, R. et al. Atomically flat silicon surface and silicon/insulator interface formation technologies for (100) surface orientation large-diameter wafers introducing high performance and low-noise metal–insulator–silicon FETs. IEEE Trans. Electron Dev. 56, 291–298 (2009).
Ohmi, S. I. Importance of Si surface flatness to realize high-performance Si devices utilizing ultrathin films with new material system. IEICE Electron. Express 11, 1–13 (2014).
Landau L. D. & Lifshitz, E. M. Fluid mechanics (Pergamon Press, Oxford, 1966).
Fischetti, M. V. & Laux, S. E. Long-range Coulomb interactions in small Si devices. Part I: performance and reliability. J. Appl. Phys. 89, 1205–1231 (2001).
Fischetti, M. V. & Laux, S. E. Monte Carlo study of electron transport in silicon inversion layers. Phys. Rev. B 48, 2244–2274 (1993).
Acknowledgements
Y.O. thanks M. Tabe and K. Takashina for valuable comments and NTT Basic Research Laboratory for technical support. H.F. thanks RISET-Pro, Kemenristekdikti, Indonesia. This work was financially supported by JSPS KAKENHI (JP15H01706, JP16H04339, JP16H02339, JP16H06087, JP17H06211, and JP18H05258).
Author information
Authors and Affiliations
Contributions
A.F. and Y.T. fabricated the device. M.H. constructed the measurement system. H.F., T.W., M.H., and Y.O. measured the device. H.F., D.M., and Y.O. analyzed the data. Y.O. wrote the manuscript with support from H.F., D.M., A.F., and Y.T., and supervised the project. All the authors discussed the results.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Firdaus, H., Watanabe, T., Hori, M. et al. Electron aspirator using electron–electron scattering in nanoscale silicon. Nat Commun 9, 4813 (2018). https://doi.org/10.1038/s41467-018-07278-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-018-07278-8
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.