Abstract
A Verwey-type charge-ordering transition in magnetite at 120 K leads to the formation of linear units of three iron ions with one shared electron, called trimerons. The recently-discovered iron pentoxide (Fe4O5) comprising mixed-valent iron cations at octahedral chains, demonstrates another unusual charge-ordering transition at 150 K involving competing formation of iron trimerons and dimerons. Here, we experimentally show that applied pressure can tune the charge-ordering pattern in Fe4O5 and strongly affect the ordering temperature. We report two charge-ordered phases, the first of which may comprise both dimeron and trimeron units, whereas, the second exhibits an overall dimerization involving both the octahedral and trigonal-prismatic chains of iron in the crystal structure. We link the dramatic change in the charge-ordering pattern in the second phase to redistribution of electrons between the octahedral and prismatic iron chains, and propose that the average oxidation state of the iron cations can pre-determine a charge-ordering pattern.
Similar content being viewed by others
Introduction
Iron oxides, composed of two of the most abundant elements in the Earth’s interior, are fundamentally important materials both for basic science and applied technologies1. The first-known magnetic mineral, magnetite (Fe3O4), was the only simple mixed-valent iron oxide known until recently, and for this reason it is a key model system for investigation of Fe2+/Fe3+ interplay and related physical phenomena. It was discovered that at 120 K magnetite exhibits an abrupt transition of a metal-insulator-type (the so-called Verwey transition), which is supposed to result from enigmatic charge ordering at the octahedral sites of its cubic spinel structure2. Numerous studies were aimed to comprehend the nature and mechanisms of this transition3. Only recently, the elusive charge-ordering pattern in the Verwey phase of magnetite below 120 K was finally solved by means of single crystal X-ray diffraction, and a novel type of quasi-particle consisting of linear units of three iron ions with one shared electron, called a trimeron, was proposed4,5. This charge ordering is highly unusual and implies a more intricate underlying phenomenon6,7,8 than ordering of separate Fe2+ and Fe3+ ions that takes place, for example, in TbBaFe2O59,10 or charge ordering during the course of charge disproportionation11.
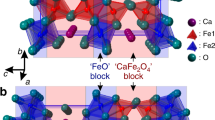
It was commonly thought that all of the simplest iron oxides fall within three basic stoichiometries, such as FeO, Fe3O4, and Fe2O3. A recent series of high-pressure high-temperature (HP-HT) studies using single crystal X-ray diffraction methods discovered and identified a number of novel iron oxides, e.g., Fe4O512,13, Fe5O614,15, Fe13O1916, Fe5O717, Fe25O3217, FeO218,19,20,21, Fe7O922, and a new monoclinic polymorph of Fe2O3 which can be stable at ambient conditions23. Some of the novel oxides, like Fe4O5, Fe5O6, and Fe7O9, were also found to be readily recoverable at ambient conditions. These discoveries open a portal to mixed-valent iron oxides and motivate investigation of their physical properties and potential for emergent innovative applications. Fe4O5 can be synthesized at moderate HP-HT conditions of about 10 GPa and 1000 °C and has appeared to be the most common of the above high-pressure iron oxides. It crystallizes in an orthorhombic CaFe3O5-type structure, one of the known Ca-ferrite (\({\mathrm{CaFe}}_n^{2 + }{\mathrm{Fe}}_2^{3 + }{\mathrm{O}}_{4 + n}\), n = 1, 2, 3, etc.) phases24,25, and this fact could explain the phase and chemical stability of Fe4O5 and its derivatives, (M,Fe)2Fe2O5 (M—Mg, Cr, Mn)26,27,28,29,30,31 at ambient conditions. The crystal structure of Fe4O5 comprises chains of both trigonal prisms Fe1 (this crystallographic position is denoted here as Fe1) with shared triangular faces, occupied by Fe2+ cations, and an octahedral network occupied by mixed Fe2+/Fe3+ cations and consisting of (i) single chains of octahedra sharing opposite edges (this crystallographic position is denoted here as Fe2), and (ii) double chains of octahedra composed of two chains similar to the above Fe2 ones, but attached together side-by-side via two other octahedron edges (this crystallographic position is denoted here as Fe3)12. Like magnetite, Fe4O5 shows a charge-ordering transition below 150 K involving the competing formation of iron trimers and dimers (two Fe ions with one shared electron) at the octahedral network32. It is interesting to note that a recent study identified coexisting trigonal and dimer-like charge ordering patterns in layered α-RuCl333.
In this work, we synthesize high-quality single crystals of Fe4O5 and investigate the effect of high pressure on charge ordering in Fe4O5 at low temperature using single crystal X-ray diffraction, Mössbauer spectroscopy, and magnetization measurements. We find that cold compression of Fe4O5 stimulates electron transfer between iron cations of different coordination and leads to the formation of novel charge-ordered phases.
Results
Phase III and two options for its crystal structure
In all experiments, we start from normal conditions (Fe4O5-I phase) (Figs. 1a and 2) and gradually decrease the temperature in the cryostat. At about 200 K and 2 GPa, we observe the appearance of weak and blurred superlattice reflections, indicating the emergence of scattered fragments of a charge-ordering pattern (Fig. 3b). With further temperature decrease and pressure increase, these reflections become progressively stronger and clearer (Fig. 3c). We verify that these reflections do not belong to the earlier-reported charge-ordered Fe4O5-II phase32, and label this phase as Fe4O5-III. Meanwhile, the presence of Fe4O5-II is noticeable at 5–7 GPa at the lowest temperature point of 30 K (Fig. 2). Upon heating at about 18 GPa, we can follow the superlattice reflections of Fe4O5-III up to at least 270 K (Fig. 2). Thus, pressure strongly enhances the temperature of the charge-ordering transition, compared to 150 K at ambient pressure32. We can index the single-crystal diffraction patterns of Fe4O5-III in either orthorhombic or monoclinic unit cells (Fig. 3d). Eventually, we determine two candidate crystal structures, namely, Fe4O5-III-a with a monoclinic C2/m lattice (Fig. 4) and Fe4O5-III-b with an orthorhombic C2221 unit cell (Fig. 5), which can equally well fit the experimental X-ray diffraction patterns (Table 1 and Supplementary Table 1). Compared to the original structure (Fe4O5-I), the crystallographic sites of the iron cations occupying the trigonal prisms in the crystal structures of both Fe4O5-III-a and Fe4O5-III-b are split into two slightly non-equivalent Fe1_1 and Fe1_2 positions; likewise the octahedral sites Fe2 and Fe3 are split into multiple non-equivalent sites, highlighted in different colors in Figs. 4 and 5. Note here that the unusual incommensurately-modulated character of the crystal structure of Fe4O5-II, reported in previous work32, could result from a lattice instability related to competition between the Fe4O5-III-a and Fe4O5-III-b phases. A similar type of incommensurability was observed, for example, in the spin-Peierls compound, TiPO434,35.
Crystal structure and image of the Fe4O5 crystal. a Orthorhombic crystal structure of Fe4O5 at ambient conditions showing the different crystallographic positions for iron atoms (Fe1, Fe2, and Fe3) in different colors. The bond valence sum values are indicated near the cations. b Image of a single crystal of Fe4O5 taken through one diamond window. A rhenium gasket of about 40 µm thickness with a circular hole of about 150 µm diameter drilled in its central part is bridged between the two opposing diamond anvils. The light background color of the central hole is due to light passing through the underlying diamond anvil. The central hole (working area) accommodates the Fe4O5 single crystal (in the center) and two small pressure markers, Au and ruby, located on the left and right sides of the crystal, respectively. The central hole is filled with a transparent neon pressure-transmitting medium. The scale bar inside the central hole corresponds to 100 µm
High-pressure low-temperature phase diagram of Fe4O5. The diagram is based on the single crystal X-ray diffraction experiments. Experimental points on the diagram corresponding to different phases are shown in different symbols. The shaded areas show the proposed stability regions of the phases. The lines and arrows show the directions of the pressure and temperature variation during the experiments. Since the basic structural reflections of Fe4O5-I and Fe4O5-III structures are identical (Fig. 3), the region of their co-existence could not be properly delineated. One cannot rule out that the region of Fe4O5-III in the phase diagram might be a superposition of stability ranges of Fe4O5-III-a and Fe4O5-III-b phases
Examples of reciprocal lattice planes (hkl) of Fe4O5. These plots correspond to different pressure and temperature conditions (indicated for each plot). a Basic reflections corresponding to the original Fe4O5-I structure, highlighted by red circles. b, c Emergence of superlattice reflections, highlighted by blue circles (in b these reflections are rather weak and blurred, but in c they are strong and clear). d Reconstruction of (hkl) reciprocal lattice planes, which reveals two possible unit cells of Fe4O5-III. The first option is an orthorhombic C-centered “average” cell, shown in the upper left corner together with its modulation wave vector q (Fe4O5-III-b). The second option is a C-centered unit cell with a tripled lattice parameter a, compared to the average cell (Fe4O5-III-a), highlighted at the bottom of the plot
Monoclinic crystal structure of Fe4O5-III-a. This structure has C2/m symmetry and plots are based on the crystal structure data refined at 11.7 GPa and 180 K. a Projection of the trigonal prisms Fe1 and single chains of Fe2 octahedra. b The unit cell projected down the b-axis. Thin solid lines indicate the unit cell edges. c Projection of the double chains of Fe3 octahedra. d Projection down the c-axis of one of the two diagonal ribbons shown in e. e Two characteristic diagonal ribbons consisting of five iron chains each. f Projection of one of two diagonal ribbons shown in e. Solid ellipsoids are dimers and trimers formed in the chains of octahedrally-coordinated iron. Dotted ellipsoids highlight Fe3–Fe1 pairs with shortened Fe–Fe length. Different crystallographic positions are shown in different colors. g Bond valence sums (BVS) values of all the iron cations in the crystal structure
Orthorhombic crystal structure of Fe4O5-III-b. The structure has C2221 symmetry and plots are based on the crystal structure data refined at 11.7 GPa and 180 K. a Projection of the trigonal prisms Fe1 and single-chains of Fe2 octahedra. b The unit cell projected down the a-axis. Thin solid lines indicate the unit cell edges. c Projection of the double chains of Fe3 octahedra. d Projection down the c-axis of one of the two diagonal ribbons shown in e. e Two characteristic diagonal ribbons consisting of five iron chains each. f Projection of one of the two diagonal ribbons shown in e. Solid ellipsoids are dimers formed in the chains of octahedrally-coordinated iron. Dotted ellipsoids highlight Fe3–Fe1 pairs with shortened Fe–Fe length. Different crystallographic positions are shown in different colors. g Bond valence sums (BVS) values of all the iron cations in the crystal structure
In magnetite, the formation of iron trimers in its charge-ordered phase is perfectly traced by anomalous shortening of some Fe–Fe distances as found by single crystal X-ray diffraction method4; hence we also apply this approach to Fe4O5. The octahedral chains occupied by mixed-valent iron cations show pronounced shortening of distances between some neighboring Fe atoms; whereas the prismatic chains of iron in both Fe4O5-III-a and Fe4O5-III-b structures are characterized by nearly equal Fe–Fe distances. For example, at 11.7 GPa and 180 K, the Fe–Fe distances in the prismatic chains of the Fe4O5-III-a structure show a periodicity consisting of one 2.8143 Å and two 2.8176 Å distances; since these two values are very similar, we cannot draw any conclusions about the formation of coupled units in these chains. Compared to the average Fe–Fe distance of ~2.8165 Å along the same crystallographic direction (b-axis), the distances between two neighboring octahedrally-coordinated Fe2_2 atoms in the single chains of Fe2 octahedra are reduced, to 2.6597 Å, and likewise those between Fe3_4 atoms in the double chains of Fe3 octahedra are reduced to 2.7279 Å (Supplementary Table 2). These dramatic shortenings in the distances suggest the formation of dimers (Fig. 4a, c). In the other octahedral chains of this Fe4O5-III-a phase, equal contractions in two neighboring Fe–Fe distances indicate the formation of trimers.
The Fe4O5-III-b structure exhibits similar features. Its prismatic iron chains show a periodicity in the Fe–Fe bond lengths consisting of one 2.8118 Å and two 2.8189 Å distances, where the difference between the two is too small to allow any conclusions about the formation of any bonded units (Fig. 5). In contrast to Fe4O5-III-a, the Fe4O5-III-b structure does not contain any trimers (Fig. 5). Both octahedral chains of the Fe4O5-III-b structure exhibit only dimers with a Fe–Fe bond length of 2.6777 Å in the single chains of Fe2 octahedra, and 2.7387 Å in the double-chains of Fe3 octahedra (Supplementary Table 2). Both Fe4O5-III-a and Fe4O5-III-b crystal structures show a strong rapprochement between free Fe3 atoms (Fe3_3 in phase III-a and Fe3_2 in phase III-b, which are unincorporated into the dimer and trimer units) and the neighboring Fe1 atoms in the prisms, which are connected to these Fe3 octahedra via one shared edge (these Fe3–Fe1 pairs are highlighted as white dashed ellipsoids in Figs. 4d and 5d). The Fe–Fe distances in these Fe3–Fe1 pairs become nearly the same as the average Fe–Fe distances in both prismatic and octahedral chains (Supplementary Table 2), thereby suggesting an enhancement of interactions between the iron ions occupying the prisms and octahedra.
We analyze the Fe–O bond lengths of all iron cations in both Fe4O5-III structures using a common bond valence sum (BVS) method (see Experimental Details)36. We estimate the average BVS values of the Fe1 atoms sitting in the prisms as +2.11 and +2.13 in Fe4O5-III-a and Fe4O5-III-b structures, respectively. The BVS analysis suggests that the dimers formed at the double chains of Fe3 octahedra of both structures consist of moderately overcharged valence-mixed Fe2.5+ ions; whereas, the dimers formed at the single-chain Fe2 octahedra have a charge as high as +5.4 (Figs. 4 and 5). Likewise, this analysis shows that, compared to a combination of one Fe2+ and two Fe3+ ions, the trimers in the Fe4O5-III-a structure are either strongly overcharged (+8.29 for the single chains of Fe2 octahedra) or strongly undercharged (+7.57 for the double chains of Fe3 octahedra) (Fig. 4).
Phase IV and charge ordering in chains of trigonal prisms
In all three experimental runs at pressures above 12 GPa and temperatures below 150 K, we observe the appearance of additional structural reflections (Supplementary Fig. 1), suggesting the beginning of another transition to a further phase, labeled as Fe4O5-IV (Fig. 2). Below 150 K this transition is nearly complete at 25 GPa, but at slightly higher temperature (200 K), minor traces of Fe4O5-III are still observable even at 36 GPa (Fig. 2). Upon heating to room temperature at 36 GPa, Fe4O5-IV gradually transforms to the original Fe4O5-I phase; meanwhile, a noticeable fraction of Fe4O5-IV persists even at 293 K (Fig. 2).
The single crystal X-ray diffraction images of Fe4O5 collected at 25.2 GPa and 120 K correspond to almost pure Fe4O5-IV (Supplementary Fig. 1), and we determine its monoclinic P21/m symmetry and atomic positions. The structure shows an overall dimerization along the c-axis involving both octahedral and prismatic chains (Fig. 6). We calculate BVS values of the iron ions in this structure using the above method36, and find an average value for the prismatic Fe1 atoms of +2.26. This value deviates from +2 established for these prismatic sites in the original Fe4O5-I phase12,32, and taking into account the emergence of dimeric ordering in these chains, we conclude that the prismatic sites in Fe4O5-IV are filled with mixed-valent iron cations. In the same way, the average BVS values of the iron in the single chains of Fe2 and double chains of Fe3 octahedra in Fe4O5-IV are found as +2.63 and +2.554, respectively (Fig. 6). These values are also consistent with the dimeric ordering in the chains. These BVS results indicate that Fe4O5 with a nominal average oxidation state of iron as Fe2.5+ tends to reach a state under pressure with more uniform charge distribution, implying an average oxidation state of Fe2.5+ in all iron chains.
Monoclinic crystal structure of Fe4O5-IV. The structure has P21/m symmetry and plots are based on the crystal structure data refined at 25.2 GPa and at 120 K. a Projection of the trigonal prisms Fe1 and single chains of Fe2 octahedra. b Two unit cells projected down the c-axis. Thin solid lines indicate the unit cell edges. c Projection of the double chains of Fe3 octahedra. d Projection down the b-axis of one of the two diagonal ribbons shown in e. e Two characteristic diagonal ribbons consisting of five iron chains each. f Projection down the b-axis of one of the two diagonal ribbons shown in e. Solid ellipsoids are dimers formed in all iron chains. Different crystallographic positions are shown in different colors. g Bond valence sums (BVS) values of all the iron cations in the crystal structure
During the Fe4O5-III → Fe4O5-IV phase transition under increasing pressure, the crystal lattice shrinks noticeably along the dimerization direction. This leads to a lattice volume collapse by about 0.5% at 120 K (Fig. 7a). This volume collapse may be attributed to a more homogeneous charge distribution in the Fe4O5-IV phase, which should lead to a volume contraction. By fitting the third-order Birch–Murnaghan equation of state37,38 to the compression data of the Fe4O5-III phase at 120 K (Fig. 7a), we determine the unit cell volume as V0 = 1063.87 Å3 and the bulk modulus as B0 = 195.3 GPa for fixed B′0 = 4. We analyze the ratios of Fe–Fe bond lengths in the dimer units compared to those in the gaps between them \(\left( {d_{{\mathrm{Fe}} - {\mathrm{Fe}}}^{{\mathrm{units}}}/d_{{\mathrm{Fe}} - {\mathrm{Fe}}}^{{\mathrm{gap}}}} \right)\) for Fe1, Fe2, and Fe3 chains, and values to be 0.93, 0.90, and 0.88, respectively (Supplementary Table 4). This difference in the \(d_{{\mathrm{Fe}} - {\mathrm{Fe}}}^{{\mathrm{units}}}/d_{{\mathrm{Fe}} - {\mathrm{Fe}}}^{{\mathrm{gap}}}\) ratios may be referred to the above average BVS values of Fe1, Fe2, and Fe3 atoms, which should approximately correspond to their oxidation states. In fact, the shortest iron dimers are formed in the double chains of Fe3 octahedra with an average BVS value equal to +2.554, i.e., nearly optimal for the formation of Fe2+ –Fe3+ pairs. In contrast, the longest dimers are formed in Fe1 prismatic chains with an average BVS value of +2.26, which deviates the most from +2.5. Furthermore, we note that the above \(d_{{\mathrm{Fe}} - {\mathrm{Fe}}}^{{\mathrm{units}}}/d_{{\mathrm{Fe}} - {\mathrm{Fe}}}^{{\mathrm{gap}}}\) ratios increase linearly with a deviation of their average BVS values from +2.5, tending to 1 for the limiting case of Fe2+ or Fe3+ (Fig. 7c). This regularity indicates that the resulting length of the dimers is determined by the balance of Fe2+ and Fe3+ cations in each linear chain.
Pressure-driven Fe4O5-III → Fe4O5-IV transition. a Equation of state of Fe4O5 at 120 K showing a volume drop of ~0.5% at the Fe4O5-III → Fe4O5-IV transition. b Edge-shared diagonal ribbons of prisms and octahedra (seen in Figs. 4–6) provide channels for charge hopping between the prisms and octahedra. c Correlation between ratios of Fe–Fe distances in dimers and trimers to those in gaps between them \(\left( {d_{{\mathrm{Fe}} - {\mathrm{Fe}}}^{{\mathrm{units}}}/d_{{\mathrm{Fe}} - {\mathrm{Fe}}}^{{\mathrm{gap}}}} \right)\) and absolute deviations of bond valence sums (BVS) values of iron in these chains from 2.5+. d Model demonstrating the coexistence of several charge-ordered phases in a single crystal of Fe4O5. The electron transfer from the prisms to octahedra leads to a short-range reorganization of ordering type
The reduced distances between the free Fe3 atoms in the double-chains of Fe3 octahedra and the neighboring Fe1 atoms in the prisms, observed in both Fe4O5-III-a and Fe4O5-III-b structures (highlighted as dashed ellipsoids in Figs. 4d and 5d), appear to be the most suitable channels for hopping of electrons from Fe2+ ions occupying Fe1 prisms to the octahedral matrix. Only 1/3 of the Fe1 atoms are involved in these channels, and hence, if the electrons of prismatically-coordinated Fe2+ ions are not delocalized within the framework of these trigonal prismatic chains, the Fe1 atoms may be maximally charged up to +2.33 on average. The actual BVS values of the two Fe1 atoms are +2.23 and +2.29 (Fig. 6), which satisfy this constraint well. The coexistence of Fe4O5-III and Fe4O5-IV phases over an extended pressure range (Fig. 2) suggests that this phase transition is rather prolonged. Likely, it is caused by the gradual pressure-driven electron transfer from the trigonal prismatic chains to the octahedral ones. The Fe4O5-III-b structure comprises only dimers; hence having free iron cations in all Fe3 chains provides twice as many channels for the charge hopping compared to the Fe4O5-III-a structure.
As mentioned above, we observe that a noticeable fraction of the Fe4O5-IV phase persists upon heating to 293 K at 35 GPa (Fig. 2). To examine the possibility of the room-temperature phase transition Fe4O5-I → Fe4O5-IV, we compress a single crystal of Fe4O5 in a separate experiment to about 45 GPa, but we see no evidence for a phase transition. Previous works also did not find any structural phase transition in this range12,39. At the maximum pressure of 45 GPa, we laser-heat the sample up to 2000 °C, and indeed we observe a structural transition to the same dimerized Fe4O5-IV structure (Fig. 2, Table 1). The unusual thermodynamic stability of the Fe4O5-IV phase might be explained by the fact that both Fe4O5-III-a and Fe4O5-III-b low-temperature structures have the above-discussed Fe3–Fe1 channels for charge hopping (Figs. 4d and 5d), which should facilitate the Fe4O5-III → Fe4O5-IV transition; whereas a direct Fe4O5-I → Fe4O5-IV transition and its related redistribution of electrons between the prismatic and octahedral chains might be hindered at room temperature, but triggered at high temperatures. We find that average BVS values36 of the iron ions in the high-temperature Fe4O5-IV (HT) phase are nearly the same as those in the low-temperature Fe4O5-IV (LT) phase, namely, +2.24 (+2.32) for prismatic Fe1_1 (Fe1_2) atoms, and +2.653 and +2.534 for the iron in the single chains of Fe2 and double chains of Fe3 octahedra, respectively. Analysis of \(d_{{\mathrm{Fe}} - {\mathrm{Fe}}}^{{\mathrm{units}}}/d_{{\mathrm{Fe}} - {\mathrm{Fe}}}^{{\mathrm{gap}}}\) ratios in the Fe4O5-IV (HT) structure shows that they do not follow the linear trend established for the Fe4O5-IV (LT) structure (Fig. 7c), and hence a distribution of Fe2+ and Fe3+ ions at least at the octahedral sites of Fe4O5-IV (HT) is more random than ordered. It can be that the transition mechanism at high temperature is different, and the dimerization observed could instead result from a Peierls transition40 rather than from the formation of electrically-bonded Fe2+–Fe3+ dimers with a shared electron.
Low-temperature high-pressure phase diagram of Fe4O5
We find the average BVS values of prismatic Fe1 atoms in Fe4O5-I, Fe4O5-III-a, Fe4O5-III-b, and Fe4O5-IV to be +2.016, +2.11, +2.13, and +2.26, respectively (Figs. 4–6). As discussed above, the average BVS value of +2.26 for Fe1 atoms in Fe4O5-IV, together with the overall structural dimerization including these Fe1 chains, unambiguously confirm the mixed-valent nature of the iron ions at the prismatic sites in this structure. The minor deviations of the BVS values from +2 for Fe1 atoms in the Fe4O5-III-a and Fe4O5-III-b phases do not allow us either to conclude a small shift in the oxidation state of these ions toward +3 or to rule that out. The co-existence of Fe4O5-III and Fe4O5-IV phases for an extended pressure range (Fig. 2) hints that this transition may follow the electron transfer between the octahedral and prismatic chains. This leads to a short-order reorganization of the charge-ordering pattern and the formation of inclusions of the novel structural order. Comparing the different charge-ordered patterns in Fe4O5-II32, Fe4O5-III-a, Fe4O5-III-b, and Fe4O5-IV (Figs. 4–6), we conclude that the average oxidation state of octahedrally-coordinated cations predetermines which ordering type would be optimal. For example, in order to form short trimers, the average oxidation state of iron should be ~+2.7 (Fig. 7c). A moderate decrease in this BVS value leads to the formation of more loosely-bonded long trimers and dimers. For BVS values tending toward +2.5, a closely-packed dimeric order becomes preferable (Fig. 6). Thus, the average oxidation state of iron ions at the octahedral chains apparently pre-determines an optimal charge-ordering scheme. One can expect, for example in the newly-discovered Fe7O9 and Fe5O6 crystallizing in similar structures14,22, that the former with a nominal oxidation state of the octahedral ions of +2.8 at ambient pressure is prone to the formation of exclusively trimers; likewise, the latter in which their oxidation state is +2.5 is prone to dimer formation only. A pressure-stimulated electron transfer from the prismatic to octahedral chains can occur inhomogeneously in the bulk of the Fe4O5 crystal and this can result in the formation of an anomalous charge-ordering pattern combining different co-existing ordering schemes (Fig. 7d).
The process of electron transfer in Fe4O5 from the trigonal prismatic to the octahedral iron chains towards charge equalization is perhaps not complete by 40 GPa, and with further pressurization the average BVS values of all iron cations can probably approach +2.5 even more closely. However, this could hardly change the dimeric charge-ordering pattern of Fe4O5-IV (Fig. 6), unless the material was to become metallic and the charge-ordering state suppressed; although the lattice symmetry may be sensitive to the charge balance. We propose that such electron transfer processes under pressure could also occur in other iron oxides crystallizing in kindred lattices, like the above-mentioned Fe5O614 and Fe7O922. However, for the ambient-pressure cubic spinel phase of magnetite with inverse electronic configuration in which tetrahedral sites are filled by Fe3+ ions and hence are already maximally charged, the possibility of an opposite electron transfer under pressure, from tetrahedral sites to the octahedral network has been suggested41. However, this conjecture was not in line with earlier work42, and was not confirmed in subsequent studies43,44,45,46. It was established for magnetite that its charge-ordered phase may be suppressed by applied pressure of about 8 GPa47,48. Thus, the behavior of Fe4O5 is remarkably different from that of magnetite and demonstrates new perspectives for charge-ordered states in iron-rich oxides. At the moment, we cannot unambiguously ascertain the driving forces of the phase transitions observed in Fe4O5 both at ambient and high pressures. In previous work investigating the Verwey transition in magnetite, it was determined that the intersite Coulomb interactions between the 3d electrons of the Fe ions alone, as well as phonon-driven lattice instability, could hardly stimulate this transition49,50. A more complex scenario, however, in which the strong electron correlations enhance the electron–phonon interactions and simultaneously reduce the mobility of the minority-spin t2g electrons of Fe2+ ions, increasing their tendency towards localization, could be an indication that electron–phonon interactions may be a driving force of the Verwey transition49,50. The phase transitions in Fe4O5 could have similar or even more complex scenarios involving the charge, lattice, spin, and orbital degrees of freedom.
Mössbauer spectroscopy of Fe4O5 at low temperature under high pressure
At ambient conditions, the Mössbauer spectra of Fe4O5 can be well fitted by the superposition of a magnetic sextet and a paramagnetic doublet with relative areas of 80(2)% and 20(2)%, respectively (Fig. 8c). The presence of the sextet component indicates the existence of magnetic order at room temperature. In the Fe4O5 crystal, 25% of iron cations occupy the trigonal prisms, and 75% have octahedral coordination (Fig. 1a). Hence, we can assign the doublet to prismatic Fe1 atoms, and likewise the sextet to octahedral Fe2 and Fe3 atoms. We determine the hyperfine parameters of these components. For example, for the spectrum collected at 295 K and 2.1 GPa, we determine the center shift of the doublet to be δCS = 1.125(12) mm/s and the quadrupole splitting to be ∆ = 1.93(2) mm/s. For the sextet, we find the center shift to be δCS = 0.568(15) mm/s, the quadrupole shift to be ε = 0.21(1) mm/s, and the hyperfine magnetic field to be Hhf = 24.96(13) T. The center shift of the Mössbauer spectral components depends primarily on the oxidation state of iron in a linear-like manner. We compare these center shifts with those reported for other iron oxides, e.g., δCS = 0.36 mm/s for octahedral Fe3+ ions in hematite (α-Fe2O3)51 and δCS = 0.67 mm/s for octahedral mixed-valent Fe2.5+ ions in magnetite51. The linear trend based on these data suggests that octahedrally-coordinated Fe2+ ions should exhibit center shifts around δCS = 0.98 mm/s; likewise the above-determined value of δCS = 0.568 mm/s for the magnetic sextet in Fe4O5 should correspond to an oxidation state of Fe2.67+, in excellent agreement with the BVS results (Fig. 1a). The large value of δCS = 1.125(12) mm/s for the Fe1 doublet unambiguously corresponds to Fe2+, in line with both BVS estimations (Fig. 1a) and earlier data for ferrous-iron compounds51.
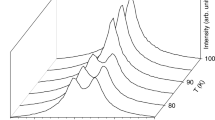
Magnetic susceptibility and Mössbauer spectra of Fe4O5. a Temperature dependence of magnetic susceptibility and inverse magnetic susceptibility measured at different hydrostatic pressures in a field of 0.5 T under field cooling. b Evolution of Mössbauer spectra upon cooling at about 2–3 GPa. Broadening of the first (low-velocity) line of the sextet starting at 150 K indicates charge ordering. c Representative Mössbauer spectra of different phases of Fe4O5 collected at different pressures and temperatures. The spectrum of phase I can be refined by superposition of a paramagnetic doublet (blue) assigned to iron in the trigonal prisms and a magnetic sextet (orange) assigned to Fe in the octahedra in a mixed-valence state. The spectra of phases II and III exhibit a complex distribution of hyperfine fields and can be refined by superposition of sextets
We note that the line widths of the sextet are roughly twice as large as those of the doublet (1.1 vs 0.5 mm/s) (Fig. 8c). This broadening results from electron exchange between the Fe2+ and Fe3+ cations occupying the octahedral sites; a similar effect was also observed in magnetite52. Upon cooling, the doublet component loses intensity and completely disappears around 150 K (Fig. 8b). Hence, Fe1 atoms occupying the oxygen prisms become magnetically ordered, and their contribution to the spectra largely overlaps with the stronger signal of Fe2 and Fe3 atoms. The Mössbauer spectra demonstrate a pronounced broadening around 150 K (Fig. 8b), where a charge ordering in Fe4O5 was observed32.
For magnetite, it has been documented that charge ordering below the Verwey transition at 120 K leads to the appearance of many closely-overlapping magnetic sextets which can be resolved only under special conditions, such as single-crystal measurements in magnetic fields52,53. Here, we collect spectra from a polycrystalline Fe4O5 sample and, together with other factors like potential phase co-existence (Fig. 2), this impedes an unambiguous fitting of the Mössbauer spectra at low temperatures. A simple single-sextet analysis of the spectra shows that the quadrupole shift has a discontinuity in its temperature dependence between 150 and 100 K (Supplementary Figure 2b and Supplementary Table 5). This feature is likely linked to changes in the magnetic properties (kink in inverse magnetic susceptibility in Fig. 7a).
The Mössbauer spectra collected in the charge-ordered states appear to be a superposition of several sextets. For instance, the spectrum acquired at 20 K and 2.6 GPa, i.e., in the stability region of the incommensurately-modulated Fe4O5-II phase with an infinite number of different environments for iron (Fig. 2), can be reasonably well described by three sextets (Fig. 8c). The center shifts of these sextets are about 0.6–0.85 mm/s, i.e., between δCS = 0.36 mm/s for Fe3+ ions in hematite51 and 0.98 mm/s estimated above for octahedral Fe2+ atoms, but at the same time quite far from both. We therefore conclude that in the charge-ordered phases of Fe4O5, the oxidation states of the octahedrally-coordinated iron did not split into Fe2+ and Fe3+ components, and hence, these ions are characterized by stable non-integer oxidation states. This finding is in line with the earlier conjecture4,32 that the minority-spin t2g electron of Fe2+ ions is shared between all ions involved in the formation of either trimers or dimers.
We do not observe any noticeable changes in the spectra with pressure up to 8 GPa at low temperatures. This fact indicates that Fe4O5-II and Fe4O5-III charge-ordered phases are not readily distinguishable by Mössbauer spectroscopy (Figs. 2 and 8c). With further compression to 16.3 GPa across the beginning of the Fe4O5-III → Fe4O5-IV transition (Fig. 2), the hyperfine field distribution changes to an apparent bimodal form (Supplementary Figure 2c). We fit these spectra by a superposition of two sextets (Fig. 8c), and for example, at 11.3 GPa and 20 K in Fe4O5-III phase, their center shifts are δCS = 0.66(3) and 0.82(3) mm/s. Taking into account the second-order Doppler shift (we use the value of 0.11 mm/s for hematite)54 and disregarding a possible pressure correction for the δCS values, we estimate the average oxidation states of iron linked to the green and purple sextets to be +2.7 and +2.45, respectively (Fig. 8c). Therefore, this case also unambiguously demonstrates that the oxidation states of the octahedrally-coordinated iron in Fe4O5 do not split into integer Fe2+ and Fe3+ components, even at 20 K. These +2.7 and +2.45 values correspond well to the average BVS values for the iron cations occupying the single chains of Fe2 and double chains of Fe3 octahedra, respectively (Figs. 4 and 5).
Magnetic properties of Fe4O5
The magnetization data for Fe4O5 collected at ambient pressure (Fig. 8a) are similar to those reported earlier32, but show slightly smaller absolute values of susceptibility. In this work, we carry out measurements on several single crystals of Fe4O5, and likely, this discrepancy may be related to a minor ferromagnetic impurity which can potentially be present in the large polycrystalline sample examined earlier32. There are two main features of the magnetization data: (i) the transformation between canted and collinear magnetic ordering (around 90 K at ambient pressure), and (ii) charge ordering that manifests itself by a kink in the 1/χ curve (around 150 K at ambient pressure) (Fig. 8a). Both features are observed up to 1.83 GPa, the maximum pressure of our measurement, and shift toward higher temperature upon compression. The size of the canted moment increases abruptly, with a large change between 0.66 and 0.90 GPa and weak changes below or above this range. Given the observation of the Fe4O5-III phase at 200 K and 2 GPa (Fig. 2), we conclude that our magnetization data extend well into its stability range, and hence, this abrupt change in the moment likely results from the phase transformation. Moreover, the kink in the 1/χ curves shifts to higher temperatures (Fig. 8a), in agreement with the positive slope of the Fe4O5-I → Fe4O5-III phase boundary. Above 0.90 GPa, the kink is strongly smeared out, probably because of more sluggish charge-ordering processes at the Fe4O5-I → Fe4O5-III phase transition, compared to Fe4O5-I → Fe4O5-II32.
The magnetization data reveal close similarities between Fe4O5-II and Fe4O5-III. Both support the formation of a canted state at low temperatures. Moreover, both charge-ordered phases emerge from the same collinear magnetic order that sets in around 320 K at ambient pressure32. As seen from the Mössbauer spectra (Fig. 8b), the initial magnetic ordering remains above room temperature at these pressures. As established earlier32, a ferromagnetic spin alignment along the a-direction (in the coordinate framework of Fe4O5-I) is essential for the formation of dimers and trimers in the charge-ordered state32, and hence magnetic ordering is a key prerequisite of the charge ordering. The same type of magnetic order would even support dimer formation in Fe4O5-IV. This demonstrates that this magnetic ordering can produce different charge-ordered states in a single structural framework.
Conclusions
We determined the low-temperature high-pressure phase diagram of Fe4O5 using single crystal X-ray diffraction and Mössbauer spectroscopy and by measurement of magnetic properties. We found two novel crystal structures of Fe4O5 and observed the extended regions of their co-existence in the phase diagram. A dramatic change in the charge-ordering pattern in the second high-pressure phase was attributed to electron hopping from the octahedral to the prismatic iron chains. We propose that the average oxidation state of the iron cations in oxides of this family can pre-determine a charge-ordering pattern. Thus, Fe4O5 demonstrates that the charge-ordering pattern can be changed by applied pressure or stress, and two or more charge-ordered phases can co-exist with each other inside one single crystal. Our work highlights the complexity of charge-ordering processes in iron-based and other transition metal oxides, but simultaneously it suggests a clue to these phenomena.
Methods
Sample preparation and characterization
The samples of Fe4O5 were synthesized in a 1200-tonne Multi-Anvil Press at BGI55 at HP-HT conditions from stoichiometric mixtures of fine powders of Fe3O4 (Aldrich, 99.99% purity) and Fe (Aldrich, 99.999% purity). The syntheses were performed at pressures of 14 GPa over several hours. Polycrystalline samples were fabricated at synthesis temperatures of about 1100–1200 °C, while higher temperatures (1350–1450 °C) enabled the growth of high-quality single crystals with linear sizes of 20–200 µm32. We employed a standard assembly including a Re cylindrical sample capsule, a LaCrO3 heater, a W3Re/W25Re thermocouple, and other components packed inside an octahedron made of 5% Cr2O3-doped MgO56,57. The procedure was similar to that described in previous work58,59. The chemical composition of the samples was verified by means of scanning electron microscopy (SEM) using a LEO-1530 instrument and by microprobe analysis using a JEOL JXA-8200 electron microscope. The crystal structure of the samples was determined by means of single crystal and powder X-ray diffraction using a high-brilliance Rigaku diffractometer (Mo Kα radiation, λ = 0.7108 Å).
Single crystal X-ray diffraction under pressure
We selected high-quality single crystals of Fe4O5 and loaded them into symmetric membrane diamond anvil cells (DACs) equipped with Boehler-Almax diamonds that enabled X-ray diffraction images to be collected over the widest range of angles. We employed three DACs with diamond anvil culet sizes of 400 and 300 µm. Together with the sample in the same cell, we loaded a ruby sphere and a chip of gold that was used for pressure determination (Fig. 2). An additional ruby sphere was placed on the outer surface of one diamond anvil to monitor the reference of its R1 line at low temperature and ambient pressure. All of the DACs were filled with Ne pressure-transmitting medium. In total, we carried out three high-pressure single crystal X-ray diffraction experiments. The first one served as an initial scanning of the low-temperature phase diagram of Fe4O5, and it was performed at the ID27 beamline of the European Synchrotron Radiation Facility (ESRF, Grenoble, France) with a wavelength of λ = 0.3738 Å. The second and third runs involved more detailed investigations, and they were accomplished in a cold-finger He cryostat on the P02.2 beamline at the Deutsches Elektronen-Synchrotron (DESY, Hamburg, Germany) using a wavelength of λ = 0.2887 Å60. Additionally, we carried out a room temperature compression experiment with laser heating at high pressures on beamline ID09a at ESRF (λ = 0.41513 Å). At each (P,T) point on the phase diagram, we acquired single-crystal X-ray diffraction images upon continuous rotation of the cell with the sample around the vertical ω-axis with a step of Δω = 0.5° and an exposure time of t = 0.5 s/frame. The diffraction data were collected by a Perkin Elmer XRD1621 detector. We analyzed these data with CrysAlisPro software, and solved the crystal structures using JANA2006 software61.
We analyze the Fe–O bond lengths of all iron cations in the different crystal structures of Fe4O5 using a common BVS method36. In this method, a bond valence is determined as (Sij = exp[(Rij − dij)/b0], where dij is the distance between atoms i and j, Rij is the bond valence parameter (empirically determined distance for this cation-anion pair), and b0 is an empirical parameter about 0.37 Å), and then, a BVS value of a cation is determined as a sum of individual bond valences \(\left( {V_i = \mathop {\sum}\nolimits_j {s_{ij}} } \right)\)36. In these calculations, we used b0=0.37 Å and the bond-valence parameters Rij determined at ambient conditions for Fe2+–O and Fe3+–O bonds as 1.734 and 1.759 Å, respectively36. Using literature data from the equation of state of hematite (α-Fe2O3) determined from single crystal X-ray diffraction experiments up to 25 GPa62, we estimated a pressure dependence of the bond-parameter Rij for the Fe3+–O bonds, and applied these values in the BVS estimations as well. Since the total cation charge in the formula unit (+10) should be conserved at all pressures and temperatures, the calculated nominal BVS values were accordingly renormalized to meet this requirement. After performing these procedures, the calculations using different starting Rij values gave identical results within experimental uncertainty.
Mössbauer spectroscopy under pressure
For Mössbauer spectroscopic examination over a wide pressure–temperature range, we synthesized a polycrystalline sample of 20% 57Fe-enriched Fe4O5. We also utilized a membrane DAC with diamond anvil culet sizes of 400 µm. The DAC was fixed inside a cryostat. We collected synchrotron Mössbauer source (SMS)63 spectra on the Nuclear Resonance beamline ID18 at ESRF64. The SMS is based on a nuclear resonant monochromator employing pure nuclear reflections of an iron borate (57FeBO3) crystal. The source provides 57Fe resonant radiation at 14.4 keV within a bandwidth of 15 neV, which is tunable in energy over a range of ~±0.6 meV63. The beam of gamma-radiation emitted by the SMS was focused to a 10 × 15 µm2 spot size. The velocity scale was calibrated relative to a natural α-Fe foil of 25 μm thickness. The center shift values are given relative to α-Fe. We monitored the width and the absolute position of the isomer shift of the source line before and after each measurement using a K2Mg57Fe(CN)6 reference single line absorber.
Magnetic measurements under pressure
The bulk magnetization measurements under hydrostatic pressure65,66 were performed in a CuBe pressure cell placed inside a Quantum Design MPMS 5S SQUID magnetometer. Daphne 7373 oil was used as a pressure-transmitting medium. One small piece of lead (~0.1 mg) was placed together with the sample inside the pressure cell, while another piece (~0.1 mg) was placed outside the pressure cell. Under pressure, the superconducting transition temperature of the inner piece decreases. The difference between the superconducting transition temperatures of the two lead samples determines the pressure value inside the pressure cell at low temperatures. Several small single crystals of Fe4O5 with a total mass of ~0.6 mg were placed into a gasket of the pressure cell along with the aforementioned piece of lead. The empty cell background data was subtracted65 using an automatic background subtraction (ABS) procedure. Field-cooling measurements of the lead and Fe4O5 samples were performed in fields of 2 mT and 0.5 T, respectively, from 300 K down to 4 K.
Data availability
The X-ray crystallographic information files (CIFs) for structures that support the findings of this study have been deposited at the Inorganic Crystal Structure Database (ICSD) with accession codes 434152, 434153, 434154, 434155, and 434156 (http://www2.fiz-karlsruhe.de/icsd_home.html). The authors declare that all other data supporting the findings of this study are available within the article and Supplementary Information files, and also are available from the corresponding author upon reasonable request.
References
Faivre, D. (ed.) Iron Oxides: From Nature to Applications (Wiley-VCH, Weinheim, 2016).
Verwey, E. J. W. Electronic conduction of magnetite (Fe3O4) and its transition point at low temperatures. Nature 144, 327–328 (1939).
Lee, S. et al. Electrically driven phase transition in magnetite nanostructures. Nat. Mater. 7, 130–133 (2008).
Senn, M. R., Wright, J. P. & Attfield, J. P. Charge order and three-site distortions in the Verwey structure of magnetite. Nature 481, 173–176 (2012).
Perversi, G., Cumby, J., Pachoud, E., Wright, J. P. & Attfield, J. P. The Verwey structure of a natural magnetite. Chem. Commun. 52, 4864–4867 (2016).
de Jong, S. et al. Speed limit of the insulator–metal transition in magnetite. Nat. Mater. 12, 882–886 (2013).
Huang, H. Y. et al. Jahn-Teller distortion driven magnetic polarons in magnetite. Nat. Commun. 8, 15929 (2017).
Cumby, J. & Attfield, J. P. Ellipsoidal analysis of coordination polyhedra. Nat. Commun. 8, 14235 (2017).
Karen, P. et al. Verwey transition in mixed-valence TbBaFe2O5: two attempts to order charges. Phys. Rev. B 64, 214405 (2001).
Pratt, D. K. et al. Checkerboard to stripe charge ordering transition in TbBaFe2O5. Phys. Rev. B 87, 045127 (2013).
Long, Y. W. et al. Temperature-induced A–B intersite charge transfer in an A-site-ordered LaCu3Fe4O12 perovskite. Nature 458, 60–63 (2009).
Lavina, B. et al. Discovery of the recoverable high-pressure iron oxide Fe4O5. Proc. Natl Acad. Sci. USA 108, 17281–17285 (2011).
Woodland, A. B., Frost, D. J., Trots, D. M., Klimm, K. & Mezouar, M. In situ observation of the breakdown of magnetite (Fe3O4) to Fe4O5 and hematite at high pressures and temperatures. Am. Mineral. 97, 1808–1811 (2012).
Lavina, B. & Meng, Y. Unraveling the complexity of iron oxides at high pressure and temperature: synthesis of Fe5O6. Sci. Adv. 1, e1400260 (2015).
Myhill, R. et al. On the P-T-fO 2 stability of Fe4O5, Fe5O6 and Fe4O5-rich solid solutions. Contrib. Mineral. Petrol. 171, 51 (2016).
Merlini, M., Hanfland, M., Salamat, A., Petitgirard, S. & Müller, H. The crystal structures of Mg2Fe2C4O13, with tetrahedrally coordinated carbon, and Fe13O19, synthesized at deep mantle conditions. Am. Mineral. 100, 2001–2004 (2015).
Bykova, E. et al. Structural complexity of simple Fe2O3 at high pressures and temperatures. Nat. Commun. 7, 10661 (2016).
Weerasinghe, G. L., Pickard, C. J. & Needs, R. J. Computational searches for iron oxides at high pressures. J. Phys. Condens. Matter 27, 455501 (2015).
Hu, Q. et al. FeO2 and FeOOH under deep lower-mantle conditions and earth’s oxygen-hydrogen cycles. Nature 534, 241–244 (2016).
Jang, G., Kim, D. Y. & Shim, J. H. Metal-insulator transition and the role of electron correlation in FeO2. Phys. Rev. B 95, 075144 (2017).
Zhang, X.-L., Niu, Z.-W., Tang, M., Zhao, J.-Z. & Cai, L.-C. First-principles thermoelasticity and stability of pyrite-type FeO2 under high pressure and temperature. J. Alloys Compd. 719, 42–46 (2017).
Sinmyo, R. et al. Discovery of Fe7O9: a new iron oxide with a complex monoclinic structure. Sci. Rep. 6, 32852 (2016).
Tuček, J. et al. Zeta-Fe2O3—a new stable polymorph in iron(III) oxide family. Sci. Rep. 5, 15091 (2015).
Evrard, O. et al. Mise en evidence de CaFe4O6 et détermination des structures cristallines des ferrites de calcium CaFe2+nO4+n (n=1, 2, 3): un nouvel exemple d’intercroissance. J. Solid State Chem. 35, 112–119 (1980).
Delacotte, C. et al. Morin-like spin canting in the magnetic CaFe5O7 ferrite: a combined neutron and Mössbauer study. J. Solid State Chem. 247, 13–19 (2017).
Woodland, A. B. et al. Fe4O5 and its solid solutions in several simple systems. Contrib. Mineral. Petrol. 166, 1677–1686 (2013).
Ishii, T. et al. High-pressure phase transitions in FeCr2O4 and structure analysis of new post-spinel FeCr2O4 and Fe2Cr2O5 phases with meteoritical and petrological implications. Am. Mineral. 99, 1788–1797 (2014).
Guignard, J. & Crichton, W. A. Synthesis and recovery of bulk Fe4O5 from magnetite, Fe3O4. A member of a self-similar series of structures for the lower mantle and transition zone. Mineral. Mag. 78, 361–371 (2014).
Ballaran, T. B., Uenver-Thiele, L. & Woodland, A. B. Complete substitution of Fe2+ by Mg in Fe4O5: the crystal structure of the Mg2Fe2O5 end-member. Am. Mineral. 100, 628–631 (2015).
Hong, K. H., McNally, G. M., Coduri, M. & Attfield, J. P. Synthesis, crystal structure, and magnetic properties of MnFe3O5. Z. Anorg. Allg. Chem. 642, 1355–1358 (2016).
Siersch, N. C., Ballaran, T. B., Uenver-Thiele, L. & Woodland, A. B. Compressibility and high-pressure structural behaviour of Mg2Fe2O5. Am. Mineral. 102, 845–850 (2017).
Ovsyannikov, S. V. et al. Charge ordering transition in iron oxide Fe4O5 involving competing dimer and trimer formation. Nat. Chem. 8, 501–508 (2016).
Ziatdinov, M. et al. Atomic-scale observation of structural and electronic orders in the layered compound alpha-RuCl3. Nat. Commun. 7, 13774 (2016).
Bykov, M. et al. Spin-Peierls distortions in TiPO4. Phys. Rev. B 88, 184420 (2013).
Bykov, M. et al. High-pressure phase transformations in TiPO4: a route to pentacoordinated phosphorus. Angew. Chem. Int. Ed. 55, 15053–15057 (2016).
Brese, N. E. & O’Keffee, M. Bond-valence parameters for solids. Acta Crystallogr. B47, 192–197 (1991).
Murnaghan, F. D. The compressibility of media under extreme pressures. Proc. Natl Acad. Sci. USA 30, 244–247 (1944).
Birch, F. Finite elastic strain of cubic crystals. Phys. Rev. 71, 809–824 (1947).
Kothapalli, K. et al. Nuclear forward scattering and first-principles studies of the iron oxide phase Fe4O5. Phys. Rev. B 90, 024430 (2014).
Friend, R. H. & Yoffe, A. D. Electronic properties of intercalation complexes of the transition metal dichalcogenides. Adv. Phys. 36, 1–94 (1987).
Rozenberg, G. Kh et al. Structural characterization of temperature- and pressure-induced inverse↔normal spinel transformation in magnetite. Phys. Rev. B 75, 020102(R) (2007).
Haavik, C., Stolen, S., Fjellvag, H., Hanfland, M. & Hausermann, D. Equation of state of magnetite and its high-pressure modification: thermodynamics of the Fe–O system at high pressure. Am. Mineral. 85, 514–523 (2000).
Klotz, S. et al. Magnetism and the Verwey transition in Fe3O4 under pressure. Phys. Rev. B 77, 012411 (2008).
Gilder, S. A. & Le Goff, M. Systematic pressure enhancement of titanomagnetite magnetization. Geophys. Res. Lett. 35, L10302 (2008).
Ovsyannikov, S. V., Shchennikov, V. V., Todo, S. & Uwatoko, Y. A new crossover in Fe3O4 magnetite under pressure near 6 GPa: modification to “ideal” inverse cubic spinel? J. Phys. Condens. Matter 20, 172201 (2008).
Ebad-Allah, J. et al. Pressure dependence of the Verwey transition in magnetite: an infrared spectroscopic point of view. J. Appl. Phys. 112, 073524 (2012).
Todo, S., Takeshita, N., Kanehara, T., Mori, T. & Mori, N. Metallization of magnetite (Fe3O4) under high pressure. J. Appl. Phys. 89, 7347–7349 (2001).
Rozenberg, G. Kh. et al. Origin of the Verwey transition in magnetite. Phys. Rev. Lett. 96, 045705 (2006).
Piekarz, P., Parlinski, K. & Oleś, A. M. Mechanism of the Verwey transition in magnetite. Phys. Rev. Lett. 97, 156402 (2006).
Piekarz, P., Parlinski, K. & Oleś, A. M. Origin of the Verwey transition in magnetite: group theory, electronic structure, and lattice dynamics study. Phys. Rev. B 76, 165124 (2007).
Menil, F. Systematic trends of the 57Fe Mössbauer isomer shifts in (FeOn) and (FeFn) polyhedra. Evidence of a new correlation between the isomer shift and the inductive effect of the competing bond T –X (→Fe) (where X is O or F and T any element with a formal positive charge). J. Phys. Chem. Solids 46, 763–789 (1985).
Hargrove, R. S. & Kundig, W. Mössbauer measurements of magnetite below the Verwey transition. Solid State Commun. 8, 303–308 (1970).
Berry, F. J., Skinner, S. & Thomas, M. F. 57Fe Mossbauer spectroscopic examination of a single crystal of Fe3O4. J. Phys. Condens. Matter 10, 215–220 (1998).
Sturhahn, W. & Chumakov, A. Lamb–Mössbauer factor and second-order Doppler shift from inelastic nuclear resonant absorption. Hyperfine Interact. 123, 809–824 (1999).
Frost, D. J. et al. A new large-volume multianvil system. Phys. Earth Planet. Inter. 143–144, 507–514 (2004).
Ovsyannikov, S. V. et al. Structural and magnetic transitions in CaCo3V4O12 perovskite at extreme conditions. Inorg. Chem. 56, 6251–6263 (2017).
Ovsyannikov, S. V. et al. Bulk silicon crystals with the high boron content, Si1−xBx: two semiconductors form an unusual metal. Chem. Mater. 26, 5274–5281 (2014).
Ovsyannikov, S. V. et al. Perovskite-like Mn2O3: a path to new manganites. Angew. Chem. Int. Ed. 52, 1494–1498 (2013).
Ovsyannikov, S. V. et al. Hard oxide semiconductor with a direct and narrow bandgap and switchable p–n electrical conduction. Adv. Mater. 26, 8185–8191 (2014).
Liermann, H.-P. et al. The extreme conditions beamline P02.2 and the extreme conditions science infrastructure at PETRA III. J. Synchrotron Radiat. 22, 908–924 (2015).
Petricek, V., Dusek, M. & Palatinus, L. Crystallographic computing system JANA2006: general features. Z. Krist. 229, 345–352 (2014).
Schouwink, P. et al. High-pressure structural behavior of α-Fe2O3 studied by single-crystal X-ray diffraction and synchrotron radiation up to 25 GPa. Am. Mineral. 96, 1781–1786 (2011).
Potapkin, V. et al. The 57Fe synchrotron Mössbauer source at the ESRF. J. Synchrotron Radiat. 19, 559–569 (2012).
Rüffer, R. & Chumakov, A. I. Nuclear resonance beamline at ESRF. Hyperfine Interact. 97–98, 589–604 (1996).
Tateiwa, N., Haga, Y., Fisk, Z. & Onuki, Y. Miniature ceramic-anvil high-pressure cell for magnetic measurements in a commercial superconducting quantum interference device magnetometer. Rev. Sci. Instrum. 82, 053906 (2011).
Tateiwa, N. et al. Improved sensitivity of magnetic measurements under high pressure in miniature ceramic anvil cell for a commercial SQUID magnetometer. Rev. Sci. Instrum. 84, 046105 (2013).
Acknowledgements
We acknowledge the ESRF for the provision of beam time at ID09a, ID18, and ID27. We also acknowledge the Sample Environment Service-HP lab and J. Jacobs for technical support of the loan pool diamond anvil cells. The authors thank D. Vasiukov for contributions to the refinement of the Mössbauer spectra and their interpretation. The authors thank M. Mezouar, G. Garbarino, and A. Cairns for assistance in the structural experiments at ID27 of ESRF (Grenoble, France). S.V.O. acknowledges the financial support of the Deutsche Forschungsgemeinschaft (DFG, project # OV-110/3-1). A.A.T. was supported by the Federal Ministry for Education and Research through the Sofja Kovalevskaya Award of the Alexander von Humboldt Foundation.
Author information
Authors and Affiliations
Contributions
S.V.O. synthesized and characterized the samples. S.V.O., M.B., E.B., K.G., A.V.K., A.S.P. and I.C. performed X-ray diffraction experiments. S.V.O., V.C., I. Kupenko, I. Kantor, A.I.C., R.R., C.M. and L.S.D. performed Mössbauer spectroscopic studies. R.S.M. and A.A.T. performed magnetic measurements and contributed to manuscript writing. M.B. solved the crystal structures and contributed to manuscript writing. S.V.O. wrote a first draft of the manuscript, and all of the co-authors read, revised, and commented on all of the versions. S.V.O. and L.S.D. initiated and designed the research.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ovsyannikov, S.V., Bykov, M., Bykova, E. et al. Pressure tuning of charge ordering in iron oxide. Nat Commun 9, 4142 (2018). https://doi.org/10.1038/s41467-018-06457-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-018-06457-x
This article is cited by
-
Monoclinic distortion and magnetic transitions in FeO under pressure and temperature
Communications Physics (2024)
-
Pressure-induced structural, electronic, and magnetic evolution in cubic inverse spinel NiFe2O4, an ab-initio study
Applied Physics A (2022)
-
Influence of applied magnetic field and heating on properties of cobalt ferrite films
Journal of Materials Science: Materials in Electronics (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.