Abstract
Strong electron correlations can give rise to extraordinary properties of metals with renormalized Landau quasiparticles. Near a quantum critical point, these quasiparticles can be destroyed and non-Fermi liquid behavior ensues. YbRh2Si2 is a prototypical correlated metal exhibiting the formation of quasiparticle and Kondo lattice coherence, as well as quasiparticle destruction at a field-induced quantum critical point. Here we show how, upon lowering the temperature, Kondo lattice coherence develops at zero field and finally gives way to non-Fermi liquid electronic excitations. By measuring the single-particle excitations through scanning tunneling spectroscopy, we find the Kondo lattice peak displays a non-trivial temperature dependence with a strong increase around 3.3 K. At 0.3 K and with applied magnetic field, the width of this peak is minimized in the quantum critical regime. Our results demonstrate that the lattice Kondo correlations have to be sufficiently developed before quantum criticality can set in.
Similar content being viewed by others
Introduction
Heavy fermion materials, i.e. intermetallics that contain rare earths (REs) like Ce, Sm, and Yb or actinides like U and Np, are model systems to study strong electronic correlations1,2. The RE-derived localized 4f states can give rise to local magnetic moments which typically order (often antiferromagnetically) at sufficiently low temperature as a result of the inter-site Ruderman–Kittel–Kasuya–Yosida interaction. In addition, the on-site Kondo effect causes a hybridization between the 4f and the conduction electrons, which eventually screens the local moments by developing Kondo spin-singlet many-body states. Hence, these two interactions directly compete with each other and lead to different (long-range magnetically ordered vs. paramagnetic Fermi-liquid) ground states3. A zero-temperature transition between the two states can be controlled through doping, pressure or magnetic field H. A quantum critical point (QCP) and concomitantly non-Fermi liquid properties ensue if the phase transition is continuous at zero temperature4,5,6.
Heavy fermion metals have been established as a canonical setting for quantum criticality2. How the Kondo lattice coherence develops upon lowering the temperature, i.e. the hierarchy of energy scales, is, however, still a matter of debate. Intuitively, the coherence temperature Tcoh is set by the single-ion Kondo temperature TK of the lowest-lying crystal-field level7 and can be further reduced by disorder8, while within another model Tcoh can exceed TK considerably9,10. The latter model might be related to the influence of crystalline electric field (CEF) effects2,11. Considerable experimental efforts have recently been devoted to the study of the quantum critical regime at sufficiently low temperatures. A key observation is that quantum criticality induces a large entropy, suggesting that it is linked with the Kondo effect. This raises the important question12 as to how the onset of Kondo lattice coherence at elevated temperatures connects with the emergence of quantum criticality at low temperatures.
The prototypical heavy fermion metal YbRh2Si2 shows an antiferromagnetic (AFM) ground state with a very low Néel temperature, TN = 70 mK, and a QCP upon applying a relatively small field μ0HN = 0.66 T parallel to the tetragonal c-axis. Non-Fermi liquid behavior has been observed in the quantum critical regime (i.e. at finite field), extending up to temperatures of about 0.5 K13, depending on the physical quantity that is measured as well as the degree of disorder14, see T–H phase diagram in Fig. 1. Isothermal magnetotransport15,16 and thermodynamic17 measurements at low temperatures have provided evidence for the existence of an additional low-energy scale T*(H), which has been interpreted as the finite-temperature manifestation of the critical destruction of the lattice Kondo effect18 and the concomitant zero-temperature jump of the Fermi surface from large to small across the QCP. Measurements of the thermal and magnetic Grüneisen ratio strongly support this picture19,20. An ever pressing issue, however, is the huge specific heat coefficient even in zero magnetic field14,21, which implies an abundance of fluctuations. Below TN, these are of Fermi-liquid type. Above TN, an obvious cause of these fluctuations are dynamical Kondo correlations, and above ~0.5 K YbRh2Si2 at zero field belongs to the quantum-critical fluctuation regime13. Yet, alternative scenarios have been proposed as well22,23,24.
Phase diagram of YbRh2Si2. Schematic temperature–magnetic field phase diagram as inferred from magnetotransport15,16, magnetostriction17, and magnetization20 measurements at low T, and STM measurements down to ~5 K7. The QCP (red dot) is located at H* ≈ 0.06 T for H⊥c and H* ≈ 0.66 T for \(H||c\). The single-ion Kondo temperatures \(T_{\mathrm{K}}^{{\mathrm{high}}}\) and TK involve all (purple shading) and the lowest-lying (white) crystal electric field levels, respectively. The lattice Kondo effect starts to develop around Tcoh ≈ TK. The Kondo-exchange interaction between the two types of spins, respectively, belonging to the local moments or the conduction electrons, gives rise to Kondo correlations in the spin-singlet channel, which are always dynamical at finite temperatures. The lattice Kondo effect (gray arrow) grows as temperature is decreased. At large magnetic fields, lowering the temperature eventually turns the short-lived lattice Kondo correlations into long-lived ones (brown region) indicating a heavy Fermi liquid with renormalized (large) Fermi surface well below TFL. For small magnetic fields the correlations stay dynamical. Here, an antiferromagnetic (AFM) order (blue region) develops below the Néel temperature TN, again with long-lived lattice Kondo correlations. The reddish regime embedding the T*(H) crossover line indicates incoherent quantum critical fluctuations as the system evolves towards the respective ground state on either side15,16,17. This scale, anchored by the QCP, marks the finite-temperature signature of the Mott-type phase transition at T = 0, additionally visualized by the red bars corresponding to the width of the crossover in Hall effect16. The green arrows indicate the parameters used in STS measurements
Scanning tunneling spectroscopy (STS) measures locally the density of states (DOS)25 through single-particle excitations7,26,27. Spectra obtained at temperatures T ≥ 4.6 K and H = 0 revealed the successive depopulation of the excited CEF states as the temperature is lowered, with essentially only the lowest crystal-field Kramers doublet occupied at lowest temperatures7. The coupling between the localized 4f electrons in this Kramers doublet and the conduction electrons gives rise to periodic Kondo-singlet correlations which start to develop below Tcoh. This coherence temperature is linked to the effective single-ion Kondo temperature TK ≈ 25 K extracted from bulk measurement28. While these properties conform to the traditional understanding of the high-temperature behavior of the Kondo lattice29,30, the questions remain open on how the Kondo coherence evolves further upon lowering the temperature13,31,32 and in applied field (green arrows in Fig. 1) and, importantly, how it connects with quantum criticality.
We therefore measure STS down to 0.3 K and in applied magnetic fields up to 12 T, complemented by magnetotransport and thermopower measurements on identical YbRh2Si2 samples. We find that lattice Kondo correlations dominate only at temperatures about an order of magnitude below the single-ion Kondo temperature. Substantial lattice Kondo correlations are a prerequisite for quantum criticality to set in.
Results
Temperature evolution of tunneling spectra down to 0.3 K
Tunneling conductance curves dI/dV = g(V,T) obtained over a wide range of temperatures are presented in Fig. 2a. Both, the peaks due to CEF splitting of the Yb3+ multiplet (marked by black dots in Fig. 2a) and the conductance dip at zero bias (V = 0), result from single-ion Kondo physics7. Specifically the latter signifies the hybridization between 4f and conduction electrons. The most striking feature, however, is the evolution of the peak at about −6 mV (red arrow in Fig. 2a). This peak initially develops below 30 K, but clearly dominates the spectra only for \(T \lesssim 3.3\,{\mathrm{K}}\).
Tunneling spectroscopy on YbRh2Si2. a Tunneling conductance g(V, T) normalized at V = −80 mV and obtained at 0.3, 1.7, 5.5, and 30 K (from bottom to top), curves at 1.7, 5.5, and 30 K are offset for clarity. The −6 meV-peak evolves strongly at low T (red arrow). Black dots mark features resulting from CEF splitting of the Yb 4f multiplet. b g(V, T)-curves at selected low T (blue: 0.3 K, magenta: 1 K, orange: 1.9 K, olive: 3.3 K) obtained on the Si-terminated surface shown in the inset. Inset: Topography indicating excellent surface quality (scale bar: 4 nm, V = 100 mV, I = 0.6 nA)
We now focus on this low-temperature regime T ≤ 3.3 K (Fig. 2b). These data were obtained on the surface shown in the inset where topography over an area of 20 × 10 nm2 is presented. Such a topography not only attests the excellent sample quality but is also indicative of Si termination (see Supplementary Note 1 and Supplementary Figs. 1, 2). This termination is pivotal to our discussion as it implies predominant tunneling into the conduction electron states. A hint toward the origin of the −6 mV-peak comes from renormalized band structure calculations33: a partially developed hybridization gap is seen in the quasiparticle DOS at slightly smaller energy. Here, as a result of the renormalization the 4f band is shifted close to the Fermi level. Since tunneling spectroscopy on Si-terminated surfaces primarily probes conduction electrons and the total number of electrons must remain constant, the hybridization gap in the 4f-band is seen as a peak in our tunneling spectroscopy. On the other hand, a multi-level, finite-U non-crossing approximation (NCA) described our temperature-dependent tunneling spectra away from the energy range of this peak reasonably well7 but presented no indication for the existence of a peak at −6 mV. Since NCA does not include intersite Kondo correlations it is very reasonable to assume that this peak results from a strong development of lattice coherence, i.e. the lattice Kondo effect, and will be referred to as the Kondo lattice peak. The bulk nature of the −6 mV peak is supported by comparison to bulk transport measurements, as discussed below.
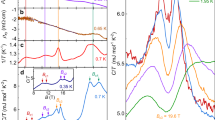
An analysis of the Kondo lattice peak is impeded by the strongly temperature-dependent zero-bias dip close by (see also Fig. 3d, Supplementary Notes 2, 3 and Supplementary Figs. 3, 4). Data \(g( V,T \,\gtrsim \, 30\,{\mathrm{K}} )\) for −15 mV ≤ V ≤−3 mV can be well approximated by a parabola and hence, we assume a parabola to describe the background below the Kondo lattice peak at low temperature, see the example of T = 0.3 K in Fig. 3a. There are finite energy ranges on both sides of the peak feature allowing to fit a parabola, cf. arrows in Fig. 3a. After background subtraction, each peak can be well described by a Gaussian (lines in Fig. 3b) from which its height and width (full width at half maximum, FWHM) is extracted. Note that the peak position in energy is independent of temperature (Fig. 3b). Clearly both, the peak height and FWHM, exhibit a significant change across TP ≈ 3.3 K, Fig. 3c. In contrast, the dip in zero-bias conductance, the hallmark of the single-ion Kondo effect, smoothly continues to deepen (Fig. 3d, for data on linear T-scale see Supplementary Fig. 4). Here, the depth of the zero-bias dip is defined as \(1 - [g(V = 0,T)/g(V = - 80\,{\mathrm{mV}},T)]\)7. This depth decreases logarithmically for 10 K < T ≤ 120 K, i.e. around TK, as predicted by dynamical mean field theory34.
Analysis of the Kondo lattice peak. a Tunneling conductance g(V, T = 0.3 K) normalized to its value at V = −80 mV, and parabola used for background subtraction (dashed line). Arrows indicate onset of deviations between data and parabola. b Examples of g(V, T, H = 0)-data after background subtraction (hollow markers, data sets at T < 5.5 K are offset). Data can be well described by Gaussians (lines). c Height (circles) and width (FWHM, crosses) of the peak at −6 mV after normalizing all g(V, T)-curves at −80 mV. At TP, indicated by the upward arrow, peak height and width change significantly. Results from different samples cause several markers to overlap. Dashed lines are guides to the eye. d Relative depth of the single-ion Kondo dip at zero-bias. Low-T data were obtained on several surfaces of two different samples, data at T ≥ 5 K from ref.7. The upward arrow indicates TP (as in c), the downward arrow TK. Dashed line is a logarithmic fit to the data as proposed in ref.34
Comparison to magnetotransport and thermopower measurements
While this temperature evolution of the single-particle spectrum is surprising, it connects well with the features that appear in bulk transport measurements14,15,16,17,35,36. Importantly, Fig. 4 shows that the thermopower divided by temperature, −S/T, has a qualitatively similar temperature dependence as the height of the STS Kondo lattice peak. Both display a plateau below about 7 K, and a subsequent strong increase upon lowering the temperature below TP ≈ 3.3 K. Here, TP is defined as the temperature at which the −6 meV-peak strongly develops. In the zero-temperature limit, a Fermi liquid is characterized by a constant value S/T. For a Kondo lattice system, this is expected to be seen at very low temperatures, i.e., once the renormalized band structure is almost fully developed37. In fact, for YbRh2Si2 heavy Fermi-liquid behavior was observed beyond the QCP: At fields μ0H = 1 T, the coefficient −S/T reaches ≈ 7 μV/K2 for temperatures up to ~0.5 K35, indicative of a very large effective charge carrier mass. The plateau in S/T seen in Fig. 4 occurs at a value almost an order of magnitude smaller and extends to a correspondingly higher temperature (see also Supplementary Note 5). This indicates some medium heavy Fermi liquid, i.e. prevailing Kondo-lattice correlations. Moreover, the nearly logarithmic increase in S/T below TP resembles that of the Sommerfeld coefficient γ of the electronic specific heat14 and is a clear signature of non-Fermi liquid behavior35. Therefore, the comparison of our STS results with those of S/T naturally leads us to propose that the incipient saturation of the Kondo lattice peak height below about 7 K (Fig. 4) signifies some prevailing Kondo–lattice correlations and, importantly, the growth of this peak below TP, as well as the concomitant drop of peak width (Fig. 3c) capture the quantum critical behavior. This leads to the insight that quantum criticality arises not before there is sufficient buildup of lattice Kondo correlations (see Supplementary Note 4 and Supplementary Fig. 5), or conversion of the local 4f electron spins into extended quasiparticle-like, but still incoherent excitations.
Development of lattice Kondo correlations. The height of the Kondo lattice peak (red squares) is compared to thermopower S divided by T (blue crosses) in dependence on T. Low-temperature data (T ≤ 6 K) were taken from ref.35. Left inset: same S/T-data on a logarithmic scale to show broader range. Right inset: Hall mobility μH vs. T. All three properties exhibit a strong upturn below TP ≈ 3.3 K and saturation at lowest T
To illustrate this point further, the Hall mobility μH = RH/ρxx as a function of temperature is also plotted in Fig. 4, right inset (RH itself is compared to S/T in Supplementary Fig. 6). In the regime where the anomalous Hall effect dominates, this quantity has been considered as capturing the buildup of the on-site Kondo resonance38. It is striking that the Hall mobility also shows a strong increase upon lowering the temperature. Yet, the Hall mobility does not show any plateau near 3 K, and neither does the resistivity nor the Sommerfeld coefficient as a function of temperature14. This implies that TP ≈ 3.3 K is not an ordinary Fermi liquid scale. The connection between the growth of the Hall mobility with quantum criticality becomes evident when we analyze its inverse 1/μH = ρxx/RH, which is equivalent to the cotangent of the Hall angle, cot θH, as a function of temperature. In YbRh2Si2, a power-law behavior of 1/μH, more specifically 1/μH ~ T2, is observed for 0.5 K \(\lesssim T \lesssim\) 5 K (see Supplementary Fig. 7). Such a behavior, as well as the T-linear electrical resistivity seen in relevant parts of the phase diagram of YbRh2Si214, has also been observed, e.g., in the cuprate high-Tc superconductors39.
Evolution of tunneling spectra in magnetic fields
To search for more direct STS evidence for quantum criticality in the H–T phase diagram of YbRh2Si2, the system was tuned by a magnetic field at T = 0.3 K ≈ 0.1TP, i.e. where coherent lattice effects are clearly dominating. Some g(V, H, T = 0.3 K)-curves are presented in Fig. 5a. No major change in the overall shape of the spectra with magnetic field is observed. The Kondo lattice peak can again be described by a Gaussian after parabolic background subtraction (Fig. 5b). Within the energy resolution of our STM the peak’s position in energy is independent on H. The resulting FWHM of the peak in dependence on H is presented in Fig. 5c. We note that the FWHM at low T and fixed H varies very little between different spectra, and even different samples, i.e. <4% (see also Fig. 3c where several data points of the FWHM fall on top of each other). This is taken as the error of FWHM, and determines the size of the error bars in Fig. 5c. Moreover, a comparison between the data and the Gaussian fit in Fig. 5b reveals an only slightly enhanced noise of g(V, H, T = 0.3 K) at elevated fields compared to zero field. Consequently, the trend displayed in Fig. 5c appears genuine.
Spectroscopy in applied field. a Tunneling conductance g(H, T = 0.3 K) measured at different magnetic fields (0, 1, 7, 11 T from bottom to top) applied parallel to the magnetically hard c-axis. Curves are offset for clarity. b Tunneling conductance data of a after parabolic background subtraction (markers) as described in Fig. 3a. Lines are the corresponding Gaussian fits; fields and color scheme as in a. c FWHM of the Kondo lattice peak for different magnetic fields at T = 0.3 K. At this temperature and field orientation, the energy scale T* (cf. Fig. 1) is located at a field of about 1.3 T (red cross15,17), approximately where a minimum is observed in the peak width. Several samples/cleaves were used to establish the existence of this minimum. The red arrow indicates the FWHM of the Hall crossover at T = 0.3 K 16. Height of blue error bars correspond to the errors of the Gaussian fits (Figs. 3a and b) and differences between samples, the line is a guide to the eye
At a field of μ0H = 1 T, the Kondo lattice peak FWHM exhibits a minimum, with a reduction of about 15% of its high-field value. This field is approximately of the value μ0H* ≈ 1.3 T at which the Hall crossover takes place at T = 0.3 K for H||c (red cross in Fig. 5c, for the field direction see Supplementary Note 6). The range in magnetic field over which the Hall crossover is observed16 is indicated by a red arrow in Fig. 5c. This implies that changes in g(V, H, T = 0.3 K) are to be expected within a similar field range, as indeed suggested by the drop in peak width vs. H at T = 0.3 K (see also Supplementary Note 7 and Supplementary Fig. 8). Note that at this low temperature Kondo lattice effects are dominating. In this regime, the observed drop of peak width at μ0H = 1 T indicates a reduced quasiparticle weight and follows the expected behavior for a critical slowing down concluded from isothermal magnetotransport (Hall coefficient, RH, and magnetoresistance, ρxx) measurements15,16, revealing thermally broadened jumps at H*(T). One may therefore expect that the drop in peak width may further increase and sharpen upon cooling, (cf. Fig. 1). In this view, all our findings reflect the finite temperature remnant of a field-induced QCP at T = 0. Data from specific-heat measurements on YbRh2Si2 in magnetic field40 confirm this assignment (cf. Supplementary Fig. 8). They yield a relative change of the Sommerfeld coefficient between critical (H*) and elevated fields of order 30% at T = 0.3 K, if scaled for the relevant field orientation. We believe that the larger change in Sommerfeld coefficient compared to the drop in FWHM of the STS Kondo lattice peak (Fig. 5c, about 15% compared to the value at 9 T at which YbRh2Si2 is almost in the Fermi liquid regime41) is related to the fact that heat capacity integrates over the whole Brillouin zone while STS is a more directional measurement. For a surface along the a–b plane (Fig. 2), tunneling along the c-direction is most relevant, yet hybridization of the Yb CEF ground state orbitals is anisotropic33, mostly with the Rh \(4d_{x^2 - y^2}\).
Remarkably, the FWHM at zero field falls in line with its trend at high fields μ0H ≥ 3.5 T, i.e. there is no significant difference at T = 0.3 K at both sides of the QCP. While the presented STS data on its own do not allow to distinguish between quantum critical scenarios, they are in good agreement with isothermal magnetotransport data. Even at a temperature as low as ~0.5 K, the Hall crossover is expected to reach all the way to H = 013. In analogy, the peak width in STS at H = 0 should be close to the one extrapolated from higher fields, where a large Fermi surface constitutes the heavy Fermi liquid. Crossing the T*-line at temperatures as high as about half a K, there is still a dominating contribution of the large Fermi surface to the quantum-critical fluctuations even at zero field42. Upon cooling, this contribution of the large Fermi surface at H = 0 is expected to decrease13. To establish this trend further, lower temperatures for our STS measurements are clearly called for. We note that Lifshitz transitions and Zeeman splitting can be ruled out as origins for the drop of the peak’s FWHM (see Supplementary Note 5).
Discussion
Our STS studies here have revealed two important insights. One is that the development of the dynamical lattice Kondo correlations in a stoichiometric material such as YbRh2Si2, while setting in at Tcoh ≈ TK, extends to considerably lower temperatures and dominate the material’s properties only at much lower temperatures (see Supplementary Note 4). In the case of YbRh2Si2, the STS Kondo lattice peak height and thermopower coefficient do not indicate dominant lattice Kondo correlations before the temperature has reached TP ~ 0.1·Tcoh. Moreover, the conductance minimum at zero bias, which has been shown to capture primarily the on-site Kondo (i.e. hybridization) effect at temperatures \(T \gtrsim 5\,{\mathrm{K}}\)7, also continues to deepen down to the lowest measured temperature as shown in Fig. 3d. Conversely, the strengthening of the lattice Kondo coherence only at much below TK implies that the on-site Kondo effect dominates many thermodynamic and transport properties at around and below Tcoh in YbRh2Si2, and gives way to the lattice Kondo correlations only slowly upon reducing the temperature. Such a persistence of this distinct signature of the single-ion Kondo effect down to temperatures substantially below Tcoh is consistent with observations based on different transport37,38 and thermodynamic8,43 properties of several other heavy-fermion metals. On the one hand, this provides a natural explanation to the applicability of single-ion-based descriptions to temperatures well below TK even though they neglect lattice Kondo coherence effects7,37,38. On the other hand, this finding supports nicely the theoretical concept of two temperature scales, i.e. a single-ion and a lattice Kondo scale29,30, including the predicted order of magnitude difference30.
The second lesson concerns the link between the development of the dynamical lattice Kondo correlations and quantum criticality. As a function of temperature, our measurements of the height and width of the Kondo lattice peak strongly suggest that, in order for the quantum criticality to set in, the lattice Kondo correlations first have to develop sufficiently upon lowering the temperature through, and well below, TK ≈ Tcoh ≅ 30 K. More specifically, as the temperature is lowered through Tcoh, both the Kondo lattice peak height and the thermopower coefficient first reach a plateau below about 7 K signifying well-developed lattice Kondo correlations. It is against this backdrop that the Kondo lattice peak height and S/T markedly increase below TP ≈ 3.3 K. This manifests quantum criticality at the level of the single-particle spectrum, which goes considerably beyond the quantum critical behavior seen in the divergent Sommerfeld coefficient of the electronic specific heat and the linear-in-T electrical resistivity14. This signature of the quantum criticality at the single-particle level is complemented by the isothermal behavior of the Kondo lattice peak with respect to the control parameter, the magnetic field, at the lowest measured temperature, T ≈ 0.3 K. The FWMH of this peak displays a minimum at a similar field value at which isothermal transport and thermodynamic measurements show a Fermi surface crossover15,16,17 indicating its relation to quantum criticality.
To put these findings into perspective, our comparative studies indicate an appealingly natural scenario: the development of the lattice Kondo correlations is the prerequisite for quantum criticality. Only if the Kondo lattice is sufficiently established quantum critical fluctuations can evolve. As such, the insights gained in our study will likely be relevant to the non-Fermi liquid phenomena in a broad range of other strongly correlated metals, such as the high-Tc cuprates and the organic charge-transfer salts, which are typically in proximity to Mott insulating states and in which quantum criticality is often observed44,45,46.
Methods
Sample characterization
High-quality single crystals of YbRh2Si2 were grown by an indium-flux method; they grow as thin platelets with a height of 0.2–0.4 mm along the crystallographic c-direction (see also Supplementary Note 6). Crystalline quality and orientation of the single crystals were confirmed by x-ray and Laue investigations, respectively. The residual resistivity ρ0 of the six samples investigated here ranged between 0.5 and 0.9 μΩ cm with no apparent differences in their spectroscopic results. The samples were cleaved in situ perpendicular to the crystallographic c direction at temperatures ~20 K. Subsequent to cleaving, the samples were constantly kept under ultra-high vacuum (UHV) conditions and did not exhibit any sign of surface degradation for at least several months, as indicated by STM re-investigation.
Scanning tunneling microscopy and spectroscopy
STM and STS was conducted (using a cryogenic STM made by Omicron Nanotechnology) at temperatures between 0.3 and 6 K, in magnetic fields μ0H ≤ 12 T (applied parallel to the crystallographic c direction) and under UHV conditions (p < 2·10−9 Pa). Spectroscopic measurements were conducted using lock-in technique with Vrms = 0.2 mV. For the tunneling spectra shown, g(V, T)-data were averaged over areas of 1 × 1 nm2 on grids of 24 × 24. In zero magnetic field, the averaging area was repeatedly varied between zero (i.e. spectroscopy repeated at a given point) and 5 × 5 nm2 to ensure local homogeneity of the g(V,T)-data. For the temperature range 4.6 K ≤ T ≤ 120 K a second UHV STM (LT-STM) was utilized (p ≤ 3·10−9 Pa).
Thermopower measurements
The thermopower S was measured by applying a temperature gradient to a rod-shaped sample of dimensions 4 × 0.5 × 0.1 mm3 out of the same batch as the samples used in STM/S measurements. For low temperatures 0.03 K \(\lesssim T \lesssim\) 6 K, a home-built, dilution refrigerator-based setup was used, while measurements between 2 and 360 K were conducted in a PPMS (Quantum Design Inc.). The overlap of the two temperature ranges between 2 and 6 K serves as consistency check. Thermopower data in the high-temperature range compare nicely to those obtained earlier47. Hall effect measurements (see ref.48 for details) were conducted on the same sample as the thermopower measurements.
Data availability
The data that support the findings of this study are available from the corresponding author upon request.
References
Grewe, N. & Steglich, F. in Handbook on the Physics and Chemistry of Rare Earths Vol. 14 (eds. Gschneidner, K. A. Jr. & Eyring, L.) 343–474 (Elsevier, Amsterdam, 1991).
Wirth, S. & Steglich, F. Exploring heavy fermions from macroscopic to microscopic length scales. Nat. Rev. Mater. 1, 16051 (2016).
Doniach, S. Kondo lattice and weak antiferromagnetism. Phys. B 91, 231–234 (1977).
Sachdev, S. Quantum Phase Transitions (Cambridge University Press, Cambridge, 2011).
Coleman, P. & Schofield, A. J. Quantum criticality. Nature 433, 226–229 (2005).
von Löhneysen, H., Rosch, A., Vojta, M. & Wölfle, P. Fermi-liquid instabilities at magnetic quantum phase transitions. Rev. Mod. Phys. 79, 1015–1075 (2007).
Ernst, S. et al. Emerging local Kondo screening and spatial coherence in the heavy-fermion metal YbRh2Si2. Nature 474, 362–366 (2011).
Pikul, A. et al. Single-ion Kondo scaling of the coherent Fermi liquid regime in Ce1−xLaxNi2Ge2. Phys. Rev. Lett. 108, 066405 (2012).
Yang, Y., Fisk, Z., Lee, H.-O., Thompson, J. D. & Pines, D. Scaling the Kondo lattice. Nature 454, 611–613 (2008).
Yang, Y. Two-fluid model for heavy electron physics. Rep. Prog. Phys. 79, 074501 (2016).
Jang, S. et al. Evolution of the Kondo lattice electronic structure above the transport coherence temperature. Preprint at http://arxiv/abs/1704.08247 (2017).
Chen, Q. Y. et al. Band dependent interlayer f-electron hybridization in CeRhIn5. Phys. Rev. Lett. 120, 066403 (2018).
Paschen, S. et al. Kondo destruction in heavy fermion quantum criticality and the photoemission spectrum of YbRh2Si2. J. Magn. Magn. Mater. 400, 17–22 (2016).
Custers, J. et al. The break-up of heavy electrons at a quantum critical point. Nature 424, 524–527 (2003).
Paschen, S. et al. Hall-effect evolution across a heavy-fermion quantum critical point. Nature 432, 881–885 (2004).
Friedemann, S. et al. Fermi-surface collapse and dynamical scaling near a quantum-critical point. Proc. Natl Acad. Sci. USA 107, 14547–14551 (2010).
Gegenwart, P. et al. Multiple energy scales at a quantum critical point. Science 315, 969–971 (2007).
Si, Q. et al. Kondo destruction and quantum criticality in Kondo lattice systems. J. Phys. Soc. Jpn. 83, 061005 (2014).
Küchler, R. et al. Divergence of the Grüneisen ratio at quantum critical points in heavy Fermion metals. Phys. Rev. Lett. 91, 066405 (2003).
Tokiwa, Y., Radu, T., Geibel, C., Steglich, F. & Gegenwart, P. Divergence of the magnetic Grüneisen ratio at the field-induced quantum critical point in YbRh2Si2. Phys. Rev. Lett. 102, 066401 (2009).
Gegenwart, P. et al. Magnetic-field induced quantum critical point in YbRh2Si2. Phys. Rev. Lett. 89, 056402 (2002).
Abrahams, E. & Wölfle, P. Critical quasiparticle theory applied to heavy fermion metals near an antiferromagnetic quantum phase transition. Proc. Natl Acad. Sci. USA 109, 3238–3242 (2012).
Wölfle, P. & Abrahams, E. Spin-flip scattering of critical quasiparticles and the phase diagram of YbRh2Si2. Phys. Rev. B 92, 155111 (2015).
Miyake, K. & Watanabe, S. Unconventional quantum criticality due to critical valence transition. J. Phys. Soc. Jpn. 83, 061006 (2014).
Fischer, Ø., Kugler, M., Maggio-Aprile, I., Berthod, C. & Renner, C. Scanning tunneling spectroscopy of high-temperature superconductors. Rev. Mod. Phys. 79, 353–419 (2007).
Schmidt, A. R. et al. Imaging the Fano lattice to ‘hidden order’ transition in URu2Si2. Nature 465, 570–576 (2010).
Aynajian, P. et al. Visualizing heavy fermions emerging in a quantum critical Kondo lattice. Nature 486, 201–206 (2012).
Köhler, U., Oeschler, N., Steglich, F., Maquilon, S. & Fisk, Z. Energy scales of Lu1−xYbxRh2Si2 by means of thermopower investigations. Phys. Rev. B 77, 104412 (2008).
Burdin, S., Georges, A. & Grempel, D. R. Coherence scale of the Kondo lattice. Phys. Rev. Lett. 85, 1048–1051 (2000).
Costi, T. A. & Manini, N. Low-energy scales and temperature-dependent photoemission of heavy fermions. J. Low Temp. Phys. 126, 835–866 (2002).
Mo, S.-K. et al. Emerging coherence with unified energy, temperature, and lifetime scale in heavy fermion YbRh2Si2. Phys. Rev. B 85, 241103(R) (2012).
Kummer, K. et al. Temperature-independent Fermi surface in the Kondo lattice YbRh2Si2. Phys. Rev. X 5, 011028 (2015).
Zwicknagl, G. Field-induced suppression of the heavy-fermion state in YbRh2Si2. J. Phys. Condens. Matter 23, 094215 (2011).
Costi, T. A. Kondo effect in a magnetic field and the magnetoresistivity of Kondo alloys. Phys. Rev. Lett. 85, 1504–1507 (2000).
Hartmann, S. et al. Thermopower evidence for an abrupt Fermi surface change at the quantum critical point of YbRh2Si2. Phys. Rev. Lett. 104, 096401 (2010).
Kimura, S. et al. Optical observation of non-Fermi-liquid behavior in the heavy fermion state of YbRh2Si2. Phys. Rev. B 74, 132408 (2006).
Sun, P. & Steglich, F. Nernst effect: evidence of local Kondo scattering in heavy fermions. Phys. Rev. Lett. 110, 216408 (2013).
Coleman, P., Anderson, P. W. & Ramakrishnan, T. V. Theory for the anomalous Hall constant of mixed-valence systems. Phys. Rev. Lett. 55, 414–417 (1985).
Chien, T. R., Wang, Z. Z. & Ong, N. P. Effect of Zn impurities on the normal-state Hall angle in single-crystal YBa2Cu3−xZnxO7−δ. Phys. Rev. Lett. 67, 2088–2091 (1991).
Oeschler, N. et al. Low-temperature specific heat of YbRh2Si2. Physica B 403, 1254–1256 (2008).
Custers, J. Quantum-Critical Behavior in the Heavy-Fermion Compounds YbRh 2 Si 2 and CeIn 3−x Sn x. PhD Thesis, Technical University Dresden (2004).
Senthil, T. Critical Fermi surfaces and non-Fermi liquid metals. Phys. Rev. B 78, 035103 (2008).
Pietri, R., Rotundu, C. R., Andraka, B., Daniels, B. C. & Ingersent, K. Absence of Kondo lattice coherence effects in Ce0.6La0.4Pb3: a magnetic-field study. J. Appl. Phys. 97, 10A510 (2005).
Lee, P. A., Nagaosa, N. & Wen, X.-G. Doping a Mott insulator: physics of high-temperature superconductivity. Rev. Mod. Phys. 78, 17–85 (2006).
Ramshaw, B. J. et al. Quasiparticle mass enhancement approaching optimal doping in a high-T c superconductor. Science 348, 317–320 (2015).
Oike, H., Miyagawa, K., Taniguchi, H. & Kanoda, K. Pressure-induced Mott transition in an organic superconductor with a finite doping level. Phys. Rev. Lett. 114, 067002 (2015).
Hartmann, S. et al. Thermal transport properties of the heavy-fermion compound YbRh2(Si1−xGex)2. Physica B 378, 70–71 (2006).
Friedemann, S. et al. The crossed-field and single-field Hall effect in LuRh2Si2. Phys. Status Solidi B 247, 723–726 (2010).
Acknowledgements
We sincerely thank U. Stockert for help with the experiments and discussions, as well as J.C. Séamus Davis for discussions. Work was partly supported by the German Research Foundation through DFG Research Unit 960 and through DFG grant KR3831/4-1. Work at Rice University has been supported by the NSF Grant DMR-1611392, the ARO grant no. W911NF-14-1-0525, and the Robert A. Welch Foundation Grant no. C-1411. Q.S. graciously acknowledges the support of the Alexander von Humboldt Foundation, the hospitality of the Karlsruhe Institute of Technology, and a QuantEmX grant from ICAM and the Gordon and Betty Moore Foundation through Grant no. GBMF5305. S.K. acknowledges support by the National Key R&D Program of the MOST of China (Nos. 2016YFA0300202 and 2017YFA0303100) and the National Science Foundation of China (Nos. 11474250 and 11774307).
Author information
Authors and Affiliations
Contributions
S.W. and F.S. designed the research. S.S., L.J. and S.W. conducted the STM experiments, S.H. the thermopower measurements and S.F. the Hall measurements. C.K. and C.G. provided the samples. S.K. and Q.S. provided theoretical insight. All authors contributed to the discussions and the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Seiro, S., Jiao, L., Kirchner, S. et al. Evolution of the Kondo lattice and non-Fermi liquid excitations in a heavy-fermion metal. Nat Commun 9, 3324 (2018). https://doi.org/10.1038/s41467-018-05801-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-018-05801-5
This article is cited by
-
Two-dimensional heavy fermions in the van der Waals metal CeSiI
Nature (2024)
-
Critical slowing down near a magnetic quantum phase transition with fermionic breakdown
Nature Physics (2023)
-
Terahertz control of many-body dynamics in quantum materials
Nature Reviews Materials (2023)
-
Inducing and tuning Kondo screening in a narrow-electronic-band system
Nature Communications (2022)
-
Superconductivity in an extreme strange metal
Nature Communications (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.