Abstract
First-order magnetic transitions (FOMTs) with a large discontinuity in magnetization are highly sought in the development of advanced functional magnetic materials. Isosymmetric magnetoelastic FOMTs that do not perturb crystal symmetry are especially rare, and only a handful of material families, almost exclusively transition metal-based, are known to exhibit them. Yet, here we report a surprising isosymmetric FOMT in a rare-earth intermetallic, Eu2In. What makes this transition in Eu2In even more remarkable is that it is associated with a large latent heat and an exceptionally high magnetocaloric effect in low magnetic fields, but with tiny lattice discontinuities and negligible hysteresis. An active role of the Eu-5d and In-4p states and a rather unique electronic structure borne by In to Eu charge transfer, altogether result in an unusual exchange mechanism that both sets the transition in motion and unveils an approach toward developing specific magnetic functionalities ad libitum.
Similar content being viewed by others
Introduction
In the solid state, phase transitions commonly lead to emergence of important properties such as superconductivity or ferroelectricity, or to a change in magnetic or crystallographic order1. In fact, phase transitions are at the heart of many functionalities. Among them, magnetic phase transitions enable a plethora of both established (magnetostrictive, magnetic shape memory, magnetoresistance) and emerging (magnetocaloric) applications2,3,4,5,6. The latter rely on the magnetocaloric effect (MCE), currently an intensely researched subject for its use in heat pumping systems, which promises transformative improvements in heating/cooling technologies, making them both energy-efficient and environmentally-benign2,3,4,5,6. In addition to obviously important applications in the room temperature range, magnetic refrigeration is also expected to create new opportunities in the low or ultra-low temperature ranges, including liquefaction of natural gas and hydrogen, and in space.
Consider a hierarchy of phase transitions illustrated in Fig. 1, focusing on those that involve magnetism. Based on the Ehrenfest classification, a distinction is usually made between the most common continuous second-order transitions, and the far less frequent discontinuous first-order magnetic transitions (FOMTs). The latter are defined in practice by the presence of a latent heat of transformation. Further, discontinuities in the entropy (ΔS), volume (ΔV), magnetization (ΔM), and other measurable quantities can be induced by the conjugate driving field(s), forming the basis for functionality of materials exhibiting FOMTs. Among those, two classes of FOMTs can be distinguished. The most frequent are magnetostructural transitions involving a simultaneous change in crystal symmetry, whereas the magnetoelastic FOMTs occur without changing the symmetry. Magnetoelastic FOMTs may be further classified as those with purely isotropic (e.g., FeRh, La(Fe,Si)13) or anisotropic (e.g., (Mn,Fe)2(P,As,Si)) discontinuities in their lattice parameters7,8,9,10,11,12. For magnetoelastic FOMTs common side effects related to hysteresis and irreversibility can be controlled and tuned by compositional adjustments and, compared to magnetostructural transitions, such adjustments are typically more successful in the design of real materials.
A classification diagram of solid-state phase transitions. Several types of magnetic phase transitions are categorized focusing on the magnetoelasticity branch, with examples of materials families7,9,10,11,12,13,14,24,38,52,53,54,55. Different sub-classes are distinguished depending on the Ehrenfest classification (first/second order), whether the magnetic transition is associated with a change in crystal symmetry (magneto-structural/magneto-elastic), and depending on the nature of the lattice parameter discontinuities (isotropic/anisotropic)
Very few material systems are known to undergo magnetoelastic FOMTs at ambient conditions with at least one phase having a large magnetization. This lack of representatives is primarily attributed to the unique underlying mechanism of magnetoelastic FOMTs. Most often these transitions involve simultaneous and cooperative discontinuities in the electronic, lattice, and magnetic properties. The most characteristic example is the FOMT between antiferromagnetic (AFM) and ferromagnetic (FM) states in FeRh8. The isostructural character of this transformation was established more than half a century ago7, yet FeRh keeps attracting a great deal of applied and fundamental interest. Though widely debated, the origin of the AFM↔FM FOMT in FeRh is most often ascribed to an evolution of the electronic density of states (DOS) near the Fermi level and an instability of Rh magnetic moments across the transition. La(Fe,Si)13 and Fe2P materials are other archetypal examples of magnetoelastic FOMTs9,10,13,14. Regardless of certain aspects that may be unique to every known family of materials, magnetoelastic FOMTs in all of them are rooted in drastic electronic reconstructions made possible by the itinerant d-states of transition metals, in turn enhancing the magnetic discontinuities. In rare-earth based materials, on the other hand, the established paradigm is that the 4f electronic states of lanthanides, while critical for the development of the largest magnetic moments and strongest magnetocrystalline anisotropies that exist in nature, are highly localized and ineffective in promoting magnetoelastic FOMTs without assistance from itinerant electrons. The latter are usually provided by transition metals whose magnetic exchange interactions spread much wider compared to lanthanides.
Here, we report on the observation of a first-order magnetoelastic transition with an entirely different mechanism in a rare-earth intermetallic, Eu2In. After establishing the first-order character of the paramagnetic (PM) ↔ FM transition by measurements of physical properties, including magnetization, heat capacity, and electrical resistivity, we address the microscopic mechanisms at its origin by temperature dependent x-ray diffraction, emission and absorption, magnetic circular dichroism, as well as first-principles calculations.
Results
Eu2In, an exception within the R2In material family
All R2In binary materials, where R = rare earth element, crystallize in the hexagonal Ni2In type with space group P63/mmc, except when R = Eu or Yb (ref.15). The magnetic properties of hexagonal R2In materials are well documented, in particular for Gd2In, which exhibits a sequence of AFM and FM transitions upon heating16. On the other hand, the crystal structure of Eu2In is known but no physical properties were reported so far. A polycrystalline Eu2In prepared by induction melting and annealing was reported to crystallize in the Co2Si-type orthorhombic structure with space group Pnma (ref.17). Our sample, synthesized by melting and annealing in a sealed Ta crucible filled with inert gas and using a conventional resistance furnace, adopts the same Co2Si-type crystal structure with lattice parameters at room-temperature a = 7.4536(6) Å, b = 5.5822(5) Å and c = 10.312(1) Å that are close to reported earlier17, and a/c and b/a ratios typical of other representatives of this type of structure18. Additional details about the crystal structure and its characterization can be found in Supplementary Notes 1 and 2.
Discontinuous FM transition
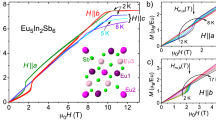
The magnetization of Eu2In is presented in Fig. 2. Upon cooling, magnetization reveals a particularly sharp (for a 1 T magnetic field) discontinuity at the Curie temperature TC(B = 1 T) = 58 K corresponding to the development of a FM phase via FOMT (AC magnetic susceptibility in Supplementary Note 3 indicates zero DC magnetic field TC of 55 K). The thermal hysteresis is however very small (~0.07 K from magnetization measurements, Supplementary Note 4). In the range 100 < T < 300 K, the magnetic susceptibility follows Curie–Weiss law with Weiss temperature of 48 K and effective magnetic moment of 8.5 μB Eu−1. Though larger than the theoretical value for non-interacting Eu2+ (7.94 μB), this indicates that both of the independent Eu-I and Eu-II sites in this intermetallic compound are populated by divalent europium. The high magnetic field magnetization measurements at 5 K shown in Fig. 2b produce a saturation magnetization of at least 14.4 μB f.u.−1, in line with a fully collinear ferromagnetism, the divalent character of Eu (gJ = 7 μB, where g is gyromagnetic ratio and J = S = total angular momentum quantum number of Eu2+), and a small but measurable additional magnetic contribution from the 5d states of Eu, even though theoretically, Eu2+ is expected to have a [Xe]4f76s25d0 configuration. Above the Curie temperature, the metamagnetic jumps observed in the isothermal measurements indicate nearly fully reversible magnetic field-induced PM↔FM transitions with a nearly negligible (≤0.1 T) magnetic hysteresis, in line with the extremely narrow thermal hysteresis.
Magnetic properties of Eu2In. a Magnetization (M) as a function of the temperature (T) measured upon cooling and heating in a magnetic field (B) of 1 T. The inverse magnetic susceptibility in B = 0.1 T in the paramagnetic regime is displayed in the inset. b Isothermal magnetization data measured upon magnetization (open symbols) and demagnetization (closed symbols) for different temperatures: 5 K (squares), then from 50 to 62 K in 2 K increments. The inset displays evolution of the Curie temperature (TC) as a function of the magnetic field derived from isothermal M(B) (circles) and isofield M(T) measurements (squares, raw data not shown). c Temperature dependence of the magnetization measured at different applied pressures upon heating in B = 0.1 T
The magnetic field dependence of TC, determined from both the isothermal and isofield measurements, is presented in the inset of Fig. 2b. Both sets of data are in good agreement, leading to ∂TC/∂B ≈ +3.5 K T−1, which is in line with TC = 55 K determined from AC measurements in 0.0005 T AC field (Supplementary Note 3) and TC = 58 K determined from the 1 T data presented in Fig. 2a. Using ΔM ≅ −90 A m2 kg−1 determined from isothermal magnetization data at T = 58 K and Clausius–Clapeyron formalism ΔST = −ΔM(∂B/∂TC) = ΔV(∂P/∂TC), the estimated entropy change at the transition is ΔST ≅ 26 J kg−1 K−1 and the latent heat ΔL = TΔST ≅ 1.4 kJ kg−1. The application of hydrostatic pressure has a minor effect on TC, and the unmodified saturation magnetization indicates that the divalent character of Eu is preserved up to 0.85 GPa (Supplementary Note 5). The shift of the ordering temperature ∂TC/∂P of about +2 K GPa−1 points to a small and positive cell volume change at the FOMT upon heating that too can be estimated from the Clausius–Clapeyron equation as ΔV/V ≈ 0.03%. Common for many other pressure-sensitive FOMTs, the transition width increases with the pressure by ~20%, as derived from the full width at half maximum of ∂M/∂T curves. As expected, the FOMT in Eu2In also leads to a sharp drop in electrical resistivity upon cooling with a narrow thermal hysteresis of about 0.1 K separating two regions with metallic behaviors (Supplementary Note 6).
Large latent heat without hysteresis
One of the most important quantities characterizing a first-order transformation—which actually is at the basis of the Ehrenfest classification—is its latent heat. However, for extremely sharp and hysteretic transitions heat capacity measurements are always challenging19. Hence, we combined the standard heat capacity data provided by a commercial semi-adiabatic calorimeter with an external analysis of a single relaxation across the FOMT (referred to as single pulse method, SPM, Supplementary Note 7)20. Figure 3 shows the extremely sharp heat capacity peak of Eu2In associated with the FOMT (the full width at half maximum is less than 1 K), and the data in the inset confirm the very small thermal hysteresis of about 0.1 K. The extremely high heat capacity maximum and the symmetrical shape of the peak unambiguously establish the first-order character of the transition. To the best of our knowledge, a nearly ideal FOMT in Eu2In is only a second such case observed among metallic solids, the first is the FM–AFM transformation in a very high-purity dysprosium metal21. This behavior can be ascribed to excellent compositional homogeneity indicating that Eu2In is a true line compound without a detectable homogeneity region, high crystallinity and low concentration of defects22,23, and/or low energy barriers involved due to limited interfacial stresses between the two phases. Using a step function to estimate the background in the transition region, the entropy change of the transition\(\Delta S_{\mathrm{T}} = \mathop {\int}\nolimits_{T = 54}^{T = 56} {\frac{{(C - C_{{\mathrm{background}}})}}{T}\mathrm{d}T \cong 27.5\;{\mathrm{J}}\;{\mathrm{kg}}^{ - 1}\;{\mathrm{K}}^{ - 1}}\) is in line with the estimate made from magnetization measurements using the Clausius–Clapeyron equation. As expected for a ferromagnet24, with the increase of the magnetic field the heat capacity peak shifts to higher temperature and broadens (Supplementary Note 8).
Heat capacity and magnetocaloric effects of Eu2In. a Heat capacity (C) as a function of the temperature (T) measured on heating in zero magnetic field. The inset shows the heating and cooling branches calculated using the single pulse method (SPM, filled squares) compared to the standard analysis of the Multiview software Quantum Design (open circles). b Adiabatic temperature change (ΔTad) for magnetic field changes of 1 and 2 T derived from calorimetry. c Isothermal entropy change (ΔS) determined from calorimetry (filled symbols) and magnetization (open symbols)
Giant MCE at low magnetic field change
In-field heat capacity measurements were performed to determine the two main quantities of the MCE: the isothermal entropy change ΔS and the adiabatic temperature change ΔTad. The maximum adiabatic temperature change is 2.2 and 5.0 K for ΔB = 1 and 2 T, respectively, starting from B = 0. These values place Eu2In on top among the best materials available for low-temperature magnetocalorics at present3,4,5,6, especially considering that in this temperature range the lattice entropy of the material is rising very rapidly, naturally suppressing ΔTad (ref.25). Due to the nearly discontinuous transition and its large sensitivity to the magnetic field, most of the latent heat is converted into a MCE even by a limited magnetic field change of 1 T. The maximum ΔS values derived from calorimetry are −24.4 and −28.2 J kg−1 K−1, for ΔB of 1 and 2 T, respectively, and are extraordinarily high as well. A good agreement is observed between the ΔS results derived from isofield magnetization and calorimetry data. In magnetic fields exceeding 2 T (Supplementary Note 8) the maximum ΔS begins to saturate, reaching −37 J kg−1 K−1 in 7 T. The steady but slow increase of ΔS with field above 2 T is due to the conventional spin contribution, but the discontinuity of ΔS observed for all ΔB ≥ 2 T remaining constant around ~−26 J kg−1 K−1 which, as expected26, is very close to the entropy change associated with FOMT determined from both the Clausius–Clapeyron equation and from heat capacity. For a field change of 1 T, the coefficient of refrigerant performance (CRP) is about 0.70 and the temperature averaged entropy change (TEC3) is about −17.1 J kg−1 K−1 27,28. These figures of merit are comparable to or higher than the most promising magnetocaloric materials in the cryogenic regime27,28. With the exceptionally small hysteresis, particularly large ΔS and ΔTad in moderate magnetic fields, Eu2In outperforms all known magnetocaloric materials in this temperature range3,4,5,6.
Unusual mechanism of FOMT in Eu2In
The unit cell parameters and crystal structure of Eu2In are presented in Fig. 4. The orthorhombic primitive unit cell consists of four formula units with two inequivalent Eu sites, both located in 4c positions. The Eu-I site (0.0287, 1/4, 0.7048) is surrounded by 6 Eu-II, 2 Eu-I, and 4 indiums atoms. The Eu-II site (0.1781, 1/4, 0.0680) is in a similar environment with slightly different interatomic distances. The Eu2In structure is effectively built by two alternating flat atomic layers stacked along the b-axis, where one layer is a mirror image of another shifted diagonally in the ac plane (Supplementary Notes 1 and 2). However, there is no significant difference between the interlayer and intralayer atomic distances suggesting that this is clearly a 3D structure.
Crystal structure and Eu electronic configuration in Eu2In. a Unit cell volume (V), b ratio c/a and b/a of the lattice parameters, determined from powder x-ray diffraction as function of the temperature. The error bars represent the standard deviation estimated during the refinement of the lattice parameters. c Schematic representation of the crystal structure. d X-ray absorption near edge spectroscopy (XANES) and normalized magnetic circular dichroism (XMCD) spectra at Eu L2,3 edges at T = 5 K and B = 3 T
To get experimental insight into the microscopic mechanisms of the FOMT in Eu2In and in particular to examine potential structural changes, powder x-ray diffraction experiments were carried out as a function of temperature. A cursory visual examination of the collected powder XRD patterns reveals only minor changes upon cooling (Supplementary Note 2) and the same crystal structure over the whole examined temperature range, indicating an isostructural transition. According to Rietveld refinements, the FOMT in Eu2In corresponds to a small discontinuous expansion of all lattice parameters: Δa/a ≅ 0.08%, Δb/b ≅ 0.04% and Δc/c ≅ 0.03%. The resulting unit cell volume change is small and positive, ΔV/V ≅ +0.1%, which is slightly larger than the rough estimate made from high pressure magnetization experiments. In comparison to the most representative examples of magnetoelastic FOMTs (FeRh, La(Fe,Si)13, MnFe(P,Si)), the transition in Eu2In manifests an order of magnitude smaller discontinuities in lattice parameters and phase volume7,9,12. This is quite surprising, as it is usually believed that either or both significant volume changes or large anisotropic distortions are required to get both a strong FOMT and a large total entropy discontinuity ΔST = ΔSM + ΔSst (where ΔSM and ΔSst reflect perturbations in the magnetic and crystallographic sublattices, respectively29) simply because ΔSst scales proportionally to ΔV/V (ref.30). On the other hand, the similarity between the lattices of FM and PM phases is the key ingredient underpinning the extremely small thermal hysteresis of the transition, requiring a minimum free energy difference to overcome strain energy. The transition in Eu2In is also in stark contrast with other types of solid–solid phase transitions such as martensitic transformations, which usually requires a fine tuning of the cell parameters to ensure lattice compatibility and approach reversibility31,32.
The actual ΔV/V ≅ 0.1% from the x-ray data (0.03% from the Clausius–Clapeyron equation) is too small to result in both the extraordinary large latent heat and the giant small-field MCE in Eu2In. Hence we must consider the magnetic entropy change across TC. The total magnetic entropy available in Eu2In is SM = Rln(2 J + 1) = 17.3 J mol(Eu2+)−1 K−1 = 82.6 J kg(Eu2In)−1 K−1, where R is the universal gas constant. When compared to the actually observed discontinuity ΔST ≅ 26–27.5 J kg−1 K−1, the compound demonstrates an exceptionally high, nearly 30% concentration of the total available spin entropy at TC. Most importantly, this large amount of entropy can also be reversibly shifted above TC by a magnetic field change as small as 1 T, generating a giant small-field MCE. This value is indeed remarkable since for comparison, a 1 T magnetic field induces an order of magnitude smaller ΔS in elemental Gd that corresponds to only ~3% of the available SM, and magnetic field change of approximately ~30 T is required to reach ΔS on the order of 30% of the available entropy33,34.
The small ΔV also makes it highly unlikely that the FOMT is associated with a Eu valence change. To confirm this, x-ray absorption near edge spectroscopy (XANES) and magnetic circular dichroism (XMCD) experiments, carried out at the europium L2,3 edges (2p → 5d) as a function of the temperature, are shown in Fig. 4d. The XANES spectra at T = 5 K present a single white line shape with a maximum at ~6974 eV at the Eu L3 edge. Both L3 and L2 spectra are typical of divalent-like Eu, which brings support to the analysis of the magnetization data. Determining the valence by the conventional spectral decomposition into Lorentzian peaks and arctangent (assuming that the broad feature about 7 eV above the white line can be attributed to Eu3+)35, an average valence of +2.03 for Eu was obtained. XANES spectra were measured as function of temperature, and confirm the absence of valence fluctuations and drastic changes in the local crystalline environment of the europium atoms (Supplementary Note 9). The sizable XMCD signals observed at both Eu L2 and L3 edges are comparable with more ionic europium materials whose divalent Eu2+ configuration is well established36, unambiguously demonstrating the FM order in Eu2In and that Eu-4f states carry about 7.0 μB Eu−1. The saturation magnetization larger than 14 μB (Eu2In)−1 should accordingly be ascribed to non-negligible magnetic moments on Eu-5d,6 s and In-5p states. The XMCD of Eu2In appears similar or larger than other europium intermetallics such as Eu8Ga16Ge30 (ref.37), but due to the inapplicability of optical sum-rules to derive the 5d magnetic moment for rare earths, a more quantitative estimate of the magnetic polarization of the conduction states will be gained through electronic structure calculations.
Specific electronic structure of Eu2In
FOMTs in solids with no change of symmetry and no substantial rearrangement of atomic bonding are rare. They have been observed in several transition-metal based compounds, but the underlying mechanisms are often challenging to address. Examples of magnetoelastic FOMTs based on rare-earth are even scarcer. One example we are aware of is Gd5Ge3.5Sb0.5, which shows a significant volume discontinuity without change in crystal symmetry and only small changes in interatomic distances between two polymorphs38. Though quite unique (no bond breaking or atomic layer displacements), the mechanisms at the origin of the FOMT remain specific to this 5:4 class of materials24,39. To get insight into the origin of the magnetism and the unusual FOMT in the virtually unexplored Eu2In, we turned toward electronic structure calculations.
FM calculations are shown in Fig. 5. Alternative calculations with opposite magnetic moments of Eu-I and Eu-II (an almost zero net magnetization used to approximate the PM state) are provided in Supplementary Note 10. Total energy of FM-Eu2In is lower by 137.7 meV f.u.−1 than the approximated PM-Eu2In, confirming the FM ground state. The 6 s, 6p, and 5d states of Eu are nearly completely hybridized with the more populated 5p states of In, in such a way that the Eu-s,p,d states fall within the envelope of the In-p states. Due to the strong hybridization of the electronic states in Eu2In, the Eu-5d states become partially occupied (~0.8 e Eu−1), rather than being empty as would have been anticipated for Eu2+ in the 4f75d0 configuration. The Eu-4f states are centered just below −2 eV, and also hybridize with the p states of In and, consequently, Eu-s,p,d states. Thus, the Eu-4f states in Eu2In are located deeper than in most EuTMX ternaries with TM a transition metal and X a p-block element. This is in line with the absence of mixed valence or valence transition of Eu in Eu2In but in contrast to EuTMX materials40,41.
The electronic structure of Eu2In also contrasts with the closely related Gd2In, where the Gd 4f states are located much deeper42,43. X-ray photoelectron spectroscopy measurements (at room temperature), Fig. 5b, show a peak at binding energy of about 2 eV, which is typical of rare-earth 4f states44 and bring direct experimental support to our predicted energy position for Eu-4f in Eu2In. The Fermi level (EF) is located on the edge of a pseudo-gap in the majority channel, while it corresponds to high Eu-5d and In-5p DOS in the minority channel. In the approximated PM state, EF falls inside a minor valley surrounded by high Eu-5d and In-5p DOS. High DOS near EF is often believed to favor instabilities in the electronic structure and magnetism when external parameters, such as temperature, magnetic field, or pressure are altered. In particular, electronic configurations which may lead to significant DOS changes at EF (and its vicinity) are considered to be at the origin of the magnetoelastic FOMTs in most prototypical transition metal-based compounds10,14,45.
Table 1 shows the magnetic moments in FM calculations. In contrast to the approximated PM calculations, there is a development of a strong exchange splitting on the hybridized Eu-5d and In-5p states in the FM state. Nearly identical (~0.67 eV) Eu-5d and In-5p exchange splitting across the Fermi level leads to similar magnetic moments of 0.22 and 0.24 μB atom−1, on Eu-5d and In-5p states, respectively. These values are in line with the experimental saturation magnetization, when the Eu-4f moment (~7.0 μB atom−1) is added, and with the large XMCD signal observed at the Eu L2,3 edges (2p → 5d). As argued below, this unusually large Eu-5d and In-5p exchange splitting is likely the key ingredient for the emergence of first-order PM↔FM transition in Eu2In.
Stoner criterion, calculated as the product of exchange splitting (in eV) at the Fermi level and DOS (in states eV−1 atom−1), is 0.76 for Eu-I 5d states—close to the unity threshold—indicating that the Eu-5d moments are metastable and may act as a trigger for the transition. The important role, the peculiar electronic structure of Eu2In plays, can be further exemplified by a stark contrast between FM Eu2In and AFM Gd2In and Eu2Sn compounds with similar compositions and related crystal structures. In the hexagonal Gd2In, the Gd-5d states develop magnetic polarization, but the In-s and In-p states are not polarized, and therefore play little, if any, part in its magnetism42,43. In AFM Eu2Sn that adopts the same crystal symmetry as Eu2In, the addition of a single p electron on Sn shifts the whole DOS so that EF falls into a deep pseudo-gap, Eu-5d and Sn-5p magnetic polarization weakens considerably, hence there is no first-order transition or ferromagnetism (see Supplementary Note 11 for more details on Eu2Sn).
In summary, an intriguing mechanism resulting in a magnetoelastic first-order FM transition is discovered in Eu2In. This transition is associated with a large latent heat while thermal and magnetic hystereses, as well as lattice discontinuities are extremely small, which leads to a remarkable combination of properties. With Eu2In we show that instabilities leading to FOMTs can be realized in rare-earth intermetallics in the absence of any structural or valence fluctuations. Electronic structure calculations indicate that key elements for the Eu2In FM transition are the filling of the Eu-5d states by hybridization with other Eu states and In-5p states, and the development of a large exchange splitting on Eu-5d and In-5p states. The strong hybridization between Eu-5d and In-5p states near the Fermi energy affects the long-range exchange interaction between Eu atoms, triggering the FM transition. Demonstrating a strong interplay between a p-block metal or a metalloid and rare-earth elements not only broadens a very exclusive class of materials, but it also highlights a favorable route to generate magnetoelastic FOMTs and paves the way for further developments in functional magnetic materials.
Methods
Sample synthesis
Polycrystalline Eu2In samples were prepared by melting stoichiometric quantities of elemental starting materials followed by annealing in a conventional resistive furnace. The high-purity europium metal was supplied by the Materials Preparation Center of the Ames Laboratory. All operations and handling of the samples were carried out in Ar glovebox. The starting materials were sealed in a Ta crucible under a partial atmosphere of ultrapure Ar. The crucible was then sealed in a quartz tube backfilled with helium gas. The sample was first melted several times at 900 °C in a resistance furnace, flipping the sample tube between each melting. Then the sample was annealed at 650 °C for 24 h. The resulting sample has a grey metallic appearance, and is relatively brittle. Exposure to air leads to darkening of the surface within a few hours. The results presented in this communication originate from the same sample, but different samples prepared to ensure reproducibility demonstrate comparable properties.
Crystal structure characterization
Temperature-dependent powder x-ray diffraction experiments were carried out on a rotating anode Rigaku TTRAX system using Mo Kα radiation. This system was modified to reach low temperatures using a cold finger He cryostat and to allow in situ application of magnetic field46. The powder consisting of particles smaller than 22 μm was mixed with petroleum jelly, then deposited on a copper sample holder. Room temperature XRD characterization was performed using a PANalytical diffractometer employing Cu Kα1 radiation. The powder XRD patterns were refined by the Rietveld method using the Fullprof software. The VESTA software has been used for structure visualization47. X-ray photon electron spectroscopy (XPS) measurements were performed at room temperature after in situ cleaning by ion bombardment of the surface of a bulk piece of Eu2In in ultra-high vacuum.
Physical property measurements
The magnetic measurements were carried out in a 7 T magnetic property measurement system MPMS (Quantum Design) magnetometer equipped with a reciprocating sample option (RSO). A quartz straw was used as a sample holder (preparation in Ar glovebox). The MCE up to 7 T was derived by applying the Maxwell equation to isofield magnetization data. The magnetic measurements under pressure were carried out using a Cu-Be mechanical cell manufactured by HMD (type CC-SPr-8.5D-MC4). The inner diameter of the cell was 2.2 mm, and lead was used as an internal manometer. Electrical resistivity measurements were performed using the AC transport option of a 14 T physical property measurement system PPMS (Quantum Design). The heat capacity measurements were performed using the heat capacity option of the same 14 T PPMS system. The sample was mounted using Apiezon N grease. Outside the transition region, the measurements were performed with the usual “2τ analysis” using 1% temperature rise and 2τ measurement time. The temperature increment was 0.5 K in the temperature range 2.0–15 K, then 1 K increment between 16 and 100 K, finally 2 K increment above. For the single pulse experiments, a temperature rise of 4 K was targeted, which was found sufficient to fully cover the transition range in zero magnetic field, but only partially covers the transition widths at higher magnetic fields.
X-ray absorption spectroscopy
X-ray absorption and magnetic circular dichroism experiments were carried out at the ID12 beamline of the European Synchrotron Radiation Facility, ESRF, France48. The experimental end station is equipped with a cold finger cryostat allowing a control of the temperature in the range 2.1–300 K, as well as magnetic field up to 17 T. The x-ray absorption spectra were recorded in fluorescence with a Si photodiode covered with polypropylene film and mounted in backscattering geometry. The x-ray absorption and consequently XMCD spectra were corrected for self-absorption effects. The XMCD spectra were obtained as difference between x-ray absorption spectra with opposite helicities of the incoming x-rays, and for two opposite directions of the magnetic field.
Computational details
First-principles electronic structure calculations were performed using the experimental crystal parameters. The local spin density approximation including onsite 4f electron correlation49 and spin orbit coupling (LSDA + U + SOC) approach has been employed. This approach is implemented in the tight binding linear muffin tin orbital (TB-LMTO, within the atomic sphere approximation, ASA) and full potential linear augmented plane wave (FP-LAPW) band structure methods50,51. Both approaches yield identical results, and those reported here are derived from TB-LMTO-ASA. Electronic structure calculations performed with different values of onsite 4f-electron correlation parameter (U) ranging from 1 eV to 7 eV. The results shown here are with U = 6.7 eV and onsite 4f-electron exchange parameter J = 0.7 eV, which are known parameters for Gd-based systems. The basis sets consisted of Eu-s, p, d, f and In-s, p, d orbitals. The calculated 4f and 5d orbital moments in Eu2In are within ~0.03 μB, and were thus neglected. The k-space integrations have been performed with 16 × 16 × 16 Brillouin zone mesh, which was sufficient for the convergence of total energies and magnetic moments.
Data availability
The data that support the findings of this study are available from the corresponding author F.G. upon reasonable request.
References
Kittel, C. Introduction to Solid State Physics. 8th edn, (Wiley, Hoboken NJ, 2005).
Gutfleisch, O. et al. Magnetic materials and devices for the 21st century: stronger, lighter, and more energy efficient. Adv. Mater. 23, 821–842 (2011).
Gschneidner, K. A. Jr, Pecharsky, V. K. & Tsokol, A. O. Recent developments in magnetocaloric materials. Rep. Prog. Phys. 68, 1479–1539 (2005).
Liu, J., Gottschall, T., Skokov, K. P., Moore, J. D. & Gutfleisch, O. Giant magnetocaloric effect driven by structural transitions. Nat. Mater. 11, 620–626 (2012).
Smith, A. et al. Materials challenges for high performance magnetocaloric refrigeration devices. Adv. Energy Mater. 2, 1288–1318 (2012).
Moya, X., Kar-Narayan, S. & Mathur, N. D. Caloric materials near ferroic phase transitions. Nat. Mater. 13, 439–450 (2014).
de Bergevin, F. & Muldawer, L. Etude cristallographique de certains alliages de fer rhodium. C. R. Hebd. Séances Acad. Sci. 252, 1347–1349 (1961).
Lewis, L. H., Marrows, C. H. & Langridge, S. Coupled magnetic, structural, and electronic phase transitions in FeRh. J. Phys. D: Appl. Phys. 49, 323002 (2016).
Hu, F. X. et al. Influence of negative lattice expansion and metamagnetic transition on magnetic entropy change in the compound LaFe11.4Si1.6. Appl. Phys. Lett. 78, 3675–3677 (2001).
Fujita, A., Fujieda, S., Hasegawa, Y. & Fukamichi, K. Itinerant-electron metamagnetic transition and large magnetocaloric effects in La(FexSi1−x)13 compounds and their hydrides. Phys. Rev. B 67, 104416 (2003).
Tegus, O., Brück, E., Buschow, K. H. J. & de Boer, F. R. Transition-metal-based magnetic refrigerants for room-temperature applications. Nature 415, 150–152 (2002).
Guillou, F., Porcari, G., Yibole, H., van Dijk, N. & Brück, E. Taming the first-order transition in giant magnetocaloric materials. Adv. Mater. 26, 2671–2675 (2014).
Kuz’min, M. D. & Richter, M. Mechanism of the strong magnetic refrigerant performance of LaFe13−xSix. Phys. Rev. B 76, 092401 (2007).
Dung, N. H. et al. Mixed magnetism for refrigeration and energy conversion. Adv. Energy Mater. 1, 1215–1219 (2011).
Palenzona, A. The crystal structure and lattice constants of RE2In and some RE5In3 compounds. J. Less-Common Met. 16, 379–384 (1968).
Gamari-Seale, H., Anagnostopoulos, T. & Yakinthos, J. K. Magnetic characteristics of rare-earth indium R2In (R=Y, Nd, Sm, Gd, Tb, Dy, Ho, Er, and Tm) intermetallic compounds. J. Appl. Phys. 50, 434–437 (1979).
Fornasini, M. L. & Cirafici, S. Crystal structures of Eu3Ga2, EuGa, Eu2In, EuIn and EuIn4. Z. Krist. 190, 295–304 (1990).
Flahaut, J. & Thévet, F. Filiation structurale des composés de formule générale AB2: Etude comparée des types Co2Si, Co2P, PbCl2, et SbSI. J. Solid State Chem. 32, 365–376 (1980).
Pecharsky, V. K. & Gschneidner, K. A. Jr. Heat capacity near first order phase transitions and the magnetocaloric effect: an analysis of the errors, and a case study of Gd5Si2Ge2 and Dy. J. Appl. Phys. 86, 6315–6321 (1999).
Hardy, V., Bréard, Y. & Martin, C. Derivation of the heat capacity anomaly at a first-order transition by using a semi-adiabatic relaxation technique. J. Phys. Condens. Matter 21, 075403 (2009).
Pecharsky, V. K., Gschneidner, K. A. Jr. & Fort, D. Superheating and other unusual observations regarding the first order phase transition in Dy. Scr. Mater. 35, 843–848 (1996).
Kurniawan, M., Perrin, A., Xu, P., Keylin, V. & McHenry, M. E. Curie temperature engineering in high entropy magnetic alloys for magnetocaloric applications. IEEE Mag. Lett. 7, 1–5 (2016).
Jones, N. J., Ucar, H., Ipus, J. J., McHenry, M. E. & Laughlin, D. E. The effect of distributed exchange parameters on magnetocaloric refrigeration capacity in amorphous and nanocomposite materials. J. Appl. Phys. 111, 07A334–336A334 (2012).
Pecharsky, V. K. & Gschneidner, K. A. Jr Giant magnetocaloric effect in Gd5Si2Ge2. Phys. Rev. Lett. 78, 4494–4497 (1997).
Pecharsky, V. K. & Gschneidner, K. A. Jr. Some common misconceptions concerning magnetic refrigerant materials. J. Appl. Phys. 90, 4614–4622 (2001).
Chernyshov, A. S. et al. Magnetic and magnetocaloric properties and the magnetic phase diagram of single-crystal dysprosium. Phys. Rev. B 71, 184410 (2005).
Brück, E., Yibole, H. & Zhang, L. A universal metric for ferroic energy materials. Philos. Trans. R. Soc. A 374, 20150303 (2016).
Griffith, L. D., Mudryk, Y., Slaughter, J. & Pecharsky, V. K. Material-based figure of merit for caloric materials. J. Appl. Phys. 123, 034902 (2018).
Pecharsky, V. K., Holm, A. P., Gschneidner, K. A. Jr. & Rink, R. Massive magnetic-field-induced structural transformation in Gd5Ge4 and the nature of the giant magnetocaloric effect. Phys. Rev. Lett. 91, 197204 (2003).
Gschneidner, K. A. Jr, Mudryk, Y. & Pecharsky, V. K. On the nature of the magnetocaloric effect of the first-order magnetostructural transition. Scr. Mater. 67, 572–577 (2012).
Bhattacharya, K., Conti, S., Zanzotto, G. & Zimmer, J. Crystal symmetry and the reversibility of martensitic transformations. Nature 428, 55–59 (2004).
Cui, J. et al. Combinatorial search of thermoelastic shape-memory alloys with extremely small hysteresis width. Nat. Mater. 5, 286–290 (2006).
Dan’kov, S. Yu, Tishin, A. M., Pecharsky, V. K. & Gschneidner, K. A. Jr. Magnetic phase transitions and the magnetothermal properties of gadolinium. Phys. Rev. B 57, 3478 (1998).
Tishin, A. M. Magnetocaloric effect in strong magnetic fields. Cryogenics 30, 127–136 (1990).
Krishnamurthy, V. V. et al. Ferrimagnetism in EuFe4Sb12 due to the interplay of f-electron moments and a nearly ferromagnetic host. Phys. Rev. Lett. 98, 126403 (2007).
Rogalev, A. & Goulon, J. X-ray magnetic circular dichroism of model Heisenberg ferromagnets. AIP Conf. Proc. 506, 336 (2000).
Krishnamurthy, V. V. et al. Temperature dependence of Eu 4f and Eu 5d magnetizations in the filled skutterudite EuFe4Sb12. Phys. Rev. B 79, 014426 (2009).
Chernyshov, A. S. et al. Magnetostructural transition in Gd5Sb0.5Ge3.5. Phys. Rev. B 80, 184416 (2009).
Haskel, D. et al. Role of Ge in bridging ferromagnetism in the giant magnetocaloric Gd5(Ge1−xSix)4 alloys. Phys. Rev. Lett. 98, 247205 (2007).
Michels, G. et al. Temperature induced valence instabilities in ternary Eu-pnictides: a comprehensive view. Z. Phys. B 98, 75–88 (1995).
Pöttgen, R. & Johrendt, D. Equiatomic intermetallic europium compounds: syntheses, crystal chemistry, chemical bonding, and physical properties. Chem. Mater. 12, 875–897 (2000).
Singh, V., Bhattacharyya, A., Majumdar, S. & Dasgupta, I. A theoretical and experimental study of magnetism in Gd2In. J. Appl. Phys. 111, 053709 (2012).
Kamali Sarvestani, N., Ahmad Ketabi, S. & Yazdani, A. Electro-mechanical character of Gd and Gd2In and possibility of a Kondo-like behavior in Gd2In. J. Alloy. Compd. 613, 62–66 (2014).
Vercaemst, R. et al. A detailed XPS study of the rare earth compounds EuS and EuF3. J. Electron. Spectrosc. Relat. Phenom. 74, 45–56 (1995).
Gray, A. X. et al. Electronic structure changes across the metamagnetic transition in FeRh via hard X-ray photoemission. Phys. Rev. Lett. 108, 257208 (2012).
Holm, A. P., Pecharsky, V. K., Gschneidner, K. A. Jr, Rink, R. & Jirmanus, M. N. X-ray powder diffractometer for in situ structural studies in magnetic fields from 0 to 35 kOe between 2.2 and 315 K. Rev. Sci. Instrum. 75, 1081–1088 (2004).
Momma, K. & Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 44, 1272–1276 (2011).
Rogalev, A. & Wilhelm, F. Magnetic circular dichroism in the hard X-ray range. Phys. Met. Metallogr. 116, 1285–1336 (2015).
Anisimov, V. I., Aryasetiawan, F. & Lichtenstein, A. I. First-principles calculations of the electronic structure and spectra of strongly correlated systems: the LDA+U method. J. Phys. Condens. Matter 9, 767 (1997).
Andersen, O. K. & Jepsen, O. Explicit, first-principles tight-binding theory. Phys. Rev. Lett. 53, 2571 (1984).
Blaha, P. et al. WIEN2k, An Augmented Plane Wave+Local Orbitals Program for Calculating Crystal Properties. (Karlheinz Schwarz, Techn. Universität Wien, Austria, 2001).
Wada, H. & Tanabe, Y. Giant magnetocaloric effect of MnAs1−xSbx. Appl. Phys. Lett. 79, 3302–3304 (2001).
Nishihara, Y. & Yamaguchi, Y. Magnetic phase transitions in itinerant electron magnets Hf1−xTaxFe2. J. Phys. Soc. Jpn. 52, 3630–3636 (1983).
Trung, N. T., Zhang, L., Caron, L., Buschow, K. H. J. & Brück, E. Giant magnetocaloric effects by tailoring the phase transitions. Appl. Phys. Lett. 96, 172504 (2010).
Radaelli, P. G. et al. Simultaneous structural, magnetic, and electronic transitions in La1−xCaxMnO3 with x=0.25 and 0.50. Phys. Rev. Lett. 75, 4488–4491 (1995).
Acknowledgements
The Ames Laboratory is operated for the U.S. Department of Energy (DOE) by Iowa State University of Science and Technology under contract No. DE-AC02-07CH11358. This work was supported by the Office of Science of the U.S. DOE, Division of Materials Sciences and Engineering, Office of Basic Energy Sciences. We thank T. Hackett for his preliminary electronic structure calculations. We acknowledge the European Synchrotron Radiation Facility for provision of synchrotron radiation at the ID12 beamline.
Author information
Authors and Affiliations
Contributions
All authors contributed equally to this work, discussed the results and commented on the manuscript at all stages. The work was initiated by V.K.P and F.G. F.G. carried out the sample synthesis and physical characterizations, A.K.P. contributed to the high pressure magnetization measurements, Y.M. the temperature dependent XRD, D.P. conducted the first principle calculations, F.W. and A.R. the XAS/XMCD measurements. The work was supervised by V.K.P.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Guillou, F., Pathak, A.K., Paudyal, D. et al. Non-hysteretic first-order phase transition with large latent heat and giant low-field magnetocaloric effect. Nat Commun 9, 2925 (2018). https://doi.org/10.1038/s41467-018-05268-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-018-05268-4
This article is cited by
-
Magnetic Phase Transitions in R5Pd2 (R = Ho, Dy, Dy0.6Gd0.4) Compounds
Journal of Superconductivity and Novel Magnetism (2023)
-
Giant low-field magnetocaloric effect of (Er,Y)Cr2Si2 compounds at ultra-low temperatures
Science China Materials (2023)
-
Introduction to magnetic refrigeration: magnetocaloric materials
International Journal of Air-Conditioning and Refrigeration (2023)
-
Materials, physics and systems for multicaloric cooling
Nature Reviews Materials (2022)
-
Tailoring the magneto-structural coupling in Mn1−xZrxCoGe alloys
Journal of Materials Science (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.