Introduction

Excitons in monolayer semiconductors, such as transition metal dichalcogenides (TMDs), are endowed with spin and valley degrees of freedom1,2,3,4,5. Recent advances in van der Waals heterojunctions formed by vertical stacking of different TMD monolayers further enable the generation of carriers in different layers with enriched valley configurations for exploring new spin/valleytronic applications6,7,8. Van der Waals heterobilayers (hBLs) of TMDs feature type-II band alignment, which can separate photoexcited electrons and holes into different layers through ultrafast charge transfer9,10,11,12,13 and can host long-lived interlayer excitons due to their spatially indirect nature6,7,8. Inheriting from the coupled spin–valley physics in the constituent monolayers, TMD hBLs further enrich the interplay of internal degrees of freedom, including the spin and valley pseudospin of electrons and holes confined in different monolayers3. In TMD homobilayers, the interplay of spin and valley pseudospins can lead to numerous exotic phenomena, such as the spin–layer locking effect14, the magnetoelectric effect15, and the electric-field-induced Zeeman-type splitting16. Recently, valley-specific interlayer excitons with long valley lifetimes have been realized in manually stacked WSe2/MoSe2 hBLs7. The valley-specific interlayer excitons were found to emit circularly polarized photoluminescence (PL) that retains the helicity of optical excitations. Theory has predicted that the valley optical selection rules and dipole strength of interlayer excitons are sensitive to the interlayer atomic registry17, 18. However, manually stacked hBLs are generally incommensurate with inevitable interlayer twist and/or lattice mismatch, which could lead to a periodic variation of the atomic registry between individual monolayers, i.e., the so-called Moiré superlattice19, 20. Conventional optical measurements are unable to resolve such variations in the atomic registry even for a very small twist angle (θ≈0.5°), where the Moiré periodicity (~40 nm) of hBLs can exceed the exciton radius (~1–2 nm), but remains much smaller than the typical spatial resolution (~1 μm) of optical measurements. Recently, periodical modulations in the local bandgap of rotationally aligned MoS2/WSe2 hBLs have been resolved by scanning tunneling microscopy and spectroscopy21. However, the experimental connection between the valley optical selection rules of interlayer excitons and the interlayer atomic registry of hBLs is still missing thus far.

Here we address how the interlayer atomic registry impacts the optical transition and polarization properties of interlayer excitons by using commensurate WSe2/MoSe2 hBLs formed by direct growth using chemical vapor deposition (CVD). The commensurate interlayer stacking with rotational alignment and long-range order facilitates us to unveil the valley optical selection rule of interlayer excitons in TMD hBLs. We observe circularly polarized photoluminescence (PL) from interlayer excitons, but with a helicity opposite to the optical excitation. The negative circular polarization arises from the quantum interference imposed by interlayer atomic registry, giving rise to distinct polarization selection rules for interlayer excitons. The impacts of stacking order on the formation processes of bright interlayer exciton states with different valley configurations are discussed. Selective excitations at different monolayers further demonstrate the optical addressability of interlayer excitons with different valley configurations and polarization helicities, providing a new scheme for exploring spin/valleytronic applications based on van der Waals heterostructures.

Results

Epitaxially grown commensurate WSe2/MoSe2 heterobilayers

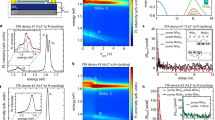
Our samples were grown on sapphire substrates (see Methods), containing WSe2/MoSe2 hBLs with parallel (AA) and antiparallel (AB) stacking, which have been identified by second harmonic generation (SHG) and annular dark-field (ADF) scanning transmission electron microscopy (STEM). In general, the hBLs consist of a monolayer WSe2 covering on top of a monolayer WSe2–MoSe2 lateral heterojunction22, 23 formed by a MoSe2 inner triangle with WSe2 epitaxially grown at the outer region. Figure 1a, b shows the optical images of hBL flakes with AA and AB stacking, respectively. PL, Raman, and atomic force microscopy characterizations (Supplementary Figs. 1, 2 and Supplementary Note 1) conclude that the inner triangles of both types are WSe2/MoSe2 hBLs, while the outer regions of AA (AB) stacking are monolayer (bilayer) WSe2, as schematically shown in Fig. 1c, d. We identified the stacking orientations (twist angle θ) by polarization-resolved SHG (Supplementary Fig. 3). In Fig. 1e, f, we show the SHG intensity maps of the AA- and AB-stacked hBLs, as shown in Fig. 1a, b, respectively. The strongly enhanced (suppressed) SHG intensity in the hBL regions is a clear evidence of AA (AB) stacking with θ=0° (θ=60°), due to the constructive (destructive) interference of SH fields from the individual layers24. We noted that the SHG intensity in the AB-stacked hBL region is not fully suppressed as that in the WSe2 bilayer region. The residual SHG intensity might be caused by the different SHG efficiencies of the two materials and the nonvanishing vertical dipole moments in the hBL regions excited and collected through the large-numerical-aperture objective. The atomic registries of the AA and AB stacking have been further identified by ADF STEM. As shown in Fig. 1g, h, the AA-stacked hBLs exhibit the 3R-like stacking (with Se atoms on top of Mo atoms), while the AB-stacked hBLs show the 2H-like stacking, as illustrated in Fig. 1i, j. Selected-area electron diffraction in the hBL region (~1-μm diameter) shows only one set of diffraction patterns (Supplementary Fig. 4 and Supplementary Note 2), which confirms that the WSe2/MoSe2 hBLs formed directly by CVD growth exhibit long-range stacking order without interlayer twists. The correlation between the morphology and stacking orientation thus facilitates the investigation of how the atomic registry affects the optical properties of WSe2/MoSe2 hBLs.

Fig. 1
figure 1

WSe2/MoSe2 hBLs with AA and AB stacking. a, b Optical images of hBLs with AA (a) and AB (b) stacking. The scale bar is 3 μm. c, d Schematics of heterostructures shown in a and b, respectively. e, f SHG intensity mapping for the hBLs with AA (e) and AB (f) stacking. The scale bar is 3 μm. g, h ADF STEM images of the hBLs with AA (g) and AB (h) stacking. The insets are filtered images. The scale bar is 0.5 nm. i, j Schematics of the top and side views of the atomic registries of AA (i) and AB (j) stacking, according to the ADF STEM results. The AA stacking corresponds to the 3R-like stacking (i), with Se atoms of WSe2 on top of Mo atoms of MoSe2. The AB stacking corresponds to the 2H-like stacking (j), with W (Se) atoms of WSe2 on top of Se (Mo) atoms of MoSe2 layer

Full size image

Stacking-dependent interlayer excitons in WSe2/MoSe2 heterobilayers

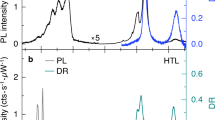
The WSe2/MoSe2 hBLs are known to exhibit a type-II band alignment25, 26 with the conduction band minimum (valence band maximum) located in the MoSe2 (WSe2) layer (Fig. 2a). Coulomb-bound electrons and holes localized in different monolayers thus form interlayer excitons (Fig. 2b). Figure 2c shows the room-temperature PL spectra for the monolayer WSe2, MoSe2, and the hBL with AB stacking. The PL emission at 1.62 eV (1.55 eV) corresponds to the excitonic states in monolayer WSe2 (MoSe2)27,28,29,30. In the hBL regions, the intralayer exciton peaks are also observed, but the intensities were quenched by a factor of ~50–100 due to the efficient interlayer carrier transfers9,10,11,12,13. In addition, we observed a lower energy peak at 1.33 eV, which is attributed to the interlayer exciton (XI) recombination6, 7. Specifically, we found that the XI peak of AA-stacked hBLs is redshifted by ~70 meV in comparison with that of AB-stacked hBLs (Fig. 2d and Supplementary Fig. 5). Band structure calculations based on density functional theory (DFT) show that the MoSe2 bands in AA stacking exhibit a rigid downshift by ~60 meV in comparison with those in AB stacking (Supplementary Fig. 6 and Supplementary Note 3). The enlarged valence band offset and the spin splitting in the MoSe2 conduction band thus account for the redshift of the XI peak in AA stacking31. Apart from XI, we found that the energies of intralayer excitons also change systematically with the atomic registry (Fig. 2e). The observed energy shifts of A and B excitons in monolayer WSe2 (\({\mathrm{X}}_{\mathrm{A}}^{\mathrm{W}}\) and \({\mathrm{X}}_{\mathrm{B}}^{\mathrm{W}}\)) and MoSe2 (\({\mathrm{X}}_{\mathrm{A}}^{{\mathrm{Mo}}}\) and \({\mathrm{X}}_{\mathrm{B}}^{{\mathrm{Mo}}}\)) agree qualitatively with the calculated band gap variation in hBLs with AA and AB stacking (Supplementary Fig. 7 and Supplementary Note 4). It has been established that the Moiré periodicity of incommensurate hBLs can induce band-gap modulations in the constituent monolayers20, 21. However, such periodicity cannot be resolved optically due to the limited spatial resolution. The agreement between the variations in the intralayer exciton energies and the calculated band gaps also suggests that the investigated WSe2/MoSe2 hBLs exhibit long-range stacking orders and well-defined atomic registries.

Fig. 2
figure 2

Interlayer excitons in WSe2/MoSe2 hBLs with AA and AB stacking. a The type-II band alignment of WSe2/MoSe2 hBLs. b Schematics of interlayer excitons with electrons (e) and holes (h) located in the MoSe2 and WSe2 layers, respectively. c PL spectra for monolayer WSe2, MoSe2, and the WSe2/MoSe2 hBL with AB stacking. The interlayer exciton XI is observed at 1.33 eV. d A comparison of XI peaks in hBLs with AA and AB stacking. The PL spectra shown in c and d were measured at room temperature (T=300 K). e Differential reflectance spectra ΔR/R for monolayer (ML) WSe2, ML MoSe2, and hBLs with AA and AB stacking. The ΔR/R spectra were measured at T=4 K. \({\mathrm{X}}_{\mathrm{A}}^{{\mathrm{Mo}}}\) and \({\mathrm{X}}_{\mathrm{A}}^{\mathrm{W}}\)(\({\mathrm{X}}_{\mathrm{B}}^{{\mathrm{Mo}}}\) and \({\mathrm{X}}_{\mathrm{B}}^{\mathrm{W}}\)) denote A (B) excitons in MoSe2 and WSe2, respectively. For each stacking, two spectra from different hBL flakes are displayed in order to demonstrate the consistent spectral features

Full size image

Valley polarization of interlayer excitons

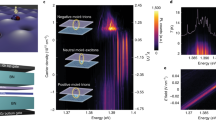
We examined the effect of atomic registry on the polarization properties of XI. Figure 3a shows the polarization-resolved PL spectra measured at T=4 K for the AA-stacked hBL using σ+ excitations at 1.96 eV (Supplementary Fig. 8 for AB hBLs). The intralayer exciton PL from the MoSe2 and WSe2 layers exhibits a stronger σ+ PL component, indicative of generating valley excitons at +K valleys in each layer by the above-gap σ+ excitations1, 2. These intralayer excitons then relax to form XI through the electron and hole transfers across the WSe2/MoSe2 interface. If the spin and/or valley indices of carriers are preserved after interlayer transfer, valley-specific XI can be formed. Interestingly, we found that the XI PL also exhibits circular polarization, but with an opposite helicity, i.e., a stronger σ− PL component under σ+ excitations. We define the degree of circular polarization as PC = (I+ − I−)/(I+ + I−), where I+ (I–) denotes the intensity of co-polarized (cross-polarized) PL component with the excitation. As shown in Fig. 3a, the intralayer exciton peak in WSe2 (MoSe2) shows \(P_{\mathrm{C}} \simeq 36\%\) (\(P_{\mathrm{C}} \simeq 18\%\)), while the XI peak exhibits \(P_{\mathrm{C}} \simeq - 7\%\). Using resonant excitation with the A exciton energy of MoSe2 (1.64 eV) markedly increases the Pc of XI up to \(\simeq - 23\%\) (Fig. 3b). Using σ+ excitations at the MoSe2 layer in AB-stacked hBLs, the XI PL also exhibits a stronger σ− PL component, but with a smaller \(P_{\mathrm{C}} \simeq - 9\%\).

Fig. 3
figure 3

Valley polarization of interlayer excitons. a Top: polarization-resolved PL spectra for the AA-stacked hBL using σ+ excitation at 1.96 eV. Bottom: the degree of circular polarization PC. b Polarization-resolved PL spectra near the XI peak using σ+ excitation at 1.64 eV (MoSe2) in AA- (top) and AB- (bottom) stacked hBLs. c The atomic registries and the phases associated with the interlayer transition dipoles in AA and AB stacking. A distinct phase factor \(e^{i{\mathrm{\tau }}{\mathbf{K}} \cdot {\mathbf{r}}_n}\) is associated with each interlayer transition dipoles between the nearest Mo and W atoms in different layers. d Left: the formation of \({\mathrm{X}}_{ + + }^{\mathrm{I}}\) state in AA-stacked hBLs using σ+ excitations at +K valleys in MoSe2 and WSe2 layers. Right: the formation of the interlayer dark state in AB-stacked hBLs using σ+ excitations at both MoSe2 and WSe2 layers. Red and blue lines are WSe2 and MoSe2 bands, respectively. Solid and dotted lines represent bands with different spins. Vertical arrows indicate optical excitations. Gray arrows represent spin-conserving interlayer transfer to the lowest energy band

Full size image

Interlayer quantum interference

The negative circular polarization arises from the interlayer quantum interference imposed by the atomic registry between the WSe2 and MoSe2 layers. We analyze the polarization properties of XI based on the theory proposed by Yu et al.17. The valley configurations of XI can be classified as \({\mathrm{X}}_{\tau \prime \tau }^{\mathrm{I}}\), i.e., electron (hole) at τ′K (τK) valley in the MoSe2 (WSe2) layer, where τ',τ = ±1 are the valley index. The Bloch function of the conduction (valence) band edge at τ'K (τK) valley consists predominantly of the \(d_{{\mathrm{z}}^2}\) (\(d_{{\mathrm{x}}^2 - {\mathrm{y}}^2} + i\tau d_{{\mathrm{xy}}}\)) orbitals with a magnetic quantum number m = 0 (m = 2τ) on Mo (W) sites in the MoSe2 (WSe2) layer. The interlayer transition dipole of \({\mathrm{X}}_{\tau \prime \tau }^{\mathrm{I}}\) can be expressed as \({\mathbf{D}}_{\tau \prime \tau } \cong \langle\psi _{{\mathrm{v}},\tau {\mathbf{K}}}^{\mathrm{W}}\left( {\mathbf{r}} \right){\mathrm{|}}{\hat{\mathbf D}}{\mathrm{|}}\psi _{{\mathrm{c}},\tau \prime {\mathbf{K}}}^{{\mathrm{Mo}}}\left( {\mathbf{r}} \right)\rangle\), which connects the orbitals on Mo and W sites in different layers17. As a first approximation, we consider the nearest-neighbor interlayer transition dipoles between Mo and W orbitals as shown in Fig. 3c. The total transition dipole is the superposition of the three dipoles associated with a distinct phase factor \(e^{ - i\tau {\mathbf{K}} \cdot {\mathbf{r}}_n}\), i.e., \({\mathbf{D}}_{\tau \prime \tau } \propto \mathop {\sum }\limits_{n = 1,2,3} e^{ - i\tau {\mathbf{K}} \cdot {\mathbf{r}}_n}\left\langle {d_{m = 2\tau }^{\mathrm{W}}({\mathbf{r}}_n){\mathrm{|}}{\hat{\mathbf D}}{\mathrm{|}}d_{m = 0}^{{\mathrm{Mo}}}(0)} \right\rangle\), where r n is the vector pointing from W to Mo sites (Supplementary Note 5). The quantum interference imposed by the atomic registry thus gives rise to a distinct polarization selection rule for XI. In general, the interlayer transition dipole also acquires contributions from coupling to intralayer excitons via interlayer hopping17. Symmetry analysis indicates that the σ+ and σ− components of \({\mathbf{D}}_{\tau \prime \tau }\) are17

$$\begin{array}{l}{\mathbf{e}}_\tau \cdot {\mathbf{D}}_{\tau \prime \tau } \propto e^{ - i\tau {\mathbf{K}} \cdot {\mathbf{r}}_1} + e^{ - i\tau {\mathbf{K}} \cdot {\mathbf{r}}_2} + e^{ - i\tau {\mathbf{K}} \cdot {\mathbf{r}}_3},\\ {\mathbf{e}}_{ - \tau } \cdot {\mathbf{D}}_{\tau \prime \tau } \propto e^{ - i\tau {\mathbf{K}} \cdot {\mathbf{r}}_1} + e^{ - i\tau({\mathbf{K}} \cdot {\mathbf{r}}_2 + 2\pi /3)} + e^{ - i\tau({\mathbf{K}} \cdot {\mathbf{r}}_3 + 4\pi /3)}\end{array}$$
(1)

where e± = (x±iy)/(2)1/2 is the unit vector of σ± polarization. From the valley optical selection rule, the PL helicity for the four possible valley configurations of bright XI states in hBLs with AA and AB stacking can be determined (Supplementary Fig. 9). Since σ+ excitation creates intralayer excitons at +K valleys in both MoSe2 and WSe2, a majority of \({\mathrm{X}}_{ + + }^{\mathrm{I}}\) is expected to form in AA-stacked hBLs via spin-conserving interlayer hopping (Fig. 3d). For \({\mathrm{X}}_{ + + }^{\mathrm{I}}\) in AA stacking, the quantum interference cancels out the σ+ component (e+ ⋅ D+ + = 0) but with the nonvanishing σ− component (e− ⋅ D + + ≠ 0), giving rise to a net σ−-polarized PL. The low PL polarization (\(P_{\mathrm{C}} \simeq - 7\%\)) of XI created by excitation at 1.96 eV arises from the valley depolarization of intralayer excitons before the formation of XI. Resonant excitation with the exciton energy in MoSe2 (1.64 eV) considerably reduces the intralayer valley depolarization and hence increases the XI PL circular polarization.

Excitation energy dependence of emission polarization

We performed PL excitation (PLE) spectroscopy to examine the energy relaxation channels for the formation of XI. Enhanced XI PL emission was observed when the excitation energy (Eex) is resonant with intralayer excitons (Fig. 4a, b), indicating that XI is formed via energy relaxation from intralayer excitons created in either MoSe2 or WSe2 layers. In AA stacking, pronounced negative PC for XI is observed when Eex < 1.73 eV, regardless of creating valley excitons in either layer. Since the K valleys of both layers are aligned in momentum space for AA stacking, the direct interlayer spin–valley transfer ensures that a majority of \({\mathrm{X}}_{ + + }^{\mathrm{I}}\) is formed via σ+ excitation at either the MoSe2 or the WSe2 layer. In AB stacking, however, the ±K valleys of MoSe2 are aligned with the opposite ∓K valleys of WSe2 in momentum space. The preferential spin–valley configurations of XI in AB stacking are therefore different. As shown in Fig. 4b, the XI PL also shows PC < 0 when creating valley excitons in the MoSe2 layer (Eex <1.65 eV), but becomes Pc > 0 when switching the excitation to the WSe2 layer (Eex~ 1.7 eV).

Fig. 4
figure 4

Excitation energy dependence of PL intensity and circular polarization of interlayer excitons. a AA stacking. b AB stacking. Top: contour plots for the XI PL spectra using different excitation energies. Middle: the corresponding PLE spectra. The differential reflectance spectra ΔR/R are also shown for comparison. Bottom: the degree of circular polarization PC as a function of excitation energy. \({\mathrm{X}}_{\mathrm{A}}^{{\mathrm{Mo}}}\) and \({\mathrm{X}}_{\mathrm{A}}^{\mathrm{W}}\)(\({\mathrm{X}}_{\mathrm{B}}^{{\mathrm{Mo}}}\) and \({\mathrm{X}}_{\mathrm{B}}^{\mathrm{W}}\)) denote A (B) excitons in MoSe2 and WSe2, respectively. The \({\mathrm{X}}_{\mathrm{A}}^{\mathrm{W}}\) peak measured by PLE and differential reflectance ΔR/R is dominated by trion absorption

Full size image

Discussion

According to the valley optical selection rule for AB stacking, the negative (positive) Pc indicates the emission of σ− (σ+) PL from the bright \({\mathrm{X}}_{ - + }^{\mathrm{I}}\) (\({\mathrm{X}}_{ + - }^{\mathrm{I}}\)) state formed by σ+ excitation at the MoSe2 (WSe2) layer. It has been established experimentally that the interlayer charge-transfer process is dominated by a spin-conserving transfer to the lowest energy band, independent of the interlayer momentum mismatch32. Our measurements based on nondegenerate optical circular dichroism (CD) spectroscopy on the AA- and AB-stacked hBLs also support this picture (Supplementary Note 6 and Supplementary Figs. 10–13). For σ+ pump at the MoSe2 layer with AB stacking, the spin-conserving transfer thus leads to the lowest valley configuration \({\mathrm{X}}_{ + + }^{\mathrm{I}}\) (Fig. 3d) in the steady state. The \({\mathrm{X}}_{ + + }^{\mathrm{I}}\) state is an intervalley dark state (Supplementary Table 1) with a large center-of-mass momentum (±ℏK), which is far beyond the light cone and unable to couple with light directly. The formation of bright XI states (\({\mathrm{X}}_{ - + }^{\mathrm{I}}\) or \({\mathrm{X}}_{ + - }^{\mathrm{I}}\)) is expected to occur by intervalley or intravalley scattering processes (Supplementary Note 7 and Supplementary Fig. 14a,b). Since the electron intervalley scattering without spin flips is expected to be more efficient, a majority of the \({\mathrm{X}}_{ - + }^{\mathrm{I}}\) will form under σ+ excitation at the MoSe2 layer, giving rise to the σ− PL emissions (Supplementary Fig. 14a). However, the presence of the lower-lying dark state makes the bright XI states in AB stacking energetically unfavorable, rendering less-efficient PL at low temperatures (Supplementary Fig. 15). As for σ+ pump at the WSe2 layer with AB stacking, the spin-conserving interlayer transfer also leads to a majority of dark \({\mathrm{X}}_{ + + }^{\mathrm{I}}\) in the steady state. However, the microscopic processes for the formation of bright XI states are intrinsically more complicated because resonant excitations at the WSe2 layer also inject carriers nonresonantly to the MoSe2 layer. The formation of bright \({\mathrm{X}}_{ + - }^{\mathrm{I}}\) state thus requires spin-flip processes (Supplementary Fig. 14c), which is expected to be energetically unfavorable. Nevertheless, the low circular polarization for XI in AB-stacked hBL suggests that there is a competing channel for the formation of \({\mathrm{X}}_{ - + }^{\mathrm{I}}\) states. While the microscopic processes remain unclear, a possible scenario is likely mediating through the generation of intralayer trions in the WSe2 layer. This explanation is also supported by the PLE spectra for AB-stacked hBLs (Fig. 4b), where the excitation resonances of higher PC are lower than the neutral exciton energy in monolayer MoSe2 and WSe2. Further studies, such as using time-resolved Kerr rotation spectroscopy33, are required in order to understand the microscopic processes for the formation dynamics of bright XI states.

In summary, we unveil the polarization properties of interlayer excitons in commensurate WSe2/MoSe2 heterobilayers with a well-defined atomic registry. The quantum interference imposed by interlayer atomic registry gives rise to distinct polarization selection rules for interlayer excitons, making the interlayer valley configurations become optically traceable. Selective excitations at different monolayers further demonstrate the optical addressability of interlayer excitons with different valley configurations and polarization helicities, providing a new scheme for exploring spin/valleytronic applications based on van der Waals heterostructures.

Methods

Material synthesis of WSe2/MoSe2 heterobilayers

High-quality single-crystal WSe2/MoSe2 heterobilayers were synthesized on sapphire substrates by chemical vapor deposition (CVD) in a horizontal hot-wall chamber using the conventional one-pot synthesis process34, 35. High-purity MoO2 (99%, Aldrich), WO3, and Se powders (99.5%, Alfa) were used as the initial reactants. The heterostructures were grown at 880 °C in Ar/H2 flowing gas at low pressure (5–40 Torr). The flow rates for Ar/H2 gas were controlled at 60/6 sccm during the growth.

ADF STEM characterizations

ADF STEM imaging was conducted using a spherical aberration-corrected transmission electron microscope (JEOL-2100F). The CVD-grown WSe2/MoSe2 flakes on the substrate were first capped with a layer of poly(methylmethacrylate) (PMMA) (950K A4) by spin-coating (step 1: 500 rpm for 10 s; step 2: 3000 rpm for 60 s), followed by baking at 100 °C for 60 min. The PMMA-capped WSe2/MoSe2 was then immersed in a BOE solution at 100 °C for 60 min. After that, the PMMA film can be exfoliated from the sapphire substrate and transferred onto a Cu grid with carbon nets (Ted Pella) after diluting etchants and residues in deionized water. Then the top PMMA film was removed by acetone, and the sample was cleaned by isopropyl alcohol and deionized water.

Optical measurements

Room-temperature optical characterizations, such as photoluminescence (PL), Raman, SHG, and differential reflectance spectroscopes were performed using a homebuilt optical microscope in the back-scattering configuration. The excitation light was focused onto the sample by a ×100 objective lens (N.A. = 0.9). The signals were collected by the same objective lens and analyzed by a 0.75-m monochromator and detected by a liquid-nitrogen-cooled CCD camera. For PL and Raman measurements, a 532-nm solid-state laser was used as the excitation source. For differential reflectance measurements, a fiber-coupled tungsten–halogen lamp was used as a white-light source. For SHG measurements, the fundamental laser field was provided by a mode-locked Ti:sapphire laser at 880 nm. Spatial mappings were performed on a fast motorized x–y stage with a step of 0.25 μm. The polarizations of fundamental and SH lights were selected and analyzed by individual linear polarizers and half-wave plates.

For low-temperature PL measurements, the sample was cooled down to T = 4 K by a cryogen-free low-vibration cryostat equipped with a three-axis piezo-positioner, an x–y scanner, and an objective lens (N.A. = 0.82) in the low-temperature chamber. Excitations at three different energies, corresponding to 1.96 (HeNe laser), 1.71, and 1.64 eV (cw-tunable Ti:sapphire laser), were used for above-gap and resonant excitations in the WSe2 and MoSe2 layers. For PL excitation (PLE) measurements, we used a supercontinuum laser equipped with a continuous tunable filter as the excitation source. The bandwidth of the tunable filter is ~1–2 nm. For polarization-resolved PL measurements, the circular polarization of the excitation laser was selected by a set of linear polarizers and quarter-wave plates, and the PL polarizations were analyzed by another set of quarter-wave plates and linear polarizers in front of the grating spectrometer. We have calibrated the circular polarization in both the detection and excitation paths. In the detection path, the degree of circular polarization is preserved up to 99.1% after passing through all optical components in the optical path. In the excitation path, the circular polarization of the excitation laser is higher than 98%.

Band structure calculations

The ab initio calculations were carried out using the Quantum ESPRESSO software36 with the LDA pseudopotentials37. An 18 × 18 × 1 k-grid is used to sample the Brillouin zone, and the energy cutoff of the plane-wave expansion is 50 Ry. Crystal structures were fully relaxed with the inclusion of the van der Waals correction to the interatomic forces by means of the DFT-D2 method38. Spin–orbit coupling was included in all calculations.

Data availability

Data described in this paper and presented in the supplementary materials are available from the corresponding author upon request.