Abstract
Hyperpolarisation of nuclear spins is important in overcoming sensitivity and resolution limitations of magnetic resonance imaging and nuclear magnetic resonance spectroscopy. Current hyperpolarisation techniques require high magnetic fields, low temperatures, or catalysts. Alternatively, the emergence of room temperature spin qubits has opened new pathways to achieve direct nuclear spin hyperpolarisation. Employing a microwave-free cross-relaxation induced polarisation protocol applied to a nitrogen vacancy qubit, we demonstrate quantum probe hyperpolarisation of external molecular nuclear spins to ~50% under ambient conditions, showing a single qubit increasing the polarisation of ~106 nuclear spins by six orders of magnitude over the thermal background. Results are verified against a detailed theoretical treatment, which also describes how the system can be scaled up to a universal quantum hyperpolarisation platform for macroscopic samples. Our results demonstrate the prospects for this approach to nuclear spin hyperpolarisation for molecular imaging and spectroscopy and its potential to extend beyond into other scientific areas.
Similar content being viewed by others
Introduction
The hyperpolarisation of nuclear spins within target molecules is a critical and complex challenge in magnetic resonance imaging (MRI)1 and nuclear magnetic resonance (NMR) spectroscopy2. Hyperpolarisation offers enormous gains in signal and spatial resolution which may ultimately lead to the development of molecular MRI and NMR3, with the prospect of revolutionising many areas of research and clinical applications. Well-known hyperpolarisation techniques include high-field/low temperature brute-force methods4, dynamic nuclear polarisation6, optical pumping5, and parahydrogen-induced polarisation7. On the other hand, the rapid advances in semiconductor spin qubit technology for quantum computing9,10 and quantum sensing11,12,13,14 has opened up the exciting possibility of hyperpolarising nuclear spins at a fundamental level via quantum mechanical protocols6,8,17,18,19,20,21,22,23,24. Despite early progress25,26, the application of quantum probe technology to this problem still faces a number of significant challenges. To be of practical use, a quantum probe must be capable of polarising a relatively large number of remote nuclear spins external to the probe substrate, ideally under ambient conditions.
In the following, we address these challenges using a quantum spin probe in diamond as an entropy pump, and, using a combined experimental and theoretical analysis, demonstrate polarisation of external molecular spin ensembles to about 50% over relatively large volumes at room temperature, with the prospect of scaling up to a universal hyperpolarisation platform suitable for clinical applications. In contrast to existing methods, our quantum polarisation approach is tunable to a range of nuclear species, is inherently free of radiofrequency (RF) or microwave fields and extraneous chemistry, and is carried out at room temperature.
Results
Principle of the technique
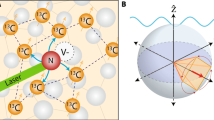
For this study, we employ a nitrogen vacancy (NV) quantum spin probe in a diamond substrate (Fig. 1a)11. Existing approaches to NV-based hyperpolarisation involve the use of an external microwave field to tune the NV Rabi frequency to the Larmor frequency of the target spins, thereby enabling rotating-frame cross-relaxation via the Az,x and Az,y components of their hyperfine interaction. Our approach, on the other hand, takes advantage of the greater (Ax,y;x,y) NV-target hyperfine interaction associated with direct lab-frame cross-relaxation, which allows for an order of magnitude greater target polarisation rate. This is achieved by using an external magnetic field, B, to tune the ground-state spin transition frequency of the NV (ωNV) into resonance with target nuclear spins (ωn) (Fig. 1b). For a given target species, the spin resonance condition is fulfilled at a magnetic field B*(γn) ≈ 2D/(γNV − γn)27, where γn, γNV are the target and NV gyromagnetic ratios, and D is the NV zero-field splitting (Fig. 1c). Entropy pumping is facilitated by repeated application of the cross relaxation induced polarisation (CRIP) sequence (Fig. 1d), wherein the NV spin is optically initialised into \(\left| 0 \right\rangle\) state and the NV-target hyperfine interaction is allowed to occur for a given period of time, τ (of order microseconds). The transfer of magnetisation caused by this interaction thus polarises the target spins into their \(\left| \downarrow \right\rangle\) state (Fig. 1c). For the sake of comparison, depolarisation may be facilitated by interleaving the initialisation of the NV spin into the opposite state \(\left| { - 1} \right\rangle\) by the application of an RF π-pulse (Fig. 1e).
Quantum probe hyperpolarisation of nuclear spin ensembles. a Schematic of the system showing a near-surface nitrogen vacancy (NV) spin probe in diamond and a hydrogen nuclear spin target ensemble in molecular Poly(methyl methacrylate) (PMMA) on the surface. The NV probe is initialised by a green laser (532 nm), and read out via its photoluminescence (PL) signal. The shaded blue surfaces denote different regimes of polarisation capabilities arising from the spatial dependence of the nuclear spin coupling to the NV qubit. b Schematic of cross relaxation induced polarisation (CRIP) implemented on a spin system illustrating the build up of polarisation from repeated application of the CRIP sequence. Diffusion effects act in competition with the CRIP entropy pumping mechanism, but also allow for polarisation at distances beyond that reachable via the hyperfine interaction. c Energy-level diagram of the NV (left) showing the relative positions of various target nuclear spins (right) resonance conditions. d, e The control sequences (laser pulses in green, RF pulses in red) used for polarising a target spin ensemble using CRIP (d) and for controlled depolarisation using the combined CRIP−1 × CRIP protocol (e). f Schematic showing the cross-relaxation spectrum obtained by measuring the PL during the CRIP (blue) or depolarisation (orange) sequence with a constant interaction time τ, while scanning the NV frequency ωNV. g Similarly, the cross-relaxation curve is obtained by scanning τ with ωNV set at the resonance
To quantitatively understand the effect of the CRIP protocol on the target spin ensemble, we developed a microscopic theory that explicitly includes the dipole interactions of ensemble spins and their interaction with a single NV quantum probe (see Supplementary Note 1 for details). We define the polarisation of a spin at position R (relative to the NV) and time t to be P(R, t); with the evolution of P(R, t) described by
subject to an initial unpolarised state P(R, t) = 0; where u(R) = A2(R)/2Γ2 is the effective cooling coefficient resulting from the hyperfine coupling A(R) with the NV spin, Γ2 is the dephasing rate of the NV spin β is the effective polarisation diffusion coefficient related to the intra-target interactions, and ΓSL is the spin-lattice relaxation rate of the target spin ensemble. This formulation allows us to predict and describe the spatial extent of polarisation for a given target sample of arbitrary geometry.
To probe the polarisation effect experimentally, we monitor the spin-dependent photoluminescence (PL) from the NV28,29,30 during the laser pulses, which decays as a function of the CRIP sequence time as \(e^{ - \Gamma _{{\mathrm{tot}}}\tau }\). Here Γtot is the NV longitudinal relaxation rate, which can be expressed as the sum Γtot = Γbg + ΓCR, where Γbg is the background rate caused by lattice phonons or surface effects, and ΓCR is due to cross-relaxation. The latter follows a Lorentzian dependence on the detuning between the probe and target transition frequencies28,
where \(A_P^2\) is the total effective hyperfine field seen by the NV due to the target ensemble, which is related to the polarisation distribution via
where nt is the density of the target spin ensemble. The key indicator of significant polarisation is therefore a reduction in ΓCR, which manifests as the disappearance of the target ensemble’s spectral feature from the cross-relaxation spectrum (Fig. 1f), and can be quantified by measuring the cross-relaxation curve at resonance (Fig. 1g).
Polarisation of internal 13C spins
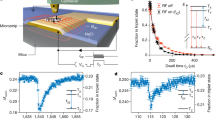
Experimentally, we first demonstrate our technique on the inherent 1.1% 13C spin ensemble surrounding a NV probe in the diamond substrate by tuning to the 13C resonant condition at B*(13C) = 1024.9 G. Comparison of the cross-relaxation spectra for CRIP and depolarisation sequences (Fig. 2a) shows the complete removal of the 13C resonance peak for interaction times of τ = 4 µs, indicating efficient polarisation of the nearest spins, as compared with the target prepared using the depolarising sequence. This is confirmed in the cross-relaxation curves as a function of τ (Fig. 2b, inset), where the polarised case shows no evolution of the NV spin state, while the unpolarised case shows coherent flip-flops between the NV and the 13C spins.
Cross-relaxation induced polarisation of 13C spins in diamond. a Cross-relaxation spectra of a single NV spin near the 13C resonance (\(\omega _{{\mathrm{N}}V} = 1.1\) MHz), obtained with an interaction time τ = 4 µs using the CRIP sequence (blue) and the depolarisation sequence (orange, only the readout following the NV initialisation in \(|0\rangle\) is shown). Sequences were repeated N = 105 times at each point. b Cross-relaxation curves obtained by increasing τ at the 13C resonance with the CRIP sequence (blue) and depolarisation sequence (orange), and off-resonance to obtain the background relaxation curve (green). Zoom-in at short times for the polarised (blue) and unpolarised case (orange, top and bottom curves correspond to the NV initialised in \(|0\rangle\) and \(| - 1\rangle\), respectively). c Calculated radial polarisation profiles relative to the NV spin (averaged over all angles), calculated from Eq. (1) for a random 1.1% 13C spin ensemble for varying total polarisation times, T = Nτ. Inset: profile along dashed line, corresponding to T = 2 h. d Three-dimensional representation of the polarisation distribution at T = 2 h
To investigate the extent of the polarisation effect, we increase the interaction time τ so as to be sensitive to more remote 13C spins, up to the limit set by the NV centre’s intrinsic spin-phonon relaxation rate, Γbg ≈ 200 s−1. The resulting cross-relaxation curves obtained at the 13C resonance using the CRIP and depolarisation sequences are shown in Fig. 2b, from which we extract the total relaxation rate, Γtot. By subtracting Γbg obtained from the off-resonance relaxation curve (Fig. 2b, green data), we deduce the 13C-induced relaxation rate ΓCR = Γtot − Γbg, which decreases from \(\Gamma _{{\mathrm{C}}\mathrm{R}}^{{\mathrm{u}}\mathrm{npol}} \approx 250\) ms−1 with the depolarisation sequence, to below the noise floor of the measurement after 5 h of CRIP, \(\Gamma _{{\mathrm{CR}}}^{{\mathrm{pol}}}\mathop { < }\limits_ \sim 19\) s−1. We use Eq. (1) (with β = 0.0335 nm2s−1 corresponding to the given 13C density) to calculate the time dependence of the radial polarisation profile for total polarisation times of 1–106 s, as depicted in Fig. 2c. By relating the spatial polarisation distribution, P(R,t), to the cross-relaxation rate, ΓCR, via Eq. (2), we find the theoretical results are consistent with the experiment for polarisation times in excess of two hours (Fig. 2c, dashed line). Examination of the spatial polarisation distribution (Fig. 2c, inset, and Fig. 2d) implies a polarisation level of more than 99% within 21 nm of the NV, equating to a 6 × 106-fold increase on thermal polarisation for 3 × 105 spins.
Polarisation of external 1H spins
With the basic protocol established, we now move to the polarisation of molecular 1H nuclear spins external to the diamond crystal. A solution of poly(methyl methacrylate), PMMA, was applied directly to a diamond surface12 with single NV spin probes located 8–12 nm below the surface with an average density of 108 cm−2. The initial criteria for finding suitable NVs involved finding a trade-off between maximising the NV-H coupling (shallow), and minimising the coupling to sparse electronic surface defects (deep) which limit the NV linewidth and the background T1 time. The surface is also known to retain a 1–2 nm thick layer of protons of density commensurate with that of PMMA15, which we therefore regard as being part of the target proton system to be polarised.
CRIP was applied with the external magnetic field tuned to resonance at B*(1H) = 1026.2 G. With a much higher diffusion constant and spin-lattice relaxation rate (β = 781 nm2 s−1, ΓSL = 1s−1)16 relative to the intrinsic 13C case, the 1H system effectively reaches steady-state within a few seconds. Application of the CRIP sequence to NV1 (data for other NVs are shown in the Supplementary Note 2) for τ = 20s (Fig. 3a) shows the removal of the hydrogen spectral feature (blue), as compared with the depolarising sequence (orange). From the cross-relaxation curves after 1 h of CRIP (Fig. 3b), we extract 1H-induced rates for the unpolarised (\(\Gamma _{{\mathrm{C}}\mathrm{R}}^{{\mathrm{u}}\mathrm{npol}}\)) and polarised (\(\Gamma _{{\mathrm{C}}\mathrm{R}}^{{\mathrm{p}}\mathrm{ol}}\)) PMMA 1H spin ensembles to be 2.71 ms−1 and 0.96 ms−1, respectively. The ratio \(\Gamma _{{\mathrm{CR}}}^{{\mathrm{unpol}}}/\Gamma _{{\mathrm{CR}}}^{{\mathrm{pol}}} = 2.8(3)\) (consistent with the value of 2.4(3) obtained using another NV), is in good agreement with the solution to Eq. (1) for the PMMA ensemble, which gives a ratio of 2.2 in the steady state. The corresponding spatial polarisation distribution is shown in Fig. 3c, indicating that the system reaches 50% average polarisation over a volume of ~ (26 nm)3. Thus, we conclude that the single spin quantum probe has increased the average polarisation of roughly a million hydrogen spins by some six orders of magnitude over the room temperature Boltzmann thermal background.
Polarisation of external molecular 1H spins. a Cross-relaxation spectra near the 1H resonance (ωNV = 4.4 MHz), for a single NV spin located 10 nm below a PMMA layer, obtained using τ = 20 μs and N = 105 with the CRIP sequence (blue) and the depolarisation sequence (orange). b Cross-relaxation curves obtained by increasing τ at the 1H resonance with the CRIP sequence (blue) and depolarisation sequence (orange), and off-resonance to obtain the background relaxation rate (green). c Three-dimensional representation of the 1H spin polarisation distribution in PMMA on the surface of a diamond (blue block), calculated from Eq. (1) in the steady state
Improvements and scaling up
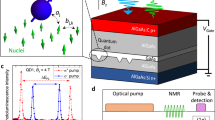
There is scope for improvement on these proof-of-concept results: for example, engineering NV depths to 5 nm would increase the rate of target spin polarisation by an order of magnitude, and improvements in the inherent NV dephasing rate Γ2 (e.g. via improved surface properties) will allow for more precise tuning to different nuclear spin species. As the protocol is all optical, scaling up for high-volume production could be achieved by stacking multiple NV arrays (Fig. 4a) and/or increasing the effective interaction area via surface patterning31, however, issues such as the creation and control of homogeneous DC magnetic fields over the spatial extent of the ensemble are ongoing endeavours that are beyond the scope of the work presented here.
Universal MRI contrast agent hyperpolarisation platform. a Schematic of a quantum polarisation stack comprising multiple diamond membranes, each containing NV array layers on both sides, in a homogeneous magnetic field tuned to the nuclear gyromagnetic ratio of the target agent spin species. The unpolarised agent in concentrated solution (orange) flows into the stack channels, where the liquid is polarised through the application of CRIP (via a pulsed laser). The out-flowing polarised liquid (blue) is then diluted for use. Zoomed schematic shows a single polarisation cell comprising a channel formed by dual diamond membranes each with a near-surface NV layer. b Average polarisation level from a single polarisation cell, for various targets (HEP, H2O, and 15N-TMPA), calculated for varying polarisation times assuming perfect mixing of a 1 M target agent solution with a cell height of 1 μm. c Outflow rate (after dilution to 1 mM for application delivery) from 10 polarisation cells at different levels of polarisation
The results presented here indicate that the CRIP protocol could produce macroscopic quantities of MRI contrast agents with high polarisation levels. For example, we consider 13C isotopically enriched HEP (hydroxyethylpropionate,13C5H10O3), a well-known MRI contrast agent32. Using a single hyperpolarisation cell comprised of two NV arrays in diamond membranes separated by 1 μm (see zoomed schematic in Fig. 4a; we assume an NV density of 4 × 1011 cm−2 over a 4 × 4 mm diamond surface33), the rate of polarisation transfer to a concentrated 1 M precursor HEP solution is 4 μL s−1 at a polarisation level of 80%. The polarisation levels for different contrast agents in 1 M precursor solutions are plotted against polarisation time (assuming perfect mixing occurs over these timescales) in Fig. 4b. In Fig. 4c, we plot the final delivery rate after dilution to 1 mM for a stack of 10 cells, showing that delivery rates of order 100 μL s−1 for clinical applications34 are achievable.
Discussion
In summary, we have experimentally demonstrated hyperpolarisation of molecular nuclear spins under ambient conditions by employing a quantum spin probe entropy pump. The technique works at low magnetic fields and room temperature conditions, requires no RF or microwave fields, and operates directly on the target molecules without the need for catalysts or free radicals. With high polarisation rates and tunability, there are excellent prospects for scale-up of the system to produce macroscopic quantities of a range of contrast agents at polarisation levels required for molecular MRI/NMR. The technique can be extended to other nuclear spin species and may also provide pathways in quantum information for initialisation of quantum simulators, or increasing the fidelity of operations through spin-bath neutralisation. Future work will involve external verification of nuclear spin polarisation using conventional NMR techniques.
Methods
Experimental apparatus
The experimental apparatus consists of a custom-built confocal microscope and a permanent magnet mounted on a scanning stage, the same setup used, and described, in29. In summary, the excitation source is a solid-state laser emitting at a wavelength λ = 532 nm (Laser Quantum Gem 532). The objective lens (Olympus UPlanSApo 100×, NA = 1.4 Oil) is mounted on an XYZ scanning stage (PI P-611.3 NanoCube) to allow fast laser scanning. The PL emitted by the diamond sample is separated from the laser light using a dichroic beam splitter and a band-pass filter, and coupled into a multimode fibre connected to a single photon counting module (Excelitas SPCM-AQRH-14-FC). For T1 measurements, the laser beam is modulated by an acousto-optic modulator (AA Opto-Electronic MQ180-A0,25-VIS) in a double pass configuration, and the PL signal is analysed by a time digitiser (FastComTec P7889). For optically detected magnetic resonance (ODMR) measurements, a 20-μm copper wire is spanned on the surface of the diamond and connected to the output of a microwave generator (Agilent N5181A) modulated by a switch (Mini-Circuits ZASWA-2-50DR+). Laser and microwave modulations are controlled by a programmable pulse generator (SpinCore PulseBlasterESR-PRO 500 MHz). The magnetic field direction and strength were varied by using a permanent magnet affixed to a set of three linear translation stages (PI M-511) allowing XYZ position control. These stages had a resolution of 100 nm which is sufficient to tune the NV into resonance and align along the field along the NV axis, thus avoiding any misalignment issues27.
Diamond samples
The sample (#132) used for the 13C measurements was a \(\left\langle {111} \right\rangle\)-oriented single crystal, electronic grade, chemical vapour deposition (CVD), 100 μm thick diamond purchased from Delaware Diamond Knives. For the measurements reported in Fig. 2, we used native (as grown) NV centres located far (several μm) from the surface. The sample (#122) used for the 1H measurements is a \(\left\langle {100} \right\rangle\)-oriented single crystal CVD overgrown on a HPHT substrate from Element Six. The overgrowth is roughly 50 μm and electronic grade. The sample has been implanted with 15N and 14N at 3 keV at a density of 5 × 108 cm−2 each. The sample was annealed at 950 °C for 2 h and was exposed to a soft O2 plasma for 1 minute36. The PMMA was baked onto the surface of the diamond by a heat gun at 85° for 40 min. The diamond has a range of near-surface NV depths (~3–13 nm) determined by NV-NMR spectroscopy using the dynamical decoupling method35.
General acquisition procedure
The spectra shown in Figs. 2 and 3 were obtained as follows. The magnetic field was first aligned along the NV axis by maximising the PL intensity30,37,38. When doing this near the GSLAC, we estimate an alignment to less than 0.1°. The magnet was then stepped along the NV direction to vary the magnetic field strength B0. For each magnet position, an ODMR spectrum was recorded for about 1 minute from which we extract ωNV via a Lorentzian fit, before the CRIP sequence is applied. The latter consists of a series of 3-μs laser pulses, sufficient to completely initialise the NV spin state, separated by a wait time τ. The signal plotted in Figs. 2a and 3a corresponds to the PL intensity integrated over the first 300 ns of the laser pulse, normalised by the intensity integrated over the last 300 ns. To compare with the non-polarised case, we repeated the scan but by interleaving CRIP and CRIP−1 pulse sequences, which acts to prevent polarisation build up in either direction. The CRIP−1 simply adds a radiofrequency (RF) pulse to flip the NV spin from |0〉 to |−1〉. This π pulse was applied 1 μs after the end of the laser pulse, was 300 ns in duration, and was followed by a wait time τ identical to that used in the preceding CRIP sequence. With the interleaved sequence, there are two independent PL readout, one during the laser pulse following the CRIP sequence, the other following the CRIP−1 sequence. Note that the interleaved sequence continuously polarises the bath but each pulse flips the direction of this polarisation. As such, because of pulse imperfections it may still partly polarise nearby spins.
For the full-length T1 measurements presented in main text Figs. 2b and 3c, a similar procedure was applied, except that the magnet was not moved throughout the acquisition, and instead the wait time τ was continuously swept. To monitor magnetic field drifts caused by thermal fluctuations, we recorded an ODMR spectrum at regular intervals. We can thus ensure that the NV remains on resonance with the target transition, within the NV linewidth (see details in Supplementary Note 2).
Model Hamiltonian
Given the generality of our approach with respect to the target species of nuclear spin, we refer to a general environmental target spin system, E. Assuming alignment of the external field with the NV axis, the Hamiltonian becomes
where Sx,y,z are the Pauli spin matrices of the spin-1 system of the NV, D = 2.87 GHz is the corresponding zero-field splitting, B0 is the external field strength, γNV and γn are the gyromagnetic ratios of the NV and target spins, \(I_{x,y,z}^{(j)}\) are the Pauli spin matrices of nuclear spin j, A j is the hyperfine tensor describing the spin-spin interaction between the NV and spin j, B jk is the tensor describing the magnetic dipole interaction between spins j and k; and summation over j,k refer to all spins in the environment. In Eq. 4, γNV is defined positive, while γn can be positive or negative depending on the species considered.
Continuum description
Solving Eq. 4 for NS spins, each having hyperfine coupling A j to the NV, mutual dipole couplings B jk , and initial state of
the population of the NV \(\left| 0 \right\rangle\) state is at a minimum when t = τ = 21/2π/A0, and is given by
where \(A_0^2 \equiv \mathop {\sum}\nolimits_j A_j^2\) is the total hyperfine coupling field, and \(A_j = \sqrt{ \left( A_{xx}^{(j)}-A_{yy}^{(j)}\right)^2 + \left(2A_{xy}^{(j)}\right)^2 }\).
The change in probability of spin j is given by
where B jk is the secular magnetic dipole coupling between spins j and k, and \(C_{jk}^2 \equiv A_j^2A_k^2/A_0^2\) is the effective hyperfine-mediated diffusion strength.
In modelling these systems, we typically consider regions of at least 200 nm in size, which means of order \(N_{\mathrm{S}} \sim 10^{10}\) spins and ~1020 couplings for the case of PMMA, thereby making modelling of discrete spin states computationally unfeasible. We therefore map Eq. 7 to a temporally and spatially continuous
In the discrete description, the probability of finding spin j in its \(\left| \uparrow \right\rangle\) state is monitored at discrete multiples of the optimal dark time, τ. As we are interested in times \(t \gg \tau\), we map changes in p j over time to
To obtain the continuum description of the spatial evolution, we put \(p_j \mapsto p\left( {{\bf{R}},t} \right)\) and \(p_k \mapsto p\left( {{\bf{R}} + {\bf{r}},t} \right)\), and discretise the Laplacian operator to get an effective diffusion term with constant β
We also map the discrete hyperfine couplings to a continuous field whose strength is determined by its position relative to the NV, R.
The summation over all hyperfine couplings is then mapped to an integral,
Finally, to account for additional sources of environmental spin-lattice relaxation, where applicable, we add an additional probability sink in which any probability outside equilibrium decays at a rate ΓSL = 1/TSL, given by
The differential equation describing the evolution of this system is thus given by
where
is the effective source, or cooling, coefficient at position R relative to the NV, Recasting Eq. 14 in terms of the polarisation P(R, t) = 1 − 2p(R, t), we obtain Equation (1) of the main text.
For cases in which the dephasing rate of the NV spin, Γ2, is greater than the hyperfine coupling to the desired target, i.e. \(\Gamma _2 \gg A_0\), the population of \(\left| 0 \right\rangle\) state of the NV spin will exhibit an exponential time dependence. As such, for this regime we instead make the replacement
where the details of this process are discussed in the Supplementary Note 1.
Experimentally, Γ2 is obtained via the T1-relaxometry spectrum (with the interleaved sequence), since Γ2 defines the width of the cross-relaxation resonances28. We note that Γ2 is expected to decrease upon polarisation of the 13C bath. However, the effect is relatively small (see section Supplementary Note 1), and as such in the calculations shown in main text Fig. 2 Γ2 is kept constant and equal to the off-resonance value (i.e. unpolarised case). For the 1H case, the dephasing is dominated by surface effects, and is therefore unaffected by the 1H polarisation.
Upon solution of Eq. 14 for the polarisation P(R, t), we may determine the total number of spins polarised at time t:
Data availability
The data that support the findings of this study are available from the corresponding author upon request.
References
Christopher deCharms, R. Applications of real-time fMRI. Nat. Rev. Neurosci. 9, 720–729 (2008).
Rossini, A. J. et al. Dynamic nuclear polarization surface enhanced NMR spectroscopy. Acc. Chem. Res. 46, 1942–1951 (2013).
Nikolaou, P., Goodson, B. M. & Chekmenev, E. Y. NMR hyperpolarization techniques for biomedicine. Chemistry 21, 3156–3166 (2015).
Bajaj, V. et al. Dynamic nuclear polarization at 9T using a novel 250GHz gyrotron microwave source. J. Magn. Reson. 160, 85–90 (2003).
Viteau, M. et al. Optical pumping and vibrational cooling of molecules. Science 321, 232–234 (2008).
London, P. et al. Detecting and polarizing nuclear spins with double resonance on a single electron spin. Phys. Rev. Lett. 111, 067601 (2013).
Bhattacharya, P. et al. Parahydrogen-induced polarization (PHIP) hyperpolarized MR receptor imaging in vivo: a pilot study of 13C imaging of atheroma in mice. NMR Biomed. 24, 1023–1028 (2011).
Álvarez, G. A. et al. Local and bulk 13C hyperpolarization in nitrogen-vacancy-centred diamonds at variable fields and orientations. Nat. Commun. 6, 8456 (2015).
Morello, A. et al. Single-shot readout of an electron spin in silicon. Nature 467, 687–691 (2010).
Zwanenburg, F. A. et al. Silicon quantum electronics. Rev. Mod. Phys. 85, 961–1019 (2013).
Doherty, M. W. et al. The nitrogen-vacancy colour centre in diamond. Phys. Rep. 528, 1–45 (2013).
Mamin, H. J. et al. Nanoscale nuclear magnetic resonance with a nitrogen-vacancy spin sensor. Science 339, 557–560 (2013).
Cole, J. & Hollenberg, L. Scanning quantum decoherence microscopy. Nanotechnology 20, 495401 (2009).
Taylor, J. M. et al. High-sensitivity diamond magnetometer with nanoscale resolution. Nat. Phys. 4, 810–816 (2008).
DeVience, S. J. et al. Nanoscale NMR spectroscopy and imaging of multiple nuclear species. Nat. Nanotechnol. 10, 129–135 (2015).
Hatada, K. et al. Mechanism of proton spin-lattice relaxation in poly(methyl methacrylate). Die Makromol. Chem. 178, 2753–2758 (1977).
Knowles, H. S., Kara, D. M. & Atatüre, M. Demonstration of a coherent electronic spin cluster in diamond. Phys. Rev. Lett. 117, 100802 (2016).
Belthangady, C. et al. Dressed-state resonant coupling between bright and dark spins in diamond. Phys. Rev. Lett. 110, 157601 (2013).
Wang, H.-J. et al. Sensitive magnetic control of ensemble nuclear spin hyperpolarization in diamond. Nat. Commun. 4, 1940 (2013).
Fischer, R. et al. Bulk nuclear polarization enhanced at room temperature by optical pumping. Phys. Rev. Lett. 111, 057601 (2013).
King, J. P. et al. Room-temperature in situ nuclear spin hyperpolarization from optically pumped nitrogen vacancy centres in diamond. Nat. Commun. 6, 8965 (2015).
Chen, Q., Schwarz, I., Jelezko, F., Retzker, A. & Plenio, M. B. Optical hyperpolarization of C 13 nuclear spins in nanodiamond ensembles. Phys. Rev. B 92, 184420 (2015).
Liu, G.-Q. et al. Protection of centre spin coherence by dynamic nuclear spin polarization in diamond. Nanoscale 6, 10134–10139 (2014).
Rej, E., Gaebel, T., Boele, T., Waddington, D. E. J. & Reilly, D. J. Hyperpolarized nanodiamond with long spin-relaxation times. Nat. Commun. 6, 8459 (2015).
Abrams, D., Trusheim, M. E., Englund, D., Shattuck, M. D. & Meriles, C. A. Dynamic nuclear spin polarization of liquids and gases in contact with nanostructured diamond dynamic nuclear spin polarization of liquids and gases in contact with nanostructured diamond. Nano Lett. 5, 2471–2478 (2014).
Chen, Q., Schwarz, I., Jelezko, F., Retzker, A. & Plenio, M. B. Resonance-inclined optical nuclear spin polarization of liquids in diamond structures. Phys. Rev. B - Condens. Matter Mater. Phys. 93, 060408 (2016).
Broadway, D. A. et al. Anticrossing spin dynamics of diamond nitrogen-vacancy centers and all-optical low-frequency magnetometry. Phys. Rev. Appl. 6, 064001 (2016).
Hall, L. T. et al. Detection of nanoscale electron spin resonance spectra demonstrated using nitrogen-vacancy centre probes in diamond. Nat. Commun. 7, 10211 (2016).
Wood, J. D. A. et al. Microwave-free nuclear magnetic resonance at molecular scales. Nat. Commun. 8, 15950 (2017).
Wood, J. D. A. et al. Wide-band, nanoscale magnetic resonance spectroscopy using quantum relaxation of a single spin in diamond. Phys. Rev. B 94, 155402 (2016).
Kehayias, P. et al. Solution nuclear magnetic resonance spectroscopy on a nanostructured diamond chip. Nat. Commun. 8, 188 (2017).
Schmidt, A. B. et al. Liquid-state carbon-13 hyperpolarization generated in an MRI system for fast imaging. Nat. Commun. 8, 14535 (2017).
Simpson, D. A. et al. Electron paramagnetic resonance microscopy using spins in diamond under ambient conditions newblock. Nat. Commun. 8, 458 (2017).
Golman, K., in't Zandt, R. & Thaning, M. Real-time metabolic imaging. Proc. Natl Acad. Sci. USA 103, 11270–11275 (2006).
Pham, LinhM. et al. NMR technique for determining the depth of shallow nitrogen-vacancy centers in diamond. Phys. Rev. B 93, 045425 (2016).
Fávaro de Oliveira, F. et al. Effect of low-damage inductively coupled plasma on shallow nitrogen-vacancy centers in diamond. Appl. Phys. Lett. 107, 073107 (2015).
Epstein, R. J. et al. Anisotropic interactions of a single spin and dark-spin spectroscopy in diamond. Nat. Phys. 1, 94–98 (2005).
Tetienne, J. P. et al. Magnetic-field-dependent photodynamics of single NV defects in diamond: an application to qualitative all-optical magnetic imaging. N. J. Phys. 14, 103033 (2012).
Acknowledgements
This work was supported in part by the Australian Research Council (ARC) under the Centre of Excellence scheme (project No. CE110001027). This work was performed in part at the Melbourne Centre for Nanofabrication (MCN) in the Victorian Node of the Australian National Fabrication Facility (ANFF). L.C.L.H. acknowledges the support of an ARC Laureate Fellowship (project No. FL130100119). J.-P.T. acknowledges support from the ARC through the Discovery Early Career Researcher Award scheme (DE170100129) and the University of Melbourne through an Establishment Grant and an Early Career Researcher Grant. D.A.B is supported by an Australian Government Research Training Program Scholarship.
Author information
Authors and Affiliations
Contributions
The CRIP protocol was conceived by L.T.H. Experiments were performed by D.A.B. and J.-P.T., with input from A.S., D.A.S., J.D.A.W., L.T.H., and L.C.L.H. L.T.H. developed the theory, with input from L.C.L.H. D.A.B., J.-P.T., A.S., and D.A.S. prepared the samples. L.C.L.H., D.A.B. and L.T.H. wrote the manuscript with input from all authors. L.C.L.H. supervised the project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Broadway, D.A., Tetienne, JP., Stacey, A. et al. Quantum probe hyperpolarisation of molecular nuclear spins. Nat Commun 9, 1246 (2018). https://doi.org/10.1038/s41467-018-03578-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-018-03578-1
This article is cited by
-
Enhancing polarization transfer from nitrogen-vacancy centers to external nuclear spins via dangling bond mediators
Communications Physics (2024)
-
Two-level system hyperpolarization using a quantum Szilard engine
Nature Physics (2023)
-
Parallel detection and spatial mapping of large nuclear spin clusters
Nature Communications (2022)
-
Learning models of quantum systems from experiments
Nature Physics (2021)
-
Utilising NV based quantum sensing for velocimetry at the nanoscale
Scientific Reports (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.