Abstract
Generally, studies of the critical current Ic are necessary if superconductors are to be of practical use, because Ic sets the current limit below which there is a zero-resistance state. Here, we report a peak in the pressure dependence of the zero-field Ic, Ic(0), at a hidden quantum critical point (QCP), where a continuous antiferromagnetic transition temperature is suppressed by pressure toward 0 K in CeRhIn5 and 4.4% Sn-doped CeRhIn5. The Ic(0)s of these Ce-based compounds under pressure exhibit a universal temperature dependence, underlining that the peak in zero-field Ic(P) is determined predominantly by critical fluctuations associated with the hidden QCP. The dc conductivity σdc is a minimum at the QCP, showing anti-correlation with Ic(0). These discoveries demonstrate that a quantum critical point hidden inside the superconducting phase in strongly correlated materials can be exposed by the zero-field Ic, therefore providing a direct link between a QCP and unconventional superconductivity.
Similar content being viewed by others
Introduction
Unconventional superconductivity (SC) often is observed in close proximity to a magnetically ordered phase, where the SC transition temperature Tc forms a dome against a non-thermal control parameter, such as the external pressure, chemical substitution, or magnetic field1,2,3,4,5,6. At an optimal value of the tuning parameter, where Tc is the highest, normal state properties do not follow predictions for Landau–Fermi liquids: the electrical resistivity (ρ) does not exhibit a T2 dependence, and the electronic specific heat coefficient (γ = C/T) does not saturate, but rather diverges with decreasing temperature1, 2, 7. These non-Fermi liquid (NFL) behaviors arise from incoherent critical fluctuations associated with a quantum critical point (QCP) hidden inside the SC dome of heavy fermion compounds and some Fe-based superconductors, such as BaFe2(As1−xPx)21, 2, 4, 6, 8. Because the zero-temperature quantum phase transition is typically not accessible without destroying SC, the role of critical magnetic fluctuations on properties of unconventional superconductors has yet to be explored in depth.
The critical current (Ic), which limits the current capacity of a zero-resistance state, is characteristically taken to depend on the strength of vortex pinning, which, in turn, is determined by the geometry and distribution of microstructural defects9,10,11. Because application of pressure should not lead to the creation of different or additional defects or to a substantial change in sample dimensions, Ic in relation to Tc should be at most weakly pressure-dependent. A substantial variation in Ic(P) or Ic/Tc(P), then, logically, should be attributed to intrinsic changes in the superconducting state itself. For example, the zero-field critical current density Jc (equal to Ic/A, where A is the sample cross sectional area perpendicular to current) of the hole-doped high-Tc cuprate superconductor Y0.8Ca0.2Ba2Cu3Oy has a sharp peak that is centered on a critical hole-doping where the pseudogap boundary line projects to zero temperature, and that is attributed in model calculations to changes in the superfluid density12, 13. These results indicate that Ic measurements may provide an opportunity to explore the relationship between unconventional SC and any QCP that is hidden beneath the SC dome.
Here we report a peak in the zero-field critical current, Ic(0), at a critical pressure Pc in pure CeRhIn5 (Rh115) and 4.4% Sn-doped CeRhIn5 (SnRh115), where their respective antiferromagnetic boundary TN(P) extrapolates to T = 0 K inside a dome of pressure-induced SC. The temperature dependence of Ic(0)s for pure Rh115 and SnRh115 under pressure is similar to that of superconducting CeCoIn5, which is close to quantum criticality at ambient pressure. Normalized values of Ic(T, P) follow a common universal curve for each material, suggesting an intrinsic, fundamental connection to quantum criticality. Supporting this conclusion, the magnetic field dependence of the flux-pinning force (Fp = Ic × μ0H), normalized to its maximum value, also forms a pressure-invariant universal curve for each compound. As will be discussed, these discoveries demonstrate that the pressure evolution of zero-field Ic is determined mainly by quantum critical fluctuations, and that the peak in Ic is a direct link to the hidden QCP.
Results
Temperature–pressure phase diagrams
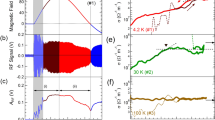
Figure 1a and b presents a contour plot of the zero-field Ic(P, T) in the SC phase and the in-plane resistivity ρab(P, T) in the normal state for pure CeRhIn5 (Rh115) and 4.4% Sn-doped CeRhSn0.22In4.78 (SnRh115) single crystals. The dependence on pressure of the in-plane resistivity and current–voltage curves upon which Fig. 1 is based is displayed in Supplementary Figs. 1 and 2, respectively. The quantum critical region veiled by the superconducting phase is fully exposed by the pressure dependence of zero-field Ic(T). A sharp peak in the value of Ic(T) is clearly observed for pressures around the QCP at Pc, where a large enhancement in the resistivity is accompanied by strong quantum fluctuations3,4,14. In addition, Ic(P) abruptly increases at pressures around Pc*, the critical pressure where coexisting phases of magnetism and SC evolve into a single SC state. In undoped Rh115, large differences between Tcs measured by heat capacity (C) and resistivity (ρ) at pressures below Pc* are ascribed to textured SC originating from an incommensurate long-range magnetic order15,16,17,18.
Temperature–pressure phase diagrams of CeRhIn5 and CeRhSn0.22In4.78 single crystals. In the superconducting state below Tc(P), false colors denote the magnitude of the zero-field critical current Ic(P, T). At temperatures above Tc(P), false colors reflect the magnitude of the in-plane resistivity ρab(P, T). a CeRhIn5 (Rh115) and b CeRhSn0.22In4.78 (SnRh115). For both materials, ρab(P, T) is enhanced around the quantum critical point Pc due to pronounced incoherent inelastic scattering. Similarly, the zero-field Ic(P, T) is largest at Pc, where the QCP is expected, as indicated by the arrow. In both a and b the vertical hashed rectangle is at Pc*, the pressure that separates a phase of coexisting superconductivity and magnetism from a purely SC phase for P > Pc*. Open squares in both a and b represent the antiferromagnetic transition temperature (TN). SC transition temperature (Tc) of Rh115 is evaluated from specific heat (Tc,C) and resistivity (Tc,ρ) measurements, and Tc of SnRh115 is determined as Tc onset (Tc,on) and 50% (Tc,50%) of the normal state resistivity value at Tc,on. AFM, SC, and NFL stand for antiferromagnetic, superconducting, and non-Fermi liquid regions, respectively
Temperature dependences of the zero-field critical current
The antiferromagnetic transition temperature (TN ~ 3.8 K) in pure Rh115 is suppressed by Sn doping, which induces a shift of its extrapolated T = 0 K antiferromagnetic transition, and pressure-induced superconductivity emanates from the tuned QCP4,5 (see Supplementary Fig. 3). Figure 2a and b shows the temperature dependence of the zero-field critical current, Ic(0), for Rh115 and SnRh115 at several pressures, respectively. Here, Ic is determined by using the voltage criterion of 0.1 μV (see Supplementary Fig. 2). Analysis of the flux-pinning force, Fp = Ic × μ0H, shows that the normalized flux-pinning force follows a power-law dependence on magnetic field, fp(h) ∝ hp(1−h)q, and is peaked around hpeak ≈ 0.6, which is characteristic of type-II superconductors with weak pinning (see Supplementary Fig. 4). Here, the normalized pinning force is fp = Fp/Fp,max and the reduced field is h = H/Hirr, where Fp,max is the maximum flux-pinning force and Hirr is the irreversible field. The dependence on temperature of the critical current has been widely explained by Ic(t)/Ic(0) = (1−t2)α(1 + t2)β for type-II superconductors, such as high-Tc cuprates, Fe-based superconductors, and MgB219,20,21,22, where t = T/Tc is the reduced temperature. When Tc variations surrounding defects are important (δTc-pinning), α = 7/6 and β = 5/6, but α = 5/2 and β = −1/2 for δl-pinning that arises from spatial variations in the charge-carrier mean free path (l) near a lattice defect10, 19, 23. These functional forms are shown by the dotted and dashed lines for δTc-pinning to δl-pinning in Fig. 2c, respectively. A crossover of the mechanism from δTc-pinning to δl-pinning has been often reported by introducing additional defects via chemical substitution or heavy ion irradiation, indicating that δTc-pinning is preferred in clean crystals19,20,21.
Temperature dependences of the zero-field critical current for Ce-based heavy fermion materials under pressure. a Temperature dependence of the zero-field critical current, Ic(0), for CeRhIn5 at various pressures. b Zero-field Ic for CeRhSn0.22In4.78 at various pressures. c Reduced temperature (t = T/Tc,0) dependence of Ic, Ic(t), normalized by its value at t = 0.4 for Rh115 and SnRh115 at representative pressures and for CeCoIn5 at ambient pressure. The normalized values of Ic(P, t) for all crystals can be described by a single curve, Ic(t) ∝ (1 − t2)5/6(1 + t2)2/3, indicating universal behavior of Ic(t) with respect to pressure in the CeMIn5 (M = Co, Rh) materials. Dotted and dashed curves are for δTc-pinning and δl-pinning, respectively, as discussed in the text
The values of Ic(t) for SnRh115 at pressures around Pc are fitted together with those for Rh115 and CeCoIn5 in Fig. 2c. The temperature dependence of Ic(0) for CeCoIn5 at ambient pressure is measured to compare it with that of CeRhIn5, because Rh115 is believed to have a SC pairing mechanism similar to that in CeCoIn5. The values of Ic(0) for all samples can be expressed well by one curve with the relation Ic(t) ∝ (1−t2)5/6(1 + t2)2/3, which is distinct from that for Ic(t) controlled by either δTc-pinning or δl-pinning. This universal curve underscores that the origin of the zero-field Ic is the same for each compound, and that it does not change under pressure for these Ce-based quantum critical materials. The fact that external pressure does not create new defects inside the crystals suggests that the pressure evolution of Ic should be related to the pressure dependence of the SC coupling strength.
Discussion
Figure 3a presents the pressure dependences of Ic(0) and Tc,0 for SnRh115, which are similar to each other. However, their relative fractional variations in Ic and Tc, γI ≡ Ic,0(P)/Ic,0(Pc) × 100 and γT ≡ Tc,0(P)/Tc,0(Pc) × 100, where Ic,0(Pc) is Ic extrapolated to zero temperature at Pc and Tc,0(Pc) is the SC transition temperature at Pc, are much different, as shown in Fig. 3b: at 1.0 GPa, the critical current is 45% of the maximum value, and Tc,0 is 67% of its maximal value. The stronger pressure dependence of Ic relative to that of Tc,0 is clearly visible in ratio Ic,0/Tc,0 for SnRh115, as presented in Fig. 3c, d. An abrupt enhancement in Ic,0/Tc,0 is observed at Pc*, and the peak in the pressure dependence of Ic,0/Tc,0 is achieved at Pc. The dc conductivity (=σdc) at Tc onset is shown as a function of pressure in the right ordinate of Fig. 3c, where a minimum value appears near Pc (see Supplementary Fig. 5). The anti-correlation between Ic,0/Tc,0 and σdc in these Ce-based quantum critical compounds may be related with the presence of the hidden QCP at Pc, because the associated critical quantum fluctuations not only act as the SC pairing glue, but also strongly enhance incoherent electron scattering, thus leading to a minimum in σdc at Pc24, 25. Homes’ scaling relation26,27,28 states that the superfluid density ns is proportional to σdcTc in many correlated superconductors and, consequently, that the ratio ns/Tc should be proportional to σdc. The fact that σdc is the minimum at Pc, where Ic,0/Tc,0 is the maximum in these Ce-based compounds, suggests a violation of Homes’ scaling if the strength of the condensate ns is proportional to the critical current Ic,0. Pressure-dependent optical conductivity and/or penetration depth experiments that directly measure ns will be important to provide a stringent test for the validity of Homes’ law in quantum critical superconductors.
Pressure evolution of the zero-field critical current in Sn-doped CeRhIn5. a Pressure dependences of Tc,0 and Ic,0 for SnRh115, where Ic,0 is the value of Ic obtained from an extrapolation of data in Fig. 2b zero Kelvin. b Fractional variations in Ic,0 and Tc,0 for SnRh115 under pressure. The fractions are defined as γI (at 0 K) ≡ Ic,0(P)/Ic,0(Pc) × 100 and γT ≡ Tc,0(P)/Tc,0(Pc) × 100, where Ic,0(Pc) is Ic extrapolated to zero temperature at Pc and Tc,0(Pc) is the superconducting transition temperature at Pc. Values of γI are plotted as a function of pressure for measured or estimated Ic(T, P) at 0 K (squares) and 0.3 K (circles). c The ratio between the critical current and SC transition temperature, Ic,0/Tc,0, plotted together with the dc conductivity at Tc onset, σdc, as a function of the pressure difference P−Pc, where Pc = 1.35 GPa is the QCP. d A contour plot of Ic,0/Tc,0 displayed in the temperature (T) and pressure (P−Pc) plane. The ratio Ic,0/Tc,0 forms a dome centered around the quantum critical point Pc and its values decrease with distance from Pc
Our study demonstrates that the critical current, a fundamental superconducting parameter, is a powerful tool for investigating the presence of a hidden QCP inside the superconducting dome without destroying the superconducting phase. The dependence on temperature of the zero-field Ic for both pure Rh115 and Sn-doped Rh115 exhibits the same functional form under pressure, underscoring that the peak at Pc in the pressure dependence of Ic arises from an enhanced fluctuations around the hidden QCP. Even though these results are specific to the Ce115 heavy-fermion materials, the prediction of similar results for the hole-doping dependence of the critical current density Jc(x) in high-Tc cuprates29 suggests a universal behavior of Jc among unconventional superconductors. These discoveries should stimulate more theoretical and experimental effort to understand the intimate link between quantum criticality and the origin of unconventional superconductivity in various families of correlated electronic systems.
Methods
Measurement outline
CeRhIn5, Sn-doped CeRhIn5, and CeCoIn5 single crystals were synthesized by the indium (In) self-flux method30,31,32. Pressure was generated in a hybrid clamp-type pressure cell with Daphne 7373 as the pressure-transmitting medium, and the pressure was determined by monitoring the shift in the value of Tc for lead (Pb). Measurements of current–voltage (I–V) characteristics under pressure were performed in a Heliox VL system (Oxford Instruments) with a vector magnet (y = 5 T and z = 9 T, American Magnetics Inc.) and in a Physical Property Measurement System (PPMS 9 T, Quantum Design), where the current was provided by a Keithley 6221 unit and the voltage was measured with a Keithley 2182A nanovoltmeter.
Measurement details
Measurements of I–V characteristics were performed in a pulsed mode to minimize Joule heating developed at Ohmic contacts to the samples and copper (Cu) wires between the pressure cell and the connector. The duration of the pulsed current was 10–11 ms, and the repetition rate was one pulse every 2 s, which was sufficient to eliminate Joule heat in the samples33, 34. A standard four-probe method was used to determine I−V, and good Ohmic contact to samples was achieved by using silver epoxy. The critical current was based on a 10−7 V criterion35, which was averaged over three measurements. The dimensions of the measured crystals were 920×330×20, 650×200×22, and 1100×200×47 μm3 for CeRhIn5 (Rh115), CeRhSn0.22In4.78 (SnRh115), and CeCoIn5, respectively. The magnetic-field dependence of the critical current was measured at several pressures and the flux-pinning force (Fp) was estimated from the relation Fp = Ic × μ0H 36,37,38
Data availability
The data sets generated and/or analyzed in this study are available from the corresponding author on reasonable request.
Change history
06 August 2019
An amendment to this paper has been published and can be accessed via a link at the top of the paper.
References
Park, T. et al. Hidden magnetism and quantum criticality in the heavy fermion superconductor CeRhIn5. Nature 440, 65–68 (2006).
Knebel, G., Aoki, D., Braithwaite, D., Salce, B. & Flouquet, J. Coexistence of antiferromagnetism and superconductivity in CeRhIn5 under high pressure and magnetic field. Phys. Rev. B 74, 020501(R) (2006).
Park, T. et al. Isotropic quantum scattering and unconventional superconductivity. Nature 456, 366–368 (2008).
Seo, S. et al. Controlling superconductivity by tunable quantum critical points. Nat. Commun. 6, 6433 (2015).
Ferreira, L. M. et al. Tuning the pressure-induced superconducting phase in doped CeRhIn5. Phys. Rev. Lett. 101, 017005 (2008).
Analytis, J. G. et al. Transport near a quantum critical point in BaFe2(As1-xPx)2. Nat. Phys. 10, 194–197 (2014).
Gegenwart, P., Si, Q. & Steglich, F. Quantum criticality in heavy-fermion metals. Nat. Phys. 145, 186–197 (2008).
Hashimoto, K. et al. A sharp peak of the zero-temperature penetration depth at optimal composition in BaFe2(As1-xPx)2. Science 336, 1554–1557 (2012).
Fang, L. et al. Huge critical current density and tailored superconducting anisotropy in SmFeAsO0.8F0.15 by low-density columnar-defect incorporation. Nat. Commun. 4, 2655 (2013).
Kunchur, M. N., Lee, S.-I. & Kang, W. N. Pair-breaking critical current density of magnesium diboride. Phys. Rev. B 68, 064516 (2003).
Dew-Hughes, D. The critical current of superconductors: an historical review. Low Temp. Phys. 27, 713–722 (2001).
Talantsev, E. F. & Tallon, J. L. Universal self-field critical current for thin-film superconductors. Nat. Commun. 6, 7820 (2015).
Talantsev, E. F., Crump, W. P. & Tallon, J. L. Thermodynamic parameters of single- or multi-band superconductors derived from self-field critical currents. Ann. Phys. 529, 1700197 (2017).
Knebel, G., Aoki, D., Brison, J.-P. & Flouquet, J. The quantum critical point in CeRhIn5: a resistivity study. J. Phys. Soc. Jpn. 77, 114704 (2008).
Park, T. et al. Textured superconducting phase in the heavy fermion CeRhIn5. Phys. Rev. Lett. 108, 077003 (2012).
Park, T. & Thompson, J. D. Magnetism and superconductivity in strongly correlated CeRhIn5. New J. Phys. 11, 055062 (2009).
Llobert, A. et al. Magnetic structure of CeRhIn5 as a function of pressure and temperature. Phys. Rev. B 69, 024403 (2004).
Yashima, M. et al. Strong coupling between antiferromagnetic and superconducting order parameters of CeRhIn5 studied by 115In nuclear quadrupole resonance spectroscopy. Phys. Rev. B 79, 214528 (2009).
Griessen, R. et al. Evidence for mean free path fluctuation induced pinning in YBa2Cu3O7 and YBa2Cu4O8 films. Phys. Rev. Lett. 72, 1910–1913 (1994).
Wen, H. H., Zhao, Z. X., Xiao, Y. G., Yin, B. & Li, J. W. Evidence for flux pinning induced by spatial fluctuation of transition temperatures in single domain (Yl-xPrx) Ba2Cu3O7-δ samples. Physica C 251, 371–378 (1995).
Xiang, F. X. et al. Evidence for transformation from δT c to δl pinning in MgB2 by graphene oxide doping with improved low and high field J c and pinning potential. Appl. Phys. Lett. 102, 152604 (2013).
Ghorbani, S. R., Wang, X. L., Shahbazi, M., Dou, S. X. & Lin, C. T. Fluctuation of mean free path and transition temperature induced vortex pinning in (Ba,K)Fe2As2 superconductors. Appl. Phys. Lett. 100, 212601 (2012).
Blatter, G., Feigel’man, M. V., Geshkenbein, V. B., Larkin, A. I. & Vinokur, V. M. Vortices in high-temperature superconductors. Rev. Mod. Phys. 66, 1125 (1994).
Howald, L., Knebel, G., Aoki, D., Lapertot, G. & Brison, J.-P. The upper critical field of CeCoIn5. New J. Phys. 13, 113039 (2011).
Miyake, K. & Narikiyo, O. Enhanced impurity scattering due to quantum critical fluctuations: perturbational approach. J. Phys. Soc. Jpn. 71, 867–871 (2002).
Homes, C. C. et al. A universal scaling relation in high-temperature superconductors. Nature 430, 539–541 (2004).
Dordevic, S. V., Basov, D. N. & Homes, C. C. Do organic and other exotic superconductors fail universal scaling relations? Sci. Rep. 3, 1713 (2013).
Uemura, Y. J. et al. Universal correlations between T c and n s/m* (carrier density over effective mass) in high-T c cuprate superconductors. Phys. Rev. Lett. 62, 2317–2320 (1989).
Tallon, J. L. et al. Critical doping in overdoped high-T c superconductors: a quantum critical point? Phys. Stat. Sol. B 251, 531–540 (1999).
Hegger, H. et al. Pressure-induced superconductivity in quasi-2D CeRhIn5. Phys. Rev. Lett. 84, 4986–4989 (2000).
Bauer, E. D. et al. Antiferromagnetic quantum critical point in CeRhIn5-xSnx. Physica B 378–380, 142–143 (2006).
Petrovic, C. et al. Heavy-fermion superconductivity in CeCoIn5 at 2.3 K. J. Phys.: Condens. Matter 13, L337–L342 (2001).
Kunchur, M. N. Current-induced pair breaking in magnesium diboride. J. Phys.: Condens. Matter 16, R1183–R1204 (2004).
Liang, M., Kunchur, M. N., Fruchter, L. & Li, Z. Z. Depairing current density of infinite-layer Sr1− xLaxCuO2 superconducting films. Physica C 492, 178–180 (2013).
Dobrovolskiy, O. V., Begun, E., Huth, M. & Shklovskij, V. A. Electrical transport and pinning properties of Nb thin films patterned with focused ion beam-milled washboard nanostructures. New J. Phys. 14, 113027 (2012).
Fietz, W. A. & Webb, W. W. Hysteresis in superconducting alloys-temperature and field dependence of dislocation pinning in niobium alloys. Phys. Rev. 178, 657–667 (1969).
Dew-Hughes, D. Flux pinning mechanisms in type-II superconductors. Philos. Mag. 30, 293–305 (1974).
Kramer, E. J. Scaling laws for flux pinning in hard superconductors. J. Appl. Phys. 44, 1360–1370 (1973).
Acknowledgements
We thank J. D. Thompson, Y. Bang, Z. Fisk, I. Vekhter, Y. Yang, J. H. Yun, and S. Oh for helpful discussions. This work was supported by a National Research Foundation (NRF) of Korea grant funded by the Korean Ministry of Science, ICT and Planning (No. 2012R1A3A2048816). S.-G.J. was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (NRF-2015R1D1A1A01060382). Work at Los Alamos National Laboratory was performed under the auspices of the U.S. Department of Energy, Office of Basic Energy Sciences, Division of Materials Sciences and Engineering. S.S. acknowledges a Director’s Postdoctoral Fellowship through the Los Alamos Laboratory Directed Research and Development program.
Author information
Authors and Affiliations
Contributions
S.-G.J. conceived the work. S.-G.J., S.S., and S.L. performed the I–V measurements at various pressures. E.D.B. and H.-O.L. synthesized the CeRhIn5, Sn-doped CeRhIn5, and CeCoIn5 single crystals. S.-G.J. analyzed the data and discussed the results with all authors. The manuscript was written by S.-G.J. and T.P. with inputs from all authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Jung, SG., Seo, S., Lee, S. et al. A peak in the critical current for quantum critical superconductors. Nat Commun 9, 434 (2018). https://doi.org/10.1038/s41467-018-02899-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-018-02899-5
This article is cited by
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.