Abstract
The upper critical field of a cuprate high-temperature superconductor, La1.84Sr0.16CuO4, was investigated by high-frequency self-resonant contactless electrical conductivity measurements in magnetic fields up to 102 T. An irreversible transition was observed at 85 T (T = 4.2 K), defined as the upper critical field. The temperature-dependent upper critical field was argued on the basis of the Werthamer-Helfand-Hohenberg theory. The Pauli-limiting pair-breaking process with a small contribution of the spin-orbit coupling explained the first-order phase transition exhibiting a hysteresis observed at low temperatures.
Similar content being viewed by others
Introduction
Magnetic field destroys superconductivity at the upper critical magnetic field, Bc2, which provides information about the pair-breaking process in the superconducting state. In addition, a magnetic-field-induced normal state is realized even at low temperatures far below the superconducting transition temperature (Tc), where the electronic state is unaffected by thermal fluctuation. Therefore, a novel quantum nature may be unveiled, which cannot be observed in the normal state in the absence of magnetic field. For example, the Fulde-Ferrell-Larkin-Ovchinnikov (FFLO) state1,2,3 and re-entrant superconductivity4,5,6 are theoretically suggested under high magnetic fields. This attracts attention of a high-field study on superconducting materials.
When a magnetic field is applied to a superconducting material, two independent mechanisms are considered to affect the pair-breaking process in the superconducting state: the orbital-limiting effect7,8 and Pauli paramagnetic (Pauli-limiting) effect9,10. In the case of the orbital-limiting effect, Cooper pair breaking is induced by the momentum, eA/ℏc, where A is the vector potential, and eventually, the kinetic energy of supercurrent exceeds the superconducting gap energy. The upper critical field is recognized as the orbital-limiting field, Borb = ϕ0/2πξ2, which depends on the coherence length of Cooper pair, ξ. By contrast, in the case of the Pauli paramagnetic effect, the Zeeman splitting energy of electronic spin exceeds the superconducting gap energy, and singlet Cooper pair becomes energetically unstable. In this case, the upper critical field is recognized as the Pauli-limiting field, Bp, where an irreversible first-order phase transition (FOT) is expected to be observed.
Cuprate high-temperature superconductors have a two-dimensional layered crystal structure, and electrical transport is confined in the CuO2 plane perpendicular to the c-axis. Therefore, the coherence length in the ab-plane is much longer than that along the c-axis, which induces an anisotropic pair-breaking mechanism depending on the direction of the magnetic fields applied to a crystal. The orbital-limiting effect is dominant under magnetic fields parallel to the c-axis (B//c). On the other hand, the Pauli-limiting effect is important under magnetic fields parallel to the CuO2 plane (B//ab), where Borb becomes larger than Bp. In general, Bc2 in the B//ab configuration is larger than that in the B//c configuration.
Because Tc in cuprate superconductors largely depends on the carrier concentration, Bc2 of the underdoped or overdoped materials can be suppressed below 100 T, which is sufficient to be generated by a non-destructive pulsed magnet. Following the pioneering work in 2007 on quantum oscillation above Bc2 to characterize the Fermi surface11, numerous research studies about Bc2 and quantum oscillations have been reported, particularly on underdoped YBa2Cu3O7-x (YBCO)12,13,14,15,16,17,18,19,20,21,22,23,24,25. However, an optimally-doped YBCO (Tc ∼ 90 K) has a Bc2 higher than 100 T, which can only be generated by a destructive pulsed magnet. For this material, extrapolation analysis has been conducted to evaluate Bc2 (T = 0)20,22,26. Above 100 T, a high-field study of cuprate superconductors is rare owing to difficulties associated with the microsecond-order pulse duration time and the exploding nature of the destructive pulsed magnet. Bc2 (T = 0 K) of YBCO has been evaluated to be 128 T and 240 T in the B//c and B//ab configurations27. In the above study, the magnetic field was generated by the electromagnetic flux compression technique28, where the measurement probe and sample were completely destroyed at the peak of a magnetic field pulse. This allowed the phase transition point at Bc2 to be observable only in ascending magnetic fields. Therefore, the details of hysteresis cannot be discussed.
In this report, we focus on another type of cuprate superconductor, La2−xSrxCuO4 (LSCO), whose Tc is approximately 40 K in the optimally-doped region (x ~ 0.16). Because its Tc is smaller than that of other typical cuprate superconductors, YBCO and Bi2Sr2CaCu2O8+x (Bi2212, Tc ~ 90 K), Bc2 (T = 0) of LSCO is easier to access. In an optimally-doped LSCO, the coherence length anisotropy takes a value between the corresponding values of YBCO and Bi2212 (YBCO: 5–729, LSCO (x = 0.15): ~1430, Bi2212: 50–20029). Because two-dimensionality is one of the distinctive features of cuprate superconductors, the research on LSCO may become a linking bridge to understand the complete physics of cuprate superconductors.
In the B//c configuration, the transport property has been investigated up to 61 T31,32,33,34,35, and Bc2 in the B//c configuration was found to be ~60 T at 4.2 K for an optimally-doped LSCO (x = 0.15)34. For an overdoped LSCO (x = 0.19), a recent high-field study up to 80 T has shown that the strength of the magnetoresistance (dρ/dB) does not depend on temperature below 25 K, which is different from the trend for conventional metals36. On the other hand, in the B//ab configuration, the measurement of Bc2 in LSCO (x = 0.08, 0.14, and 0.18) has been performed only up to 17.5 T in the vicinity of Tc37 and there has been no direct measurement of Bc2 for an optimally-doped LSCO at low temperatures. In this study, we have directly observed Bc2 of LSCO (x = 0.16) in the B//ab configuration by applying ultra-high magnetic fields up to 102 T.
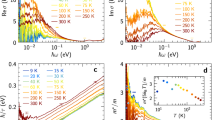
The results of the high-frequency electrical conductivity measurement using the self-resonant coil (SRC) at 4.2 K (#1) are displayed in Fig. 1(a–c), where the time evolution of the probe signal and its amplitude ARF are presented with the waveform of the pulsed magnetic field. ARF(t) was analyzed in (i) an elevating and (ii) a descending slope of magnetic field pulse. The data in the first 1 μs in region (i) was excluded in the analysis (the hatched region in gray) owing to the condenser discharging large noises that disturb the probe signal.
(a) Waveform of the magnetic field generated by the single-turn coil (STC) megagauss generator, (b) the RF probe signal, and (c) amplitude of (b) obtained in experiment #1 at 4.2 K. (d–f) Magnetic field dependence of the electrical conductivity at various temperatures. The down triangles denote Bc2. The horizontal arrows indicate the values of the normal-state DC electrical conductivity at zero magnetic field. The colored broken lines show the data with electromagnetic discharging noise in the elevating slope of the magnetic field pulse. The panel (d) is based on the data published in Nakamura et al.38.
The magnetic field dependence of the electrical conductivity, σ, at 4.2 K (#1), 30 K (#2), and above Tc (100 K, #3) is shown in Fig. 1(d–f). ARF was converted to the value of σ by using a formula based on the electromagnetic analysis of the SRC described in ref.38 (also see Supplementary Fig. S3). The horizontal arrows in Fig. 1(d,e) indicate the electrical conductivity in the normal state at zero magnetic field (σDC)31. The values of σDC below Tc were taken from σDC just above Tc (Fig. 1(d,e)). At 4.2 K (experiment #1, Fig. 1(d)), σ decreased with magnetic field and saturated at approximately 85 T (indicated by the down triangle), with evidence of a clear hysteresis. This type of magnetic field dependence was reproduced by an independent experiment (see Supplementary Fig. S4).
At 30 K (experiment #2), σ(B) decreased with magnetic field, and saturated at 46 T (down triangle). In the experiment far above Tc (100 K, #3), σ(B) exhibited a practically constant value in magnetic fields. This is consistent with a previous report of measurements up to 61 T32, stating that a change in the magnetoresistance above Tc is small for an optimally-doped LSCO.
σ(B) at 4.2 K (#1, Fig. 1(d)) continuously decreased up to Bc2. In the B//ab configuration, the quantum flux called as the Josephson vortex selectively penetrates between the CuO2 layers. The decrease in σ(B) is considered to arise from the flow resistance of the Josephson vortex39. In addition, a magnetic field induces an energy shift of the quasiparticle excitation (Doppler effect40), which causes an increase in the density of the quasiparticle state for an anisotropic pairing symmetry, such as d-wave superconductor41. This effect also contributes to the decrease in σ. The kink structure around 10 T is considered to arise from a change in the Josephson vortex state. Various vortex states are theoretically suggested, which appear as a consequence of competition between the vortex-vortex interaction and the pinning force42,43,44,45. We note that σ in Fig. 1(d,e) does not diverge near zero magnetic field. The divergence in σ is difficult to observe by a contactless technique, because it has a finite measurable frequency range. In addition, a high-frequency probe signal induces a finite dissipation of the quasiparticle in the core of quantum flux, even in the superconducting state.
The hysteresis in σ(B) observed at 85 T is considered as an evidence of FOT at Bc2. The melting transition of the vortex lattice cannot account for the hysteresis observed in Fig. 1(d). If this is the case, the high-field region above 85 T becomes the vortex liquid phase, where the superconducting order parameter remains, and σ continues to decrease with increasing magnetic field. However, our result in Fig. 1(d) shows that σ above 85 T is nearly constant within experimental error. Therefore, the high-field region above 85 T could be regarded as a magnetic-field-induced normal state, which arises after the Cooper pair breaking takes place completely.
Joule heating induced by the short pulse magnetic field cannot be a major cause of the hysteresis observed in σ (B). Typical phenomena caused by Joule heating can be represented in Fig. 2(b) of the previous report by Sekitani et al.46, in which σ(B) shows significant deviation in the entire region of ascending and descending magnetic fields. In order to confirm the effect of Joule heating on our sample, we have conducted similar contactless transport measurements by using long pulse magnet (Magnetic fields up to 55 T with a duration time 35 ms, indicating that dB/dt is reduced by four orders of magnitude. See Supplementary Fig. S5.), to see a good coincidence except a tiny difference of Bc2 at 30 K. Therefore, we believe that the Joule heating effect is not significant in this study.
(a) B-T phase diagram of an optimally-doped LSCO. The open circles denote Bc2 measured by using an STC magnet in this study, and the open diamonds (colored in pink) are Bc2s near Tc reported in ref.30. The open squares are Bc2 in the B//c configuration determined by Ando et al.34. The solid line shows the upper critical field of the WHH theory, BWHH. Tr* is the temperature at the local maxima of BWHH(T). The dotted line is a guide for the eye, indicating the critical field of the first-order transition, BFOT. (b) Enlarged plot of (a). Several BWHH and BFOT (guide) are displayed as solid and dotted lines, respectively.
A superconducting-normal (S-N) transition is expected to be the FOT, when the Pauli paramagnetism causes the pair-breaking of superconductivity9,10. The Pauli-limiting field is expressed as Bp = ΔSC/\(\surd 2\) μB, where μB is the Bohr magneton and ΔSC is the superconducting gap energy. Given ΔSC of LSCO as 2ΔSC = 4.3 kBTc evaluated from the ARPES measurement47, Bp is estimated to be 83 T in our sample, which is close to Bc2 assigned in Fig. 1(d). It should be noted that the relationship, 2ΔSC ~ 5 kBTc, has been confirmed for a number of cuprate superconductors48. The common relation held in LSCO implies that the superconducting energy scale in cuprate superconductors is governed by a universal mechanism.
The upper critical fields were plotted against temperature to display the magnetic field-temperature (B-T) phase diagram in Fig. 2(a). The lower abscissa in Fig. 2(a) is the reduced temperature, Tr = T/Tc. The open circles are the Bc2(Tr) values obtained in this study in the B//ab configuration, and the error bars indicate an accuracy of the estimation of Bc2 in the descending slope of the magnetic field pulse in Fig. 1(d,e). The open squares plot Bc2 (Tr) in the B//c configuration of LSCO (x = 0.15), as reported by Ando et al.34. It is noted in Fig. 2(a) that the anisotropy of Bc2 is reduced at low temperatures, where the Pauli paramagnetic effect becomes a dominating factor. This tendency is in contrast to the orbital-limiting case. The Bc2(Tr) data just below Tc (open diamonds) determined by ref.30 are added to the plot in Fig. 2(a). We note that the carrier concentration (x = 0.15) of LSCO in refs30,34 is slightly different from that of our sample (x = 0.16). The Bc2 (Tr) values for LSCO with x = 0.15 and 0.16 are expected to practically coincide, because both enter into an optimally-doped region, where Tc takes a broad maximum in the electronic phase diagram.
A magnitude of the Pauli paramagnetic effect is described by the Maki parameter, α, which is defined as the ratio of the orbital-limiting field, Borb, and Bp49,
According to Maki’s theory, α is experimentally evaluated from the slope of Bc2 close to Tc. In LSCO, dBc2/dT was estimated to be 8.33 T/K at around Tc, indicating α = 4.4. This value is compatible with those for other examples. The heavy fermion compound, CeCoIn5, is a typical Pauli-limiting superconductor50, and α is evaluated to be 4.6 in the B//ab configuration and 5.0 in the B//c configuration51. In CeCoIn5, a discernible hysteresis is observed to exhibit the FOT in the magnetization curve52.
Bc2(Tr) in Fig. 2(a) was analyzed by using the Werthamer-Helfand-Hohenberg (WHH) theory8, which considered both the Pauli paramagnetic effect and the spin-orbit interaction. The Maki parameter and the WHH theory have been used to analyze Bc2(T) in high-temperature superconductors such as cuprates27,46 and iron-pnictides53,54,55,56. The temperature dependence of the upper critical field based on the WHH theory is described as follows8:
where the dimensionless magnetic field, Br = 2eBWHH vF2τ / (6πkBTc), is defined by using the upper critical field within the frameworks of the WHH theory, BWHH, Fermi velocity, vF, and carrier scattering time, τ. λSO is the spin-orbit coupling parameter, which provides the magnitude of the spin-flip scattering in material. In our analysis, the Fermi velocity and scattering time cannot be evaluated separately. Because the Maki parameter is described as \(\alpha =3\hslash /2{m}_{e}{v}_{F}^{2}\tau \) in the WHH theory8, vF2τ is calculated to be 3.9 × 10−5 m2/s for α = 4.4. This is smaller than 5.8 × 10−4 m2/s evaluated from the results of the ARPES measurements; vF = 2.9 × 105 m/s57 and the inverse of mean free path 1/vFτ = 0.05 × 1010 m−1 58. The difference in vF2τ may come from the simplification in the WHH theory, ignoring the Fermi surface anisotropy and strong electron-phonon coupling. In relation to this issue, we need an additional scaling factor s to fit Bc2 by BWHH; Br = 2eBWHH vF2τ s/ (6πkBTc). Therefore, we calculated Br(Tr) for parameters (α, λSO), and then, determined s (~1.5) to fit Bc2 = 46 T of the experiment #2.
In the case of (α, λSO) = (0, 0), the pair-breaking is solely caused by the orbital-limiting effect (BWHH = Borb). In this case, BWHH(T = 0) is evaluated to be 0.69Tc(dBc2/dT)T=Tc = 211 T for a dirty superconductor8, which is much different from the experimental result. Using α = 4.4 determined by the dBc2/dT slope near Tc, BWHH(Tr) for (α, λSO) = (4.4, 0.0) is presented as a solid curve in Fig. 2(a), which exhibits a local maximum at Tr* = 0.34. At low temperatures, Bc2 are evidenced to deviate from BWHH. According to the WHH theory8, BWHH represents the critical field of the second-order S-N transition. When the Pauli paramagnetic effect is dominant, BWHH takes a local maximum at a finite temperature, Tr*. The Pauli paramagnetic effect on the upper critical field has been described in detail by Maki and Tsuneto10. The FOT occurs at the upper critical field, BFOT (>BWHH), below Tr*. In this case, BWHH below Tr* does not represent the phase transition point, but becomes the supercooling field. Accordingly, the hysteresis observed in Bc2 at 4.2 K (Tr = 0.11) is a natural consequence when the upper critical field is dominantly determined by the Pauli paramagnetic effect. In Fig. 2(a), a dotted line was added as a guide for eyes, where the critical field becomes BFOT.
The spin-orbit coupling parameter λSO is also estimated in the following way. In Fig. 2(b), we show the enlarged plot of the B-T phase diagram at low temperatures. When we set α = 4.4, BWHHs for several values of λSO are plotted as solid curves. BFOT (dotted guideline) is considered to locate above BWHH(Tr*), because BFOT has a negative slope at the low-temperature limit (BFOT = (ΔSC2/2 −(πT)2/3)0.5)10. Therefore, the upper limit value of λSO is determined from the relation, BWHH(Tr*) = 84. In this manner, the spin-orbit coupling parameter was estimated to be less than 0.1 as is notified from the plot in Fig. 2(b). λSO relates to the spin-flip scattering time τ2, λSO = 1/3πTcτ28. The condition λSO < 0.1 indicates that τ2 > 1.4 × 10−12 s, which is far larger than the total scattering time τ = 6.9 × 10−15 s evaluated from the results of the ARPES measurements57,58. The magnitude relation between τ and τ2 is consistent with the assumption of the WHH theory, stating that the spin-flip scattering process is infrequent compared with the spin-independent scattering process (τ < < τ2)8.
The spin-orbit coupling suppresses the Pauli paramagnetic effect, because the spin-flip scattering induces an effective reduction of the Zeeman splitting of the energy levels of electrons in the singlet Cooper pair. In the α-λSO diagram shown in Fig. 3, a FOT occurs at Bc2 when α > αc (pink-colored region)8, where
α - λSO phase diagram. In the pink-colored region above αc, the first-order phase transition at Bc2 is predicted by the WHH theory. The cross symbols denote (α, λSO) parameters for materials with a lack of hysteresis at Bc227,53,54,55. The open circles represent the values of α for materials with a hysteresis observed at Bc251,56. We note that the parameter, λSO, is not considered in the analysis in refs51,56.
The parameter (α, λSO) of LSCO (x = 0.16) is located inside the pink-colored region. In contrast, Bc2(T) of another typical cuprate superconductor, YBCO, is well fitted by the WHH parameter (α, λSO) = (5.1, 1.5) in the B//ab configuration27, which is outside of the pink-colored region in Fig. 3. Therefore, from the discussion above, it could be inferred that the S-N transition in YBCO can hardly be a FOT at low temperatures. In Fig. 3, (α, λSO) of other superconductors are also shown as blue cross symbols (no hysteresis observed at Bc253,54,55) and blue open circles (hysteresis observed at Bc251,56). We note that the parameter λSO is not included in the analysis in refs51,56.
In cuprate superconductors, the magnitude of the spin-orbit coupling is considered to depend on the buckling in the CuO2 plane. When the inversion symmetry perpendicular to the CuO2 plane breaks, a Rashba-type spin-orbit coupling occurs59. Among the cuprate superconductors, the buckling in YBCO is the largest, where the Cu-O-Cu angle is approximately 165 deg60,61. Actually, the strong spin-orbit coupling in YBCO was evidenced by the high-field quantum oscillation of side-frequencies in the nodal direction of the d-wave order parameter62. Contrastingly, in LSCO, the Cu-O-Cu angle is approximately 177 deg63, indicating that the CuO2 plane is practically flat. Therefore, the spin-orbit coupling is suggested to be much smaller than that in YBCO, which is consistent in our study, as shown in Fig. 3. In terms of the spin-flip scattering time, τ2 of YBCO can be evaluated to be 3.8 × 10−14 s, from Tc ~ 90 K and λSO = 1.527. This value is considerably smaller than that of LSCO.
From the above discussion, FOT at Bc2 induced by the Pauli paramagnetic effect is only realized in cuprate superconductors when the strict conditions, (i) the B//ab configuration and (ii) a small buckling in the CuO2 plane, are satisfied. In this respect, LSCO can be regarded as a rare case among cuprate superconductors, in which Bc2 is studied as the FOT. A comparison with a typical Pauli-limiting superconductor, CeCoIn5, which exhibits an exotic high-field phase such as the FFLO state in the vicinity of Bc2, might impose a novel guideline to reveal the magnetic-field-induced superconducting properties.
Conclusion
In summary, the electrical conductivity measurements using the SRC method were performed for a cuprate high-temperature superconductor, La1.84Sr0.16CuO4, under ultra-high magnetic fields up to 102 T using a single-turn coil megagauss generator. The upper critical field was investigated in the B//ab configuration, where a first-order phase transition was observed at low temperature. Comparison with the WHH theory indicated that both a large Maki parameter and a small amount of the spin-orbit coupling parameter were necessary to explain the temperature dependence of Bc2 and the Pauli-limiting first-order phase transition. These conditions were only realized for the B//ab configuration and a small buckling of the CuO2 plane in La1.84Sr0.16CuO4.
Experimental methods
The optimally-doped LSCO (x = 0.16, Tc = 36.7 K) single crystal was synthesized by the traveling-solvent floating-zone method64. The concentration of Sr ion was determined by inductively-coupled-plasma optical-emission-spectrometry65. The samples were cut to a thin tabular shape parallel to the ab-plane, whose dimension was 1 × 1 × 0.05–0.07 mm3.
Magnetic fields up to 102 T were generated by a vertical single-turn coil (STC) megagauss generator66. The duration of the pulsed magnetic field with a damped sinusoidal shape is 6 μs. Because the destruction of the magnet coil takes place in outward direction, a measurement sample is intact after the magnetic field generation. Therefore, a hysteresis phenomenon, if any, would be observable on the elevating and descending slopes of the magnetic field pulse. The magnetic field was applied along the ab-plane of LSCO sample (B//ab). In the STC magnet, a liquid helium cryostat was set, enabling the measurements at temperatures down to 2 K67.
The in-plane electrical conductivity of LSCO sample was measured by the contactless self-resonant coil method38,68. A home-made planar probe coil worked by itself as an LCR resonant circuit (self-resonant coil, hereafter called as SRC). The ab-plane of sample was mounted on the SRC, and radio-frequency (RF) current was applied to the SRC as a probe signal. The experimental set-up and measurement conditions are described in Supplementary Materials. When the electrical conductivity of a sample changes, the resonant spectrum of an SRC is affected by the electromagnetic coupling between a sample and an SRC. Therefore, when an RF current closely tuned to the resonant frequency (fres, ~800 MHz) was applied to an SRC, the return RF voltage responded sensitively to changes in the electrical conductivity of the sample, σ. The amplitude of the return RF voltage, ARF, was monitored by a high-resolution (12 bit) digital oscilloscope.
Data availability
The datasets generated during and/or analyzed during the current research are available from the corresponding author on reasonable request.
References
Fulde, P. & Ferrell, R. A. Superconductivity in a strong spin-exchange field. Phys. Rev. 135, A550 (1964).
Larkin, A. I. & Ovchinnikov, Y. N. Nonuniform state of superconductors. Sov. Phys. JETP 20, 762 (1965).
Bianchi, A., Movshovich, R., Capan, C., Pagliuso, P. G. & Sarrao, J. L. Possible Fulde-Ferrell-Larkin-Ovchinnikov superconducting state in CeCoIn5. Phys. Rev. Lett. 91, 187004 (2003).
Lebed, A. G. & Yamaji, K. Restoration of superconductivity in high parallel magnetic fields in layered superconductors. Phys. Rev. Lett. 80, 2697 (1998).
Uji, S. et al. Magnetic-field-induced superconductivity in a two-dimensional organic conductor. Nature 410, 908 (2001).
Lévy, F., Sheikin, I., Grenier, B. & Huxley, A. D. Magnetic field-induced superconductivity in the ferromagnet URhGe. Science 309, 1343 (2005).
Helfand, E. & Werthamer, N. R. Temperature and purity dependence of the superconducting critical field, H c2. II. Phys. Rev. 147, 288 (1966).
Werthamer, N. R., Helfand, E. & Hohenberg, P. C. Temperature and purity dependence of the superconducting critical field, H c2. III. electron spin and spin-orbit effects. Phys. Rev. 147, 295 (1966).
Sarma, G. On the influence of a uniform exchange field acting on the spins of the conduction electrons in a superconductor. J. Phys. Chem. Solids 24, 1029 (1963).
Maki, K. & Tsuneto, T. Pauli paramagnetism and superconducting state. Prog. Theor. Phys. 31, 945 (1964).
Doiron-Leyraud, N. et al. Quantum oscillations and the Fermi surface in an underdoped high-Tc superconductor. Nature 447, 565 (2007).
LeBoeuf, D. et al. Electron pockets in the Fermi surface of hole-doped high-T c superconductors. Nature 450, 533 (2007).
Yelland, E. A. et al. Quantum oscillations in the underdoped cuprate YBa2Cu4O8. Phys. Rev. Lett. 100, 047003 (2008).
Bangura, A. F. et al. Small Fermi surface pockets in underdoped high temperature superconductors: observation of Shubnikov–de Haas oscillations in YBa2Cu4O8. Phys. Rev. Lett. 100, 047004 (2008).
Jaudet, C. et al. de Haas-van Alphen oscillations in the underdoped high-temperature superconductor YBa2Cu3O6.5. Phys. Rev. Lett. 100, 187005 (2008).
Audouard, A. et al. Multiple quantum oscillations in the de Haas-van Alphen spectra of the underdoped high-temperature superconductor YBa2Cu3O6.5. Phys. Rev. Lett. 103, 157003 (2009).
Singleton, J. et al. Magnetic quantum oscillations in YBa2Cu3O6.61 and YBa2Cu3O6.69 in fields of up to 85 T: patching the hole in the roof of the superconducting dome. Phys. Rev. Lett. 104, 086403 (2010).
Ramshaw, B. J. et al. Angle dependence of quantum oscillations in YBa2Cu3O6.59 shows free-spin behaviour of quasiparticles. Nat. Phys. 7, 234 (2010).
LeBoeuf, D. et al. Lifshitz critical point in the cuprate superconductor YBa2Cu3Oy from high-field Hall effect measurements. Phys. Rev. B 83, 054506 (2011).
Ramshaw, B. J. et al. Vortex lattice melting and H c2 in underdoped YBa2Cu3Oy. Phys. Rev. B 86, 174501 (2012).
Sebastian, S. E. et al. Normal-state nodal electronic structure in underdoped high-T c copper oxides. Nature 511, 61 (2014).
Grissonnanche, G. et al. Direct measurement of the upper critical field in cuprate superconductors. Nat. Commun. 5, 3280 (2014).
Yu, J. F. et al. Magnetization of underdoped YBa2Cu3Oy above the irreversibility field. Phys. Rev. B 92, 180509 (2015).
Doiron-Leyraud, N. et al. Evidence for a small hole pocket in the Fermi surface of underdoped YBa2Cu3Oy. Nat. Commun. 6, 6034 (2015).
Ramshaw, B. J. et al. Quasiparticle mass enhancement approaching optimal doping in a high-T c superconductor. Science 348, 317 (2015).
Rullier-Albenque, F., Alloul, H. & Rikken, G. High-field studies of superconducting fluctuations in high-T c cuprates: Evidence for a small gap distinct from the large pseudogap. Phys. Rev. B 84, 014522 (2011).
Sekitani, T., Miura, N., Ikeda, S., Matsuda, Y. & Shiohara, Y. Upper critical field for optimally-doped YBa2Cu3O7−δ. Physica B: Condensed Matter 346-347, 319 (2004).
Takeyama, S. & Kojima, E. A copper-lined magnet coil with maximum field of 700 T for electromagnetic flux compression. J. Phys. D: Appl. Phys. 44, 425003 (2011).
Blatter, G., Feigel’man, M. V., Geshkenbein, V. B., Larkin, A. I. & Vinokur, V. M. Vortices in high-temperature superconductors. Rev. Mod. Phys. 66, 1125 (1994).
Suzuki, M. Thermally activated resistive behavior and flux motion in La2−xSrxCuO4 single-crystal thin films. Phys. Rev. B 46, 14230 (1992).
Ando, Y., Boebinger, G. S., Passner, A., Kimura, T. & Kishio, K. Logarithmic divergence of both in-plane and out-of-plane normal-state resistivities of superconducting La2-xSrxCuO4 in the zero-temperature limit. Phys. Rev. Lett. 75, 4662 (1995).
Boebinger, G. S. et al. Insulator-to-metal crossover in the normal state of La2−xSrxCuO4 near optimum doping. Phys. Rev. Lett. 77, 5417 (1996).
Ando, Y. et al. Normal-state Hall effect and the insulating resistivity of high-T c cuprates at low temperatures. Phys. Rev. B 56, R8530 (1997).
Ando, Y. et al. Resistive upper critical fields and irreversibility lines of optimally doped high- T c cuprates. Phys. Rev. B 60, 12475 (1999).
Cooper, R. A. et al. Anomalous Criticality in the Electrical Resistivity of La2−xSrxCuO4. Science 323, 603–607 (2009).
Giraldo-Gallo, P. et al. Scale-invariant magnetoresistance in a cuprate superconductor. Science 361, 479 (2018).
Iwasaki, H. et al. Vortex glass transition of the Josephson vortex system in LSCO crystals. Physica C: Superconductivity 388–389, 735 (2003).
Nakamura, D., Altarawneh, M. M. & Takeyama, S. Radio frequency self-resonant coil for contactless AC-conductivity in 100 T class ultra-strong pulse magnetic fields. Meas. Sci. Technol. 29, 035901 (2018).
Clem, J. R. & Coffey, M. W. Viscous flux motion in a Josephson-coupled layer model of high-T c superconductors. Phys. Rev. B 42, 6209 (1990).
Fulde, P. Tunneling Phenomena in Solids. p.427 (Plenum Press New York, 1969).
Volovik, G. E. Superconductivity with lines of GAP nodes: density of states in the vortex. JETP Letters 58, 469 (1993).
Larkin, A. I. & Ovchinnikov, Y. N. Pinning in type II superconductors. J. Low Temp. Phys. 34, 409 (1979).
Ikeda, R. & Adachi, H. Josephson-Vortex-glass transition in strong fields. J. Phys. Soc. Jpn. 69, 2993 (2000).
Doussal, P. L. & Giamarchi, T. Moving glass theory of driven lattices with disorder. Phys. Rev. B 57, 11356 (1998).
Domínguez, D. Dynamic transition in vortex flow in strongly disordered Josephson junction arrays and superconducting thin films. Phys. Rev. Lett. 82, 181 (1999).
Sekitani, T., Matsuda, Y. H. & Miura, N. Measurement of the upper critical field of optimally-doped YBa2Cu3O7-δ in megagauss magnetic fields. New J. Phys. 9, 47 (2007).
Yoshida, T. et al. Universal versus material-dependent two-gap behaviors of the high-T c cuprate superconductors: angle-resolved photoemission study of La2-xSrxCuO4. Phys. Rev. Lett. 103, 037004 (2009).
Hüfner, S., Hossain, M. A., Damascelli, A. & Sawatzky, G. A. Two gaps make a high-temperature superconductor? Rep. Prog. Phys. 71, 062501 (2008).
Maki, K. Effect of Pauli paramagnetism on magnetic properties of high-field superconductors. Phys. Rev. 148, 362 (1966).
Bianchi, A. et al. First-order superconducting phase transition in CeCoIn5. Phys. Rev. Lett. 89, 137002 (2002).
Kumagai, K. et al. Fulde-Ferrell-Larkin-Ovchinnikov state in a perpendicular field of quasi-two-dimensional CeCoIn5. Phys. Rev. Lett. 97, 227002 (2006).
Tayama, T. et al. Unconventional heavy-fermion superconductor CeCoIn5: dc magnetization study at temperatures down to 50 mK. Phys. Rev. B 65, 180504(R) (2002).
Terashima, T. et al. Resistivity and upper critical field in KFe2As2 single crystals. J. Phys. Soc. Jpn. 78, 063702 (2009).
Zhang, J. L. et al. Upper critical field and its anisotropy in LiFeAs. Phys. Rev. B 83, 174506 (2011).
Khim, S. et al. Evidence for dominant Pauli paramagnetic effect in the upper critical field of single-crystalline FeTe0.6Se0.4. Phys. Rev. B 81, 184511 (2010).
Mun, E. et al. Anisotropic H c2 up to 92 T and the signature of multiband superconductivity in (Ca10Pt4As8)((Fe1-xPtx)2As2)5. Phys. Rev. B 85, 100502 (2012).
Zhou, X. J. et al. Universal nodal Fermi velocity. Nature 423, 398 (2003).
Yoshida, T. et al. Low-energy electronic structure of the high-Tc cuprates La2−xSrxCuO4 studied by angle-resolved photoemission spectroscopy. J. Phys.: Condens. Matter 19, 125209 (2007).
Silsbee, R. H. Spin-orbit induced coupling of charge current and spin polarization. J. Phys.: Condens. Matter 16, R179 (2004).
Krüger, C., Conder, K., Schwer, H. & Kaldis, E. The dependence of the lattice parameters on oxygen content in orthorhombic YBa2Cu3O6+x: a high precision reinvestigation of near equilibrium samples. J. Solid State Chem. 134, 356 (1997).
Yamashita, E. T. & Tanabe, K. Advances in Superconductivity XII: Proceedings of the 12th International Symposium on Superconductivity (ISS'99) (Springer, 2000).
Harrison, N., Ramshaw, B. J. & Shekhter, A. Nodal bilayer-splitting controlled by spin-orbit interactions in underdoped high-T c cuprates. Sci. Rep. 5, 10914 (2015).
Dabrowski, B. et al. Dependence of superconducting transition temperature on doping and structural distortion of the CuO2 planes in La2−xMxCuO4 (M = Nd, Ca, Sr). Phys. Rev. Lett. 76, 1348 (1996).
Adachi, T., Omori, K., Tanabe, Y. & Koike, Y. Magnetic-susceptibility and specific-heat studies on the inhomogeneity of superconductivity in the underdoped La2−xSrxCuO4. J. Phys. Soc. Jpn. 78, 114707 (2009).
Boss, C. B. & Fredeen, K. J. Concept, Instrumentation and Techniques in Inductively Coupled Plasma Optical Emission Spectrometry, 2nd edition (Perkin-Elmer, Norwalk, CT, 1997).
Miura, N., Osada, T. & Takeyama, S. Research in super-high pulsed magnetic fields at the Megagauss Laboratory of the University of Tokyo. J. Low Temp. Phys. 133, 139 (2003).
Takeyama, S., Sakakura, R., Matsuda, Y. H., Miyata, A. & Tokunaga, M. Precise magnetization measurements by parallel self-compensated induction coils in a vertical single-turn coil up to 103 T. J. Phys. Soc. Jpn. 81, 014702 (2012).
Altarawneh, M. M. Note: Radio frequency inductance-capacitance band-stop filter circuit to perform contactless conductivity measurements in pulsed magnetic fields. Rev. Sci. Instrum. 83, 096102 (2012).
Acknowledgements
We would like to thank Dr. Moaz M. Altarawneh for the technical support of measurement. We also thank to Prof. Y. Kohama for providing us with the data obtained by a non-destructive pulsed magnet. This work was financially supported by JSPS KAKENHI Grant Number 16K17737.
Author information
Authors and Affiliations
Contributions
D.N. and S.T. conceived the project. T.A., K.O. and Y.K. grew the crystals. D.N. performed the high-field measurements and the simulations. D.N. and S.T. wrote the manuscript with help of T.A. and Y.K.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Nakamura, D., Adachi, T., Omori, K. et al. Pauli-limit upper critical field of high-temperature superconductor La1.84Sr0.16CuO4. Sci Rep 9, 16949 (2019). https://doi.org/10.1038/s41598-019-52973-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-019-52973-1
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.