Abstract
The weak value concept has enabled fundamental studies of quantum measurement and, recently, found potential applications in quantum and classical metrology. However, most weak value experiments reported to date do not require quantum mechanical descriptions, as they only exploit the classical wave nature of the physical systems. In this work, we demonstrate measurement of the sequential weak value of two incompatible observables by making use of two-photon quantum interference so that the results can only be explained quantum physically. We then demonstrate that the sequential weak value measurement can be used to perform direct quantum process tomography of a qubit channel. Our work not only demonstrates the quantum nature of weak values but also presents potential new applications of weak values in analyzing quantum channels and operations.
Similar content being viewed by others
Introduction
Measurement plays a quintessential role in quantum theory and is tied to many peculiarities of quantum physics. The projection postulate stipulates that a quantum system is irrecoverably collapsed into one of the eigenstates of the observable, resulting in maximum state disturbance. Weak measurement, however, relaxes this constraint and has enabled novel research into important problems in quantum physics and quantum information, e.g., minimum-disturbance measurement1,2, relation between information gain and reversibility of measurement3, protecting quantum states from decoherence4,5, measurement based quantum state manipulation6,7,8, etc. In particular, the “weak value”, obtained from a weak measurement followed by a strong measurement, is quite peculiar in that it is in general a complex number and is not bounded by the eigenvalue spectrum of the associated observable9,10. Since the first demonstration of the weak value concept11,12, the physical properties of the weak value have been studied extensively both theoretically and experimentally13,14,15,16 and these properties have been used to explore a variety of fundamental problems in quantum physics17,18,19,20,21. In recent years, the weak value concept is being actively exploited for quantum technology, for instance, in precision measurement and metrology22,23,24,25, and in quantum information as a tool for direct characterization of quantum states26,27,28,29,30,31,32,33,34.
As the weak measurement does not irrecoverably collapse the quantum state, it opens up the possibility of sequential quantum measurement for two non-commuting observables. While such sequential weak value measurement has been reported very recently33,34, these experiments are classical in that the results can be fully explained with the classical electromagnetic theory. Note that, despite a nonclassical single-photon state is used in ref.34, the weak value measuring apparatus itself is classical. In fact, it is worth noting that optical weak value experiments to date are mostly classical with a few rare exceptions14,20.
In this work, we report measurement of the sequential weak value of two incompatible observables by making use of two-photon quantum interference35 so that the results can only be explained quantum physically. We then demonstrate that the sequential weak value measurement can be used to perform direct quantum process tomography of a quantum channel. The genuine quantum nature of the sequential weak value for two incompatible observables reported in this work will be instrumental in rigorous tests quantum contextuality36,37 and macroscopic realism38,39. Moreover, direct quantum process tomography (d-QPT) based on sequential weak value measurement offers a way for characterizing quantum channels and gates. We also compare and identify advantages and disadvantages, via experiment and numerical simulation, of d-QPT via sequential weak value, standard QPT, and compressive-sensing QPT40,41.
Results
Schematic and theory
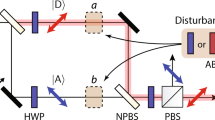
The experimental schematic of the sequential weak value measurement apparatus for two non-commuting observables \(\hat A\) and \(\hat B\) is shown in Fig. 1. First, two single-photons are prepared by spontaneous parametric down-conversion (SPDC). The system and ancilla qubits are encoded, respectively, on the polarization and path modes of one of the photons42. The meter qubit is encoded on the polarization mode of the other photon. The system qubit is measured with the help of the ancilla qubit and the meter qubit is used for the read-out of the measurement outcome. The computational basis {|0〉, |1〉} is used throughout the text with the understanding that, for the polarization qubit, it refers to horizontal and vertical polarization states and, for the path qubit, it refers to upper and lower path modes. The system qubit is prepared in an arbitrary initial state |ψ〉s = α|0〉s + β|1〉s and the ancilla and meter qubits are initialized to |0〉a and |0〉m, respectively. The three qubits are initially in the product state |ψ〉s |0〉a |0〉m.
Schematic of experimental setup. The system and meter qubits are encoded in the polarization state of single-photons. The ancilla qubit is encoded on the path mode of the single-photon carrying the system qubit. Measurement of the observables \(\hat A\) and \(\hat B\) are sequentially applied to the system qubit |ψ〉s. Projection measurement of the observable \(\hat A\), arbitrarily set by the angle θA of HWP, is accomplished by interacting it with the ancilla qubit |0〉a. Likewise, weak measurement of the observable \(\hat B\), arbitrarily set by the angle θB of HWP, is accomplished by interacting the system and ancilla qubits with the meter qubit |0〉m. The weak measurement strength is parameterized by g = 4θ g where θ g is the angle of HWP. The sequential weak value \(\langle {\hat B\hat A} \rangle _{\mathrm{w}}\) is obtained from the expectation values of the meter qubit conditioned on the post-selective projection measurements on the system and ancilla qubits \({{\hat {\mathrm \Pi}}}_{\mathrm{s}}^\phi\) and \({{\hat {\mathrm \Pi}}}_{\mathrm{a}}^ +\). To perform direct quantum process tomography of a quantum channel \(\hat {\cal E}\) with sequential weak values, an arbitrary quantum operation \(\hat {\cal E}\) is inserted between the observables \(\hat A\) and \(\hat B\). BD (beam displacer), PBS (polarizing beam splitter), PPBS (partially polarizing beam splitter), QWP (quarter wave plate), SPCM (single-photon counting module)
To measure the sequential weak value of two non-commuting observables, measurement of the observables \(\hat A\) and \(\hat B\) are sequentially applied to the system qubit |ψ〉s. Measurement of the observable \(\hat A\) is accomplished by interacting it with the ancilla qubit |0〉a. As shown in Fig. 1, the interaction \(\hat U_{\mathrm{{A}}}\) between the system qubit and the ancilla qubit is a controlled-σ x type operation which can be written as
where \(\hat {\Bbb I}\) is the identity operation. This interaction is implemented in experiment with a beam displacer (BD) and wave plates42. The observable \(\hat A\) may be arbitrarily set by choosing the angle θA of HWP in Fig. 1. For instance, choosing \(\theta _{\mathrm{A}} = \frac{\pi }{4},0, - \frac{\pi }{8}\), and \(\frac{\pi }{8}\) rotates the bases |0〉, |1〉, |+〉, and |−〉 into |1〉, thereby implementing the observable \(\hat A = \left| 0 \right\rangle \left\langle 0 \right|,\left| 1 \right\rangle \left\langle 1 \right|,\left| + \right\rangle \left\langle + \right|\), and, \(\left| - \right\rangle \left\langle - \right|\) respectively. Here, \(\left| + \right\rangle \equiv \left( {\left| 0 \right\rangle + \left| 1 \right\rangle } \right){\mathrm{/}}\sqrt 2\) and \(\left| - \right\rangle \equiv \left( {\left| 0 \right\rangle - \left| 1 \right\rangle } \right){\mathrm{/}}\sqrt 2\).
The complete state of the three qubits after the first interaction is given by
Note the measurement interaction for \(\hat A\) is considered to be strong or projective in the sense that \(\hat A\left| \psi \right\rangle _{\mathrm{s}}\) is completely discriminated from its orthogonal counterpart \(\left( {\hat {\Bbb I} - \hat A} \right)\left| \psi \right\rangle _{\mathrm{s}}\) by the ancillary qubit state.
Measurement of the observable \(\hat B\) is accomplished by interacting the system and ancilla qubits with the meter qubit |0〉m as shown in Fig. 1. The interaction \(\hat U_{\mathrm{B}}\) involving the three qubits is effectively a controlled–controlled-σ z type operation which can be written as
where the single-qubit operation R(θ) is defined by \(R\left( \theta \right)\left| 0 \right\rangle \to {\mathrm{cos}}{\kern 1pt} 2\theta \left| 0 \right\rangle + {\mathrm{sin}}{\kern 1pt} 2\theta \left| 1 \right\rangle\) and \(R\left( \theta \right)\left| 1 \right\rangle \to {\mathrm{sin}}{\kern 1pt} 2\theta \left| 0 \right\rangle - {\mathrm{cos}}{\kern 1pt} 2\theta \left| 1 \right\rangle\). The rotation of angle θ g determines the measurement strength g = 4θ g . For example, \(\hat U_{\mathrm{B}}\) becomes the identity operation (i.e., null measurement) when g = 0 and, at g = π/2, it becomes the controlled–controlled–σ x operation, a strong measurement. Note that the weak measurement condition is valid when \(\left| g \right| \ll 1\).
In experiment, the measurement interaction for the observable \(\hat B\) is realized by the two-photon quantum interference at a partially polarizing beam splitter (PPBS), where \(\hat B\) is set arbitrarily by the angle θB of HWPs. The PPBS partially reflects vertical polarization with transmittance TV = 1/3 and transmits horizontal polarization with TH = 1. Since two-photon quantum interference occurs only for the ancilla qubit in the |1〉a state35, the π-phase shift due to the quantum interference is only induced when the system, ancilla, and meter qubits are in the |1〉s |1〉a |1〉m. Two additional PPBS-HWP sets are used to equalize the probability amplitudes at the output ports for arbitrary input polarization states43.
The three-qubit quantum state after the \(\hat U_{\mathrm{B}}\) interaction, evaluated up to the first-order of the weak interaction strength g is given by
where the last term clearly shows that the result of the sequential observables \(\hat B\hat A\) is registered on the meter. The superfluous second term can be eliminated by subjecting the ancilla qubit into projection measurement \({{\hat {\mathrm \Pi}}}_{\mathrm{a}}^ + = \left| + \right\rangle \left\langle + \right|\)44, resulting in the joint state of the system and the meter qubits
The quantum erasure works in a probabilistic way if only one POVM element \({{\hat {\mathrm \Pi}}}_{\mathrm{a}}^ +\) is considered. However, the erasure scheme can be deterministic if the other POVM element \({{\hat {\mathrm \Pi}}}_{\mathrm{a}}^ - = \hat {\Bbb I} - {{\hat {\mathrm \Pi}}}_{\mathrm{a}}^ +\) is also taken into account, in that an additional interaction between the system and the meter qubits is required. See Supplementary Note 1 for more details.
Finally, we project the system qubit onto the projector \({{\hat {\mathrm \Pi}}}_{\mathrm{s}}^\phi = \left| \phi \right\rangle \left\langle \phi \right|\), leaving the meter qubit in the state
where \(\left\langle {\hat B\hat A} \right\rangle _{\mathrm{w}} \equiv \left\langle {\phi \left| {\hat B\hat A} \right|\psi } \right\rangle {\mathrm{/}}\left\langle {\phi |\psi } \right\rangle\) is the sequential weak value for the two non-commuting observables \(\hat B\) and \(\hat A\).
Since the sequential weak value \(\left\langle {\hat B\hat A} \right\rangle _{\mathrm{w}}\) is registered in the meter qubit, it can be read out by obtaining certain expectation values for the meter qubit. For instance, the real part of \(\left\langle {\hat B\hat A} \right\rangle _{\mathrm{w}}\) is obtained from \(\left\langle {{\mathrm{{\Phi}}}\left| {\hat \sigma _x} \right|{\mathrm{{\Phi}}}} \right\rangle _{\mathrm{m}} \equiv \left( {N^ + - N^ - } \right){\mathrm{/}}\left( {N^ + + N^ - } \right)\), where N+ (N−) is the coincidence counts of D1 and D2 when the meter qubit is projected on the |+〉 (|−〉) state. The complex sequential weak value is thus given by
As our scheme combines two-photon quantum interference for the measurement interaction and sequential measurement of two non-commuting observables, it is able to demonstrate the genuine quantum nature of the sequential weak value. Moreover, unlike prior sequential weak value experiments33,34 in which the sequential weak values were inferred from the covariance of two meter variables, our scheme allows direct measurement of the sequential weak value. We also point out that, even though the first measurement interaction is strong, the sequential weak value for two observables can be obtained by erasing the information registered on the ancilla qubit44.
Experimental sequential weak values
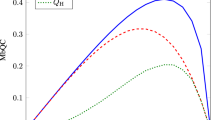
As described in Eq. (7), the sequential weak value \(\left\langle {\hat B\hat A} \right\rangle _{\mathrm{w}}\) can be obtained by measuring the expectation values \(\left\langle {\hat \sigma _x} \right\rangle _{\mathrm{m}}\) and \(\left\langle {\hat \sigma _y} \right\rangle _{\mathrm{m}}\) for the meter qubit. The results of the meter qubit readout, i.e., \(\left\langle {\hat \sigma _x} \right\rangle _{\mathrm{m}}\) and \(\left\langle {\hat \sigma _y} \right\rangle _{\mathrm{m}}\), as a function of the measurement strength parameter g is shown in Fig. 2. For this measurement, the system qubit is first prepared in a specific state \(\left| \psi \right\rangle _{\mathrm{s}} = \left( {\left| 0 \right\rangle - i\sqrt 3 \left| 1 \right\rangle } \right){\mathrm{/}}2\). The two incompatible observables are chosen to be \(\hat A = \left| - \right\rangle \left\langle - \right|\) and \(\hat B = \left| 0 \right\rangle \left\langle 0 \right|\), and the final projection basis for the system qubit is chosen to be \({{\hat {\mathrm \Pi}}}_{\mathrm{s}}^\phi = \left| - \right\rangle \left\langle - \right|\).
Extracting sequential weak values. The data points indicate the measured expectation values for the meter photon as a function of the weak measurement strength g. The system qubit is initially prepared in \(\left| \psi \right\rangle _{\mathrm{s}} = \left( {\left| 0 \right\rangle - i\sqrt 3 \left| 1 \right\rangle } \right){\mathrm{/}}2\) and the final post-selective projection measurement is defined by \({{\hat {\mathrm \Pi}}}_{\mathrm{s}}^\phi = \left| - \right\rangle \left\langle - \right|\). For a, the two non-commuting observables are \(\hat A = \left| - \right\rangle \left\langle - \right|\) and \(\hat B = \left| 0 \right\rangle \left\langle 0 \right|\). For b, \(\hat A\) and \(\hat B\) are exchanged. The black solid lines are the exact theoretical curves. The dashed lines are the first-order dependence of g obtained from the polynomial fit to the data from which the sequential weak value is extracted. The shaded regions represent simulated errors assuming the phase instability of ±π/36 radians in the BD interferometer. Note that shaded regions for a are too narrow to be visible. The measured sequential weak values are in good agreement with the theoretical values \(\langle {\hat B\hat A} \rangle _{\mathrm{w}} = 0.5\) and \(\langle {\hat A\hat B} \rangle _{\mathrm{w}} = 0.250 - 0.433i\). Error bars represent one standard deviation due to Poissonian counting statistics
While it is possible to obtain the sequential weak value for a fixed g in the limit of \(\left| g \right| \ll 1\), this may introduce systematic errors, such as, inaccurate reading of waveplate angles. To avoid this, the data set shown in Fig. 2 is fully fitted with a polynomial function of g. The first-order linear dependence of the polynomial fit (red dashed line) exactly corresponds to the sequential weak value. The measured values are in good agreement with the theoretical predictions.
Note that, for the sequential weak value, the measurement interaction strength g is very small so that the measurement process may be considered to be non-invasive. Classical intuition then may lead that the time ordering should be irrelevant to the measurement outcome45, i.e., \(\langle {\hat A\hat B} \rangle _{\mathrm{w}} = \langle {\hat B\hat A} \rangle _{\mathrm{w}}\). However, this is not the case because \(\langle {\hat A\hat B} \rangle _{\mathrm{w}} \ne \langle {\hat B\hat A} \rangle _{\mathrm{w}}\) as clearly demonstrated in Fig. 2. This result clearly distinguishes quantum measurement from classical measurement even in when the measurement strength is extremely weak so that the measurements may be considered non-perturbing46. It should be noted that the result \(\langle {\hat A\hat B} \rangle _{\mathrm{w}} \ne \langle {\hat B\hat A} \rangle _{\mathrm{w}}\) cannot be interpreted as the consequence of the non-commuting nature of the measurement interactions. Note also that weak value measurement allows one to directly characterize quantum states26. We have also carried out direct quantum state tomography (d-QST) of the system qubit by using the sequential weak value32,33, see Methods section for details.
Direct quantum process tomography
Identifying an unknown quantum process or operation is a crucial task in quantum information technology. We now show that the sequential weak value measurement demonstrated so far allows one to perform direct quantum process tomography (d-QPT). Typically, a quantum process \(\hat {\cal E}:\hat \rho _{{\mathrm{in}}} \to \hat \rho _{{\mathrm{out}}}\) in a d-dimension Hilbert space is represented as \(\hat {\cal E}\left( {\hat \rho _{{\mathrm{in}}}} \right) = \mathop {\sum}\nolimits_{i = 1}^{d^2} {\kern 1pt} \mathop {\sum}\nolimits_{j = 1}^{d^2} {\kern 1pt} \chi _{ij}{\hat{\mathrm E}}_i\hat \rho _{{\mathrm{in}}}{\hat{\mathrm E}}_j^{\mathrm{\dagger }}\), where \(\left\{ {\hat E_i} \right\}\) is the operator basis set. The quantum process \(\hat {\cal E}\) is completely characterized by matrix elements χ ij of the process matrix χ. For a single-qubit operation, the usual choice for \(\left\{ {\hat E_i} \right\}\) is the Pauli basis set \(\left\{ {\hat I,\hat \sigma _x,\hat \sigma _y,\hat \sigma _z} \right\}\), but this is not a unique choice. In particular, we consider the following basis set \(\left\{ {\hat S_1 = {\textstyle{1 \over {\sqrt 2 }}}\left| 0 \right\rangle \left\langle + \right|,\hat S_2 = {\textstyle{1 \over {\sqrt 2 }}}\left| 0 \right\rangle \left\langle - \right|} \right.\), \(\left. {\hat S_3 = {\textstyle{1 \over {\sqrt 2 }}}\left| 1 \right\rangle \left\langle + \right|,\hat S_4 = {\textstyle{1 \over {\sqrt 2 }}}\left| 1 \right\rangle \left\langle - \right|} \right\}\), referred to as the Dirac basis following the analogy with the Dirac distribution, which characterizes a quantum state in complementary bases26,47. We now rewrite the quantum process in the Dirac basis as
where \(\chi _{ij}^S\) is the χ-matrix elements in the Dirac basis.
To perform direct quantum process tomography via sequential weak value measurement in the Dirac basis, an arbitrary single-qubit quantum process \(\hat {\cal E}\) is placed between the two non-commuting observables \(\hat A\) and \(\hat B\) as shown in Fig. 1. By choosing a specific set of the input system qubit |ψ〉s, measurement observables \(\hat A\) and \(\hat B\), and the final projection basis for the system qubit \({{\hat {\mathrm \Pi}}}_{\mathrm{s}}^\phi = \left| \phi \right\rangle \left\langle \phi \right|\), we are able to directly measure \(\chi _{ij}^S\) from the sequential weak values, see Methods section for the specific settings. In experiment, we have tested d-QPT via sequential weak value measurement for trace-preserving and non-trace-preserving maps. The experimental process matrices are shown in Fig. 3 and they are indeed very close to the ideal process matrices, showing high fidelity of \({\cal F} > 0.96\) for all cases.
Direct-QPT via sequential weak values. The quantum operation \(\hat {\cal E}\) inserted between the observables \(\hat A\) and \(\hat B\) can be characterized by measuring the sequential weak values. a \(\hat {\cal E}\) is the Hadamard operation implemented by HWP set at 22.5°. b \(\hat {\cal E}\) is the \({\cal R}_x\)-gate operation implemented by QWP set at 45°, the polarization rotating operation along x-axis. c \(\hat {\cal E}\) is the PPBS operation. The directly measured raw process matrices \(\chi _{ij}^S\) in Dirac basis are shown at left. The corresponding process matrices \(\chi _{ij}^\sigma\) in the standard Pauli basis \(\{ {\hat I,\hat \sigma _x,\hat \sigma _y,\hat \sigma _z} \}\) are shown at right, where the process matrices are reconstructed to be physical matrices via the maximum likelihood estimation technique. Solid (empty) bars represent experimental (theoretical) results. The fidelities between the measured and the ideal \(\chi _{ij}^\sigma\) are a \({\cal F} = 0.974 \pm 0.022\), b \({\cal F} = 0.963 \pm 0.007\) and c \({\cal F} = 0.973 \pm 0.007\). The errors in \({\cal F}\) are obtained by performing 500 Monte–Carlo simulation runs by taking into account of the statistical errors in measured weak values
One of the key purposes of quantum process tomography in experiment is to quantitatively compare a physically implemented quantum operation with the intended ideal operation. The d-QPT via sequential weak value is uniquely well suited for this purpose over standard full quantum process tomography48,49,50. For instance, consider a trace-preserving operation such as the Hadamard gate operation. In order to judge the fidelity of the physical operation to the ideal Hadamard operation, it is not essential to know the full process matrix which may contain 16 non-zero elements. In fact, the fidelity \({\cal F}\) for Hadamard operation can be obtained with only three real or imaginary process matrix elements and is given by \({\cal F} = \sqrt {{\mathrm{Re}}\left( {\chi _{11}^S + \chi _{44}^S} \right){\mathrm{/}}2 + {\mathrm{Re}}\left( {\chi _{14}^S} \right)}\). For the \({\cal R}_x\)-gate operation, the fidelity calculations requires four process matrix elements and is given by \({\cal F} = \sqrt {{\mathrm{Re}}\left( {2\chi _{13}^S - 2\chi _{24}^S + 1} \right){\mathrm{/}}4 + {\mathrm{Im}}\left( {\chi _{12}^S - \chi _{34}^S} \right)}\). \({\cal R}_x\)-gate operation is a polarization rotating operation along x-axis, that is defined as \({\cal R}_x\left| 0 \right\rangle \to \left( {\left| 0 \right\rangle + i\left| 1 \right\rangle } \right){\mathrm{/}}\sqrt 2\), \({\cal R}_x\left| 1 \right\rangle \to \left( {\left| 0 \right\rangle - i\left| 1 \right\rangle } \right){\mathrm{/}}\sqrt 2\). See Supplementary Note 3 for details. The resulting fidelity values are \({\cal F} = 0.973 \pm 0.023\) for the Hadamard operation and \({\cal F} = 0.970 \pm 0.011\) for the \({\cal R}_x\)-gate operation and these fidelity values are indeed in good agreement with the fidelity values from the full quantum process tomography.
We now compare d-QPT-based fidelity estimation with the compressive-sensing quantum process tomography (cs-QPT)40,41. Even though our d-QPT method requires additional resource qubits, both d-QPT and cs-QPT are equally more efficient than the standard full QPT in the sense that the fidelity of a quantum process can be quantified without complete measurements. However, the difference is in the requirement of prior knowledge and assumptions. In cs-QPT, an unknown quantum process can be accurately quantified with the assumption that it can be represented by a sparse or low-rank matrix. Thus, if the sparsity assumption is not valid, cs-QPT would give incorrect fidelity estimation. In contrast, d-QPT-based fidelity estimation always produces faithful results with the prior knowledge of the target operation.
It is also interesting to consider the possibility of combining cs-QPT and d-QPT based on sequential weak values for more efficient characterization of a quantum process. In cs-QPT, incomplete sets of experimentally measured outcomes with randomly chosen input states and projective measurement settings are fed in to the compressive-sensing algorithm. Interestingly, we have found that certain sequential weak values corresponding to specific process matrix elements in Dirac basis could be used as the input to cs-QPT for more efficient characterization of a quantum process. More details of the cs-QPT with sequential weak values may be found in Supplementary Note 3. For instance, one first measure an incomplete set of sequential weak values (or randomly chosen process matrix elements in Dirac basis) for an unknown quantum process. The results are then fed into cs-QPT and the reliability of the cs-QPT is evaluated accurately via d-QPT fidelity estimation, which may require measuring a few more sequential weak values. This process may be repeated until a certain reliability bound is reached.
Discussion
We have demonstrated measurement of the sequential weak values of two incompatible observables. By making use of two-photon quantum interference for the measurement interaction, our measurement scheme can be viewed as an unambiguous quantum physical implementation of sequential weak measurement. The genuine quantum nature of the sequential weak value for two incompatible observables reported in this work will be instrumental in rigorous tests quantum contextuality36,37, macroscopic realism38,39, uncertainty relations51, measurement induced geometric phase52, etc. Furthermore, our sequential measurement scheme is in principle nondestructive and its measurement strength is controllable. We anticipate such features will be useful for quantum feedback control via measurement53,54. We have also demonstrated for the first time that the sequential weak value measurement can be used to perform direct quantum process tomography of a quantum channel. By combining the idea of compressing sensing with d-QPT fidelity estimation, an efficient strategy for characterizing an unknown quantum process can be established.
Methods
Photon pair source
The two single-photons in the experiment are generated via ultrafast-pumped spontaneous parametric down-conversion (SPDC) in a 1 mm thick type-II BBO crystal in the beamlike configuration. The central wavelengths of the pump photon and the SPDC photons are 390 nm and 780 nm, respectively. The SPDC photons are collected into a single-mode fiber via interference filters having 3 nm full-width at half-maximum bandwidth.
Details for direct-QST
To directly measure elements of the density matrix for the system qubit, the sequential weak values are measured with a specific setting for the observables \(\hat A\) and \(\hat B\) and the post-selection projection \({{\hat {\mathrm \Pi}}}_{\mathrm{s}}^\phi = \left| \phi \right\rangle \left\langle \phi \right|\). The sequential weak value for the system qubit having the density matrix \(\hat \rho _{{\mathrm{in}}}\) is given as \(\left\langle {\hat B\hat A} \right\rangle _{\mathrm{w}} = {\mathrm{Tr}}[ {{{\hat {\mathrm \Pi}}}_{\mathrm{s}}^\phi \hat B\hat A\hat \rho _{{\mathrm{in}}}} ]{\mathrm{/}}p\), where \(p = {\mathrm{Tr}}\left[ {{{\hat {\mathrm \Pi}}}_{\mathrm{s}}{\kern 1pt} \hat \rho _{{\mathrm{in}}}} \right]\) is the post-selection probability. For simplicity, let us denote {|a1〉 = |0〉, |a2〉 = |1〉} and {|b1〉 = |+〉, |b2〉 = |−〉}. The observables are \(\hat A = \left| {a_m} \right\rangle \left\langle {a_m} \right|\) and \(\hat B = \left| {b_1} \right\rangle \left\langle {b_1} \right|\). The projector is given by \({{\hat {\mathrm \Pi}}}_{\mathrm{s}} = \left| {a_n} \right\rangle \left\langle {a_n} \right|\). Then, the elements of \(\hat \rho _{{\mathrm{in}}}\) can be directly obtained from the sequential weak values, i.e., \(\rho _{mn} = \left\langle {\hat B\hat A} \right\rangle _{\mathrm{w}}^{mn} \times 2p^n\). We have tested d-QST with sequential weak value measurement and the results are in good agreement with the ideal target density matrix with fidelity better than \({\cal F} = 0.994 \pm 0.008\). See Supplementary Note 2 for more details and experimental data.
Details for direct-QPT
For a single-qubit quantum process, there are 16 elements for the χ-matrix and it is possible to access these matrix elements directly via sequential weak value measurement with specific choices of settings. We first define \(\hat \rho _{{\mathrm{in}}}^{n\prime } = \left| {a_{n\prime }} \right\rangle \left\langle {a_{n\prime }} \right|\), \(\hat A^k = \left| {b_k} \right\rangle \left\langle {b_k} \right|\), \(\hat B^n = \left| {a_n} \right\rangle \left\langle {a_n} \right|\), and \({{\hat {\mathrm \Pi}}}_{\mathrm{s}}^{k\prime } = \left| {b_{k\prime }} \right\rangle \left\langle {b_{k\prime }} \right|\). The sequential weak values are corresponding to the process matrix elements as \(\chi _{ij}^S = \chi _{knk{\prime}n{\prime}}^S = \left\langle {\hat B^n\hat A^k} \right\rangle _{\mathrm{w}}^{n{\prime}k{\prime}} \times 2p^{n{\prime}k{\prime}} \times \left( { - 1} \right)^{\delta _{k2}\delta _{n\prime 2}}\left( { - 1} \right)^{\delta _{k\prime 2}\delta _{n2}}\), where \(p^{n\prime k\prime } = {\mathrm{Tr}}[ {{{\hat {\mathrm \Pi}}}_{\mathrm{s}}^{k\prime }{\cal E}( {\hat \rho _{{\mathrm{in}}}^{n\prime }} )} ]\) is the post-selection probability, δi2 is the Kronecker delta, and the subscripts kn and kʹnʹ are the binary number representations of i and j, respectively. See Supplementary Note 3 for more details.
Data availability
The data sets analyzed during this study are available from the corresponding author on reasonable request.
Change history
22 February 2018
In the original version of this Article, the penultimate sentence of the second paragraph of the “Schematic and theory” section of the Results originally incorrectly read as “For instance, choosing θA = π/4, 0, −π/8 and π/8 rotates the bases |0>, |1>, |+>, and |−> into |1>, thereby implementing the observableÂ=|0><0|, |1><1|, |+><+| and, respectively.” In the corrected version, “|−><−|” has been added before “, respectively”. This error has been corrected in both the PDF and HTML versions of the Article.
References
Banaszek, K. Fidelity balance in quantum operations. Phys. Rev. Lett. 86, 1336–1369 (2001).
Baek, S.-Y., Cheong, Y. W. & Kim, Y.-H. Minimum-disturbance measurement without postselection. Phys. Rev. A 77, 060308(R) (2008).
Lim, H.-T., Ra, Y.-S., Hong, K.-H., Lee, S.-W. & Kim, Y.-H. Fundamental bounds in measurements for estimating quantum States. Phys. Rev. Lett. 113, 020504 (2014).
Kim, Y.-S., Lee, J.-C., Kwon, O. & Kim, Y.-H. Protecting entanglement from decoherence using weak measurement and quantum measurement reversal. Nat. Phys. 8, 117–120 (2014).
Kim, Y.-S., Cho, Y.-W., Ra, Y.-S. & Kim, Y.-H. Reversing the weak quantum measurement for a photonic qubit. Opt. Express. 17, 11978–11985 (2009).
Vijay, R. et al. Stabilizing Rabi oscillations in a superconducting qubit using quantum feedback. Nature 490, 77–80 (2012).
Hatridge, M. et al. Quantum back-action of an individual variable-strength measurement. Science 339, 178–181 (2013).
Blok, M. S. et al. Manipulating a qubit through the backaction of sequential partial measurements and real-time feedback. Nat. Phys. 10, 189–193 (2014).
Aharonov, Y., Albert, D. Z. & Vaidman, L. How the result of a measurement of a component of the spin of a spin-1/2 particle can turn out to be 100. Phys. Rev. Lett. 60, 1351–1354 (1988).
Dressel, J., Malik, M., Miatto, F. M., Jordan, A. N. & Boyd, R. W. Colloquium: Understanding quantum weak values: Basic and applications. Rev. Mod. Phys. 86, 307–316 (2014).
Duck, I. M., Stevenson, P. M. & Sudarshan, E. C. G. The sense in which a “weak measurement” of a spin-1/2 particle’s spin component yields a value 100. Phys. Rev. D. 40, 2112–2117 (1989).
Ritchie, N. W. M., Story, J. G. & Hulet, R. G. Realization of a measurement of a “weak value”. Phys. Rev. Lett. 66, 1107–1110 (1991).
Cho, Y.-W., Lim, H.-T., Ra, Y.-S. & Kim, Y.-H. Weak value measurement with an incoherent measuring device. New J. Phys. 12, 023036 (2010).
Pryde, G. J. et al. Measurement of quantum weak values of photon polarization. Phys. Rev. Lett. 94, 220405 (2005).
Groen, J. P. et al. Partial-measurement backaction and nonclassical weak values in a superconducting circuit. Phys. Rev. Lett. 111, 090506 (2013).
Mitchison, G., Jozsa, R. & Popescu, S. Sequential weak measurement. Phys. Rev. A 76, 062105 (2007).
Lundeen, J. S. & Steinberg, A. M. Experimental Joint Weak Measurement on a Photon Pair as a Probe of Hardy’s Paradox. Phys. Rev. Lett. 102, 020404 (2009).
Denkmayr, T. et al. Observation of a quantum Cheshire Cat in a matter-wave interferometer experiment. Nat. Commun. 5, 4492 (2014).
Kocsis, S. et al. Observing the average trajectories of single photons in a two-slit interferometer. Science 332, 1170–1173 (2011).
Goggin, M. E. et al. Violation of the Leggett-Garg inequality with weak measurements of photons. Proc. Natl Acad. Sci. USA 108, 1256–1261 (2011).
Mahler, D. H. et al. Experimental nonlocal and surreal Bohmian trajectories. Sci. Adv. 2, e1501466 (2016).
Hosten, O. & Kwiat, P. Observation of the spin hall effect of light via weak measurements. Science 319, 787–790 (2008).
Hallaji, M. et al. Weak-value amplification of the nonlinear effect of a single photon. Nat. Phys. 13, 540–544 (2017).
Dixon, P. B., Starling, D. J., Jordan, A. N. & Howell, J. C. Ultrasensitive beam deflection measurement via interferometric weak value amplification. Phys. Rev. Lett. 102, 173601 (2009).
Magaña-Loaiza, O. S., Mirhosseini, M., Rodenburg, B. & Boyd, R. W. Amplification of angular rotations using weak measurements. Phys. Rev. Lett. 112, 200401 (2014).
Salvail, J. Z. et al. Full characterization of polarization states of light via direct measurement. Nat. Photonics 7, 316–321 (2013).
Bolduc, E., Gariepy, G. & Leach, J. Direct measurement of large-scale quantum states via expectation values of non-Hermitian matrices. Nat. Comm. 7, 10439 (2016).
Lundeen, J. S. et al. Direct measurement of the quantum wavefunction. Nature 474, 188–191 (2011).
Mirhosseini, M. et al. Compressive direct measurement of the quantum wave function. Phys. Rev. Lett. 113, 090402 (2014).
Shi, Z. et al. Scan-free direct measurement of an extremely high-dimensional photonic state. Optica 2, 388–392 (2015).
Malik, M. et al. Direct measurement of a 27-dimensional orbital-angular-momentum state vector. Nat. Commun. 5, 3115 (2014).
Lundeen, J. S. & Bamber, C. Procedure for direct measurement of general quantum states using weak measurement. Phys. Rev. Lett. 108, 070402 (2012).
Thekkadath, G. S. et al. Direct measurement of the density matrix of a quantum system. Phys. Rev. Lett. 117, 120401 (2016).
Piacentini, F. et al. Measuring incompatible observables by exploiting sequential weak values. Phys. Rev. Lett. 117, 170402 (2016).
Hong, C. K., Ou, Z. Y. & Mandel, L. Measurement of subpicosecond time intervals between two photons by interference. Phys. Rev. Lett. 59, 2044–2046 (1987).
Budroni, C., Moroder, T., Kleinmann, M. & Gühne, O. Bounding temporal quantum correlations. Phys. Rev. Lett. 111, 020403 (2013).
Kochen, S. & Specker, E. P. The Problem of hidden variables in quantum mechanics. J. Math. Mech. 17, 59–87 (1967).
Leggett, A. J. & Garg, A. Quantum mechanics versus macroscopic realism: Is the flux there when nobody looks? Phys. Rev. Lett. 54, 857–860 (1985).
Avella, A. et al. Anomalous weak values and the violation of a multiple-measurement Leggett-Garg inequality. Phys. Rev. A 96, 052123 (2017).
Shabani, A. et al. Efficient measurement of quantum dynamics via compressive sensing. Phys. Rev. Lett. 106, 100401 (2011).
Riofrío, C. A. et al. Efficient measurement of quantum dynamics via compressive sensing. Nat. Commun. 8, 15305 (2017).
Kim, Y.-H. Single-photon two-qubit entangled states: preparation and measurement. Phys. Rev. A 67, 040301(R) (2003).
Kiesel, N. et al. Linear optics controlled-phase gate made simple. Phys. Rev. Lett. 95, 210505 (2005).
Brodutch, A. & Cohen, E. Nonlocal measurements via quantum erasure. Phys. Rev. Lett. 116, 070404 (2016).
Bednorz, A., Franke, K. & Belzig, W. Noninvasiveness and time symmetry of weak measurements. New J. Phys. 15, 023043 (2013).
Piacentini, F. et al. Experiment investigating the connection between weak values and contextuality. Phys. Rev. Lett. 116, 180401 (2016).
Hofmann, H. F. Complex joint probabilities as expressions of reversible transformations in quantum mechanics. New J. Phys. 14, 043031 (2012).
Schmiegelow, C. T., Bendersky, A., Larotonda, M. A. & Paz, J. P. Selective and efficient quantum process tomography without ancilla. Phys. Rev. Lett. 107, 100502 (2011).
Mohseni, M. & Lidar, D. A. Direct characterization of quantum dynamics. Phys. Rev. Lett. 97, 170501 (2006).
Schmiegelow, C. T., Larotonda, M. A. & Paz, J. P. Selective and efficient quantum process tomography with single photons. Phys. Rev. Lett. 104, 123601 (2010).
Rozema, L. A. et al. Violation of heisenberg’s measurement-disturbance relationship by weak measurements. Phys. Rev. Lett. 109, 100404 (2012).
Samuel, J. & Bhandari, R. General setting for berry’s phase. Phys. Rev. Lett. 60, 2339–2342 (1988).
Brańczyk, A. M. et al. Quantum control of a single qubit. Phys. Rev. A 75, 012329 (2007).
Gillett, G. G. et al. Experimental feedback control of quantum systems using weak measurements. Phys. Rev. Lett. 104, 080503 (2010).
Acknowledgements
This work was supported by the KIST institutional programs (Project Nos 2E27231, 2E26780, and 2E27230-17-P005), by the National Research Foundation of Korea (Grant Nos 2016R1A2A1A05005202 and 2016R1A4A1008978) and by ICT R&D program of MSIP/IITP (Grant No. B0101-16-1355). Y.K. acknowledges support from the Global Ph.D. Fellowship by the National Research Foundation of Korea (Grant No. 2015H1A2A1033028).
Author information
Authors and Affiliations
Contributions
Y-W.C. and Y-H.K.: Planned and supervised the research. The experiment was designed by Y-W.C. and further developed with all other authors. Y.K. and Y-W.C. carried out the experiment and the theoretical calculations. Y.K., Y-W.C., Y-S.K. and Y-H.K.: Analyzed the data. Y-S.K., S-Y.L., S-W.H., and S.M.: Contributed the discussion of the results. Y-W.C., Y-H.K., and Y.K.: Wrote the manuscript. All authors commented on the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
A correction to this article is available online at https://doi.org/10.1038/s41467-018-03305-w.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kim, Y., Kim, YS., Lee, SY. et al. Direct quantum process tomography via measuring sequential weak values of incompatible observables. Nat Commun 9, 192 (2018). https://doi.org/10.1038/s41467-017-02511-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-017-02511-2
This article is cited by
-
Implementing efficient selective quantum process tomography of superconducting quantum gates on IBM quantum experience
Scientific Reports (2022)
-
Observing the quantum Cheshire cat effect with noninvasive weak measurement
npj Quantum Information (2021)
-
True experimental reconstruction of quantum states and processes via convex optimization
Quantum Information Processing (2021)
-
Emergence of the geometric phase from quantum measurement back-action
Nature Physics (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.