Abstract
Strong spin–orbit coupling lifts the degeneracy of t 2g orbitals in 5d transition-metal systems, leaving a Kramers doublet and quartet with effective angular momentum of J eff = 1/2 and 3/2, respectively. These spin–orbit entangled states can host exotic quantum phases such as topological Mott state, unconventional superconductivity, and quantum spin liquid. The lacunar spinel GaTa4Se8 was theoretically predicted to form the molecular J eff = 3/2 ground state. Experimental verification of its existence is an important first step to exploring the consequences of the J eff = 3/2 state. Here, we report direct experimental evidence of the J eff = 3/2 state in GaTa4Se8 by means of excitation spectra of resonant inelastic X-ray scattering at the Ta L3 and L2 edges. We find that the excitations involving the J eff = 1/2 molecular orbital are absent only at the Ta L2 edge, manifesting the realization of the molecular J eff = 3/2 ground state in GaTa4Se8.
Similar content being viewed by others
Introduction
The quantum effects of electronic orbitals are pronounced in degenerate systems where the orbital degrees of freedom have to be considered on equal footing with spins as in, e.g., the Kugel–Khomskii model1. Examples include some cubic perovskite compounds of early 3d transition metals, in which the degeneracy of t 2g orbitals is large and the oxygen octahedra are only weakly distorted. For heavy 5d electrons, the strong spin–orbit coupling (SOC) can reduce the degeneracy by splitting the t 2g orbitals into a Kramers doublet (J eff = 1/2) and quartet (J eff = 3/2), and recovers the orbital angular momentum2,3,4. Recently, iridates with 5d 5 have drawn much attention because the half-filled state near the Fermi level (E F) is a Kramers doublet and a relatively weak electron correlation leads to the J eff = 1/2 Mott ground state5,6,7. This state offers opportunities to explore quantum phases such as a topological Mott insulator8, unconventional superconductivity9,10,11,12,13 and quantum spin liquid14,15,16,17.
At present, theories, modeling constructs and experimental investigations of relativistic J eff ground state systems are still emerging. Beyond the well-known 5d 5 iridates, the main challenge in other 5d electron systems is to build a concrete understanding of the exotic quantum effects with the J eff state. A relatively simple, but more interesting case is the 5d 1 system, which results in a J eff = 3/2 effective moment. Examples can be found in double perovskites such as Sr2MgReO6 18, Ba2YMoO6 19,20,21 and Ba2NaOsO6 22, 23. In the ionic limit, the magnetic moment of J eff = 3/2 vanishes because the orbital component cancels the spin component3, 4. The spin–orbital entanglement leads to a strong multipolar exchange of the same order as the ordinary bilinear exchange3, 4, giving access to a variety of exotic phenomena in multipolar systems such as 4f-/5f- heavy Fermion compounds24. While recent advanced X-ray spectroscopic studies showed clear signatures in Sr2IrO4 and the other iridates6, 25,26,27,28,29 for the case of J eff = 1/2, the physics of the J eff = 3/2 state has to date remained elusive in experiment.
Recently, a lacunar spinel compound, GaTa4Se8, was suggested as a model system for the molecular J eff = 3/2 Mott insulating ground state30. As shown in Fig. 1a, the basic building block is a tetramerized Ta4Se4, or simply so-called Ta4 cluster. The short intra-cluster having a Ta–Ta distance of ≤3 Å naturally induces the molecular orbital (MO) states residing on the cluster30, 31. The MO calculation for the Ta–Ta bonding orbitals of Ta4 cluster and the ab-initio band structure calculation found that one electron occupies the MO states with t 2 (or, t 2g-like) symmetry near E F 30,31,32,33,34,35]. The strong SOC of the Ta atom splits the three-fold degenerate t 2 MO states into Kramers doublet (J eff = 1/2 MO states) and quartet (J eff = 3/2 MO states), and the quarter-filled state near E F is the Kramers quartet as shown in Fig. 1b. Due to the large inter-cluster distance (≥4 Å), the bandwidth of the band formed by J eff = 3/2 MO states is small (~0.7 eV) and the relative strength of on-site Coulomb correlation, i.e., U (~ 2 eV), is sizable, rendering GaTa4Se8 a rare example of a molecular J eff = 3/2 Mott insulator30.
Crystal structure, MO levels, and RIXS process in GaTa4Se8. a The crystal structure of GaTa4Se8 (cubic \({\rm{F}}\bar 43m\)). The red, black and green spheres represent Ga, Ta and Se atoms, respectively. The Ta4 tetrahedron clusters (shaded in gray) form a face-centered-cubic lattice. b The MO energy levels of Ta4 cluster near the Fermi level (E F). Due to the SOC, three-fold degenerate t 2 MO states split into Kramers quartet (J eff = 3/2) and doublet (J eff = 1/2) MO states. The former has the mixed character of the atomic j = 3/2 and j = 5/2, whereas the latter is branched off from the j = 5/2. c Schematic diagram for RIXS processes involving the J eff = 1/2 and J eff = 3/2 MO states. The low-energy dipole allowed non-elastic L2- and L3-edge RIXS processes are indicated by red and blue arrows, respectively. Ta 2p electrons in p 1/2 and p 3/2 core states are denoted by orange circles and 5d electrons occupying MO states near E F are represented by green circles. Since 2p 1/2 → J eff = 1/2 transition is forbidden, orbital excitations involving the J eff = 1/2 MO states are absent in the L2-edge RIXS. Therefore, only two elementary processes are allowed for the inelastic L2-edge RIXS. This should be contrasted with the inelastic L3-edge RIXS where five different processes are expected in low-energy excitations
Experimental identification of the relativistic J eff state is necessary to understand the underlying mechanisms of quantum phenomena that have been reported and speculated for this material and others3, 18,19,20,21,22,23, 30, 32, 36,37,38,39,40,41,42. At low temperature, for example, GaTa4Se8 exhibits an intriguing transition38,39,40 towards a non-magnetic and possibly spin singlet state, which are presumably related to a peculiar bump observed in the susceptibility and specific heat39, 40. Furthermore, this non-trivial magnetic and electronic behavior could be related to superconductivity observed under pressure32, 37, 38. Considering that the previous studies do not take the SOC into account30, determining the nature of its magnetic moment is essential to elucidate the physics of GaTa4Se8 and to address the related issues that have been theoretically discussed largely for the 5d oxides.
In the case of the J eff = 1/2 ground state in Sr2IrO4, the salient experimental evidence has been that the magnetic resonant X-ray scattering (MRXS) intensity of the Néel-ordered state is nearly absent at the L2 edge6. The destructive quantum interference at L2 edge only occurs in the complex J eff = 1/2 state \(\left( { \propto \left| {xy, \mp \sigma } \right\rangle \mp \left| {yz, \mp \sigma } \right\rangle + i\left| {zx, \mp \sigma } \right\rangle } \right)\), ruling out all single orbital S = 1/2 states of real wave functions. A few magnetically ordered iridium compounds were found to show the same phenomenon26,27,28,29. On the other hand, verifying the J eff = 3/2 state in non-magnetic GaTa4Se8 is a greater challenge. MRXS analysis, which is only possible for magnetically ordered materials, cannot be exploited.
Here we used the high-resolution resonant inelastic X-ray scattering (RIXS) technique to explore the J eff = 3/2 state. At the Ta L edges, dipole transitions give rise to the direct RIXS via 2p→5d absorption and subsequent 5d→2p decay, which directly probes the valence and conduction band states43. As depicted in Fig. 1b, c, the J eff = 1/2 MO level is branched off from the atomic j = 5/2 and the absorption transition between L2 (2p 1/2) and j = 5/2 is naturally dipole-forbidden44. In contrast, the J eff = 3/2 MO states are composed of both the atomic j = 5/2 and j = 3/2 states. Therefore, we were able to establish the molecular J eff = 3/2 ground state in GaTa4Se8 by examining the excitation spectra at both the Ta L3 and L2 absorption edges. This is the first spectroscopic evidence for a molecular J eff = 3/2 ground state in a real material.
Results
Ta L3 and L2 edge XAS and RIXS
Figure 2a, b show the high-resolution Ta L3- and L2-edge X-ray absorption spectroscopy (XAS) spectra, respectively, which were measured in the partial yield mode by recording the shallow core–hole emissions (see also Supplementary Fig. 1). The L3- and L2-edge spectra comprise one primary peak at ~ 9.8825 and ~ 11.1365 keV, respectively, and a shoulder peak at ~ 5 eV higher photon energy. Figure 2c, d show the high-resolution Ta L3- and L2-edge RIXS spectra, respectively, as a function of the incident photon energy (E i). Both RIXS spectra show basically the same resonant profiles. It should be noted that broad excitation peaks ~3.5 and 7 eV are resonantly enhanced when E i is tuned near to the primary XAS peak. On the other hand, the narrow excitation peaks below 2 eV are resonantly enhanced when E i is tuned to the ~ 2 eV below the XAS maximum.
XAS and RIXS spectra and the projected DOS. a, b High-resolution Ta L3-edge a and L2-edge b XAS spectra of GaTa4Se8 measured in the partial yield mode. c, d High-resolution Ta L3-edge c and L2-edge d RIXS spectra as functions of the incident photon energy (E i) and energy loss. Both spectra show the broad excitation over the three −7 eV energy loss. Below 2 eV, the three narrow peaks are clearly visible in the L3-edge RIXS spectra. But the third peak at 1.3 eV is missing in the L2-edge RIXS spectra. e The calculated DOS projected onto Ta-e g (black), Ta-t 2g (cyan) and Se-p (yellow) orbitals. In the region of E F ± 2 eV, the t 2g states are dominant and responsible for the narrow peak excitations noticed in c and d
The XAS and RIXS spectra clearly reveal the overall structure of the unoccupied states guided by insights from the band structure calculations. Figure 2e shows the wide energy range density of states (DOS), projected onto Ta atomic t 2g and e g symmetry orbitals from the ab-initio band structure calculations. A quite large portion of the unoccupied states is located above 2 eV and has a mixed character of t 2g and e g symmetry, which explains the overall XAS feature and the broad high-energy RIXS peaks above the 2 eV energy loss. Regarding these broad peaks, there is no distinct difference between the Ta L3- and L2-edge RIXS spectra.
On the other hand, the t 2g symmetry character dominates the energy range near E F (±2 eV). In the XAS spectra, excitations to these t 2g states, including the possible relativistic J eff states, do not show up as a distinct peak but are located in the lower-energy shoulder region of the large XAS peak. The narrow RIXS peaks below the 2 eV energy loss are assigned to orbital excitations within these t 2g manifolds. In the case of the L3-edge RIXS (Fig. 2c), three narrow peaks are located at 0.27, 0.7 and 1.3 eV energy loss positions. Remarkably, the 1.3 eV peak disappears in the L2-edge RIXS spectra (Fig. 2d). In the sections below, to shed light on the physical origin, we further investigate the orbital excitation spectra in terms of the momentum transfer dependence, and analyze the RIXS spectra based on the band structure calculations and the cluster model calculations.
The absence of 1.3 eV orbital excitation in the L2 edge RIXS
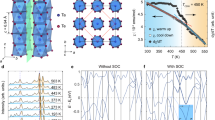
Figure 3a shows the momentum transfer dependence of the L3-edge RIXS (E i = 9.879 keV) excitations along (hhh) high-symmetry direction. Three orbital excitation peaks at the 0.27, 0.7 and 1.3 eV energy loss positions are clearly identified for all momentum transfers with some intensity modulations. Within the instrument energy resolution (~ 100 meV), no dispersion is observed for these three excitations.
L3- and L2-edge RIXS spectra. a, b L3-edge (E i = 9.879 keV) a and L2-edge (E i = 11.133 keV) b RIXS spectra as a function of momentum transfer Q and energy loss. Three orbital excitations are clearly noticed at the 0.27, 0.7, 1.3 eV energy-loss positions in a. In sharp contrast, only two peaks at 0.27 and 0.7 eV are visible in b, and the broad peak at 1.3 eV is not observed. c, d L3-edge c and L2-edge d RIXS spectra as a function of incident sample angle θ and energy loss. 2θ is fixed at 90°. Clearly, the broad peak at 1.3 eV is absent for L2-edge
Figure 3b shows the momentum transfer dependence of the L2-edge RIXS (E i = 11.133 keV) excitations along the (hhh) high-symmetry direction. Like the L3-edge RIXS excitations (Fig. 3a), two sharp peaks at the 0.27 and 0.7 eV energy loss positions are observed for all momentum transfers with some intensity modulations. Unlike the L3-edge RIXS excitations, however, there is no peak at the 1.3 eV region in the L2-edge RIXS excitations for all measured momentum transfers. This is our main observation which is attributed to the destructive interference of molecular J eff = 1/2 state at the L2 edge as will be further discussed below.
Figure 3c shows the incident sample angle (θ) dependence of the L3-edge RIXS excitations where the scattering angle (2θ) is fixed to 90°. When a grazing angle (θ = 30°) is used, the 1.3 eV peak is largely enhanced while the 0.27 eV peak is suppressed. Figure 3d shows the θ dependence of the L2-edge RIXS excitations where 2θ is fixed to 90°. For all θ angles, no peak structure shows up in the 1.3 eV energy loss region (also see Supplementary Fig. 2). Instead, a concave spectral shape is formed in the 1.3 eV energy loss region, indicating the total absence of the 1.3 eV peak.
Band structure and cluster model RIXS calculations
Having the solid experimental observation that there is no 1.3 eV peak only in the L2-edge RIXS excitations, we now investigate the detailed electronic structure near E F and perform the cluster model RIXS calculations to find its origin. Figure 4a shows the schematics of the band structure near E F corresponding to the cases with and without SOC and electron correlation U. Without a sizable SOC, only a strong enough U can split the t 2 MO band into a narrow lower Hubbard band (LHB) and a broad upper Hubbard band (UHB). In this case, a broad orbital excitation between LHB and UHB is expected. Importantly, no contrast between the L3- and L2-edge RIXS spectra is expected. On the other hand, with a strong SOC, the well-defined J eff = 1/2 MO band is branched off, leaving out the J eff = 3/2 MO band near E F. A moderate U opens a gap, making it a molecular J eff = 3/2 Mott insulator. Multiple orbital excitations are expected between the occupied bands (a 1, e and J eff = 3/2 LHBs), and the unoccupied J eff = 3/2 and J eff = 1/2 bands.
Schematic representation DOS and the electronic structure near E F. a Schematic representation DOS for cases with and without SOC and electron correlation U. Without SOC and U, t 2 MO band prevails over E F with six-fold degeneracy. SOC (without U) splits this degenerate band into the four-fold degenerate J eff = 3/2 and two-fold degenerate J eff = 1/2 MO bands. On-site correlation U (without SOC) can split the t 2 MO band into lower Hubbard band (LHB) and upper Hubbard band (UHB). With both SOC and U, the quarter-filled J eff = 3/2 MO band splits to LHB and UHB with the higher-lying J eff = 1/2 MO band. Red, blue, green, pink and black colors represent the J eff = 1/2, J eff = 3/2, e, a 1 and t 2 MO characters, respectively. b The calculated band dispersion (right) and DOS (middle) projected onto the MO states (a 1, e, J eff = 3/2 and J eff = 1/2) formed in the Ta4 cluster, and the calculated DOS projected onto the Ta atomic j = 3/2 and j = 5/2 states (left). Red, blue, green and pink colors represent the J eff = 1/2, J eff = 3/2, e and a 1 MO characters, respectively. In the band dispersion the J eff = 1/2 and 3/2 character is also represented by the line thickness. Gray and orange colors indicate the j = 3/2 and j = 5/2 Ta atomic characters, respectively. Notice that the J eff = 1/2 MO band is mostly composed of the atomic j = 5/2 states
Figure 4b shows the calculated band dispersion (right) and DOS (middle) near E F, which were projected onto the low-energy MO states (a 1, e, J eff = 3/2, and J eff = 1/2) formed in the Ta4 tetrahedron cluster (see Fig. 1a, b). The band gap is formed within the J eff = 3/2 MO bands, indicating the formation of a molecular J eff = 3/2 Mott state. The unoccupied J eff = 1/2 MO band is well separated from the J eff = 3/2 MO bands. The DOS projected onto the Ta atomic j = 5/2 and 3/2 states is shown on the left of Fig. 4b. It demonstrates that the J eff = 1/2 MO band comprises mostly the atomic j = 5/2 states, whereas the a 1, e and J eff = 3/2 MO bands are composed of both the atomic j = 5/2 and 3/2 states (see also Fig. 1b).
To clarify the nature of the observed excitations, we have carried out the cluster model calculations for RIXS spectra within the fast collision approximation (zeroth order of the ultrashort core–hole lifetime expansion) and the dipole approximation45 (for details, see Supplementary Note 2). The calculated L3-edge RIXS spectrum in Fig. 5a reveals four low-energy peaks. Peaks A and B originate from the excitations from the fully occupied e and a 1 MO states to the partially occupied J eff = 3/2 MO state, respectively. The excitations from the e and a 1 MO states to the unoccupied J eff = 1/2 MO state are well separated and comprise the remaining two peaks C and D, respectively (see Supplementary Note 4). The excitation from the J eff = 3/2 MO state to the J eff = 1/2 MO state is coincidently located at the second peak B. Figure 5b shows the corresponding experimental L3-edge RIXS spectra. We find reasonable agreement between the calculations and the experimental observations: A and B correspond to the first two peaks experimentally observed at 0.27 and 0.7 eV, and C and D correspond to the broad peak observed at 1.3 eV.
Cluster model calculations of the L3 and L2 RIXS spectra. a RIXS spectra calculated within the fast collision approximation (zeroth order of the ultrashort core–hole lifetime expansion) and the dipole approximation using the model parameters U = 2 eV, λ SO = 0.4 eV, t σ = −1.41 eV, t δ = 0.213 eV and t π = 0.1 eV. U and λ SO denote strengths of the on-site Coulomb repulsion and SOC, respectively, and t σ,δ (t π ) denote diagonal (off-diagonal) nearest neighbor hoppings (see Supplementary Note 2). The spectral functions are convoluted with a Lorentzian function of 0.1 eV width. The lowest two peaks A and B are excitations from the fully occupied e and a 1 MO states, respectively, to the partially occupied J eff = 3/2 MO states. The excitation from the J eff = 3/2 MO states to the unoccupied J eff = 1/2 MO states is coincidently located at the second peak B. The excitations from the e and a 1 MO states to the J eff = 1/2 MO states are well separated and comprise the higher two peaks C and D, respectively. The latter three excitations involving the J eff = 1/2 MO states are absent in the L2-edge RIXS spectrum. b The corresponding experimental RIXS spectra at L3- and L2-edge with error bars. The error bars indicate the standard deviation to the number of detected photons
The excitations involving the unoccupied J eff = 3/2 MO states (peaks A and B) are also revealed in the calculated L2-edge RIXS spectrum in Fig. 5a. Compared to the L3-edge RIXS calculations, the intensity of peak B is much weaker than that of peak A. This is understood because peak B contains the excitation from the J eff = 3/2 MO states to the J eff = 1/2 MO states, and its spectral weight is partially suppressed for the L2-edge RIXS excitations in the following reason. For the RIXS process to occur, both photon absorption and emission must be the allowed transitions43. In the L2-edge RIXS excitations, the photon absorption between 2p 1/2 and the J eff = 1/2 MO states is naturally dipole-forbidden because the J eff = 1/2 MO states mostly comprise the Ta atomic j = 5/2 states as shown in Fig. 4b44. This is clearly seen in peaks C and D, which are totally absent in the calculated L2-edge RIXS spectrum in the Fig. 5a, indicating that excitations involving the J eff = 1/2 MO states was totally suppressed at the L2 edge. Hence, the total absence of the 1.3 eV peak in the L2-edge RIXS spectra of GaTa4Se8 can be identified as arising from the destructive interference at the L2 edge of the J eff = 1/2 MO states, thereby establishing the molecular J eff = 3/2 ground state in GaTa4Se8.
Discussion
We have focused on spectroscopic evidence in search for the destructive quantum interference of J eff states. With the help of the band structure and the cluster model calculations, the RIXS excitation spectra taken at L3 and L2 edges provide clear evidence that the J eff = 1/2 MO band is well separated from the J eff = 3/2 MO band and the excitations involving the J eff = 1/2 MO band are totally suppressed only at L2 edge, verifing the molecular J eff = 3/2 ground state in GaTa4Se8. Unlike MRXS, the RIXS technique can be useful even for a system with no long-range magnetic order (namely, a typical case rather than an exception) as demonstrated in the current study. Considering a strong SOC (~ 0.5 eV) of 5d orbital, this type of study is possible with a moderate energy resolution of ~ 100 meV, which is easily achievable for all 5d transition-metal L edges in the current state-of-the-art RIXS spectrometer46.
Establishing the molecular J eff = 3/2 nature of GaTa4Se8 does not only just provide the opportunities for investigating J eff physics but also elucidates the current important issues in GaTa4Se8 and its close cousins such as GaNb4 X 8 and GaMo4 X 8 (X = Se, Te). In GaTa4Se8, for example, the underlying mechanism is not clearly understood for the ‘paramagnetic’ insulator to metal transition and the superconductivity under pressure32,33,34, 37, 38. Furthermore, the magnetic behavior of this material at low temperatures does not seem to support a simple ‘paramagnetic’ Mott phase33, 34. It should be emphasized that the relativistic J eff state has not been identified in the previous studies, since it is a recent theoretical finding30 and is experimentally established in this study. On the basis of the current spectroscopic evidence, one can consider the ground state of GaTa4Se8 as the manifestation of the frustrated magnetic phase emerging from the non-trivial interactions among the relativistic J eff = 3/2 moments3, 19,20,21. Moreover, we speculate that the superconductivity reported in this material is also related to this phase. We note that the other related lacunar spinel compound, GaNb4Se8 which is also expected to have the molecular J eff = 3/2 nature30, exhibits a quite similar low-temperature behavior and becomes superconducting. On the other hand, the molecular J eff = 1/2 material with basically the same structure, GaMo4 X8 (X = S, Se), is well understood as a ferromagnet41 and does not exhibit superconductivity47. Our total energy calculation shows that the molecular J eff = 3/2 moments of the Ta4 cluster are in fact antiferromagnetically coupled between neighboring clusters (E AFM-FM = −7.4 meV per cluster). Considering the fcc arrangement of this cluster unit, this strongly suggests magnetic frustration48, 49. In this regard, our current study may indicate that the molecular J eff moments are frustrated in this material. This is compatible with recent experimental observations of the specific heat and magnetic susceptibility, interpreted as a formation of dimerization and a spin singlet state36, 39.
Methods
Partial-yield L-edge XAS
Diced spherical analyzers were used to record L3- and L2-edge XAS spectra by analyzing resonant emission signals. The incident photon bandpass is ~0.8 eV. In the case of the L3 edge, the Lβ2 emission, which leaves out a shallow (~ 230 eV) core–hole of 4d, was analyzed by the Ge (555) analyzer, which was on the 1 m Rowland circle. Because of a long lifetime of the shallow core–hole, a high-resolution (<2 eV) XAS was obtained50. In the case of the L2 edge, the Lγ1 emission, which leaves out a shallow (~ 230 eV) core–hole of 4d, was analyzed by the Si (466) analyzer. Note that the use of the analyzer is essential for the L2-edge XAS because a poor resolution of an energy-resolving detector cannot totally eliminate the Ga K-edge emission (~ 10.2 keV) from the Ta Lγ1 emission (10.9 keV).
RIXS measurements
The sample grown by the vapor transport method in a sealed quartz tube was mounted in a displex closed-cycle cryostat and measured at 15 K. The RIXS measurements were performed using the MERIX spectrometer at the 27-ID B beamline46 of the Advanced Photon Source. X-rays were monochromatized to a bandwidth of 70 meV, and focused to have a beam size of 40(H) × 15(V) μm2. A horizontal scattering geometry was used with the incident photon polarization in the scattering plane. For the L3-edge RIXS, a Si (066) diced spherical analyzer with 4 inches radius and a position-sensitive silicon microstrip detector were used in the Rowland geometry. For the L2-edge RIXS, a Si (466) diced spherical analyzer with 4 inches radius was used. The overall energy resolution of the RIXS spectrometer at both edges was 100 meV, as determined from the full-width-half-maximum of the elastic peak.
Sample synthesis
Single crystal samples of GaTa4Se8 were obtained by the selenium transport method51. The pure powders of GaTa4Se8 were placed in an evacuated silica tube with a small excess of Se and heated at 950 °C for 24 h and then slowly cooled (2 °C h−1) to room temperature.
Band structure calculations
Electronic structure calculations were performed by OpenMX software package52, which is based on the linear combination of pseudo-atomic-orbital basis formalism. The exchange-correlation energy was calculated within the LDA (local density approximation) functional53. The energy cutoff The exchange-correlation energy was calculated within the LDA (local density approximation) functional of 400 Rydberg was used for the real-space integration and the 8 × 8 × 4 Monkhorst-Pack k-point grid was used for the momentum-space integration. The SOC was treated within the fully relativistic j-dependent pseudopotential and non-collinear scheme54. DFT + U (density functional theory + U) formalism by Dudarev et al.55, 56 was adopted for our calculations. Our main result is based on U eff = U−J = 2.3 eV, and we found that our conclusion and discussion are valid for different U eff in a reasonable range (see Supplementary Fig. 4 and Supplementary Note 1). The experimental structure taken from X-ray diffraction32 has been used for our calculation and there is no significant difference found in electronic and magnetic properties when the optimized structure is used. Total energy calculations have been performed with several different non-collinear magnetic configurations, and the most stable (a kind of antiferromagnetic) order has been taken to present the electronic structure. We found that the magnetic order does not change the band characters or their relative positions, and therefore, it does not affect any of our conclusion or discussion.
Cluster model calculations
We have adopted a three-band Hubbard model in a four-site tetrahedron cluster with seven electrons (for detail, see Supplementary Note 2). The model was solved numerically with the help of the Lanczos exact diagonalization method57. We have employed the Kramers–Heisenberg formula of the RIXS scattering operator45 and calculated the RIXS spectra by using the continued fraction method58. The RIXS scattering operator was determined with the zeroth order of the ultrashort core–hole lifetime expansion and the dipole approximation was applied with taking the experimental X-ray beam geometry (see Supplementary Note 3).
Data availability
The data that support these findings are available from the corresponding authors (M.J.H. and J.K.) on reasonable request.
References
Kugel, K. I. & Khomskii, D. I. The Jahn-Teller effect and magnetism: transition metal compounds. Sov. Phys. Usp. 25, 231–256 (1982).
Jackeli, G. & Khaliullin, G. Mott insulator in the strong spin-orbit coupling limit: from Heisenberg to a quantum compass and Kitaev Models. Phys. Rev. Lett. 102, 017205 (2009).
Chen, G., Pereira, R. & Balents, L. Exotic phases induced by strong spin-orbit coupling in ordered double perovskites. Phys. Rev. B 82, 174440 (2010).
Witczak-Krempa, W., Chen, G., Kim, Y. B. & Balents, L. Correlated quantum phenomena in the strong spin-orbit regime. Annu. Rev. Condens. Matter Phys. 5, 57–82 (2014).
Kim, B. J. et al. Novel J eff = 1/2 Mott state induced by relativistic spin-orbit coupling in Sr2IrO4. Phys. Rev. Lett. 101, 076402 (2008).
Kim, B. J. et al. Phase-sensitive observation of a spin-orbital Mott state in Sr2IrO4. Science 323, 1329–1332 (2009).
Watanabe, H., Shirakawa, T. & Yunoki, S. Microscopic study of a spin-orbit-induced mott insulator in Ir oxides. Phys. Rev. Lett. 105, 216410 (2010).
Pesin, D. & Balents, L. Mott physics and band topology in materials with strong spin-orbit interaction. Nat. Phys. 6, 376–381 (2010).
Wang, F. & Senthil, T. Twisted hubbard model for Sr2IrO4: magnetism and possible high temperature superconductivity. Phys. Rev. Lett. 106, 136402 (2011).
Kim, J. et al. Magnetic excitation spectra of Sr2IrO4 probed by resonant inelastic x-ray scattering: establishing links to cuprate superconductors. Phys. Rev. Lett. 108, 177003 (2012).
Watanabe, H., Shirakawa, T. & Yunoki, S. Monte Carlo study of an unconventional superconducting phase in Iridium oxide Jeff = 1/2 Mott insulators induced by carrier doping. Phys. Rev. Lett. 110, 027002 (2013).
Kim, Y. K. et al. Fermi arcs in a doped pseudospin-1/2 Heisenberg antiferromagnet. Science 345, 187–190 (2014).
Kim, Y. K., Sung, N. H., Denlinger, J. D. & Kim, B. J. Observation of d-wave gap in electron-doped Sr2IrO4. Nat. Phys. 12, 37–41 (2016).
Chaloupka, J., Jakeli, G. & Khaliullin, G. Kitaev-Heisenberg model on a Honeycomb lattice: possible exotic phases in iridium oxides A2IrO3. Phys. Rev. Lett. 105, 027204 (2010).
Kimchi, I. & Vishwanath, A. Kitaev-Heisenberg model for iridates on the triangular, hyperkagome, kagome, fcc, and pyrochlore lattices. Phys. Rev. B 89, 014414 (2014).
Chun, S. H. et al. Direct evidence for dominant bond-directional interactions in a honeycomb lattice iridates Na2IrO3. Nat. Phys. 11, 462–466 (2015).
Dey, F. et al. Spin-liquid behavior in Jeff = 1/2 triangular lattice compound Ba3IrTi2O9. Phys. Rev. B 86, 140405 (2012).
Wiebe, C. R. et al. Frustration-driven spin freezing in the S = 1/2 fcc perovskite Sr2MgReO6. Phys. Rev. B 68, 134410 (2003).
de Vries, M. A., Mclaughlin, A. C. & Bos, J.–W. G. Valence bond glass on an fcc lattice in the double perovskite Ba2YMoO6. Phys. Rev. Lett. 104, 177202 (2010).
Aharen, T. et al. Magnetic properties of the geometrically frustrated S = 1/2 antiferromagnets, La2LiMoO6 and Ba2YMoO6, with the B-site ordered double perovskite structure: evidence of collective spin-singlet ground state. Phys. Rev. B 81, 224409 (2010).
Carlo, J. P. et al. Triplet and in-gap magnetic states in the ground state of the quantum frustrated fcc antiferomagnet Ba2YMoO6. Phys. Rev. B 84, 100404 (2011).
Erickson, A. S. et al. Ferromagnetism in the Mott insulator Ba2NaOsO6. Phys. Rev. Lett. 99, 016404 (2007).
Gangopadhyay, S. & Pickett, W. E. Spin-orbit coupling, strong correlation, and insulator-metal transitions: the J eff = 3/2 ferromagnetic Dirac-Mott insulator Ba2NaOsO6. Phys. Rev. B 91, 045133 (2015).
Mydosh, J. A. & Oppeneer, P. M. Colloquium: hidden order, superconductivity, and magnetism: the unsolved case of URu2Si2. Rev. Mod. Phys. 83, 1301–1322 (2011).
Boseggia, S. et al. Antiferromagnetic order and domains in Sr3Ir2O7 probed by x-ray resonant scattering. Phys. Rev. B 85, 184432 (2012).
Kim, J. W. et al. Dimensionality driven spin-flop transition in layered iridates. Phys. Rev. Lett. 109, 037204 (2012).
Boseggia, S. et al. Robustness of basal-plane antiferromagnetic order and the J eff = 1/2 state in single-layer iridate spin-orbit Mott insulators. Phys. Rev. Lett. 110, 117207 (2013).
Ohgushi, K. et al. Resonant x-ray diffraction study of the strongly spin-orbit-coupled Mott insulator CaIrO3. Phys. Rev. Lett. 110, 217212 (2013).
Calder, S. et al. Jeff = 1/2 Mott spin-orbit insulating state close to the cubic limit in Ca4IrO6. Phys. Rev. B 89, 081104 (2014).
Kim, H.-S., Im, J., Han, M. J. & Jin, H. Spin-orbital entangled molecular j eff states in lacunar spinel compounds. Nat. Commun. 5, 3988 (2014).
Johrendt, D. Crystal and electronic structure of the tetrahedral V4 cluster compounds GeV4Q8 (Q = S, Se). Z. Anorg. Allg. Chem. 624, 952–958 (1998).
Pocha, R., Johrendt, D., Ni, B. & Abd-Elmeguid, M. M. Crystal structures, electronic properties, and pressure-induced superconductivity of the tetrahedral cluster compounds GaNb4S8, GaNb4Se8, and GaTa4Se8. J. Am. Chem. Soc. 127, 8732–8740 (2005).
Ta Phuoc, V. et al. Optical conductivity measurements of GaTa4Se8 under high pressure: evidence of a bandwidth-controlled insulator-to-metal Mott transition. Phys. Rev. Lett. 110, 037401 (2013).
Camjayi, A. et al. First-order insulator-to-metal transition in the paramagnetic 3D system GaTa4Se8. Phys. Rev. Lett. 113, 086404 (2014).
Guiot, V., Janod, E., Corraze, B. & Cario, L. Control of the electronic properties and resistive switching in the new series of Mott insulators GaTa4Se8-yTey (0 ≤ y ≤ 6.5). Chem. Mater. 23, 2611–2618 (2011).
Waki, T. et al. Spin-singlet state formation in the cluster Mott insulator GaNb4S8 studied by μSR and NMR spectroscopy. Phys. Rev. B 81, 020401 (2010).
Abd-Elmeguid, M. et al. Transition from Mott insulator to superconductor in GaNb4Se8 and GaTa4Se8 under high pressure. Phys. Rev. Lett. 93, 126403 (2004).
Ni, B. Pressure-Induced Superconductivity in the Semiconducting Metal-Cluster Compounds Ga(Ta,Nb) 4 (Se,S) 8 (Mensch-und-Buch-Verl., 2002).
Kawamoto, S. et al. Frustrated magnetism in a Mott insulator based on a transition metal chalcogenide. J. Phys. Conf. Ser. 683, 012025 (2016).
Yaich, H. B. et al. Nouveaux chalcogénures et chalcohalogénures à clusters tétraédriques Nb4 ou Ta4. J. Less-Common Met. 102, 9–22 (1984).
Rastogi, A. K. et al. Itinerant electron magnetism in the Mo4 tetrahedral cluster compounds GaMo4S8, GaMo4Se8, and GaMo4Se4Te4. J. Low Temp. Phys. 52, 539–557 (1983).
Rastogi, A. K. & Wohlfarth, E. P. Magnetic field-induced transitions in the Mo4 cluster compounds GaMo4S8 and GaMo4Se8 showing heavy Fermion behaviour. Phys. Stat. Sol. b 142, 569–573 (1987).
Ament, L. J. P., van Veenendaal, M., Devereaux, T. P., Hill, J. P. & van den Brink, J. Resonant inelastic x-ray scattering studies of elementary excitations. Rev. Mod. Phys. 83, 705–767 (2011).
Di Matteo, S. & Norman, M. R. Magnetic ground state of Sr2IrO4 and implications for second-harmonic generation. Phys. Rev. B 94, 075148 (2016).
Kramers, H. A. & Heisenberg, W. Über die streuung von strahlung durch atome. Z. Phys. 31, 681–708 (1925).
Gog, T. et al. Spherical analyzers and monochromators for resonant inelastic hard X-ray scattering: a compilation of crystals and reflections. J. Synchrotron Rad. 20, 74–79 (2013).
Asano, M. et al. Metallization of Mo-Cluster compound Ga0.5Mo2S4 at 38 GPa. J. Phys. Soc. Jpn 59, 2179–2182 (1990).
Mackenzie, N. D. & Young, A. P. Low-temperature series expansion for the FCC Ising antiferromagnet. J. Phys. C Solid State Phys. 14, 3927–3934 (1981).
Kuz’min, E. V. J. Quantum spin liquid in the FCC lattice. Exp. Theor. Phys. 96, 129–139 (2003).
Hämäläinen, K., Siddons, D. P., Hastings, J. B. & Berman, L. E. Elimination of the inner-shell lifetime broadening in x-ray-absorption spectroscopy. Phys. Rev. Lett. 67, 2850 (1991).
Vaju., C. et al. Electric-pulse-driven electronic phase separation, insulator-metal transition, and possible superconductivity in a Mott insulator. Adv. Mater. 20, 2760–2765 (2008).
Ozaki, T. Variationally optimized atomic orbitals for large-scale electronic structures. Phys. Rev. B 67, 155108 (2003).
Ceperley, D. M. & Alder, B. J. Ground state of the electron gas by a stochastic method. Phys. Rev. Lett. 45, 566–569 (1980).
MacDonald, A. H. & Vosko, S. H. Spin-polarized relativistic exchange energies and potentials. J. Phys. C Solid State Phys. 12, 2977–2990 (1979).
Dudarev, S., Botton, G., Savrasov, S., Humphreys, C. & Sutton, A. Electron-energy-loss spectra and the structural stability of nickel oxide:An LSDA+U study. Phys. Rev. B 57, 1505–1509 (1998).
Han, M. J., Ozaki, T. & Yu, J. O(N) LDA+U electronic structure calculation method based on the nonorthogonal pseudoatomic orbital basis. Phys. Rev. B 73, 045110 (2006).
Wu, K. & Simon, H. Thick-restart Lanczos method for large symmetric eigenvalue problems. SIAM J. Matrix Anal. Appl. 22, 602–616 (2000).
Kim, B. H., Shirakawa, T. & Yunoki, S. From a quasimolecular band insulator to a relativistic Mott insulator in \(t_{2g}^5\) systems with a honeycomb lattice structure. Phys. Rev. Lett. 117, 187201 (2016).
Acknowledgements
We are grateful to Yang Ding, In Chung, Heung-Sik Kim, Jino Im, Hosub Jin and Michel van Veenendaal for helpful discussion. The use of the Advanced Photon Source at the Argonne National Laboratory was supported by the US DOE under Contract No. DE-AC02-06CH11357. M.Y.J., J.-H.S. and M.J.H. were supported by Basic Science Research Program through NRF (2014R1A1A2057202). The computing resource was supported by KISTI (KSC-2014-C2-046) and the RIKEN supercomputer system (HOKUSAI GreatWave). S.H.C. was supported by Basic Science Research Program through NRF (2016K1A3A7A09005337). B.H.K. was supported by the RIKEN iTHES Project. S.Y. was supported by Grant-in-Aid for Scientific Research from MEXT Japan under the Grant No. 25287096.
Author information
Authors and Affiliations
Contributions
S.H.C., M.J.H. and J.K. conceived and performed the experiment. A.S., D.C. and T.G. developed analyzers. E.J. and L.C. prepared the sample. M.Y.J., J.-H.S. and M.J.H. performed the band structure calculations. B.H.K. and S.Y. performed the cluster model calculations. All authors discussed the results. J.K. and M.J.H. led the manuscript preparation with contributions from all authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Jeong, M.Y., Chang, S., Kim, B. et al. Direct experimental observation of the molecular J eff = 3/2 ground state in the lacunar spinel GaTa4Se8 . Nat Commun 8, 782 (2017). https://doi.org/10.1038/s41467-017-00841-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-017-00841-9
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.