Abstract
Experimental and theoretical investigations on itinerant ferromagnetic systems under pressure have shown that ferromagnetic quantum criticality is avoided either by a change of the transition order, becoming of the first order at a tricritical point, or by the appearance of modulated magnetic phases. In the first case, the application of a magnetic field reveals a wing-structure phase diagram as seen in itinerant ferromagnets such as ZrZn2 and UGe2. In the second case, no tricritical wings have been observed so far. Here, we report on the discovery of wing-structure as well as the appearance of modulated magnetic phases in the temperature-pressure-magnetic field phase diagram of LaCrGe3. Our investigation of LaCrGe3 reveals a double-wing structure indicating strong similarities with ZrZn2 and UGe2. But, unlike these simpler systems, LaCrGe3 also shows modulated magnetic phases similar to CeRuPO. This finding provides an example of an additional possibility for the phase diagram of metallic quantum ferromagnets.
Similar content being viewed by others
Introduction
Suppressing a second-order, magnetic phase transition to zero temperature with a tuning parameter (pressure, chemical substitutions, magnetic field) has been a very fruitful way to discover many fascinating phenomena in condensed matter physics. In the region near the putative quantum critical point (QCP), superconductivity has been observed in antiferromagnetic1 as well as ferromagnetic (FM) systems2,3,4. One peculiarity of the clean FM systems studied so far is that the nature of the paramagnetic-ferromagnetic (PM-FM) phase transition always changes before being suppressed to zero temperature5: in most cases, the transition becomes of the first order6,7,8,9,10,11. Recently, another possibility, where a modulated magnetic phase (AFM Q ) appears (spin-density wave, antiferromagnetic order), has been observed in CeRuPO12, 13, MnP14, 15, and LaCrGe3 16.
Several theories have been developed to explain those possibilities17,18,19,20,21,22,23,24,25,26. When a FM transition becomes of the first order at a tricritical point (TCP) in the temperature T pressure p plane, the application of a magnetic field H along the magnetization axis reveals a wing structure phase diagram in the T-p-H space20, 27. This is seen in UGe2 28, 29 and ZrZn2 30 and is schematically represented in Fig. 1a. This phase diagram shows the possibility of a different kind of quantum criticality at the quantum wing critical point (QWCP). In contrast with the conventional QCP, symmetry is already broken by the magnetic field at a QWCP. In the more recently considered case where the transition changes to a AFM Q phase, no wing structure phase diagram has been reported, but it is found that the AFM Q is suppressed by moderate magnetic field12, 13. This second possible T-p-H phase diagram has been schematically presented in a recent review5 and reproduced in Fig. 1b.
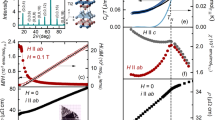
Temperature–pressure phase diagram. a Schematic T-p-H phase diagram of a quantum ferromagnet: the paramagnetic-ferromagnetic (PM-FM) transition becomes of the first order at a tricritical point (TCP) after which there is a quantum phase transition (QPT) at 0 K. Tricritical wings emerge from the TCP under magnetic field and terminate at quantum wing critical points (QWCP). b Schematic T-p-H phase diagram of a quantum ferromagnet when a modulated magnetic phase (SDW/AFM) emerges from the Lifshitz point (LP). c New possible schematic T-p-H phase diagram for which tricritical wings as well as a new magnetic phase are observed. d T-p phase diagram of LaCrGe3 from electrical resistivity measurements16 showing two FM regions (FM1 and FM2) separated by a crossover. The solid lines are guides to the eye
Here, we report electrical resistivity measurements on LaCrGe3 under pressure and magnetic field. We determine the T-p-H phase diagram and find that it corresponds to a third possibility where tricritical wings emerge in addition to the AFM Q phase. This type of phase diagram is illustrated in Fig. 1c: it includes both the tricritical wings and the AFM Q phase. In addition, the phase diagram of LaCrGe3 shows a double wing structure similar to what is observed in the itinerant ferromagnets UGe2 31 and ZrZn2 32, but with the additional AFM Q phase. LaCrGe3 is the first example showing such a phase diagram.
Results
T-p phase diagram
Recently, we reported on the T-p phase diagram of LaCrGe3 16, which is reproduced in Fig. 1d. At ambient pressure, LaCrGe3 orders ferromagnetically at TC = 86 K. Under applied pressure, TC decreases and disappears at 2.1 GPa. Near 1.3 GPa, there is a Lifshitz point33 at which a new transition line appears. The transition corresponds to the appearance of a modulated magnetic phase (AFM Q ) and can be tracked up to 5.2 GPa. Muon-spin rotation (μSR) measurements show that the AFM Q phase has a similar magnetic moment as the FM phase but without net macroscopic magnetization16. In addition, band structure calculations suggest that the AFM Q phase is characterized by a small wave-vector Q and that several small Q phases are nearly degenerate. Below the PM-AFM Q transition line, several anomalies marked as gray cross in Fig. 1d can be detected in ρ(T)16. These other anomalies within the AFM Q phase are compatible with the near degeneracy of different Q-states (shown as AFM Q and AFM Q′) with temperature and pressure driven transitions between states with differing wavevectors.
In this article, we determine the three dimensional T-p-H phase diagram of LaCrGe3 by measuring the electrical resistivity of single crystals of LaCrGe3 under pressure and magnetic field.
FM1 and FM2 phases
Whereas most of the features in Fig. 1d were well understood in ref. 16, we also indicate the pressure dependence of T x (dρ/dT max) at which a broad maximum is observed in dρ/dT below TC and shown as orange triangles in Fig. 1d. At ambient pressure, T x ≈ 71 K. No corresponding anomaly can be observed in magnetization16, internal field16 or specific heat34. Under applied pressure, T x decreases and cannot be distinguished from TC (dρ/dT mid) above 1.6 GPa. As will be shown, application of magnetic field allows for a much clearer appreciation and understanding of this feature.
Figure 2a shows the anomalies at T x and T C observed in the electrical resistivity and its temperature derivative at 1.14 GPa. For comparison, Fig. 2b shows ambient pressure data for UGe2 28 where a similar anomaly at T x can be observed. In UGe2, this anomaly was studied intensively35,36,37. It corresponds to a crossover between two ferromagnetic phases FM1 and FM2 with different values of the saturated magnetic moment35, 36. Under pressure, there is a critical point at which the crossover becomes a first-order transition, which eventually vanishes where a maximum in superconducting-transition temperature is observed2. In the case of LaCrGe3, we cannot locate where the crossover becomes a first order transition, since the anomaly merges with the Curie temperature anomaly near 1.6 GPa, very close to the TCP. However, as we will show below, the two transitions can be separated again with applied magnetic field above 2.1 GPa. This is similar to what is observed in UGe2 where the PM-FM1 and FM1-FM2 transition lines separate more and more as the pressure and the magnetic field are increased. Because of such similarities with UGe2, we label the two phases FM1 and FM2 and assume that the anomaly at T x corresponds to a FM1-FM2 crossover. A similar crossover was also observed in ZrZn2 32. In refs 18, 25, a Stoner model with two peaks in the density of states near the Fermi level was proposed to account for the two phases FM1 and FM2, reinforcing the idea of the itinerant nature of the magnetism in LaCrGe3.
Comparison of ρ(T) and its dρ(T)/dT between LaCrGe3 and UGe2. Temperature dependence of the resistivity (black line, left axis) and its derivative (blue line, right axis) of a LaCrGe3 at 1.14 GPa and b UGe2 at 0 GPa from ref. 28. The crossover between the two ferromagnetic phases (FM1 and FM2) is inferred from the maximum in dρ/dT (T x ) and marked by a red triangle, whereas the paramagnetic-ferromagnetic transition is inferred from the middle point of the sharp increase in dρ/dT (TC) and indicated by a blue circle
Field-dependent resistivity measurement under pressure
In zero field, for applied pressures above 2.1 GPa, both FM1 and FM2 phases are suppressed. Upon applying a magnetic field along the c-axis, two sharp drops of the electrical resistivity can be observed (Fig. 3a) with two corresponding minima in the field derivatives (Fig. 3b). At 2 K, clear hysteresis of ΔH ~ 0.7 T can be observed for both anomalies indicating the first order nature of the transitions. The emergence of field-induced first-order transitions starting from 2.1 GPa and moving to higher field as the pressure is increased (Supplementary Note 1) is characteristic of the FM quantum phase transition: when the PM-FM transition becomes of the first order, a magnetic field applied along the magnetization axis can induce the transition resulting in a wing structure phase diagram such as the one illustrated in Fig. 1a. In the case of LaCrGe3, evidence for a first order transition was already pointed out because of the very steep pressure dependence of T C near 2.1 GPa and the abrupt doubling of the residual (T = 2 K) electrical resistivity16. In UGe2 or ZrZn2, the successive metamagnetic transitions correspond to the PM-FM1 and FM1-FM2 transitions. In LaCrGe3, at 2 K, due to the presence of the AFM Q′ phase at zero field, the transitions correspond to AFM Q′-FM1 and FM1-FM2.
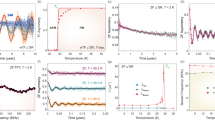
Determination of wing critical point at 2.39 GPa. a Field dependence of the electrical resistivity at 2, 13.5, and 30 K at 2.39 GPa with applied field along the c-axis. Continuous and dashed lines represent the field increasing and decreasing, respectively. When the continuous and dashed lines do not overlap, there is indication for hysteresis. b Corresponding field derivatives (dρ/dH). The curves are shifted by 15 μΩ cm T−1 for clarity. Vertical arrows represent the minima. The transition width is determined by the full width at half minimum as represented by horizontal arrows. Solid and open symbols in a, b represent the transition fields for field increasing and decreasing (squares for AFM Q -FM1 and circles for FM1-FM2). The blue cross symbols in a, b represent the AFM Q -PM transition at this pressure. The temperature dependence of the hysteresis width of H min1 and H min2 (solid symbols) are shown in c, d (left axes). The hysteresis width gradually decreases with increasing temperature and disappears at Tw corresponding to the wing critical point (vertical red arrows). The right axes show the temperature dependence of the transition widths (open symbols). Dashed lines are guides to the eye. The width is small for the first-order transition and becomes broad in the crossover region. The blue-color shaded area represents the first order transition region, whereas the white color area represents the crossover region. These allow for the determination of the wing critical point of the FM1 transition at 13.5 ± 1.5 K, 2.39 GPa, and 5.1 T and the one for the FM2 transition at 12 ± 1 K, 2.39 GPa and 7.7 T
Determination of the wing structure phase diagram
As the temperature is increased, the hysteresis decreases for both transitions, as can be seen in Fig. 3c, d and disappears at a wing critical point (WCP). Also, the transition width is small and weakly temperature dependent below the WCP and it broadens when entering in the crossover regime. Similar behavior has been observed in UGe2 29. At 2.39 GPa for example, we locate the WCP of the first-order FM1 transition around 13.5 K and the one of the first-order FM2 transition around 12 K. At this temperature and pressure, the transitions occur at 5.1 and 7.7 T, respectively. This allows for the tracking of the wing boundaries in the T-p-H space up to our field limit of 14 T. At low field, near the TCP, the wing boundaries are more conveniently determined as the location of the largest peak in dρ/dT (Supplementary Note 2).
The projections of the wings lines T w(p, H) in the T-H, T-p, and H-p planes are shown in Fig. 4a–c, respectively. The metamagnetic transitions to FM1 and FM2 start from 2.1 GPa and separate in the high field region as the pressure is further increased. For the FM1 wing, the slope dT w/dH w is very steep near H = 0 (Fig. 4a), whereas dH w/dp w is very small (Fig. 4c). This is in agreement with a recent theoretical analysis based on the Landau expansion of the free energy, which shows that dT w/dH w and dp w/dH w are infinite at the TCP27. This fact was overlooked in the previous experimental determinations of the wing structure phase diagram in UGe2 28, 29 and ZrZn2 30, but appears very clearly in the case of LaCrGe3. In the low field region, there are no data for the FM2 wing since the transition is not well separated from the FM1 wing, but there is no evidence for an infinite slope near H = 0. The wing lines can be extrapolated to QWCPs at 0 K in high magnetic fields of the order of ~30 T (Fig. 4a) and pressures around ~3 GPa (Fig. 4b).
Shape of the tricritical wing lines (T w, p w, H w). Projection of the wings in a T-H, b T-p and c H-p planes. Black solid squares and green solid circles represent the FM1-wing and FM2-wing, respectively. Red lines (represented in the T-p-H space in Fig. 5) are guides to the eyes and open symbols represent the extrapolated quantum wing critical point (QWCP). d H-p phase diagram at 2 K. The arrow represents the pressure p c = 2.1 GPa. The green color cross symbols represent the AFM Q′ phase boundary. Dark blue, light blue, and green color shaded areas represent the FM2, FM1, and AFM Q′ phases, respectively. The error bars in pressure for b–d are determined by the superconducting transition width of the Pb manometer. For a–d, the error bars in temperature and magnetic field are determined as half the data spacing
Figure 4d shows the H-p phase diagram at low temperature (T = 2 K). The magnetic field at the transition to the FM1 phase increases rapidly, whereas the field suppressing the AFM Q′ phase does not exceed 7 T. Above 2.5 GPa, the AFM Q′ and FM1 phases are separated by a region corresponding to the polarized PM phase. We note that a similar diagram where the wings extend beyond the AFM phase was recently obtained theoretically in the case of strong quantum fluctuations effects38. The similarity of the H-p phase diagram at 2 K (Fig. 4d) and the projection of the wings in the H-p plane (Fig. 4c) reveals the near vertical nature of the wings.
T-p-H phase diagram of LaCrGe3
The resulting three-dimensional T-p-H phase diagram of LaCrGe3 is shown in Fig. 5, which summarizes our results (Several of the constituent T-H phase diagrams, at various pressures, are given in Supplementary Fig. 3). The double wing structure is observed in addition to the AFM Q phase. This is the first time that such a phase diagram is reported. Other materials suggested that there is either a wing structure without any additional magnetic phase28,29,30, or a magnetic phase without a wing structure12, 13. The present study illustrates a third possibility where all such features are observed. The phase diagram of LaCrGe3 and the existence of wings clearly establish that the quantum phase transition from FM to AFM Q′ is of the first order. It is plausible that the reason is the same as for the FM to PM transition, but no theory is available for this case, as pointed out in a recent review5. Another interesting aspect is the existence of the two metamagnetic transitions (to FM1 and FM2) which suggests that this might be a generic feature of itinerant ferromagnetism. Indeed, it is observed in ZrZn2, UGe2, and LaCrGe3, although these are very different materials with different electronic orbitals giving rise the the magnetic states. We note that a wing structure has also been determined in the PM compounds UCoAl39,40,41 and Sr3Ru2O7 42, implying that a FM state probably exists at negative pressures in these materials. Strikingly, two anomalies could be detected upon crossing the wings in UCoAl (two kinks of a plateau in electrical resistivity39, two peaks in the ac susceptibility41), as well as in Sr3Ru2O7 (two peaks in the ac susceptibility42). These double features could also correspond to a double wing structure.
T-p-H phase diagram of LaCrGe3. Red solid lines are the second order phase transition and blue color planes are planes of first order transitions. Green color areas represent the AFM Q and AFM Q′ phases. For clarity, only data points at 2 K and along the transitions lines are shown. Black circles indicate the paramagnetic (PM)-ferromagnetic (FM) transition. Black squares indicate the wing critical line for FM1 and empty squares indicate the wing critical line for FM2. Blue diamonds indicate the first order transition to the FM1 state at 2 K and empty diamonds, the first order transition to FM2 at 2 K. Empty triangles indicate the PM-modulated magnetic phase (AFM Q ) and “+” indicate the AFM Q′ boundary. “×” indicate the AFM Q or AFM Q′ boundary at 2 K. The full set of data points can be found in Supplementary Note 3. For clarity, the green surfaces representing the boundaries for the AFM Q or AFM Q′ phases are shown only in the region of positive magnetic field
Conclusions
To conclude, the T-p-H phase diagram of LaCrGe3 provides a distinct example of possible outcomes of FM quantum criticality. At zero field, quantum criticality is avoided by the appearance of a new modulated magnetic phase, but the application of magnetic field shows the existence of a wing structure phase diagram leading towards QWCP at high field. These experimental findings reveal insights into the possible phase-diagrams of FM systems. The emergence of the wings reveals a theoretically predicted tangent slope27 near the TCP, a fact that was overlooked in previous experimental determination of phase diagrams of other compounds because of the lack of data density in that region. In addition, the double nature of the wings appears to be a generic feature of itinerant ferromagnetism, as it is observed in several, a priori, unrelated materials. This result deserves further theoretical investigations and unification.
Methods
Sample preparation
Single crystals of LaCrGe3 were grown using a high-temperature solution growth technique43, 44. A mixture of La, Cr, and Ge with a molar ratio of La:Cr:Ge = 13:13:74 was premixed by arc melting. The material was then placed in a 2-mL alumina crucible and sealed in a silica ampoule under partial pressure of high purity argon gas. The sealed ampoule was heated to 1100 °C over 3 h and held for 5 h. After that, it was cooled to 825 °C and the remaining liquid was decanted using a centrifuge. Details about the crystal growth procedure and sample characterization at ambient pressure is described in ref. 34.
The resistivity measurements under pressure
The samples for the pressure study were selected after ambient pressure characterization by the magnetization and resistivity measurements. Temperature and field dependent resistance measurements were carried out using a Quantum Design Physical Property Measurement System from 1.8 to 300 K. The resistivity was measured by the standard four-probe method with the current in the ab plane. Four Au wires with diameter of 12.5 μm were spot welded to the sample. A magnetic field, up to 9 or 14 T, was applied along the c-axis, which corresponds to the magnetization easy axis34, 45.
Two types of pressure cells were used for this experiment. A Be-Cu/Ni-Cr-Al hybrid piston-cylinder cell, similar to the one described in ref. 46, was used for pressures up to 2.1 GPa. A mixture of 4:6 light mineral oil: n-pentane46 used as a pressure medium, which solidifies at ~3–4 GPa at room temperature47. For higher pressures, a modified Bridgman cell48 was used to generate pressure up to 6 GPa. A 1:1 mixture of n-pentane:iso-pentane was used as a pressure medium. The solidification of this medium occurs around ~6–7 GPa at room temperature47, 49. For both cells, the pressure at low temperature was determined by the superconducting transition temperature of Pb50 measured by the resistivity.
The resistivity measurement under pressure at zero field is described in ref. 16.
Data availability
The data that support the findings of this study are available on request from the corresponding authors.
References
Mathur, N. et al. Magnetically mediated superconductivity in heavy fermion compounds. Nature 394, 39–43 (1998).
Saxena, S. S. et al. Superconductivity on the border of itinerant-electron ferromagnetism in UGe2. Nature 406, 587–592 (2000).
Aoki, D. et al. Coexistence of superconductivity and ferromagnetism in URhGe. Nature 413, 613–616 (2001).
Huy, N. T. et al. Superconductivity on the border of weak itinerant ferromagnetism in UCoGe. Phys. Rev. Lett. 99, 067006 (2007).
Brando, M., Belitz, D., Grosche, F. M. & Kirkpatrick, T. R. Metallic quantum ferromagnets. Rev. Mod. Phys. 88, 025006 (2016).
Goto, T., Shindo, Y., Takahashi, H. & Ogawa, S. Magnetic properties of the itinerant metamagnetic system Co(S1−x Se x )2 under high magnetic fields and high pressure. Phys. Rev. B 56, 14019–14028 (1997).
Huxley, A. D., Sheikin, I. & Braithwaite, D. Metamagnetic behavior near the quantum critical point in Uge2. Physica B 284, 1277–1278 (2000).
Uhlarz, M., Pfleiderer, C. & Hayden, S. M. Quantum phase transitions in the itinerant ferromagnet ZrZn2. Phys. Rev. Lett. 93, 256404 (2004).
Colombier, E., Braithwaite, D., Lapertot, G., Salce, B. & Knebel, G. High-pressure transport and microcalorimetry studies on high quality YbCu2Si2 single crystals. Phys. Rev. B 79, 245113 (2009).
Araki, S. et al. Pressure-temperature-field phase diagram in the ferromagnet U3P4. J. Phys. Soc. Jpn 84, 024705 (2015).
Shimizu, Y. et al. Unusual strong spin-fluctuation effects around the critical pressure of the itinerant ising-type ferromagnet URhAl. Phys. Rev. B 91, 125115 (2015).
Kotegawa, H. et al. Pressure-temperature-magnetic field phase diagram of ferromagnetic Kondo Lattice CeRuPO. J. Phys. Soc. Jpn 82, 123711 (2013).
Lengyel, E. et al. Avoided ferromagnetic quantum critical point in CeRuPO. Phys. Rev. B 91, 035130 (2015).
Cheng, J.-G. et al. Pressure induced superconductivity on the border of magnetic order in MnP. Phys. Rev. Lett. 114, 117001 (2015).
Matsuda, M. et al. Pressure dependence of the magnetic ground states in MnP. Phys. Rev. B 93, 100405 (2016).
Taufour, V. et al. Ferromagnetic quantum critical point avoided by the appearance of another magnetic phase in LaCrGe3 under pressure. Phys. Rev. Lett. 117, 037207 (2016).
Belitz, D., Kirkpatrick, T. R. & Vojta, T. First order transitions and multicritical points in weak itinerant ferromagnets. Phys. Rev. Lett. 82, 4707–4710 (1999).
Sandeman, K. G., Lonzarich, G. G. & Schofield, A. J. Ferromagnetic superconductivity driven by changing Fermi surface topology. Phys. Rev. Lett. 90, 167005 (2003).
Chubukov, A. V., Pepin, C. & Rech, J. Instability of the quantum-critical point of itinerant ferromagnets. Phys. Rev. Lett. 92, 147003 (2004).
Belitz, D., Kirkpatrick, T. R. & Rollbuhler, J. Tricritical behavior in itinerant quantum ferromagnets. Phys. Rev. Lett. 94, 247205 (2005).
Conduit, G. J., Green, A. G. & Simons, B. D. Inhomogeneous phase formation on the border of itinerant ferromagnetism. Phys. Rev. Lett. 103, 207201 (2009).
Karahasanovic, U., Krüger, F. & Green, A. G. Quantum order-by-disorder driven phase reconstruction in the vicinity of ferromagnetic quantum critical points. Phys. Rev. B 85, 165111 (2012).
Thomson, S. J., Krüger, F. & Green, A. G. Helical glasses near ferromagnetic quantum criticality. Phys. Rev. B 87, 224203 (2013).
Pedder, C. J., Krüger, F. & Green, A. G. Resummation of fluctuations near ferromagnetic quantum critical points. Phys. Rev. B 88, 165109 (2013).
Wysokinski, M. M., Abram, M. & Spalek, J. Ferromagnetism in Uge2: A microscopic model. Phys. Rev. B 90, 081114 (2014).
Abdul-Jabbar, G. et al. Modulated magnetism in PrPtAl. Nat. Phys 11, 321–327 (2015).
Taufour, V., Kaluarachchi, U. S. & Kogan, V. G. Constraints on the merging of the transition lines at the tricritical point in a wing-structure phase diagram. Phys. Rev. B 94, 060410 (2016).
Taufour, V., Aoki, D., Knebel, G. & Flouquet, J. Tricritical point and wing structure in the itinerant ferromagnet Uge2. Phys. Rev. Lett. 105, 217201 (2010).
Kotegawa, H., Taufour, V., Aoki, D., Knebel, G. & Flouquet, J. Evolution toward quantum critical end point in Uge2. J. Phys. Soc. Jpn 80, 083703 (2011).
Kabeya, N. et al. Non-fermi liquid state bounded by a possible electronic topological transition in ZrZn2. J. Phys. Soc. Jpn 81, 073706 (2012).
Taufour, V., Villaume, A., Aoki, D., Knebel, G. & Flouquet, J. Magnetic field evolution of critical end point in UGe2. J. Phys. Conf. Ser. 273, 012017 (2011).
Kimura, N. et al. de Haas-van Alphen effect in ZrZn2 under pressure: Crossover between two magnetic states. Phys. Rev. Lett. 92, 197002 (2004).
Hornreich, R. M., Luban, M. & Shtrikman, S. Critical behavior at the onset of \(\overrightarrow {\rm{k}}\)-space instability on the λ line. Phys. Rev. Lett. 35, 1678–1681 (1975).
Lin, X., Taufour, V., Bud’ko, S. L. & Canfield, P. C. Suppression of ferromagnetism in the LaV x Cr1−x Ge3 system. Phys. Rev. B 88, 094405 (2013).
Pfleiderer, C. & Huxley, A. D. Pressure dependence of the magnetization in the ferromagnetic superconductor Uge2. Phys. Rev. Lett. 89, 147005 (2002).
Hardy, F. et al. Two magnetic Gruneisen parameters in the ferromagnetic superconductor Uge2. Phys. Rev. B 80, 174521 (2009).
Palacio Morales, A. et al. Thermoelectric power quantum oscillations in the ferromagnet UGe2. Phys. Rev. B 93, 155120 (2016).
Belitz, D. & Kirkpatrick, T. R. Quantum triple point and quantum critical endpoints in metallic magnets. Preprint at http://arxiv.org/abs/1708.00103 (2017).
Aoki, D. et al. Ferromagnetic quantum critical endpoint in UCoAl. J. Phys. Soc. Jpn 80, 094711 (2011).
Combier, T., Aoki, D., Knebel, G. & Flouquet, J. Ferromagnetic quantum criticality studied by hall effect measurements in UCoAl. J. Phys. Soc. Jpn 82, 104705 (2013).
Kimura, N. et al. Quantum critical point and unusual phase diagram in the itinerant-electron metamagnet UCoAl. Phys. Rev. B 92, 035106 (2015).
Wu, W. et al. Quantum critical metamagnetism of Sr3Ru2O7 under hydrostatic pressure. Phys. Rev. B 83, 045106 (2011).
Canfield, P. C. & Fisk, Z. Growth of single-crystals from metallic fluxes. Philos. Mag. B-Phys. Condens. Matter Stat. Mech. Electron. Opt. Magn. Prop 65, 1117–1123 (1992).
Canfield, P. C. & Fisher, I. R. High-temperature solution growth of intermetallic single crystals and quasicrystals. J. Cryst. Growth. 225, 155–161 (2001).
Cadogan, J. M., Lemoine, P., Slater, B. R., Mar, A. & Avdeev, M. Neutron diffraction study of the hexagonal perovskite-type compound lacrge3. Solid State Phenom 194, 71–74 (2013).
Bud’ko, S. L., Voronovskii, A. N., Gapotchenko, A. G. & Itskevich, E. S. The Fermi surface of cadmium at an electron-topological phase transition under pressure. Zh. Eksp. Teor. Fiz. 86, 778-783 (1984).
Torikachvili, M. S., Kim, S. K., Colombier, E., Bud’ko, S. L. & Canfield, P. C. Solidification and loss of hydrostaticity in liquid media used for pressure measurements. Rev. Sci. Instrum. 86, 123904 (2015).
Colombier, E. & Braithwaite, D. Simple adaptation of the Bridgman high pressure technique for use with liquid media. Rev. Sci. Instrum. 78, 093903 (2007).
Tateiwa, N. & Haga, Y. Evaluations of pressure-transmitting media for cryogenic experiments with diamond anvil cell. Rev. Sci. Instrum. 80, 123901 (2009).
Bireckoven, B. & Wittig, J. A diamond anvil cell for the investigation of superconductivity under pressures of up to 50 GPa: Pb as a low temperature manometer. J. Phys. E: Sci. Instrum 21, 841–848 (1988).
Acknowledgements
We would like to thank S.K. Kim, X. Lin, V.G. Kogan, D.K. Finnemore, E.D. Mun, H. Kim, Y. Furukawa, R. Khasanov for useful discussions. This work was carried out at the Iowa State University and the Ames Laboratory, US DOE, under Contract No. DE-AC02-07CH11358. This work was supported by the Materials Sciences Division of the Office of Basic Energy Sciences of the U.S. Department of Energy. V.T. was partly supported by Ames Laboratorys laboratory-directed research and development (LDRD) funding.
Author information
Authors and Affiliations
Contributions
V.T. and P.C. initiated this study. U.K., V.T., and P.C. prepared the single crystals. U.K, V.T., and S.B. performed the pressure measurements. U.K., V.T., S.B., and U.K. analyzed and interpreted the pressure data. U.K. and V.T. wrote the manuscript with the help of all authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kaluarachchi, U.S., Bud’ko, S.L., Canfield, P.C. et al. Tricritical wings and modulated magnetic phases in LaCrGe3 under pressure. Nat Commun 8, 546 (2017). https://doi.org/10.1038/s41467-017-00699-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-017-00699-x
This article is cited by
-
Machine learning guided discovery of ternary compounds involving La and immiscible Co and Pb elements
npj Computational Materials (2022)
-
Ferroelectric phase-transition frustration near a tricritical composition point
Nature Communications (2021)
-
Fragmentation in Frustrated Magnets: A Review
Journal of Low Temperature Physics (2020)
-
Mechanism for transitions between ferromagnetic and antiferromagnetic orders in d-electron metallic magnets
Scientific Reports (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.