Abstract
American marten (Martes americana) are a conservation priority in many forested regions of North America. Populations are fragmented at the southern edge of their distribution due to suboptimal habitat conditions. Facilitating gene flow may improve population resilience through genetic and demographic rescue. We used a multiscale approach to estimate the relationship between genetic connectivity and landscape characteristics among individuals at three scales in the northeastern United States: regional, subregional, and local. We integrated multiple modeling techniques and identified top models based on consensus. Top models were used to parameterize resistance surfaces at each scale, and circuit theory was used to identify potential movement corridors. Regional gene flow was affected by forest cover, elevation, developed land cover, and slope. At subregional and local scales, the effects were site specific and included subsets of temperature, elevation, developed land cover, and slope. Developed land cover significantly affected gene flow at each scale. At finer scales, lack of variance in forest cover may have limited the ability to detect a relationship with gene flow. The effect of slope on gene flow was positive or negative, depending on the site examined. Occupancy probability was a relatively poor predictor, and we caution its use as a proxy for landscape resistance. Our results underscore the importance of replication and multiscale approaches in landscape genetics. Climate warming and landscape conversion may reduce the genetic connectivity of marten populations in the northeastern United States, and represent the primary challenges to marten conservation at the southern periphery of their range.
Similar content being viewed by others
Introduction
Habitat conversion for human use has reduced the ranges of many species and fragmented them into smaller isolated patches (Hanski 2011). Population persistence in areas where species are patchily distributed is positively influenced by connectivity and exchange of individuals between patches (Beier and Noss 1998; Haddad et al. 2003; Whiteley et al. 2015). Connectivity reduces the probability of extinction from stochastic events, provides rescue effects following local extirpations, and increases genetic diversity within populations, which can reduce the likelihood of inbreeding depression (Hanski 1997; Quinn et al. 2019). For species affected by habitat fragmentation, identifying and protecting corridors that facilitate dispersal and gene flow between disjunct populations is a conservation priority (Tischendorf and Fahrig 2000).
The American marten (Martes americana) is a forest carnivore species that depends on deep snow pack to outcompete larger mesocarnivores (Carroll 2007; Kelly et al. 2009). Martens occur throughout the boreal forests of Canada and Alaska, and were historically widespread in forested regions of the northeastern United States (US) and Great Lakes region (Hagmeier 1956). During the nineteenth and twentieth centuries, anthropogenic land development and unregulated harvest led to widespread population declines, and contracted the southern extent of their range (Hagmeier 1956; Gibilisco 1994).
The southernmost extant population occurs in the northeastern US (O’Brien et al. 2018). Historically, the landscape was almost entirely forested, and the marten population was likely panmictic (Foster et al. 2002). Habitat fragmentation in the nineteenth- to mid-twentieth centuries led to population declines (Gibilisco 1994). As forests have recovered in recent decades, demographic and genetic data suggest that marten populations have also re-expanded (Kelly et al. 2009; Aylward et al. 2019). Nonetheless, the species is regionally considered rare, threatened, or endangered, and maintaining genetic connectivity is a conservation priority (Vermont Wildlife Action Plant Team 2015; New Hampshire Department of Fish and Game 2015). Furthermore, this system affords an opportunity to better understand gene flow dynamics that likely resulted from relatively recent landscape changes.
Gene flow is affected by the extent of landscape connectivity, which is often estimated based on measures of habitat quality like occupancy probability (O’Brien et al. 2006; Stevenson-Holt et al. 2014; Spear et al. 2015; Aylward et al. 2018). However, it is often unclear whether measures of landscape connectivity accurately represent functional connectivity (Tischendorf and Fahrig 2000). Landscape-genetic approaches infer landscape effects on dispersal and migration by examining relationships between genetic differentiation and landscape conditions between sampling locations (Spear et al. 2005; Epps et al. 2007). Identifying landscape characteristics that have positive or negative effects on gene flow can improve management strategies for population connectivity. For example, identifying the impact of major roadways on wildlife population genetic structure contributed to the creation of forested overpass structures that facilitate large mammal gene flow across highways in Banff National Park in Canada (Sawaya et al. 2014).
A common landscape genetics approach involves estimating relationships between genetic distance and an estimated cost of movement between sample locations. This movement cost is often calculated by using a resistance surface, a gridded representation of the landscape in which each cell value represents the degree to which the landscape conditions inhibit dispersal (Spear et al. 2015). Next, techniques like circuit theory can be applied to estimate the likelihood of dispersal and the most probable movement corridors between two points (McRae 2006). Resistance surfaces are challenging to parameterize, often relying on a priori assignment of resistance values to certain landscape characteristics (Spear et al. 2015). One approach, called causal modeling, limits biases associated with a priori resistance assignments by allowing the genetic data to determine the optimal parameterization scheme (Cushman et al. 2006). Causal modeling involves testing a wide range of resistance values for each landscape variable, and identifying the optimal parameterization based on correlation coefficients or information criteria (Smouse et al. 1986; Legendre et al. 1994; Burnham and Anderson 2002).
In this study, we used a hierarchical approach to parameterize models that predict how landscape conditions affect genetic connectivity of American marten populations in the northeastern US. The landscape conditions that facilitate or inhibit long-distance dispersal between subpopulations may differ from those that facilitate or inhibit local dispersal within subpopulations (Parks et al. 2013). Furthermore, observed landscape-genetic relationships may vary in different parts of a species’ range (Short Bull et al. 2011). Therefore, we estimated landscape-genetic relationships across the entire study area (“regional” scale), among groups of subpopulations (“subregional” scale), and within subpopulations (“local” scale). We used multiple analytical approaches to construct candidate models and verify their predictive power. We also identified potential dispersal corridors at each spatial scale.
Methods
Study area
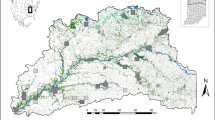
The study area included the US states of Vermont, New Hampshire (NH), and Maine (ME), the Adirondack Mountain region of New York (NY), and part of the Canadian province of Quebec, south of the St. Lawrence River (total area = 220,132 km2, Fig. 1). This area occurred along the southern limit of marten distribution. The study area was defined by regions harboring marten populations in the northeastern US and areas most likely to be used for long-distance dispersal between populations. The region is characterized by historically widespread forests that experienced significant fragmentation following European colonization (Foster et al. 2002). Forests have been in recovery in the region since the mid-1900s (Foster et al. 2002). Today, the study area is ~80% forested land cover, and more specifically, 20% spruce–fir forest, which may be the preferred cover type for martens (Bowman and Robitaille 1997; Godbout and Ouellet 2010). Demographics of forest mammals in the region are believed to have followed a similar trajectory, declining through the 1800s and recovering within the past several decades (Foster et al. 2002; Giblisco 1994; Hapeman et al. 2011; Aylward et al. 2019).
Dots represent individual marten sample locations used in this study. Blue polygons show the extent of subregional study areas, which were determined from broad-scale genetic population clusters (Aylward et al. 2019). Purple polygons show the extent of local study areas, which were determined by finer-scale population genetic clustering (Aylward et al. 2019). The inset shows the location of the study area (dark shading) in relation to the Atlantic coast of the United States. Samples in southern Vermont were not used for model development because of human-mediated gene flow from a reintroduction attempt. However, this location was used in corridor modeling due to the importance of identifying corridors for genetic connectivity to this population.
Genetic data
Genetic data used in this study were a subset of microsatellite data previously used to estimate genetic structure in the northeastern US (Aylward et al. 2019). Genetic material was obtained from tissue samples of animals collected by trappers in NY and ME, where martens are legally harvested, and incidental take by trappers and road kill in Vermont and NH, where martens are endangered and threatened, respectively. Previous estimates suggest hierarchical genetic structure within the region (Aylward et al. 2019). At a broad scale, two genetic clusters were present, which are referred to as “subregional” sites in this study: (1) NY and (2) New England (NHME). At a fine scale, five subpopulations were present: (1) ME, (2) New Hampshire and north-eastern Vermont, (3) southern Vermont (VT-S), (4) eastern New York (NY-E), and (5) western New York (NY-W). These fine-scale subpopulations are referred to as “local” sites in this study. We removed the subpopulation in VT-S from this analysis, as it was likely reintroduced from ME (Aylward et al. 2019), and translocations result in genetic patterns that are not indicative of natural processes (Colella et al. 2019). Furthermore, we removed any individual whose township locality could not be determined. The dataset for this analysis included ten microsatellite loci from 102 individuals from the four remaining subpopulations. We used these data to produce a novel analysis of landscape effects on the observed genetic distances between individuals.
Individual-based genetic distance was estimated in the R package “Gstudio” (Dyer 2012; R Core Team 2018) using the dist_euclidean function. Euclidean genetic distance has been shown to perform well in individual-based landscape genetics analysis (Shirk et al. 2018). Sample locations were obtained at the township level. Although precise GPS locations would be preferable, township-level data were the finest scale available for the majority of samples. To facilitate an individual-based approach, we assigned a location for each sample within its given township. Locations were randomly selected 1–3 km from the geographic center of their township.
Landscape data
Spatial data for landscape variables were obtained from public sources and scaled to the raster resolution of the coarsest dataset (800 × 800 m, Supplementary Information I). Based on previous research of marten habitat use, we considered seven landscape variables: (1) forest land cover, (2) spruce–fir land cover, (3) developed land cover, (4) elevation, (5) winter (Nov–Mar) temperature, (6) road density, and (7) slope (Bowman and Robitaille 1997; Kelly et al. 2009; Godbout and Ouellet 2010). We also tested the performance of estimated occupancy probability as a predictor using a model derived from expert-opinion data in the northeastern US (Aylward et al. 2018). Incongruence of spatial data across state or country boundaries limited our ability to include other desirable variables, such as tree canopy cover.
For each landscape variable, we constructed resistance surfaces for a range of maximum resistance (Rmax) values ranging from Rmax = 2–500 (Roffler et al. 2016; Supplementary Information II). Landscape variables were coded such that features hypothesized to reduce gene flow were assigned higher values in the resistance surface. Variables hypothesized to be positively related to gene flow included forest land cover, spruce–fir land cover, elevation, and estimated occupancy. Therefore, these variables were reverse transformed to create resistance surfaces (e.g., 100% forested cover = 1 and 0% forested cover = Rmax). Landscape variables hypothesized to have a negative relationship with gene flow included winter temperature, developed land cover, road density, and slope.
We then estimated the resistance distance between each individual using Circuitscape (McRae et al. 2008). The resistance distance based on a model of isolation by distance (IBD) was estimated by creating a null resistance surface in which the resistance value of each cell was 1, which is considered the appropriate null model for Circuitscape-based analyses (Roffler et al. 2016; Tucker et al. 2017).
Resistance surface parameterization
The optimal Rmax for each landscape variable was determined by estimating the relationship between genetic distance and landscape resistance distance for univariate models. For analyses with underlying population substructure (regional and subregional scale), we used maximum-likelihood population effects (MLPE) models constructed using lme4 (Bates et al. 2015) to estimate landscape-genetic relationships (Clarke et al. 2002). For analyses within a single population (local scale), we conducted partial Mantel tests (Smouse et al. 1986) using Ecodist (Goslee and Urban 2007). MLPE models outperform Mantel and other regression methods when population structure is present, whereas Mantel methods perform well in the absence of population structure (Franckowiak et al. 2017; Row et al. 2017; Shirk et al. 2018). The optimal Rmax for each landscape variable was determined by the Rmax with the lowest AICc in MLPE models and highest R2 in Mantel models (Shirk et al. 2018).
Multivariate models were then constructed by combining subsets of landscape variables. Only the optimal Rmax was used for each landscape variable in multivariate models. We removed geographic distance from each landscape variable to isolate the impact of the landscape variable on landscape resistance (Tucker et al. 2017). Regional and subregional analyses used MLPE modeling for multivariate models, and local analyses used multiple regression of distance matrices (MRDM; Legendre et al. 1994) in Ecodist. We identified several criteria to ensure that models contained informative and uncorrelated variables. First, we restricted multivariate models to include no more than one variable from each of the following categories: forest characteristics (forest land cover; spruce–fir land cover), anthropogenic land covers (developed land cover; road density), and climatic variables (elevation; winter temperature). Estimated occupancy was not included in multivariate analyses, serving as an alternative hypothesis. Next, we excluded all models with significant multicollinearity (one or more variables with a variance inflation factor, VIF > 5) or uninformative landscape variables (β coefficient 95% confidence intervals included 0).
Multivariate models were ranked by AICc, which had strong concordance with R2 in MRDM models. For each study site at each scale, the top models that contributed to 99% of the AICc weight were identified. One common approach is to model-average top scoring models (Symonds and Moussalli 2011), however, this could reintroduce predictor variables that were previously excluded from inclusion in the same model. As an alternative, we conducted a commonality analysis (CA; e.g., Prunier et al. 2015) in the R program “yhat” (Nimon et al. 2013) to select a single model from the top AICc model set to represent the resistance surface for each study site. We computed structure coefficients (rs) for each variable, an estimate of the amount of variance in the dependent variable explained by each predictor irrespective of collinearity among predictors (Prunier et al. 2015). We eliminated any model with an independent variable whose rs did not differ significantly from 0. We then used CA to estimate the amount of variance in genetic distance explained uniquely by each independent variable (U) and shared among other predictors (C), which sum to the total explanatory contribution of the variable (T) (Nimon and Oswald 2013; Prunier et al. 2015). The model with the set of predictors that contributed to the greatest amount of variance in genetic distance (based on the summed T of independent variables) was chosen to parameterize the resistance surface for each study site. Resistance surface parameterization was conducted based on β weights of predictor variables in the resistance surface model.
Corridor mapping
Resistance surfaces for each site at each scale were created in Raster Calculator in ArcGIS 10 (ESRI, Redlands, California, USA) by calculating a dot product of β-coefficients in the model expression with the respective landscape variable values. Resistance surface rasters were scaled 1–100 for use in Circuitscape (McRae et al. 2008). At the regional scale, where conservation objectives are often to identify long-distance corridors between isolated subpopulations, we used Linkage Mapper (McRae and Kavanagh 2011) to estimate corridors. Focal nodes were represented by the minimum convex polygon of marten locations for each local population. At the subregional and local scales, where practical corridor end points are less clear, we used Circuitscape to estimate current density, as a proxy for probability of gene flow, throughout each study site. To limit focal node attraction bias, according to recommendations by Koen et al. (2014a), we buffered each site by ~20% the width of the study site and placed 30 focal nodes evenly spaced along the perimeter of the buffer.
Results
Regional
Sixty-five models were fitted for the regional univariate analysis: eight Rmax values for seven landscape variables and occupancy probability plus the null IBD model (Supplementary Information II). Selected Rmax values ranged from the highest value tested (Rmax = 500; developed land cover) to the lowest value tested (Rmax = 2; slope; Supplementary Information II). The range of Rmax values tested in our analysis is considered extensive based on previously published literature (Roffler et al. 2016; Tucker et al. 2017), and we considered it unnecessary to expand the range of values tested.
After identifying the optimal Rmax for each landscape variable, 55 multivariate models were fitted (Supplementary Information III). After removing models with significant VIF and uninformative parameters, seven models contributed to 99% of the AICc weight (Table 1). Variables included in these models were forest land cover, spruce–fir land cover, elevation, winter temperature, developed land cover, and slope. The For + Elev + Dev + Slope model had the greatest explanatory power (T = 17.9; Table 1), and was used to create the resistance surface.
Subregional
In each subregion, 65 models were fitted for univariate analyses, and 55 models were fitted for multivariate analyses, coinciding with the model set tested in the regional analysis. In the NY subregion, most landscape variables had an optimal Rmax of 2, with the exception of forest land cover (Rmax = 50), developed land cover (Rmax = 500), and slope (Rmax = 10; Supplementary Information II). After removing models with high VIF and uninformative landscape variables, five models contributed to 99% of the AICc weight (Table 1; Supplementary Information III). Variables included in these models were spruce–fir land cover, elevation, developed land cover, roads, and slope. The SF + Dev + Slope model had the greatest explanatory power (T = 4.6; Table 1), but spruce–fir land cover had nonsignificant rs. The Dev + Slope model (T = 4.2) was selected to create the resistance surface.
In the northern New England (NHME) subregion, most landscape variables had an optimal Rmax of 2, with the exception of developed land cover (Rmax = 10) and slope (Rmax = 10, Supplementary Information II). After removing models with high VIF or uninformative landscape variables, eight models contributed to 99% of the AICc weight (Table 1; Supplementary Information III). All landscape variables tested were included in this set of models (Table 1). The For + Elev + Dev + Slope model had the greatest explanatory power (T = 10.2) but forest had nonsignificant rs. The Elev + Dev + Slope model was the second-most explanatory (T = 6.6) and was used to create the resistance surface.
Local
Each local analysis included the same set of 65 univariate and 55 multivariate models fitted in the regional and subregional analyses. In NY-W, optimal Rmax = 500 for all landscape variables except forest land cover (Rmax = 2), spruce–fir land cover (Rmax = 2), and developed land cover (Rmax = 50; Supplementary Information II). After removing models with high VIF or uninformative landscape variables, one model (Dev + Slope) contributed to 99% of the AICc weight (Table 1; Supplementary Information III). CA revealed developed land cover and slope as meaningful predictors, and the Dev + Slope model (T = 10.0) was used to create the resistance surface.
In NH, the optimal Rmax was 2 for all landscape variables, except developed land cover (Rmax = 5), forest land cover (Rmax = 200), and road density (Rmax = 500; Supplementary Information II). After removing models with high VIF or uninformative landscape variables, three models contributed to 99% of the AICc weight (Table 1; Supplementary Information III). Landscape variables in these models included winter temperature, road density, and slope (Table 1). The Temp + Slope model had the greatest explanatory power (T = 8.0) and was used to create the resistance surface.
In NY-E and ME, all models included uninformative landscape variables. These sites had the smallest sample sizes (n = 16 for NY-E and n = 18 for ME), which may be responsible for low statistical power in the study areas.
Corridors
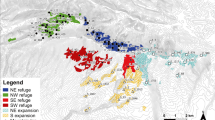
At the regional scale, the resistance surface included the effects of forest land cover (U = 0.4) and elevation (U = 1.2), both negatively correlated with landscape resistance, and developed land cover (U = 1.2) and slope (U = 0.1), both positively correlated with landscape resistance (Table 2). Corridors connected core populations via relatively straight paths with notable avoidance of developed land cover (Fig. 2).
Gray polygons show the location of focal areas, which were the five fine-scale genetic clusters identified based on microsatellite data in a previous study (Aylward et al. 2019). Within corridors, hot colors (red) indicate higher corridor quality and cool colors (blues) indicate lower quality corridors. Corridors are cut off at resistance cost of 10 cost-weighted kilometers. Apparent holes within corridors occur where small patches of developed land create high landscape resistance and are completely avoided.
In the NY subregion, the resistance surface included the effects of developed land cover (positive, U = 2.1) and slope (Table 2). Current density (proxy for probability of gene flow) was relatively high throughout the study area, with notable small patches of low current density in developed areas (Fig. 3b). In the NHME subregion, the resistance surface included the effects of elevation (negative, U = 0.7), developed land cover (positive, U = 0.6), and slope (Table 2). A complex mosaic of current densities occurred throughout NHME (Fig. 4b). In general, current densities were highest in the northern parts of the study site.
Current density estimated across the NY-W local site (a) and NY subregion (b) using Circuitscape, based on resistance surfaces parameterized by landscape genetics models. Dark shading on the inset indicates the extent of the NY-W local site and intermediate shading indicates the extent of the NY subregion. Current density serves as a proxy for probability of gene flow such that high current density areas are more likely to be used as corridors for movement. In both sites, landscape resistance was predicted by developed land cover (positively correlated with landscape resistance) and slope (negative).
Current density estimated across the NH local site (a) and NHME subregion (b) in Circuitscape, based on resistance surfaces parameterized by landscape genetics models. Dark shading on the inset indicates the extent of the NH local site and intermediate shading indicates the extent of the NHME subregion. Current density serves as a proxy for probability of gene flow such that high current density areas are more likely to be used as corridors for movement. In the NHME subregional site, landscape resistance was predicted by elevation (negatively correlated with landscape resistance), developed land cover (positive), and slope (positive). In the NH local site, landscape resistance was predicted by winter temperature (positive) and slope (positive).
In the NY-W local site, the resistance surface included the effects of developed land cover (positive, U = 7.7) and slope (Table 2). High current densities occurred in the steep ridgelines in the south and east parts of the site (Fig. 3a). In the NH local site, the resistance surface included the effects of winter temperature (positive; U = 3.3) and slope (Table 2). High current densities occurred in the highlands in the north and northwest of the study area, while low current densities occurred on steep slopes and in the warmer lowlands in the center of the study site (Fig. 4a).
Discussion
Regional scale
The resistance surface at the regional scale included effects from all four categories of landscape variables examined (forest characteristics, climate variables, anthropogenic land cover, and slope). Corridors were relatively nonspecific with the exception of movement barriers where developed land cover occurred. Contrary to previous corridor estimates based on occupancy (Aylward et al. 2018), the central and northern Green Mountains of Vermont were not considered an important corridor between populations in VT-S, NH, and NY. Martens are considered extraordinarily successful dispersers, exhibiting low levels of genetic distance per geographic distance compared with other mammals of similar or larger body size (Kyle and Strobeck 2003). The misalignment of corridors identified from occupancy-based and landscape genetics analyses may be due to greater flexibility in habitat use during dispersal than residency, as has been observed in other carnivore species (Palomares et al. 2000).
Subregional scale
Both subregional sites included developed land cover and slope as effects in their resistance surfaces. In NY these were the only two variables in the resistance surface. In NHME, elevation was also included. Landscape resistance was associated with low elevations in NHME and high developed land cover in both sites. Interestingly, the correlation between landscape resistance and slope was positive in NHME and negative in NY. This pattern was observed across all top models that included slope in both NHME and NY subregions (data not shown). Slope may facilitate gene flow due to spatial correlation with elevation or low temperatures in NY. However, including elevation or temperature in NY models (i.e., Elev + Dev + Slope or Temp + Dev + Slope models) did not change the sign or significance of the effect of slope in the NY subregion. In other species, steep slopes can be positively correlated with genetic distance due to increased energetic cost of travel (Funk et al. 2005, Spear et al. 2005) or negatively correlated with genetic distance due to “escape habitat” from larger predators or better opportunities for vigilance (Epps et al. 2007; Portanier et al. 2018). The site-dependent reversal of the relationship between slope and genetic distance in our study shows that sampling site selection can significantly alter landscape-genetic inferences.
Local scale
The NY-W resistance surface included the same landscape effects (Dev + Slope) as the NY subregion. Steep areas in the south of NY-W were identified as having the highest current density, in agreement with results from the subregional scale. Winter temperature and slope were included in the NH resistance surface. Similar to the subregional results, slope was positively associated with landscape resistance in NH despite having a negative relationship in NY-W. At the local level, the suite of landscape variables in top-performing landscape genetics models was site dependent. This result underscores that results obtained from landscape genetics modeling may not apply outside the specific study area (Short Bull et al. 2011; Castillo et al. 2016).
Scale dependence of landscape-genetic relationships
Developed land cover negatively affected gene flow in all sites at all scales. Forest land cover was present in the regional resistance surface but was absent from resistance surfaces at smaller scales. The smaller study areas are constrained to areas where martens occur, thus contain comparatively little unforested land (<12% for all local study areas, 20% in the regional study area; Supplementary Information IV). The lack of an observed effect of forest characteristics on gene flow at finer scales is probably not biological, and may be a product of the lack of variance in forest cover at finer-scale sites. This is an important consideration for future landscape genetics studies, as the lack of an observed statistical effect may be more related to sampling decisions than to biological relationships between landscape conditions and gene flow.
We expected the effect of climate variables to be the strongest in NY sites, which experience higher temperatures that would be more likely to constrain marten habitat use and gene flow (mean winter temperature [°C]: NY = 0.085, NHME = −1.22, Supplementary Information IV). However, NY and NY-W were the only sites in which a climate variable (elevation/temperature) did not play a role in the resistance surface. The NY sites have relatively low variance in elevation and winter temperature (Supplementary Information IV). Consequently, the lack of an observed effect of climate on gene flow in NY may be nonbiological; these sites may simply lack adequate spatial heterogeneity in temperature and elevation to produce a detectable effect.
Occupancy probability was not a strong predictor of genetic connectivity at any scale compared with multivariate models parameterized by genetic distance. Habitat suitability or occupancy models are often used as a proxy for landscape permeability (O’Brien et al. 2006; Stevenson-Holt et al. 2014; Spear et al. 2015; Aylward et al. 2018). Our results caution that occupancy does not necessarily predict genetic connectivity in a landscape genetics framework, perhaps due to animals exhibiting greater flexibility in habitat use while transient than when selecting home ranges (Mateo-Sanchez et al. 2015). Occupancy-based predictions of genetic connectivity may be more suitable for species with highly restrictive habitat use or low mobility (Wang et al. 2008).
Context
Genetic connectivity of marten populations in the interior of their range is better predicted by IBD than additional landscape effects (Kyle et al. 2000; Kyle and Strobeck 2003; Broquet et al. 2006; Koen et al. 2012). In our study area at the southern periphery of marten range, connectivity was better described by models that included landscape covariates (Supplementary Information V). In particular, at least one site at each scale examined included a climate-related variable and developed land cover in the top-performing model. Martens are considered deep-wood specialists (Buskirk and Powell 1994), and thus the strong negative effect of developed land cover on genetic connectivity is expected. In addition, previous studies have highlighted the effect of elevation on gene flow in mountainous regions of Pacific marten (M. caurina) distribution (Wasserman et al. 2010).
Genetic drift may represent another major influence on observed genetic distances in our study area. The observed subpopulations are believed to have become isolated during the late nineteenth or early twentieth centuries, and likely persisted for several generations in isolated relicts with low population sizes (Aylward et al. 2019). Random loss of alleles in isolated relicts is believed to have occurred, which may heterogeneously inflate the observed genetic distance between local populations in our study area (Richardson et al. 2016). Indeed, the effects of genetic drift in subpopulations have been estimated to contribute up to 41% of the variance in genetic distance (T) in empirical data sets (Prunier et al. 2017a).
Landscape connectivity during population declines in the 1800s may explain some variance in genetic distance that is unexplained by current landscape conditions. Historical landscape data are not available at the appropriate scale and resolution to investigate these effects. Based on estimates of T in this study, landscape predictors in our models contributed up to 17.9% of the total variance in genetic distance (range = 4.2–17.9; Table 1). These numbers are within the typical range of previously published landscape genetics studies using CA with microsatellite data (Renner et al. 2016; Prunier et al. 2017b); however, the majority of variance in genetic distance remains unexplained (Table 2).
Management implications
Although vegetation conditions in the region are improving for forest carnivores such as martens (Foster et al. 2002), climate conditions and increasing development may allow larger carnivores such as red fox (Vulpes vulpes), coyote (Canis latrans), and fisher (Pekania pennanti), to outcompete martens (Carroll 2007; Sirén et al. 2017). Climate change is predicted to decrease demographic potential and contract the range of martens in the northeastern US (Carroll 2007). Our results show that a warming climate could also decrease gene flow, a pattern also observed in Canada lynx (Lynx canadensis) at their southern periphery (Koen et al. 2014b). Furthermore, the regional corridor map indicated complete avoidance of developed areas (Fig. 2). Future expansion of urban and residential areas would likely have adverse effects on genetic connectivity of marten populations in the northeastern US.
Replication in landscape genetics
Landscape genetics is a developing field with a broad array of methodological approaches and study design considerations (Richardson et al. 2016). Previous studies have shown that results from different portions of species’ ranges do not necessarily align (Short Bull et al. 2011; Castillo et al. 2016). Our study further demonstrates that the choice of study location, spatial scale, and modeling technique can yield different results across subsets of a study system. We also showed that replicating study sites across multiple scales can help elucidate where potential sampling biases are affecting landscape-genetic inferences. These are important results to highlight from a practical perspective, as conclusions drawn from just one of the sites in our study area could potentially encourage management strategies that appear counterproductive in other sites within the region.
Data availability
The genetic data used in this study are available through the Dryad Digital Repository, https://doi.org/10.5061/dryad.p8cz8w9kr.
References
Aylward CM, Murdoch JD, Donovan TM, Kilpatrick CW, Bernier C, Katz J (2018) Estimating distribution and connectivity of recolonizing American marten in the northeastern United States using expert elicitation techniques. Anim Conserv 21:483–495
Aylward CM, Murdoch JD, Kilpatrick CW (2019) Genetic legacies of translocation and relictual populations of American marten at the southeastern margin of their distribution. Conserv Genet 20:275–286
Bates D, Machler M, Bolker B, Walker S (2015) Fitting linear mixed-effects models using lme4. J Stat Softw 67:51
Beier P, Noss RF (1998) Do habitat corridors provide connectivity? Conserv Biol 12:1241–1252
Broquet T, Johnson CA, Petit E, Thompson I, Burel F, Fryxell JM (2006) Dispersal and genetic structure in the American marten, Martes americana. Mol Ecol 15:1689–1697
Bowman JC, Robitaille JF (1997) Winter habitat use of American martens Martes americana within second-growth forest in Ontario, Canada. Wildl Biol 3:97–105
Burnham KP, Anderson DR (2002) Model selection and inference—a practical information-theoretic approach. Springer, New York, NY, USA
Buskirk SW, Powell RA (1994) Habitat ecology of fishers and martens. In: Buskirk SW, Harestad AS, Raphael MG, Powell RA (eds) Martens, sables, and fishers: biology and conservation. Cornell University Press, Ithaca, New York, USA, 283–296
Carroll C (2007) Interacting effects of climate change, landscape conversion, and harvest on carnivore populations at the range margin: marten and lynx in the northern Appalachians. Conserv Biol 21:1092–1104
Castillo JA, Epps CW, Jeffress MR, Ray C, Rodhouse TJ, Schwalm D (2016) Replicated landscape genetic and network analyses reveal wide variation in functional connectivity for American pikas. Ecol Appl 26:1660–1676
Clarke RT, Rothery P, Raybould AF (2002) Confidence limits for regression relationships between distance matrices: estimating gene flow with distance. J Agric Biol Environ Stat 7:361–372
Colella JP, Wilson RE, Talbot SL, Cook JA (2019) Implications of introgression for wildlife translocations: the case of North American martens. Conserv Genet 20:153–166
Cushman SA, McKelvey KS, Jayden J, Schwartz MK (2006) Gene flow in complex landscapes: testing multiple hypotheses with causal modeling. Am Nat 168:486–499
Dyer RJ (2012) The gstudio package. Virginia Commonwealth University, Richmond, Virginia, USA
Epps CW, Wehausen JD, Bleich VC, Torres SG, Brashares JS (2007) Optimizing dispersal and corridor models using landscape genetics. J Appl Ecol 44:714–724
Foster DR, Motzkin G, Bernardos D, Cardoza J (2002) Wildlife dynamics in the changing New England landscape. J Biogeogr 29:1337–1357
Franckowiak RP, Panasci M, Jarvis KJ, Acuna-Rodriguez IS, Landguth EL, Fortin MJ et al. (2017) Model selection with multiple regression on distance matrices leads to incorrect inferences. PLoS ONE 12:e175194. https://doi.org/10.1371/journal.pone.0175194
Funk WC, Blouin MS, Corn PS, Maxell BA, Pilliod DS, Amish S et al. (2005) Population structure of Columbia spotted frogs (Rana luteiventris) is strongly affected by the landscape. Mol Ecol 14:483–496
Gibilisco CJ (1994) Distributional dynamics of martens and fishers in North America. In: Buskirk SW, Harestad AS, Raphael MC, Powell RA (eds) Martens, sables, and fishers: biology and conservation. Cornell University Press, Ithaca, New York, NY, USA, p 59–71
Godbout G, Ouellet JP (2010) Fine-scale habitat selection of American marten at the southern fringe of the boreal forest. Ecoscience 17:175–185
Goslee SC, Urban DL (2007) The ecodist package for dissimilarity-based analysis of ecological data. J Stat Softw 22:1–19
Haddad NM, Bowne DR, Cunningham A, Danielson BJ, Levey DJ, Sargent S et al. (2003) Corridor use by diverse taxa. Ecology 84:609–615
Hagmeier EM (1956) Distribution of marten and fisher in North America. Can Field-Nat 70:149–168
Hanski I (1997) Metapopulation dynamics: from concepts and observations to predictive models. In: Hanski I, Gilpin ME (eds) Metapopulation biology: ecology, genetics and evolution. Academic Press, Cambridge, Massachusetts, USA, p 69–92
Hanski I (2011) Habitat loss, the dynamics of biodiversity, and a perspective on conservation. Ambio 40:248–255
Hapeman P, Latch EK, Fike JA, Rhodes OE, Kilpatrick CW (2011) Landscape genetics of fishers (Martes pennanti) in the northeast: dispersal barriers and historical influences. J Heredity 102:251–259
Kelly JR, Fuller TK, Kanter JJ (2009) Records of recovering American marten in New Hampshire. Can Field-Nat 123:1–6
Koen EL, Bowman J, Garroway CJ, Mills SC, Wilson PJ (2012) Landscape resistance and American marten gene flow. Landsc Ecol 27:29–43
Koen EL, Bowman J, Sadowski C, Walpole AA (2014a) Landscape connectivity for wildlife: development and validation of multispecies linkage maps. Methods Ecol Evol 5:626–633
Koen EL, Bowman J, Murray DL, Wilson PJ (2014b) Climate change reduces genetic diversity of Canada lynx at the trailing range edge. Ecography 37:754–762
Kyle CJ, Davis CS, Strobeck C (2000) Microsatellite analysis of North American pine marten (Martes americana) populations from the Yukon and Northwest Territories. Can J Zool 78:1150–1157
Kyle CJ, Strobeck C (2003) Genetic homogeneity of Canadian mainland marten populations underscores the distinctiveness of Newfoundland pine martens (Martes americana atrata). Can J Zool 66:57–66
Legendre P, Lapointe FJ, Casgrain P (1994) Modeling brain evolution from behavior: a permutational regression approach. Evolution 48:1487–1499
Mateo-Sanchez MC, Balkenhol N, Cushman S, Perez T, Dominguez A, Saura S (2015) Estimating effective landscape distances and movement corridors: comparison of habitat and genetic data. Ecosphere 6:1–16
McRae BH (2006) Isolation by resistance. Evolution 60:1551–1561
McRae BH, Dickson BG, Keitt TH, Shah VB (2008) Using circuit theory to model connectivity in ecology and conservation. Ecology 10:2712–2724
McRae BH, Kavanagh DM (2011) Linkage Mapper Connectivity Analysis Software. The Nature Conservancy. Seattle, Washington, USA. http://www.circuitscape.org/linkagemapper
New Hampshire Department of Fish and Game (2015) New Hampshire Wildlife Action Plan 2015. New Hampshire Department of Fish and Game, Concord, New Hampshire, USA
Nimon KF, Oswald FL (2013) Understanding the results of multiple linear regression: beyond standardized regression coefficients. Organ Res Methods 16:650–674
Nimon KF, Oswald FL, Roberts JK (2013) Interpreting regression effects. R package version 2.0.0. http://cran.r.project.org/web/packages/yhat/index.html
O’Brien D, Manseau M, Fall A, Fortin MJ (2006) Testing the importance of spatial configuration of winter habitat for woodland caribou: an application of graph theory. Biol Conserv 130:70–83
O’Brien P, Bernier C, Hapeman P (2018) A new record of an American marten (Martes americana) population in southern Vermont. Small Carniv Conserv 56:68–75
Palomares F, Delibes M, Ferreras P, Fedriani JM, Calzada J, Revilla E (2000) Iberian lynx in a fragmented landscape: predispersal, dispersal, and postdispersal habitats. Conserv Biol 14:809–818
Parks SA, McKelvey KS, Schwartz MK (2013) Effects of weighting schemes on the identification of wildlife corridors generated with least-cost methods. Conserv Biol 27:145–154
Portanier E, Jarroque J, Garel M, Marchand P, Maillard D, Bourgoin et al. (2018) Landscape genetics matches with behavioral ecology and brings new insight on the functional connectivity in Mediterranean mouflon. Landsc Ecol 33:1069–1085
Prunier JG, Colyn M, Legendre X, Nimon KF, Flamand MC (2015) Multicollinearity in spatial genetics: separating the wheat from the chaff using commonality analyses. Mol Ecol 24:263–283
Prunier JG, Dubut V, Chikhi L, Blanchet S (2017a) Contribution of spatial heterogeneity in effective population sizes to the variance in pairwise measures of genetic differentiation. Methods Ecol Evol 8:1866–1877
Prunier JG, Colyn M, Legendre X, Flamond MC (2017b) Regression commonality analyses on hierarchical genetic distances. Ecography 40:1412–1425
Quinn CB, Alden PB, Sacks BN (2019). Noninvasive sampling reveals short-term genetic rescue in an insular red fox population. J Heredity. https://doi.org/10.1093/jhered/esz024
R Core Team (2018). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria.
Renner SC, Suarez-Rubio M, Wiesner KR, Drogmuller C, Gockel S, Kalko EKV et al. (2016) Using multiple landscape genetic approaches to test the validity of genetic clusters in a species characterized by an isolation-by-distance pattern. Biol J Linn Soc 118:292–303
Richardson JL, Brady SP, Wang IJ, Spear SF (2016) Navigating the pitfalls and promise of landscape genetics. Mol Ecol 25:849–863
Roffler GH, Schwartz MK, Pilgrim K, Talbot SL, Sage GK, Adams LG et al. (2016) Identification of landscape features influencing gene flow: how useful are habitat selection models. Evol Appl 9:805–817
Row JR, Knick ST, Oyler-McCance SJ, Lougheed SC, Fedy BC (2017) Developing approaches for linear mixed modeling in landscape genetics through landscape-directed dispersal simulations. Ecol Evol 7:3751–3761
Sawaya MA, Kalinowski ST, Clevenger AP (2014) Genetic connectivity for two bear species at wildlife crossing structures in Banff National Park. Proc R Soc Biol Sci 281: 20131705
Sirén APK, Pekins PJ, Kilborn JR, Kanter JJ, Sutherland CS (2017) Potential influence of high-elevation wind farms on carnivore mobility. J Wildl Manag 81:1505–1512
Shirk AJ, Landguth EL, Cushman SA (2018) A comparison of regression methods for model selection in individual-based landscape genetic analysis. Mol Ecol Resour 18:55–67
Short Bull R, Cushman SA, Mace R, Chilton T, Kendall KC, Landguth EL et al. (2011) Why replication is important in landscape genetics: American black bear in the Rocky Mountains. Mol Ecol 20:1092–1107
Smouse PE, Long JC, Sokal RR (1986) Multiple regression and correlation extensions of the mantel test of matrix correspondence. Syst Zool 4:627–632
Spear SF, Peterson CR, Matocq MD, Storfer A (2005) Landscape genetics of the blotched tiger salamander (Ambystoma tigrinum melanostictum). Mol Ecol 14:2553–2564
Spear SF, Cushman SA, McRae BH (2015) Resistance surface modeling in landscape genetics. In: Balkenhol N, Cushman SA, Storfer AT, Waits LP (eds) Landscape genetics: concepts, methods, applications. John Wiley & Sons, Hoboken, New Jersey, USA, 129–144
Stevenson-Holt CD, Watts K, Bellamy CC, Nevin OT, Ramsey AD (2014) Defining landscape resistance values in least-cost connectivity models for the invasive grey squirrel: a comparison of approaches using expert-opinion and habitat suitability modeling. PLoS ONE 9:e112119. https://doi.org/10.1371/journal.pone.0112119
Symonds MRE, Moussalli A (2011) A brief guide to model selection, multimodel inference, and model averaging in behavioral ecology using Akaike’s information criterion. Behav Ecol Sociobiol 65:13–21
Tischendorf L, Fahrig L (2000) On the usage and measurement of landscape connectivity. Oikos 90:7–19
Tucker JM, Allendorf FW, Truex RL, Schwartz MK (2017) Sex-biased dispersal and spatial heterogeneity affect landscape resistance to gene flow in fisher. Ecosphere 8:e01839
Vermont Wildlife Action Plant Team (2015) Vermont Wildlife Action Plan 2015. Vermont Department of Fish and Wildlife, Montpelier, Vermont, USA
Wang YH, Yang KC, Bridgman CL, Lin LK (2008) Habitat suitability modeling to correlate genet flow with landscape connectivity. Landsc Ecol 23:989–1000
Wasserman TN, Cushman SA, Schwartz KM, Wallin DO (2010) Spatial scaling and multi-model inference in landscape genetics: Martes americana in northern Idaho. Landsc Ecol 25:1601–1612
Whiteley AR, Fitzpatrick SW, Funk WC, Tallmon DA (2015) Genetic rescue to the rescue. Trends Ecol Evol 30:42–49
Acknowledgements
Tissue samples for genetic analyses were provided by Paul Jensen (New York Department of Environmental Conservation), Chris Bernier and Kim Royar (Vermont Department of Fish and Wildlife), Alexej Sirén and Jill Kilborn (New Hampshire Department of Fish and Game), Cory Mosby (Maine Department of Inland Fisheries and Wildlife), and volunteer trappers from Maine. We thank Liz Kierepka for helpful technical advice on methods and analysis. We also thank Jeremy Larroque for a constructive review. We thank the Vermont Department of Fish and Wildlife for funding genetic analyses and the University of Vermont for publishing funds.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Aylward, C.M., Murdoch, J.D. & Kilpatrick, C.W. Multiscale landscape genetics of American marten at their southern range periphery. Heredity 124, 550–561 (2020). https://doi.org/10.1038/s41437-020-0295-y
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41437-020-0295-y
This article is cited by
-
Highland forest’s environmental complexity drives landscape genomics and connectivity of the rodent Peromyscus melanotis
Landscape Ecology (2022)
-
Landscape genetics of an endangered salt marsh endemic: Identifying population continuity and barriers to dispersal
Conservation Genetics (2022)
-
Comparison of methods for estimating omnidirectional landscape connectivity
Landscape Ecology (2021)