Abstract
Although nonparametric methods in genome-wide association studies (GWAS) are robust in quantitative trait nucleotide (QTN) detection, the absence of polygenic background control in single-marker association in genome-wide scans results in a high false positive rate. To overcome this issue, we proposed an integrated nonparametric method for multi-locus GWAS. First, a new model transformation was used to whiten the covariance matrix of polygenic matrix K and environmental noise. Using the transferred model, Kruskal–Wallis test along with least angle regression was then used to select all the markers that were potentially associated with the trait. Finally, all the selected markers were placed into multi-locus model, these effects were estimated by empirical Bayes, and all the nonzero effects were further identified by a likelihood ratio test for true QTN detection. This method, named pKWmEB, was validated by a series of Monte Carlo simulation studies. As a result, pKWmEB effectively controlled false positive rate, although a less stringent significance criterion was adopted. More importantly, pKWmEB retained the high power of Kruskal–Wallis test, and provided QTN effect estimates. To further validate pKWmEB, we re-analyzed four flowering time related traits in Arabidopsis thaliana, and detected some previously reported genes that were not identified by the other methods.
Similar content being viewed by others
Introduction
The genome-wide association study (GWAS) has become a very effective approach to identifying the genetic loci associated with complex traits (Sladek et al. 2007; WTCCC 2007; Li et al. 2013). Since the establishment of mixed linear model (MLM) based GWAS methods (Zhang et al. 2005; Yu et al. 2006), then there has been an increasing interest in using MLM in GWAS, because of their demonstrated effectiveness in accounting for relatedness between individuals and in controlling population stratification. This has stimulated the development of the MLM-based GWAS methods (Kang et al. 2008; Zhang et al. 2010; Lippert et al. 2011; Zhou and Stephens 2012; Segura et al. 2012; Wang et al. 2016). Furthermore, these methods have been widely used in GWAS; the loci identified in GWAS explain only a fraction of heritability of complex trait, indicating that additional loci influencing those traits exist.
To increase the robustness of quantitative trait nucleotide (QTN) detection in GWAS, nonparametric approaches have been recommended. Up to now several existing nonparametric methods have been used to conduct GWAS. For example, Atwell et al. (2010) adopted Wilcoxon rank-sum test (Wilcoxon 1945; Mann and Whitney 1947) to carry out GWAS for 107 phenotypes in a common set of Arabidopsis thaliana inbred lines; the 107 phenotypes were re-analyzed by Kruskal–Wallis test (Kruskal and Wallis 1952) and more significantly associated SNPs were identified as compared with those using efficient mixed model association (EMMA) (Filiault and Maloof 2012); the Kruskal–Wallis test was also generalized to group uncertainty when comparing k samples, and one application to a GWAS of type 1 diabetic complications demonstrated the utility of the generalized Kruskal–Wallis test for study with group uncertainty (Acar and Sun 2013). Similarly, Beló et al. (2008) used Kolmogorov–Smirnov test (Kolmogorov 1933; Smirnov 1948) to detect an allelic variant of fad2 associated with increased oleic acid levels in maize, and Terao et al. (2014) and Tan et al. (2014) adopted Jonckheere–Terpstra test (Terpstra 1952; Jonckheere 1954) to detect a T allele of rs2395185 in human leukocyte antigen locus and a T allele of rs1260326 and rs780094 in glucokinase regulatory loci, respectively. None of the above approaches have included population structure in their genetic model. Thus, Yang et al. (2014) integrated Anderson–Darling test with a population structure correction. This method was used to analyze 17 agronomic traits in maize, and some important loci were identified. In practice, the true model for a quantitative trait is rarely known, and model misspecification can lead to a loss of power. To address this issue, Kozlitina and Schucany (2015) proposed a rank-based maximum test (MAX3), which has favorable properties relative to other tests, especially in the case of symmetric distributions with heavy tails. We found that all the above methods have high false positive rates (FPRs) in our simulation experiments. To overcome this problem, multi-locus model methodologies should be recommended. For example, Li et al. (2014) proposed a two-stage nonparametric approach, in which all the markers potentially associated with quantitative trait are identified and their effects in one multi-locus model are estimated by shrinkage estimation for true QTN detection. However, none of the above methods have controlled polygenic background in single-marker association in genome scans.
In this study, we proposed a two-stage method for multi-locus GWAS. First, the model transformation of Wen et al. (2017) was used to control polygenic background in single-marker association in genome scans. Using the transformed model, Kruskal–Wallis test along with least angle regression (LARS) of Efron et al. (2004) was then used to select all the markers that were potentially associated with the trait. Finally, all the selected markers were placed into multi-locus model, these effects were estimated by empirical Bayes, and all the nonzero effects were further identified by a likelihood ratio test. Clearly, this method integrates the Kruskal–Wallis test with empirical Bayes under polygenic background control. This method, named pKWmEB, was validated by a series of Monte Carlo simulation studies and real data analyses for four flowering time related traits in Arabidopsis.
Materials and methods
The Arabidopsis thaliana data set
The Arabidopsis thaliana data set was downloaded from http://www.arabidopsis.usc.edu/ (Atwell et al. 2010) and used to conduct simulation experiments and real data analysis. This data set contained 199 accessions each with 216130 genotyped SNPs.
Genetic model and model transformation
The standard MLM for an n × 1 phenotypic vector y of quantitative trait is
where n is the number of individuals; 1 is a n × 1 vector of 1; μ is overall average; Q is an n × c matrix of fixed effects, including population structure (Yu et al. 2006) or principle component (Price et al. 2010), and v is a c × 1 vector of fixed effects excluding the intercept μ; G is an n × 1 vector of putative QTN genotypes, and β is fixed effect of putative QTN; \({\mathbf{u}}\sim {\mathrm{MVN}}_m({\mathbf{0}},\sigma _g^2{\mathbf{K}})\) is an m × 1 vector of polygenic effects, K is an m × m kinship matrix, \(\sigma _g^2\) is polygenic variance, and MVN denotes multivariate normal distribution; Z = (zij)n × m is the corresponding designed matrix for u, zij = 1 if individual i comes from family j (j = 1, …, m) and zij = 0 otherwise; and \({\mathrm{\varepsilon \sim }}{\mathrm{MVN}}_n({\mathbf{0}},\sigma _e^2{\mathbf{I}}_n)\) is an n × 1 vector of residual errors, \(\sigma _e^2\) is residual error variance, In is an n × n identity matrix. To simplify population structure, let m = n and Z = In in this study (Atwell et al. 2010). Note that the observed data is (y, G), matrices Q and K can be calculated from G, and the parameters to be estimated are μ, v, β, \(\sigma _g^2\) and \(\sigma _e^2\).
Based on model (1), phenotypic values y were affected by population structure, QTN and polygenes. In other words, a nonparametric test for k samples cannot be directly applied. Thus, we must remove the effects for population structure and polygenes before using a nonparametric test.
Population structure correction
If we delete Gβ and Zu in model (1), its reduced model is
Using least squares method, the effect of v, denoted by \(\hat{\bf v}\), can be estimated from y, Q and 1. Thus, we can correct the effect of population structure from
Polygenic background correction
Based on model (3), the variance of y−Q is
where \(\lambda _g = \sigma _g^2/\sigma _e^2\). Using the EMMA algorithm of Kang et al. (2008), the estimate of λg, denoted by \(\hat \lambda _g\), can be easily obtained. Replacing λg in (4) by \(\hat \lambda _g\), so
where \({\mathbf{B}} = \hat \lambda _g{\mathbf{ZKZ}}^{\rm T} + {\mathbf{I}}_n\). An eigen decomposition of positive semi-definite matrix B is
where QB is orthogonal, Λr is a diagonal matrix with positive eigen values, r = Rank(B), Q1 and Q2 are the n × r and n × (n − r) block matrices of QB, and 0 is the corresponding block zero matrix (Wen et al. 2017).
Let \({\mathbf{C}} = {\mathbf{Q}}_1{\mathbf{\Lambda }}_r^{ - \begin{array}{*{20}{c}} {} \end{array}{\textstyle{1 \over 2}}}{\mathbf{Q}}_1^{\rm T}\), a new model with polygenic background control is
where yc = Cy−Q, 1c = C1, Gc = CG and εc = C(Zu + ε). Clearly, the observed data is (yc,Gc), and the parameter to be estimated is β. Using \(\lambda _g = \hat \lambda _g\), equation (6) and \({\mathbf{Q}}_1^{\rm T}{\mathbf{Q}}_1 = {\mathbf{I}}_r\), so
It should be noted that model (7) includes QTN variation and normal residual error (Wen et al. 2017). Although the polygenic background has been corrected, nonparametric test cannot be implemented owing to continual Gc values.
Kruskal–Wallis test
Based on model (7), we used Kruskal–Wallis test to detect whether one SNP was associated with the trait. However, the values of Gc were not binary variable. Thus, we must transfer Gc into binary variable. Let Gc = (gij)n × p, \({\bf{G}}_c^*{\mathrm{ = }}\left( {g_{ij}^*} \right)_{n \times p}\), p is the number of QTNs under study and \(\bar g_{ \cdot j} = \frac{1}{n}\mathop {\sum}\nolimits_{i = 1}^n {g_{ij}}\), so
Therefore, \(\left( {{\mathbf{y}}_c,{\bf{G}}_c^*} \right)\) is the data set for Kruskal–Wallis test. All the transferred phenotypes yc were grouped by the values of \({\bf{G}}_c^*\). In this situation, there are two groups for the transferred phenotypes yc. In the two groups, let their sizes be ni, and their cumulative distribution functions be Fi(y|θi) (i = 1, 2). The null hypothesis for Kruskal–Wallis test was
When precise category assignment of \({\bf{G}}_c^*\) is available, Kruskal–Wallis test for equation (9) is conducted by ranking all the transferred phenotypes yc together and comparing the rank sum for each group. If H0:θ1 = θ2, so the estimate for β in equation (7) equals to zero. The statistic H
follows an asymptotic χ2 distribution with one degree of freedom (Kruskal 1952), where rj is the rank of the jth phenotype of yc in the overall sample; and \(R_i = \mathop {\sum}\limits_{j = 1}^n {I_{ij}} r_j\) (i = 1, 2), Iij is an indicator variable, Iij = 1 if the jth phenotype of yc belongs to the ith group and Iij = 0 otherwise; and \(n_i = \mathop {\sum}\limits_{j = 1}^n {I_{ij}}\).
Empirical Bayes estimation for QTN effects
In GWAS, the number of SNPs is frequently 1000 times larger than sample size. In this situation, fitting all the genome markers in one model is not feasible. As we know, most SNPs are not associated with the trait. Once we delete these SNPs with zero effects, the reduced model is estimable. The purpose of the above Kruskal–Wallis test is to select all the potentially associated SNPs. If the number of markers passing the 0.05 level of significance test is more than oi (oi = 50, 100, and 150), we invoke LARS of Efron et al. (2004) to select oi variables that are most likely associated with the trait of interest. LARS is a flexible method for variable selection, which is implemented by lars package in R language (http://cran.r-project.org/web/packages/lars/). The oi markers are then included in a multi-locus model. If the number of markers passing the initial test is less than oi, we skip the LARS step and proceed to include all the selected markers in a multi-locus model
where y, 1, μ, and ε are the same as those in model (1); q is the number of markers selected in Krusal–Wallis test; βi is the effect for marker i, and Gi is the corresponding designed matrix for βi. Clearly, the observed data is (y, G1, …,Gq), the parameters to be estimated are β1,…,βq. In model (11), the polygenic background is not considered. In theory, this is because all the potentially associated loci have been included in this model. However, we should determine whether population structure is considered. To solve this issue, the linkage disequilibrium score regression test of Bulik-Sullivan et al. (2015) is used (see Discussion). In the selection of markers, a less stringent criterion is adopted.
Empirical Bayes of Xu (2010) was used to estimate the SNP effects in model (11). In this method, each SNP effect βi is viewed as random. We adopt normal prior for βi, \(P(\beta _i|\sigma _i^2){\mathrm{ = }}N\left( {0,\sigma _i^2} \right)\), and the scaled inverse χ2 prior for \(\sigma _i^2\), \(P(\sigma _i^2|\tau ,\omega ) \propto \left( {\sigma _i^2} \right)^{{\mathrm{ - }}{\textstyle{1 \over 2}}\left( {\tau + 2} \right)}\exp \left( { - \frac{\omega }{{2\sigma _i^2}}} \right)\), where (τ,ω) = (0,0), which represents the Jeffreys’ prior (Figueiredo 2003), \(P\left( {\sigma _i^2|\tau ,\omega } \right){\mathrm{ = 1/}}\sigma _i^2\). The procedure for parameter estimation in empirical Bayes is as follows.
-
1.
Initial-step: To initialize parameters with
$$\begin{array}{l}\mu = {\bf{1}}^{\rm T}{\mathbf{y}}/n\\ \sigma _e^2 = \frac{1}{n}\left( {{\mathbf{y}} - {\bf{1}}\mu } \right)^{\rm T}\left( {{\mathbf{y}} - {\bf{1}}\mu } \right)\\ \sigma _i^2 = \left[ {\left( {{\mathbf{G}}_i^{\rm T}{\mathbf{G}}_i} \right)^{{\mathrm{ - }}1}{\mathbf{G}}_i^{\rm T}\left( {{\mathbf{y}} - {\bf{1}}\mu } \right)} \right]^2 + \left( {{\mathbf{G}}_i^{\rm T}{\mathbf{G}}_i} \right)^{{\mathrm{ - }}1}\sigma _e^2\end{array}$$ -
2.
E-step: marker effect can be predicted by
$$E\left( {\beta _i} \right) = \sigma _i^2{\mathbf{G}}_i^{\rm T}{\bf{V}}^{ - 1}\left( {{\mathbf{y}} - {\bf{1}}\mu } \right)$$(12)where \({\bf{V}} = \mathop {\sum}\limits_{i = 1}^q {{\mathbf{G}}_i^{}} {\mathbf{G}}_i^{\rm T}\sigma _i^2 + {\bf{I}}\sigma _e^2\).
-
3.
M-step: To update parameters \(\sigma _i^2\), μ and \(\sigma _e^2\)
where \(E\left( {\beta _i^T\beta _i} \right)\) \(= E\left( {\beta _i^T} \right)E\left( {\beta _i} \right) + tr\left[ {var\left( {\beta _i} \right)} \right]\), \(var\left( {\beta _i} \right) = {\bf{I}}\sigma _i^2 - \sigma _i^2{\mathbf{G}}_i^T{\bf{V}}^{ - 1}{\mathbf{G}}_i\sigma _i^2\) and (τ,ω) = (0,0).
Repeat E-step and M-step until convergence is satisfied.
Owing to oi = 50, 100, and 150, so three models would be established by the above procedures. Their AIC values were calculated in order to pick up an optimal model.
Likelihood ratio test
Based on the estimate of marker effect βi in the optimal model, all the markers with \(\left| {\hat \beta _i} \right| \le 10^{ - 4}\) are deemed not to be associated with the trait. The other markers with the effects θ = {β(1),…,β(O)} are potentially associated with the trait. To test the null hypothesis H0:β(i) = 0, which is no QTN linked to the ith marker, LR test was conducted by
where \(\theta _{ - i} = \left\{ {\beta _{(1)}, \cdots ,\beta _{(i - 1)},\beta _{(i + 1)}, \cdots ,\;\beta _{(O)}} \right\}^{\rm T}\), \(L(\theta ) = \mathop {\sum}\nolimits_{i = 1}^n {\ln } \phi (y_i;{\mathbf{1}}\mu + \mathop {\sum}\nolimits_{o = 1}^O {{\mathbf{G}}_o\beta _o} ,\sigma _e^2)\) is log-likelihood function, \(\phi (y_i;{\mathbf{1}}\mu + \mathop {\sum}\nolimits_{o = 1}^O {{\mathbf{G}}_o\beta _o} ,\sigma _e^2)\) is a normal density with mean \({\mathbf{1}}\mu + \mathop {\sum}\nolimits_{o = 1}^O {{\mathbf{G}}_o\beta _o}\) and variance \(\sigma _e^2\), and LOD = LR/4.605. Although the general 0.05 critical value may be used for significance test, we decided to set up a slightly more stringent criterion of LOD = 3.0. The criterion is frequently adopted in linkage analysis and is the equivalent of \(P = \Pr (\chi _1^2 > 3.0 \times 4.605) \approx 0.0002\), in which \(\chi _1^2\) under H0, follows a \(\chi _{}^2\) distribution with one degree of freedom.
The flow diagram of pKWmEB is shown in Fig. 1. pKWmEB has been implemented in R and its software can be downloaded from https://cran.r-project.org/web/packages/mrMLM/index.html.
Genome-wide efficient mixed model association
This is an existing GWAS method (Zhou and Stephens 2012) and used as a gold standard for comparison. This method is the fixed model version of the original MLM, in which βi was treated as fixed effect with no distribution assigned. The method was implemented in the C software GEMMA (Zhou and Stephens 2012) (http://www.xzlab.org/software.html). The threshold of P-value was set as 0.05/p after Bonferroni correction for multiple tests, where p is the number of markers.
Monte Carlo simulation experiments
Five Monte Carlo simulation experiments were used to validate pKWmEB. In the first experiment, all the SNP genotypes were derived from 216,130 SNPs in Atwell et al. (2010) and 2000 SNPs were randomly sampled from each chromosome. The positions for the sampled SNPs were described by Wang et al. (2016). The sample size was the number of accessions (199) in Atwell et al. (2010). Six QTNs were simulated and placed on the SNPs with allelic frequencies of 0.30; their heritabilities were set as 0.10, 0.05, 0.05, 0.15, 0.05, and 0.05, respectively; and their positions and effects were listed on Table S1. Using \(h_{\rm T}^2 = \sigma _G^2/\left( {\sigma _G^2 + \sigma _e^2} \right)\) = 0.05 × 4 + 0.10 + 0.15 = 0.45 and residual variance \(\sigma _e^2 = 10.0\), total genetic variance for six simulated QTNs (\(\sigma _G^2\)) and individual genetic variance for each simulated QTN (\(\sigma _r^2\),r = 1,…,6) could be obtained. \(\sigma _r^2\) was a function of QTN effect and frequency of common allele. Thus, QTN effect could be obtained. The average was set at 10.0. The new phenotypes were simulated by the model: \(y = \mu + \mathop {\sum}\limits_{i = 1}^6 {x_ib_i + \varepsilon }\), where ε~MVNn(0,10 × In). The simulation was replicated 1000 times. In the Kruskal–Wallis test, the oi most associated SNPs were selected and placed into multi-locus model. A detected QTN within 1 kb of the simulated QTN was considered to be a true QTN. For each simulated QTN, we counted the samples in which the LOD statistic exceeded 3.0. The ratio of the number of such samples to the total number of replicates (1000) represented the empirical power of this QTN. FPR was calculated as the ratio of the number of false positive effects to the total number of zero effects considered in the full model. To measure the variance and bias of gene effect estimate, mean squared error (MSE)
was calculated, where \(\hat \beta _{k(i)}\) is the estimate of βk in the ith sample.
To investigate the effect of polygenic background on pKWmEB, polygenic effects were simulated in the second experiment by multivariate normal distribution \({\mathrm{MVN}}_n(0,\sigma _{pg}^2{\mathbf{K}})\), where \(\sigma _{{\rm pg}}^2\) is polygenic variance and K is kinship matrix between a pair of individuals. Here \(\sigma _{{\rm pg}}^2 = 2\), so \(h_{pg}^2 = 0.092\). The QTN size (h2), average, residual variance, and other parameter values were the same as those in the first experiment, and all the parameters were listed on Table S2. The new phenotypes were simulated by the model: \(y = \mu + \mathop {\sum}\nolimits_{i = 1}^6 {x_ib_i + u + \varepsilon }\), where u~MVNn(0,2 × K) and ε~MVNn(0,10 × In).
To investigate the effect of epistatic background on pKWmEB, three epistatic QTNs were simulated in the third simulation experiment. The related parameters for the three epistatic QTNs were described in Wang et al. (2016). The QTN sizes (h2), average, residual variance, and other parameter values were also the same as those in the first experiment, and all the parameters were listed on Table S3. The new phenotypes were simulated by \(y = \mu + \mathop {\sum}\nolimits_{i = 1}^6 {x_ib_i + \mathop {\sum}\nolimits_{j = 1}^3 {(A_j\# B_j)b_{jj}} + \varepsilon }\), where ε~MVNn(0,10 × In), bjj is the epistatic effect and Aj#Bj is its incidence coefficient.
All simulated data sets are available from https://doi.org/10.5061/dryad.sk652 (the Dryad Digital Repository).
To investigate the effect of skewed phenotypic distribution on pKWmEB, normal distribution for residual error in the first simulation experiment was replaced by log-normal distribution in the fourth simulation experiment and logistic distribution in the fifth simulation experiment, and other parameter values were the same as those in the first simulation experiment. To let residual error variance be 10, the standard deviation was set at 1.144 in log-normal distribution and 1.743 in logistic distribution. The means for the two skewed distributions were also zero. The two simulation data sets were included in Data set S2.
Results
Monte Carlo simulation studies
Statistical power for QTN detection
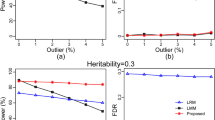
To validate pKWmEB, five simulation experiments were conducted. In the first simulation experiment, each sample was analyzed by five methods: pKWmEB, the new method without polygenic background control (KWmEB), Kruskal–Wallis test with Bonferroni correction (KWsBC), genome-wide EMMA (GEMMA), and multi-locus random-SNP-effect MLM (mrMLM). All the power results are shown in Table S1 and Fig. 2a. Clearly, the average powers for the above five methods were 69.8, 67.3, 60.7, 46.0, and 68.6 (%), respectively, indicating the highest average power of pKWmEB (Fig. 2a). More importantly, the power using pKWmEB was significantly higher than those using KWmEB and GEMMA (Table 1). Note that there were four QTNs with the same 5% heritability. The standard deviation of powers across the four QTNs might be used to measure the robustness of each method. As a result, the standard deviation was 13.01 for pKWmEB, 11.98 for KWmEB and 10.57 for mrMLM, which were much less than 35.17 for KWsBC, indicating the better stability of pKWmEB. On one occasion, the power for the fifth QTN using pKWmEB was 47.7% less than that using KWsBC. To further confirm the effectiveness of pKWmEB, polygenic effect simulated by multivariate normal distribution (r2 = 9.2%) was added to each phenotypic observation in the second simulation experiment and the polygenic background was replaced by three epistatic QTN (r2 = 15%) in the third simulation experiment. These results are listed in Tables S2 and S3, which show that the average powers for the above five methods were 69.1, 67.7, 58.9, 42.5, and 67.6 (%) in the second simulation experiment (Table S2; Fig. 2b), and 61.9, 59.9, 54.9, 39.1, and 58.9 (%), respectively, in the third simulation experiment (Table S3; Fig. 2c). The standard deviation of statistical powers among all the 5% QTNs was 21.31 for pKWmEB and 31.39 for KWsBC in the second simulation experiment, and 15.05 for pKWmEB and 40.77 for KWsBC in the third simulation experiment. Similarly, the power for the fifth QTN using pKWmEB was 47.2 and 68.3 (%) less than those using KWsBC in the second and third simulation experiments, respectively. In addition, residual error distributions in the above three experiments were replaced by log-normal (the fourth simulation experiment) and logistic (the fifth simulation experiment) distributions. The average powers for the above five methods were 76.2, 74.4, 80.1, 53.9, and 78.3 (%) in the fourth simulation experiment (Table S4; Fig. 2d), and 68.7, 66.9, 60.9, 44.1, and 68.0 (%), respectively, in the fifth simulation experiment (Table S5; Fig. 2e). Similar phenomena were observed for the fifth QTN and the standard deviation of statistical powers across all the 5% QTNs in the last two experiments. In summary, pKWmEB with polygenic background control is better than KWmEB without polygenic background control; pKWmEB retains the high power of KWsBC, and it is better in the stability of statistical power than KWsBC.
Comparison of statistical powers of six simulated QTNs using five GWAS methods (pKWmEB, KWmEB, KWsBC, GEMMA, and mrMLM). a No polygenic background; b an additive polygenic variance (explaining 0.092 of the phenotypic variance); c three epistatic QTNs each explaining 0.05 of the phenotypic variance. Residual error is normal distribution with mean zero and variance 10 in (a) to (c), log-normal distribution with mean zero and standard deviation 1.144 (d), and logistic distribution with mean zero and standard deviation 1.743 (e)
Accuracies of estimated QTN effects
The accuracy of QTN effect estimation was measured by MSE and smaller MSE indicates higher accuracy of parameter estimation. All the MSE results from four approaches in the five simulation experiments are shown in Fig. 3 and Tables S6–S10, because KWsBC does not provide the estimates for QTN effects. Results showed that the average MSEs using pKWmEB, KWmEB, GEMMA, and mrMLM were 0.0797, 0.0825, 0.5467, and 0.0940 in the first simulation experiment, respectively, indicating the minimum average MSE of pKWmEB (Fig. 3a and Table S6). More importantly, the MSE using pKWmEB was almost significantly less than that using GEMMA (Table 1). Almost similar trends were found in the other simulation experiments (Tables S16–S19, Figs. 3a–e). Average value of each QTN effect across 1000 replicates was listed in Tables S11–S15. These results were also confirmed the above trends.
Comparison of mean squared errors of each simulated QTN effect using four GWAS methods (pKWmEB, KWmEB, GEMMA, and mrMLM). The descriptions in (a) to (e) are the same as those in Fig. 2
False positive rate
The FPR is similar to the empirical Type 1 error rate. The FPRs in all the five simulation experiments were 0.0356 ± 0.0085 (%) for pKWmEB, 0.0385 ± 0.0073 (%) for KWmEB, 0.6130 ± 0.1644 (%) for KWsBC, 0.0290 ± 0.0094 (%) for GEMMA and 0.0214 ± 0.0043 (%) for mrMLM (Fig. 4 and Tables S1–S5). In summary, the FPRs are less than 0.05 % for pKWmEB, KWmEB, mrMLM, and GEMMA, and more than 0.60 % for KWsBC, indicating the best FPR control of pKWmEB even if a less stringent significant criterion was adopted.
Comparison of false positive rates using five GWAS methods (pKWmEB, KWmEB, KWsBC, GEMMA, and mrMLM). The descriptions in (a) to (e) are the same as those in Fig. 2
Computational efficiency
Each sample in the first simulation experiment was analyzed by pKWmEB, KWmEB, KWsBC, mrMLM, and GEMMA. These analyses were implemented on the computer (Intel(R) Xeon(R) CPU E5-2637 v2 @ 3.50 GHz CPU). As a result, the computing times using the above five methods were 35.30, 35.20, 32.63, 13.08, and 1.63 (hours), respectively (Fig. S1). Although pKWmEB runs slightly longer than KWsBC, pKWmEB has significantly lower FPR than KWsBC.
Real data analysis in Arabidopsis thaliana
Four flowering time related traits in Arabidopsis thaliana derived from Atwell et al. (2010) were re-analyzed by pKWmEB, KWmEB, mrMLM, and GEMMA. The four flowering time related traits were FLC gene expression (FLC), FRI gene expression (FRI), days to flowering of plants grown in the field (FT Field) and days to flowering growth in greenhouse (FT GH). We also downloaded the results of EMMA from Atwell et al. (2010), with the significance criterion of Bonferroni correction (0.05/p, p is the number of markers). All the results are listed in Table S23. Results showed that the numbers of SNPs significantly associated with the four traits were 80 for pKWmEB, 77 for KWmEB, 56 for mrMLM, and 53 for GEMMA.
These significantly associated SNPs were used to mine candidate genes associated with the traits. These candidate genes were compared with those in previous studies. All the previously reported genes detected by the above four methods are listed in Table S24. As a result, 23, 16, 10, and 5 previously reported genes were found to be in the region of the significantly associated SNPs detected by pKWmEB, KWmEB, mrMLM, and GEMMA, respectively (Table S23), indicating that pKWmEB identified the most previously reported genes. Among these known genes, five were identified only by pKWmEB and were not included in the list of the previously reported genes in Atwell et al. (2010) (Table 2).
Discussion
Recently, our group has developed several multi-locus GWAS methods, i.e., mrMLM (Wang et al. 2016), FASTmrEMMA (Wen et al. 2017), ISIS EM-BLASSO (Tamba et al. 2017), and pLARmEB (Zhang et al. 2017). Actually, these are parametric methods. As we know, nonparametric GWAS methods are also very useful in GWAS. However, polygenic background in the nonparametric methods isn’t controlled, so their FPRs are high. To overcome this issue, we developed pKWmEB in this study. In addition, pKWmEB can find some previously reported genes that aren’t detected by parametric methods (Table 2).
No existing nonparametric methods in GWAS have considered polygenic background control. This leads to the inflation of FPR. To overcome this issue, the model transformation of Wen et al. (2017) is used to whiten the covariance matrix of the polygenic matrix K and environmental noise. Meanwhile, genotypic incidence matrix and phenotypes are also transferred. Owing to continually transferred genotypic values, it is necessary to change the transferred genotypic values into binary variables (1 and −1) in order to carry out Kruskal–Wallis test. The question is how to conduct this transfer. If the values are larger than their mean or median, the values are transferred into 1. If the values are not larger than their mean or median, the values are transferred into −1. Thus, new incidence values are obtained. These new incidence values along with new phenotypes are used to conduct the Kruskal–Wallis test. Using this test, all the markers potentially associated with the trait are identified. These selected markers are placed into a multi-locus model, and original genotype and phenotype information is used to estimate their effects using empirical Bayes. Thus, true QTNs can be identified. Our results showed that mean threshold is better than median threshold in statistical power (Fig. S3 and Table S22). Although the Kruskal–Wallis test is used in this study, in addition, other nonparametric tests are also available, for example, the Jonckheere–Terpstra test (Terpstra 1952; Jonckheere 1954) and Anderson–Darling test (Anderson and Darling 1952 1954). As compared with the methods without polygenic background control, the new method demonstrates a significant improvement in statistical power and robustness for QTN detection and in accuracy for QTN-effect estimation.
In real data analysis, we should consider whether it is necessary to include population structure in the genetic model. Recently, Bulik-Sullivan et al. (2015) proposed a linkage disequilibrium score regression test to solve this issue. This method is to test the significance of difference between regression intercept and one. Results showed that population structure should be included in multi-locus model for all the four traits in this study (Table S25). Principal component analysis is also available for this purpose. We also need to consider the heterozygotes. In this case, a heterozygote is coded as zero and the others are the same as those in pKWmEB. If so, there is no significant power difference between the two homozygote genotypes (AA and aa) and the three genotypes (AA, Aa, and aa). However, the accuracy of QTN effect estimation significantly decreased as compared with no heterozygotes (Table S20 and S21).
The current nonparametric GWAS methods are almost a single-locus genome scan analysis, and such a single-marker test often requires a Bonferroni correction. To control the experimental error at a genome-wide significance level of 0.01, the significance level for each test should be adjusted as 0.01/p, which is 1e−8 if there are one million markers (p). This criterion is too stringent to detect many important loci. To avoid this issue, many multi-locus approaches have been suggested (Segura et al. 2012; Moser et al. 2015; Wang et al. 2016). In these multi-locus approaches, there is no need for such a multiple test correction. At this situation, less stringent critical P-value (~2e−4, which is the equivalent of LOD = 3.0) can be adopted. This is because its FPR is similar to that from single-locus genome scan analysis with a stringent significance criterion.
In Monte Carlo simulation studies, the estimates of powers for the four QTNs with the same effect size are highly variable. This is different from the situation in quantitative trait locus mapping. To dissect this phenomenon, the simulated data sets in this study were also analyzed by ADGWAS of Yang et al. (2014) and Jonckheere–Terpstra test with Bonferroni correction (Liu 2016). As a result, similar phenomenon was observed as well. This may be due to two reasons. One is about the genotypic data sets, which are derived from the 216130 SNPs in Atwell et al. (2010). Several significant correlations of genotypes between a pair of QTNs were observed. This is not similar to ideal segregation populations in linkage analysis. Another is about single-locus genome-wide scanning of nonparametric tests. When KWsBC is implemented in the first simulation experiment, the 85.6, 46.9, 14.2, and 70.9 (%) P-values in the detection of the second, third, fifth, and sixth QTNs are between 5e−6 and 0.01. Owing to the stringent Bonferroni correction criterion, QTN2 and QTN6 were not detected in most situations.
We compared the results in this study with those in Atwell et al. (2010), and found that individual previously reported genes are common, for example, FLA, AT4G00690 (similar to ESD4, 268809/276143 bp on chromosome 4) and ATARP4 (6371569 bp on chromosome 1) are detected by all the four methods. However, most previously reported genes depend on methods (Table S24) and some previously reported genes are detected only by pKWmEB (Table 2). This indicates that pKWmEB is a complement to the widely used GWAS methods (such as GEMMA). The possible reason is that each method has its own distinct assumptions.
Data archiving
All simulated data sets are available from the Dryad Digital Repository: https://doi.org/10.5061/dryad.sk652 and supplementary file (Simulated phenotypes Data Sets). The real data set can be retrieved from: http://www.arabidopsis.org/.
References
Acar EF, Sun L (2013) A generalized Kruskal-Wallis test incorporating group uncertainty with application to genetic association studies. Biometrics 69:427–435
Anderson TW, Darling DA (1954) A test of goodness-of-fit. J Am Stat Assoc 49:765–769
Anderson TW, Darling DA (1952) Asymptotic theory of certain “goodness-of-fit” criteria based on stochastic processes. Ann Math Stat 23:193–212
Atwell S, Huang YS, Vilhjálmsson BJ, Willems G, Horton M, Li Y et al. (2010) Genome-wide association study of 107 phenotypes in a common set of Arabidopsis thaliana inbred lines. Nature 465:627–631
Beló A, Zheng P, Luck S, Shen B, Meyer DJ, Li B et al. (2008) Whole genome scan detects an allelic variant of fad2, associated with increased oleic acid levels in maize. Molec Genet Genomics 279:1–10
Bulik-Sullivan BK, Loh PR, Finucane HK, Ripke S, Yang J, Schizophrenia Working Group of the Psychiatric Genomics Consortium et al. (2015). LD score regression distinguishes confounding from polygenicity in genome-wide association studies. Nat Genet. 47: 291–295.
Efron B, Hastie T, Johnstone I, Tibshirani R (2004) Least angle regression. Ann Statist 32:407–451
Figueiredo MA (2003) Adaptive sparseness for supervised learning. IEEE T Pattern. Anal 25:1151–1159
Filiault DL, Maloof JN (2012) A genome-wide association study identifies variants underlying the Arabidopsis thaliana shade avoidance response. PLoS Genet 8:e1002589
Holt BF, Boyes DC, Ellerström M, Siefers N, Wiig A, Kauffman S et al. (2002) An evolutionarily conserved mediator of plant disease resistance gene function is required for normal Arabidopsis development. Dev Cell 2:807–817
Huang Z, Shi T, Zheng B, Yumul RE, Liu X, You C, Gao Z et al. (2016) APETALA2 antagonizes the transcriptional activity of AGAMOUS in regulating floral stem cells in Arabidopsis thaliana. New Phytol 215:1197–1209
Izawa T, Takahashi Y, Yano M (2003) Comparative biology comes into bloom: genomic and genetic comparison of flowering pathways in rice and Arabidopsis. Curr Opin Plant Biol 6:113–120
Jonckheere AR (1954) A distribution-free k-sample test against ordered alternatives. Biometrika 41:133–145
Kang HM, Zaitlen NA, Wade CM, Kirby A, Heckerman D, Daly MJ et al. (2008) Efficient control of population structure in model organism association mapping. Genetics 178:1709–1723
Kolmogorov AN (1933) Sulla determinazione empirica di una legge di distribuzione. Giornale dell’Istituto Italiano degli Attuari 4:83–91
Kozlitina J, Schucany WR (2015) A robust distribution-free test for genetic association studies of quantitative traits. Stat Appl Genet Mol Biol 14:443–464
Kruskal WH (1952) A nonparametric test for the several sample problem. Ann Math Stat 23:525–540
Kruskal WH, Wallis WA (1952) Use of ranks in one-criterion variance analysis. J Am Stat Assoc 47:583–621
Li J, Zhang J, Wang X, Chen J (2010) A membrane-tethered transcription factor ANAC089 negatively regulates floral initiation in Arabidopsis thaliana. Sci China Life Sci 53:1299–1306
Li JH, Dan J, Li CL, Wu RL (2014) A model-free approach for detecting interactions in genetic association studies. Brief Bioinform 15:1057–1068
Li QZ, Li ZB, Zheng G, Gao GM, Yu K (2013) Rank-based robust tests for quantitative-trait genetic association studies. Genet Epidemiol 37:358–365
Lippert C, Listgarten J, Liu Y, Kadie CM, Davidson RI, Heckerman D (2011) FaST linear mixed models for genome-wide association studies. Nat Methods 8:833–835
Liu Q (2016). A multi-locus Jonckheere-Terpstra method for genome-wide association study. Master of Science, Nanjing Agricultural University, Nanjing, China
Mann HB, Whitney DR (1947) On a test of whether one of two random variables is stochastically larger than the other. Ann Math Stat 18:50–60
Moser G, Lee SH, Hayes BJ, Goddard ME, Wray NR, Visscher PM (2015) Simultaneous discovery, estimation and prediction analysis of complex traits using a Bayesian mixture model. PLoS Genet 11:e1004969
Price AL, Zaitlen NA, Reich D, Patterson N (2010) New approaches to population stratification in genome-wide association studies. Nat Rev Genet 11:459–463
Segura V, Vilhjálmsson BJ, Platt A, Korte A, Seren Ü, Long Q et al. (2012) An efficient multi-locus mixed-model approach for genome-wide association studies in structured populations. Nat Genet 44:825–830
Sladek R, Rocheleau G, Rung J, Dina C, Shen L, Serre D et al. (2007) A genome-wide association study identifies novel risk loci for type 2 diabetes. Nature 445:881–885
Smirnov N (1948) Table for estimating the goodness of fit of empirical distributions. Ann Math Stat 19:279–281
Tamba CL, Ni YL, Zhang YM (2017) Iterative sure independence screening EM-Bayesian LASSO algorithm for multi-locus genome-wide association studies. PLoS Comput Biol 13:e1005357
Tan HL, Zain SM, Mohamed R, Rampal S, Chin KF, Basu RC et al. (2014) Association of glucokinase regulatory gene polymorphisms with risk and severity of non-alcoholic fatty liver disease: an interaction study with adiponutrin gene. J Gastroenterol 49:1056–1064
Terao C, Ohmura K, Yamada R, Kawaguchi T, Shimizu M, Tabara Y et al. (2014) Association between antinuclear antibodies and the HLA class II locus and heterogeneous characteristics of staining patterns. Arthritis Rheumatol 66:3395–3403
Terpstra TJ (1952) The asymptotic normality and consistency of Kendalls test against trend, when ties are present in one ranking. Indagat Math 14:327–333
The Wellcome Trust Case Control Consortium (WTCCC) (2007) Genome-wide association study of 14,000 cases of seven common diseases and 3,000 shared controls. Nature 447:661–678
Wang SB, Feng JY, Ren WL, Huang B, Zhou L, Wen YJ et al. (2016) Improving power and accuracy of genome-wide association studies via a multi-locus mixed linear model methodology. Sci Rep 6:19444
Wen YJ, Zhang H, Ni YL, Huang B, Zhang J, Feng JY et al. (2017). Methodological implementation of mixed linear models in multi-locus genome-wide association studies. Brief Bioinformatics. https://doi.org/10.1093/bib/bbw145.
Wilcoxon F (1945) Individual comparisons by ranking methods. Biometrics Bull 1:80–83
Xu S (2010) An expectation-maximization algorithm for the Lasso estimation of quantitative trait locus effects. Heredity 105:483–494
Yang N, Lu Y, Yang X, Huang J, Zhou Y, Ali F et al. (2014) Genome wide association studies using a new nonparametric model reveal the genetic architecture of 17 agronomic traits in an enlarged maize association panel. PLoS Genet 10:821–833
Yu J, Pressoir G, Briggs WH, Vroh BiI, Yamasaki M, Doebley JF et al. (2006) A unified mixed-model method for association mapping that accounts for multiple levels of relatedness. Nat Genet 38:203–208
Zhang J, Feng JY, Ni YL, Wen YJ, Niu Y, Tamba CL et al. (2017) pLARmEB: integration of least angle regression with empirical Bayes for multi-locus genome-wide association studies. Heredity 118:517–524
Zhang YM, Mao Y, Xie C, Smith H, Luo L, Xu S (2005) Mapping quantitative trait loci using naturally occurring genetic variance among commercial inbred lines of maize (Zea mays L.). Genetics 169:2267–2275
Zhang Z, Ersoz E, Lai CQ, Todhunter RJ, Tiwari HK, Gore MA et al. (2010) Mixed linear model approach adapted for genome-wide association studies. Nat Genet 42:355–360
Zhao XY, Wang Q, Li S, Ge FR, Zhou LZ, McCormick S et al. (2013) The juxtamembrane and carboxy-terminal domains of Arabidopsis PRK2 are critical for ROP-induced growth in pollen tubes. J Exp Bot 64:5599–5610
Zhou X, Stephens M (2012) Genome-wide efficient mixed model analysis for association studies. Nat Genet 44:821–824
Acknowledgements
This work was supported by the National Natural Science Foundation of China (31571268, U1602261), Huazhong Agricultural University Scientific & Technological Self-innovation Foundation (Program No. 2014RC020) and State Key Laboratory of Cotton Biology Open Fund (CB2017B01).
Author contributions
Y.-M.Z. conceived and supervised the study, and improved the manuscript. W.-L.R. and Y.-J.W. performed the experiments, analyzed the data, and wrote the draft. W.-L.R. wrote the R software. J.M.D. improved the language within the manuscript. All authors reviewed the manuscript.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conlict of interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, which permits any non-commercial use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. If you remix, transform, or build upon this article or a part thereof, you must distribute your contributions under the same license as the original. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/4.0/.
About this article
Cite this article
Ren, WL., Wen, YJ., Dunwell, J.M. et al. pKWmEB: integration of Kruskal–Wallis test with empirical Bayes under polygenic background control for multi-locus genome-wide association study. Heredity 120, 208–218 (2018). https://doi.org/10.1038/s41437-017-0007-4
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41437-017-0007-4
This article is cited by
-
Multi-omics analysis reveals novel loci and a candidate regulatory gene of unsaturated fatty acids in soybean (Glycine max (L.) Merr)
Biotechnology for Biofuels and Bioproducts (2024)
-
Insights into the genetic architecture of Phytophthora capsici root rot resistance in chile pepper (Capsicum spp.) from multi-locus genome-wide association study
BMC Plant Biology (2024)
-
Unveiling genetic signatures associated with resilience to neonatal diarrhea in lambs through two GWAS approaches
Scientific Reports (2024)
-
Multi-locus genome-wide association analysis for root and shoot traits at seedling stage in Ethiopian sorghum (Sorghum bicolor (L.) Moench) accessions
Genetic Resources and Crop Evolution (2024)
-
Association mapping in multiple yam species (Dioscorea spp.) of quantitative trait loci for yield-related traits
BMC Plant Biology (2023)