Abstract
The spin–orbit torque (SOT) resulting from a spin current generated in a nonmagnetic transition metal layer offers a promising magnetization switching mechanism for spintronic devices. To fully exploit this mechanism, in practice, materials with high SOT efficiencies are indispensable. Moreover, new materials need to be compatible with semiconductor processing. This study introduces W–Ta and W–V alloy layers between nonmagnetic β-W and ferromagnetic CoFeB layers in β-W/CoFeB/MgO/Ta heterostructures. We carry out first-principles band structure calculations for W–Ta and W–V alloy structures to estimate the spin Hall conductivity. While the predicted spin Hall conductivity values of W–Ta alloys decrease monotonically from −0.82 × 103 S/cm for W100 at% as the Ta concentration increases, those of W–V alloys increase to −1.98 × 103 S/cm for W75V25 at% and then gradually decrease. Subsequently, we measure the spin Hall conductivities of both alloys. Experimentally, when β-W is alloyed with 20 at% V, the absolute value of the spin Hall conductivity considerably increases by 36% compared to that of the pristine β-W. We confirm that the W–V alloy also improves the SOT switching efficiency by approximately 40% compared to that of pristine β-W. This study demonstrates a new material that can act as a spin current-generating layer, leading to energy-efficient spintronic devices.
Similar content being viewed by others
Introduction
In recent decades, there has been tremendous advancement in spintronics. Spin–orbit torque (SOT)1,2, which is significantly more rapid and energy-efficient than spin-transfer torque (STT)3,4, has generated interest from technological and scientific perspectives. SOT is a critical part of magnetization switching, facilitating devices with magnetic memory and logic5,6,7,8. In a typical nonmagnetic transition metal (NM)/ferromagnet (FM) heterostructure, polarized spin moments carried by the spin current and accumulated at the NM and FM interface generate a SOT. The spin current, in turn, is known to be generated by the spin–orbit interaction at the NM or NM/FM interface9,10. Recently, FMs (e.g., NiFe)11 have been shown to generate a spin current. Other material classes, such as topological insulators and Weyl semimetals, have also been studied12,13,14. However, their application in device manufacturing appears to be limited due to the complexity of the growth method and low thermal stability. Therefore, it is essential to design NMs with manufacturing process-friendly materials, such as W, commonly used in the current semiconductor industry. It is also equally essential to identify material combinations that possess perpendicular magnetic anisotropy (PMA), which is the key to achieving high bit density15,16. Two orthogonal torques contribute to the SOT: damping-like (DL) and field-like (FL) SOTs. Note that the DL-SOT efficiency per unit current density (ξDL) is correlated to the spin Hall angle (θSH), which is the charge-to-spin conversion ratio, as follows: ξDL = Tint θSH, where Tint is the interfacial spin transparency. Unless we know the exact value of Tint, the value of θSH is not equal to ξDL.
Of the various NMs, β-W is a good candidate, showing PMA with CoFeB and a high DL-SOT efficiency ξDL of −0.33 to −0.4017,18. There have been several efforts made to improve the ξDL of β-W derivatives, e.g., the deposition of W by sputtering under an oxygen atmosphere19 and multistep W deposition to form a thick β-W layer of up to 16 nm20. Both methods achieved ξDL values of approximately −0.5. In the former study, the PMA strength weakened due to oxygen incorporation, whereas the processing time increased in the latter. Moreover, Ta substitution into β-W was theoretically predicted to achieve a ξDL of −0.5 due to intrinsic band structure modification21.
This study extends this Ta-based theoretical investigation. In addition, we expect V to play a similar role in A15-structured β-W because V has the same number of valence electrons as Ta. Thus, we explore Ta and V substitutions in β-W for a wide range of alloy concentrations. Based on our first-principles band calculations, an alloy layer, W100−xXx (where X is either Ta or V), was introduced between the β-W and CoFeB layers. We fabricated β-W/W100−xXx/CoFeB/MgO/Ta heterostructure film stacks on Si wafers coated with thermal oxides for various alloy compositions, 0 < x < 100 at%. Due to the presence of bottom β-W layers, the β-phase in the W100−xXx alloy layers was expected to be maintained to the maximum extent. Over most of the composition range, PMA was exhibited. Harmonic Hall measurements confirmed that ξDL increased to −0.49, corresponding to an approximately 40% enhancement compared to that of β-W, which agreed well with the calculated results. This large SOT was further validated using other measurement methods, such as domain wall depinning and the propagation model22. This combined theoretical and experimental study provides insight into engineering opportunities for developing materials exhibiting high SOT efficiency.
Materials and methods
Theoretical calculations
First-principles calculations were performed using the Vienna Ab Initio Simulation Package23 with the projector augmented wave basis24. An energy cutoff of 500 eV was selected, with a 16 × 16 × 16 k-point mesh for summation in the Brillouin zone. The generalized gradient approximation was employed for the exchange-correlation potential as parametrized by Perdew, Burke, and Ernzerhof25. The spin Hall conductivity (σSH) was calculated using the Kubo formula in the linear response theory26 as follows
where \(f_{{{{\boldsymbol{k}}}}n}\) is the Fermi–Dirac function for the nth band at k; therefore, the Berry curvature of the n-th band at k is expressed as
where \(j_x = \frac{\beta }{2}\left\{ {{\Sigma},v_x} \right\}\) is the spin current and Σ is the spin operator in the full relativistic formalism. In this study, the interpolation technique27,28 using Wannier90 was employed with s, p, and d orbitals of W, Ta, and V atoms. Throughout this study, the xy component of the spin Hall conductivity with the spin axis along the z-direction was considered. For the alloys, the spin Hall conductivity at concentration x was calculated for all possible configurations and was thermodynamically averaged using the Boltzmann factor by considering the relative energies.
Sample preparation
Samples were sputtered onto 1.25 × 1.25 cm2 thermally oxidized Si wafers under a base pressure below 5 × 10−9 Torr. The thickness of the Si-oxide layer was 300 nm. The stacking structure of each sample was W (4)/W100−xXx (2)/CoFeB (0.9)/MgO (1)/Ta (2) (the number in parentheses represents the thickness in nanometers), where X is either Ta or V. A 4-nm-thick β-W layer was employed to maintain the β-phase in the 2-nm-thick W100−xXx alloy layer. The alloy layer composition was varied in 10 at% steps by changing the sputtering power densities of the W and Ta (or V) targets during co-deposition. The composition of the CoFeB target was Co40Fe40B20 in at%. The metallic layers and the MgO interlayer were produced by DC and radio frequency magnetron sputtering, respectively. All samples were post-annealed at 300 °C for 1 h under a magnetic field of 6 kOe applied perpendicular to the film plane under a base pressure of 10−6 Torr. Each film was patterned into a 5-μm-wide and 35-μm-long Hall cross-device by photolithography (Karl Suss MA6) and Ar ion milling. An electrical contact pad of a Ti/Au bilayer was fabricated using an e-beam evaporator followed by a lift-off process. We also constructed 4 × 4 μm2-sized ferromagnetic islands at the center of the Hall bar devices for current-induced SOT switching, in which all parts excluding the islands were W/W–Ta or W/W–V layers.
Measurements
Hysteresis loops were measured using a vibrating sample magnetometer (Microsense EV9). To evaluate the SOT efficiency, the harmonic Hall response method was employed (Supplementary Note 1, Figs. S1a, b). Two lock-in amplifiers were also utilized to simultaneously access the first- and second-harmonic responses of the magnetization. An alternating current (AC) of frequency 13.7 Hz and amplitude 1 mA was applied during the measurement while changing the external magnetic field from −18,000 to 18,000 Oe with different azimuthal angles φ. The polar angle of the sample was tilted (~5°) to prevent the formation of multiple domains.
The current-induced SOT switching was measured by the anomalous Hall voltage of the samples. The Hall voltage was detected by a 100-μA direct current (DC) after applying each current pulse is 0.5-mA steps and a 10-μs width from −15 to 15 mA under a constant external field along the x-direction. The resistivity of the alloyed layer was evaluated using a constant DC supply. Both switching and resistivity were examined using a four-point electrical property measurement station (MSTECH M7VC). The crystal structures of the W/W–Ta, and W/W–V layers were characterized by grazing incidence (GI) X-ray diffraction (XRD, Rigaku ATX-G) with incident angles ranging from 30° to 80° in 0.02° steps. The atomic distribution after annealing at 300 °C was evaluated by scanning transmission electron microscopy (STEM, FEI Double Cs Corrected Titan3 G2 60-300) with energy-dispersive X-ray spectroscopy (EDS). For the STEM sampling, a focused ion beam (FIB, FEI Quanta3D) system was used. Secondary ion mass spectrometry (SIMS, ION-TOF TOF, SIMS 5) was also used to examine the atomic distribution.
Results and discussion
Materials screening by ab initio calculations
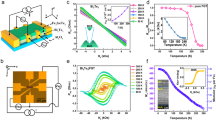
A previous investigation21 on x = 12.5 at% Ta alloying was extended in this study to other concentrations of Ta and V. The crystal structure of A15 β-W comprises two symmetrically inequivalent sites: body-centered cubic (bcc) and chain (c) sites. Due to the presence of these two inequivalent sites, several configurations are possible for each x, where the acceptance of a configuration is determined by energetics. The spin Hall conductivity is estimated by thermodynamic averaging (Supplementary Note 2). In particular, for an alloy with a solute composition x = 25 at%, there are four possible configurations: cc, bc, cc’, and bb’, where b and c denote either a bcc site or a chain site. Specifically, the cc and cc’ configurations exist when the solute atoms, either Ta or V, occupy the same and different chain sites, respectively. Similarly, bb’ denotes the case when two different bcc sites are replaced, and bc represents the case when each of the bcc and chain sites is substituted (Supplementary Fig. S2a–d).
The σSH values were calculated as a function of x (see Fig. 1a, b), and the k-resolved Berry curvatures were obtained for both W–Ta and W–V alloys at x = 25 at% (see Fig. 1c, d). The two alloys exhibit quite different behaviors based on their composition. σSH for W–Ta decreases monotonically with x, whereas that of the W–V alloy is enhanced as x increases from 12.5 to 50 at%. The W–Ta alloy favors the cc’ configuration with a 96% probability; hence, other configurations are not considered. In comparison, for the W–V alloy, the bb’ configuration has the highest probability (60.5%), and the bc configuration has a lower probability (35%). The probabilities are estimated using Boltzmann factors, considering the relative total energies at room temperature (Supplementary Fig. S2e).
The spin Hall conductivity of the bc configuration reaches as high as −1.98 × 103 S/cm, equivalent to 141% enhancement relative to that of β-W (−0.82 × 103 S/cm) (Supplementary Fig. S2f). This enhancement is attributed to the occurrence of strong symmetry breaking when V simultaneously adopts bcc and chain sites. Specifically, the Berry curvatures with opposite signs, a characteristic of β-W with a resonant double degenerate state, no longer cancel out (Supplementary Note 3 and Fig. S3a–d). Moreover, the increased degeneracies associated with the lowered symmetry increase the spin Hall conductivity, whose effect is most drastic when x = 25 at% in the W–V alloy. Based on the calculations, a W–V alloy with a composition range of 12.5–50 at% is explored experimentally, as discussed below.
SOT efficiency estimation employing the harmonic Hall method
Based on first-principles calculations, various alloy layers were introduced between the β-W and CoFeB layers in a heterostructure consisting of β-W/CoFeB/MgO/Ta. The employment of the alloy layer was motivated by our previous study29, which showed that a W layer could not maintain the β-W phase when it was alloyed with 10 at% Ta. A film stack of β-W (4)/W100−xXx (2)/CoFeB (0.9)/MgO (1)/Ta (2) (thickness in nm) was fabricated with alloy X (Ta or V) to prevent the phase transition of W from β to α. Note that the β-phase is a fundamental assumption in the theoretical calculations.
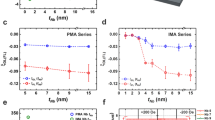
The alloyed layer composition ranged from 0 to 100 at% X in 10 at% steps. After annealing at 300 °C for 1 h in a vacuum, most film structures present PMA. However, when the V composition exceeds 80 at%, a PMA to in-plane magnetic anisotropy transition occurs. At this composition, the effective magnetic anisotropy energy (\(K_u^{\rm{eff}}\)) decreases. (Supplementary Note 4, Fig. S4a–f, and Table S1). At x = 100 at%, the magnetic hysteresis loop is not observed; hence, the sign of \(K_u^{\rm{eff}}\) cannot be determined. The degradation of the magnetic properties when x > 80 at% is attributed to the formation of a magnetic dead layer between V and CoFe30,31. Thus, in the following, the SOT efficiency is discussed for the composition range exhibiting PMA.
Harmonic Hall measurements32 were performed to assess the SOT efficiencies. Figure 2a schematically illustrates the harmonic Hall measurement, where an AC is applied along the x-direction, following which the Hall voltage (VH) along the y-direction is measured. During the VH measurement, sweeping the external in-plane magnetic field parallel (perpendicular) to the current yields traces of DL-SOT (FL-SOT). Fig. 2b, c shows the DL-SOT (ξDL) and FL-SOT (ξFL) efficiencies per unit current density of the W/W100−xTax/CoFeB/MgO/Ta and W/W100−xVx/CoFeB/MgO/Ta heterostructures versus alloy composition x (in at%), respectively. The changes in ξDL and ξFL with respect to x are quite different. As the Ta content increases, ξDL gradually decreases from −0.35 ± 0.002 for a 6-nm-thick W to −0.06 ± 0.06 for the W/W0Ta100 bilayer. Notably, the ξDL of the W/W0Ta100 bilayer is similar to that of the highly resistive material β-Ta33. This suggests that the spin current generated in W inefficiently penetrates the W–Ta alloy layer and further intensifies with increasing Ta composition. Consequently, in the extreme case of a bilayer NM structure, most of the DL torque occurs due to the spin current generated in Ta. Furthermore, this is consistent with previous studies on the spin diffusion length of Ta, which is 2–3 nm34,35. However, the ξDL values of the W/W100−xVx/CoFeB/MgO/Ta heterostructure exhibit interesting composition-dependent behavior. At V = 20 at%, the ξDL value reaches a maximum of −0.49 ± 0.05. This large value is in agreement with that of a W-based SOT tunnel junction19,20.
The FL-SOT (ξFL) efficiencies do not present any distinct compositional dependence, as depicted in Fig. 2c. In both the Ta and V cases, ξFL \(\approx\) −0.10 to −0.20, suggesting that the potential gradient at the interface (i.e., the Rashba effect) has a slight correlation with the alloy layer. In addition, in the thin FM layer, in the layered structure with PMA, ξFL depends on the magnetic anisotropy energy and temperature36. Moreover, the PMA in the NM/CoFeB/MgO structure mainly originates from the CoFeB/MgO interfacial anisotropy energy, and the portion of NM/CoFeB is relatively small. Thus, the insensitive behavior of ξFL in this study is in line with a previous report because only the W/CoFeB interface is modified.
In accordance with the ab initio calculations, the spin Hall conductivity was estimated by employing the relationship between the resistivity and the spin Hall angle, \(\theta _{\rm{SH}} = \sigma _{\rm{SH}}\rho _{xx} + b\)37, where σSH comprises the intrinsic and side-jump contributions, ρxx is the longitudinal resistivity, and b represents the skew-scattering contribution. Presumably, parameter b is negligible because of the high impurity content in the studied system, and it is assumed that Tint is 1. Hence, the spin Hall conductivity can be expressed by the ratio of θSH to ρxx. The ρxx value of each device was determined by employing the parallel resistance model assuming ρxx = 170 μΩ cm for CoFeB (Supplementary Note 5, Fig. S5a, b). The results are displayed in Fig. 2d, and the maximum SHC value is (−2.77 ± 0.31) × 103 S/cm at 20 at% V. This is reasonably consistent with the first-principles calculation results of this study, which yield a maximum value of −1.98 × 103 S/cm at 25 at% V. Consequently, by using the W−V alloy layer, the band structure modification predicted by the calculations is successfully captured.
Assessment of SOT switching
Current-induced SOT switching in patterned devices was examined. A current sweep was applied from –15 to 15 mA. The current pulse width was 10 μs and was changed in 0.5-mA steps while the external magnetic field strength was varied from −100 to 100 Oe in the x-direction. An additional fabrication process was utilized to form an island pattern on the devices to test the current-induced SOT switching (Methods).
Figure 3a shows the switching loops for a heterostructure with a 20 at% V alloy, which shows the highest ξDL. The sample clearly exhibits external field dependence. When the polarity of the external field is varied, the switching polarity also changes. A strong applied magnetic field implies a small observed switching current. Furthermore, magnetization switching was examined in all patterned devices used in the harmonic measurements. As depicted in Fig. 3b, the magnetization direction was successfully manipulated by applying an in-plane current pulse and a constant external field, 100 Oe. The switching current density (JSW) and ξDL are inversely proportional in single-domain devices as follows38:
where tFM represents the thickness of the FM layer and \(H_K^{\rm{eff}}\) and \(H_{\rm{ext}}\) are the anisotropy field and the external field, respectively. However, based on Figs. 2b and 3b, ξDL and JSW do not show inverse proportionality. A 4 μm × 4 μm-sized island pattern was used to test the SOT switching, and this size of the island was extremely large to maintain a single-domain state. Therefore, this deviation is attributed to the existence of domains and domain walls39. The next section describes tests on whether SOT switching entails domain wall motion and double-checks of the high SOT efficiency. To this end, a domain wall depinning and propagation model for the 20 at% V-incorporated devices was employed.
Domain wall depinning and propagation model
To examine the high SOT efficiency in the 20 at% V alloy sample, the domain wall depinning and propagation model was applied. First, we determined whether SOT switching occurs through domain wall propagation or single domain reversal under the current application. Hp(θ) is defined as the external switching field at polar angle θ. Figure 4a shows that the Hp(θ)/Hp(0) ratio accurately presents a 1/cos θ dependence, which confirms that in the studied Hall cross-device, magnetization switching involves a domain wall-mediated process.
a Polar angle dependence of the switching field. The green dotted line represents the fitted line for 1/cos θ. b Measuring time (tm)-dependent behavior of the switching field. Error bars represent the standard deviation from 35 independent measurements. c Switching state diagram as a function of the external field in the x-direction. d Effective DL field evaluated from the switching state diagram. The red dotted line represents the effective DL field estimated from the harmonic measurement. The error bars in the figures represent the standard error.
Based on the SOT evaluation process, the measuring time (tm) dependence of Hp was also examined, as shown in Fig. 4b. We find that the intrinsic coercive field (Hc0) is 393.03 Oe and that the coercivity of the device is 274.82 Oe (Supplementary Fig. S6a). In addition, the Joule heating coefficient (κ) was determined utilizing two different channel resistance (Rxx) measurements: the temperature dependence of Rxx was determined by heating the device externally (Supplementary Fig. S6b), and the current dependence of Rxx was determined from the relationship T(I) ≈T0 + κI2, where T0 is the room temperature and I is the amplitude of the input current (Supplementary Fig. S6c).
When a current of I = 4.22 mA is applied, the temperature of the device increases by 157 K relative to room temperature, where κ is determined to be 0.02485 K/mA2. Using these parameters, the switching state diagram (Fig. 4c) is converted into the DL effective field normalized by the input current density (Fig. 4d). The detailed conversion process is described in Supplementary Note 6.
The DL effective field saturates at approximately 24.7 ± 2.33 Oe cm2/MA when the external field exceeds 120 Oe. This is consistent with the effective DL field obtained using the harmonic Hall method, as indicated by the red dotted line in Fig. 4d. Because the two measurement schemes yield similar magnitudes for the DL-SOT effective field, it is concluded that the enhancement in the SOT originates from the 20 at% V incorporation in the film structure.
Furthermore, we examine the 1/cos θ dependence of all devices and confirm that SOT switching occurs in a domain wall-mediated process. From this perspective, the SOT switching efficiency (η), considering the domain wall depinning field, is investigated (Supplementary Note 7 and Fig. S7a). The enhancement ratio of the SOT switching efficiency between pristine W and the 20 at% V-incorporated samples is qualitatively consistent with the enhancement ratio of ξDL (Supplementary Fig. S7b). Therefore, increasing the switching current per increase in the V content, as shown in Fig. 3b, does not consider the effect of the domain wall depinning field. When the domain wall depinning field during magnetization switching is considered, the W–V alloy achieves a higher SOT switching efficiency than that in the single W layer.
Note that if domain wall depinning and propagation occur during SOT switching, Jsw follows Eq. (4)40.
where e, μ0, Ms, tFM, and Hc represent the elementary charge of an electron, vacuum permeability, saturation magnetization, thickness of the FM layer, and coercivity of the ferromagnetic layer, respectively. The W–V alloyed structures reasonably follow the coercivity of CoFeB with regard to V composition (Supplementary Note 8 and Fig. S8a, b).
Improvement in the DL-SOT efficiency of W–V alloys
To elucidate the increase in the ξDL in a W–V alloy, the microstructure of the films was analyzed. GI-XRD was used to examine the phases of the W/W–Ta and W/W–V layers, and the results are shown in Fig. 5a and b. Because the layers are ultrathin, the XRD spectra show no peaks corresponding to CoFeB, MgO, or Ta. The W–Ta alloy retains the β-W phase up to 80 at% Ta content. For the W–V alloy, as illustrated in Fig. 5b, the characteristic peak for α-W appears when 100 at% V is incorporated. β-W has the A15 structure, which is an energetically unstable phase. In addition, the atomic radii of W, Ta, and V are 135, 146, and 135 pm, respectively; therefore, the residual stress in the W–Ta alloy promotes the phase transition of β-W. Consequently, the phase stability of β-W in the W–V alloy is one of the reasons for the enhancement in ξDL.
Because V is a lighter element than W, we examined atomic interdiffusion after annealing at 300 °C. To test whether ξDL was enhanced due to its atomic interdiffusion of V, atomic distribution profiles employing STEM were obtained. Figure 6a, b clearly shows the layered structures. Schematics of the layered structures are placed on the right side of the figures. The interfaces between each layer become clear and sharp after the films undergo 300 °C annealings. EDS was conducted to locate the atomic positions in the film structure. To obtain the EDS intensity, the sample prepared for high-resolution (HR) TEM measurement was extremely thin (20–30 nm), and thus, a relatively thick specimen (80–100 nm) was prepared using a FIB system. The atomic positions in the film structure were assigned by EDS, as presented in Fig. 6c, d. Note that the high-angle annular dark-field images appear blurred because of the TEM sampling thickness.
We also conducted EDS on the samples used in the HR-TEM measurement (Supplementary Fig. S9a, b). Based on Fig. 6c and d, V atoms are located under the CoFe layer, regardless of heat treatment. The elemental profile of V observed in the SiO2/W and Ta layers is confirmed to be an EDS measurement artifact (Supplementary Note 9 and Fig. S10a–f). Furthermore, SIMS was performed, showing that the atomic interdiffusion of V is negligibly small (Supplementary Note 10 and Fig. S11a–d). Therefore, we can exclude the notion of atomic interdiffusion in the heterostructures.
Conclusion
A combined theoretical and experimental study was presented for W/W−Ta/CoFeB/MgO/Ta and W/W–V/CoFeB/MgO/Ta heterostructures. A series of first-principles calculations were conducted to investigate the W–Ta and W–V alloy compositions leading to high spin Hall conductivity. Subsequently, fabrication and measurement were performed by experimentally compiling the composition dependencies of the SOT efficiency. The W–Ta alloy presented a gradually decreasing ξDL as the Ta content increased, and the ξDL of the W–V alloy demonstrated interesting composition-dependent behavior. Specifically, for the 20 at% V alloy layer, ξDL became −0.49 ± 0.05, an enhancement of 40% over that of pristine β-W. This significant enhancement in ξDL was confirmed by two different measurement schemes: harmonic measurements and a domain wall depinning and propagation model. The domain wall depinning and propagation model presented a reasonable value for the DL-SOT effective field 24.7 ± 2.33 Oe cm2/MA.
The SOT switching efficiency (η) also improved, similar to the enhancement ratio of ξDL. The XRD and TEM analyses confirmed that the high ξDL was attributed to the phase stability of β-W achieved by employing the W–V alloy layer. We expect that the optimized composition of the W80V20 alloy layer could become an energy-efficient spin current source layer because of its high ξDL and good process compatibility for semiconductor manufacturing.
References
Miron, I. M. et al. Perpendicular switching of a single ferromagnetic layer induced by in-plane current injection. Nature 476, 189–193 (2011).
Liu, L. et al. Spin torque switching with the giant spin Hall effect of tantalum. Science 336, 555–558 (2012).
Slonczewski, J. C. Current-driven excitation of magnetic multilayers. J. Magn. Magn. Mater. 159, L1–L7 (1996).
Berger, L. Emission of spin waves by a magnetic multilayer traversed by a current. Phys. Rev. B 54, 9353 (1996).
Fukami, S., Anekawa, T., Zhang, C. & Ohno, H. A spin-orbit torque switching scheme with collinear magnetic easy axis and current configuration. Nat. Nanotechnol. 11, 621–625 (2016).
Baek, S. C. et al. Complementary logic operation based on electric-field controlled spin-orbit torques. Nat. Electron. 1, 398–403 (2018).
Zhang, J. et al. Role of micromagnetic states on spin-orbit torques-switching schemes. Nano Lett. 18, 4074–4080 (2018).
Song, C. et al. Spin-orbit torques: materials, mechanisms, performances, and potential applications. Prog. Mater. Sci. 118, 100761 (2021).
Sinova, J., Valenzuela, S. O., Wunderlich, J., Back, C. H. & Jungwirth, T. Spin Hall effects. Rev. Mod. Phys. 87, 1213–1259 (2015).
Manchon, A. & Zhang, S. Theory of nonequilibrium intrinsic spin torque in a single nanomagnet. Phys. Rev. B 78, 212405 (2008).
Wang, W. et al. Anomalous spin-orbit torques in magnetic single-layer films. Nat. Nanotech. 14, 819–824 (2019).
Fan, Y. et al. Magnetization switching through giant spin-orbit torque in a magnetically doped topological insulator heterostructure. Nat. Mater. 13, 699–704 (2014).
Wang, Y. et al. Room temperature magnetization switching in topological insulator-ferromagnet heterostructures by spin-orbit torques. Nat. Commun. 8, 1364 (2017).
Li, P. et al. Spin-momentum locking and spin-orbit torques in magnetic nano-heterojunctions composed of Weyl semimetal WTe2. Nat. Commun. 9, 3990 (2018).
Mangin, S. et al. Current-induced magnetization reversal in nanopillars with perpendicular anisotropy. Nat. Mater. 5, 210–215 (2006).
Ikeda, S. et al. A perpendicular-anisotropy CoFeB-MgO magnetic tunnel junction. Nat. Mater. 9, 721–724 (2010).
Pai, C.-F. et al. Spin transfer torque device utilizing the giant spin Hall effect of tungsten. Appl. Phys. Lett. 101, 122404 (2012).
Hao, Q. & Xiao, G. Giant Spin Hall Effect and switching induced by spin-transfer torque in a W/Co40Fe40B20/MgO structure with perpendicular magnetic anisotropy. Phys. Rev. Appl. 3, 034009 (2015).
Demasius, K.-U. et al. Enhanced spin-orbit torques by oxygen incorporation in tungsten films. Nat. Commun. 7, 10644 (2016).
Chen, W., Xiao, G., Zhang, Q. & Zhang, X. Temperature study of the giant spin Hall effect in the bulk limit of β-W. Phys. Rev. B 98, 134411 (2018).
Sui, X. et al. Giant enhancement of the intrinsic spin Hall conductivity in β-tungsten via substitutional doping. Phys. Rev. B 96, 241105(R) (2017).
Lee, O. J. et al. Central role of domain wall depinning for perpendicular magnetization switching driven by spin torque from the spin Hall effect. Phys. Rev. B 89, 024418 (2014).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169 (1996).
Blöchl, P. Projector augmented-wave method. Phys. Rev. B 50, 17953 (1994).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).
Guo, G. Y., Murakami, S., Chen, T.-W. & Nagaosa, N. Intrinsic spin Hall effect in platinum: first principles calculations. Phys. Rev. Lett. 100, 096401 (2008).
Souza, I., Marzari, N. & Vanderbilt, D. Maximally localized Wannier functions for entangled energy bands. Phys. Rev. B 65, 035109 (2001).
Mostofi, A. A. et al. wannier90: a tool for obtaining maximally-localised Wannier functions. Comput. Phys. Commun. 178, 685 (2008).
Cha, I. H., Kim, T., Kim, Y. J., Kim, G. W. & Kim, Y. K. Thickness and composition-dependent spin-orbit torque behaviors in perpendicular magnetized Ta/W (t)/CoFeB and Ta1-xWx/CoFeB junction structures. J. Alloy. Compd. 823, 153744 (2020).
Devolder, T., Tahmasebi, T., Eimer, S., Hauet, T. & Andrieu, S. Compositional dependence of the magnetic properties of epitaxial FeV/MgO thin films. Appl. Phys. Lett. 103, 242410 (2013).
Fackler, S. W. et al. Combinatorial study of Fe-Co-V hard magnetic thin films. Sci. Tech. Adv. Mater. 18, 231 (2017).
Avci, C. O. et al. Interplay of spin-orbit torque and thermoelectric effects in ferromagnet/normal-metal bilayers. Phys. Rev. B 90, 224427 (2014).
Yu, R. et al. Determination of spin Hall angle and spin diffusion length in β-phase dominated tantalum. Phys. Rev. Mater. 2, 074406 (2018).
Niimi, Y. et al. Extrinsic spin Hall effects measured with lateral spin valve structures. Phys. Rev. B 89, 054401 (2014).
Kim, D.-J., Kim, S.-I., Park, S.-Y., Lee, K.-D. & Park, B.-G. Ferromagnetic resonance spin pumping in CoFeB with highly resistive nonmagnetic electrodes. Curr. Appl. Phys. 14, 1344–1348 (2014).
Ou, Y., Pai, C.-F., Shi, S., Ralph, D. C. & Buhrman, R. A. Origin of field-like spin-orbit torques in heavy metal/ferromagnet/oxide thin film heterostructures. Phys. Rev. B 94, 140414(R) (2016).
Fritz, K., Wimmer, S., Ebert, H. & Menert, M. Large spin Hall effect in an amorphous binary alloy. Phys. Rev. B 98, 094433 (2018).
Lee, K.-S., Lee, S.-W., Min, B.-C. & Lee, K.-J. Thermally activated switching of perpendicular magnet by spin-orbit spin torque. Appl. Phys. Lett. 104, 072413 (2014).
Emori, S., Bauer, U., Ahn, S.-M., Martinez, E. & Beach, G. S. D. Current-driven dynamics of chiral ferromagnetic domain walls. Nat. Mater. 12, 611–616 (2013).
Zhu, L., Ralph, D. C. & Buhrman, R. A. Lack of simple correlation between switching current density and spin-orbit torque efficiency of perpendicularly magnetized spin-current-generator-ferromagnet heterostructures. Phys. Rev. Appl. 15, 024059 (2021).
Acknowledgements
The authors thank Yun Jung Jang of the Korea Institute of Science and Technology for helping us with the ToF-SIMS experiments. This research was supported by the National Research Foundation (NRF) of Korea (2015M3D1A1070465 and 2020M3F3A2A01082591). Y. K. Kim was supported by Samsung Electronics Co., Ltd. (IO201211-08104-01). O. Lee was supported by the NRF of Korea (2020M3F3A2A01081635). The study at the University of Ulsan was supported by the Basic Research Lab Program through the NRF of Korea (2018R1A4A1020696).
Author information
Authors and Affiliations
Contributions
G.W.K. and Y.K.K. conceived and designed the experiments. D.D.C., S.C.H., and S.H.R. performed the first-principles calculations. G.W.K., T.K., and M.H.L. fabricated the film structures and devices. G.W.K., Y.J.K., and I.H.C. conducted the SOT efficiency evaluation and analyzed the microstructural transition of β.-W. G.W.K. conducted the domain wall propagation experiments with the help of O.J.L. H.B. performed the TEM experiment and analyzed the atomic distribution. G.W.K. and D.D.C. wrote the paper after discussion with all the authors. Y.K.K. supervised the entire project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kim, G.W., Cuong, D.D., Kim, Y.J. et al. Spin–orbit torque engineering in β-W/CoFeB heterostructures with W–Ta or W–V alloy layers between β-W and CoFeB. NPG Asia Mater 13, 60 (2021). https://doi.org/10.1038/s41427-021-00326-8
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41427-021-00326-8