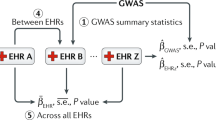
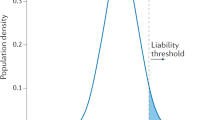
Key Points
-
Evaluation of the utility of genetic risk assessment for disease prevention requires the development of models incorporating both genetic and non-genetic (environmental) risk factors for predicting the absolute risk of diseases. Development of models for absolute risk may require combining data from various sources, including epidemiological cohort, case–control and family-based studies, population-based disease and death registries, and national health surveys.
-
Complex diseases are likely to be associated with thousands or tens of thousands of common single-nucleotide polymorphisms (SNPs), each with small effects, but cumulatively they may explain substantial variation in disease risks. The extreme polygenic architecture of many common diseases implies that the predictive performance of polygenic risk scores (PRSs) will slowly rise in the future with increasingly large studies and will reach a plateau only after genome-wide association studies (GWAS) reach huge sample sizes, possibly involving hundreds of thousands of individuals.
-
Development of optimal PRSs based on data from a given GWAS data set requires careful consideration of the threshold for SNP selection, weights for selected SNPs, linkage disequilibrium and any external knowledge — including functional, annotation and pleiotropic information — that can be utilized to prioritize the SNPs.
-
Development of multifactorial risk models, including PRSs and environmental risk factors, requires characterization of the risk associated with individual factors, exploration of interactions and assessment of the goodness of fit of models. Use of information on disease rates and mortality from population-based registries can improve the generalizability of absolute risk models.
-
Before clinical applications, models need to be assessed for calibrations — that is, their ability to produce an unbiased estimate of risks in prospective cohort studies. The clinical utility of well-calibrated models depends on the degree of risk stratification they can produce for the population, but the optimal criterion for evaluating risk stratification depends on the clinical application under consideration.
Abstract
Knowledge of genetics and its implications for human health is rapidly evolving in accordance with recent events, such as discoveries of large numbers of disease susceptibility loci from genome-wide association studies, the US Supreme Court ruling of the non-patentability of human genes, and the development of a regulatory framework for commercial genetic tests. In anticipation of the increasing relevance of genetic testing for the assessment of disease risks, this Review provides a summary of the methodologies used for building, evaluating and applying risk prediction models that include information from genetic testing and environmental risk factors. Potential applications of models for primary and secondary disease prevention are illustrated through several case studies, and future challenges and opportunities are discussed.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$189.00 per year
only $15.75 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
References
Gabai-Kapara, E. et al. Population-based screening for breast ovarian cancer risk due to BRCA1 and BRCA2. Proc. Natl Acad. Sci. USA 111, 14205–14210 (2014).
King, M. C., Levy-Lahad, E. & Lahad, A. Population-based screening for BRCA1 and BRCA2: 2014 Lasker Award. JAMA 312, 1091–1092 (2014).
Easton, D. F. et al. Gene-panel sequencing and the prediction of breast-cancer risk. N. Engl. J. Med. 372, 2243–2257 (2015).
Evans, B. J., Burke, W., & Jarvik, G. P. The FDA and genomic tests — getting regulation right. N. Engl. J. Med. 372, 2258–2264 (2015).
Thomas, D. M., James, P. A. & Ballinger, M. L. Clinical implications of genomics for cancer risk genetics. Lancet Oncol. 16, e303–e308 (2015).
Grosse, S. D. & Khoury, M. J. What is the clinical utility of genetic testing? Genet. Med. 8, 448–450 (2006).
German National Cohort (GNC) Consortium. The German National Cohort: aims, study design and organization. Eur. J. Epidemiol. 29, 371–382 (2014).
Pharoah, P. D. et al. Polygenic susceptibility to breast cancer and implications for prevention. Nat. Genet. 31, 33–36 (2002). These authors use key mathematical relationships between heritability and the discriminatory ability of polygenic scores to illustrate potential utility of breast cancer risk stratification models.
Wray, N. R. et al. The genetic interpretation of area under the ROC curve in genomic profiling. PLoS Genet. 6, e1000864 (2010).
Witte, J. S., Visscher, P. M. & Wray, N. R. The contribution of genetic variants to disease depends on the ruler. Nat. Rev. Genet. 15, 765–776 (2014).
Yang, J. et al. Common SNPs explain a large proportion of the heritability for human height. Nat. Genet. 42, 565–569 (2010). These authors develop mixed-model techniques to estimate heritability of height that could be explained by common SNPs included in GWAS platforms. This technique and various extensions of it have been used to characterize the GWAS heritability of many complex diseases.
Yang, J. et al. Advantages and pitfalls in the application of mixed-model association methods. Nat. Genet. 46, 100–106 (2014).
Yang, J. et al. GCTA: a tool for genome-wide complex trait analysis. Am. J. Hum. Genet. 88, 76–82 (2011).
Lee, S. H. et al. Estimation of SNP heritability from dense genotype data. Am. J. Hum. Genet. 93, 1151–1155 (2013).
Lee, S. H. et al. Estimating missing heritability for disease from genome-wide association studies. Am. J. Hum. Genet. 88, 294–305 (2011).
Lee, S. H. et al. Estimating the proportion of variation in susceptibility to schizophrenia captured by common SNPs. Nat. Genet. 44, 247–250 (2012).
Lee, S. H. et al. Estimation and partitioning of polygenic variation captured by common SNPs for Alzheimer's disease, multiple sclerosis and endometriosis. Hum. Mol. Genet. 22, 832–841 (2013).
Lu, Y. et al. Most common 'sporadic' cancers have a significant germline genetic component. Hum. Mol.Genet. 23, 6112–6118 (2014).
Chen, G. B. et al. Estimation and partitioning of (co)heritability of inflammatory bowel disease from GWAS and immunochip data. Hum. Mol. Genet. 23, 4710–4720 (2014).
Gusev, A. et al. Partitioning heritability of regulatory and cell-type-specific variants across 11 common diseases. Am. J. Hum. Genet. 95, 535–552 (2014).
Sampson, J. N. et al. Analysis of heritability and shared heritability based on genome-wide association studies for thirteen cancer types. J. Natl Cancer Inst. 107, djv279 (2015).
Zaitlen, N. et al. Using extended genealogy to estimate components of heritability for 23 quantitative and dichotomous traits. PLoS Genet. 9, e1003520 (2013).
Zaitlen, N. et al. Leveraging population admixture to characterize the heritability of complex traits. Nat. Genet. 46, 1356–1362 (2014).
Lichtenstein, P. et al. Environmental and heritable factors in the causation of cancer — analyses of cohorts of twins from Sweden, Denmark, and Finland. N. Engl. J. Med. 343, 78–85 (2000).
Polderman, T. J. et al. Meta-analysis of the heritability of human traits based on fifty years of twin studies. Nat. Genet. 47, 702–709 (2015).
Chang, E. T. et al. Reliability of self-reported family history of cancer in a large case-control study of lymphoma. J. Natl Cancer Inst. 98, 61–68 (2006).
Mitchell, R. J. et al. Accuracy of reporting of family history of colorectal cancer. Gut 53, 291–295 (2004).
Kerber, R. A. & Slattery, M. L. Comparison of self-reported and database-linked family history of cancer data in a case-control study. Am. J. Epidemiol. 146, 244–248 (1997).
Speed, D. et al. Improved heritability estimation from genome-wide SNPs. Am. J. Hum. Genet. 91, 1011–1021 (2012).
Golan, D. Lander, E. S. & Rosset S. Measuring missing heritability: inferring the contribution of common variants. Proc. Natl Acad. Sci. USA 111, E5272–E5281 (2014).
Goldgar, D. E. et al. Systematic population-based assessment of cancer risk in first-degree relatives of cancer probands. J. Natl Cancer Inst. 86, 1600–1608 (1994).
Kerber, R. A. & O'Brien, E. A cohort study of cancer risk in relation to family histories of cancer in the Utah population database. Cancer 103, 1906–1915 (2005).
Czene, K. Lichtenstein, P. & Hemminki, K. Environmental and heritable causes of cancer among 9.6 million individuals in the Swedish Family-Cancer Database. Int. J. Cancer 99, 260–266 (2002).
Mucci, L. A. et al. Familial risk and heritability of cancer among twins in nordic countries. JAMA 315, 68–76 (2016).
Cox, D. R. Regression models and life-tables. J. R. Stat. Soc. Series B Stat. Methodol. 34, 187–220; discussion 202–220 (1972). The author proposes the proportional hazard regression model and partial-likelihood method for statistical inference. In the discussion following the paper, N.E. Breslow proposes an estimator for baseline hazard function that is required for absolute risk estimation.
Prentice, R. L. & Breslow, N. E. Retrospective studies and failure time models. Biometrika 65, 153–158 (1978). The authors show a relationship between risk parameters in a proportional hazard and logistic regression model when the latter model is finely adjusted for age.
Hill, G. et al. Neyman's bias re-visited. J. Clin. Epidemiol. 56, 293–296 (2003).
Wacholder, S. et al. Selection of controls in case-control studies: I. Principles. Am. J. Epidemiol. 135, 1019–1028 (1992).
Falconer, D. S. Inheritance of liability to diseases with variable age of onset with particular reference to diabetes mellitus. Ann. Hum. Genet. 31, 1–20 (1967).
Aldrich, J. H. & Nelson, F. D. Linear Probability, Logit and Probit Models (SAGE, 1984).
Rothman, K. J., Greenland, S. & Lash, T. L. Modern Epidemiology 3rd edn (Lippincott, Williams and Wilkins, 2008).
Joshi, A. D. et al. Additive interactions between susceptibility single-nucleotide polymorphisms identified in genome-wide association studies and breast cancer risk factors in the Breast and Prostate Cancer Cohort Consortium. Am. J. Epidemiol. 180, 1018–1027 (2014).
Song, M. et al. Testing calibration of risk models at extremes of disease risk. Biostatistics 16, 143–154 (2015).
Barrdahl, M. et al. Post-GWAS gene–environment interplay in breast cancer: results from the Breast and Prostate Cancer Cohort Consortium and a meta-analysis on 79,000 women. Hum. Mol. Genet. 23, 5260–5270 (2014).
Langenberg, C. et al. Gene-lifestyle interaction and type 2 diabetes: the EPIC interact case-cohort study. PLoS Med. 11, e1001647 (2014).
Rudolph, A. et al. Investigation of gene-environment interactions between 47 newly identified breast cancer susceptibility loci and environmental risk factors. Int. J. Cancer 136, E685–E696 (2015).
Chatterjee, N. et al. Projecting the performance of risk prediction based on polygenic analyses of genome-wide association studies. Nat. Genet. 45, 400–405 (2013).
Talmud, P. J. et al. Sixty-five common genetic variants and prediction of type 2 diabetes. Diabetes 64, 1830–1840 (2014).
Dudbridge, F. Power and predictive accuracy of polygenic risk scores. PLoS Genet. 9, e1003348 (2013). In this paper, along with Ref. 47, the authors derive a mathematical relationship between the predictive performance of polygenic models, the sample size of training data, heritability and the underlying effect-size distribution of traits. Their analyses indicate that the predictive performance of polygenic models for diseases with extreme polygenic architecture will slowly improve in the future with larger sample sizes.
Lee, S. H. & Wray, N. R. Novel genetic analysis for case-control genome-wide association studies: quantification of power and genomic prediction accuracy. PLoS ONE 8, e71494 (2013).
Stahl, E. A. et al. Bayesian inference analyses of the polygenic architecture of rheumatoid arthritis. Nat. Genet. 44, 483–489 (2012).
Mavaddat, N. et al. Prediction of breast cancer risk based on profiling with common genetic variants. J. Natl Cancer Inst. 107, djv036 (2015).
Hsu, L. et al. A model to determine colorectal cancer risk using common genetic susceptibility loci. Gastroenterol. 148, 1330–1339 (2015).
Bao, W. et al. Predicting risk of type 2 diabetes mellitus with genetic risk models on the basis of established genome-wide association markers: a systematic review. Am. J. Epidemiol. 178, 1197–1207 (2013).
Krarup, N. T. et al. A genetic risk score of 45 coronary artery disease risk variants associates with increased risk of myocardial infarction in 6041 Danish individuals. Atherosclerosis 240, 305–310 (2015).
Weissfeld, J. L. et al. Lung cancer risk prediction using common SNPs located in GWAS-identified susceptibility regions. J. Thorac. Oncol. 10, 1538–1545 (2015).
Scott, I. C. et al. Predicting the risk of rheumatoid arthritis and its age of onset through modelling genetic risk variants with smoking. PLoS Genet. 9, e1003808 (2013).
Abraham, G. et al. Accurate and robust genomic prediction of celiac disease using statistical learning. PLoS Genet. 10, e1004137 (2014).
Romanos, J. et al. Improving coeliac disease risk prediction by testing non-HLA variants additional to HLA variants. Gut 63, 415–422 (2014).
Schizophrenia Working Group of the Psychiatric Genomics Consortium. Biological insights from 108 schizophrenia-associated genetic loci. Nature 511, 421–427 (2014).
International Schizophrenia Consortium. Common polygenic variation contributes to risk of schizophrenia and bipolar disorder. Nature 460, 748–752 (2009).
Psychiatric GWAS Consortium Bipolar Disorder Working Group. Large-scale genome-wide association analysis of bipolar disorder identifies a new susceptibility locus near ODZ4. Nat. Genet. 43, 977–983 (2011).
Bush, W. S. et al. Evidence for polygenic susceptibility to multiple sclerosis — the shape of things to come. Am. J. Hum. Genet. 86, 621–625 (2010).
Wu, J., Pfeiffer, R. M. & Gail, M. H. Strategies for developing prediction models from genome-wide association studies. Genet. Epidemiol. 37, 768–777 (2013).
Purcell, S. et al. PLINK: a tool set for whole-genome association and population-based linkage analyses. Am. J. Hum. Genet. 81, 559–575 (2007).
Vilhjalmsson, B. J. et al. Modeling linkage disequilibrium increases accuracy of polygenic risk scores. Am. J. Hum. Genet. 97, 576–592 (2015).
Golan, D. & Rosset, S. Effective genetic-risk prediction using mixed models. Am. J. Hum. Genet. 95, 383–393 (2014).
Moser, G. et al. Simultaneous discovery, estimation and prediction analysis of complex traits using a Bayesian mixture model. PLoS Genet. 11, e1004969 (2015).
Speed, D. & Balding, D. J. MultiBLUP: improved SNP-based prediction for complex traits. Genome Res 24, 1550–1557 (2014).
Zhou, X. Carbonetto, P. & Stephens, M. Polygenic modeling with Bayesian sparse linear mixed models. PLoS Genet. 9, e1003264 (2013).
Schork, A. J. et al. All SNPs are not created equal: genome-wide association studies reveal a consistent pattern of enrichment among functionally annotated SNPs. PLoS Genet. 9, e1003449 (2013).
Pickrell, J. K. Joint analysis of functional genomic data and genome-wide association studies of 18 human traits. Am. J. Hum. Genet. 94, 559–573 (2014).
Andreassen, O. A. et al. Improved detection of common variants associated with schizophrenia by leveraging pleiotropy with cardiovascular-disease risk factors. Am. J. Hum. Genet. 92, 197–209 (2013).
Andreassen, O. A. et al. Improved detection of common variants associated with schizophrenia and bipolar disorder using pleiotropy-informed conditional false discovery rate. PLoS Genet. 9, e1003455 (2013).
Maier, R. et al. Joint analysis of psychiatric disorders increases accuracy of risk prediction for schizophrenia, bipolar disorder, and major depressive disorder. Am. J. Hum. Genet. 96, 283–294 (2015).
Li, C. et al. Improving genetic risk prediction by leveraging pleiotropy. Hum. Genet. 133, 639–650 (2014).
Gusev, A. et al. Partitioning heritability of regulatory and cell-type-specific variants across 11 common diseases. Am. J. Hum. Genet. 95, 535–552 (2014).
Wacholder, S., Chatterjee, N. & Hartge, P. Joint effect of genes and environment distorted by selection biases: implications for hospital-based case-control studies. Cancer Epidemiol. Biomarkers Prev. 11, 885–889 (2002).
Piegorsch, W. W., Weinberg, C. R. & Taylor, J. A. Non-hierarchical logistic models and case-only designs for assessing susceptibility in population-based case-control studies. Stat. Med. 13, 153–162 (1994).
Umbach, D. M. & Weinberg, C. R. Designing and analysing case-control studies to exploit independence of genotype and exposure. Stat. Med. 16, 1731–1743 (1997).
Chatterjee, N. & Carroll, R. J. Semiparametric maximum-likelihood estimation in case-control studies of gene-environment interactions. Biometrika 92, 399–418 (2005).
Lee, A. J. et al. BOADICEA breast cancer risk prediction model: updates to cancer incidences, tumour pathology and web interface. Br. J. Cancer 110, 535–545 (2014).
Mazzola, E. et al. Recent enhancements to the genetic risk prediction model BRCAPRO. Cancer Inform. 14 (Suppl. 2), 147–157 (2015).
Aschard, H. et al. Inclusion of gene-gene and gene-environment interactions unlikely to dramatically improve risk prediction for complex diseases. Am. J. Hum. Genet. 90, 962–972 (2012).
Ganna, A. & Ingelsson, E. 5 year mortality predictors in 498,103 UK Biobank participants: a prospective population-based study. Lancet 386, 533–540 (2015).
Hosmer, D. W. & Lemeshow, S. Applied Logistic Regression (Wiley, 1989).
DeFilippis, A. P. et al. An analysis of calibration and discrimination among multiple cardiovascular risk scores in a modern multiethnic cohort. Ann. Intern. Med. 162, 266–275 (2015).
Pfeiffer, R. M. & Gail, M. H. Two criteria for evaluating risk prediction models. Biometrics 67, 1057–1065 (2011).
So, H. C. et al. Risk prediction of complex diseases from family history and known susceptibility loci, with applications for cancer screening. Am. J. Hum. Genet. 88, 548–565 (2011).
Park, J. H. et al. Potential usefulness of single nucleotide polymorphisms to identify persons at high cancer risk: an evaluation of seven common cancers. J. Clin. Oncol. 30, 2157–2162 (2012).
Pencina, M. J. et al. Evaluating the added predictive ability of a new marker: from area under the ROC curve to reclassification and beyond. Stat. Med. 27, 157–172; discussion 207–212 (2008).
Pencina, M. J., D'Agostino, R. B., & Steyerberg, E. W. Extensions of net reclassification improvement calculations to measure usefulness of new biomarkers. Stat. Med. 30, 11–21 (2011).
Kerr, K. F. et al. Net reclassification indices for evaluating risk prediction instruments: a critical review. Epidemiology 25, 114–121 (2014).
Pepe, M. S., Janes, H. & Li, C. I. Net risk reclassification P values: valid or misleading? J. Natl Cancer Inst. 106, dju041 (2014).
Stone, N. J. et al. 2013 ACC/AHA guideline on the treatment of blood cholesterol to reduce atherosclerotic cardiovascular risk in adults: a report of the American College of Cardiology/American Heart Association Task Force on Practice Guidelines. Circulation 129, S1–S45 (2014).
Mega, J. L. et al. Genetic risk, coronary heart disease events, and the clinical benefit of statin therapy: an analysis of primary and secondary prevention trials. Lancet 385, 2264–2271 (2015). This study illustrates the utility of PRSs for primary and secondary prevention of CHD by reanalysis of data from randomized trials of statin treatment.
Meads, C. Ahmed, I. & Riley, R. D. A systematic review of breast cancer incidence risk prediction models with meta-analysis of their performance. Breast Cancer Res. Treat. 132, 365–377 (2012).
Burton, H. et al. Public health implications from COGS and potential for risk stratification and screening. Nat. Genet. 45, 349–351 (2013).
Garcia-Closas, M., Gunsoy, N. B. and Chatterjee, N. Combined associations of genetic and environmental risk factors: implications for prevention of breast cancer. J. Natl Cancer Inst. 106, dju305 (2014).
US Preventive Services Task Force. Final Update Summary — Colorectal Cancer: Screening. US Preventive Services Task Force [online], http://www.uspreventiveservicestaskforce.org/Page/Document/UpdateSummaryFinal/colorectal-cancer-screening(Oct 2008; updated Jul 2015).
Garcia-Closas, M. et al. Common genetic polymorphisms modify the effect of smoking on absolute risk of bladder cancer. Cancer Res. 73, 2211–2220 (2013).
Do, R. et al. Exome sequencing identifies rare LDLR and APOA5 alleles conferring risk for myocardial infarction. Nature 518, 102–106 (2015).
Purcell, S. M. et al. A polygenic burden of rare disruptive mutations in schizophrenia. Nature 506, 185–190 (2014).
The UK10K Consortium. The UK10K project identifies rare variants in health and disease. Nature 526, 82–90 (2015).
Mancuso, N. et al. The contribution of rare variation to prostate cancer heritability. Nat. Genet. 48, 30–35 (2016).
Rogowski, W. H., Grosse, S. D. & Khoury, M. J. Challenges of translating genetic tests into clinical and public health practice. Nat. Rev. Genet. 10, 489–495 (2009).
Grimshaw, J. M. et al. Knowledge translation of research findings. Implement Sci. 7, 50 (2012).
Dent, T. et al. Stratified screening for cancer: recommendations and analysis from the COGS project (PHG Foundation, 2014).
Khoury, M. J., Janssens, A. C. & Ransohoff, D. F. How can polygenic inheritance be used in population screening for common diseases? Genet. Med. 15, 437–443 (2013).
Grosse, S. D., Wordsworth, S. & Payne, K. Economic methods for valuing the outcomes of genetic testing: beyond cost-effectiveness analysis. Genet. Med. 10, 648–654 (2008).
Goddard, K. A. et al. Building the evidence base for decision making in cancer genomic medicine using comparative effectiveness research. Genet. Med. 14, 633–642 (2012).
Gonzales, R. et al. A framework for training health professionals in implementation and dissemination science. Acad. Med. 87, 271–278 (2012).
Gail, M. H. et al. Projecting individualized probabilities of developing breast-cancer for white females who are being examined annually. J. Natl Cancer Inst. 81, 1879–1886 (1989). The authors develop the first risk-prediction model for breast cancer and define the methodology for absolute risk estimation using external information on rates of disease and competing mortality in the underlying population.
Acknowledgements
The research was supported by intramural funding from the National Cancer Institute, which is part of the US National Institutes of Health, and a Bloomberg Distinguished Professorship endowment from Johns Hopkins University.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information S1 (table)
Study designs and methods used for model building, validation and assessment ofclinical utility in case studies (PDF 71 kb)
Glossary
- Penetrance
-
The proportion of individuals in a population with a genetic variant who develop the disease associated with that variant. Common single-nucleotide polymorphisms (SNPs) are referred to as low-penetrant, as risk alleles typically confer modest risk.
- Polygenic disease
-
A disease caused by a large number of underlying susceptibility genes.
- Prospective cohort studies
-
Studies that collect information on potential risk factors (based on questionnaires, devices and biological samples) in a sample of healthy individuals and then longitudinally follow them to record future disease incidence. Information on risk factors can be updated longitudinally over time.
- Heritability
-
The proportion of phenotypic variation attributed to genetic variation among individuals in a population.
- Polygenic risk score
-
(PRS). A score for predicting disease risk, calculated as the weighted sum of risk alleles with the weights specified by association coefficients.
- Ascertainment
-
Non-random selection of study participants, often arising in genetic studies owing to the selection of subjects based on personal and/or family history of disease.
- Ethnically admixed samples
-
Samples from subjects who have inherited genetic materials from two or more previously separated populations.
- Confounding
-
A false association between a disease and an exposure caused by the presence of a risk factor for the disease that is correlated with the exposure.
- Case–control studies
-
Studies that sample subjects with and without a disease and collect information on potential risk factors in a retrospective fashion.
- Incidence rates
-
(Also known as hazard rates). The rates at which new diseases are observed in a population during a specific time interval (for example, between specific ages).
- Proportional hazard model
-
A model for incidence rate that assumes a multiplicative effect of risk factors on the age-specific incidence rate of a disease.
- Hazard ratio
-
The ratio of hazard rates (also known as incidence rates) between groups of subjects with different risk factor profiles.
- Incident case–control studies
-
Case–control studies that aim to recruit representative samples of new cases that arise in a population during a specified time period.
- Odds ratios
-
Quantitative measures of the strength of association between a binary disease end point and risk factors that can be estimated by logistic regression models.
- Prevalent cases
-
The number of individuals with a disease condition in a population at a given time point.
- Selection bias
-
Bias in risk estimates due to non-random selection of study participants. Case–control studies can be particularly prone to selection bias, as the likelihood of participation may be affected by both disease status and risk factor history.
- Logit
-
The transformation log{p/(1−p)} where p is the probability of disease occurrence in a population.
- Liability score
-
A score that represents the underlying progression of a disease through the accumulation of risks on a continuous scale. The risk of binary disease outcomes can be modelled by assuming the existence of an underlying, normally distributed liability score that leads to the manifestation of disease when it exceeds a threshold.
- Probit
-
The transformation Φ−1(p) where Φ−1 denotes the inverse of the cumulative distribution function for a standard normal random variable and p is the probability of disease occurrence in a population.
- Additive interaction
-
The presence of non-additive effects of multiple risk factors on the risk of a disease. Absence of additive interaction indicates that the risk difference parameter associated with one factor does not vary with that of other factors.
- Genome-wide significance
-
A stringent level of statistical significance, often set at p − val = 5 × 108 for genome-wide association studies (GWAS) of common variants, for the avoidance of false positives.
- Linkage disequilibrium
-
(LD). The non-random association of alleles at different loci, frequently measured by r2, the square of the genotypic correlation between two single-nucleotide polymorphisms (SNPs).
- Pleiotropic analysis
-
Analysis to identify variants associated with two or more distinct phenotypic traits.
- Recall bias
-
Bias in risk estimates that could arise in case–control studies owing to differential recall or reporting of disease status by study participants.
- Multiplicative interactions
-
Presence of the non-multiplicative effects of multiple factors on the risk of a disease. Absence of multiplicative interaction implies that the risk ratio parameter associated with one factor does not depend on that of the other factors.
Rights and permissions
About this article
Cite this article
Chatterjee, N., Shi, J. & García-Closas, M. Developing and evaluating polygenic risk prediction models for stratified disease prevention. Nat Rev Genet 17, 392–406 (2016). https://doi.org/10.1038/nrg.2016.27
Published:
Issue Date:
DOI: https://doi.org/10.1038/nrg.2016.27
This article is cited by
-
Comprehensive analysis of a tryptophan metabolism-related model in the prognostic prediction and immune status for clear cell renal carcinoma
European Journal of Medical Research (2024)
-
Recent advances in polygenic scores: translation, equitability, methods and FAIR tools
Genome Medicine (2024)
-
Principles and methods for transferring polygenic risk scores across global populations
Nature Reviews Genetics (2024)
-
Improving fine-mapping by modeling infinitesimal effects
Nature Genetics (2024)
-
Progress and Implications from Genetic Studies of Bipolar Disorder
Neuroscience Bulletin (2024)