Abstract
Magneto-optical trapping and sub-Doppler cooling have been essential to most experiments with quantum degenerate gases, optical lattices, atomic fountains and many other applications. A broad set of new applications await ultracold molecules1, and the extension of laser cooling to molecules has begun2,3,4,5,6. A magneto-optical trap (MOT) has been demonstrated for a single molecular species, SrF7,8,9, but the sub-Doppler temperatures required for many applications have not yet been reached. Here we demonstrate a MOT of a second species, CaF, and we show how to cool these molecules to 50 μK, well below the Doppler limit, using a three-dimensional optical molasses. These ultracold molecules could be loaded into optical tweezers to trap arbitrary arrays10 for quantum simulation11, launched into a molecular fountain12,13 for testing fundamental physics14,15,16,17,18, and used to study collisions and chemistry19 between atoms and molecules at ultracold temperatures.
Similar content being viewed by others
Main
We first focus on the MOT, which is likely to become a workhorse for cooling molecules just as it is for atoms. Previously, only SrF had been trapped this way. For SrF, two types of MOT have been developed, a d.c. MOT where the lifetime was short and the temperature high7,8, and a radiofrequency (rf) MOT where longer lifetimes and lower temperatures were achieved9,20. In the rf MOT, optical pumping into dark states is avoided by rapidly reversing the magnetic field and the handedness of the MOT laser. It has been suggested that the detrimental effects of dark states can also be avoided in the d.c. MOT by driving the cooling transition with two oppositely polarized laser components, one red- and one blue-detuned21. We use this dual-frequency technique to make a d.c. MOT of CaF and find that it works just as well as the rf MOT. Thus, we demonstrate a MOT of a second molecular species, which is important for applications of ultracold molecules, and also verify the effectiveness of this new scheme.
Figure 1 illustrates the experiment, which is described in more detail in Methods. A pulse of CaF molecules produced at time t = 0 is emitted from a cryogenic buffer gas source, then decelerated by frequency-chirped counter-propagating laser light, and finally captured in the MOT between t = 16 and 40 ms. Figure 2a shows the molecules in the MOT, imaged on a charge-coupled device (CCD) camera by collecting their fluorescence. We estimate that there are (1.3 ± 0.3) × 104 molecules in this MOT (see Methods), with a peak density of n = (1.6 ± 0.4) × 105 cm−3. These are similar to the best values achieved for SrF20. To determine the MOT lifetime, we fit the decay of its fluorescence to a single exponential. Figure 2b shows this lifetime as a function of the scattering rate. The lifetime is typically 100 ms and decreases with higher scattering rate, suggesting loss by optical pumping to a state not addressed by the lasers. We do not see the precipitous drop in lifetime observed at low scattering rate in the d.c. MOT of SrF9. To watch the molecules oscillate in the trap, we push them radially by pulsing on the slowing laser for 500 μs at t = 50 ms, and then image them for 1 ms after a fixed delay, τ. Figure 2c shows ρ(τ), the mean radial displacement of the molecules as a function of this delay. Describing ρ(τ) by the damped harmonic oscillator equation, ρ′′ + βρ′ + ω2ρ = 0, we determine an oscillation frequency of ω = 2π × (94.4 ± 0.2) Hz and a damping constant of β = 390 ± 4 s−1. Similar values were found in SrF MOTs (refs 8,9). The oscillation frequency is within 20% of the value predicted from rate-equation simulations21, where it was established that the dual-frequency mechanism is mainly responsible for the trapping force. By contrast, the damping constant is 14 times smaller than predicted by these simulations. The reduced damping may be caused by polarization-gradient forces which oppose the Doppler cooling force in the molecule MOT and dominate at low velocities22. This is in contrast to normal atomic MOTs, where both forces damp the motion.
a, Fluorescence image of the MOT, averaged over 100 shots with 50 ms exposure starting at t = 40 ms. Also shown are the 1D axial and radial density profiles obtained by integrating the image along each axis. Gaussian fits to these yield the axial and radial centres and r.m.s. widths, and associated 1σ standard deviations. b, MOT lifetime versus scattering rate. The lifetime, and its 1σ standard deviation, are found by fitting the decay of the MOT fluorescence to an exponential decay. The scattering rate is controlled via the intensity of the main MOT laser and determined as described in Methods. c, Radial displacement of the cloud versus time after pushing it. Each point is obtained by summing 50 images each of 1 ms exposure. Solid line: fit to the motion of a damped harmonic oscillator. d, Temperature measurement using the free-expansion method. The mean squared width of the cloud is plotted against the square of the free-expansion time, for (i) the axial and (ii) the radial directions. Each point is obtained by summing 50 images each of 1 ms exposure. The top row shows typical images. Solid lines: quadratic fit to the data (see Methods). Where error bars are not visible in b–d, they are smaller than the point size.
We turn now to the temperature, which we measure by turning off the MOT and then imaging the cloud after various free-expansion times τ. Figure 2d shows the mean squared widths in the axial and radial directions versus τ2, together with fits to the model described in Methods, which give temperatures of Tz = 11.0 ± 0.3 mK and Tρ = 12.3 ± 0.5 mK. A 10–20% variation between the two directions is typical of all our data. Hereafter, we use the geometric mean temperature, T = Tρ2/3Tz1/3, giving T = 11.4 ± 0.3 mK in this case. This temperature is similar to that observed in SrF MOTs (refs 7,8,9). We may compare this to the Doppler temperature (see Methods), which for our intensity and detuning is 830 μK, 14 times lower than measured. The elevated temperature is consistent with the reduced damping constant already noted above.
This MOT has a phase-space density of ρ = h3n/(2πmkBT)3/2 = (1.5 ± 0.4) × 10−15. We now show how we increase this by lowering the temperature. In the rf MOT of SrF, lowering the laser intensity reduced the temperature from 10 mK to 400 μK without loss of molecules9, and even to 250 μK (ref. 20), although at substantial cost to the number and density. This method was not useful for cooling the d.c. MOT of SrF because of its short lifetime at low intensity. By contrast, the lifetime of our d.c. CaF MOT increases at lower intensity, so this method is open to us. We decrease the power of the main MOT laser between t = 50 and 70 ms, hold it for 5 ms, then measure the MOT temperature. Figure 3 shows both the temperature and the size of the MOT versus final intensity, together with the expected Doppler temperature, TD (see equation (6) in Methods). At 9.2 mW cm−2 we find a minimum of 960 μK, which is about 4TD. Extending the ramp to lower intensities increases the temperature again. Optimization of the detuning and the bias magnetic field lowers the minimum temperature to about 500 μK, but we do not pursue that further here. Figure 3 shows that the MOT size first decreases as the intensity decreases, but then grows once the intensity is below 50 mW cm−2. At the minimum MOT size the density is 2.5 × 105 cm−3. The maximum phase-space density in the MOT is obtained near 25 mW cm−2, where it is ρ = (3.4 ± 0.9) × 10−14, almost the same as the compressed rf MOT of SrF20. This ability to reach similar temperatures and phase-space densities in a d.c. MOT as in an rf MOT is an important advance.
Temperature (blue filled circles) and geometric mean r.m.s. width of the MOT (red open circles) versus total intensity of the MOT laser at the end of the ramp. Dashed line: Doppler temperature (Methods, equation (6)). Error bars are 1σ standard deviations of fits similar to those in Fig. 2d, and are smaller than the points.
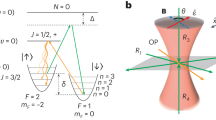
To lower T and increase ρ further, we transfer into a three-dimensional blue-detuned optical molasses where we find remarkably effective sub-Doppler cooling. Sub-Doppler cooling usually occurs in a light field with non-uniform polarization, where optical pumping between sub-levels sets up a friction force at low velocity much stronger than the Doppler force23,24. Details of the polarization-gradient cooling mechanism depend on the ground- and excited-state angular momenta, F and F′. In our case F ≥ F′ (Supplementary Fig. 1), so there are dark ground states that cannot couple to the local laser polarization, and bright states that can. A bright-state molecule loses kinetic energy on moving into blue-detuned light, and pumps to a dark state when the light has sufficient intensity. The dark molecule moves through changing polarization and switches non-adiabatically back to a bright state, preferentially at low intensity where the energies of dark and bright states are similar. This cooling method25, often called ‘grey molasses’, has been used to cool atoms. Magnetically induced laser cooling24 is similar, but uses a magnetic field instead of polarization gradients so that Larmor precession transfers molecules between dark and bright sub-levels. This mechanism has been used to cool molecules in one dimension2,6, but sub-Doppler temperatures were not reached.
The procedure we use to transfer from MOT to molasses is detailed in Methods. Figure 4a shows the molecules cooling in the molasses towards a base value of ∼100 μK, which is half the Doppler limit. The 1/e time constant is 361 ± 2 μs, implying a damping constant of 1,400 s−1. We find that the base temperature is sensitive to all three components of the background magnetic field. Figure 4b shows the variation of temperature versus one field component after optimizing the other two. We find a quadratic dependence on magnetic field, consistent with the model outlined in Methods. Figure 4c shows the temperature versus the laser intensity during the molasses phase. The temperature has a minimum of 46 μK near 100 mW cm−2, increases rapidly at lower intensities and more gradually at higher intensities. The temperature dependencies shown in Fig. 4a–c are all similar to those observed in atomic grey molasses25,26, so we conclude that the cooling process is indeed the grey molasses mechanism. Figure 4d shows the thermal expansion of a cloud after cooling for 5 ms in a 93 mW cm−2 molasses. The average of six such temperature measurements gives T = 55 ± 2 μK. To within our 5% uncertainty, no molecules are lost between the initial MOT and this ultracold cloud, excepting loss due to the MOT lifetime. The cloud now has n = (0.8 ± 0.2) × 105 cm−3 and ρ = (2.4 ± 0.6) × 10−12, 1,500 times higher than in the initial MOT and 40 times higher than previously achieved for laser-cooled molecules. It also exceeds that obtained by other molecule cooling methods that have reached sub-millikelvin temperatures13,27.
a, Temperature versus time in molasses, when intensity is 460 mW cm−2. Solid line: fit to an exponential decay towards a base temperature, giving a 1/e time constant of 361 ± 2 μs. Dashed line: minimum Doppler temperature. b, Temperature versus magnetic field produced at the cloud by one of three shim coils during the molasses phase. Intensity is 460 mW cm−2 and molasses hold time is 5 ms. Solid line: quadratic fit giving curvature of 5,740 ± 30 μK mT−2. c, Temperature versus molasses intensity, with molasses hold time of 5 ms. d, Temperature measurement after a period of 5 ms in a molasses. Intensity is 93 mW cm−2. Inset: images at each time point, from which cloud sizes in the axial (red) and radial (blue) directions are obtained from Gaussian fits. Error bars are 1σ standard deviations. Solid lines: straight line fits. Temperature from six repeated measurements is 55 ± 2 μK.
Single molecules from this ultracold gas could be loaded into low-lying motional states of microscopic optical tweezer traps and formed into regular arrays10 for quantum simulation11. They could be loaded into chip-based electric traps and coupled to transmission line resonators, forming the elements of a quantum processor28. By mixing the molecules with atoms, it will be possible to explore collisions, chemistry19 and sympathetic cooling29 in the ultracold regime. Our cooled molecules could be used to search for a time variation of the electron-to-proton mass ratio16, while application of the methods to other amenable molecules will advance measurements of electric dipole moments12,17 and nuclear anapole moments18. All these applications are feasible with the phase-space densities achieved in the present work. For other applications, it is desirable to increase the density towards 1012 cm−3, as often achieved for ultracold atomic gases. Major increases in density are likely to come by compressing the MOT20 and from more efficient slowing methods30 along with transverse cooling2 prior to slowing. The resulting dense, ultracold sample would be an ideal starting point for sympathetic or evaporative cooling to quantum degeneracy.
Methods
Laser cooling scheme.
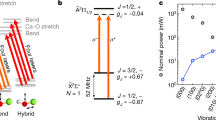
Supplementary Fig. 1 shows the energy levels in CaF relevant to the experiment, and the branching ratios between them. The two excited states, A2Π1/2 and B2Σ+, have decay rates of Γ = 2π × 8.3 MHz (ref. 31) and 2π × 6.3 MHz (ref. 32), respectively. The main slowing laser ( ) drives the B2Σ+(v′ = 0) ← X2Σ+(v′′ = 0) transition at 531.0 nm. Population that leaks to v′′ = 1 during the slowing is returned to the cooling cycle by a repump slowing laser (
) drives the B2Σ+(v′ = 0) ← X2Σ+(v′′ = 0) transition at 531.0 nm. Population that leaks to v′′ = 1 during the slowing is returned to the cooling cycle by a repump slowing laser ( ) that drives the A2Π1/2(v′ = 0) ← X2Σ+(v′′ = 1) transition at 628.6 nm. The hyperfine interval of about 20 MHz in the lowest level of the B2Σ+ excited state is inconvenient for making a MOT, and our modelling21 suggests that a higher capture velocity is obtained by using the A2Π1/2 state where the hyperfine structure is unresolved. The MOT uses four lasers, denoted
) that drives the A2Π1/2(v′ = 0) ← X2Σ+(v′′ = 1) transition at 628.6 nm. The hyperfine interval of about 20 MHz in the lowest level of the B2Σ+ excited state is inconvenient for making a MOT, and our modelling21 suggests that a higher capture velocity is obtained by using the A2Π1/2 state where the hyperfine structure is unresolved. The MOT uses four lasers, denoted  , to drive the A2Π1/2(v′ = j) ← X2Σ+(v′′ = i) transitions. These are
, to drive the A2Π1/2(v′ = j) ← X2Σ+(v′′ = i) transitions. These are  at 606.3 nm (called the main MOT laser in the main paper),
at 606.3 nm (called the main MOT laser in the main paper),  at 628.6 nm,
at 628.6 nm,  at 628.1 nm and
at 628.1 nm and  at 627.7 nm. All lasers drive the P(1) component so that rotational branching is forbidden by the electric dipole selection rules33. Each of the levels of the X state shown in Supplementary Fig. 1 is split into four components due to the spin–rotation and hyperfine interactions. The splittings for the v′′ = 0 state are shown in the figure, while those for the other states are similar. Radiofrequency (rf) sidebands are added to each laser (see discussion of Supplementary Fig. 2 below) to ensure that all these components are addressed. The frequency component of
at 627.7 nm. All lasers drive the P(1) component so that rotational branching is forbidden by the electric dipole selection rules33. Each of the levels of the X state shown in Supplementary Fig. 1 is split into four components due to the spin–rotation and hyperfine interactions. The splittings for the v′′ = 0 state are shown in the figure, while those for the other states are similar. Radiofrequency (rf) sidebands are added to each laser (see discussion of Supplementary Fig. 2 below) to ensure that all these components are addressed. The frequency component of  that addresses the upper F = 1 state has the opposite circular polarization to the other three. Thus, when the overall detuning of
that addresses the upper F = 1 state has the opposite circular polarization to the other three. Thus, when the overall detuning of  is negative, as in Supplementary Fig. 1, the F = 2 component is driven simultaneously by two frequencies with opposite circular polarization, one red- and the other blue-detuned. This configuration produces the dual-frequency MOT described in ref. 21. The simulations presented there suggest that most of the confining force in the MOT is due to this dual-frequency effect.
is negative, as in Supplementary Fig. 1, the F = 2 component is driven simultaneously by two frequencies with opposite circular polarization, one red- and the other blue-detuned. This configuration produces the dual-frequency MOT described in ref. 21. The simulations presented there suggest that most of the confining force in the MOT is due to this dual-frequency effect.
Set-up and procedures.
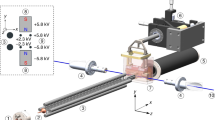
Figure 1 illustrates the experiment. A short pulse of CaF molecules is produced at t = 0 by laser ablation of a Ca target in the presence of SF6. These molecules are entrained in a continuous 0.5 sccm flow of helium gas cooled to 4 K, producing a pulsed beam with a typical mean forward velocity of 150 m s−1. The beam exits the source through a 3.5-mm-diameter aperture at x′ = 0, passes into the slowing chamber through an 8-mm-diameter aperture at x′ = 15 cm, and then through a 20-mm-diameter, 200-mm-long differential pumping tube whose entrance is at x′ = 90 cm, reaching the MOT at x′ = 130 cm. The pressure in the slowing chamber is 6 × 10−8 mbar, and in the MOT chamber is 2 × 10−9 mbar. The experiment runs at a repetition rate of 2 Hz.
The beam is slowed using the methods described in ref. 34. The slowing light is combined into a single beam, containing 100 mW of  and 100 mW of
and 100 mW of  . This beam has a 1/e2 radius of 9 mm at the MOT, converging to 1.5 mm at the source. The changes in frequency and intensity of
. This beam has a 1/e2 radius of 9 mm at the MOT, converging to 1.5 mm at the source. The changes in frequency and intensity of  are illustrated in the timing diagram in Supplementary Fig. 3. The initial frequency of
are illustrated in the timing diagram in Supplementary Fig. 3. The initial frequency of  is set to a detuning of −270 MHz so that molecules moving at 145 m s−1 are Doppler-shifted into resonance. The light is switched on at t = 2.5 ms and frequency chirped at a rate of 23 MHz ms−1 between 3.4 ms and 15 ms. The frequency of
is set to a detuning of −270 MHz so that molecules moving at 145 m s−1 are Doppler-shifted into resonance. The light is switched on at t = 2.5 ms and frequency chirped at a rate of 23 MHz ms−1 between 3.4 ms and 15 ms. The frequency of  is not chirped, which differs from the procedure used previously34. Instead, it is frequency broadened as described below, and its centre frequency detuned by −200 MHz. Both
is not chirped, which differs from the procedure used previously34. Instead, it is frequency broadened as described below, and its centre frequency detuned by −200 MHz. Both  and
and  are turned off at t = 15 ms. A 0.5 mT magnetic field, directed along y′, is applied throughout the slowing region and is constantly on.
are turned off at t = 15 ms. A 0.5 mT magnetic field, directed along y′, is applied throughout the slowing region and is constantly on.
The MOT light is combined into a single beam containing 80 mW of  , 100 mW of
, 100 mW of  , 10 mW of
, 10 mW of  and 0.5 mW of
and 0.5 mW of  . This beam is expanded to a 1/e2 radius of 8.1 mm, and then passed through the centre of the MOT chamber six times, first along y, then x, then z, then −z, then −x, then −y. In this paper, intensity refers always to the full intensity at the MOT due to
. This beam is expanded to a 1/e2 radius of 8.1 mm, and then passed through the centre of the MOT chamber six times, first along y, then x, then z, then −z, then −x, then −y. In this paper, intensity refers always to the full intensity at the MOT due to  , which is six times the intensity of the
, which is six times the intensity of the  beam entering along y. The light is circularly polarized each time it enters the chamber, and returned to linear polarization each time it exits, following ref. 7. For any given frequency component of the light, the handedness is the same for each pass in the horizontal plane, but opposite in the vertical direction. All MOT lasers have zero detuning, apart from
beam entering along y. The light is circularly polarized each time it enters the chamber, and returned to linear polarization each time it exits, following ref. 7. For any given frequency component of the light, the handedness is the same for each pass in the horizontal plane, but opposite in the vertical direction. All MOT lasers have zero detuning, apart from  , which has variable detuning Δ. The MOT field gradient, which is 2.9 mT cm−1 in the axial direction, is produced by a pair of anti-Helmholtz coils inside the vacuum chamber. The MOT vanishes when this field gradient is reversed or turned off. Three bias coils, with axes along x′, y′ and z, are used to tune the magnetic field in the MOT region to trap the most molecules. The MOT fluorescence at 606 nm is collected by a lens inside the vacuum chamber and imaged onto a CCD camera with a magnification of 0.5. An interference filter blocks background light at other wavelengths.
, which has variable detuning Δ. The MOT field gradient, which is 2.9 mT cm−1 in the axial direction, is produced by a pair of anti-Helmholtz coils inside the vacuum chamber. The MOT vanishes when this field gradient is reversed or turned off. Three bias coils, with axes along x′, y′ and z, are used to tune the magnetic field in the MOT region to trap the most molecules. The MOT fluorescence at 606 nm is collected by a lens inside the vacuum chamber and imaged onto a CCD camera with a magnification of 0.5. An interference filter blocks background light at other wavelengths.
Supplementary Fig. 2 shows the frequency spectrum of each laser. For  , a 73.5 MHz electro-optic modulator (EOM) generates the sidebands that drive the F = 2, F = 0 and lower F = 1 states, while a 48 MHz acousto-optic modulator (AOM) generates the light of opposite polarization to address the upper F = 1 state4. The rf sidebands for
, a 73.5 MHz electro-optic modulator (EOM) generates the sidebands that drive the F = 2, F = 0 and lower F = 1 states, while a 48 MHz acousto-optic modulator (AOM) generates the light of opposite polarization to address the upper F = 1 state4. The rf sidebands for  ,
,  ,
,  and
and  are generated using 24 MHz EOMs. We spectrally broaden
are generated using 24 MHz EOMs. We spectrally broaden  to approximately 500 MHz using three consecutive EOMs, one driven at 72 MHz, one at 24 MHz and one at 8 MHz. For each laser, we find the frequency that maximizes the laser-induced fluorescence (LIF) from the molecular beam when that laser is used as an orthogonal probe. These frequencies define zero detuning for each laser, with the exception of
to approximately 500 MHz using three consecutive EOMs, one driven at 72 MHz, one at 24 MHz and one at 8 MHz. For each laser, we find the frequency that maximizes the laser-induced fluorescence (LIF) from the molecular beam when that laser is used as an orthogonal probe. These frequencies define zero detuning for each laser, with the exception of  . For
. For  , we find that there is a critical frequency where an observable MOT is only formed in half of all shots. These large fluctuations in molecule number seem to come from a strong sensitivity to the approximately 1 MHz frequency fluctuations of
, we find that there is a critical frequency where an observable MOT is only formed in half of all shots. These large fluctuations in molecule number seem to come from a strong sensitivity to the approximately 1 MHz frequency fluctuations of  at this frequency. We define this critical frequency to be zero detuning, Δ = 0. At Δ = −0.25Γ the MOT is stable, and at Δ = 0.25Γ there is never a MOT (recall that Γ = 2π × 8.3 MHz). We find that this method is more sensitive and reproducible than maximizing the LIF. When
at this frequency. We define this critical frequency to be zero detuning, Δ = 0. At Δ = −0.25Γ the MOT is stable, and at Δ = 0.25Γ there is never a MOT (recall that Γ = 2π × 8.3 MHz). We find that this method is more sensitive and reproducible than maximizing the LIF. When  is used as an orthogonal probe, the LIF is maximized at Δ = 0.25Γ ± 0.5Γ. We observe MOTs when 0 > Δ > −1.8Γ, and we load the most molecules when Δ = −0.75Γ, the value used for all data in this paper.
is used as an orthogonal probe, the LIF is maximized at Δ = 0.25Γ ± 0.5Γ. We observe MOTs when 0 > Δ > −1.8Γ, and we load the most molecules when Δ = −0.75Γ, the value used for all data in this paper.
The complete procedure for cooling to the lowest temperatures is illustrated in Supplementary Fig. 3. The intensity of  is ramped down by a factor 100 to 4.6 mW cm−2 between t = 50 and 70 ms to lower the MOT temperature (see Fig. 3), while keeping the detuning at −0.75Γ. At t = 72 ms, the shim coil currents are switched from those that load the most molecules in the MOT to those that give the lowest temperature in the molasses, thereby optimizing both molecule number and temperature. The MOT coils are turned off at t = 75 ms. At t = 76 ms we jump
is ramped down by a factor 100 to 4.6 mW cm−2 between t = 50 and 70 ms to lower the MOT temperature (see Fig. 3), while keeping the detuning at −0.75Γ. At t = 72 ms, the shim coil currents are switched from those that load the most molecules in the MOT to those that give the lowest temperature in the molasses, thereby optimizing both molecule number and temperature. The MOT coils are turned off at t = 75 ms. At t = 76 ms we jump  to a detuning of +2.5Γ, and to a (variable) higher intensity, to form the molasses (see Fig. 4c). After allowing the molasses to act for a variable time (see Fig. 4a)
to a detuning of +2.5Γ, and to a (variable) higher intensity, to form the molasses (see Fig. 4c). After allowing the molasses to act for a variable time (see Fig. 4a)  is turned off so that the cloud can expand for a variable time (see Fig. 4d) before it is imaged for 1 ms at full intensity with Δ = −0.75Γ.
is turned off so that the cloud can expand for a variable time (see Fig. 4d) before it is imaged for 1 ms at full intensity with Δ = −0.75Γ.
Scattering rate and saturation intensity.
Despite the complexity of the multi-level molecule, it is useful to use a simple rate model12 to predict some of the properties of the MOT, as done previously9. In this model, ng ground states are coupled to ne excited states, and the steady-state scattering rate is found to be

Here, Ij is the intensity of the light driving transition j, Δj is its detuning, and Is, j = πhcΓ/(3λj3) is the two-level saturation intensity for a transition of wavelength λj. In applying this model we need to include the ng = 24 Zeeman sub-levels of the v = 0 and v = 1 ground states, all of which are coupled to the same ne = 4 levels of the excited state. The v = 2 and v = 3 ground states can be neglected since they are repumped through other excited states with sufficient intensity that their populations are always small. Because  is detuned whereas
is detuned whereas  is not, and because the
is not, and because the  intensity is always higher than the
intensity is always higher than the  intensity, the transitions driven by
intensity, the transitions driven by  make only a small contribution to the sum in equation (1) and we neglect them. This is a reasonable approximation at full
make only a small contribution to the sum in equation (1) and we neglect them. This is a reasonable approximation at full  power, and a very good approximation once the power of
power, and a very good approximation once the power of  is ramped down. The 12 transitions driven by
is ramped down. The 12 transitions driven by  have common values for Δ and Is, and the total intensity, I00, is divided roughly equally between them so that we can write Ij = I00/(ng/2). With these simplifications, we can rewrite equation (1) in the form
have common values for Δ and Is, and the total intensity, I00, is divided roughly equally between them so that we can write Ij = I00/(ng/2). With these simplifications, we can rewrite equation (1) in the form

where

and

Writing seff = I00/Is, eff, we find an effective saturation intensity of

We have measured the scattering rate at various  intensities, using the method described in the next paragraph. These measurements show that the scattering rate does indeed follow the form of equation (2), but suggest that Γeff is roughly a factor of 2 smaller than equation (3) while Is, eff is roughly a factor of 2 smaller than equation (5). However, the determination of Is, eff is sensitive to the value of the detuning, which is imperfectly defined for the multi-level molecule. Fortunately, none of our conclusions depend strongly on knowing the values of either Γeff or Is, eff.
intensities, using the method described in the next paragraph. These measurements show that the scattering rate does indeed follow the form of equation (2), but suggest that Γeff is roughly a factor of 2 smaller than equation (3) while Is, eff is roughly a factor of 2 smaller than equation (5). However, the determination of Is, eff is sensitive to the value of the detuning, which is imperfectly defined for the multi-level molecule. Fortunately, none of our conclusions depend strongly on knowing the values of either Γeff or Is, eff.
Number of molecules.
To estimate the number of molecules in the MOT, we need to know the photon scattering rate per molecule. We measure this by switching off  and recording the decay of the fluorescence as molecules are optically pumped into v′′ = 2. The decay is exponential with a time constant of 570 ± 10 μs at full
and recording the decay of the fluorescence as molecules are optically pumped into v′′ = 2. The decay is exponential with a time constant of 570 ± 10 μs at full  intensity. Combining this with our measured branching ratio of (8.4 ± 0.5) × 10−4 to v′′ = 2 (ref. 35) gives a scattering rate of 2.1 × 106 s−1. This is about 2.5 times below the value predicted by equation (2). The detection efficiency is 1.6 ± 0.2% and is determined by numerical ray tracing together with the measured transmission of the optics and the specified quantum efficiency of the camera. For the MOT shown in Fig. 2a, the detected photon count rate at the camera is 4.3 × 108 s−1. From these values, we estimate that there are (1.3 ± 0.3) × 104 molecules in this MOT. From one day to the next, using nominally identical parameters, and after optimization of the source, the molecule number varies by about 25%. We assign this uncertainty to all molecule number estimates in this paper.
intensity. Combining this with our measured branching ratio of (8.4 ± 0.5) × 10−4 to v′′ = 2 (ref. 35) gives a scattering rate of 2.1 × 106 s−1. This is about 2.5 times below the value predicted by equation (2). The detection efficiency is 1.6 ± 0.2% and is determined by numerical ray tracing together with the measured transmission of the optics and the specified quantum efficiency of the camera. For the MOT shown in Fig. 2a, the detected photon count rate at the camera is 4.3 × 108 s−1. From these values, we estimate that there are (1.3 ± 0.3) × 104 molecules in this MOT. From one day to the next, using nominally identical parameters, and after optimization of the source, the molecule number varies by about 25%. We assign this uncertainty to all molecule number estimates in this paper.
Temperature.
In the standard theory of Doppler cooling, the equilibrium temperature is reached when the Doppler cooling rate equals the heating rate due to the randomness of photon scattering. Because both rates are proportional to the scattering rate, the multi-level system is expected to have the same Doppler-limited temperature as a simple two-level system. This is

We measure the temperature using the standard ballistic expansion method. We turn off the magnetic field and  , then turn
, then turn  back on after a delay time τ to image the cloud using a 1 ms exposure. For a thermal velocity distribution and an initial Gaussian density distribution of r.m.s. width σ0, the density distribution after a free-expansion time τ is a Gaussian with a mean squared width given by σ2 = σ02 + kBTτ2/m, where m is the mass of the molecule. Thus, a plot of σ2 against τ2 should be a straight line whose gradient gives the temperature.
back on after a delay time τ to image the cloud using a 1 ms exposure. For a thermal velocity distribution and an initial Gaussian density distribution of r.m.s. width σ0, the density distribution after a free-expansion time τ is a Gaussian with a mean squared width given by σ2 = σ02 + kBTτ2/m, where m is the mass of the molecule. Thus, a plot of σ2 against τ2 should be a straight line whose gradient gives the temperature.
There are several potential sources of systematic error in this measurement which we address here. First we consider whether the finite exposure time of 1 ms introduces any systematic error. While the image is being taken using the MOT light, the magnetic quadrupole field is off. Thus, there is no trapping force, but there is a velocity-dependent force which, according to ref. 22, may either accelerate or decelerate the molecules depending on whether their velocity is above or below some critical value. To quantify the effect, we have made temperature measurements using various exposure times. For a 12 mK cloud we estimate that the 1 ms exposure time results in an overestimate of the temperature by about 0.3 ± 0.5 mK. For a 50 μK cloud, the overestimate is about 0 ± 0.3 μK. These corrections are insignificant.
With a MOT that is centred on the light beams, the intensity of the imaging light is higher in the middle of the cloud than it is in the wings, making the cloud look artificially small. This skews the temperature towards lower values because the effect is stronger for clouds that have expanded. The error is mitigated by using laser beams that are considerably larger than the cloud and that strongly saturate the rate of fluorescence. Using a three-dimensional model of the MOT beams and equations (2) and (5) for the dependence of the scattering rate on intensity, we have simulated the imaging to determine the functional form of σ2(τ2) expected in our experiment. The model suggests that a simple τ4 correction—σ2 = σ02 + kBTτ2/M + a2τ4—will fit well to all our ballistic expansion data, will recover the correct temperature, and will give a significantly non-zero a2 for our T ∼ 10 mK data, but a negligible one for all our data where T ≤ 1 mK. We have investigated this in detail using σ2 versus τ2 data with a higher density of data points (12 points, instead of our usual 6). For a hot MOT (T ∼ 12 mK), we see a nonlinear expansion and find that a fit to the above ‘quadratic model’ gives a temperature that is typically about 10% higher than a linear fit. For an ultracold molasses (T ∼ 100 μK) linear fits to the earliest six points and the latest six points of the ballistic expansion give the same temperature to within the statistical uncertainty of 4%. For the data in Figs 2 and 3 we use the quadratic model, while for the data in Fig. 4 we use the linear model. We determine the minimum temperature of 55 ± 2 μK from the weighted mean of six measurements at a molasses intensity of 93 mW cm−2. None of these six datasets show a statistically significant nonlinearity in the plots of σ2 versus τ2, so we use the linear model. Using the quadratic model instead of the linear one changes the temperature to 66 ± 7 μK.
The magnification of the imaging system may not be perfectly uniform across the field of view. This can alter the apparent size of the cloud as it drops under gravity and expands. We have measured the magnification across the whole field of view that is relevant to our data and find that the uniformity is better than 3%. At this level, the effect on the temperatures is negligible.
Finally, a non-uniform magnetic field can result in an expansion that does not accurately reflect the temperature. A magnetic field gradient accelerates the molecules, and since the magnetic moment depends on the hyperfine component and Zeeman sub-level, this acceleration is different for different molecules. We calculate that this effect contributes a velocity spread less than 0.5 cm s−1 after 10 ms of free expansion. This is negligible, even for a 50 μK cloud. The second derivative of the magnetic field causes a differential acceleration across the cloud, but this effect is even smaller.
The temperature reached in the molasses depends on the background magnetic field, as shown in Fig. 4a. The sub-Doppler cooling mechanism relies on optical pumping into a dark state near the intensity maxima of the light field, and motion-induced non-adiabatic transitions back to a bright state near the intensity minima25,36. This process becomes ineffective if the Larmor precession time between bright and dark states is comparable to the time taken by a molecule to move from a minimum to a maximum. Therefore, in the presence of a magnetic field B, the cooling will not reduce the mean velocity much below v ≈ μλB/(4h), where μ is the magnetic moment and λ is the wavelength. Converting from mean speed to temperature we find the relation T ≈ (πm/8kB)(μλB/4h)2. Taking μ ≈ μB we obtain T = aB2 with a ≈ 12,500 μK mT−2. Our data fits well to this quadratic dependence on B and gives a = 5,740 ± 30 μK mT−2, consistent with our model, given its approximate nature.
Data availability.
Data underlying this article can be accessed from Zenodo (https://doi.org/10.5281/zenodo.264440) and may be used under the Creative Commons CCZero licence.
Additional Information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Carr, L. D., DeMille, D., Krems, R. V. & Ye, J. Cold and ultracold molecules: science, technology and applications. New J. Phys. 11, 055049 (2009).
Shuman, E. S., Barry, J. F. & DeMille, D. Laser cooling of a diatomic molecule. Nature 467, 820–823 (2010).
Hummon, M. T. et al. 2D magneto-optical trapping of diatomic molecules. Phys. Rev. Lett. 110, 143001 (2013).
Zhelyazkova, V. et al. Laser cooling and slowing of CaF molecules. Phys. Rev. A 89, 053416 (2014).
Hemmerling, B. et al. Laser slowing of CaF molecules to near the capture velocity of a molecular MOT. J. Phys. B 49, 174001 (2016).
Kozyryev, I. et al. Sisyphus laser cooling of a polyatomic molecule. Phys. Rev. Lett. 118, 173201 (2017).
Barry, J. F., McCarron, D. J., Norrgard, E. B., Steinecker, M. H. & DeMille, D. Magneto-optical trapping of a diatomic molecule. Nature 512, 286–289 (2014).
McCarron, D. J., Norrgard, E. B., Steinecker, M. H. & DeMille, D. Improved magneto-optical trapping of a diatomic molecule. New J. Phys. 17, 035014 (2015).
Norrgard, E. B., McCarron, D. J., Steinecker, M. H., Tarbutt, M. R. & DeMille, D. Submillikelvin dipolar molecules in a radio-frequency magneto-optical trap. Phys. Rev. Lett. 116, 063004 (2016).
Barredo, D., de Léséleuc, S., Lienhard, V., Lahaye, T. & Browaeys, A. An atom-by-atom assembler of defect-free arbitrary 2d atomic arrays. Science 354, 1021–1023 (2016).
Micheli, A., Brennen, G. K. & Zoller, P. A toolbox for lattice-spin models with polar molecules. Nat. Phys. 2, 341–347 (2006).
Tarbutt, M. R., Sauer, B. E., Hudson, J. J. & Hinds, E. A. Design for a fountain of YbF molecules to measure the electron’s electric dipole moment. New J. Phys. 15, 053034 (2013).
Cheng, C. et al. Molecular fountain. Phys. Rev. Lett. 117, 253201 (2016).
Hudson, J. J. et al. Improved measurement of the shape of the electron. Nature 473, 493–496 (2011).
Baron, J. et al. Order of magnitude smaller limit on the electric dipole moment of the electron. Science 343, 269–272 (2014).
Kajita, M. Variance measurement of mp/me using cold molecules. Can. J. Phys. 87, 743–748 (2009).
Hunter, L. R., Peck, S. K., Greenspon, A. S., Alam, S. S. & DeMille, D. Prospects for laser cooling TlF. Phys. Rev. A 85, 012511 (2012).
Cahn, S. B. et al. Zeeman-tuned rotational-level crossing spectroscopy in a diatomic free radical. Phys. Rev. Lett. 112, 163002 (2014).
Krems, R. V. Cold controlled chemistry. Phys. Chem. Chem. Phys. 10, 4079–4092 (2008).
Steinecker, M. H., McCarron, D. J., Zhu, Y. & DeMille, D. Improved radio-frequency magneto-optical trap of SrF molecules. Chem. Phys. Chem. 17, 3664–3669 (2016).
Tarbutt, M. R. & Steimle, T. C. Modeling magneto-optical trapping of CaF molecules. Phys. Rev. A 92, 053401 (2015).
Devlin, J. A. & Tarbutt, M. R. Three-dimensional Doppler, polarization-gradient, and magneto-optical forces for atoms and molecules with dark states. New J. Phys. 18, 123017 (2016).
Dalibard, J. & Cohen-Tannoudji, C. Laser cooling below the Doppler limit by polarization gradients: simple theoretical models. J. Opt. Soc. Am. B 6, 2023–2045 (1989).
Ungar, P. J., Weiss, D. S., Riis, E. & Chu, S. Optical molasses and multilevel atoms: theory. J. Opt. Soc. Am. B 6, 2058–2071 (1989).
Boiron, D., Triché, C., Meacher, D. R., Verkerk, P. & Grynberg, G. Three-dimensional cooling of cesium atoms in four-beam gray optical molasses. Phys. Rev. A 52, R3425–R3428 (1995).
Fernandes, D. R. et al. Sub-Doppler laser cooling of fermionic 40K atoms in three-dimensional gray optical molasses. Europhys. Lett. 100, 63001 (2012).
Prehn, A., Ibrügger, M., Glöckner, R., Rempe, G. & Zeppenfeld, M. Optoelectrical cooling of polar molecules to submillikelvin temperatures. Phys. Rev. Lett. 116, 063005 (2016).
André, A. et al. A coherent all-electrical interface between polar molecules and mesoscopic superconducting resonators. Nat. Phys. 2, 636–642 (2006).
Lim, J., Frye, M. D., Hutson, J. M. & Tarbutt, M. R. Modeling sympathetic cooling of molecules by ultracold atoms. Phys. Rev. A 92, 053419 (2015).
Fitch, N. J. & Tarbutt, M. R. Principles and design of a Zeeman-Sisyphus decelerator for molecular beams. Chem. Phys. Chem. 17, 3609–3623 (2016).
Wall, T. E. et al. Lifetime of the A(v′ = 0) state and Franck–Condon factor of the A − X(0 − 0) transition of CaF measured by the saturation of laser-induced fluorescence. Phys. Rev. A 78, 062509 (2008).
Dagdigian, P. J., Cruse, H. W. & Zare, R. N. Radiative lifetimes of the alkaline earth monohalides. J. Chem. Phys. 60, 2330–2339 (1974).
Stuhl, B. K., Sawyer, B. C., Wang, D. & Ye, J. Magneto-optical trap for polar molecules. Phys. Rev. Lett. 101, 243002 (2008).
Truppe, S. et al. An intense, cold, velocity-controlled molecular beam by frequency-chirped laser slowing. New J. Phys. 19, 022001 (2017).
Williams, H. J. et al. Characteristics of a magneto-optical trap of molecules. Preprint at http://arxiv.org/abs/1706.07848 (2017).
Weidemüller, M., Esslinger, T., Ol’shanii, M. A., Hemmerich, A. & Hänsch, T. W. A novel scheme for efficient cooling below the photon recoil limit. Europhys. Lett. 27, 109–114 (1994).
Acknowledgements
We thank J. Devlin for his assistance and insight. We are grateful to J. Dyne, G. Marinaro and V. Gerulis for technical assistance. The research has received funding from EPSRC under grants EP/I012044, EP/M027716, and EP/P01058X/1, and from the European Research Council under the European Union’s Seventh Framework Programme (FP7/2007-2013)/ERC grant agreement 320789.
Author information
Authors and Affiliations
Contributions
All authors contributed to all aspects of this work.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 341 kb)
Rights and permissions
About this article
Cite this article
Truppe, S., Williams, H., Hambach, M. et al. Molecules cooled below the Doppler limit. Nature Phys 13, 1173–1176 (2017). https://doi.org/10.1038/nphys4241
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys4241
This article is cited by
-
Raman sideband cooling of molecules in an optical tweezer array
Nature Physics (2024)
-
Precision spectroscopy and laser-cooling scheme of a radium-containing molecule
Nature Physics (2024)
-
Laser cooling of molecules
Journal of the Korean Physical Society (2023)
-
Magneto-optical trapping and sub-Doppler cooling of a polyatomic molecule
Nature (2022)
-
Simulation of EOM-based frequency-chirped laser slowing of MgF radicals
Frontiers of Physics (2022)